Abstract
We propose a novel representation of continuous, closed curves in ℝn that is quite efficient for analyzing their shapes. We combine the strengths of two important ideas - elastic shape metric and path-straightening methods -in shape analysis and present a fast algorithm for finding geodesics in shape spaces. The elastic metric allows for optimal matching of features while path-straightening provides geodesics between curves. Efficiency results from the fact that the elastic metric becomes the simple  2 metric in the proposed representation. We present step-by-step algorithms for computing geodesics in this framework, and demonstrate them with 2-D as well as 3-D examples.
2 metric in the proposed representation. We present step-by-step algorithms for computing geodesics in this framework, and demonstrate them with 2-D as well as 3-D examples.
1. Introduction
Over the last few years, a number of mathematical representations and metrics have been proposed to analyze shapes of planar, closed curves. Despite the multitudes of metrics proposed, there is an emerging consensus on the suitability of the elastic metric for curve-shape analysis. This metric uses a combination of bending and stretching/compression to find optimal deformations from one shape to another. These deformations are studied as the shortest paths, or geodesics, under this chosen metric on a certain shape space. This metric was first suggested by Younes [10] and subsequently utilized by Mio et al. [6], who developed an algorithm to compute geodesic paths between arbitrary shapes. Several other authors, including Michor and Mumford [5], and Shah [9] have highlighted the advantages of the elastic metric.
In view of the past ideas on representations and metrics, is there really a need or scope for yet another representation, or a new shape analysis method in this area? It is widely known that the elastic metric is better suited for shape analysis of curves, as it is the only metric that remains invariant under re-parameterizations. It is closely related to the Fisher-Rao metric used in information geometry. Parameterized curves can be represented in a variety of ways: normal vector fields, coordinate functions, angle functions, curvature functions, speed functions, etc, and the form of elastic metric depends on the representation. However we argue that the computational evaluations of different approaches are yet to be performed. More importantly, we consider the question: Under what representation of curves is the analysis using this metric most efficient? For a parameterized curve β in ℝ2, the velocity vector β̇(s) can be identified with a complex scalar r(s)eiθ(s). Here r(s) is the instantaneous speed and θ(s) is the angle made by β(s) with the positive X axis. Mio et al. used the pair (ϕ, θ), with ϕ = log(r), to represent and analyze shape of β. In this case, the Riemannian metric that translates into elastic deformations of shapes is:
| (1) |
Here a and b are the positive weights assigned to the bending and the stretching energies, respectively, in search for optimal deformation. Some other researchers have used r directly, or its integral form ∫ r(s)ds as representatives of speeds of curves. This gives rise to various difficulties. Firstly, the elastic metrics under these representations, owing to speed-invariance, assume complicated forms. Secondly, they may not be computationally efficient. As an example, the elastic metric under the log-speed (ϕ, θ) representation (Eqn. 1) varies from point to point on the shape manifold, and is thereby complicated to implement.
We propose a new representation using the square-root velocity function, . This choice has the following advantages:
It uses a single function, instead of a pair, to represent the curve.
It is the only representation in which the elastic metric reduces to a simple
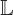 2 metric. Not only is the metric same at all points, but also much simpler to implement and analyze. With this representation, the pre-shape space is actually a subset of a unit sphere inside a Hilbert space. The use of geometry of the sphere helps simplify computations to a large extent.
2 metric. Not only is the metric same at all points, but also much simpler to implement and analyze. With this representation, the pre-shape space is actually a subset of a unit sphere inside a Hilbert space. The use of geometry of the sphere helps simplify computations to a large extent.There are convenient, isometric mappings from this representation to other forms used previously.
In this representation, the re-parameterization of curves by diffeomorphisms is an action by isometries.
Another contribution of this paper is that it combines the strengths of the elastic metric and the path straightening method for finding geodesics. Path straightening is an approach for finding geodesics between points on a Riemannian manifold. The basic idea is to connect the points with arbitrary paths and to iteratively straighten the paths, using the gradient of an energy function, until the path becomes a geodesic. This framework of elastic shape analysis and path-straightening is general enough to be applied to closed curves in ℝn.
This paper is organized as follows. Section 2 introduces the proposed representation of curves for shape analysis. Section 3 defines the pre-shape space of open as well as closed curves in ℝn. A Riemannian structure is imposed on this pre-shape space in Sec. 4 followed by the computation of geodesics in Sec. 5. We also provide step-by-step procedures for implementations of the ideas presented in the paper.
2. Curve Representation
For an unit interval I ≡ [0, 2π], let β : I → ℝn be an
curve. Any function f is said to be an
function, if both f and its derivative f′ are 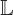 2(I) functions. In order for the curve to stretch, shrink and bend freely, we represent the shape of the elastic curve β by the function q : I → ℝn as follows,
2(I) functions. In order for the curve to stretch, shrink and bend freely, we represent the shape of the elastic curve β by the function q : I → ℝn as follows,
| (2) |
Here, s ∈ I, , and (·, ·)ℝn is taken to be the standard Euclidean inner product in ℝn. The quantity ‖q(s)‖ is the square-root of the instantaneous speed, and the ratio is the instantaneous direction along the curve. Thus, the curve β can be recovered within a translation, using .
3. Pre-Shape Space of Curves
Let 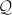 ≡ {q = (q1,q2, …, qn)∣q(s) : I → ℝn} be the space of all vector valued functions representing all elastic curves described above. This is an infinite-dimensional vector space of all functions in
≡ {q = (q1,q2, …, qn)∣q(s) : I → ℝn} be the space of all vector valued functions representing all elastic curves described above. This is an infinite-dimensional vector space of all functions in 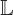 2(ℝn). Each element of this set represents an elastic curve (not necessarily closed) on ℝn. Similar to Kendall's shape analysis [2], we would eventually like to study shapes of curves as equivalences under rigid motions, uniform scaling and other such “shape-preserving” transformations. However, in this paper we restrict only to the removal of translations and scaling. We refer to such spaces as pre-shape spaces of elastic curves in ℝn.
2(ℝn). Each element of this set represents an elastic curve (not necessarily closed) on ℝn. Similar to Kendall's shape analysis [2], we would eventually like to study shapes of curves as equivalences under rigid motions, uniform scaling and other such “shape-preserving” transformations. However, in this paper we restrict only to the removal of translations and scaling. We refer to such spaces as pre-shape spaces of elastic curves in ℝn.
3.1. Open curves
We denoted
as the space of all unit-length, elastic curves. The space 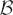 is in fact an infinite-dimensional unit-sphere and represents the pre-shape space of all open elastic curves invariant to translation and uniform scaling. The tangent space of
is in fact an infinite-dimensional unit-sphere and represents the pre-shape space of all open elastic curves invariant to translation and uniform scaling. The tangent space of 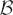 is easy to define and is given as
.
is easy to define and is given as
.
Geodesics on a sphere are great circles and can be specified analytically. The geodesic on 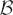 between the two points x1, x2 ∈
between the two points x1, x2 ∈ 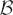 along a unit direction f ∈ Tx1 (
along a unit direction f ∈ Tx1 (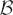 ) towards x2 for time t is given as,
) towards x2 for time t is given as,
| (3) |
Any tangent vector transported along this geodesic preserves its length as well as its angle w.r.t the geodesic. For any two points x1 and x2 on this unit sphere, the map π : Tx1 (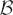 ) → Tx2 (
) → Tx2 (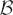 ) parallel-transports a tangent vector a from x1 to x2 and is given by,
) parallel-transports a tangent vector a from x1 to x2 and is given by,
| (4) |
3.2. Closed curves ( )
)
Although, matching of open curves has important applications involving 2-D or 3-D anatomical or biological curves, it is a relatively easier problem than comparing closed curves. The closure condition imposes a nonlinear constraint on the elements of 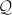 . Furthermore, handling the variability in placement of origin also becomes an important issue. The closure condition for a curve β requires that
. For our shape representation scheme, this translates to
. We define a mapping
. Furthermore, handling the variability in placement of origin also becomes an important issue. The closure condition for a curve β requires that
. For our shape representation scheme, this translates to
. We define a mapping 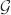 ≡ (
≡ (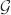 1,
1, 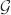 2, …,
2, …, 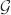 n) as
,
. The space obtained by the inverse image
is the space of all closed, elastic (arbitrary speed parameterizations) curves. Then the subset
n) as
,
. The space obtained by the inverse image
is the space of all closed, elastic (arbitrary speed parameterizations) curves. Then the subset  =
= 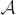 ∩
∩ 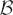 ⊂
⊂ 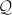 is the space of all unit-length, closed, elastic curves, invariant to translation and scaling.
is the space of all unit-length, closed, elastic curves, invariant to translation and scaling. 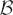 is the set of unit-length curves and
is the set of unit-length curves and 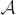 is the set of closed curves.
is the set of closed curves.
For the remainder of this paper, we shall concentrate on the pre-shape space of closed curves ( ) and study its structure under the elastic metric.
) and study its structure under the elastic metric.
4. Riemannian Geometry of 
The length of a geodesic or the “shortest path” between two points on a manifold depends on the Riemannian metric, or the inner product defined on the tangent spaces of that manifold. Note that the tangent space of 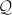 at any point is
at any point is 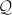 itself. Any tangent vector w of
itself. Any tangent vector w of 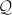 , where w = (w1, w2, …, wn)∣ w(s) : I → ℝn ∀s ∈ [0, 2π) of
, where w = (w1, w2, …, wn)∣ w(s) : I → ℝn ∀s ∈ [0, 2π) of 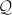 has the property that ‖w(s)‖ ∈
has the property that ‖w(s)‖ ∈ 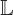 2, ∀s.
2, ∀s.
Definition 1. Given a curve q ∈ 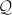 , and the first order perturbations of q given by u, v ∈ Tq(
, and the first order perturbations of q given by u, v ∈ Tq(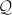 ), respectively, the inner product between the tangent vectors u, v to
), respectively, the inner product between the tangent vectors u, v to 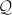 at q is defined as,
at q is defined as,
| (5) |
In the following section, we will see that the inner product given by Def. 1 imposes a symmetric, bilinear positive-definite form on Tq( ) and results in
) and results in  being a Riemannian manifold. We proceed by specifying the tangent space Tq(
being a Riemannian manifold. We proceed by specifying the tangent space Tq( ) for a q ∈
) for a q ∈  .
.
4.1. Tangent Space of 
In order to specify Tq( ), we derive the normal space of
), we derive the normal space of  at q at first. The directional derivative of the map
at q at first. The directional derivative of the map 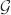 at a point q in the direction of w ∈ Tq(
at a point q in the direction of w ∈ Tq(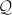 ) is given by
) is given by
where ei is the ith column of In, an identity matrix. The normal space of 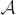 is now the span of the gradient vectors of
is now the span of the gradient vectors of 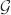 as follows,
as follows,
| (6) |
Remark 1. Given a curve q ∈ 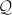 , and the tangent vector w to
, and the tangent vector w to 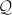 at q, the tangent space of
at q, the tangent space of  at q is defined as Tq(
at q is defined as Tq( ) = {w : I → ℝn∣w ∈ Tq(
) = {w : I → ℝn∣w ∈ Tq(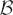 ), w ⊥ Nq(
), w ⊥ Nq(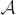 )}.
)}.
A useful tool in constructing geodesics under this Riemannian metric is the projection of a curve q ∈ 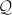 in the space of closed curves
in the space of closed curves  . This is achieved by projecting the curve q to
. This is achieved by projecting the curve q to 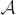 by an iterative method and further projecting it to
by an iterative method and further projecting it to  . The idea is to define a residual vector l(q) = −
. The idea is to define a residual vector l(q) = −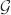 (q), l ∈ ℝn and evolve q in the direction normal to the level set of
(q), l ∈ ℝn and evolve q in the direction normal to the level set of  so as to move the residual l quickly to the origin 0. Algorithm 1 provides a procedure for projecting an open curve q ∈
so as to move the residual l quickly to the origin 0. Algorithm 1 provides a procedure for projecting an open curve q ∈  onto the nearest point in
onto the nearest point in  .
.
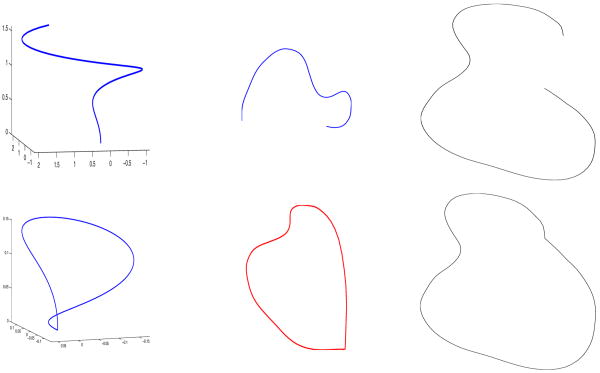
Figure 1 shows examples of projecting 2-D and 3-D open curves q ∈  onto
onto  using Algorithm 1.
using Algorithm 1.
Figure 1.
Algorithm 1 applied to project open curves (top row) into the set  (bottom row).
(bottom row).
Algorithm 1 Projection of q ∈  to to 
| |||
| 1: | Initialize l(q)i = 1n. Let ε > 0. | ||
| 2: | while ‖l(q)‖ > ε do | ||
| 3: | Compute l(q)i = −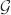 i(q), i = 1, …, n. i(q), i = 1, …, n. |
||
| 4: | Calculate the Jacobian matrix, Ji,j = 〈∇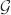 i(q), ∇ i(q), ∇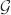 j(q)〉 as follows, j(q)〉 as follows,
|
||
| 5: | Solve the equation J(q)xT = lT(q) for x. | ||
| 6: | Update , δ > 0. | ||
| 7: |
|
||
| 8: | end while | ||
Another important tool in constructing geodesic paths is the projection of a tangent vector w ∈ Tq(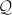 ) into Tq(
) into Tq( ). Algorithm 2 outlines a procedure for doing that.
). Algorithm 2 outlines a procedure for doing that.
Algorithm 2 Projection of w ∈ Tq( ) into Tq( ) into Tq( ) ) | |||
| 1: | Start by projecting w into Tq( ) by ) by
|
||
| 2: | Compute an orthonormal basis
for {∇ i(s)}, i = 1, …, n. w.r.t. the inner product given in Eqn. 5. i(s)}, i = 1, …, n. w.r.t. the inner product given in Eqn. 5. |
||
| 3: | Then the projection of w̃ into Tq( ) is given as, ) is given as,
|
||
5. Geodesics using Path straightening Flows
There have been two prominent approaches for computing geodesic paths between shapes of closed curves. One approach uses the shooting method [4, 6], where, given a pair of shapes, one finds a tangent direction at the first shape such that a geodesic along that direction reaches the second shape in unit time. The search for this tangent direction uses a gradient update that iteratively refines the tangent direction. We will use another, more stable approach that uses path-straightening flows to find a geodesic between two shapes. This approach, introduced by Klassen et al. [3] iteratively straightens a path between shapes until it becomes a geodesic. Similar variational methods have also been proposed by other researchers [8].
Given two curves q0 and q1, our goal is to find a geodesic between them. Let α : [0, 1] →  be any path connecting q0, q1 ∈
be any path connecting q0, q1 ∈  . Then, the critical points of the energy
. Then, the critical points of the energy
| (9) |
are geodesics in  . In order to minimize the integral in Eqn. 9, we need to find the gradient of the energy E[α] in the space of all paths on
. In order to minimize the integral in Eqn. 9, we need to find the gradient of the energy E[α] in the space of all paths on  . For this purpose, we define
. For this purpose, we define  as the collection of all paths in
as the collection of all paths in  , and
, and  0 ⊂
0 ⊂  as the collection of all paths going from q0 to q1. Since each element along the path α is actually an element of
as the collection of all paths going from q0 to q1. Since each element along the path α is actually an element of  , the tangent space Tα(
, the tangent space Tα( ) is written as Tα(
) is written as Tα( ) = {w∣w(t) ∈ Tα(t)(
) = {w∣w(t) ∈ Tα(t)( ) ∀t ∈ [0, 1]}. We adopt the Palais metric [7] on Tα(
) ∀t ∈ [0, 1]}. We adopt the Palais metric [7] on Tα( ) to impose a Riemannian structure on the space of all paths
) to impose a Riemannian structure on the space of all paths  . For u1, u2 ∈ Tα(
. For u1, u2 ∈ Tα( ), the Palais metric is given by the inner product,
), the Palais metric is given by the inner product,
| (10) |
The gradient of E[α] is a vector field in the tangent space of  0, where Tα(
0, where Tα( 0) = {w ∈ Tα(
0) = {w ∈ Tα( )∣w(0) = w(1) = 0}. Here w(t) is a tangent vector field on the curve α(t) ∈
)∣w(0) = w(1) = 0}. Here w(t) is a tangent vector field on the curve α(t) ∈  . Before deriving the energy minimization framework in the space
. Before deriving the energy minimization framework in the space  , we review some definitions below.
, we review some definitions below.
Definition 2. Covariant derivative [1]: For a path α ∈  , the covariant derivative of a vector field w ∈ Tα(
, the covariant derivative of a vector field w ∈ Tα( ) is defined as the orthogonal projection of the derivative
on the tangent space Tα(t) (
) is defined as the orthogonal projection of the derivative
on the tangent space Tα(t) ( ) for all t and is denoted as
.
) for all t and is denoted as
.
Similarly the covariant integral of w along α is given by the vector field u ∈ Tα such that
. Algorithm 3 describes the procedure for computing the covariant integration of the velocity vector field
along α. To derive the gradient vector field of E[α] on Tα(
such that
. Algorithm 3 describes the procedure for computing the covariant integration of the velocity vector field
along α. To derive the gradient vector field of E[α] on Tα( ), we state the following theorem without proof.
), we state the following theorem without proof.
| Algorithm 3 Covariant integration of | |||
| 1: | Let w(0) = 0. | ||
| 2: | for τ = 1 to k do | ||
| 3: |
|
||
| 4: | Project into using Algorithm 2. | ||
| 5: | end for | ||
Theorem 1. The gradient vector field of E in Tα( ) is given by v such that
, and v(0) = 0.
) is given by v such that
, and v(0) = 0.
Theorem 1 implies that the gradient of E in Tα( ) is given by covariant integration of the velocity vector field along the curve α. For this purpose, we need to compute the path velocity
. Since we are dealing with discretized curves in computer implementations, we will compute an approximation to the velocity vector field for discrete intervals along the path by computing the derivative of α(τ) on the sphere
) is given by covariant integration of the velocity vector field along the curve α. For this purpose, we need to compute the path velocity
. Since we are dealing with discretized curves in computer implementations, we will compute an approximation to the velocity vector field for discrete intervals along the path by computing the derivative of α(τ) on the sphere  , and projecting it on
, and projecting it on  .
.
| Algorithm 4 Velocity vector field for a path α. | ||
| 1: | Let . | |
| 2: | for τ = 1 to k do | |
| 3: |
|
|
| 4: |
|
|
| 5: |
|
|
| 6: | Project into using Algorithm 2 | |
| 7: | end for | |
Definition 3. Parallel Transport: Let w0 ∈ Tα(0)( ) be a vector field along a curve α : [0, 1] →
) be a vector field along a curve α : [0, 1] →  . Then there exists a unique parallel vector field w(t) such that
and w(0) = w0. Furthermore w(t1) (w̃(t1) = w(1 − t1))is the forward (backward) parallel transport of w0 along α at t1.
. Then there exists a unique parallel vector field w(t) such that
and w(0) = w0. Furthermore w(t1) (w̃(t1) = w(1 − t1))is the forward (backward) parallel transport of w0 along α at t1.
Algorithm 5 outlines the procedure for the parallel transport of a tangent vector field w ∈ Tα(τ) to w‖ ∈ Tα(τ+1)
to w‖ ∈ Tα(τ+1) . It is noted that the same algorithm can perform forward as well as a backward parallel transport.
. It is noted that the same algorithm can perform forward as well as a backward parallel transport.
| Algorithm 5 Parallel transport of tangent vector field w from to denoted as | ||
| 1 | Let lw = 〈w, w〉. | |
| 2: |
|
|
| 3: | Project w‖ into using Algorithm 2 and call it . | |
| 4: | Rescale the length as | |
Definition 4. Geodesic: A path α : [0, 1] →  is a geodesic if the covariant derivative of it's velocity vector field is identically zero at all t ∈ [0, 1], i.e.
, ∀t ∈ [0, 1].
is a geodesic if the covariant derivative of it's velocity vector field is identically zero at all t ∈ [0, 1], i.e.
, ∀t ∈ [0, 1].
Lemma 1. The orthogonal complement of the tangent space Tα( 0) is given by
.
0) is given by
.
Proof. Let w ∈ Tα( ) be a vector field such that
. In this case w(t) is a covariantly linear vector field. Let u ∈ Tα(
) be a vector field such that
. In this case w(t) is a covariantly linear vector field. Let u ∈ Tα( 0) be an arbitrary vector field. Then
0) be an arbitrary vector field. Then
Using Lemma 1, a tangent vector field v ∈ Tα( ) can be projected onto Tα(
) can be projected onto Tα( ) by subtracting a covariantly linear vector field given by tṽ(t), where ṽ(t) is a backward parallel transport of the vector field v(1) along α. Algorithm 6 describes the procedure for backward parallel transport of the gradient vector field w(1) along α̃ = α(1 − τ). The verification that tṽ(t) is a covariantly linear vector field is straightforward. Algorithm 7 describes the procedure for projecting the gradient vector field w ∈ Tα(
) by subtracting a covariantly linear vector field given by tṽ(t), where ṽ(t) is a backward parallel transport of the vector field v(1) along α. Algorithm 6 describes the procedure for backward parallel transport of the gradient vector field w(1) along α̃ = α(1 − τ). The verification that tṽ(t) is a covariantly linear vector field is straightforward. Algorithm 7 describes the procedure for projecting the gradient vector field w ∈ Tα( ) to v ∈ Tα(
) to v ∈ Tα( 0). After obtaining the gradient of the energy E[α] in
0). After obtaining the gradient of the energy E[α] in  0, we can update the path α in the direction of the gradient field v. Algorithm 8 describes the simple procedure for updating the path α.
0, we can update the path α in the direction of the gradient field v. Algorithm 8 describes the simple procedure for updating the path α.
| Algorithm 6 Backward parallel transport of w(1) along α̃ = α(1 − τ) | ||
| 1: | Let w̃(1) = w(1) | |
| 2: | for τ = k − 1 to 0 do | |
| 3: |
|
|
| 4: | end for | |
Algorithm 7 Project the gradient vector field w ∈ Tα( ) to v ∈ Tα( ) to v ∈ Tα( 0) 0) | ||
| 1: | for τ = 0 to k do | |
| 2: |
|
|
| 3: | end for | |
| Algorithm 8 Gradient update for α in the direction v | ||
| 1: | for τ = 0 to k do | |
| 2: |
|
|
| 3: | Project
into  using Algorithm 1 using Algorithm 1 |
|
| 4: | end for | |
5.1. Computing geodesics between q0 and q1 on 
In this subsection, we combine all the algorithms described above and use them to compute geodesics in the pre-shape space  . In practice, we deal with discretized versions of the curves and tangent spaces. The first step is the initialization of a path α on
. In practice, we deal with discretized versions of the curves and tangent spaces. The first step is the initialization of a path α on  and is described in Algorithm 9.
and is described in Algorithm 9.
Algorithm 9 Initialization of a path α on  between q0, q1 ∈ between q0, q1 ∈  . . | ||
| 1: | Let α(0) = q0. Let k be the number of steps along the discretized path. | |
| 2: | f = q1 − 〈q1, q0〉q0, | |
| 3: | for all τ = 1 to k do | |
| 4: |
|
|
| 5: | Project
into  using Algorithm 1. using Algorithm 1. |
|
| 6: | end for | |
Using the initialized path α, Algorithm 10 summarizes various steps using the path-straightening approach in computing the geodesic. The geodesic distance between the two curves is then given by , where α̂ is the resulting geodesic path.
Algorithm 10 Given q0, q1 ∈  , compute a geodesic between them , compute a geodesic between them | |
| 1: | Initialize a path α between q0 and q1 using Algorithm 9. |
| 2: | repeat |
| 3: | Compute the path velocity along α using Algorithm 4. |
| 4: | Calculate the covariant integral (w) of αt using Algorithm 3. |
| 5: | Parallel translate (backward) w(1) along α as w̃ using Algorithm 6. |
| 6: | Compute the gradient of the energy E and project it to  0 as v using Algorithm 7. 0 as v using Algorithm 7. |
| 7: | Update the path α in the direction v using Algorithm 8. |
| 8: | Compute path energy . |
| 9: | until ‖∇E‖ > ε |
6. Experimental Results and Future Directions
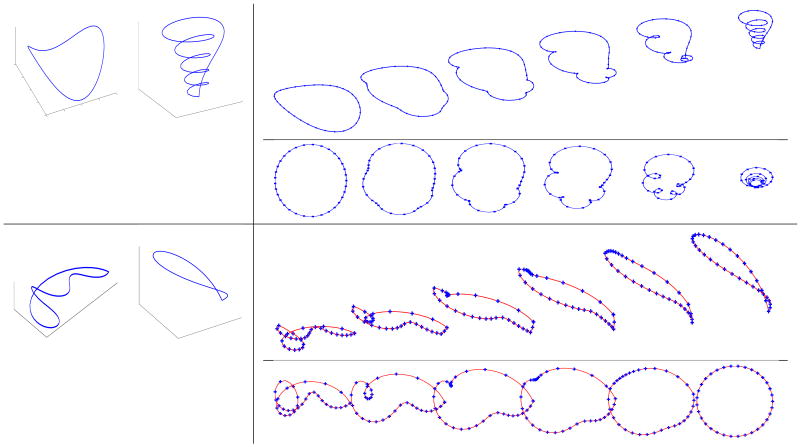
Here we present some experimental results for computing elastic geodesics by implementing the above algorithms in MATLAB®. Figure 2 shows pairwise geodesics between some 2-D curves in the set  . Intermediate shapes along the geodesics have tick-marks placed around the curve, that help identify parts of the curve traversed by non-uniform speed. Figure 3 shows two different views of a geodesic path computed between a pair of 3-D curves. It is emphasized that the intermediate curves along the geodesic do not cross each other.
. Intermediate shapes along the geodesics have tick-marks placed around the curve, that help identify parts of the curve traversed by non-uniform speed. Figure 3 shows two different views of a geodesic path computed between a pair of 3-D curves. It is emphasized that the intermediate curves along the geodesic do not cross each other.
Figure 2.
Row-wise geodesic paths in  between the pair of curves shown to the left.
between the pair of curves shown to the left.
Figure 3.
Examples of geodesics between a pair of 3-D curves shown to the left. Two different views of the geodesic are shown to the right.
In the previous sections, we have constructed geodesics in the pre-shape space of translation and scale invariant curves. In fact, the shape of a curve is also invariant to rigid rotations. Furthermore, if we are dealing with a closed curve, the shape is also invariant to change of starting points along that curve. Since we allow the curves to stretch, shrink and bend freely, its shape also remains invariant to the speed of traversal along the curve. Then we can define the elastic shape space as the quotient space 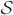 =
=  /(
/(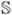 1 × SO(n) ×
1 × SO(n) × 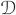 ). The problem of finding geodesics between two shapes in
). The problem of finding geodesics between two shapes in 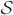 can now be modified as finding the shortest path among all possible paths between the equivalence classes of the given pair of shapes. This is a consideration for future work.
can now be modified as finding the shortest path among all possible paths between the equivalence classes of the given pair of shapes. This is a consideration for future work.
7. Summary
We have presented a differential geometric approach for studying shapes of elastic curves in ℝn. The novelty in our approach is the representation of elastic curves by a single vector valued function that incorporates both stretching and bending along the curve. The Riemannian metric is a simple 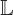 2 metric that remains same at all points in the space. Geodesics between curves are obtained using a path-straightening approach. We have also provided detailed algorithms for computing these geodesics, along with examples.
2 metric that remains same at all points in the space. Geodesics between curves are obtained using a path-straightening approach. We have also provided detailed algorithms for computing these geodesics, along with examples.
Acknowledgments
This research was partially supported by the following grants: ARO W911NF-04-01-0268 and AFOSR FA9550-06-1-0324 to Anuj Srivastava and NSF 0430954 to Eric Klassen. It was also supported by INRIA/Florida State University Associated Team “SHAPES” grant. Additionally, Anuj Srivastava was supported from a Visiting Professorship from INRIA in summer 2006.
Contributor Information
Shantanu H. Joshi, Email: joshi@eng.fsu.edu, Department of Electrical Engineering, Florida State University, Tallahassee, FL.
Eric Klassen, Email: klassen@math.fsu.edu, Department of Mathematics, Florida State University, Tallahassee, FL.
Anuj Srivastava, Email: anuj@stat.fsu.edu, Department of Statistics, Florida State University, Tallahassee, FL.
Ian Jermyn, Email: ian.jermyn@sophia.inria.fr, ARIANA Group, INRIA, Sophia Antipolis, France.
References
- 1.Boothby WM. An Introduction to Differential Manifolds and Riemannian Geometry. Academic Press, Inc.; 2003. [Google Scholar]
- 2.Kendall DG. Shape manifolds, Procrustean metrics and complex projective spaces. Bulletin of London Mathematical Society. 1984;16:81–121. [Google Scholar]
- 3.Klassen E, Srivastava A. Geodesics between 3D closed curves using path-straightening. Proceedings of ECCV, Lecture Notes in Computer Science. 2006:I:95–106. [Google Scholar]
- 4.Klassen E, Srivastava A, Mio W, Joshi SH. Analysis of planar shapes using geodesic paths on shape spaces. IEEE Trans Pattern Analysis and Machine Intelligence. 2004;26(3):372–383. doi: 10.1109/TPAMI.2004.1262333. [DOI] [PubMed] [Google Scholar]
- 5.Michor PW, Mumford D. Riemannian geometries on spaces of plane curves. J Eur Math Soc. 2006;8:1–48. [Google Scholar]
- 6.Mio W, Srivastava A, Joshi SH. On shape of plane elastic curves. Intl Journal of Computer Vision. 2007;73(3):307–324. [Google Scholar]
- 7.Palais RS. Morse theory on Hilbert manifolds. Topology. 1963;2:299–349. [Google Scholar]
- 8.Schmidt FR, Clausen M, Cremers D. Pattern Recognition (Proc DAGM), volume 4174 of LNCS. Berlin, Germany: Springer; Sep, 2006. Shape matching by variational computation of geodesics on a manifold; pp. 142–151. [Google Scholar]
- 9.Shah J. An H2 type Riemannian metric on the space of planar curves. Workshop on the Mathematical Foundations of Computational Anatomy, MICCAI; 2006. [Google Scholar]
- 10.Younes L. Computable elastic distance between shapes. SIAM Journal of Applied Mathematics. 1998;58(2):565–586. [Google Scholar]