Density Estimation with Replicate Heteroscedastic Measurements

Abstract

We present a deconvolution estimator for the density function of a random variable from a set of independent replicate measurements. We assume that measurements are made with normally distributed errors having unknown and possibly heterogeneous variances. The estimator generalizes the deconvoluting kernel density estimator of Stefanski and Carroll (1990), with error variances estimated from the replicate observations. We derive expressions for the integrated mean squared error and examine its rate of convergence as n → ∞ and the number of replicates is fixed. We investigate the finite-sample performance of the estimator through a simulation study and an application to real data.

1 Introduction

We consider estimating the density function of an unobservable random variable from a set of replicate measurements. Let X have unknown density function f_x. Suppose that X₁, …, X_n are measured independently and repeatedly as ${\{W_{r,j}\}}_{r=1,j=1}^{n,m_r}$, where W_r,j = X_r + U_r,j and m_r ≥ 2. Then the density of the observed W_r,j is related to f_x by the convolution, f_Wr,j= f_x * f_Ur,j. We present an estimator for f_x under the assumption that $U_{r,j}\sim \text{N}(0,{\sigma }_r^2)$, independent of X_r, r = 1, …, n and j = 1, …, m_r. We do not model the error variances ${\sigma }_r^2$, and thus our methods are completely general. We note that in applications where reliable models for variances (say, as functions of the means) can be specified, more efficient estimators can likely be obtained.

Several authors have studied estimation of f_x when measurement errors are identically distributed with a known density function. The approach we take is closely related to that of Stefanski and Carroll (1990), who presented deconvoluting kernel density estimators appropriate for a wide class of error distributions. The properties of deconvoluting estimators have been studied in detail (see, for example, Carroll and Hall, 1988; Devroye, 1989; Stefanski, 1990; Fan, 1991a, 1991b, 1992; Wand, 1998). Recently, authors have studied deconvolution under less restrictive assumptions. Estimating f_x when errors are identically distributed with an unknown density function has been addressed by Diggle and Hall (1993), Patil (1996), Li and Vuong (1998), Meister (2006), Neumann (2007) and Delaigle et al. (2007, 2008), among others.

Fewer authors have addressed deconvolution in the presence of heteroscedastic measurement error. Staudenmayer et al. (2007) assume the availability of replicate measurements and model measurement error variances as functions of the unobserved data. The density function f_x is modeled as a convex mixture of B-spline densities. Delaigle and Meister (2007, 2008) present a generalization to the deconvoluting kernel estimator for the case where measurement errors are heteroscedastic and have known distributions. The characteristic function for the measurement error density is described by a weighted average of characteristic functions. Additionally they discuss estimation when error densities are imperfectly known but estimable, for example, from replicate measurements. Under certain conditions, the known error densities may be replaced with their estimates without affecting convergence properties.

We assume a fixed number of replicate measurements and approach the problem via the conditional distributions of the sample means and variances of these measurements. A natural estimator arises from the results of Stefanski et al. (2005), and generalizes the deconvoluting estimator of Stefanski and Carroll (1990). Measurement errors are assumed normal, but not identically distributed. The estimator accommodates heteroscedastic and homoscedastic measurement errors. However as the main focus of this paper is estimation in the presence of heteroscedastic error, a detailed examination of our estimator’s properties is restricted to this case.

We start with a brief review of the results of Stefanski et al. (2005). In Section 2, we define our estimator and show its connection to the Stefanski and Carroll (1990) estimator. We derive and examine the asymptotic mean integrated squared error in Section 3, and in Section 4 we investigate finite-sample properties via simulation. We address bandwidth estimation in Section 5, describing a bootstrap bandwidth selection procedures. In Section 6 we present an application to real data.

1.1 Background

Our estimator of f_x uses results of Stefanski et al. (2005), who presented a method for constructing unbiased estimators of g(μ) where μ is the mean of a normally distributed random variable and g() is an entire function over the complex plane. For reference, we present the following theorem, without proof, from Stefanski et al. (2005).

Theorem 1.1.1

Suppose μ̂ and σ̂² are independent random variables such that μ̂ ~ N (μ, τ̂²) and (dσ̂²/σ²) ~ Chi-Squared(d). Define $T=Z_1/\sqrt{Z_1^2+\cdots +Z_d^2}$, where Z₁, …, Z_d are independent and identically distributed N(0, 1) random variables, and let $i=\sqrt{-1}$. Let g() be an entire function, so that g() has a series expansion defined at each point in the complex plane, and suppose that the interchange of expectation and summation in this expansion is justified. Then the estimator,

$$\widehat{\theta }=E\left\{g(\widehat{\mu }+i{(\tau d)}^{1/2}\widehat{\sigma }T)|\widehat{\mu },{\widehat{\sigma }}^2\right\}$$ (1)

is uniformly minimum variance unbiased for g(μ) provided Var(θ̂)< ∞.

A proof and discussion may be found in Stefanski et al. (2005) and Stefanski (1989). However, a few comments about the estimator θ̂ are in order. Although g() is complex-valued, θ̂ is real-valued, because the imaginary part of g() has expectation 0. For most functions g(), however, finding a closed-form expression for the estimator in (1) is difficult. A Monte Carlo approximation to θ̂ is given by

$${\widehat{\theta }}_B=\frac{1}{B}\sum _{b=1}^{B}Re\{g(\widehat{\mu }+i{(\tau d)}^{1/2}\widehat{\sigma }{T}_b)\},$$ (2)

where T₁, …, T_B are independent replicates of the variable T. Variances of (1) and (2) are real-valued, but generally do not have closed-form expressions. However, Monte Carlo methods can be used to estimate both as described in Stefanski et. al (2005).

2 The Deconvolution Estimator

2.1 Heteroscedastic Measurement Errors

The estimators in (1) and (2) can be used to estimate the density function of a random variable X that is measured with normally distributed error having unknown, nonconstant variance, provided each value of X is measured at least twice, and that the measurement error variance is constant among replicates but may differ between replicates. Suppose that the variables X₁, …, X_n are measured independently and repeatedly as ${\{W_{r,j}\}}_{r=1,j=1}^{n,m_r}$, m_r ≥ 2, where for each r = 1, …, n and j = 1, …, m_r,

$$W_{r,j}=X_r+U_{r,j},U_{r,j}\sim \text{iid}\text{N}(0,{\sigma }_r^2),$$ (3)

U_r,j is independent of X_r and ${\sigma }_r^2$ is unknown. Define the sample moments ${\overline{W}}_r=m_r^{-1}{\sum }_{j=1}^{m_r}{W}_{r,j}$ and ${\widehat{\sigma }}_r^2={(m_r-1)}^{-1}{\sum }_{j=1}^{m_r}{(W_{r,j}-{\overline{W}}_r)}^2$. Then conditioned on X_r, the following are true: 1) W̄_r and ${\widehat{{\sigma }_r}}^2$ are independent random variables, 2) ${\overline{W}}_r\sim \text{N}(X_r,{\sigma }_r^2/m_r)$, and 3) $(m_r-1){\widehat{{\sigma }_r}}^2/{\sigma }_r^2\sim \text{Chi}-\text{squared}(m_r-1)$. Let Q(x) be a probability density function that is entire over the complex plane, and for each r = 1, …, n define $T_{r,m_r-1}=Z_{r,1}/\sqrt{Z_{r,1}^2+\cdots +Z_{r,m_r-1}^2}$, where the Z_r,j are independent N(0, 1) random variables. It follows from Theorem 1.1.1 that the estimator

$${\widehat{f}}_{\mathit{het}}(x)=\frac{1}{n\lambda }\sum _{r=1}^{n}E\left\{Q\left(\frac{x-\left\{{\overline{W}}_r+i{(\frac{m_r-1}{m_r})}^{1/2}{\widehat{\sigma }}_r{T}_{r,m_r-1}\right\}}{\lambda }\right)|{\overline{W}}_r,{\widehat{\sigma }}_r^2\right\}$$ (4)

is such that

$$E\{{\widehat{f}}_{\mathit{het}}(x)\mid X_1,\cdots ,X_n\}=\frac{1}{n\lambda }\sum _{r=1}^{n}Q\left(\frac{x-X_r}{\lambda }\right).$$ (5)

The right hand side of (5) is a kernel density estimator of f_x(x), with bandwidth λ> 0. Thus it follows that unconditionally, f̂_het(x) has the same expectation and same bias as the kernel density estimator constructed from the true, unobserved data.

Note that Theorem 1.1.1 also applies to the case where the measurement error variance in (3) is constant and data are pooled to estimate the common variance σ². Let ${\widehat{\sigma }}^2=d^{-1}{\sum }_{r=1}^n(m_r-1){\widehat{\sigma }}_r^2$ be the pooled estimator of the measurement error variance based on $d={\sum }_{r=1}^n(m_r-1)$ degrees of freedom, and let $T_{r,d}=Z_{r,1}/\sqrt{Z_{r,1}^2+\cdots +Z_{r,d}^2}$ where the Z_r,j are independent N(0, 1) random variables. It follows from Theorem 1.1.1 that the estimator

$${\widehat{f}}_{\mathit{hom}}(x)=\frac{1}{n\lambda }\sum _{r=1}^{n}E\left\{Q\left(\frac{x-\left\{{\overline{W}}_r+i{(\frac{d}{m_r})}^{1/2}\widehat{\sigma }{T}_{r,d}\right\}}{\lambda }\right)|{\overline{W}}_r,{\widehat{\sigma }}^2\right\}$$ (6)

possesses the key property in (5), i.e., that conditioned on the true data, it is an unbiased estimator of a true-data, kernel density estimator.

2.1.1 Connection to the Deconvoluting Kernel Density Estimator

The estimators in (4) and (6) generalize the deconvoluting kernel density estimator of Stefanski and Carroll (1990). They considered the case with data ${\left\{W_r\right\}}_{r=1}^n$, such that W_r = X_r + U_r, and ${\left\{U_r\right\}}_{r=1}^n$ are independent and identically distributed with known characteristic function Φ_u(t) = E(e^itu), and are independent of ${\left\{X_r\right\}}_{r=1}^n$. Their estimator is based on Fourier inversion of the empirical characteristic function of the kernel density estimator of the observed-data density, f_w(w). Let Q(x) be a probability density function whose extension to the complex plane is entire throughout the complex plane, and denote the characteristic function of Q(x) by Φ_Q(t). For the case of N(0, σ²) measurement errors, the deconvoluting estimator is given by

$${\widehat{f}}_{sc}(x)=\frac{1}{n\lambda }\sum _{r=1}^n{Q}_d\left(\frac{x-W_r}{\lambda },\lambda ,\sigma \right),$$ (7)

where Q_d() is the deconvoluting kernel defined as

$$Q_d(z,\lambda ,\sigma )=\frac{1}{2\pi }\int e^{-\mathit{itz}}{e}^{t^2{\sigma }^2/2{\lambda }^2}{\mathrm{\Phi }}_Q(t)dt.$$ (8)

We now establish the connection between f̂_sc(x) and our estimator under heteroscedastic errors, f̂_het(x). Arguments similar to those presented below also apply to the homoscedastic-error estimator f̂_hom(x). Consider again f̂_het(x) in (4). Define

$$Q_r^{\ast }(z,\lambda ,m_r,{\widehat{\sigma }}_r)=E\left\{Q\left(z-\frac{i{(\frac{m_r-1}{m_r})}^{1/2}{\widehat{\sigma }}_r{T}_{r,m_r-1}}{\lambda }\right)|{\overline{W}}_r,{\widehat{\sigma }}_r^2\right\},$$ (9)

and note that $Q_r^{\ast }(z,\lambda ,m_r,{\widehat{\sigma }}_r)$ is real-valued. With this definition we write

$${\widehat{f}}_{\mathit{het}}(x)=\frac{1}{n\lambda }\sum _{r=1}^n{Q}_r^{\ast }\left(\frac{x-{\overline{W}}_r}{\lambda },\lambda ,m_r,{\widehat{\sigma }}_r\right).$$ (10)

The connection between the estimators f̂_het(x) in (10) and f̂_sc(x) in (7) is made clear through examination of the functions $Q_r^{\ast }()$ and Q_d(). For each r = 1, …, n, the sample mean W̄_r measures X_r with a normally distributed measurement error that has variance ${\sigma }_r^2/m_r$. The deconvoluting kernel in equation (8) depends on the assumed known inverse of the measurement-error characteristic function ${\mathrm{\Phi }}_{u_r}^{-1}(t)=e^{t^2{\sigma }_r^2/2m_r{\lambda }^2}$. However, when ${\sigma }_r^2$ is unknown, so too is ${\mathrm{\Phi }}_{u_r}^{-1}(t)$. As we show next, $Q_r^{\ast }(z,\lambda ,m_r,{\widehat{\sigma }}_r)$ unbiasedly estimates $Q_d(z,\lambda ,{\sigma }_r^2/m_r)$ through unbiased estimation of ${\mathrm{\Phi }}_{u_r}^{-1}(t)$.

First, applying the Fourier inversion formula and interchanging the operations of integration and expectation in (9) yields

$$Q_r^{\ast }(z,\lambda ,m_r,{\widehat{\sigma }}_r)=\frac{1}{2\pi }\int e^{-\mathit{itz}}E\left\{exp\left(\frac{-t}{\lambda }{\left(\frac{m_r-1}{m_r}\right)}^{1/2}{\widehat{\sigma }}_r{T}_{r,m_r-1}\right)|{\overline{W}}_r,{\widehat{\sigma }}_r^2\right\}{\mathrm{\Phi }}_Q(t)dt.$$ (11)

Because T_r,mr−1 is independent of the data, the conditional expectation in (11) is the characteristic function of T_r,mr−1 evaluated at the argument θ (t) = it{(m_r − 1)/m_r}^1/2σ̂_r/λ. By construction, T_r,mr−1= T^Te₁, where T^T is a random vector uniformly distributed on the (m_r−1) dimensional unit sphere, and e₁ is the (m_r−1)×1 dimensional unit vector having a one in the first position. The characteristic function of T^Te₁ is given by (Watson, 1983)

$${\mathrm{\Phi }}_T(\theta (t))=\mathrm{\Gamma }\left(\frac{m_r-1}{2}\right)J_{\frac{m_r-1}{2}-1}(\theta (t)){\left(\frac{\theta (t)}{2}\right)}^{1-\frac{m_r-1}{2}}.$$ (12)

Here J_ν(z) denotes a Bessel function of the first kind,

$$J_v(z)=\sum _{k=0}^{\infty }\frac{{(-1)}^k}{k!\mathrm{\Gamma }(\nu +k+1)}{\left(\frac{z}{2}\right)}^{\nu +2k}.$$

Substituting equation (12) into equation (11) yields

$$\begin{array}{l}{Q}_r^{\ast }(z,\lambda ,m_r,{\widehat{\sigma }}_r)=\frac{1}{2\pi }\int e^{-\mathit{itz}}\mathrm{\Gamma }\left(\frac{m_r-1}{2}\right)J_{\frac{m_r-1}{2}-1}(\theta (t)){\left\{\frac{\theta (t)}{2}\right\}}^{1-\frac{m_r-1}{2}}{\mathrm{\Phi }}_Q(t)dt\\ =\frac{1}{2\pi }\int e^{-\mathit{itz}}{\mathrm{\Phi }}_Q(t){\widehat{\mathrm{\Phi }}}_{u_r}^{-1}(t/\lambda )dt,\end{array}$$ (13)

where

$$\begin{array}{l}{\mathrm{\Phi }}_{u_r}^{-1}(t/\lambda )=\mathrm{\Gamma }\left(\frac{m_r-1}{2}\right)J_{\frac{m_r-1}{2}-1}(\theta (t)){\left\{\frac{\theta (t)}{2}\right\}}^{1-\frac{m_r-1}{2}}\\ =\sum _{k=0}^{\infty }\frac{{\left(\frac{t^2}{4{\lambda }^2}\frac{m_r-1}{m_r}{\widehat{\sigma }}_r^2\right)}^k\mathrm{\Gamma }\left(\frac{m_r-1}{2}\right)}{k!\mathrm{\Gamma }\left(k+\frac{m_r-1}{2}\right)}.\end{array}$$ (14)

The only random quantity in $Q_r^{\ast }(z,\lambda ,m_r,{\widehat{\sigma }}_r)$ is the sample variance, ${\widehat{\sigma }}_r^2$, which appears in ${\widehat{\mathrm{\Phi }}}_{u_r}^{-1}(t/\lambda )$. From the relationship

$$E\{{\widehat{\sigma }}_r^{2k}\}=\frac{\mathrm{\Gamma }\left(k+\frac{m_r-1}{2}\right){\left(\frac{2{\sigma }_r^2}{m_r-1}\right)}^k}{\mathrm{\Gamma }\left(\frac{m_r-1}{2}\right)},$$ (15)

it follows that $E\left\{{\widehat{\mathrm{\Phi }}}_{u_r}^{-1}(t/\lambda )\right\}=e^{t^2{\sigma }_r^2/2m_r{\lambda }^2}$, the inverse of the characteristic function of a $\text{N}(0,{\sigma }_r^2/m_r)$ random variable evaluated at t/λ. Substitution into (13) yields

$$E\{Q_r^{\ast }(z,\lambda ,m_r,{\widehat{\sigma }}_r)\}=\frac{1}{2\pi }\int e^{-\mathit{itz}}{e}^{t^2{\sigma }_r^2/2m_r{\lambda }^2}{\mathrm{\Phi }}_Q(t)dt.$$

Comparison with (8) reveals that $Q_r^{\ast }(z,\lambda ,m_r,{\widehat{\sigma }}_r)$ is unbiased for $Q_d(z,\lambda ,{\sigma }_r^2/m_r)$.

2.2 Monte Carlo Estimation

In most cases, the estimators in (4) and (6) do not have simple closed-form expressions. However, Monte Carlo approximations to the conditional expectations in equations (4) and (6) follow directly from (2). Consider the expression for f̂_het(x) in (4). For each r = 1, …, n, generating T_r,1, …, T_r,B as independent replicates of $T_r=Z_{r,1}/\sqrt{Z_{r,1}^2+\cdots +Z_{r,m_r-1}^2}$ yields an approximation to f̂_het(x),

$${\widehat{f}}_{B,\mathit{het}}(x)=\frac{1}{n\lambda }\sum _{r=1}^n\frac{1}{B}\sum _{b=1}^{B}Re\left\{Q\left(\frac{x-\left\{{\overline{W}}_r+i{(\frac{m_r-1}{m_r})}^{1/2}{\widehat{\sigma }}_r{T}_{r,b}\right\}}{\lambda }\right)\right\}.$$

Note that when m_r = 2, T_r,mr−1 in (4) is equal to either 1 or −1, each with probability 1/2. Thus in the special case of two replicate measurements, the conditional expectation in (4) can be evaluated without Monte Carlo approximation, and is

$${\widehat{f}}_{\mathit{het}}(x)=\frac{1}{2n\lambda }\sum _{r=1}^n\sum _{k=1}^{2}Re\left\{Q\left(\frac{x-\left\{{\overline{W}}_r+{(-1)}^{k}i\mid W_{r,1}-W_{r,2}\mid /2\right\}}{\lambda }\right)\right\}.$$

In the case of homoscedastic measurement error, the Monte Carlo version of (6) is

$${\widehat{f}}_{B,\mathit{hom}}(x)=\frac{1}{n\lambda }\sum _{r=1}^n\frac{1}{B}\sum _{b=1}^{B}Re\left\{Q\left(\frac{x-\left\{{\overline{W}}_r+i{(\frac{d}{m_r})}^{1/2}\widehat{\sigma }{T}_{r,b}\right\}}{\lambda }\right)\right\},$$

where T_r,1, …, T_r,B are independent copies of $T_r=Z_{r,1}/\sqrt{Z_{r,1}^2+\cdots +Z_{r,d}^2}$ for each r.

3 Mean Integrated Squared Error

We now derive the mean integrated squared error (MISE) of the heteroscedastic-error estimator in (4). An objective is to compare the asymptotic properties of (4) to those of the known-variance deconvolution estimator. It was shown by Carroll and Hall (1988) that when measurement errors are normally distributed with constant variance, the optimal rate at which any deconvolution estimator can converge to f_x(x) is {log(n)}⁻². The deconvoluting kernel density estimator achieves this rate of convergence (Stefanski and Carroll, 1990), and does so with the optimal bandwidth of λ= σ{log(n)}^−1/2 (Stefanski, 1989).

For each X_r, assume a fixed number m_r ≥ 2 of replicate measurements are observed and used to estimate ${\sigma }_r^2$. The independence of the summands in (4) simplifies the derivation of the MISE and results in closed-form expressions for certain special cases of m_r. In practice, it is common that the number of replicates is small and we examine in detail the case of two replicate measurements, m_r = 2 for all r. In addition, we present a weighted estimator, a natural extension in the case of nonconstant variances, where weights are selected to minimize the asymptotic integrated variance. We derive the MISE of the weighted estimator under the assumption that the weights are known. We note that, although we limit our asymptotic analysis to n → ∞, it is also reasonable to consider asymptotic behavior as the number of replicates increases to infinity. Delaigle (2007) provides convincing arguments for this approach.

3.1 Heteroscedastic Measurement Errors

We obtain expressions for the MISE of f̂_het(x) using results on hypergeometric series. We start with notation and definitions. For all real x define the rising factorial

$${(x)}_k=\{\begin{array}{ll}1\hfill & \text{if}k=0;\hfill \\ x(x+1)(x+2)\cdots (x+k-1)\hfill & \text{if}k=1,2,3,\dots \hfill \end{array}$$

and note that for real x ≠ 0 and y ≠ 0,

$$\begin{array}{l}{(1)}_k=k!\text{for}k=1,2,3,\dots \\ \frac{{(xy)}_k}{{(x)}_k}=y\frac{{(xy+1)}_{k-1}}{{(x+1)}_{k-1}}\text{for}k=1,2,3,\dots \\ \underset{x\to 0}{lim}\frac{{(xy)}_k}{{(x)}_k}=\{\begin{array}{ll}1,\hfill & \text{if}k=0;\hfill \\ y,\hfill & \text{if}k=1,2,3,\dots \hfill \end{array}\end{array}$$ (16)

Denote the generalized hypergeometric series (Erdelyi, 1953) by

$${{}_{p}F}_q(a_1,\dots ,a_p;b_1,\dots ,b_q;x)=\sum _{k=0}^{\infty }\frac{{(a_1)}_k{(a_2)}_k\dots {(a_p)}_k}{{(b_1)}_k{(b_2)}_k\dots {(b_q)}_k}\frac{x^k}{k!},$$ (17)

where it is assumed that the a_j and b_j are such that division by 0 does not arise. We use the relationships (for b ≠ 1/2)

$${\{{{}_{0}F}_1(;b;x)\}}^2={{}_{2}F}_3(b,b-\frac{1}{2};b,b,2b-1;4x)={{}_{1}F}_2(b-\frac{1}{2};b,2b-1;4x).$$ (18)

A proof of the first equality appears in Bailey (1928); the second follows upon simplification after substitution into (17). Because ₀F₁(; b; x) is well-defined and continuous in b at b = 1/2, the identity in (18) can be extended via

$$\begin{array}{l}{\{{{}_{0}F}_1(;.5;x)\}}^2=\underset{b\to 1/2}{lim}{{}_{1}F}_2(b-\frac{1}{2};b,2b-1;4x)\\ =1+\frac{{{}_{0}F}_1(;.5;4x)-1}{2}.\end{array}$$ (19)

The limit in (19) is readily verified using the properties in (16). We now state and prove our main result.

Theorem 3.1.1

Consider data following model (3) and the estimator f̂_het(x) in (4). As n → ∞ and λ → 0, with ${\mu }_{Q,2}^2=\int z^{2}Q(z)dz$,

$$\mathit{MISE}\{{\stackrel{\sim }{f}}_{\mathit{het}}(x)\}\sim \frac{1}{2\pi n^2\lambda }\sum _{r=1}^n\int {\mathrm{\Phi }}_Q^2(t)H(m_r,2t^2{\lambda }^{-2}{\sigma }_r^2/m_r)dt+\frac{{\lambda }^4}{4}{\mu }_{Q,2}^2\int {\{f_x^{″}(x)\}}^{2}dx,$$ (20)

where

$$H(m,z)=\{\begin{array}{ll}(e^z+1)/2\hfill & ifm=2;\hfill \\ {{}_{1}F}_1(\frac{m-2}{2};m-2;z)\hfill & ifm\ge 3.\hfill \end{array}$$ (21)

Proof

First from (14) we write ${\widehat{\mathrm{\Phi }}}_{u_r}^{-1}(t/\lambda )={{}_{0}F}_1(;(m_r-1)/2;\widehat{\theta })$ where

$$\widehat{\theta }={\left(\frac{t^2(m_r-1){\widehat{\sigma }}_r^2}{4{\lambda }^2{m}_r}\right)}^k.$$

Now consider the decomposition of MISE{f̂_het(x)},

$$\text{MISE}\{{\widehat{f}}_{\mathit{het}}(x)\}=\int \text{Var}\{{\widehat{f}}_{\mathit{het}}(x)\}dx+\int {\text{Bias}}^2\{{\widehat{f}}_{\mathit{het}}(x)\}dx.$$ (22)

It follows from (5) that as λ → 0,

$$\int {\text{Bias}}^2\{{\widehat{f}}_{\mathit{het}}(x)\}dx\sim \frac{{\lambda }^4}{4}{\mu }_{Q,2}^2\int {\{f_x^{″}(x)\}}^{2}dx.$$ (23)

The integrated variance can be further decomposed and from (10), ∫Var{f̂_het(x)}dx = V₁ − V₂ where

$$\begin{array}{l}{V}_1=\frac{1}{n^2{\lambda }^2}\sum _{r=1}^n\int E\left[{\left\{Q^{\ast }\left(\frac{x-{\overline{W}}_r}{\lambda },\lambda ,m_r,{\widehat{\sigma }}_r\right)\right\}}^2\right]dx\\ =\frac{1}{n^2\lambda }\sum _{r=1}^{n}E\int {\{Q^{\ast }(z,\lambda ,m_r,{\widehat{\sigma }}_r)\}}^{2}dz\\ =\frac{1}{2\pi n\lambda }E\int {\mathrm{\Phi }}_Q^2(t){\widehat{\mathrm{\Phi }}}_{u_r}^{-2}(t/\lambda )dt\\ =\frac{1}{2\pi n\lambda }\int {\mathrm{\Phi }}_Q^2(t)E\left[{\{{{}_{0}F}_1(;(m_r-1)/2;\widehat{\theta })\}}^2\right]dt\end{array}$$ (24)

using a change of variables and Parseval’s Identity, and

$$\begin{array}{l}{V}_2=\frac{1}{n^2{\lambda }^2}\sum _{r=1}^n\int {\left\{E\left[Q^{\ast }\left(\frac{x-{\overline{W}}_r}{\lambda },\lambda ,m_r,{\widehat{\sigma }}_r\right)\right]\right\}}^{2}dx\\ =\frac{1}{n^2{\lambda }^2}\sum _{r=1}^n\int {\left\{E\left[Q\left(\frac{x-X_r}{\lambda }\right)\right]\right\}}^{2}dx\\ =\frac{1}{n}\int {\left\{\int Q(z)f_x(x-\lambda z)dz\right\}}^{2}dx\\ =\frac{1}{2\pi n}\int {\mid {\mathrm{\Phi }}_f(t)\mid }^2{\mathrm{\Phi }}_Q^2(\lambda t)dt.\end{array}$$ (25)

The second equality is a consequence of Theorem 1.1.1. The last two follow from a change of variables and Parseval’s Identity. It remains to evaluate the expectation of {₀F₁(; (m_r −1)/2; θ̂)}² in (24). Using equations (15), (17), and (18) (for m_r ≥ 3) or (19) (for m_r = 2), it is easily verified that

$$E[{\{{{}_{0}F}_1(;(m_r-1)/2;\widehat{\theta })\}}^2]=H(m_r,2t^2{\lambda }^{-2}{\sigma }_r^2/m_r),$$ (26)

so that

$$V_1=\frac{1}{2\pi n^2\lambda }\sum _{r=1}^n\int {\mathrm{\Phi }}_Q^2(t)H(m_r,2t^2{\lambda }^{-2}{\sigma }_r^2/m_r).$$ (27)

The result follows from (22) and the fact that V₂ = o{(nλ)⁻¹}.

The infinite sum makes the asymptotic behavior of the MISE difficult to examine for general sequences m_r, r = 1, 2, …. This sum converges for m_r ≥ 2, and closed-form expressions can be obtained for special cases of m_r. We focus the remainder of our analysis on the important case of two replicate measurements.

3.1.1 Heteroscedastic Measurement Errors: m_r = 2

When m_r = 2 for all r, the expectation in equation (26) simplifies to

$$E[{\{{{}_{0}F}_1(;(m_r-1)/2;\widehat{\theta })\}}^2]=\frac{1}{2}{e}^{t^2{\sigma }_r^2/{\lambda }^2}+\frac{1}{2},$$

and V₁ in equation (27) becomes

$$\begin{array}{l}{V}_1=\frac{1}{4\pi n^2\lambda }\sum _{r=1}^n\int {\mathrm{\Phi }}_Q^2(t)e^{t^2{\sigma }_r^2/{\lambda }^2}dt+\frac{1}{4\pi n\lambda }\int {\mathrm{\Phi }}_Q^2(t)dt\\ =\frac{1}{4\pi n^2\lambda }\sum _{r=1}^n\int {\mathrm{\Phi }}_Q^2(t)e^{t^2{\sigma }_r^2/{\lambda }^2}dt+o({\{n{\lambda }^2\}}^{-1}),\end{array}$$

so that as n → ∞ and λ → 0,

$$\text{MISE}\{{\stackrel{\sim }{f}}_{\mathit{het}}(x)\}\sim \frac{1}{4\pi n^2\lambda }\sum _{r=1}^n\int {\mathrm{\Phi }}_Q^2(t)e^{t^2{\sigma }_r^2/{\lambda }^2}dt+\frac{{\lambda }^4}{4}{\mu }_{Q,2}^2\int {\{f_x^{″}(x)\}}^{2}dx.$$ (28)

Asymptotic analysis of the MISE (n → ∞, λ → 0) in equation (28) is difficult because of the dependence of the MISE on the particular sequence of variances ${\sigma }_1^2,{\sigma }_2^2$,…. However useful insights can be gained under the assumption that the empirical distribution function of ${\sigma }_1^2$,…, ${\sigma }_n^2$ converges to an absolutely continuous distribution. McIntyre (2003) shows that when measurement error variances are distributed uniformly over a finite interval, the rate of convergence of f̂_het is proportional to {log(n)}⁻², the same rate found by Stefanski and Carroll (1990) for the deconvoluting estimator when measurement errors are normally distributed with known, constant variance. Furthermore, both the optimal bandwidth and the optimal rate of convergence depend on the upper support boundary of the variance distribution. The indicated conclusions are that estimating heteroscedastic error variances from just two replicates has no effect on the asymptotic rate of convergence, but that the constant multiplying this rate, and also the bandwidth needed to achieve the rate, are dependent on the larger error variances.

3.2 Heteroscedastic Measurement Errors: Weighting

We next investigate the use of weights to reduce the variability of f̂_het(x) in (4). As f̂_het(x) is the sum of independent components, having a common mean but different variances, it is reasonable to expect that weighting will reduce variability.

Optimal weights for the weighted estimator are derived under the assumption that the measurement error variances are known, and weights are selected to minimize the asymptotic integrated variance. We examine the asymptotic properties of the estimator calculated with these optimal weights, and our results provide intuition for the properties of f̂_wt(x), which uses the set of estimated weights calculated with the unknown measurement error variances replaced by their sample estimates.

The optimal weighted estimator has the general form

$${\stackrel{\sim }{f}}_{wt}(x)=\frac{1}{\lambda }\sum _{r=1}^n{w}_{r}E\left\{Q\left(\frac{x-\left\{{\overline{W}}_r+i{(\frac{m_r-1}{m_r})}^{1/2}{\widehat{\sigma }}_r{T}_r\right\}}{\lambda }\right)|{\overline{W}}_r,{\widehat{\sigma }}_r^2\right\},$$ (29)

where w₁, …, w_n are known constants, w_r ≥ 0 for all r and ${\sum }_{r=1}^n{w}_r=1$. The integrated variance of f̃_wt(x) is ∫Var{f̃ (x)}dx = Ṽ₁ − Ṽ₂ where

$${\stackrel{\sim }{V}}_1=\frac{1}{{\lambda }^2}\sum _{r=1}^n{w}_r^2\int E\left\{{\left[Q^{\ast }\left(\frac{x-{\overline{W}}_r}{\lambda },\lambda ,m_r,{\widehat{\sigma }}_r\right)\right]}^2\right\}dx,$$ (30)

and

$${\stackrel{\sim }{V}}_2=\frac{1}{{\lambda }^2}\sum _{r=1}^n{w}_r^2\int {\left\{E\left[Q^{\ast }\left(\frac{x-{\overline{W}}_r}{\lambda },\lambda ,m_r,{\widehat{\sigma }}_r\right)\right]\right\}}^{2}dx,$$

and Q^*(z, λ, m_r, σ̂_r) is defined as in equation (9).

It follows from equation (25) that, provided w_r ≤ B/n for r = 1, …, n and some 0< B < ∞, Ṽ₂ = o{(nλ)⁻¹}. Thus asymptotically, Ṽ₁ is the dominant term in the integrated variance, and we select weights to minimize this quantity. Using (21), let

$$h_r({\sigma }_r^2,m_r,\lambda )=\int {\mathrm{\Phi }}_Q^2(t)H(m_r,2t^2{\lambda }^{-2}{\sigma }_r^2/m_r)dt$$

and note from equation (27) that $h_r({\sigma }_r^2,m_r,\lambda )$ is proportional to the contribution to the asymptotic integrated variance from the rth component of f̂_het(x). Define

$$w_r=\frac{{\{h_r({\sigma }_r^2,m_r,\lambda )\}}^{-1}}{{\sum }_{r=1}^n{\{h_r({\sigma }_r^2,m_r,\lambda )\}}^{-1}}$$ (31)

for r = 1, …, n. A straightforward application of the Cauchy-Schwartz inequality shows that these weights minimize (30). Substitution into (30) yields

$${\stackrel{\sim }{V}}_1={\left\{2\pi \lambda \sum _{r=1}^n{\left\{\int {\mathrm{\Phi }}_Q^2(t)H(m_r,2t^2{\lambda }^{-2}{\sigma }_r^2/m_r)dt\right\}}^{-1}\right\}}^{-1}.$$ (32)

Finally, substituting the sample variances, ${\widehat{\sigma }}_1^2$,…, ${\widehat{\sigma }}_n^2$ for the true variances in equation (31) forms the set of estimated weights, ŵ₁, …, ŵ_n, and the estimator

$${\widehat{f}}_{wt}(x)=\frac{1}{\lambda }\sum _{r=1}^n{\widehat{w}}_{r}E\left\{Q\left(\frac{x-\left\{{\overline{W}}_r+i{(\frac{m_r-1}{m_r})}^{1/2}{\widehat{\sigma }}_r{T}_r\right\}}{\lambda }\right)|{\overline{W}}_r,{\widehat{\sigma }}_r^2\right\}.$$ (33)

3.2.1 Mean Integrated Squared Error of f̃_wt(x)

We now consider the asymptotic properties of f̃_wt(x), calculated with the optimal weights in equation (31). We derive an expression for the MISE of f̃_wt(x) under the assumption that the sequence of measurement error variances, ${\sigma }_1^2$,…, ${\sigma }_n^2$, is known. This analysis provides guidelines for the asymptotic behavior of f̂_wt(x) in equation (33). Because the estimated weights are not consistent for the true weights, the resulting estimator is not guaranteed to perform as well as the true-weight estimator asymptotically. Nevertheless, the simulation results reported in Section 4 indicate the approximate weighting has a significant beneficial effect in finite samples.

The estimator f̃_wt(x) has the same key property in equation (5) as f̂_het(x), and so has the same integrated squared bias as the kernel density estimator of f_x(x) based on the true data. Combining (23) and (32), we have that as n → ∞ and λ → 0,

$$\text{MISE}\{{\stackrel{\sim }{f}}_{wt}(x)\}\sim {\left\{2\pi \lambda \sum _{r=1}^n{\left\{\int {\mathrm{\Phi }}_Q^2(t)H(m_r,2t^2{\lambda }^{-2}{\sigma }_r^2/m_r)dt\right\}}^{-1}\right\}}^{-1}+\frac{{\lambda }^4}{4}{\mu }_{Q,2}^2\int {\{f_x^{″}(x)\}}^{2}dx.$$ (34)

The expression simplifies in the case of two replicate measurements. From equations (32) and (21), when m_r = 2 for all r, as n → ∞ and λ → 0,

$${\stackrel{\sim }{V}}_1\sim {\left\{4\pi \lambda \sum _{r=1}^n{\left\{\int {\mathrm{\Phi }}_Q^2(t)e^{t^2{\sigma }_r^2/{\lambda }^2}dt\right\}}^{-1}\right\}}^{-1},$$

and the MISE becomes

$$\text{MISE}\{{\stackrel{\sim }{f}}_{wt}(x)\}\sim {\left\{4\pi \lambda \sum _{r=1}^n{\left\{\int {\mathrm{\Phi }}_Q^2(t)e^{t^2{\sigma }_r^2/{\lambda }^2}dt\right\}}^{-1}\right\}}^{-1}+\frac{{\lambda }^4}{4}{\mu }_{Q,2}^2\int {\{f_x^{″}(x)\}}^{2}dx.$$

The asymptotic behavior of MISE again depends on the sequence of variances ${\sigma }_1^2$,…, ${\sigma }_n^2$. McIntyre (2003) shows that when the variances are uniformly distributed over a finite interval, the MISE of f̂_wt(x) converges to 0 at a rate proportional to {log(n)}⁻², the same rate achieved by the unweighted estimator under that assumption. The result implies that when measurement error variances are known and uniformly distributed, there is no advantage to weighting in terms of the rate of convergence of the MISE. However, the constant multiplying the rate is reduced. Furthermore, the primary advantage of weighting is in finite samples as we study via simulation in Section 4.

4 Simulation Study

We performed a simulation study to investigate the finite-sample properties of the proposed estimators in equations (4), (29), and (6). These were calculated using the kernel Q(x) ∝ {sin(x)/x}⁴, where Q(x) was scaled to have mean 0 and variance 1. We also included in the study the so-called naive estimator which ignores measurement error. Specifically, we studied the naive estimator to be the kernel density estimator calculated with the sample means of the replicate measurements,

$${\widehat{f}}_{\mathit{naive}}(x)=\frac{1}{n\lambda }\sum _{r=1}^n\phi \left(\frac{x-{\overline{W}}_r}{\lambda }\right),$$

where φ(x) is the standard normal density.

Estimators were compared on the basis of average integrated squared error (ISE). For each simulated data set, estimators were computed at their optimal bandwidths, found by minimizing the integrated squared error. As this requires knowledge of the unknown density f_x(x), the estimators in this study are not true estimators. However our results provide insight into their relative optimal performances, independent of the problem of estimating a bandwidth. We defer a discussion of bandwidth estimation to Section 5. For additional comparison, however, we also calculated the naive estimator using the popular normal reference bandwidth estimator, τ̂ = 1.06σ̂_W̄n^−1/5 where ${\widehat{\sigma }}_{\overline{W}}^2$ is the sample variance of the means W̄₁, …, W̄_n (Silverman, 1986).

We examined three factors in this study. First, six different sample sizes were considered, n = 100, 500, 1000, 2000 and 2500. Second, we examined the effect of the true-data density, generating data, X₁, …, X_n, from the N(0, 1) density and the Chi-squared(4) density, standardized to have mean 0 and variance 1. Finally, we examined the effect of the homogeneity of measurement error variances on the performance of each estimator. Observed data were generated with normal measurement errors having variances ${\sigma }_1^2=\cdots ={\sigma }_n^2=1$ for the case of constant variances, and ${\sigma }_1^2$,…, ${\sigma }_n^2$ chosen uniformly over the interval (0, 2) for the case of nonconstant variances. All estimators were computed on each set of observed data.

In practice, often only a small number of replicate measurements is observed, with m_r = 2 common. Thus in our simulations, we considered only the case of m_r = 2 replicate measurements. All results are based on fifty simulated data sets.

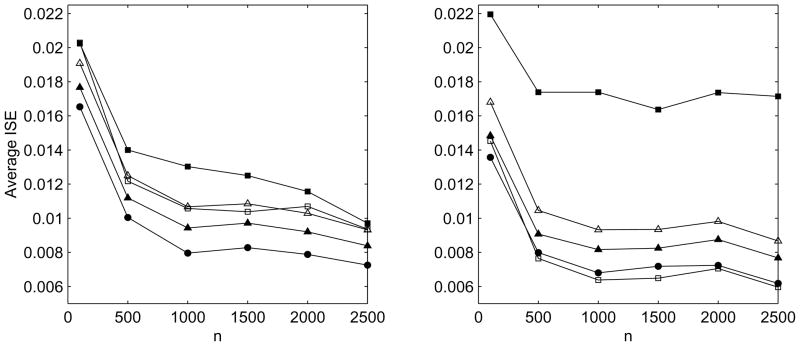
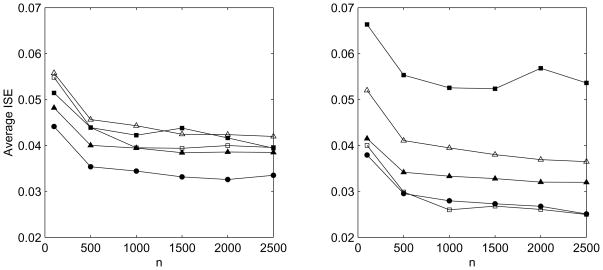
Average ISEs are plotted by sample size in Figure 1 for X_r ~ N(0, 1) and Figure 2 for X_r ~ Chi-squared(4). For simulations that considered homoscedastic measurement error, the average ISE for f̂_hom(x) was significantly smaller (α=0.05) than that of the other estimators for each sample size except n=100, where all estimators were most variable. For simulations that considered heteroscedastic measurement errors, f̂_het(x) had a significantly higher average ISE than all other estimators for sample sizes of n ≥ 500, and was also much more variable. The estimators f̂_hom(x) and f̂_wt(x) had significantly lower average integrated squared errors than all other estimators for n ≥ 500, but differences between the two were generally not significant.

Figure 1.

Average ISE by sample size for X ~ N(0, 1). Left: homoscedastic measurement errors, N(0, 1). Right: heteroscedastic measurement errors, $\text{N}(0,{\sigma }_r^2)$ with ${\sigma }_r^2$ uniform on (0, 2). Open triangle: f̂_naive with plug-in bandwidth; Closed triangle: f̂_naive with optimal bandwidth; Closed square: f̂_het; Open square: f̂_wt; Closed circle: f̂_hom.

Figure 2.

Average ISE by sample size for $X\sim {\chi }_4^2$. Left: homoscedastic measurement errors, N(0, 1). Right: heteroscedastic measurement errors, $\text{N}(0,{\sigma }_r^2)$ with ${\sigma }_r^2$ uniform on (0, 2). Open triangle: f̂_naive with plug-in bandwidth; Closed triangle: f̂_naive with optimal bandwidth; Closed square: f̂_het; Open square: f̂_wt; Closed circle: f̂_hom.

It is evident from the simulations that weighting is effective in reducing the ISE of f̂_het(x), and f̂_wt(x) is preferred. In almost every case, the average ISE of f̂_wt(x) was significantly less than that of f̂_het(x). However, even the weighted estimator performed relatively poorly when measurement error variances were constant, not surprising considering that here f̂_wt(x) relies on n estimates of the constant variance each obtained from only two replicate measurements. The estimator for homoscedastic errors performed well for both types of measurement errors, suggesting it is a good choice even when there is doubt about the homogeneity of the error variances, provided the heterogeneity is not too great. It is encouraging that for the sample sizes considered here, the measurement error-corrected estimators perform as well or better than the naive estimator. This suggests that given a reliable rule for selecting a bandwidth, correcting for measurement errors is worthwhile in many situations.

5 A Bootstrap Method for Bandwidth Selection

We now describe a bootstrap bandwidth selection procedure, and illustrate it with data in Section 6. The bootstrap has been used for bandwidth selection in traditional kernel density estimation (Marron, 1992). Delaigle and Gijbels (2004) extended it to the deconvolution estimator (7). With the bootstrap method the bandwidth estimate can be obtained without resampling. We note that the bandwidth-selection method proposed by Delaigle and Hall (2008) based on SIMEX (Cook and Stefanski, 1994; Stefanski and Cook, 1995) could also be applied to our estimators.

We obtain an initial estimate of bandwidth, τ̂, used to construct an initial density estimate for generating bootstrap samples. For our deconvolution problem, we use the naive estimator,

$${\widehat{f}}_{\mathit{naive}}(x;\widehat{\tau })=\frac{1}{n\widehat{\tau }}\sum _{r=1}^n\phi \left(\frac{x-{\overline{W}}_r}{\widehat{\tau }}\right),$$

where τ̂ is the normal reference bandwidth (Silverman 1986). This provides a reasonable, though overly smoothed, estimate of f_x(x).

For heteroscedastic measurement errors, bootstrap data are generated for r = 1, …, n and j = 1, …, m_r as $W_{r,j}^{\ast }=X_r^{\ast }+{\widehat{\sigma }}_r{Z}_{r,j}$, where $X_r^{\ast }$ is generated from the density f̂_naive(x; τ̂), σ̂_r is the estimate of σ_r from the original data and Z_r,j ~ N(0, 1). In the case of homoscedastic measurement errors, σ̂_r is replaced with the pooled estimate of variance, σ̂.

Let ${\widehat{f}}_{·}^{\ast }(x;h)$ denote any of the three deconvolution estimators from (4), (6) or (29) computed with the bootstrap sample. The bootstrap estimate of the optimal bandwidth for a measurement error-corrected estimator is the value h that minimizes

$${\text{MISE}}^{\ast }(h)=E_{BS}\left[\int {\left\{{\widehat{f}}_{.}^{\ast }(x;h)-{\widehat{f}}_{\mathit{naive}}(x;\widehat{\tau })\right\}}^{2}dx\right],$$

where E_BS denotes expectation with respect to the bootstrap distribution. The optimal bandwidth can be determined empirically by computing a large number of bootstrap estimates over a dense grid of bandwidths and selecting the value of h that achieves the smallest average ISE. However because f̂_naive(z, τ̂) replaces the unknown f(x), the optimal bandwidth can also be determined by direct calculation of MISE^*(h) over the grid of bandwidths, using analytical expressions for MISE, e.g., equations (20) and (34). For more details see McIntyre (2003).

6 An Application

We illustrate the bootstrap bandwidth procedure using data from a U.S. EPA study of automobile emissions. Measurements of carbon monoxide (CO) in automobile emissions were collected with a remote sensing device stationed at a highway entrance ramp in North Carolina. The device measured CO in the exhaust of passing automobiles, and also photographed their license plates. Measurements were taken on several different dates resulting in replicate measurements from cars that passed the location multiple times. Of a total of 3002 automobiles observed, 1233 had multiple measurements (946 with m_r = 2 and 287 with m_r = 3).

An objective of the study was to characterize average CO emissions among the population of automobiles. Measurements of CO taken from a stationary point on the roadway are subject to error from several sources including meteorological conditions, variations in engine temperature, speed and acceleration, and instrument error. The multiple sources of variation are expected to result in multiplicative errors. Thus we log-transformed the CO measurements.

The log-transformed data showed evidence of heteroscedastic measurement errors. A loess curve fit to the scatter plot of σ̂_r versus W̄_r exhibited substantial nonlinearities over the range of sample means, although globally there was a tendency for larger sample standard deviations to be associated with larger sample means. Testing the latter via a simple linear regression of the sample standard deviations on the sample means resulted in a significant slope of 0.0936 (p < .0001).

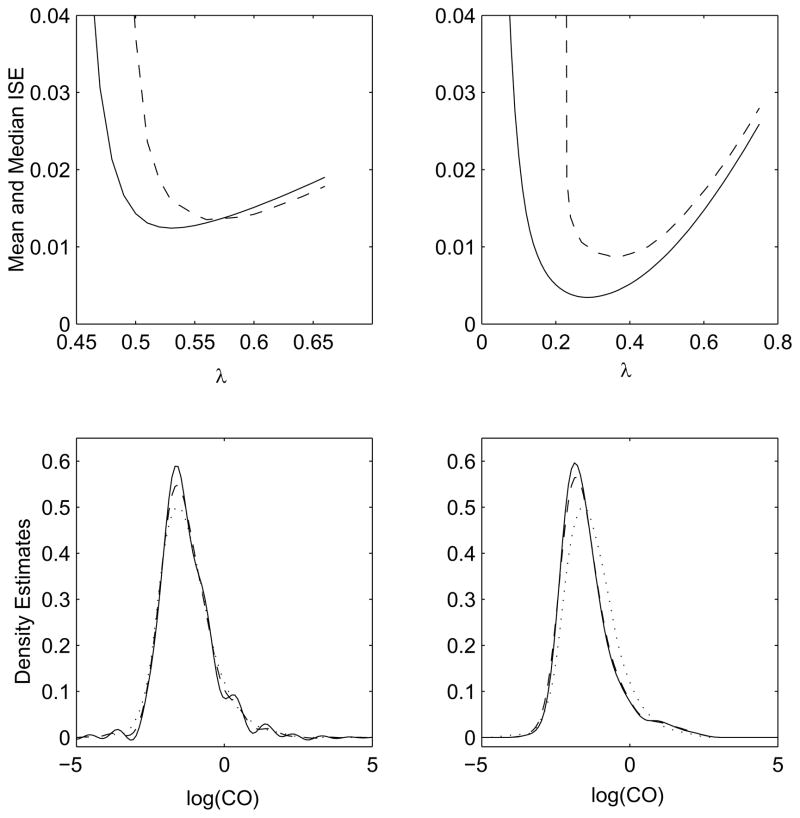
We estimated the density function of the log-transformed CO measurements using the 1233 automobiles with multiple measurements. For comparison, we fit the weighted estimator for heteroscedastic errors and the estimator for homoscedastic errors. Bandwidths were selected using both analytical and empirical calculation of the bootstrap bandwidth estimate as described in Section 5. Each empirical estimate was based on 100 bootstrap data sets and the bandwidth was selected to minimize the median integrated squared error. Results are shown in Figure 3. Also shown is the naive estimate, calculated using the sample means of replicate observations and the normal reference bandwidth. All measurement error-corrected estimators show a higher peak and slightly thinner tails than the naive estimator. This is expected when the effects of measurement error are removed from the observed-data estimate.

Figure 3.

Top row: Analytical mean (Solid line) and empirical median (Dashed line) ISE of bootstrap density estimates as a function of bandwidth. Left: Homoscedastic estimator; Right: Weighted estimator; Bottom row: Density estimates with bandwidth minimizing bootstrap MISE (solid line) and median ISE (dashed line). Left: Homoscedastic estimator; Right: Weighted estimator. Dotted line in both panels is the naive estimator with plug-in bandwidth.