Abstract
Much progress has been made in automated facial image analysis, yet current approaches still lag behind what is possible using manual labeling of facial actions. While many factors may contribute, a key one may be the limited attention to dynamics of facial action. Most approaches classify frames in terms of either displacement from a neutral, mean face or, less frequently, displacement between successive frames (i.e. velocity). In the current paper, we evaluated the hypothesis that attention to dynamics can boost recognition rates. Using the well-known Cohn-Kanade database and support vector machines, adding velocity and acceleration decreased the number of incorrectly classified results by 14.2% and 11.2%, respectively. Average classification accuracy for the displacement and velocity classifier system across all classifiers was 90.2%. Findings were replicated using linear discriminant analysis, and found a mean decrease of 16.4% in incorrect classifications across classifiers. These findings suggest that information about the dynamics of a movement, that is, the velocity and to a lesser extent the acceleration of a change, can helpfully inform classification of facial expressions.
1. Introduction
Facial expression is a rich and intricate source of information about the current affective state of a human being [20]. While humans routinely extract much of this information automatically in real life situations, the systematic classification and extraction of facial expression information in the laboratory has proven a more difficult task. Human-coded classification systems, such as the Facial Action Coding System (FACS) [18, 19] rely on people examining individual frames of video to determine the specific units of deformation of the face shown in each video frame. This type of analysis requires long training times, and still shows subjective error in rating [25, 12].
Yet why should this seem so difficult when a variant of it is performed routinely in everyday life? Converging evidence from psychology indicates that one major aspect that aids in the recognition of facial expression and affect is information about the dynamics of movement. For example, Ambadar et al. [1] demonstrated differences between the dynamic characteristics of true versus false smiles. Similarly, Bassili [5, 6] showed that humans can detect the emotional content of facial expressions merely from a moving point-light display of those expressions.
In spite of this converging evidence most automatic recognition engines use only static displacement; that is, the distance between the features on the current image and the location of the same features on a canonical “neutral” face at a single moment in time. In general, the procedure for this sort of classifier involves extracting features from a video stream and examining the parameter values for each frame of that video in isolation. The general architecture of such a classification system usually consists of some form of tracking, such as optical flow [14] or a feature detector like Gabor filters [4] to find features in each frame of raw video, and then a second stage that operates on the frame-by-frame output of the feature detector. Even those classifiers that do utilize frame-to-frame changes, (such as Pantic and Patras [27]) use an explicitly-built set of rules customized to the specific AUs and viewpoints of their study. Their approach is therefore limited to the views and action units for which the dynamic profiles have been explicitly characterized; and is particularly constrained to the analysis of single expressions as opposed to a stream of many successive expressions. The current paper provides a general means of allowing standard classifiers to learn how to incorporate velocity and acceleration information and use that information without explicitly designed rules of motion, and explores the relative contributions of velocity and acceleration across several different action units. It further presents the method of Local Linear Approximation as a computationally efficient method for calculating acceleration and velocity in a manner robust to noise and easy to calculate “on the fly”.
In order to avoid the need for a more complex classifier to handle this added information, instantaneous velocity and acceleration are estimated at each video frame, and presented as additional feature vectors for use by a standard frame-by-frame classifier. The current paper presents a technique for extracting these dynamic components of movement using a local linear approximation of velocity and acceleration, and provides a comparison between a standard, displacement-only, technique and a similar technique applied to displacements with velocity and acceleration information included.
2. Methods
2.1. Image Processing
Facial Action Coding System (FACS)
The FACS [18, 19] is the most comprehensive, psychometrically rigorous, and widely used manual method of annotating facial actions [13, 20]. Using FACS and viewing video-recorded facial behavior at frame rate and slow motion, coders can manually annotate nearly all possible facial expressions, which are decomposed into action units (AUs). Action units, with some qualifications, are the smallest visually discriminable facial movements. FACS has been selected as the coding system for this paper because of its ubiquity and comprehensiveness.
We selected 16 AUs for this study, following the selections made in [14]: FACS AUs 1, 2, 4, 5, 6, 7, 9, 12, 15, 17, 20, 23, 24, 25, 26 and 27. Together, these provide a relatively complete sampling of the different regions of the face, including brow, mouth, and eye regions. We intend these only as a demonstration of the benefit of using velocity and acceleration information, not as a exhaustive list of the abilities of the technique.
Image Corpus
Image data were from the Cohn-Kanade Facial Expression Database [14, 22]. Subjects were 100 university students enrolled in introductory psychology classes. They ranged in age from 18 to 30 years. Sixty-five percent were female, 15 percent were African-American, and three percent were Asian or Latino. They were recorded using two hardware synchronized cameras while performing directed facial action tasks [17]. Video was digitized into 640 × 480 grayscale pixel arrays.
The apex of each facial expressions was coded using the FACS [18] by a certified FACS coder. Seventeen percent of the data were comparison coded by a second certified FACS coder. Inter-observer agreement was quantified with coefficient kappa, which is the proportion of agreement above what would be expected to occur by chance [11, 21]. The mean kappa for inter-observer agreement was 0.86, indicating good agreement. Action units which occurred a minimum of 25 times and were performed by a minimum of 10 different people were selected for analysis.
Active Appearance Models
Active Appearance Models (AAMs) are a compact mathematical representation of the appearance and shape of visual objects [15]. After model training, AAMs can be used to recreate the shape and appearance of the object modeled. By using a gradient-descent analysis-by-synthesis approach, AAMs can track the deformation of a variety of facial features including both shape deformations (such as jaw movements) and appearance deformations (such as changes in shading) in real-time [26]. Each image sequence was processed using AAMs. The AAMs applied to this corpus tracked 68 point locations on the face of each individual. Figure 1 shows the arrangement of points on two different video frames, as placed by the AAM. The locations of these points, as placed by the AAM, serve as the initial primary data for this study.
Figure 1.
Examples of facial images. Colored dots indicate AAM-tracked point locations.
Image Alignment
As with prior studies (e.g. [14]), all image sequences began with a canonically neutral face. Each sequence was aligned so that the location of the first image was taken to be zero. Hence every image in sequence is defined in terms of displacement from the neutral face.
Velocity and Acceleration Estimates
Given a time series, like a sequence of feature point locations, one can estimate the instantaneous rate of change in position (i.e. velocity) and also estimate the change in velocity, known as acceleration. The instantaneous rate of change is estimated by using the change in position. Similarly, the acceleration is estimated by using the change in velocity. After a time series is collected, the first estimation step is to perform a time-delay embedding [29]. The basic principle is to put the one-dimensional time series into a higher-dimensional space that can accurately represent the dynamics of the system of interest. As an example, consider the time series P given by p1, p2, p3, …, p8. The one-dimensional time-delay embedding of P is given by P itself and cannot account for dynamical information. The time-delay embedding in dimension two is given by a two-column matrix with pi in the ith entry of the first column, and pi+1 in the ith entry of the second column. A four-dimensional embedding was performed for the present analysis to allow for the use of dynamical information and to filter some noise from the data. The four-dimensional embedding of our example time series P is given by P(4) in equation 1.
| (1) |
The next step, after a time series is embedded is to estimate velocity and acceleration by local linear approximation, a variant of a Savitzky-Golay filtering [30]. To do this for velocity, we calculate the change in position between the same point at two adjacent times, and average over several of these changes. The simplest version of this velocity calculation uses only two time-points per estimate and takes the frame-to-frame differences. However, because of the use of only two frames, this does not allow for an estimate of acceleration. Moreover, using three time points can be overly sensitive to error [8]. Thus, a weighted sum of four frames of positions was used to calculate a more robust estimate of velocity. A similar process is used to average the differences between estimated velocities to estimate the instantaneous acceleration.
When using four time-points, and hence a four-dimensional embedding, to estimate position, velocity, and acceleration, the weighting matrix W is always given by equation 2
| (2) |
where the first column provides the weights for the re-estimation of position, which here is displacement from the neutral face; the second column estimates velocity; and the third column, acceleration. These weights are determined analytically based on the ubiquitous relationship between position, velocity, and acceleration. See [7] for details.
The approximate derivatives of any four-dimensionally embedded time series X(4) are given by equation 3,
| (3) |
where W is the weighting matrix, and Y contains the position, velocity, and acceleration estimates. As can be seen from equation 3, velocity and acceleration for an arbitrarily long but finite time series are calculated with a single matrix multiplication which, on virtually every platform, is fast and computationally efficient. Moreover, in the case where velocity and acceleration are being estimated in real-time concurrently with the feature points, then using these dimensions at each time point only requires an extra 12 multiplications and 9 additions per feature point, which should not cause any significant slowdown.
Additionally, if one desires to estimate the dynamics of many feature points instead of only a single point, then one merely constructs block diagonal matrices for the embedded sequences and for the weighting matrix. There will be a separate block for each feature point used; and the original weighting matrix is same for every one of its blocks. An example using three embedded point sequences is provided by equation 4, where Y contains the position, velocity, and acceleration for feature points one, two, and three; W is the weighting matrix, and Xi is the embedded time series for feature point i.
| (4) |
One should also note, because of the sparseness of the matrices involved in the multiplication, this calculation is also highly efficient.
2.2. Data Analysis
Classifiers
In order to evaluate the added benefit of including information about the dynamics of facial movement on classification accuracy, support vector machines (SVMs) were chosen. SVMs are linear classifiers that have been commonly used in the literature (for example, [3, 2, 32]), and are available in many pieces of software. For this analysis, the kernlab package in R was used to train and evaluate SVM performance [23, 31]. The kernlab package provides an interface to the commonly used libsvm framework [10]. SVMs were chosen for this analysis because they represent a simple, common classifier that is well-known in the community.
Support Vector Machines are a form of classifier used to distinguish exemplars of different classes in multidimensional space. Each SVM essentially forms an n − 1 dimensional hyperplane in the space created by the n feature vectors, oriented so as to maximize the distance between the hyperplane and the nearest exemplars of each class. Objects falling on one side of the hyperplane are considered to be in one class. More information about SVMs is available from [16].
In order to demonstrate that the benefits of this added dynamic information are not unique to a single type of classifier, we replicated our study using Linear Discriminant analysis. Linear Discriminant analysis has also been used previously in the facial expression literature, and details on both the mathematics behind it and an example usage can be found in [14].
10-Fold Cross-validation
Subjects were divided randomly into ten subsets, with random redraws occurring until each subset included at least one exemplar for each of the AUs of interest. Each subject was included in only one subset, with all images of that subject being relegated to that subset. 10-fold cross-validation was then performed, where a classifier was trained on 9 of the subsets, and then tested on the 10th. This was repeated, leaving a different subset out of the training set each time. Thus each subject was tested once by a classifier which was not trained on data that included that subject's face. A total of 6770 individual frames were estimated, of which roughly ten percent exhibited any given facial action unit.
In each case, first a classifier was trained using only displacement data, that is, the distance at each time point between the current facial location and the location during the first (neutral) frame. A second classifier was trained using position, and the velocity estimated by the local linear approximation procedure described above. Finally, a third classifier was trained using displacement, estimated velocity, and estimated acceleration. In each case, classifiers evaluated each image in a sequence as though it were an independent observation; that is, no time information other than the estimated positions, velocities, and accelerations was used. A separate classifier was trained for each action unit to be classified.
Independence
It is worth noting that the addition of velocity and acceleration information causes a dependency to develop between successive frames. That is, the velocity data from frame 3 is influenced not only by frame 3, but by the locations of features in frames 1, 2, 3, and 4. Similarly, the velocity estimate for frame 4 is influenced by frames 2, 3, 4, and 5. This necessarily induces some dependency between successive measures, and violates the standard regression assumption of independence. However, because the testing set is entirely distinct from the training set (that is, there is no dependence between any measure in the testing set and any measure in the training set), dependencies within the training set have no effect on our estimates of precision and accuracy of the classifier. No attempt is made to remove these dependencies within the testing set, since, in general, such a classifier is likely to be used on real video data, and as such be faced with the same sorts of dependencies we present here. In short, we allow for some violation of the standard assumptions used for classification in order to provide estimates that are likely to be more valid for the application of this technique.
Because the three classifiers evaluating a given action unit are trained and tested in the same way, meaningful comparisons can be made. The difference between these classifiers can be attributed solely to the inclusion of information about the estimated dynamics of the expression.
3. Results
When velocity information was included as input to the classifier, it showed a median increase in true positive identification of 4.2% over displacement-only classification for the testing set with a corresponding 3.1% reduction in false positive rate. Because each individual classification carried only a small proportion (mean: 21.3%, median: 14.6%) of the total set, mean change in total accuracy was only 2.9%. While this number is relatively small in absolute value, it results in as much as 31% fewer incorrectly classified instances for some AUs (mean: 14.2%, N = 16).
It is worth noting that not all AUs are better classified in all cases by the addition of this information. For example, AUs 4 and 26 appear to show no real gain, or even a slight loss overall. This is likely due to the already high classification rate of that classifier, and the relatively poor performance of an SVM when faced with noisy data. It is worth noting that the only classifier to actively lose accuracy with the addition of velocity or acceleration information is AU 26, which is demonstrated in less than 10% of the training examples–a larger proportion of training examples might show better results. Acceleration information does not provide a consistent benefit above velocity information (mean: .4%), but does provide some benefit in finding many AUs (range: –.3% to 2.1% increase in true positive classification). Taken together, these results imply that acceleration information plays a differential role in identification of distinct AUs.
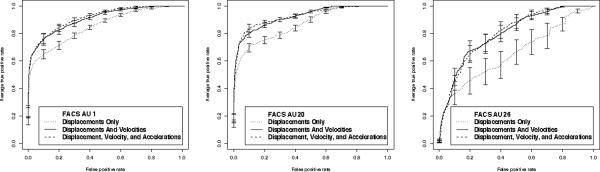
Examination of the Reciever Operating Characteristic (ROC) curves for the specific classifiers, however, shows that acceleration information does have some influence at different levels of discrimination. Figure 2 shows some of the common patterns of influence. It is worth noting that even in AU 26, where the gain is lowest, velocity information does play a role if a stricter (< 50% probability) requirement is enforced.
Figure 2.
Representative ROC curves for classifiers trained using displacement only, displacement and velocity only, or displacement, velocity, and acceleration. Error bars indicate estimated standard errors of the mean true positive rates over 10-fold cross-validation. In all cases, addition of velocity and acceleration improved or unchanged fit along the entire curve.
Details about the individual benefit provided for the classification of each of the individual AUs is shown in Table 1, and percentage reduction in false negative results corrected is shown in Table 2.
Table 1.
Proportion of correctly classified instances using displacement, displacement and velocity, or displacement, velocity, and acceleration. Second column indicates percentage of total instances exhibiting the given AU.
| AU | AU Percentage | X only | X+X' | X + X' + X” |
|---|---|---|---|---|
|
| ||||
| 1 | 28.2 | 0.840 | 0.877 | 0.872 |
| 2 | 18.2 | 0.917 | 0.940 | 0.942 |
| 4 | 34.7 | 0.802 | 0.831 | 0.834 |
| 5 | 14.6 | 0.887 | 0.905 | 0.896 |
| 6 | 23.9 | 0.935 | 0.956 | 0.954 |
| 7 | 24.3 | 0.940 | 0.955 | 0.950 |
| 9 | 10.0 | 0.951 | 0.964 | 0.963 |
| 12 | 26.8 | 0.909 | 0.935 | 0.928 |
| 15 | 14.6 | 0.909 | 0.928 | 0.923 |
| 17 | 33.9 | 0.857 | 0.902 | 0.910 |
| 20 | 13.4 | 0.906 | 0.919 | 0.917 |
| 23 | 12.5 | 0.899 | 0.916 | 0.916 |
| 24 | 12.2 | 0.905 | 0.916 | 0.918 |
| 25 | 57.8 | 0.860 | 0.898 | 0.896 |
| 26 | 8.3 | 0.918 | 0.915 | 0.913 |
| 27 | 14.6 | 0.918 | 0.952 | 0.944 |
Table 2.
Proportion of reduction in false negative classifications
| AU | X vs. X+X' | X vs X+X'+X” |
|---|---|---|
|
| ||
| 1 | 0.127 | 0.034 |
| 2 | 0.255 | 0.253 |
| 4 | −0.036 | −0.121 |
| 5 | 0.125 | 0.147 |
| 6 | 0.082 | 0.016 |
| 7 | 0.092 | 0.131 |
| 9 | 0.218 | 0.222 |
| 12 | 0.158 | 0.028 |
| 15 | 0.116 | −0.002 |
| 17 | 0.237 | 0.357 |
| 20 | 0.246 | 0.193 |
| 23 | 0.169 | 0.199 |
| 24 | 0.133 | 0.096 |
| 25 | 0.026 | −0.144 |
| 26 | 0.006 | 0.027 |
| 27 | 0.315 | 0.364 |
In order to ensure that the improvement was not solely due to the SVM classifier, the experiment was repeated with linear discriminant analysis (LDA) classification. Again, the mean increase in overall classification was 4.5%, now accounting for 16% of the incorrectly classified instances.
For training set, the impact of velocity and acceleration was larger. SVM classifiers using velocity information increased in overall accuracy by about 1%, decreasing the number of incorrect instances by 32.3%. LDA classifiers using velocity information also increased accuracy by about 1%, about 51.7% of incorrectly classified instances.
4. Discussion
Psychological evidence shows that humans are able to distinguish facial expressions using primarily motion information and that modification of the characteristics of motion influence the interpretation of the affective meaning of facial expressions [28]. The dynamics of facial movements, therefore, carry information valuable to the classification of facial expression.
Several recent attempts have been made to incorporate some form of time-related information into the classification of facial expression. For example, Tong et al. [32] used dynamic interrelations between FACS codes to provide better informed priors to a Bayesian classifier tree. Lien [24] used Hidden Markov Models (HMMs) for classification, which take into account some measure of the relationship between successive frames of measurement. Yet these approaches are primarily focused on using co-occurrence and common transitions to influence the bias (specifically, the Bayesian priors or HMM transition probabilities) of other analyses on a larger scale. Yet a large amount of local information is available as well, in the form of instantaneous velocities and accelerations. This information is local, easy to approximate on-the-fly, and can be passed to existing classification engines with minimal changes to the classifier structure. We have demonstrated that this information can be calculated with minimal computational overhead, and provides a noticeable gain in classification accuracy.
The classifiers used for this example are relatively simple and are intended primarily as an illustration of the benefit to be gained by the addition of dynamic information. It is important to note, however, that the benefits of estimated dynamics are independent of the specific model being used. While velocities and accelerations are easiest to understand concerning a structural model of the face, even such higher-level constructs as the formation of wrinkles must have a rate of change, such as might be evidenced by the rate of increase in the classification probability being reported by a Gabor-filter-based classifier. This rate-of-change information could be calculated in a manner identical to the calculation of the velocities of point movements described here, and included as regular features in the higher-level model.
This study is limited by the use of laboratory-collected, intentionally expressed faces. It is possible that real-world faces will have different profiles of velocity and acceleration than laboratory-collected facial expressions. Even if this should be the case, a classifier trained on real-world expressions should still benefit from the addition of velocity information, and might even be able to distinguish between intentional and unintentional faces in this way.
No examination of the race or gender of the participants was made with reference to either the testing or training sets. Because participants were randomly assigned to cross-validation subsets and all testing subsets were evaluated, the impact of such groups should be minimal. An interesting question about the generalizability of dynamic profiles across race and gender remains open.
Another possible limitation is the potential impact of global head movements on the accuracy of classification. With only a few minor exceptions in the Cohn-Kanade Database [22], variation in head translation, rotation, and scale is negligible; and each frame sequence begins with a neutral expression. Therefore, because every head began and generally remained in a canonical position, every frame in a sequence was not first normalized to a canonical head position; and generally did not need to be. Hence, some small amount of variance in the displacements, estimated velocities, and estimated accelerations can be attributed to global head movements. If these head movements do not covary with facial expressions, then they are inhibiting accurate classification by adding noise. On the other hand, if global head movements meaningfully co-occur with facial expressions, then this aids accurate classification. The current study also examines only a series of intentional, face-forward facial movements in a laboratory setting, which may always reduce the frequency and magnitude of these head movements. Further work includes studying these effects in a more general setting, such as natural conversation.
As opposed to being a handicap, some of the benefit from velocities may be attributable to the covariance of global head movement and facial expression. For example, the smiles used to indicate embarrassment and enjoyment are characterized by many of the same facial muscle movements (e.g. open mouth, intense contraction of the modioli), but differ markedly in the associated head movements. Similarly, surprise is often associated with upward head movement [9]. The dynamics of head motion and facial action each provide important information for the understanding of affect as related by facial expression. This implies that in addition to helping the classification of AUs, velocity and acceleration information might be more beneficial to the classification of affective state given a set of classified AUs.
This paper has demonstrated a computationally light technique for online calculation of velocity and acceleration of feature points, and provided evidence for the benefits that this technique provides to classification accuracy. We have presented an argument that the use of this form of dynamic information will provide a benefit to a wide range of classification techniques.
References
- [1].Ambadar Z, Cohn JF, Reed LI. All smiles are not created equal: Morphology and timing of smiles perceived as amused, polite, and embarrassed/nervous. J Nonverbal Behav. 2009 Mar;33(1):17–34. doi: 10.1007/s10919-008-0059-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Ashraf AB, Lucey S, Cohn JF, Chen T, Prkachin KM, Soloman P, Theobald BJ. The painful face: Pain expression recognition using acttive appearacne models. Proceedings of the ACM International Conference on Multi-modal Interfaces. 2007:9–14. [Google Scholar]
- [3].Barlett MS, Littlewort G, Lainscsek C, Fasel IR, Movellan F. Machine learning methods for fully automated recognition of facial expressions and facial actions. Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics. 2004 [Google Scholar]
- [4].Bartlett M, Littlewort G, Frank M, Lainscsek C, Fasel I, Movellan J. Automatic recognition of facial actions in spontaneous expressions. Journal of Multimedia. 2006;1(6):22–35. [Google Scholar]
- [5].Bassili JN. Facial motion in the perception of faces and of emotional expression. Journal of Experimental Psychology: Human Perception and Performance. 1978 Aug;4(3):373–379. doi: 10.1037//0096-1523.4.3.373. [DOI] [PubMed] [Google Scholar]
- [6].Bassili JN. Emotion recognition: The role of facial movement and the relative importance of upper and lower areas of the face. Journal of Personality and social Psychology. 1979 Nov;37(11):2049–2058. doi: 10.1037//0022-3514.37.11.2049. [DOI] [PubMed] [Google Scholar]
- [7].Boker SM, Deboeck PR, Edler C, Keel PK. Generalized local linear approximation of derivatives from time series. In: Chow S-M, Ferrer E, editors. Statistical Methods for Modeling Human Dynamics: An Interdisciplinary Dialogue. Taylor and Francis; Boca Raton, FL: In Press. [Google Scholar]
- [8].Boker SM, Nesselroade JR. A method for modeling the intrinsic dynamics of intraindividual variability: Recovering the parameters of simulated oscillators in multi-wave panel data. Multivariate Behavioral Research. 2002;37:127–160. doi: 10.1207/S15327906MBR3701_06. [DOI] [PubMed] [Google Scholar]
- [9].Camras LA. Surprise! Facial expressions can be coordinative motor structures. In: Lewis MD, Granic I, editors. Emotion, Development, and Self-Organization. 2000. pp. 100–124. [Google Scholar]
- [10].Chih-Chung C, Chih-Jen L. Libsvm: a library for support vector machines. 2001 [Google Scholar]
- [11].Cohen J. Coefficient of agreement for nominal scales. Educational and Psychological Measurement. 1960;20(1):37–46. [Google Scholar]
- [12].Cohn JF, Ambadar Z, Ekman P. Observer-based measurement of facial expression with the Facial Action Coding System. In: Coan JA, Allen JB, editors. The Handbook of Emotion Elicitation and Assessment. Oxford University Press; New York: 2007. pp. 203–221. [Google Scholar]
- [13].Cohn JF, Ekman P, Scherer RRK. Measuring facial action by manual coding, facial emg, and automatic facial image analysis. In: Harrigan JA, editor. Handbook of nonverbal behavior research methods in the affective sciences. 2005. pp. 9–64. [Google Scholar]
- [14].Cohn JF, Zlochower AJ, Lien J, Kanade T. Automated face analysis by feature point tracking has high concurrent validity with manual facs coding. Psychophysiology. 1999;36(01):35–43. doi: 10.1017/s0048577299971184. [DOI] [PubMed] [Google Scholar]
- [15].Cootes T, Edwards G, Taylor C. Active appearance models. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2001 Jun;23(6):681–685. [Google Scholar]
- [16].Cortes C, Vapnik V. Support vector networks. Machine Learning. 1995;20:273–297. [Google Scholar]
- [17].Ekman P. The directed facial action task: Emotional responses without appraisal. In: Coan JA, Allen JJB, editors. The Handbook of emotion elicitation and assessement. Oxford University Press; Oxford: 2007. pp. 47–53. [Google Scholar]
- [18].Ekman P, Friesen W, Hager J. Facial action coding system manual. Consulting Psychologists Press. 1978 Jan; [Google Scholar]
- [19].Ekman P, Friesen WV, Hager JC. Facial action coding system. Research Nexus, Network Research Information; Salt Lake City, UT: 2002. [Google Scholar]
- [20].Ekman P, Rosenberg EL, editors. What the face reveals: Basic and applied studies using the facial action coding system. second edition Oxford University Press; New York: 2005. [Google Scholar]
- [21].Fleiss JL. Measuring nominal scale agreement among many raters. Psychological Bulletin. 1971;76(5):378–382. [Google Scholar]
- [22].Kanade T, Cohn JF, Tian Y. Comprehensive database for facial expression analysis. Fourth IEEE International Conference on Automatic Face and Gesture Rcognition; Grenoble, France. 2000. pp. 46–53. [Google Scholar]
- [23].Karatzoglou A, Smola A, Hornik K, Zeileis A. kern-lab – an S4 package for kernel methods in R. Journal of Statistical Software. 2004;11(9):1–20. [Google Scholar]
- [24].Lien J, Kanade T, Cohn JF, Li CC. Detection, tracking, and classification of subtle changes in facial expression. Journal of Robotics and Autonomous Systems. 2000;46(3):1–48. [Google Scholar]
- [25].Marin P, Bateson P. Measuring Behavior: An Introductory Guide. Cambridge University Press; Cambridge: 1986. [Google Scholar]
- [26].Matthews I, Baker S. Active appearance models revisited. International Journal of Computer Vision. 2004;60(20):135–164. [Google Scholar]
- [27].Pantic M, Patras I. Dynamics of facial expression: Recognition of facial actions and their temporal segments from face profile image sequences. IEEE Transactions on Systems, Man, and Cybernetics, Part B. 2006;36(2):433–449. doi: 10.1109/tsmcb.2005.859075. [DOI] [PubMed] [Google Scholar]
- [28].Pollick FE, Hill H, Calder A, Paterson H. Recognising facial expression from spatially and temporally modified movements. Perception. 2003 Jan;32(7):813–826. doi: 10.1068/p3319. [DOI] [PubMed] [Google Scholar]
- [29].Sauer T, Yorke J, Casdagli M. Embedology. Journal of Statistical Physics. 1991 Nov;65(3,4):579–616. [Google Scholar]
- [30].Savitzky A, Golay MJE. Smoothing and differentiation of data by simplified least squares procedures. Analytical Chemistry. 1964 Jul;36(9):1627–1639. [Google Scholar]
- [31].Team RDC. R: A language and environment for statistical computing. R Foundation for Statistical Computing. 2005 [Google Scholar]
- [32].Tong Y, Liao W, Ji Q. Facial action unit recognition by exploiting their dynamic and semantic relationships. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2007;29(10):1683–1699. doi: 10.1109/TPAMI.2007.1094. [DOI] [PubMed] [Google Scholar]