Investigating the predictability of essential genes across distantly related organisms using an integrative approach

Abstract

Rapid and accurate identification of new essential genes in under-studied microorganisms will significantly improve our understanding of how a cell works and the ability to re-engineer microorganisms. However, predicting essential genes across distantly related organisms remains a challenge. Here, we present a machine learning-based integrative approach that reliably transfers essential gene annotations between distantly related bacteria. We focused on four bacterial species that have well-characterized essential genes, and tested the transferability between three pairs among them. For each pair, we trained our classifier to learn traits associated with essential genes in one organism, and applied it to make predictions in the other. The predictions were then evaluated by examining the agreements with the known essential genes in the target organism. Ten-fold cross-validation in the same organism yielded AUC scores between 0.86 and 0.93. Cross-organism predictions yielded AUC scores between 0.69 and 0.89. The transferability is likely affected by growth conditions, quality of the training data set and the evolutionary distance. We are thus the first to report that gene essentiality can be reliably predicted using features trained and tested in a distantly related organism. Our approach proves more robust and portable than existing approaches, significantly extending our ability to predict essential genes beyond orthologs.

INTRODUCTION

The recent success of ‘synthetic bacteria’ has rekindled people’s enthusiasm for using systems and synthetic biology to serve the needs of humanity by re-engineering microorganisms (1,2). Essential genes are important in these bioengineering efforts because any functional microorganism must contain a minimal set of essential genes that are required for survival and carrying out desired functions. Studying gene essentiality is also important in basic science because it is a crucial step toward understanding the complex relationship between genotype and phenotype (3). To date, genomic-scale knockout experiments in over a dozen microorganisms have shown that different organisms share a very limited number of essential genes. Therefore, rapid and accurate identification of essential genes in an under-studied organism, especially those unique to this organism, poses a significant challenge in this post-genomic era. The lack of this ability has prevented us from fully comprehending how a cell works as well as efficiently re-engineering microorganisms that will have energy, bioremediation, pharmaceutical and biodefence applications (4–6).

Experimental identification of essential genes can be accomplished either by targeted mutagenesis, where specific genes are identified prior to genetic manipulations and confirmatory studies based upon the experimental data, or by random mutagenesis, where the target genes are identified only after the experimental disruptions (7). While targeted mutagenesis produces more reliable results with higher accuracy, random mutagenesis appears to be more cost-effective. Nonetheless, genomic-scale systematic screening for lethal gene disruptions by either approach is a formidable undertaking. Taken together, a universal consensus of arguably multiple laboratories is required to ensure that the results are accurate, often requiring a consortium of labs many years of research.

To circumvent the expense and difficulty of these screens, researchers attempting to identify essential genes in under-studied organisms often have to rely on homology mapping to help elucidate essential genes. However, this method has several limitations. First, homology mapping is limited to the conserved orthologs between species, which often correspond to a small portion of a target bacterial genome (8). For example, Escherichia coli and Pseudomonas aeruginosa share <35% of their genes as orthologs. In addition, although essential genes tend to be conserved, conserved genes are often not essential. For example, less than a quarter of the highly conserved bacterial genes were essential when tested experimentally in model bacteria (9–12). Finally, beyond the testability of homology mapping, differences in genetic regulation or protein modification, genetic redundancy or divergence in cellular pathways or processes between organisms may also have great bearing on relative essentiality. For example, alaS gene that encodes alanyl-tRNA synthetase is essential in E. coli but non-essential in P. aeruginosa. It is non-essential in P. aeruginosa probably because it has a paralog (PA2106) that carries out the same function. Considering all these limitations, a group of researchers reached a disappointing conclusion that ‘gene conservation among bacteria does not necessarily indicate that essentiality in one organism can be extrapolated to others’ (12).

Thus, in this study, we developed a machine learning-based integrative approach as an alternative to transfer gene essentiality annotations between organisms. In contrast to homology mapping that relies strictly on the similarity of nucleotide sequences, this approach identifies relevant features of essential genes and makes predictions using a weighted combination of hallmark features.

By taking advantage of the near-complete mapping of the essential genes in Saccharomyces cerevisiae (13–14) and E. coli (15–17), a collection of genomic features have been identified to correlate with gene essentiality (Table 1). These features can be broadly classified into two categories: intrinsic and context-dependent features. Intrinsic features are determined by the genomic sequences, e.g. GC content, and do not depend on external conditions. Context-dependent features cannot be derived from an organism’s genome alone and may vary under different conditions, e.g. fluctuations in mRNA expression. The dependency of essentiality on both categories of features suggests that multiple aspects of biology unite to make a gene essential. Therefore, taking into account only the similarity in genomic sequences provides a limited perspective on this highly complex property.

Table 1.

Features correlated with gene essentiality in S. cerevisiae and E. coli

References	Genomic features
Jeong et al. (41)	(i) Fluctuation in mRNA expression; (ii) Protein functions; (iii) Connectivity in protein–protein interaction (PPI) network
Chen and Xu (18)	(i) Evolutionary rate; (ii) Duplication rate; (iii) Gene expression correlation network; (iv) Connectivity in PPI network
Saha and Heber (20)	(i) Phylogenetic conservation; (ii) Degree of paralogy; (iii) Number of PPIs
Seringhaus et al. (22)	14 intrinsic features, such as: GC content; length of protein; hydrophobicity; codon adaptation index; predicted subcellular localization in six compartments, etc
Gustafson et al. (21)	(i) Codon usage; (ii) Paralogs; (iii) Size and localization; (iv) Protin interaction network degree; (v) Phyletic retention measure; (vi) Recombination rate; (vii) Strand bias; (viii) Regulatory complexity, etc

A number of machine learning systems have been developed to integrate a subset of these features for cross-validation of essential genes in S. cerevisiae and E. coli, showing various degrees of prediction accuracy (AUC: 0.7–0.82; PPV: 0.34–0.68) (18–21). However, these studies do not address the applicability of such methods to novel genomes. Such applicability is important, because a useful predictor must perform well outside the organism on which it was trained. Seringhaus et al. (22) recently developed a method to train classifiers on S. cerevisiae essential genes and applied them to predict those in S. mikatae. However, due to the limited knowledge of essential genes in S. mikatae, it is impossible to systematically assess the performance of the classifiers in transferring gene essentiality. More importantly, when predicting essential genes in an unstudied organism, a closely related yet well-studied organism on which classifiers could be trained is often unavailable. Therefore, it would be most useful if a machine learning-based approach can be proven applicable to more distantly related species.

In this study, we re-examined the question of whether gene essentiality can be accurately transferred between organisms by a machine learning approach. We first focused on two bacterial species: E. coli and Acinetobacter baylyi ADP1. Both bacteria have well-characterized essential genes by targeted mutagenesis. For this pair, we developed a classifier to learn traits of essential genes in one organism and then predict those in the other. We then systematically evaluated the predictions by examining the overlaps with the known essential genes in the target organism, and compared its performance with homology mapping. To examine the applicability of our approach, we also tested the transferability on two other pairs of bacteria: E. coli and P. aeruginosa PAO1, and E. coli and Bacillus subtilis.

MATERIALS AND METHODS

Data sources

E. coli K-12 (EC) sequence data were downloaded from Comprehensive Microbial Resource (CMR) database at http://cmr.jcvi.org/. It contains 4289 protein sequences in total (23). The essential genes of E. coli K-12 were downloaded from the PEC database (17). The Kato data set contains 302 essential genes from gene deletion experiments.

P. aeruginosa PAO1 (PA) sequence data were downloaded from http://www.pseudomonas.com/ (Pseudomonas_aeruginosa_PAO1.faa, revision 17 July 2009). PA essential genes were downloaded from (24). The Jacobs dataset contains 678 essential genes from transponson mutagenesis in PAO1.

A. baylyi ADP1 (AB) sequences were collected from the Magnifying Genomes database (http://www.genoscope.cns.fr/). Out of a total of 3308 genes, 499 are essential genes from (25).

B. subtilis (BS) sequence data were downloaded from Microbial Genome Database (http://mbgd.genome.ad.jp/). This data set contains 4117 ORFs. The essential gene list was downloaded from (26) and consists of three data sets: (i) 150 essential genes determined by Kobayashi’s mutantgenesis experiments; (ii) 42 known essential genes from previous studies; (iii) 79 essential genes by homology mapping to other bacteria, most of which encode proteins involved in ribosome or synthesis.

Gene expression data in these bacteria were downloaded from NCBI GEO (27), ArrayExpress (28), as well as from Gasch et al. (29).

Homology mapping by reciprocal best hit

We developed a reciprocal best hit (RBH) method to identify the orthologs between EC and PA: We first queried an ORFⁱ in PA against all known ORFs in EC by Blastp, with an E-value threshold of 10⁻⁵, to yield the set of hits {W}. Then, we queried the hit with the lowest E-value in {W} (ORF^j) against all ORFs in PA to yield the set of hits {Y}. A pair of proteins (ORFⁱ, ORF^j) are considered putative orthologs if ORFⁱis the hit in {Y} with the lowest E-value, and if they also meet two strict criteria: (i) 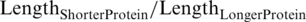≥80%; (ii)  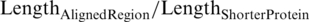≥ 80% to ensure sufficient coverage of aligned regions.

Homology mapping by COG groups

We implemented an alternative approach for homology mapping by using COG groups (30). The COG groups contain a list of genes of organisms from the same distinct phylogenetic lineage. We used these COG groups to map the essential genes from one organism to the other. Thus, if one gene in EC is essential, then all PA genes in the same COG group are assumed to be essential.

COG groups are unavailable for genes from AB. Therefore, we performed homology mapping between EC and AB based on sequence identity groups. We clustered AB proteins into groups based on their sequence identities with each other. Each protein sequence in AB was searched against all protein sequences in AB by Blastp with an E-value cutoff of 1e–5. Proteins are considered in the same sequence identity group if every pair of proteins has (i) sequence similarity that satisfies the E-value cutoff mutually and (ii) sequence identities >35%. Similarly, protein sequence identity groups were extracted for EC. If a protein in one organism is essential, then all proteins of the other organism in the same sequence identity group as the essential protein predicted by RBH are considered essential.

Intrinsic and context-dependent genomic features

To create a training dataset for our classifier, features are extracted where available for each ORF in each organism and annotated with known essentiality values from the essential gene data sets. Our study considered three main types of features: (i) those intrinsic to a gene’s sequence (e.g. GC content, protein length); (ii) those derived from genomic sequence (e.g. localization signals and codon adaptation measures) and (iii) experimental functional genomics data (e.g. gene-expression microarray data) (Supplementary Table S1).

(i-a) Genomic sequence properties. Evolutionary selection of genes can often be detected from the base composition of a genome, e.g. GC content, and the overall amino acid composition, e.g. hydrophobicity (31). Essential genes have been found to be more evolutionarily conserved than non-essential genes in bacteria and the negative selection on essential genes are more stringent than for non-essentials (32). Therefore, correlating the base or amino acid composition with essentiality may reveal the evolutionary constraints that are predictive of essential genes. We used CodonW (http://bioweb.pasteur.fr/) to calculate the following properties associated with genomic sequences: Kyte and Doolittle’s grand average of hydropathicity (GRAVY) (33), protein length (amino acids), GC content and two measures of codon usage: effective Nc (34–35) and CAI (36).

(ii-a) Predicted subcellular localization. Subcellular localization is potentially predictive of gene essentiality because gene products that carry out specific functions are often confined to certain subcellular compartments. For example, proteins involved in the essential functions of information storage and processing such as DNA replication, recombination and mRNA synthesis locate in nucleus in Eukaryotes and cytoplasm in Prokaryotes (37). In contrast, most membrane proteins function as transporters or participate in metabolic related processes. This also explains why a protein has more transmembrane helix (PredHel) are more likely to be non-essential (Supplementary Figure S1). We used the PA-SUB Server v2.5 to obtain these features (38). Gram-negative bacteria (EC, PA and AB) have five predicted localizations: inner membrane, extracellular, cytoplasm, periplasm and outer membrane. Gram-positive bacteria (BS) have three predicted localizations: extracellular, cytoplasm and plasma membrane.

(ii-b) Transmembrane helices for each ORF. The putative transmembrane helices were calculated by TMHMM Web server v2.0 (39,40).

(ii-c) Phylogenetic profile of a gene. Essential genes are more evolutionarily conserved than non-essential genes (14,20–21). This is because essential genes are more likely involved in basic cellular processes, thus the negative selection acting on essential genes are more stringent than for non-essentials (32). We used the RBH method to search orthologs in multiple complete genomes for each gene of the target organism (PA, EC, AB and BS). The number of genomes that have orthologous hits was used as a measure of evolutionary conservation of a gene. Such conservation has been shown to correlate well with the dispensability of a gene (18).

(ii-d) Paralogy. Duplicated genes in an organism are often referred to as paralogs. Paralogs typically have a similar function because they arose from gene duplication events within the same species. It is expected that essential genes should have a fewer number of paralogs than non-essential genes because an essential gene’s function is indispensable and less likely to be compensated by its paralogs (14,20). An all-against-all FASTA search was conducted for the whole set of ORFs in the target organism (PA, EC, AB and BS) to identify the paralogs with an E-value threshold of 10⁻²⁰.

(ii-e) Domain enrichment. In contrast to the evolutionary conservation of a gene in (ii-c), domain enrichment reflects the conservation of local sequences rather than the entire gene. For each individual domain, we collected its occurrence in each organism (PA, EC, AB and BS) using the Pfam database (http://pfam.sanger.ac.uk). 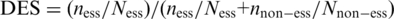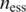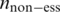Then we estimated the domain enrichment score according to the ratio of occurrence frequencies between essential gene sets and the total genes in the target organism: , here and represent a domain’s occurrence frequency in the essential and non-essential data set, respectively. 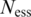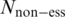and represent the size of the essential and non-essential dataset, respectively. For each round of training-testing, we re-computed the DES scores based on available data except the testing data. For example, in EC → PA, for a given domain in PA, DES is computed by calculating the ratio of essential to non-essential genes among all EC genes that encode this domain. Therefore, we did not use the information regarding PA essential genes, ensuring a correct training and testing.

(iii-a) Fluctuation in gene-expression. The mRNA expression levels of essential genes often vary, on average, within a narrower range, whereas the expression of non-essential genes fluctuates more widely (41). This is due to the potential existence of feedback mechanisms that can stabilize the expression level of essential genes. It has been observed that wide fluctuation in the expression level of essential genes could cause the death of an organism (41). The variance of each gene was calculated from these gene expression profiles as a measure of the fluctuation of gene expression.

(iii-b) Topology in gene co-expression network. Previous research has shown that in protein–protein interaction (PPI) network, hubs or highly connected proteins, are more likely to be essential and evolve slowly (42–44). It has also been shown that interacting proteins tend to be co-expressed because they are often involved in the same pathway (45,46). 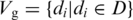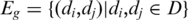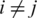From gene expression microarray data, a gene-expression cooperativity graph is constructed as G_g (D) = (V_g, E_g), with the vertex set and the edge set for and 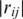 ≥ 0.7. Each vertex represents a gene and each edge represents a gene pair whose gene expression profiles correlation coefficient 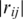is >0.7. This cutoff value of 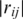is determined based on our previous work (46). The hubs (nodes with high degrees) and bottlenecks (nodes with high betweenness or shortest paths occurrence) have been found to have correlations with gene essentiality (42). The network statistics are calculated using tYNA (http://tyna.gersteinlab.org/).

Feature evaluation and selections

We used three criteria as described in the ‘Results’ section to select suitable features.

To measure the predictive power of different features, we performed a Naïve Bayes analysis and ranked all features according to the coverage length of log-odds ratio (Supplementary Figure S1). The longer the overall coverage length is, the greater the contribution of the corresponding feature has to the target class, i.e. gene essentiality. Since we are interested in predicting essential genes but not non-essential genes, the features with a positive coverage length are considered as useful features.

The log-odds ratio was calculated for each feature and compared with all other features in nomograms. Comparing the span of an attribute axis in nomograms easily identifies the important attributes. The effects of each attribute value are also clearly represented in a nomogram, making it easy to spot a direction and magnitude of the influence. Attribute axis are aligned to zero-point influence (prior probability), which allows for a straightforward comparison of contributions across different values and attributes (Supplementary Figure S1).

For each feature, we ranked the features according to their positive influence on gene essentiality. Those with high positive influence and monotonic relationship with essentiality are our candidate features. Specifically, in feature Category (A), we kept CBI, CAI, Fop, Nc, L_aa, Aromo and removed GC, C3s, A3s, T3s, Gravy and G3s. In Category (B), we kept DES, PHYS, Cytoplasm, Extracellular, PA and Inner Membrane and removed Periplasm, Outer Membrane, ExpAA, First60 and PredHel. In Category (C), we kept CEB, CEH and FLU.

Next, we considered prior biological information to remove feature redundancy. For example, CBI has Pearson correlation coefficients of 0.92 and 0.99 with CAI and Fop, respectively (Supplementary Figure S2), because these features are all derived from the codon usage of a gene and share similar biological meanings. Therefore, we removed CBI and Fop from Category (A) which resulted in the 13 candidate features (Table 2).

Table 2.

Thirteen features that are selected for 10-fold cross-validation in EC

Intrinsic features		Context-dependent features (From functional genomics experiment)
Sequence based	Sequence derived
Codon bias index (CBI)	Domain enrichment score (DES)	Fluctuation in gene expression (FLU)
Hydrophobicity score (Nc)	Phylogenetic score (PHYS)	Co-expression network bottlenecks (CEB)
Length of Amino Acid (L_aa)	Subcellular localization: cytoplasm (Cyto)	Co-expression network hubs (CEH)
Aromaticity (Aromo)	Subcellular localization: extracellular (Extra)
	Paralogy (PA)
	Subcellular localization: inner membrane (Inner)

Training and testing sets preparation

The training data included the attribute values for each feature and the class assignments. Each gene was assigned a Boolean value regarding its essentiality (1—essential; 0—non-essential). The feature values may be Boolean or real depending on the type of individual features (Supplementary Table S1). The training data were divided into 10 equal parts. Nine-folds were used to train the classifiers and the remaining one fold was used for testing. The control training set was generated by randomly assigning essential labels to all E. coli genes. The same number of random ‘essential genes’ as the number of true essential genes was used in the training and testing frame.

Classifier design

We used four classifiers to train and test the model: (i) Naïve Bayes classifier; (ii) a logistical regression model; (iii) a C4.5 decision tree; and (iv) CN2 rule. Each classifier scheme independently generates a separate probability score of gene essentiality. The performances of these classifiers are different but complementary. The best performance was obtained by combining the outputs of these diverse classifiers using an unweighted average approach. All classifiers were implemented using the Orange software package (http://www.ailab.si/orange/).

RESULTS

Comparing the genomes and essential genes of E. coli and A. baylyi

In order to test the hypothesis that essential gene annotations can be transferred between distantly related organisms, we chose to perform an analysis on a pair of relatively distantly related organisms: E. coli (EC) and A. baylyi (AB). The reasons to select this organism pair are:

1. Essential genes are well-characterized in both organisms. Large-scale gene-knockout experiments have identified 302 (or 7%) essential genes in E. coli K-12 out of a total of 4289 genes (17). In A. baylyi ADP1, from a total of 3308 genes, 499 (or 15%) essential genes have been identified from large-scale gene-knockout experiments (25). Both mutagenesis experiments were performed under aerobic conditions, with the former on standard laboratory rich (LB) media and the latter on minimal medium supplemented with succinate.

2. Both AB and EC are γ-proteobacteria in taxonomy; however, they are not closely related—the time frame of divergence is estimated to be 50–200 myrs (47–48) (Supplementary Figure S3). Because our approach would be most useful if proven applicable to distantly related species, this pair of species provides an excellent testing ground for examining the accuracy and coverage of our approach.

If our hypothesis is true, we rationalize that the genomic features trained and tested using EC essential genes should be able to produce reliable predictions of essential genes in AB, and vice versa. To provide an objective assessment of the accuracy and coverage of the predictions, the known annotations of gene essentiality in the target organism will only be used in the evaluation stage.

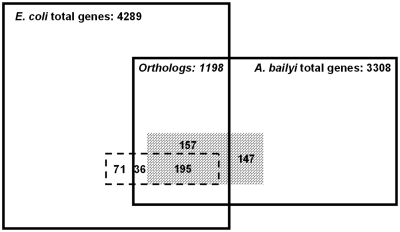
We first used a reciprocal best hit (RBH) method to compare the genomes between the two organisms (see ‘Materials and Methods’ section) (18). Between EC and AB, there are 1198 orthologs. This represents 28 or 36% of the EC or AB genomes, respectively (Figure 1).

Figure 1.

Comparison of genomes and essential genes in EC and AB. The square represents 4289 EC total genes; the rectangle represents 3308 AB total genes. The overlap of the two represents 1198 orthologs determined by the RBH method. The rectangle with dashed border represents the total 302 EC essential genes. The rectangle with diagonal brick shades represents the total 499 AB essential genes. The rectangle within the dashed border and with diagonal brick shades represents the common essential genes in both species. The area of each rectangle is approximately proportional to the number of genes it represents.

We also examined the overlaps between the two essential gene datasets based on identifying orthologs (Figure 1). There are 195 essential genes in common between the EC and AB essential datasets, making up 65 and 39% of the two essential gene sets, respectively. It is clear that both pathogens have a substantial portion of unique essential genes, consistent with a previous report that bacterial species share a limited number of common essential genes (12).

Selecting suitable features for predicting gene essentiality

It is becoming increasingly apparent that genomic sequences represent only one aspect of the complex genetic relationships that have evolved under diverse selection pressures (49); therefore, it is necessary to consider a variety of features, including both intrinsic and context-dependent features. We used three criteria to select the most suitable features.

First, the features should be easily obtained and available to most microorganisms. Intrinsic features can be easily extracted as long as a microorganism has a completely sequenced genome. For context-dependent features, we only considered the gene expression profiles measured by microarray experiments. We did not include functional annotations, pathway or protein–protein interactions (PPIs) in our method because they are often unavailable to under-studied organisms.

Second, the features should have high predictive power of gene essentiality. To quantify the predictive power of each feature, we performed a Naïve Bayes analysis and ranked all features according to the coverage length of log-odds ratio (Supplementary Figure S1).

Third, the features should minimize biological redundancy. Biologically redundant features are often derived from a similar source and have high correlations with each other. For example, CBI has Pearson correlation coefficients of 0.92 and 0.99 with CAI and Fop, respectively (Supplementary Figure S2), because these features are all derived from the codon usage of a gene and have similar biological meanings. Including such redundant features will not only create problems for some types of classifiers, e.g. Naïve Bayes classifier, but also increase the complexity without necessarily increasing the inferential and predictive power of the classifier (Supplementary Table S2).

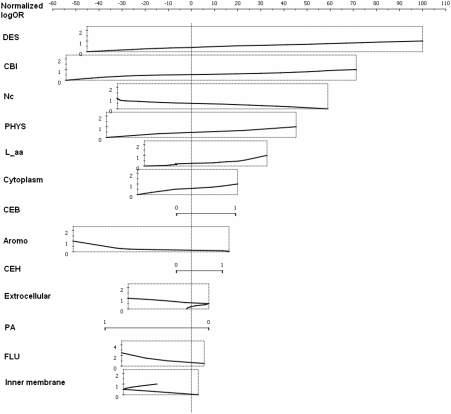
Using the above criteria, among a total of 28 characteristic features that we considered (Supplementary Table S1), we identified 13 of them potentially associated with gene essentiality in EC with relatively weak correlations among themselves (Table 2 and Figure 2). Interestingly, these features represent different aspects from sequence to function. These diverse aspects of the correlated features suggest that gene essentiality is likely determined not solely by the genomic sequence of a gene, but by multiple aspects of biology. Among the 13 features, the strongest turns out to be DES (domain enrichment in essential genes), which has not been considered by previous studies. The next four strongest features are CBI, Nc, PHYS and L_aa, consistent with previous studies (18,21–22) (Table 1).

Figure 2.

The Nomogram for visualization of the 13 selected features. Each feature has a corresponding line indicating the relationship between a feature value and its predictive contribution assessed by Naïve Bayes analysis. The number on the line is the value of the feature and each value corresponds to a point score above. The longer the line is, the more predictive power the feature has in prediction.

Cross-validations of the classifier using E. coli essential gene set

The 13 selected features (Table 2) were then used as input variables for four classifiers: Naïve Bayes, logistical regression, decision tree and CN2 rule. The input of the classifiers contained the features of each gene and the class labels if they were used as the training data. Each classifier scheme independently generated a probability score of gene essentiality. The best performance was obtained by combining the output probability scores of these diverse classifiers using an unweighted approach and hence was used as the final prediction.

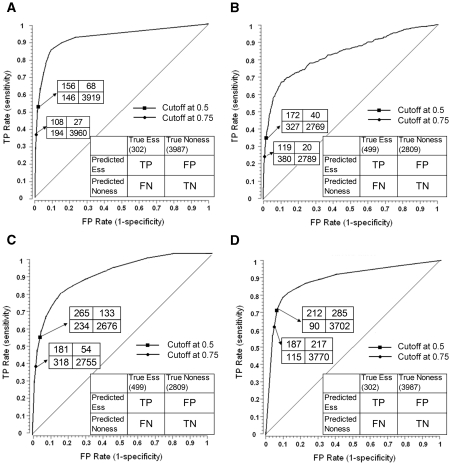
The 10-fold cross-validation result shown in the ROC curve indicated that, at the level of 1% FPR, the classifier achieved 45% TPR (Figure 3A). The area under curve (AUC) score of the classifier is 0.93 and the positive predictive value (PPV or precision) is 0.70 with the probability threshold set at 0.5. Our classifier represented a significant improvement over the classifier that integrates only sequence features in S. cerevisiae (22) (AUC = 0.70). Our results also outperformed a recent study in E. coli by a considerable margin (21) (AUC = 0.70).

Figure 3.

ROC curves plot the TPR versus FPR for different thresholds of classifier probability output. (A) and (B): EC → AB; (C) and (D): AB → EC. (A) Ten-fold cross-validations on the EC essential gene data set. (B) Predictions of AB essential genes. The classifier was trained on EC dataset and evaluated on AB essential genes. (C) Ten-fold cross-validations on the AB essential gene data set. (D) Predictions of EC essential genes. The classifier was trained on AB data set and evaluated on EC essential genes.

Because of the imbalanced training dataset (essential:non-essential = 1:13), to avoid making excessive false positive predictions, a slightly higher cost can be assigned against false positives. This is equivalent to raising the probability threshold for the predictions which yields fewer false positives. At the probability threshold set at 0.75, the precision of our predictions increased 14% to 0.80 (108/135) (Figure 3A).

The control training set was generated by randomly assigning essential labels to all E. coli genes (50). The same number of random ‘essential genes’ was assigned as in the original training and testing sets. The performance of the classifiers on the random set was significantly lower than that using the real training set (Supplementary Figure S4). This suggested that our method was indeed learning the features characteristic to gene essentiality.

Predicting AB essential genes by integrating intrinsic and context-dependent features

After the 10-fold cross-validation on known essential genes in EC, we applied the classifier to predict AB essential genes, denoted as EC → AB.

A. baylyi is a Gram-negative bacterium commonly found in aquatic and soil environments. It belongs to the same class of γ-proteobacteria as EC (Supplementary Figure S3). A set of 499 AB essential genes has been identified by targeted mutagenesis (25). Because the targeted mutagenesis was performed on minimal media, many genes involved in the biosynthesis of essential compounds became essential that are otherwise not required under rich media. This difference in media results in a substantially higher percentage of essential genes in AB (16%) compared to EC (7%).

When applying the classifier across organisms, the distributions of each raw feature were compared first to ensure they are comparable in both organisms. Between a pair of organisms, the same feature can be sufficiently different that they follow completely different distributions even after normalized into the same range (Supplementary Figure S5). We quantified the similarity of two distributions by their overlapping area. Two distributions with an overlapping area >0.5 are considered as similar. As a result, a subset of 10 features (Supplementary Table S2A) that have a similar distribution in EC and AB was compiled for each of the 3308 AB ORFs, and the classifier trained on EC was then applied to this dataset. The accuracy was evaluated by examining the agreement with the assignments from the gene knockout experiments in AB.

At the level of 1% FPR, the result indicated that the classifier achieved a 28% TPR (Figure 3B). The AUC score is 0.80 and PPV is 0.81 at the threshold of 0.5. That is, among the 212 predictions that received the highest scores in AB, about 172 are true essential genes. The prediction accuracy is excellent considering that a random selection of 212 AB genes would contain only 32 essential genes.

We then performed a reciprocal prediction of EC essential genes using the AB essential gene data set, denoted as AB → EC. The prediction yielded a ROC curve with an AUC score of 0.89 and a PPV of 0.43 (Figure 3C and D). We speculated that the lower precision was because the AB data set contained ∼100 genes associated with biosynthesis function (e.g. amino acids, cofactors) that are needed for survival only on minimal media (25). Inclusion in the training set of the genes that are essential only on minimal media may have led our classifier to learn characteristics unique to these genes, thereby resulting in a poorer classification of the ‘true’ essential genes. To test whether a more refined AB training set would lead to increased precision of prediction, we removed 82 genes associated with biosynthesis function from the AB essential gene set. The refined data set achieved a substantially better precision (PPV = 0.53) in predicting EC essential genes, most obvious at their top 10% predictions (Supplementary Figure S6).

Prediction of essential genes between E. coli and P. aeruginosa

To show that the transferability of essential genes is not limited between EC and AB, it is important to extend the analysis to other pairs of organisms. We next conducted predictions between EC and P. aeruginosa PAO1 (PA).

PA is a ubiquitous and opportunistic pathogen capable of causing chronic infection of the lungs of cystic fibrosis patients. It is Gram-negative and belongs to the same class of γ-proteobacteria as EC and AB (Supplementary Figure S3). A set of 678 PA essential genes, or 12% of its total genes, has been identified by transposon mutagenesis (24). Due to the random nature of transposon insertion events, the results of transposon mutagenesis often contain systematic bias. For example, the essential genes determined by transposon mutagenesis contain a disproportionately higher percentage of short proteins because shorter proteins are more likely to be missed by transposons (24,51). Comparison of orthologs and essential genes between EC and PA is shown in (Supplementary Figure S7A).

Using the same feature selection strategy as we employed to predict essential genes between EC and AB, we identified a set of nine features in EC (Supplementary Table S2B). Note that they are different from those used in EC → AB (Supplementary Table S2A). We then used the same method to predict essential genes in PA by learning the features from EC, denoted as EC → PA, and generated a ROC curve with an AUC score of 0.69 and PPV = 0.57 (Supplementary Figure S8A and B). The reciprocal PA 678 → EC prediction showed a similar pattern of decreased accuracy (AUC = 0.79 and PPV = 0.41).

The relatively lower accuracy of transferring essentiality between EC and PA is likely due to the lower quality (i.e. more errors) associated with the essential gene set produced by transposon mutagenesis (52). A subset of 335 genes, consensus of the PAO1 and another Pseudomonas species PA14 essential gene sets (51), is believed to be more accurate. We then trained our classifier on these 335 PA essential genes and predicted those in EC, denoted PA 335 → EC. Training on this refined data set achieved an improved performance over PA 678 → EC (AUC = 0.82 and PPV = 0.47).

Prediction of essential genes between E. coli and B. subtilis

To explore the limit of the transferability, we also attempted to predict essential genes in B. subtilis (BS). Unlike EC, PA and AB, BS is Gram-positive bacteria. The evolutionary distance between EC and BS is substantially farther than the other two species: estimated to be around 3000 myrs (Supplementary Figure S3). Among the 271 essential genes listed in (26), we included 192 that were determined by experimental techniques and disregarded 79 genes that were predicted by homology mapping from other bacteria, mostly E. coli. A comparison of orthologs and essential genes between EC and BS is shown in (Supplementary Figure S7B).

Using the strategy described in previous sections, we applied our methods to transfer essential gene annotations from EC to BS, denoted EC → BS, and compared the predictions with the available known essential gene dataset in BS. The prediction in BS generated a ROC curve with an AUC score of 0.80 and PPV 0.54 (Supplementary Figures S8C and D). Similarly, the reciprocal BS → EC prediction yielded a ROC curve with an AUC score of 0.86 and PPV 0.48.

The results suggest that despite the long evolutionary distance between BS and EC, there are common characteristics underlying EC and BS essential genes represented by features that can still be recognized by our machine learning approach.

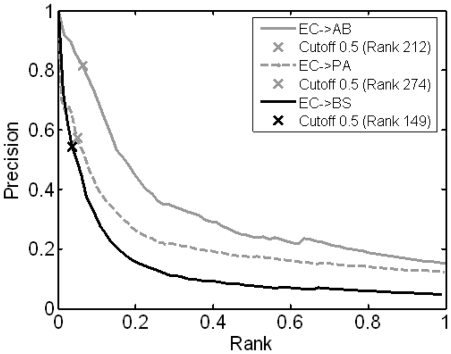
Although an AUC score in an ROC curve provides a useful estimation of the predictive accuracy of our models, it weights the false positive and false-negative errors equally (53). Because the ratio of essential genes in the genome is different among organisms, e.g. 4% in BS and 16% in AB, when evaluating the transferability from EC to the three target organisms, we should not directly compare the AUC scores. In addition, when predicting essential genes in an unstudied organism, precision of the prediction (PPV), or how many genes predicted as essential are indeed essential, is often more useful. Therefore, we plotted the precision of our predictions from EC to the three target organisms (Figure 4). The result clearly indicated that EC→AB achieved the highest precision, while the lower precisions in EC→PA and EC→BS were likely due to the lower quality of the dataset and the greater evolutionary distance as we mentioned in previous sections.

Figure 4.

Precision of predictions from EC to three target organisms. The Precision versus Rank plot for the three pairs of bacteria: EC→AB (Gray solid), EC→PA (Gray dashed) and EC→BS (Black solid). The little cross on the curve represents the precision or PPV with the corresponding probability threshold set at 0.5.

Integrative genomics significantly improves the accuracy and coverage compared with homology mapping

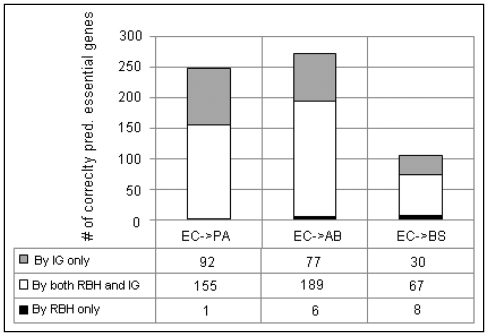
In order to illustrate the substantial improvement in coverage by our method, we first used homology mapping to transfer essential gene annotations from EC to AB. Among the 302 known essential genes in EC, 234 genes could be directly mapped to the AB genes using an RBH approach. Therefore, the corresponding 234 orthologous genes in AB were predicted by RBH to be essential. Among these 234 predictions, 195 were true essential as determined by the AB essential gene dataset (Figure 5). Please note, these 234 orthologs are the maximal number of predictions homology mapping can make, given the definition of orthologs.

Figure 5.

The integrative approach significantly extends the coverage of homology mapping. IG stands for the integrative approach. RBH stands for the reciprocal best hit approach. For the IG method, the cutoffs are set to be the same as the number of essential genes in each organism, i.e. (PA: 678, AB: 499, BS: 192).

We then selected appropriate cutoffs so that our method made the same number of predictions as the number of essential genes in the target organism, i.e. 499 in AB. Compared with homology mapping, among the 195 genes correctly predicted by homology mapping, our approach also predicted 189 (97%) as true essential. On the other hand, our approach predicted 77 unique predictions that could not be made by homology mapping.

We used the following three examples to illustrate the discrepancies between our method and homology mapping (Table 3). For example, ACIAD0822 was determined as essential by both targeted mutagenesis (25) and our prediction. This gene has been annotated with the function of aspartyl/glutamyl-tRNA amidotransferase with no ortholog in EC (54). Its closest homolog in EC is b1394 involved in fatty acid metabolic process (GO:0006631), different from that of ACIAD0822. In addition, b1394 is a non-essential gene. In this case, homology mapping is unable to predict ACIAD0822 as essential. In contrast, the integrated effect of four strong features (PHYS, PA, CAI and Cyto) enabled our method to correctly assign this gene as essential. In another example, ACIAD2634 was determined as essential by both targeted mutagenesis (25) and our prediction. Its closest homology in EC is b2499, a non-essential gene with the same function. In this case, RBH incorrectly predicted it as non-essential. However, the combined influence of DES, PHYS, Nc and CAI allowed our method to successfully override the incorrect assignment by RBH. These two examples highlighted the power of the integrative approach.

Table 3.

Examples of correct and incorrect predictions

The number in the parenthesis indicates the normalized log-odds ratio (points). The larger number indicates a higher correlation with essentiality. Shaded features are those that determine the prediction outcome in each case.

On the other hand, ACIAD2640 was determined as an essential gene by both targeted mutagenesis (25) and the RBH approach, while our method incorrectly predicted it as non-essential. The main reason we failed to predict it as essential is this gene has a paralog in AB, which resulted in a strongly unfavorable PA score. Its predicted subcellular localization further cemented the incorrect assignment.

Our predictions in PA and BS suggested a similar conclusion (Figure 5). The RBH method is sometimes considered too stringent for mapping orthologs (55), because if the forward BLAST yields a paralogous best hit, regardless of whether the reciprocal BLAST corrects the error by recovering an actual ortholog, both pairs will be excluded. Therefore, we also performed homology mapping using COG groups. Using this alternative method of homology mapping did not change our conclusions (Supplementary Figure S9).

A simple way to increase the coverage of homology mapping is to include homologs that are not orthologs by choosing a more relaxed E-value cutoff. By gradually loosening the E-value thresholds, we compared our approach with the RBH method in ROC curves (Supplementary Figure S10). It was clear that our method dominated the RBH method in the entire range of the ROC curves.

DISCUSSIONS

By taking advantage of the abundant genomic sequences and functional genomics data available in four bacterial species, EC, PA, AB and BS, we have developed a machine learning-based approach that predicts essential genes by integrating features potentially associated with gene essentiality in Prokaryotes. Although essential gene data sets are also available in many other genomes (56), most of them were determined by transposon mutagenesis whose results may contain systematic biases (24,52). To strike a balance between comprehensiveness and validity of our analysis, we chose to include all three bacterial species (EC, AB and BS) whose essential gene were determined by targeted mutagenesis, which are considered the highest quality, and the one (PA) whose essential genes were determined by transposon mutagenesis by two independent groups.

Our 10-fold cross-validations in four organisms showed AUC scores ∼0.9, suggesting that gene essentiality, albeit a complex property is highly predictable by learning the characteristics underlying gene essentiality. We believe this is the best cross-validation result in the same organism to date in predicting essential genes. We attributed this significant improvement over previous studies to incorporating both intrinsic and context-dependent features. In particular, we discovered domain enrichment, which has not been considered in previous studies, as the strongest feature.

Our results that protein domain enrichment is a much stronger feature in predicting gene essentiality than orthologs (PHYS) suggests that gene essentiality is likely preserved through the function of protein domains or domain combinations instead of through the conservation of the entire genes. This is unexpected but reasonable because numerous examples can be found in literature that supports this postulation. For example, DNA polymerase III subunits τ and γ domain III (PF12169) (57) only has a single copy in EC, PA and BS. The host gene of this domain, dnaX, is essential in all three species; however, the sequence identity among them is low. To further support the modularity within essential genes, previous studies have discovered that although some genes as a whole are essential, not all domains are required for the essential function. For example, E. coli ftsK (b0890) is an essential gene consisting of two domains: N-terminal (amino acid 1–780) and C-terminal (amino acid 780–1329) domains. Only the N-terminal domain of this gene is required for its role in cell division and viability (58).

Another reason DES is more predictive than orthologs is that protein domains are more transferable between organisms than orthologs. For example, our data showed that EC and PA share <35% of their genes as orthologs, but they share almost 70% of domains. A list of domains that have the highest and lowest DES is given in Supplementary Table S4. Identifying and exploring such domains that are actually responsible for carrying out the essential function, or ‘essential domains’, will greatly improve our understanding of the mechanistic basis of gene essentiality.

Other dominant features besides DES are mostly intrinsic features while the strongest context-dependent feature CEB ranks seventh among the 13 features. This suggests that a gene’s essentiality is primarily determined by its biochemical functions, while whether these functions are essential can also be influenced by the bacteria’s growth conditions. For instance, the rewiring of the gene regulatory networks under different conditions may alter the degree of a gene’s essentiality to the organism. Further investigations on the influence from the context-dependent features may shed light on the conditional gene essentiality.

Most of the errors in our current method are influenced by strong features. For example, false positive predictions often have high Phylogenetic score (PHYS). Although essential genes tend to be more evolutionarily conserved than non-essential genes, less than a quarter of the highly conserved bacterial genes were essential when tested experimentally in model bacteria (9–12). Therefore, assigning an excessive weight on gene conservation will inevitably create false positive errors. On the other hand, false negative errors, i.e. essential genes that were incorrectly predicted as non-essential, are often the result of combined effect of other features failing to override the decisions made by strong features. These errors can be corrected by further studying the role each feature plays in determining essentiality and adjusting their relative weights.

Our study is also significant in that this is the first report that gene essentiality can be reliably transferred between distantly related organisms using a machine learning-based approach. When using our method to transfer essentiality between distantly related organisms, the accuracy of predicting essential genes can be affected by the following four factors:

First, the essential gene data set on which the classifiers are trained should be of high quality. Errors in the training dataset will significantly reduce the accuracy of predictions, as we observed in PA → EC.

Second, the essentiality should be transferred under the same or highly similar growth conditions. Gene essentiality is likely a contextual property (49). Organisms are likely to use different sets of essential genes under different conditions. Predicting essential genes under different conditions than those of the training set will likely result in decreased predictive accuracy, as we observed between EC and AB. However, a recent study on E. coli conditional essential genes showed that <20% of the total essential genes are different between glycolysis and glucose metabolisms (59). Therefore, our algorithm will still be useful in capturing the majority of the essential genes in the target organism even when the growth conditions are different, although the best performance will be achieved under the same or highly similar growth conditions.

Third, the evolutionary distance seems to play an important role in the accuracy of predictions. It is encouraging to see that the classifier can transfer gene essentiality between Gram-negative and Gram-positive bacteria, although the accuracy of transferring is lower than between gram-negative bacteria. An interesting future direction would be to investigate further to what extent our method can be applicable. For example, to what extent can essential genes be transferred between Prokaryotes and Eukaryotes?

Fourth, the prediction also depends on the availability of features with a similar distribution between organisms. To be useful in the prediction, the features have to have a similar distribution in both organisms in order to allow accurate training and testing (Supplementary Figure S5).

The comparison between our method and homology mapping highlights the limitations of homology mapping. Homology mapping is most useful in closely related organisms, such as S. cerevisiae and S. mikatae (22). However, in more divergent organisms, it is severely limited by the number of conserved orthologs. In contrast, our approach does not have this limitation because the prediction is based on the features that can be computed for all genes; therefore, it can easily explore the gene space for which homology mapping is inapplicable of.

Another advantage is that because our approach can incorporate organism-specific and context-dependent features, e.g. gene expression or the number of paralogs in the target organism, it can potentially identify in one organism essential genes whose orthologs are non-essential in other organisms, e.g. ACIAD2634 in Table 3.

Our method can be easily extended to predict essential genes in an unstudied organism. The genomic sequences of the genes and functional genomics data from microarray gene-expression analysis are often available in an organism before the whole-genome mutagenesis experiments are carried out. As a result, the essentiality prediction could be done prior to a costly whole-genome screening using mutagenesis experiments.

In summary, by integrating features available to all genes, our method provides a valuable alternative for predicting essential genes beyond orthologs. The application of our approach to bacterial species has tremendous potential to significantly improve our ability to re-engineer microorganisms as well as to respond to many emergency situations, such as bioterrorist attack or bioremediation of oil-spilled Gulf regions. Although our research was performed in Prokaryotes, where the highest quality essential gene datasets are available, the conclusions drawn from this study are expected to be also valid in other domains of life.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Cincinnati Children's Hospital Medical Center (CCHMC) Trustee Grant awarded (to L.J.L.); National Institutes of Health grant GM69845 (to D.J.H.). Funding for open access charge: CCHMC Trustee Grant.

Conflict of interest statement. None declared.