Predicting translational diffusion of evolutionary conserved RNA structures by the nucleotide number

Abstract

Ribonucleic acids are highly conserved essential parts of cellular life. RNA function is determined to a large extent by its hydrodynamic behaviour. The presented study proposes a strategy to predict the hydrodynamic behaviour of RNA single strands on the basis of the polymer size. By atom-level shell-modelling of high-resolution structures, hydrodynamic radius and diffusion coefficient of evolutionary conserved RNA single strands (ssRNA) were calculated. The diffusion coefficients D of 17–174 nucleotides (nt) containing ssRNA depended on the number of nucleotides N with D = 4.56 × 10⁻¹⁰ N^−0.39 m² s⁻¹. The hydrodynamic radius R_H depended on N with R_H = 5.00 × 10⁻¹⁰ N^0.38 m. An average ratio of the radius of gyration and the hydrodynamic radius of 0.98 ± 0.08 was calculated in solution. The empirical law was tested by in solution measured hydrodynamic radii and radii of gyration and was found to be highly consistent with experimental data of evolutionary conserved ssRNA. Furthermore, the hydrodynamic behaviour of several evolutionary unevolved ribonucleic acids could be predicted. Based on atom-level shell-modelling of high-resolution structures and experimental hydrodynamic data, empirical models are proposed, which enable to predict the translational diffusion coefficient and molecular size of short RNA single strands solely on the basis of the polymer size.

INTRODUCTION

Ribonucleic acids are evolutionary conserved essential parts of cellular life, most prominently represented by messenger RNA (mRNA). While the biological function of mRNA is mainly determined by its nucleotide sequence, ribozymatic activity of rRNA and transcriptional or translational regulation by riboswitches (1), miRNAs (2) or internal ribosome entry sites (IRESs) (3) depend on the molecular structure. Insights into structural principles of ribonucleic acids have been gained by X-ray crystallographic studies of evolutionary conserved RNA. Although crystal structures represent static views, they allow to draw conclusions to the hydrodynamic behaviour, which inherently determines life processes (4).

By studying hydrodynamics, free two- or three-dimensional diffusion, active transport and anomalous diffusion can be distinguished from each other. Prominent methods to characterize translational diffusion are fluorescence correlation spectroscopy (FCS) (5,6) and dynamic light scattering (DLS) (7,8). These methods also allow monitoring and quantifying molecular interaction under physiological conditions. DLS does not require labelling of the molecule. Micro- to millimolar concentrations are necessary to achieve an appropriate signal-to-noise ratio. The optimum concentration range for FCS is nano- to micromolar, mimicking physiological concentrations and minimizing sample amounts. These methods have been applied on the characterization of ribonucleic acids in vitro (9,10).

By FCS, hydrodynamics of fluorescence-labelled single molecules can be studied in vivo, enabling to gain realistic knowledge about live processes. The potential of the method has been demonstrated when characterizing the mechanism of nuclear RNA-induced silencing complex formation in living cells (11).

In vivo, RNA single strands are found almost exclusively as part of RNA–protein complexes (RNP) (12). However, to design experiments or to interpret hydrodynamic data, predictions about the hydrodynamic behaviour of isolated RNA single strands (ssRNA) are useful.

The compared to ssRNA high number of experimental studies of proteins and double stranded nucleic acids allowed to develop hydrodynamic models for these molecule species. Assuming short dsDNA molecules to be cylinders (13) and globular proteins to be spheres (4,14,15), translational diffusion velocity can be approximated solely based on the number of base pairs or amino acids, respectively. Because of its complex and heterogeneous structure, which limits the number of crystallographic studies, no analogue strategy has been published so far for ssRNA (16,17). In the presented work, the question is addressed, how ssRNA translational diffusion depends on the polymer length.

Predictions by using models, which simplify the molecular shape to rigid geometric bodies, may largely deviate from experimental data. The largest coincidence between theoretical and experimental data can be reached, when structural information about the molecule is included in the model (18). Ellipsoids introduce the ratio of perpendicular axes into the prediction (19). They enable a significant higher accuracy in the description of the translational diffusion of proteins. A more pronounced reference to structural information is enabled by bead- or shell-modelling, therefore reaching higher degrees of coincidence with the experimentally determined shape of the molecule (20–22). As proposed by José García de la Torre, atom-level resolution can be reached by representing the hydration shells of single non-hydrogen atoms as overlapping beads. Applying the software HYDROPRO, which was developed for this approach, the diffusion coefficients or molecular sizes of the 76 nucleotides (nt) Saccharomyces cerevisiae tRNA^Phe (23), the 85 nt hepatitis delta virus self-cleaving ribozyme (HDV) and the 160 nt P4–P6 domain of the Tetrahymena thermophila group I self-splicing intron (24) could be predicted accurately.

High-resolution structures are not always available. Referring to the growing number of X-ray crystallographic data of RNA, the purpose of the presented study is to define by atom-level shell-modelling of a large number of crystal structures an empirical model, which enables to predict the diffusional behaviour of ssRNA solely based on the number of nucleotides.

In the presented work, atom-level shell-modelling is applied to high-resolution structural data of naturally occurring evolutionary conserved RNA single strands. The dependence of the translational diffusion coefficients and hydrodynamic radii on the number of nucleotides is investigated and its validity tested by a comparison with experimental data.

MATERIALS AND METHODS

Atom-level shell-modelling was carried out by applying the software HYDROPRO (20). The radius of the atomic elements was defined to be 2.8 Å and the partial specific volume to be 0.55 cm³ g⁻¹ (23). It should be noted, that the atomic hydrodynamic radius, applied for globular proteins, is usually 3.4 Å. In addition, the radius of the mini beads was set to −1, letting the program estimate SIGMIN and SIGMAX. The temperature was defined to be 293 K.

Translational diffusion of short dsDNA molecules can be predicted by using a model for cylinders (13,23). Double stranded RNA forms an A-form α-helix (25,26). The model for dsDNA is transferred to dsRNA by setting the width of an A-form α-helix to 26 Å (27) and the internucleotide distance to 2.9 Å nt⁻¹ (26). The parameter A describes the ratio between the length L and the width d of a molecule with 2 < L/d < 30 (dsRNA: 40 < nt < 550 or 20 < base pairs < 275) using

(1)

By a modified Stokes–Einstein equation, the translational diffusion coefficient D of dsRNA is calculated using

(2)

with the Boltzmann constant k (1.38 × 10⁻²³ kg m² s⁻² K⁻¹), the viscosity η (1.002 × 10⁻³ kg m⁻¹ s⁻¹) and the temperature T (295 K).

Translational diffusion of globular molecules was predicted by assuming the shape of a sphere with the molecular mass m of 309 g mol⁻¹ per nucleotide, the volumic mass ρ of 1.8 g cm⁻³ (28) and the Avogadro constant N_A of 6.023 × 10²³ mol⁻¹ using (29,30)

(3)

Applying the Stokes–Einstein equation, the hydrodynamic radius R_H was transformed into

(4)

Assuming in a simplification RNA to be a homopolymer, which consist of equally sized and freely rotating rigid units, the dependence of D on the unit number N can be described, in reference to J.P. Flory (14,15), using

(5)

and for R_H and the radius of gyration R_G by

(6)

RESULTS AND DISCUSSION

Diffusion coefficients and hydrodynamic radii, determined by shell-modelling of high-resolution ssRNA structures

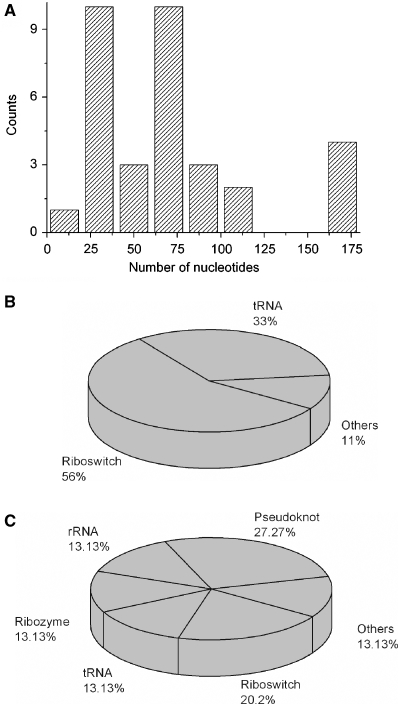
Protein Data Bank (PDB) files (31), resulting from a search of the criteria (i) exclusion of DNA and protein, (ii) a single chain containing biological assembly and (iii) a single chain containing asymmetric unit, were chosen for shell-modelling. To truly refer to the structural properties of naturally occurring RNA, mutated variants were excluded from the study. Hydrodynamic data were calculated for the selected ∼70 PDB files using the software HYDROPRO as described in the ‘Materials and Methods’ section. Predicted translational diffusion coefficients and hydrodynamic radii are summarized in Supplementary Data, Table S1. To balance the contribution of the different polymer sizes, diffusion coefficients of structures of the same species were averaged. Different crystallization conditions or phylogenetic origins led to an average standard deviation of 0.6% in the predicted values; influencing translational diffusion only to a minor extent (Supplementary Data, Table S2). The polymer sizes of the RNA species are shown in Figure 1A. The largest number of high-resolution structures ranged between 25 and 75 nt. Full-length structures and truncated sequences contributed equally to the 33 RNA species. Three-quarters of the truncated sequences consisted of <50 nt.

Figure 1.

Oligonucleotide size distribution and biological origin of structural data. (A) The nucleotide distribution of the investigated 33 ssRNA molecule species are represented as histogram with a bin width of 20 nt. (B and C) The biological origin of the full-length RNA (B) and truncated ssRNA (C) is represented as histogram.

The biological origin of the oligonucleotides is presented in Figure 1B and C. Fifty-six percent of all full-length molecule species originated from riboswitches and 33% from tRNAs (Figure 1B). Twenty percent of the truncated sequences originated from riboswitches and 13% from rRNAs, ribozymes or tRNAs, respectively (Figure 1C). The oligonucleotides represented highly conserved RNA species with very different functions, e.g. being scaffolding molecule, molecular sensor or chemical catalyst. Due to the high fraction of 27% of the tertiary structural motif of pseudoknots, pseudoknots were defined as an additional category for truncated sequences.

Dependence of predicted ssRNA diffusion coefficients and molecular sizes on the nucleotide number

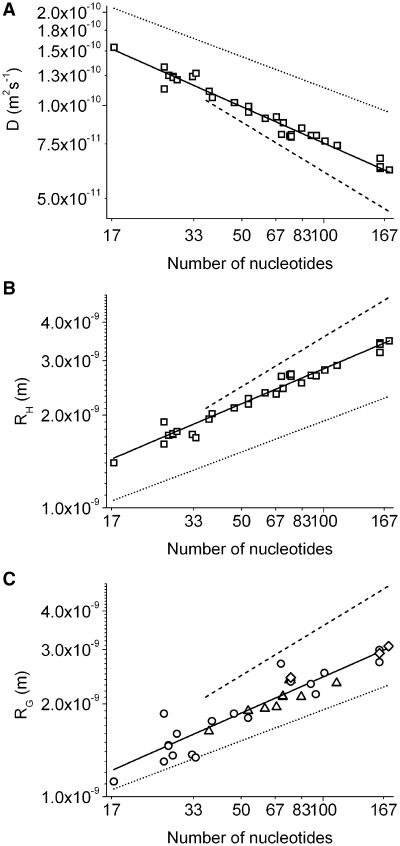
To investigate the dependence of the translational diffusion on the length of the polymer, the predicted diffusion coefficients were plotted against the nucleotide number N (Figure 2A). In the following, the diffusion coefficients were compared with two models for rigid bodies. In highly structured ssRNA, 79% of nucleotides have been found to form Watson–Crick base pairs (32). Furthermore, double helices are prominent parts of ssRNA folding. On the common phenomenon of self-dimerization (33,34) was referred to, when predicting the hydrodynamic behaviour by a cylindrical model [Figure 2 dashed line; please also see ‘Materials and Methods’ Equations (1) and (2)]. To represent a maximally compact conformation a spherical model was included into Figure 2 [dotted line; Equations (3) and (4)]. All diffusion coefficients predicted by shell-modelling were larger than the values, determined by the cylindrical model and smaller than the values, determined by the spherical model.

Figure 2.

Translational diffusion coefficient, hydrodynamic radius and radius of gyration of evolutionary conserved RNA single strands, determined by shell-modelling of high-resolution structures. The diffusion coefficient D, the hydrodynamic radius R_H and the radius of gyration R_G were logarithmically plotted against the number of nucleotides N. Models for rigid spheres, representing maximum compact conformation, and cylinders, assuming self-dimerization, are compared with predicted values. A comparison of different models is facilitated by representing the number of base pairs as (doubled) nucleotide number for the cylindrical model. (A) The dependence of D on N was fitted to Equation (5), D = a N^−v. The cylindrical model revealed a = 7.17 × 10⁻¹⁰ and v = 0.54 (dashed line), the spherical model a = 5.30 × 10⁻¹⁰ and v = 0.33 (dotted line). The by shell-modelling predicted translational diffusion coefficients of monomeric ssRNAs of 17–174 nt are shown as open squares. A fit to Equation (5) revealed a = (4.58 ± 0.25) 10⁻¹⁰ and v = 0.39 ± 0.01 (R²= 0.96, reduced Χ²= 2.2 × 10⁻²³; solid line). (B) The dependence of the hydrodynamic radius R_H on N was described by Equation (6), R_H/G = a N^v, represented analogously to (A). The cylindrical model revealed a = 3.05 × 10⁻¹⁰ and v = 0.54, the spherical model a = 4.12 × 10⁻¹⁰ and v = 0.33. The predicted hydrodynamic radii were fit in dependence on N with a = (5.00 ± 0.28) 10⁻¹⁰ and v = 0.38 ± 0.01 (R²= 0.97, reduced Χ²= 1.1 × 10^-20). (C) Radii of gyration R_G of unbound state (circles), ligand-bound state (triangles) and average R_G of bound and unbound state (rhombes). The dependence of R_G on N was determined by Equation (6) with a = (4.06 ± 0.47) 10⁻¹⁰ and v = 0.39 ± 0.03 (R²= 0.87, reduced Χ²= 3.5 × 10⁻²⁰).

The dependence of hydrodynamic parameters on the number of nucleotides was described by Flory’s law (please see ‘Materials and Methods’ section). The fit to the power law revealed for dsRNA an exponent of 0.54 [Equation (5); Figure 2A], which corresponds with a previously experimentally determined value of 0.57 for 5–100 nt containing dsDNA (35). The hydrodynamic behaviour of a sphere is defined by an exponent of 0.33. Predicted diffusion coefficients showed a well-defined dependency on the number of nucleotides, which allowed highly accurate fits to a power law. The diffusion coefficients of evolutionary conserved ssRNA depended on N with D = (4.58 ± 0.25) 10⁻¹⁰ N^{(−0.39 ± 0.01)} m² s⁻¹ [Equation (5); Figure 2A]. The exponent 0.39 represented an intermediate value between the exponents of the rigid models, 0.33 and 0.54, biased towards the spherical model.

The hydrodynamic radii of ssRNA, predicted by applying HYDROPRO, depended on the nucleotide number with R_H = (5.00 ± 0.28) 10⁻¹⁰ N^{(0.38 ± 0.01)} m (Figure 2B). The spherical model defined minimum molecular sizes, resulting from maximum compaction. The hydrodynamic radii of the cylindrical model were larger than the predicted data, but allowed a more accurate approximation of the absolute molecular sizes than the spherical model. The exponent 0.33 resulting from fitting the data of the spherical model to a power law, equalled that of the by shell-modelling predicted value 0.38 to a larger extent than the exponent 0.54, which has been determined for the cylindrical model.

Hydrodynamic data of truncated sequences, representing the oligonucleotide lengths of 17 to 50 nt, and full length sequences, dominating the oligonucleotide lengths of 50–174 nt, did not show systematic deviations in their dependence on N. Therefore, it seemed not to be necessary to differ between the hydrodynamic behaviour of tertiary structural motifs and full-length oligonucleotides.

The radius of gyration depended on N with R_G = (4.06 ± 0.47) 10⁻¹⁰ N^{(0.38 ± 0.03)} m (Figure 2C). This result corresponds with a previously described compact conformation of short ssRNA (36). In a recent study, which investigated crystal structures of monomeric RNA single strands of up to 160 nt, a nearly identical model was determined with R_G = 3.8 × 10⁻¹⁰ N^0.41 m (37).

In solution measured hydrodynamic radii and radii of gyration of evolutionary conserved ssRNA

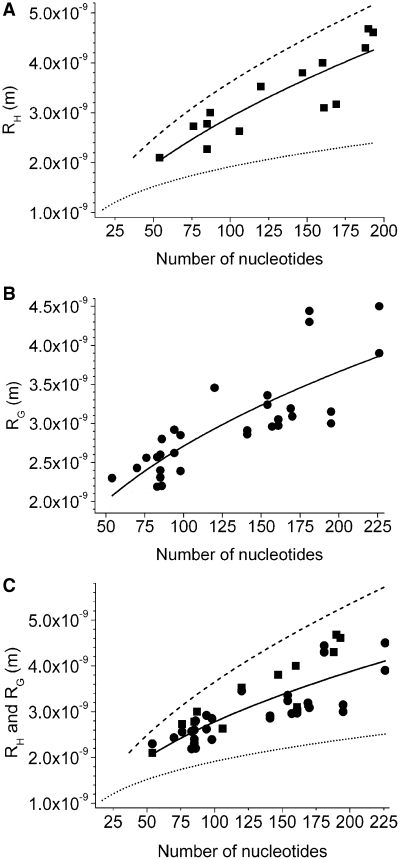
Several in solution measured hydrodynamic radii of the evolutionary conserved structures riboswitches, ribozymes, tRNA, rRNA, IRES and aptamers have been published (Table 1). The hydrodynamic data originate from analytical ultracentrifugation (AUC), DLS and FCS. The fit of 14 hydrodynamic radii of ssRNA of 54–193 nt to Equation (6) in dependence on N revealed R_H = (2.05 ± 0.10) 10⁻¹⁰ N^{(0.58 ± 0.10)} m (Figure 3A, Table 3, R²= 0.75).

Table 1.

Experimentally in solution determined hydrodynamic radii of evolutionary conserved RNA and their deviation from the hydrodynamic crystal-structure-based model

Molecule	Citation	Method	nt	RH_exp (10−9 m)	Deviation from RH_pred (%)
Sulforhodamine B binding aptamer	(10)	FCS	54	2.10	8
S. cerevisiae tRNAPhe	(24)	AUC	76	2.67	–3
S. cerevisiae tRNAPhe	(44)	DLS	76	2.73	–5
S. cerevisiae tRNAPhe	(45)	GF	76	2.80	–7
tRNAPhe average (SD)			76	2.73 (0.07)	–5
Hepatites delta virus	(24)	AUC	85	2.78	–3
Turnip yellow mosaic virus tRNA-like structure	(46)	AUC	85	2.27	19
Class III self-ligating ribozyme	(24)	AUC	87	3.00	−9
Tobacco mosaic virus tRNA-like structure	(46)	AUC	106	2.63	12
X. laevis 5S rRNA	(47)	AUC	120	3.5	–12
E. coli 5S rRNA	(48)	DLS	120	3.60	–14
E. coli 5S rRNA	(49)	DLS	120	3.4	–9
Rat liver 5S rRNA	(49)	DLS	120	3.6	–14
5S rRNA average (SD)			120	3.53 (0.10)	–13
P. stali intestinal virus IRES Δregion 3	(50)	AUC	147	3.80	–12
T. thermophila P4-P6	(24)	AUC	160	4.00	14
B. subtilis mgtE 5′ UTR sequence	(51)	AUC	161	3.1	11
Brome mosaic virus tRNA like structures	(46)	AUC	169	3.17	11
P. stali intestinal virus IRES	(50)	AUC	188	4.30
Dicistroviridae intergenic region IRES	(50)	AUC	190	4.68
Himetobi P virus intergenic region IRES	(50)	AUC	193	4.61

Hydrodynamic radii were measured by analytical ultracentrifugation (AUC), dynamic light scattering (DLS), gel filtration (GF) or fluorescence correlation spectroscopy (FCS). Literature values which approximate a MgCl₂ concentration of 5 mM were chosen.

Figure 3.

Molecular sizes of RNA of evolutionary conserved structure, determined in solution experiments. Spherical and cylindrical models are shown in analogy to Figure 2 in a linear representation. Experimental solution data are represented by filled symbols and their fit to Equation 6, R_H/G = a N^v, as solid lines. (A) The fit of hydrodynamic radii of ssRNA of 54–193 nt revealed a = (2.05 ± 0.10) 10⁻¹⁰ and v = 0.58 ± 0.10 (R²= 0.75, reduced Χ²= 1.8 × 10⁻¹⁹). (B) The fit of the in solution measured radii of gyration of ssRNA of 54–226 nt revealed a = (3.67 ± 1.08) 10⁻¹⁰ and v = 0.43 ± 0.06 (R²= 0.64, reduced Χ²= 1.4 × 10⁻²⁰). (C) The fit of hydrodynamic radii and radii of gyration of 54–226 nt revealed a = (3.05 ± 0.84) 10⁻¹⁰ and v = 0.48 ± 0.06 (R²= 0.64, reduced Χ²= 1.8 × 10⁻¹⁹).

Table 3.

Molecular size and hydrodynamic parameters of monomeric single stranded RNA in dependence on the nucleotide number

Parameter	Method	N	Data sets	R2	Dependence on N
D	Crystal	17–174	33	0.96	(4.58 ± 0.25) 10−10 N(–0.39 ± 0.01)
RH	Crystal	17–174	33	0.97	(5.00 ± 0.28) 10−10 N(0.38 ± 0.01)
RH	Solution	54–169	11	0.58	(4.11 ± 2.26) 10−10 N(0.42 ± 0.12)
RH	Solution	54–193	14	0.75	(2.05 ± 0.10) 10−10N(0.58 ± 0.10)
RG	Crystal	17–174	33	0.87	(4.06 ± 0.47) 10−10 N(0.38 ± 0.03)
RG	Solution	54–170	26	0.61	(5.35 ± 1.44) 10−10 N(0.35 ± 0.06)
RG	Solution	54–226	31	0.64	(3.67 ± 1.08) 10−10 N(0.43 ± 0.06)
RG + RH	Solution	54–170	37	0.57	(4.86 ± 1.27) 10−10 N(0.38 ± 0.05)
RG + RH	Solution	54–226	45	0.64	(3.05 ± 0.84) 10−10 N(0.48 ± 0.05)

The dependence of the molecular size and hydrodynamic parameters of monomeric single stranded RNA on the nucleotide number N was determined based on atom-level shell-modelling of high-resolution structures (Crystal) or in solution experiments (Solution).

Molecular size and diffusion coefficient are related by the Stokes–Einstein equation. Applying Equation (4) it is, therefore, possible to calculate by the model for R_H expected diffusion coefficients. Although, the correlation coefficient of 0.75 was relatively high, it has to be taken into account that the number of experimentally determined hydrodynamic radii is with 14 very small and limits the accuracy of the fit.

One frequently applied method to receive structural information from solution measurements is small angle X-ray scattering (SAXS). The by SAXS available radius of gyration R_G describes the mass distribution of a macromolecule about its centre of gravity. It provides a measure for the molecular size. In addition, its ratio to the hydrodynamic radius is a measure for the shape of a molecule. Thirty-one published radii of gyration of 54 to 226 nt containing ssRNA depended on N with R_G = (3.67 ± 1.08) 10⁻¹⁰ N^{(0.43 ± 0.06)} m (Figure 3B, Tables 2 and 3).

Table 2.

Experimentally in solution determined radii of gyration of evolutionary conserved RNA and their deviation from the hydrodynamic crystal-structure-based model

Molecule	Citation	nt	RG_exp (10−9 m)	SD (%)	Deviation from RH_pred (%)
Sulforhodamine B binding aptamer	(10)	54	2.3		−1
Yeast tRNAPhe	(46)*	70	2.43		3
Yeast tRNAPhe	(46)	76	2.56		1
E. coli tRNAPhe	(52)	76	2.56		1
E. coli thiM thiamin pyrophosphate riboswitch	(53)	83	2.19/2.57	10	22/4
Adenine-dependent hairpin ribozyme	(33)	85	2.4/2.6	6	11/4
Turnip yellow mosaic virus tRNA-like structures	(46)	85	2.31		14
A. thaliana thiamine pyrophosphate riboswitch	(54)	86	2.2/2.8	19	23/–3
T. tengcongensis SAM-I riboswitch aptamer domain	(53)	94	2.62/2.92	7	7/–4
V. cholerae cyclic diguanylate riboswitch	(55)	98	2.39/2.85	14	0/19
X. laevis 5S rRNA	(47)	120	3.6		−14
Th. flavus 5S rRNA	(56)	120	3.44		−10
E. coli 5S rRNA	(57)	120	3.61		−15
E. coli 5S rRNA	(49)	120	3.27		−6
Rat liver 5S rRNA	(49)	120	3.31		−7
5S rRNA average (SD)		120	3.46 (0.16)		−17
B. subtilis ribD flavin mononucleotide riboswitch	(53)	141	2.86/2.91	1	15/13
B. subtilis S-domain RNA	(58)	154	3.24		5
E. coli S-domain RNA	(58)	154	3.36		1
T. thermophila P4–P6	(59)*	157	2.96		14
T. maritima lysine riboswitch	(60)*	161	2.97/3.05	2	16/13
Brome Mosaic virus tRNA-like structure	(46)	169	3.19		10
Brome Mosaic virus tRNA-like structure	(46)*	170	3.09		14
B. subtilis lysC lysine riboswitch	(53)	181	4.30/4.44	2
Azoarcus group I ribozyme	(61)	195	3.15
Azoarcus group I ribozyme	(62).	195	3.00
V. cholera glycine riboswitch	(63)	226	3.9/4.5	9

Radii of gyration were measured by small angle X-ray scattering.

In the references (34,48), neutron scattering was applied.

Literature values which approximate a MgCl₂ concentration of 5 mM were chosen.

Two values refer to the ligand-bound and unbound state.

The stars mark the database Bioisis of J. Tainer and G. Hura (http://www.bioisis.net).

In the following the ratio of R_G and R_H was investigated. Hydrodynamic radii and radii of gyration of the 54 nt Sulforhodamine B binding aptamer RNA, the 76 nt tRNA^Phe, the 85 nt Turnip yellow mosaic virus tRNA-like structure, the 120 nt 5S rRNA, the 160 nt P4–P6 domain of the T. thermophila group I self-splicing intron and the 169 nt Brome mosaic virus tRNA-like structure coincided to a high extent (Tables 1 and 2). An average value R_G/R_H = 0.98 ± 0.08 was calculated. A significant deviation from the theoretical R_G/R_H 0.78 of a sphere and 1.30 of a flexible Gaussian chain was observed (38). This result is in correspondence to crystal structures previously determined compact prolate shape of ssRNA (36). Referring to the numerical similarity of R_G and R_H, the dependency of the molecular size in solution on N was determined to be (3.05 ± 0.84) 10⁻¹⁰ N^{(0.48 ± 0.05)} (Figure 3C, Table 3).

Comparison of in solution measured radii of gyration and hydrodynamic radii with from crystal structures predicted values

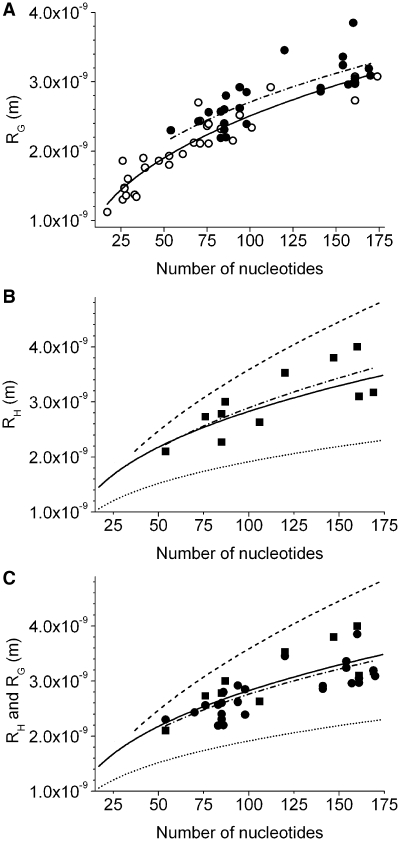
Conformations might differ in crystals and in solution, e.g. as has been observed for the four stranded G-quadruplex (39). In crystal structures, certain conformations might dominate, while heterogeneous conformations are enabled in solution experiments. To estimate the extent, to which molecular sizes in solution and in crystals might deviate, from crystal structures calculated radii of gyration were compared with in solution determined radii of gyration of evolutionary conserved RNA structures (Tables 1 and 2, Figure 4A). In solution measured radii of gyration of 54–170 nt containing oligonucleotides depended on N with R_G = (3.19 ± 0.93) 10⁻¹⁰ N^{(0.47 ± 0.06)} m. Although the radii of gyration calculated from crystal structures showed a comparable dependency on N with (4.06 ± 0.47) 10⁻¹⁰ N^{(0.38 ± 0.03)}, a slightly more extended conformation was found in solution (Table 3). Comparable observations have been made in several multidomain protein studies (40).

Figure 4.

Comparison of molecular sizes of RNA of evolutionary conserved structure, determined in solution experiments, with by shell-modeling of crystal structures predicted values. Spherical, cylindrical and empirical models are shown in analogy to Figure 2 in a linear representation. Solution data are represented by filled symbols and their fit to Equation (6,) R_H/G = a N^v, by a dashed-dotted line. (A) The fit of in solution measured radii of gyration R_G revealed a = (5.35 ± 1.44) 10⁻¹⁰ and v = 0.35 ± 0.06 (R²= 0.61, reduced Χ²= 6.8 × 10⁻²⁰). (B) The fit of in solution measured hydrodynamic radii R_H revealed a = (4.11 ± 2.26) 10⁻¹⁰ and v = 0.42 ± 0.12 (R²= 0.58, reduced Χ²= 1.5 × 10⁻¹⁹). (C) Comparison of in solution measured R_G and R_H with the hydrodynamic empirical model. The fit of R_G and R_H revealed a = (4.86 ± 1.27) 10⁻¹⁰ and v = 0.38 ± 0.05 (R²= 0.57, reduced Χ²= 9.8 × 10⁻²⁰).

Considering the influence of ligand interaction on the molecular size, a relative high responsiveness was found in solution experiments. The standard deviations of the radii of gyration of bound and unbound species were in solution in average 8% (Table 2). Only in a small number of high-resolution studies it was possible to compare the molecular sizes of unbound and bound state, giving a standard deviation of 1% (Figure 2C, routes, Supplementary Data, Table S2). Both species were equally represented in the 33 crystal structure data sets and showed no significant difference in their dependency on N (Figure 2C, circles and triangles).

Despite deviations between conformations in solution and in their crystallized form, it has been demonstrated, that the knowledge of high-resolution structures enables to approximate the hydrodynamic behaviour (20). To test, if the empirical model, which bases on atom-level shell-modelling of high-resolution structures, precisely predicts translational diffusion, hydrodynamic radii of RNA of published hydrodynamic behaviour were calculated depending on the oligonucleotide length (Table 1). The empirical model allowed approximating the hydrodynamic behaviour with an average deviation of 9%. The fit of hydrodynamic radii of 54–170 nt ssRNA revealed R_H = (4.11 ± 2.26) 10⁻¹⁰ N^{(0.42 ± 0.12)} m (Figure 4B), which is in the range of the from crystal structures determined model R_H = (5.00 ± 0.28) 10⁻¹⁰ N^{(0.38 ± 0.01)} m (Table 3). Comparable to the hydrodynamic data, the radii of gyration differed from the by the hydrodynamic structure-based model predicted values in average with 11% and revealed with (5.35 ± 1.44) 10⁻¹⁰ N^{(0.35 ± 0.06)} m a fit result in the range of the shell-modelling-based law (Tables 1 and 3). A large difference between the exponents of the power laws for R_H and R_G determined for up to 170 and 220 nt containing ssRNA is obvious (please see Table 3). This observation could be explained by a tendency to more extended conformations at larger oligonucleotide sizes.

To further validate the high-resolution structure-based model, the in solution determined hydrodynamic radii and radii of gyration of 54–170 nt were fitted to Flory’s law. The molecular size depended on N with (4.86 ± 1.27) 10⁻¹⁰ N^{(0.38 ± 0.05)} m (Figure 4C, Table 3). The power laws, determined from 37 solution experiment and 33 high-resolution structure data sets, corresponded to a very high extent. It was concluded, that the by atom-level shell-modelling of crystal structures determined empirical model approximates the hydrodynamic behaviour of ssRNA with very high accuracy.

In solution measured hydrodynamic radii of ssRNA of arbitrary sequences

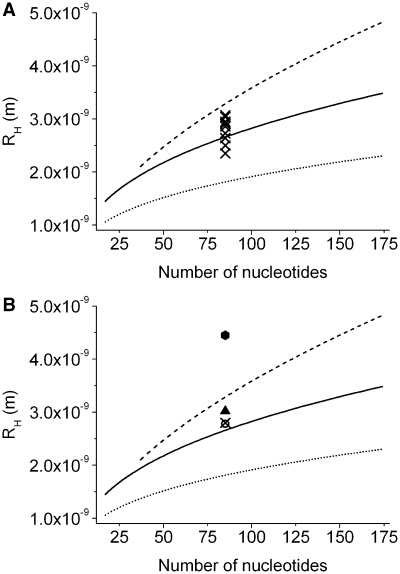
Not in its three-dimensional structure conserved RNA might adopt less compact conformations, as has been shown by secondary structure analysis of large viral RNA and randomly permuted sequences (41). By analytical ultracentrifugation it has been shown, that randomly generated 85 nt containing oligonucleotides form structures of similar compactness as naturally selected RNA (24). The experimental results of the cited study allowed to test the validity of the empirical model on arbitrary, evolutionary unevolved sequences. In the presented study, the values, which were predicted by the empirical model, were compared with the experimentally determined hydrodynamic radii of 10 randomly permuted 85-nt sequences, which equal in nucleotide base composition and length HDV. An average deviation of 8% was found, which was even smaller than the average deviation of the experimentally determined data of evolutionary conserved RNA structures (Figure 5A, crosses; Supplementary Data, Table S3). The hydrodynamic radii of the transcripts of 10 isoheteropolymers of 85 nt (24) deviated from the empirical model in average with 11% to a larger extent.

Figure 5.

Molecular sizes of RNA of arbitrary sequences, determined in solution experiments. Spherical, cylindrical and the by shell-modelling determined empirical model of evolutionary conserved ssRNA are shown in analogy to Figure 2B in a linear representation. (A) Hydrodynamic radii of 10 randomly permuted sequences of HDV (crosses; Supplementary Data, Table S3). (B) Hydrodynamic radius of HDV (open square), Poly(U)₈₅ (hexagon) and the average value of 10 isoheteropolymers of 85 nt (triangle) and of 10 randomly permuted sequences of HDV (cross) (please see also Supplementary Data, Table S3).

The hydrodynamic radius of HDV of 2.78 nm was nearly identical to the average hydrodynamic radius of 2.80 nm of the transcripts of randomly permuted sequences (please see also Figure 5B). Differences in sequence, therefore, do not seem to lead to systematic deviations in the hydrodynamic behaviour. In contrast, the average molecular size of the isoheteropolymer, which differed in sequence and nucleotide base composition, was 3.02 nm and therefore slightly larger than the values of RNAs, whose nucleotide base composition had been evolved by evolution. It is suggested that the degree of compaction is influenced by the nucleotide base composition (42). This conclusion is supported by a correspondence between nucleotide base composition and secondary structure element formation (43). A further support for this assumption is provided by the molecular size of Poly(U)₈₅ (24) (Figure 5B hexagon). The hydrodynamic radius of Poly(U)₈₅ of 4.45 nm clearly ranges outside of the empirical and cylindrical models. This observation can be explained by a lack of Watson–Crick base pairing and stacking interactions, which hinder secondary structure formation. The shift to more extended structures due to a larger distance from an evolutionary evolved nucleotide base composition is expected to reach a maximum with Poly(U)_n.

These results suggest that the extent to which the hydrodynamic behaviour of arbitrary sequences equals that of evolutionary evolved sequences is not defined by sequence but by nucleotide base composition. It is expected that the hydrodynamic behaviour of arbitrary sequences shows a broader distribution than that of evolutionary evolved sequences and a bias towards larger hydrodynamic radii and smaller diffusion coefficients.

CONCLUSIONS

In the presented work, an empirical law is presented for the dependence of the translational diffusion of short evolutionary conserved RNA single strands on the number of nucleotides. Based on atom-level shell-modelling of high-resolution structures, a hydrodynamic model is proposed, which is highly consistent with in solution measured hydrodynamic radii and radii of gyration. The dependency of the molecular size on the oligonucleotide length allowed assuming a compact aspherical shape of ssRNA. In correspondence, the ratio of the radius of gyration and hydrodynamic radius was equal to 1.

Comparing radii of gyration in crystal structures and in solution, slightly more extended conformations were found in solution, which points to limitations of the transfer of knowledge from the crystallized state to the solution state.

The empirical hydrodynamic models, determined from crystal structures and solution data, are expected to facilitate the planning of experimental studies of RNA function and the interpretation of data resulting from DLS, AUC or FCS experiments.

The empirical laws for ssRNA translational diffusion and size have been derived from and validated by evolutionary evolved structures. Furthermore, the hydrodynamic behaviour of several unevolved heterogeneous sequences could be, depending on the nucleotide base composition, accurately predicted. However, to define the hydrodynamic behaviour of arbitrary sequences more accurately, a higher number of experimental data would be required.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Funding for open access charge: Waived by the Oxford University Press.

Conflict of interest statement. None declared.