Improved Prediction of Cardiovascular Disease Based on a Panel of Single Nucleotide Polymorphisms Identified Through Genome-Wide Association Studies

Abstract

Background

Genome-wide association studies (GWAS) have identified single-nucleotide polymorphisms (SNPs) at multiple loci that are significantly associated with coronary artery disease (CAD) risk. In this study, we sought to determine and compare the predictive capabilities of 9p21.3 alone and a panel of SNPs identified and replicated through GWAS for CAD.

Methods and Results

We used the Ottawa Heart Genomics Study (OHGS) (3323 cases, 2319 control subjects) and the Wellcome Trust Case Control Consortium (WTCCC) (1926 cases, 2938 control subjects) data sets. We compared the ability of allele counting, logistic regression, and support vector machines. Two sets of SNPs, 9p21.3 alone and a set of 12 SNPs identified by GWAS and through a model-fitting procedure, were considered. Performance was assessed by measuring area under the curve (AUC) for OHGS using 10-fold cross-validation and WTCCC as a replication set. AUC for logistic regression using OHGS increased significantly from 0.555 to 0.608 (P=3.59×10^–14) for 9p21.3 versus the 12 SNPs, respectively. This difference remained when traditional risk factors were considered in a subgroup of OHGS (1388 cases, 2038 control subjects), with AUC increasing from 0.804 to 0.809 (P=0.037). The added predictive value over and above the traditional risk factors was not significant for 9p21.3 (AUC 0.801 versus 0.804, P=0.097) but was for the 12 SNPs (AUC 0.801 versus 0.809, P=0.0073). Performance was similar between OHGS and WTCCC. Logistic regression outperformed both support vector machines and allele counting.

Conclusions

Using the collective of 12 SNPs confers significantly greater predictive capabilities for CAD than 9p21.3, whether traditional risks are or are not considered. More accurate models probably will evolve as additional CAD-associated SNPs are identified.

The last 3 years have seen the completion of a series of genome-wide association studies (GWAS) that were designed to elucidate DNA sequence variations that are associated with coronary artery disease (CAD) or its related phenotype, myocardial infarction (MI). These studies have all identified a robust locus that is risk-conferring located at 9p21.3.^1–4 Several other loci that impart a more modest population attributable risk have also been shown to associate with CAD.^5–9

After identification of DNA sequence variation associated with the development of CAD, 2 lines of investigation emerge. The first involves elucidation of the biological mechanisms that underlie association; this may reveal novel therapeutic targets because many loci do not exert their effect via the known modifiable risk factors. The second line of investigation is to determine the ability of these markers to predict disease above and beyond standard risk algorithms, such as the Framingham risk score, both individually and in concert. Thus far, such studies generally fall into 2 categories: those that feature a prospective cohort and use well-established statistical methodology, and case-control studies, which tend to experiment more with their statistical approach. Case-control studies for CAD have generally used simple methodology such as allele counting to generate genetic risk scores,¹⁰ or logistic regression.⁵ Case-control studies for other phenotypes, such as type I diabetes, have had limited success with alternative statistical methodology from the field of machine learning, particularly support vector machines.¹¹

The first objective of the present study was to evaluate whether the incorporation of a collective of single nucleotide polymorphisms (SNPs) recently identified to be associated with CAD adds to the predictive power provided by 9p21.3 alone, and whether any difference remained significant when traditional risk factors were also considered. Second, the study tested which of 2 common prediction methods, allele counting and logistic regression, and 1 more complicated algorithm from the field of machine learning, support vector machines, conferred the best predictive capabilities for CAD using the collective of SNPs. Access to a large, well-powered GWAS, the Ottawa Heart Genomics Study, and an independent replication cohort, the Wellcome Trust Case Control Consortium, has provided appropriate data sets to address the impact of genetic variants on predicting CAD.

Materials and Methods

Determining Eligible GWAS SNPs

To determine eligible SNPs, we searched the National Human Genome Research Institute catalog for SNPs identified before January 25, 2010,¹² in a manner slightly more restrictive than a similar approach by Ioannidis.¹³ For this study, we sought to include SNPs that had been identified through GWAS to associate with CAD. However, as the phenotypes of CAD and MI are highly correlated and are generally overlapping in GWAS; we also accepted SNPs that had been identified through GWAS to be associated with MI. To ensure robustness of the loci we considered, variants were required to associate with CAD or MI with a probability value ≤5×10^–7 in the original discovery report, a threshold that has been used previously to assess genome-wide significance.³ SNPs were also included if the primary analysis was with a related cardiovascular phenotype, such as hypertension, lipids, diabetes, or body mass index, and included a subgroup analysis with CAD or MI meeting GWAS significance. However, we did not include SNPs if the primary analysis of the report in which they are identified focused on a measure whose effect on cardiovascular disease is contentious, for example, C-reactive protein. A full list of related phenotypes that were considered is available in the online-only Data Supplement Methods. Articles were examined in detail if the primary analysis focused on either CAD or MI or a mention of a subanalysis of CAD or MI was made in the abstract.

Studies

The Ottawa Heart Genomics Study

Details of the Ottawa Heart Genomics Study (OHGS) have been published previously.¹⁴ In brief, subjects were recruited from the University of Ottawa Heart Institute (UOHI) lipid clinic, catheterization laboratory, or from the Cleveland Clinic. Cases either had an MI, had undergone coronary artery bypass grafting, had percutaneous coronary intervention, or had a coronary angiography or computed tomography angiography demonstrating a stenosis of at least 50% in at least 1 epicardial vessel. Control subjects were either healthy individuals asymptomatic for ischemic cardiovascular disease or individuals with minimal disease burden determined by angiography (no stenosis exceeding 30% in a major coronary vessel). Cases were age ≤55 years for men and ≤65 years for women; control subjects were ≥65 years for men and ≥70 years for women. All cases with a history of diabetes or subjects with nonEuropean ancestry were excluded. A subgroup of OHGS for which traditional risk factors (TRFs) were available was used to evaluate the influence of traditional TRFs alongside genetic TRFs. We considered TRFs as included in Table 6 of Wilson et al, ¹⁵ specifically age, diabetes, hypertension (yes/no), smoking current versus not current, total cholesterol, high-density lipoprotein, and sex. Because of the nature of the OHGS study, we were not able to include age and diabetes as covariates.

The Wellcome Trust Case Control Consortium

Details on the Wellcome Trust Case Control Consortium (WTCCC) have been published previously.³ In brief, cases had MI, coronary artery bypass grafting, or percutaneous coronary intervention before the age of 66 years. Control subjects were recruited from both the 1958 Birth Cohort and the UK Blood Services. Control subjects were not screened by phenotype or age.

Sample Genotyping and Processing

OHGS samples were genotyped at the John and Jennifer Ruddy Canadian Cardiovascular Genetics Centre at the UOHI. Samples were genotyped using either the Affymetrix GeneChip 500K or 6.0 (Affymetrix, Santa Clara, Calif). Genotype calling was performed using the BRLMM and Birdseed algorithms on the 500K and 6.0 chips, respectively. Removal of individuals of non-European ancestry was performed using the SMARTPCA program within the EIGENSOFT suite of software.¹⁶ WTCCC samples were genotyped at the Affymetrix Services laboratory using the Affymetrix GeneChip 500K. Genotype calling was performed using CHIAMO. Details of the method by which individuals of non-European ancestry were removed can be found in the original publication.³

Imputation, Haplotyping, and Quality Control

Imputation was used both to fill in uncalled genotypes for genotyped SNPs and to impute SNPs that were not genotyped and for which a tag SNP could not be found. Imputation was carried out using IMPUTE v1 using default settings.¹⁷ Hapmap3 (release2) haplotypes from NCBI Build 36 (dbSNP b126) were used from the CEU (Utah residents with Western European ancestry) and TSI (Toscans in Italy) populations, as downloaded from the IMPUTE website (https://mathgen.stats.ox.ac.uk/impute/impute.html). Genotypes that were not called using either the arrays or imputation at a posterior probability threshold of 0.90 were “forced” to their most likely genotype on the basis of posterior probability from the IMPUTE program. Unless otherwise stated, call rate refers to the percent of genotypes called before forcing, which may include imputation of missing genotype data.

Haplotyping was carried out after imputation to “impute” untyped SNPs using the haplo.stats package in R (R Foundation for Statistical Computing, Vienna, Austria). The posterior probability of haplotype assignment based on haplotype frequency and available haplotypes was used to assess quality. A haplotype was deemed to be satisfactorily assigned if a particular pair of haplotypes explained the observed genotypes with a posterior probability of >0.90. If no haplotype pair had a posterior probability of >0.90, the most likely haplotype pair was forced.

SNPs were excluded if call rate before forcing was <90% or if the Hardy Weinberg equilibrium exact test probability value was <0.001.

Model Fitting

Although the SNPs under consideration in this study had previously passed “genome-wide” significance, this does not preclude the possibility that some of these SNPs act on similar pathways, and as such there may be SNPs with only marginal association in a multivariable model. As such, we performed a model-fitting procedure after identification and selection of the set of GWAS validated SNPs. We performed a backwards stepwise removal procedure via logistic regression, where we first fit a model with all SNPs and then iteratively removed the SNP with the highest probability value until the highest probability value was <0.05.

Algorithms

A more detailed description of the 3 algorithms we considered can be found in the online-only Data Supplement Methods. In brief, we considered: logistic regression (LR), which uses a linear weighting of the input variables; allele counting, which uses a literature-derived “count” of risk alleles; and support vector machines (SVM), which work in a higher dimensional analog of the input variables and create a highly nonlinear function of the original variables. SVMs were constructed using the e1071 package in R using the radial kernel and default settings. Receiver operator characteristic (ROC) curves were generated by comparing the numeric scores resulting from the algorithms to a series of thresholds, calling “case” if above and “control” if below the threshold. Sensitivity, specificity, and accuracy were calculated from the resulting 2×2 tables. A measure of the performance of a classifier was taken as the area under the curve (AUC), calculated using caTools in R. Statistical differences between AUCs were assessed using the nonparametric method of DeLong et al.¹⁸

The OHGS was considered to be the training set and the WTCCC the test set. To obtain an estimate of training set performance, we used k-fold cross-validation (CV). In k-fold CV, the training set is divided into k roughly equal sets. For each of the k-folds, a classifier is built on the remaining k-1 folds and tested using the k^th fold. This should ensure that every member in the training set is tested using a classifier it did not help train and hence minimize bias. We used 10-fold CV on the OHGS training set.

Results

Characteristics of Study Populations

Specific details on the processing of OHGS and WTCCC have already been published.^3,14 After removal of ineligible individuals, there were 5642 subjects available from the OHGS, of which 3323 were cases and 2319 control subjects, and 4864 subjects available from the WTCCC, of which 1926 were cases and 2938 control subjects. Phenotypic characterization of the OHGS population is given in Table 1.

Table 1.

Clinical Characteristics of Ottawa Heart Genomics Study

	Cases	Control Subjects
No.	3323	2319
Age*	48.6±7.2	75.0±5.2
Men, %	75.9	51.7
Body mass index	29.0±5.2	26.2±4.1
Smoke current, %	21.3	2.5
Hypertension, %	58.9	39.1
Cholesterol, mmol/L†	5.92±1.2	5.67±1.0
TG, mmol/L†	2.07±1.1	1.33±0.7
LDL-C, mmol/L†	3.84±1.1	3.59±0.9
HDL-C, mmol/L†	1.16±0.4	1.48±0.4

TG indicates triglyceride; LDL, low-density lipoprotein; and HDL, high-density lipoprotein.

Values reported are mean±1 SD. All measures are significantly different (P<0.001) between cases and control subjects as measured by t tests for the continuous variables and χ² tests for the binary traits.

^*Age refers to age at diagnosis (cases) and age at consent (control subjects).

^†All 4 lipid measures were available for 1248 cases and 2016 control subjects at baseline.

Previously Established Loci

An investigation of the literature revealed 5 publications from 2009 reporting loci associated with CAD^5–9 and 3 publications from 2007.^2–4 Note that McPherson et al also identified the 9p21.3 locus at the same time as Helgadottir et al¹ but did not include a formal meta-analysis probability value and so failed our probability value requirement. A description of the loci and SNPs identified in these 8 reports is given in Table 2.

Table 2.

Details of Previously Identified SNPs

Studies	Locus	Physical Location, Mb	Using SNP	SNP Type	Original SNP	Genes in Region	OHGS, OR (95% CI)
5	1p32	55.27	rs11206510	G	rs11206510	PCSK9	1.00 (0.91,1.10)*
2, 5	1p13	109.62	rs646776	I	rs646776	CELSR2/PSRC1/SORT1	1.18 (1.08,1.30)
5	1q41	220.87	rs17465637	G	rs17465637	MIA3	1.15 (1.06,1.25)
5	2q33	203.45	rs6725887	G	rs6725887	WDR12	1.28 (1.14,1.43)
7	3q22	139.60	rs9818870	G	rs9818870	MRAS	1.13 (1.02,1.25)
5	6p24	13.04	rs12526453	G	rs12526453	PHACTR1	1.11 (1.03,1.21)
8	6q26-27	160.88	CCTC haplo	H	rs3798220	SLC22A3/LPAL2/LPA	1.79 (1.38,2.31)
2-5	9p21	22.09	rs4977574	G	rs4977574	CDKN2A/CDKN2B	1.46 (1.35,1.57)
2, 5	10q11	44.10	rs1746049	G-T	rs1746048	CXCL12	1.17 (1.04,1.31)
6, 9	12q24	111.36	rs11066301	I	rs11066301	SH2B3/ATXN2/PTPN11	1.17 (1.08,1.26)
7	12q24	119.92	rs2259816	G	rs2259816	HNF1A/C12orf43	1.13 (1.04,1.22)
5	19p13	11.02	rs1122608	G	rs1122608	LDLR	1.20 (1.09,1.31)
5	21q22	34.52	rs9978407	G-T	rs9982601	SLC5A3/MRPS6/KCNE2	1.25 (1.12,1.40)

Original SNP refers to the SNP as identified through the relevant GWAS; using refers to the SNP being used in our analysis. SNP type refers to whether the SNP being used was the original genotype SNP (G), a tag SNP of the genotype SNP (G-T), an imputed SNP (I), or a haplotype (H). Odds ratios (ORs) and 95% confidence intervals (CIs) are given for the risk allele for a logistic regression model containing all 13 SNPs.

^*rs1120650 was removed after the model-fitting procedure.

Among reports published in 2007, only Samani et al² identified loci other than 9p21.3, with SNPs in 1p13, 2q36, 6q25, 10q11, and 15q22 meeting a 5×10^–7 probability value requirement. However, in a later report, the Myocardial Infarction Genomics Consortium (MIGC) performed a meta-analysis including data from the Samani report and did not show convincing evidence of replication for the 2q36, 6q25, and 15q22 loci; hence, we did not include these 3 loci in this analysis.⁵ For the 9p21.3 locus, we took forward the SNP identified by the MIGC because it was based on the largest sample size.

In the 2009 publications, the only loci in which multiple SNPs were reported were the 12q24 region near the genes SH2B3/ATXN2/PTPN11 and the 6q26-27 region near the genes SLC22A3/LPAL2/LPA. The 12q24 region was reported by Gudbjartsson et al⁶ and Soranzo et al,⁹ who identified SNPs rs11066301 and rs3184504, respectively. Given that the r² between these 2 SNPs is 0.671 in HapMap and the reported odds ratios of 1.15 for rs11066301 and 1.13 for rs3184504 are quite similar, we chose to retain the rs11066301 SNP in our analysis because it was more easily imputed using data from the Affymetrix arrays. Note that the r² and D′ between the SNPs representing the 2 loci in the 12q24 chromosomal band, rs11066301 in the SH2B3 locus, and rs2259816 in the HNF1A locus, as measured among the OHGS samples, are both 0.0.

At the 6q26-27 locus, Trégouët et al⁸ reported a haplotypic association among 4 SNPs (rs2048327, rs3127599, rs7767084, and rs10755578). Among those SNPs, rs2048327 showed the strongest individual association, although it was noted that it did not fully explain the association in the region, which was mostly due to 2 haplotypes among the 4 SNPs, CCTC and CTTG. In a recent report, Clarke et al¹⁹ used a custom array specifically targeting certain genomic regions, among them the LPA gene at 6q26-27. They reported 2 SNPs, rs3798220 and rs10455872, which accounted for the majority of the association between the LPA locus and CAD. Although determining linkage based on HapMap between these 2 SNPs is not an option because rs3798220 is monomorphic in the CEU population, the online-only Data Supplement Information included with the Clarke report allows one to calculate that the r² and D′ between these 2 SNPs are 0.0 and 1.0.

The first of these SNPs, rs3798220, has an r² of 0.86, with the CCTC haplotype as reported by Clarke et al.¹⁹ rs3798220 represents a nonsynonymous variant at LPA and is therefore of high biological plausibility. Although rs3798220 is not on the Affymetrix arrays used in this study and is not imputable because of its monomorphism in the HapMap CEU population, the 4 SNPs from the Trégouët et al study were, so the CCTC haplotype was available for analysis. The other SNP, rs10455872, has an r² of 0.51 with the CTTG haplotype; however, we were unable to impute rs10455872 (call rate <80%). Given the stronger reported odds ratio for the CCTC haplotype as compared with the CTTG haplotype, and to avoid including 2 haplotypes that necessarily have a D′ of 1, we carried forward only the CCTC haplotype from the LPA locus for analysis.

Results From Quality Control and Model Fitting

Online-only Data Supplement Table 1 contains measures pertaining to quality control analysis of the eligible SNPs in the 2 sample populations. Except for rs3798220, which was tagged with a haplotype, we were able to generate genotypes using either the original SNP or a perfect tag SNP (r²=1) for all SNPs identified from previous studies. All SNPs were deemed to have passed quality control.

Performing the backwards elimination stepwise logistic regression procedure identified 1 SNP, rs11206510, with a high multivariable probability value (P=0.99). In the second iteration, no SNPs were removed (max P=0.023<0.05).

Of the 12 SNPs we carried forward, 8 SNPs in OHGS and WTCCC had a 100.0% call rate when including both geno-type calls and imputation of uncalled genotypes. Of the 5642 subjects from the OHGS, 5221 subjects had a call rate of 100.0% across all SNPs, whereas 410 subjects had 1 genotype forced and 11 had 2 genotypes forced. For the WTCCC, 4333 subjects had call rates of 100.0%, whereas 511 had 1 genotype forced and 20 had 2 genotypes forced.

Results of the Algorithms

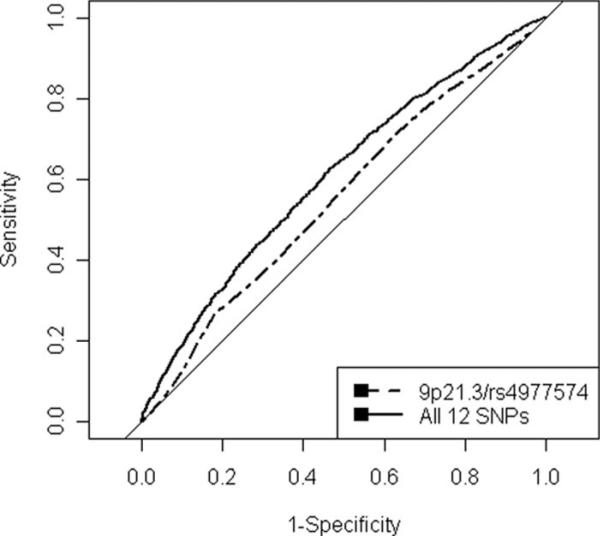
Results for the various algorithms are available in Table 3. CV results for OHGS using LR are available in the Figure and showed a benefit with the inclusion of more SNPs, with AUCs increasing from 0.555 to 0.608 with the inclusion of all 12 SNPs (P=3.59×10^–14). Results for the WTCCC were quite similar, with AUCs for LR increasing from 0.556 to 0.602 (P=3.50×10^–11).

Table 3.

Results for Models Trained Using Sets of SNPs

	OHGS			WTCCC
	LR	AC	SVM	LR	AC	SVM
9p21.3/rs4977574	0.555	0.555	0.555	0.556	0.556	0.556
All	0.608	0.599	0.581	0.602	0.593	0.579

Values are AUCs for both LR and SVM trained on either 9p21.3 alone or using 12 SNPs.

Figure.

ROC curves for OHGS logistic regression model. Plot of ROCs from OHGS data using 10-fold CV with the logistic regression algorithm for 9p21.3 alone and for all 12 SNPs.

When 5 TRFs were used as covariates with LR in a subgroup of OHGS (1388 cases, 2038 control subjects), the increase in AUC achieved using the 12 SNPs as compared with 9p21.3 alone remained significant, with an increase in AUC from 0.8044 to 0.8097 (P=0.037). Whereas the added predictive value of 9p21.3 over the TRFs does not quite reach significance (0.8013 versus 0.8044, P=0.097), the collective of 12 SNPs offers an even greater benefit than 9p21.3 versus the TRFs (0.8013 versus 0.8097 P=0.0073).

As for the different algorithms using the 12 SNPs, LR marginally outperformed allele counting, with AUCs decreasing from 0.608 to 0.599 (P=0.016), whereas LR outperformed SVM by a larger margin with AUCs decreasing from 0.608 to 0.581 (P=3.79×10^–6). Results were quite similar between WTCCC and OHGS across the various algorithms considered. A sensitivity analysis for CV, comparing OHGS results using the 12 SNPs for the 3 algorithms, showed that whereas LR and SVM were relatively insensitive to CV (AUCs of 0.608 versus 0.615 for LR, AUCs of 0.599 versus 0.599 for allele counting), SVM was highly sensitivity to CV, achieving an AUC of 0.715 when the OHGS data served both as the training and test set.

Discussion

We demonstrate in 2 large case-control populations that the addition of other CAD-associated loci to 9p21.3 improves discriminatory capability. The incorporation of these additional SNPs resulted in a significant improvement in the AUC whether or not traditional risk factors were considered. In addition, we found that the model consisting of the traditional risk factors plus the collective of SNPs significantly outperformed the model consisting solely of TRFs.

Previous attempts to quantify the effect of using 9p21.3 for cardiovascular risk prediction have not been able to show a clinically meaningful benefit when used alongside TRFs.^20–22 More recently, Paynter et al²³ used 2 literature-derived, allele counting–based genetic risk scores in an attempt to predict cardiovascular risk in a prospective cohort, using either robustly associated CAD-SNPs or a larger set of SNPs that are related to either CAD risk factors or surrogate phenotypes. Paynter et al were not able to demonstrate that either of their genetic risk scores led to meaningful improvements in risk prediction over that of traditional CAD risk factors.

The 12-SNP set that we investigated shares overlap with the SNPs used by Paynter et al. However, there exist important distinctions; we include other GWAS-identified variants, including 2 chromosome 12 loci and the CCTC haplotype/rs3798220 in the LPA locus. In our data set, the CCTC haplotype/rs3798220 is the single most potent genetic variant, with an odds ratio of 1.79, as compared with the next most potent, with an odds ratio of 1.46. Furthermore, we were also able to exclude variants whose association was not confirmed by more recent studies, such as rs6922269.⁵

Given that derivation of weights for genetic risk scores and testing their predictive capabilities on the same data set would bias the results, Paynter at al²³ used allele counting. Given our larger sample of cases, as well as a second independent data set, we were able to experiment with methodologies and could construct a weighted genetic risk score using logistic regression. Our results showed that a weighted genetic risk score using logistic regression outperforms allele counting, even if the differences in AUCs is slight. It should also be noted that with the exception of 9p21.3, which has been robustly replicated in multiple independent populations, and the SH2B3 locus, which used a subset of the OHGS samples analyzed here, the 12 SNPs reported on here were discovered using data derived separately from the present study. Therefore, any bias in favor of a larger effect that might arise from performing discovery and effect size estimation in the same data set is unlikely to have adversely influenced these results.

As for the results of the analysis with TRFs, our results seem to be in line with simulation work performed by Talmud et al,²⁰ who showed that adding 9p21.3 to a prospective model did not add significantly to risk prediction, whereas simulating a second independent locus of equal effect and adding it with 9p21.3 would add significantly to the model. We speculate, based on differences in AUC with only the genetic variants, where the difference in AUC between the 12 SNPs and the null AUC of 0.5 is twice that for 9p21.3 alone, we might be at the stage where we have the equivalent effect of 2 9p21.3 risk alleles. Although our results offer hope that as more loci are gradually identified and verified, the ability to construct genetic risk scores that add discrimination on top of TRFs increases, we caution that our study population is not without biases, as discussed further below in the limitations.

Therefore, the present novel genetic risk score, which features the improvement of weighting via logistic regression and the benefit of using the most robust set of CAD associated SNPs, should offer improvement over previously published genetic risk scores for CAD. The present study also suggests that genetic risk scores derived from allele counting are a good “first start” but that measurable improvements are likely to be obtained by using weighted scores from a method such as logistic regression.

A secondary objective of this study was to assess the predictive capabilities of more complicated prediction algorithms, namely, support vector machines versus traditional logistic regression or allele counting. The results that show that there is little benefit derived from the use of this more complicated algorithm.

It should be noted that recently a similar analysis was completed in a type 1 diabetes population, where the abilities of SVM using a radial kernel and LR for prediction were compared.¹¹ In their population, diagnostic performance far exceeded that in our population, where test set AUCs using SNPs only of 0.84 were achieved for SVM, whereas those for LR were marginally lower. The improved predictive accuracy in this analysis probably stems from the greater heritability associated with type 1 diabetes as compared with CAD and the larger number of genetic variants that have been found to associate with type 1 diabetes.

Although the discrepancy in AUCs can easily be explained by a larger number of variants that have been identified to associate with type 1 diabetes, the difference in performance between SVM and LR requires more careful analysis. Wei et al suggest several reasons for the increased performance of SVMs in their data set. One of these is that interactions have been found between genetic loci in the major histocompatibility region on chromosome 6 and other validated loci for diabetes. To date, no such interactions have been identified for CAD, and an interaction analysis of the 12 SNPs in our study, evaluating interactions among (12*11)/2=66 pairs of SNPs, did not yield a probability value that withstood Bonferroni correction (minimum P=0.0010>0.05/66). Additionally, whereas our study used only SNPs in linkage equilibrium, Wei et al included several SNPs from the same locus in their predictive models. Although they used ridge regression for LR, it is likely that SVM, which is inherently more capable of handling correlated data, would more accurately predict disease. It is likely for these reasons that the more flexible SVM was able to outperform LR in their data set but not in ours.

Although promising, the present study is not without limitations. We selected only the most robustly associated CAD SNPs, so it is likely that future genetic risk scores will be more successful because it is likely that future studies will continue to identify variants associated with CAD. In addition, more precise phenotyping may facilitate risk prediction in that currently both MI and CAD are treated as the same entity. Although these phenotypes are generally linked, it is likely that they are driven in part by separate biological processes that are genetically determined. By considering these entities as one, the effect of genetic variants for nonoverlapping processes, such as plaque rupture or thrombosis, may be obscured.

As for study design, we used elderly asymptomatic control subjects because younger control subjects may harbor a significant burden of occult atherosclerosis and have development of symptomatic CAD at an age only slightly higher than that of the CAD case population. However, recent analysis has suggested that 9p21.3 might be associated with longevity, although the association was hypothesized to act through avoidance of CAD as an age-related phenotype.²⁴ To determine if any of the SNPs used in this study were associated with either age of onset for the cases or age of consent for the control subjects, we performed a subanalysis by stratifying the OHGS case and control groups into young and old, splitting according to the median age in each group. We subsequently determined the ability of each SNP to explain the binary trait of young versus old using logistic regression. Only 1 SNP, the CCTC haplotype representing rs3798220 in the LPA locus, approached a Bonferroni-adjusted cutoff, with a probability value of P=0.004 for the case group and nonsignificance for the control group (MAFs of 3.8 and 2.6 for young and old cases, and 1.8 and 2.0 for young and old control subjects, respectively); therefore, we believe that differences in SNP allele frequency with age are unlikely to play a major role in the creation of the observed genetic risk scores.

Finally, by using elderly control subjects, for whom traditional risk factors may be less strongly related to CAD risk, the effect of genetic risk factors on top of TRFs may differ from that observed in a prospective cohort study. Although these results are certainly promising and offer useful insight into the relative contributions of statistical methods and usefulness of SNP/disease associations, further investigations are required in prospective population cohorts.

Conclusion

We demonstrate the ability of multiple robustly associated CAD loci to augment the ability of CAD risk prediction above and beyond 9p21.3. Logistic regression proved superior to both the more complicated support vector machines and the simpler allele counting. More accurate models probably will evolve as additional CAD-associated SNPs are found. Moreover, the identification of causal variants, for which the index SNPs are mere surrogates, will facilitate more accurate disease prediction.

CLINICAL PERSPECTIVE.

In the past 3 years, several genome-wide association studies have identified common genetic variants at multiple loci that are significantly associated with coronary artery disease (CAD) risk. The most robust of these is a risk allele at 9p21 that has been shown to modestly but inconsistently improve CAD risk prediction over and above conventional risk factors. However, the extent to which additional recently identified genetic variants of more modest effect size cumulatively improve risk prediction remains controversial. In the present study, we demonstrate, in 2 large CAD case-control populations, that a collective of 12 previously replicated CAD-associated single nucleotide polymorphisms confers significantly greater predictive capabilities than do traditional risk factors or traditional risk factors plus 9p21. We also show that logistic regression performs better than more complicated machine-learning approaches. Large meta-analyses of CAD case-control data sets including >100 000 individuals are underway. Relevant to the goal of personalized medicine, more informative risk prediction models can be expected as additional CAD-associated single nucleotide polymorphisms are identified and more refined phenotypic data become available.