A Framework for the Automatic Generation of Surface Topologies for Abdominal Aortic Aneurysm Models

Abstract

Patient-specific abdominal aortic aneurysms (AAAs) are characterized by local curvature changes, which we assess using a feature-based approach on topologies representative of the AAA outer wall surface. The application of image segmentation methods yields 3D reconstructed surface polygons that contain low-quality elements, unrealistic sharp corners, and surface irregularities. To optimize the quality of the surface topology, an iterative algorithm was developed to perform interpolation of the AAA geometry, topology refinement, and smoothing. Triangular surface topologies are generated based on a Delaunay triangulation algorithm, which is adapted for AAA segmented masks. The boundary of the AAA wall is represented using a signed distance function prior to triangulation. The irregularities on the surface are minimized by an interpolation scheme and the initial coarse triangulation is refined by forcing nodes into equilibrium positions. A surface smoothing algorithm based on a low-pass filter is applied to remove sharp corners. The optimal number of iterations needed for polygon refinement and smoothing is determined by imposing a minimum average element quality index with no significant AAA sac volume change. This framework automatically generates high-quality triangular surface topologies that can be used to characterize local curvature changes of the AAA wall.

INTRODUCTION

Abdominal aortic aneurysms (AAAs) are localized dilations of the abdominal artery that commonly form below the renal arteries. Depending on the size of the aneurysm at the time of diagnosis, it should either be closely monitored or repaired to prevent rupture. Evaluating rupture risk is critically important as aneurysm rupture carries high mortality rates. Two-hundred thousand new AAA cases are diagnosed each year in the United States and 15,000 people die from AAA rupture each year. AAA rupture is the 13th leading cause of death in this country and affects 1 in 250 individuals over 50 years of age.²² Currently, a maximum transverse diameter of 5.5 cm or greater and an expansion rate of 1 cm/year are the standard for estimating rupture risk and are commonly used thresholds for elective repair. It is a known fact, however, that basing the clinical management of this disease on maximum diameter alone is not a reliable measure of individual rupture risk. This is evident by the small aneurysms that rupture (prior to reaching the critical diameter of 5.5 cm) and the large aneurysms that do not rupture (at the critical size for which elective repair is recommended) after they are either diagnosed at an advanced stage of growth or are in patients who are unfit for repair.

Recent studies reveal that aneurysm diameter is not the sole determinant for rupture and that biomechanical and biological factors may influence AAA rupture risk. Peak wall stress has been shown to be a more reliable parameter than maximum diameter for predicting aneurysm rupture, and the stresses acting on the wall of an aneurysm are highly dependent on aneurysm shape.²⁶ Wall stress alone is not sufficient to predict rupture risk; regional estimations of wall strength are also necessary.²⁴ The degeneration of aortic wall connective tissue causes a significant loss of structural integrity of the aortic wall,³ increasing the risk of rupture for an individual aneurysm. Moreover, the presence of intraluminal thrombus, which forms as a result of disturbed blood flow conditions and blood stagnation, has an effect on aortic wall degeneration.²³

Quantifying the shape and size of patient-specific AAAs can be valuable for predicting individual rupture and operative risks in pre-surgical planning, establishing index thresholds for patient selection, and for customizing designs of endovascular grafts. Accurate geometrical characterization requires taking into consideration the 3D complexity of the shape, tortuosity, and asymmetry of the randomly formed AAA sac. Recent studies have shown that AAAs with an asymmetric geometry exhibit higher wall stress²⁷ and that ruptured aneurysms show evidence of more out of plane growth than axial growth.¹² A complex AAA geometry contributes to an equivalently complex wall stress distribution over the entire AAA, with the highest stresses associated with regions of high curvature. ¹⁷ It has been proposed that geometric parameters may be able to accurately predict wall stress distributions.⁴ Mean and maximum centerline curvature were highly correlated with peak wall stress⁷ and the location of maximum stress coincided with peaks in Gaussian curvature, a parameter that indicates the existence of concave and convex regions on the vessel surface.¹¹ Parameters such as the Gaussian curvature are important since they offer information unattainable with simple visual inspection: a measure of the degree to which the AAA wall geometry is irregular. It has also been proposed that the role of AAA geometry should not be underestimated in wall stress analysis of small AAAs with diameters of 5.0–5.5 cm.⁶

Mechanical analysis requires the accurate quantification of 3D anatomic structures since the surface geometry can have a direct impact on their mechanical behavior in health and disease.¹⁹ A recent study described the derivation of a set of global indices for the size and shape of cerebral aneurysms for assessment of their rupture potential and choosing the appropriate clinical treatment modality.^8,15 It was reported that quantified shape was more effective than size in discriminating between ruptured and non-ruptured cerebral aneurysms.

We previously reported on a novel, semi-automatic vessel segmentation algorithm (VESSEG v.1.0.2, Carnegie Mellon University) used to analyze the CT images of a pilot subject population and estimate local measures of wall thickness.¹⁸ Patient-specific 3D models of nine electively repaired AAAs were constructed from the segmented data and characterized quantitatively by calculating 28 size and shape indices and regional variations in aortic wall thickness.⁹ In this study, we describe an automated method to generate outer wall surface topologies from AAA segmented images. The framework described herein is simple to use, yields polygons of high quality, and can also generate unstructured volume meshes. The surface topologies can be used to quantify geometric indices that could be construed as potential predictors of AAA rupture risk. An application of the surface polygon generation framework is presented with a population subset of ten ruptured and ten unruptured AAA datasets for which polygon-dependent shape and curvature-based indices are quantified.

IMAGE PROCESSING AND SURFACE TOPOLOGY GENERATION METHODS

Segmentation Algorithm

The segmentation methods used in this study are described in detail in Shum et al.¹⁸ In brief, three different algorithms form the basis of the segmentation and wall thickness detection tools applied for this study. The lumen segmentation is performed via the intensity gradient that exists between the lumen and surrounding structures. The outer wall contour can be determined either manually or automatically. In the manual method, the image is reduced to a small region containing the aorta and an array of contours, or isolines, are provided to the user for manual selection. In the automatic method, the outer wall is detected by using intensity thresholding and additional control rules to ensure that the segmentation of the slice is discarded when no possible boundaries can be created. The threshold is changed accordingly to attempt a new segmentation. The inner wall is detected by training a neural network to recognize regions where the inner wall could reside.

Polygon Generation and Refinement

The polygon generation algorithm described by Persson and Strang¹³ was modified to produce high-quality triangular surface topologies using the outer wall contour of the segmented AAA. From the segmentation algorithm, the outer wall contours are exported as a set of point clouds to generate an initial tetrahedral volume mesh using a signed distance function. A boundary box containing a uniformly distributed set of nodes and a signed distance function yield the initial aneurysm topology by rejecting nodes positioned outside the outer wall contours. A coarse mesh is generated from the remaining nodes using a restricted Delaunay triangulation scheme. A force displacement function is used iteratively to move the nodes to an equilibrium position with a uniform length between each node by updating the nodal positions. This causes a repulsive force between nodes that spreads them across the aneurysm geometry and refines the mesh. From the volume mesh, the external triangular faces of the tetrahedrals are extracted to generate an initial, coarse surface topology.

The initial surface topology contains low-quality elements, unrealistic sharp corners, and surface irregularities that result from the slice spacing between images and from the image segmentation method. To address this, the point clouds of the outer wall contours are converted to cylindrical coordinates and linearly interpolated between the slices to generate additional wall points. The new sets of points are then converted back to Cartesian coordinates and binary masks are created to approximate a signed distance function. The region within the mask is assigned a negative value while the region outside is assigned a positive value. This approximated signed distance function in conjunction with the boundary box is used to reject nodes located outside the boundary, or those nodes with a positive value.

A uniform edge length distribution was used to allocate the initial point cloud with a length equal to the pixel size. Using a non-linear distribution where the point clouds are denser at highly tortuous regions and coarser at less tortuous regions might be more effective for generating tetrahedral meshes for finite element analysis (FEA). However, we evaluated the effect of the initial point cloud density against the average element quality index and found that densities in which the point clouds are distributed with a length equal to the pixel size gave the highest average element quality (Q_ave > 0.75).

The average element quality index, Q_ave, is calculated after each iteration of refinement. Element quality is defined as:

$$Q_{\text{ave}}=\frac{2\sqrt{3}r}{h_{\text{max}}},$$ (1)

where r is the radius of the largest circle inscribed in a triangle and h_max is the length of the longest edge of a triangle. An equilateral triangle would yield a Q_ave = 1.

Polygon Smoothing

After the refinement process, a surface smoothing algorithm based on Taubin’s low-pass filter method²¹ is applied to remove sharp corners. The implemented algorithm is linear in space and time, and produces no shrinkage of the surface topology. Moreover, the topology is not distorted because the low-pass filter preserves low-curvature components (the underlying shape of the aneurysm) while it attenuates high-curvature components (sharp peaks).

For each iteration of smoothing, a new nodal position is calculated by performing two consecutive weighted averaging steps: one with a positive scaling factor, λ, and the other with a negative scaling factor, μ. For each scaling factor, we obtain the set of elements that each node v_i is adjacent to (neighboring nodes, i*). The new position of each node is updated using the following formula:

$$v_i^{\prime }=v_i+c{\displaystyle \sum _{j\in i*}\frac{v_j-v_i}{|i*|}},$$ (2)

where c is either the λ or μ scaling factor and v_j is the neighbor of node v_i for j ∈ i*.

A smooth surface, x^N, is produced by iteratively applying a low-pass filter to the original surface signal, x, such that

$$x^N=f{(K)}^{N}x$$ (3)

$$f{(K)}^N={((I-\mu K)(I-\lambda K))}^2,$$ (4)

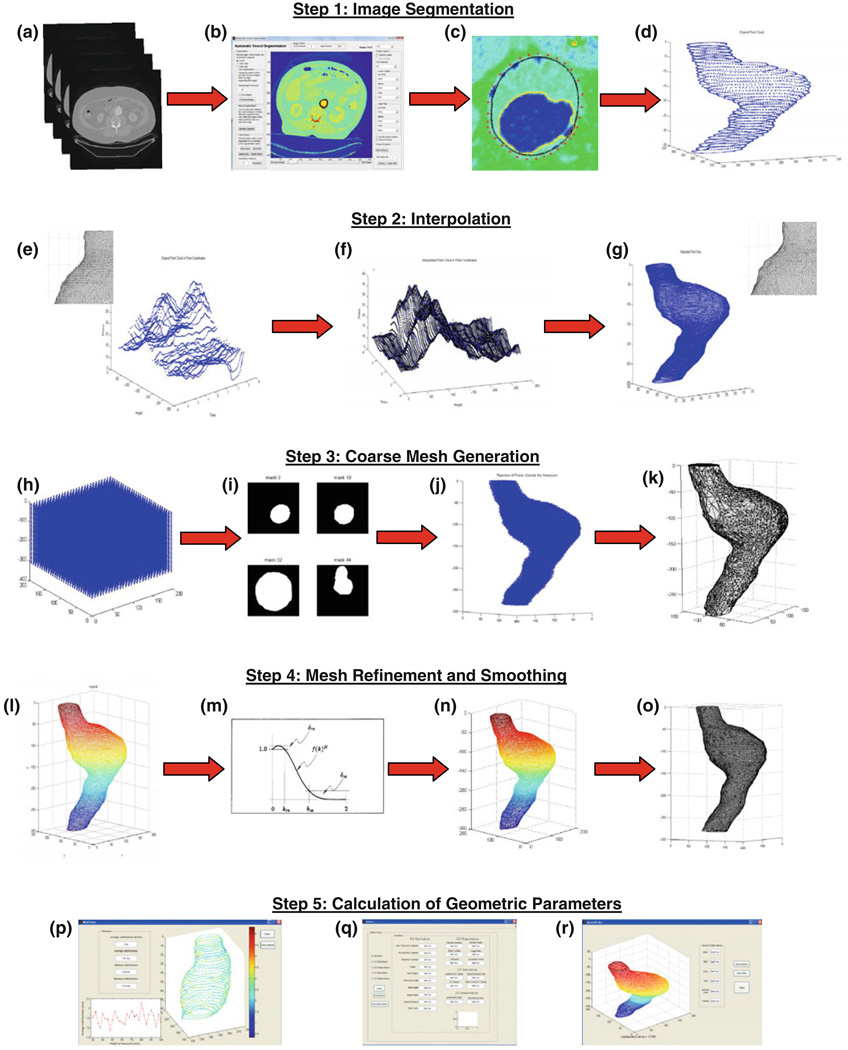
where f(K) is the transfer function of the low-pass filter and N is the number of iterations. It can be observed that f(K)^N ≈ 1 for low frequencies and f(K)^N ≈ 0 for high frequencies. In the transition band, the rate of decrease of this function is determined by the number of iterations N and the scaling factor λ in the transfer function equation (4). The transfer function decreases faster with larger N or λ. Since the function mimics a typical low-pass filter, by applying Eq. (4) the high-curvature components can be removed while the low-curvature components remain unchanged. The polygon generation, refinement, and smoothing steps of the framework are illustrated in Fig. 1.

FIGURE 1.

Flowchart for calculation of geometric parameters: (a) Load DICOM CT image; (b) vessel segmentation program; (c) segmented image; (d) point clouds generated from outer wall points; (e)–(g) interpolation; (h)–(j) uniformly distribute points; (k) generate coarse topology; (l) polygon refinement; (m, n) polygon smoothing; (o) final topology generated; (p)–(r) quantification of geometric indices and wall thickness.

Implementation of the Algorithms

The optimal number of iterations needed for polygon refinement and smoothing is determined by calculating an acceptable Q_ave (≥0.75) with minimal AAA sac volume change (≤1.5%). Polygon refinement ends when the surface polygon reaches a maximum Q_ave with no improvement after 15 consecutive iterations. We determined that a nodal distance equivalent to the interpolated slice spacing resulted in the highest Q_ave. However, an interpolated slice spacing less than the original CT slice spacing greatly increased the computational time. To achieve the maximum Q_ave without compromising on computational time, the interpolated slice spacing was set equal the pixel size of the CT images. For datasets where the pixel size exceeded 0.8 mm, a slice spacing of 0.75 mm was used as a default for the interpolation step to yield a high Q_ave.

CASE STUDY APPLICATION METHODS: TOPOLOGY-BASED AAA GEOMETRY QUANTIFICATION

Subjects and Image Data

The study population consists of 20 human subjects with AAAs; 10 ruptured (“R”) and 10 unruptured (“U”) datasets. Noteworthy is that the term “ruptured” is used in the context of this investigation to designate those aneurysms that were detected as ruptured in the last CT exam prior to emergent intervention, as well as those that ruptured within a month after the last CT exam and prior to the intervention. Abdominal DICOM images were acquired using contrast enhanced CT with the following imaging parameters: (i) scan matrix size = 512 × 512; (ii) average pixel size = 0.8874 mm (0.7031–1 mm); (iii) pixel intensity = 0–2000; and (iv) median slice thickness = 3.0 mm (1–10 mm).

Size, Shape, and Curvature Indices

Nine indices were calculated to quantify the size, shape, and curvature of each AAA model, as described by Martufi et al.⁹ We computed three 3D size indices: AAA volume (V), surface area (S), and intra-luminal thrombus volume (V_ILT), and two 3D shape indices based on V and S: the isoperimetric ratio (IPR) and non-fusiform index (NFI). In addition, we also calculated four second-order curvature-based indices: area-averaged Gaussian and Mean curvatures (GAA and MAA) and the L2-norms of these curvatures (GLN and MLN). All indices are calculated for the 20 AAA geometries using the framework described herein. The reader is referred to the “Appendix” for a complete mathematical description of the indices used in this feature-based approach of geometry quantification.

Wall Thickness

As described in Shum et al.¹⁸ 72 pointwise estimations of wall thickness are calculated for each cross section in a CT image stack, yielding the average thickness per cross section. We define wall thickness as the shortest distance between a point on the inner wall contour and another point on the outer wall contour. Computing the shortest distance between the two sets of points and multiplying by the pixel dimension yields a wall thickness estimate. The average wall thickness of the aneurysm sac (t_w,ave) was calculated based on the mean of the average cross-sectional wall thicknesses.

Statistical Analysis

The indices were calculated for the two population subgroups: unruptured aneurysms (n₁ = 10) and ruptured aneurysms (n₂ = 10). A multivariate analysis of variance (MANOVA) using the rupture status as a factor was performed for all indices as dependent variables to determine statistical significance (α = 0.05). Box and Whisker plots and ROC curves were generated for all the statistically significant indices. The area under the curve (AUC), which quantifies the predictability of each index, was calculated in addition to the cut-off value for each index that results in the highest Youden index. The Youden index is given as J = max(sensitivity + specificity − 1) and it corresponds to the point on the ROC curve that provides the highest accuracy. Sensitivity, or the true positive rate, and specificity, or the true negative rate, are calculated as the percentage of instances classified correctly for the given cut-off value.

Sensitivity to Random Noise

Due to inter-user variability in the segmentation process, which we quantified in our previous work,¹⁸ uncertainty errors exist in the nodal positions of the surface topology. A topology sensitivity analysis was performed by perturbing the surface triangles with random noise to mimic the inter-user variability in yielding different AAA geometries. Random noises were added to the nodal positions of the original topology of one AAA model, namely U8. Multiple noisy surface topologies were created at ten different noise amplitudes (in the 0.1–1.0 mm range). At each noise amplitude, 27 random generations of the topology were created yielding 270 topology variants of aneurysm U8. The topology-dependent geometric indices were calculated using the 270 noisy topologies and compared to the original, noise-free indices. The percent error at each noise amplitude and the 95% confidence intervals were calculated using the noise-free model as a reference standard.

RESULTS

A validation study was completed generating three idealized fusiform aneurysms of random dimensions using SolidWorks (Dassault Systèmes SolidWorks Corp., Concord, MA, USA). The volumes and surface areas were computed with this software and compared to those calculated with the corresponding surface topologies of five mesh densities for each of the fusiform shapes. This comparison revealed average relative percent errors ranging from 0.02 to 0.68% for these two geometric indices.

Table 1 shows the final average quality element index after smoothing for the study population, as well as the number of elements (N_elements) and nodes (N_nodes), volume prior to and after smoothing (V_inital and V_final, respectively), and number of iterations needed for polygon refinement (N_refine) and smoothing (N_smooth). The surface topology generation metrics averaged for the 20 AAA models are Q_ave = 0.77 (range: 0.75–0.78), N_elements = 87,546 (26,205 to 178,146), N_nodes = 42,931 (12,679 to 87,576), V_initial = 256.80 cm³ (24.79–638.52 cm³), V_final = 260.54 cm³ (35.31–644.56 cm³), N_refine = 238 (50–300), and N_smooth = 292 (12–863). The code written for this framework was run on 64-bit Windows workstations with up to 16 Gb RAM; the median CPU time required to obtain a surface topology [steps illustrated in Figs. 1e to 1o] was 17 min.

TABLE 1.

Average element quality index (Q_ave), number of nodes (N_nodes), number of elements (N_elements), initial and final volumes of the aneurysm model (V_initial and V_final), and number of iterations of polygon refinement and smoothing (N_refine and N_smooth).

AAA model	Qave	Nelements	Nnodes	Vinitial (cm3)	Vfinal (cm3)	Nrefine	Nsmooth
U1	0.77	46,313	22,671	101.94	103.47	205	243
U2	0.77	107,501	52,665	202.59	205.63	237	118
U3	0.76	64,436	31,602	173.31	175.91	215	200
U4	0.77	57,485	28,223	107.78	109.40	272	131
U5	0.77	60,508	29,734	96.00	97.44	180	198
U6	0.77	26,205	12,856	38.88	39.46	171	12
U7	0.75	27,069	12,679	24.79	35.31	50	151
U8	0.77	41,344	20,285	81.62	82.84	208	98
U9	0.77	46,300	22,594	94.95	96.37	272	237
U10	0.76	31,298	15,198	48.49	49.21	118	116
R1	0.76	105,929	52,071	311.46	316.12	300	352
R2	0.77	168,531	82,967	615.22	624.44	296	816
R3	0.76	63,680	31,097	151.16	153.42	251	235
R4	0.77	11,8921	58,255	296.57	301.01	290	863
R5	0.76	85,360	42,000	228.85	232.27	300	412
R6	0.77	143,882	70,508	632.52	635.59	300	43
R7	0.76	159,747	78,322	616.86	623.63	299	419
R8	0.78	76,085	37,326	186.72	189.52	300	208
R9	0.77	178,146	87,576	638.52	644.56	275	317
R10	0.76	142,187	69,995	487.84	495.16	229	662

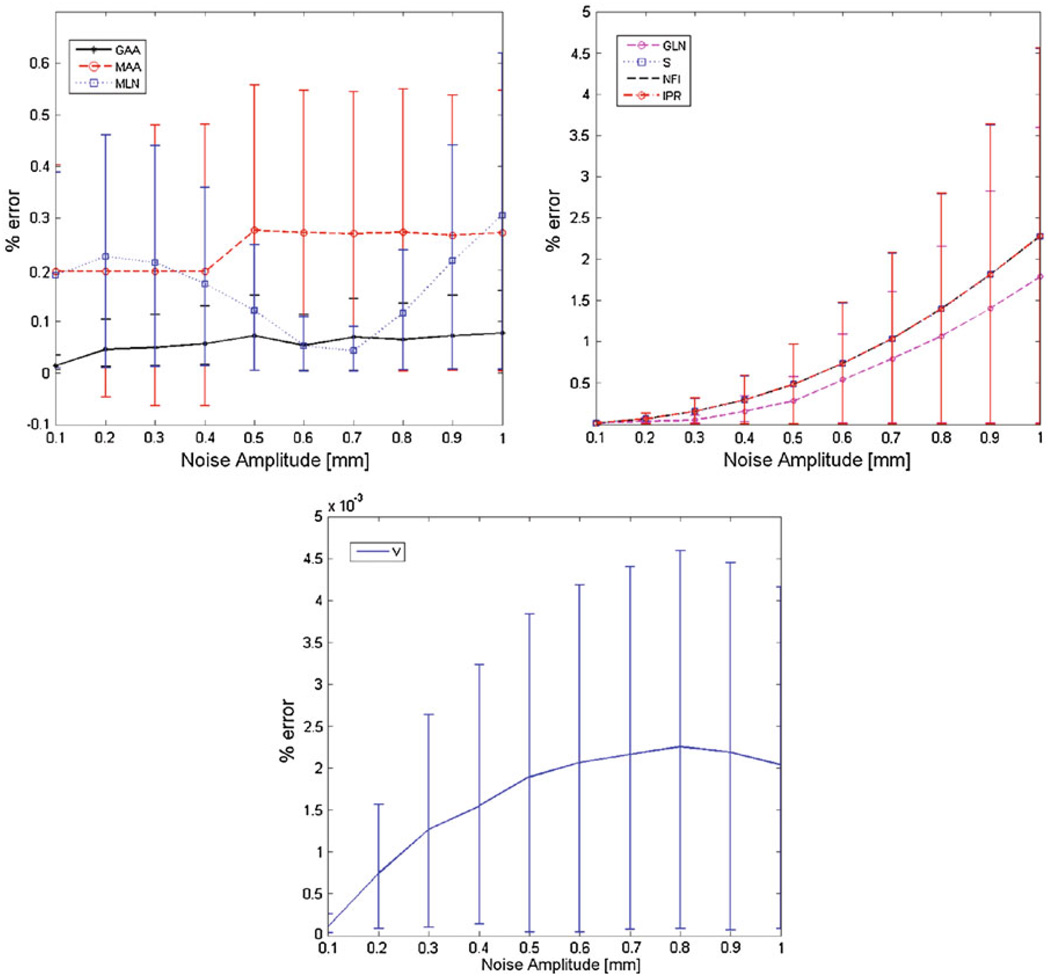
The topology sensitivity analysis (Fig. 2) reveals that GLN, S, NFI, and IPR have the highest percent errors, and as the noise amplitude increases, the percent error increases exponentially. All indices exhibited errors less than 3.4%, even at the highest noise amplitude of 1.0 mm. Among the curvature-based indices, GAA had the smallest error, which is less than 0.8% across all noise levels, and GLN had the largest error: 1.8% at a noise amplitude of 1.0 mm. NFI and IPR have similar error distributions since they are both calculated as a function of S and V. When compared to the pixel size of the original CT images (0.742 mm), the maximum noise amplitude due to CT resolution is 0.371 mm. At a noise amplitude of 0.371 mm, all topology-dependent indices yielded errors less than 0.3%, indicating that the geometry quantification approach is almost unaltered by the appearance of random noise in the original topology.

FIGURE 2.

Percent error and 95% confidence intervals for the topology-dependent indices: (a) GAA, MAA, and MLN; (b) GLN, S, IPR, and NFI; and (c) V for different noise amplitudes.

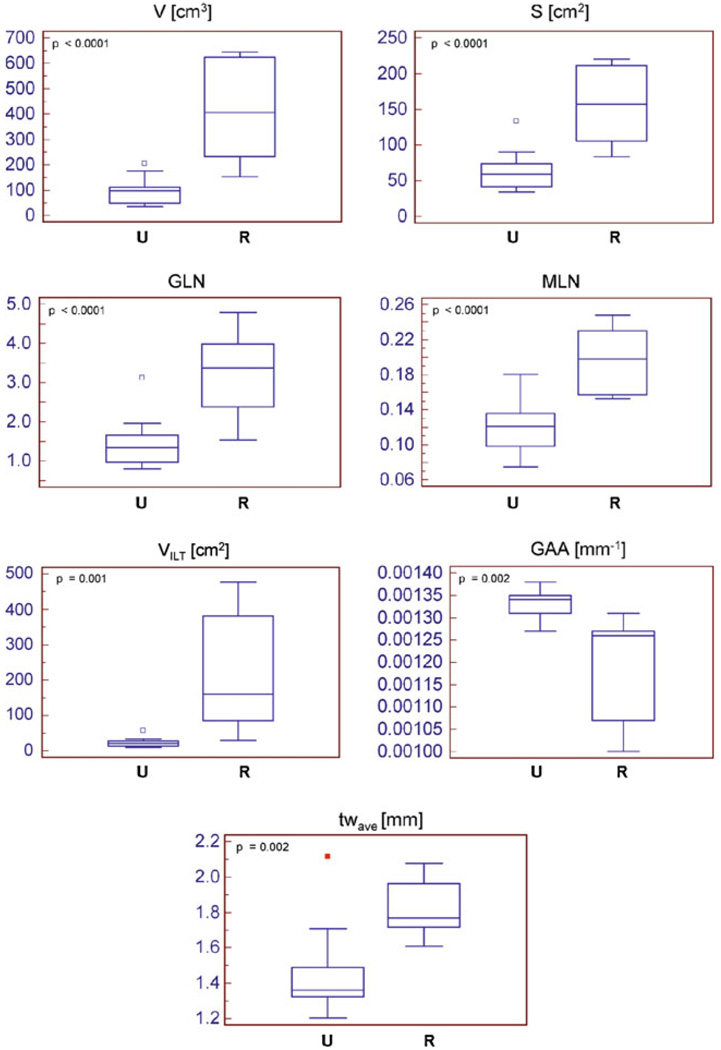
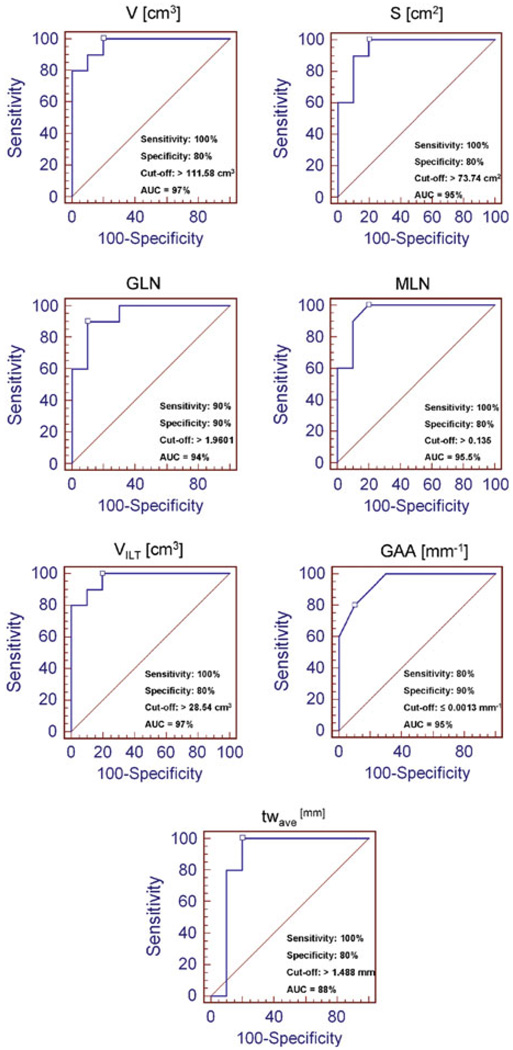
The mean and standard of deviation for each index were calculated for two population subgroups: ruptured (“R”) and unruptured (“U”) aneurysm datasets (Table 2). From the MANOVA, the statistically significant indices were V (p < 0.0001), S (p < 0.0001), GLN (p < 0.0001), MLN (p < 0.0001), V_ILT (p = 0.001), GAA (p = 0.002), and t_w,ave (p = 0.002). Box and Whisker plots were generated for these seven indices to visualize their distribution between the two subgroups, as shown in Fig. 3. Based on ROC curve analysis (Fig. 4), the indices with the highest prediction accuracy were V_ILT and V with AUCs of 97%, sensitivities of 100%, and specificities of 80% for V_ILT = 28.54 cm³ and V = 111.58 cm³.

TABLE 2.

Mean ± standard deviation, p-values, and AUC for all geometric indices for groups U (unruptured) and R (ruptured).

Index	Group U	Group R	p-Value	AUC
3D size indices
V (cm3)	100.32 ± 52.81	421.57 ± 192.40	<0.0001	0.97
S (cm2)	64.33 ± 28.25	154.93 ± 50.61	<0.0001	0.95
VILT (cm3)	20.06 ± 7.63	226.90 ± 168.90	0.001	0.97
3D shape indices (non-dimensional)
NFI	0.62 ± 0.08	0.58 ± 0.04	0.167	0.69
IPR	3.04 ± 0.33	2.83 ± 0.15	0.095	0.725
Second-order curvature-based indices
GAA (mm−1)	0.00133 ± 0.00003	0.00119 ± 0.00011	0.002	0.95
MAA (mm−1)	0.01338 ± 0.00084	0.01391 ± 0.00070	0.162	0.69
GLN (non-dim)	1.47 ± 0.64	3.26 ± 1.08	<0.0001	0.94
MLN (non-dim)	0.1215 ± 0.0290	0.1963 ± 0.0344	<0.0001	0.955
Wall thickness index (mm)
tw,ave	1.45 ± 0.26	1.82 ± 0.16	0.002	0.88

FIGURE 3.

Box and Whisker plots of the seven statistically significant indices.

FIGURE 4.

ROC curves for the seven statistically significant indices and computed AUC (%), sensitivity, specificity, and cut-off values.

DISCUSSION

Recent studies show that wall stress may be a better indicator for aneurysm rupture risk assessment than AAA maximum diameter. Fillinger et al.⁵ showed the feasibility of using FEA for patient-specific wall stress calculations and reported statistically significant differences in peak stress for ruptured/symptomatic AAAs (46.8 N/cm²) in comparison with those electively repaired (38.1 N/cm²). Another study reports that the site of rupture and the peak wall stress were correlated and that ruptured AAAs had significantly higher peak wall stress than non-ruptured AAAs.²⁵

A factor of significant importance in AAA rupture risk prediction is the non-uniformity of the aortic wall thickness. Di Martino et al.² using a laser micrometer, measured the thickness of AAA wall specimens obtained fresh from operating room patients undergoing surgical repair. A significant difference was found in wall thickness between ruptured (3.6 ± 0.3 mm) and electively repaired (2.5 ± 0.1 mm) aneurysms, as well as an inverse correlation between wall thickness and local tissue strength. In an autopsy study, Raghavan et al.¹⁴ analyzed the tissue properties of three un-ruptured and one ruptured AAA revealing that all aneurysms had considerable regional variation in wall thickness and a significant reduction in wall thickness near the rupture site. Similarly, Mower et al.¹⁰ demonstrated that wall thickness is a major parameter influencing wall stress distribution, rather than aneurysm maximum diameter alone.

This study demonstrates that seven of the ten reported indices, namely V, S, GLN, MLN, V_ILT, GAA, and t_w,ave, were statistically significant with all except GAA being larger for the ruptured aneurysms (Fig. 3). Ruptured aneurysms generally tend to be larger than non-ruptured aneurysms, which could explain the strong relationship between the three size indices (V, V_ILT,, and S) and rupture. Also, the non-ruptured aneurysms chosen in this study were smaller in size than the ruptured AAAs with respect to the maximum diameter (D_max,U = 40.31 ± 5.78 mm, D_max,R = 78.44 ± 13.16 mm, p < 0.0001). Based on the ROC curve analysis, V, V_ILT, and S, in addition to being the most statistically significant indices, also had the highest AUC. All the ruptured aneurysms had V > 111.58 cm³, V_ILT > 28.54 cm³, and S > 73.74 cm², indicating that, in general, they were larger in size. Eighty percent of the non-ruptured aneurysms had V ≤ 111.58 cm³, V_ILT ≤ 28.54 cm³, and S ≤ 73.74 cm². However, the curvature indices have similar significance levels and AUC as V and S, whereas GLN and GAA are able to classify the non-ruptured aneurysms better, giving 90% specificity for GLN > 1.9601 and GAA ≤ 0.00013 mm⁻¹. Previous reports show that peak wall stress is localized near the aorta–aneurysm inflection point where the aneurysm curvature changes.⁵ Moreover, the maximum stress being located at the posterior wall seems to coincide with peaks in the Gaussian curvature.¹¹

From ROC curve analysis, t_w,ave had an AUC = 88% and sensitivity = 100% and specificity = 80% for t_w,ave ≥ 1.488 mm. These results, in addition to the Box and Whisker plots, show that the average wall thickness of the aneurysm sac is larger for ruptured aneurysms (p = 0.002), with all ruptured AAAs having t_w,ave ≥ 1.488 mm and 80% of the non-ruptured aneurysms having t_w,ave < 1.488 mm. Previous studies^2,18 also report that ruptured aneurysms have thicker walls than non-ruptured aneurysms, though clinically relevant thresholds of wall thickness as they relate to AAA rupture potential have not been established elsewhere.

In the proposed framework, we defined two metrics to evaluate the quality of the polygons and determined the optimal number of iterations needed to achieve satisfactory smoothing, while avoiding oversmoothing. However, inter-user variability in the segmentation method could lead to the reconstruction of different AAA geometries, thereby yielding dissimilar index quantifications. We attempt to account for this variability in our topology sensitivity analysis by introducing randomly generated topologies of the same AAA dataset. Our analysis shows that when the maximum noise amplitude due to CT resolution is evaluated, the maximum error in the prediction of the topology-dependent geometric indices is 0.3%, indicating that the noise introduced to the polygons does not affect the indices significantly. The surface topologies generated with the proposed framework are dense and of high average element quality, which likely contributes to suppressing the errors resulting from user-dependent segmentation variability or noise.

The reliability of the geometry quantification approach relies on the accuracy of the segmentation algorithm. We have previously addressed the limitations of the algorithm and quantified VESSEG’s inter-user variability and reproducibility measures.¹⁸ In addition to these, the feature-based approach tends to reduce the geometric characterization to a relatively small number of indices. Without a priori knowledge of the exact discriminator of AAA rupture risk, a preconceived set of indices may omit important information necessary for evaluating size and shape differences between two population groups. The size difference between the two groups is also a limiting factor as it is difficult to interpret the differences in the geometric parameters between these two groups of aneurysms. Another limitation of the study is that the use of area-averaged curvatures may lead to the exclusion of local changes in curvature in the statistical comparison of the population subgroups. A direct comparison of the spatial distributions of the Gaussian and mean curvatures could be performed although this would likely consist of a qualitative analysis. Conversely, computing the root mean square curvature, which was first described by Ateshian et al.¹ and also used to characterize heart valves,^16,19 can provide a measure of surface flatness. To this end, additional geometric indices should be defined to describe both the global and local curvature characterizations along the aneurysm surface, as well as geometric quantities associated with surface deformation, changes in curvature and strain, as described by Smith et al.²⁰

CONCLUSIONS

The objectives of this study were to develop a framework for the automatic generation of AAA outer wall surface topologies and apply it to compute a set of indices that accurately describe the aneurysm geometry. Based on Delaunay triangulation, node-based interpolation for polygon refinement, and volume-preserving smoothing algorithms, the proposed framework can automatically generate the surface polygons from masks resulting from a prior image segmentation step. While yielding a minimum average quality index of 0.75 and a maximum reduction in aneurysmal sac volume of 1.5%, the surface topologies can be used for geometric characterization of AAA size, shape, and local curvature. The sensitivity of the geometric indices due to human intervention in the image segmentation step revealed index prediction errors of up to 0.3% at the maximum noise amplitude due to medical image resolution. Applying the framework to a pilot population study comprised of ten ruptured and unruptured AAA datasets yielded seven statistically significant indices that discriminate between the two groups. These are AAA volume, ILT volume, and surface area (size indices), aneurysm sac averaged wall thickness, and the area-averaged Gaussian curvature and L2 norms of the Gaussian and mean curvatures (curvature-based indices). Future work would involve statistical analysis of aneurysms that are size matched. In addition, a larger population study is required to confirm the significance of this feature-based approach in individualized predictions of rupture-risk assessment.

The surface topologies could also be used in FEA to obtain regional mappings of wall stress. Due to the inability to measure wall thickness non-invasively, a uniform thickness of 1.5 mm is typically assumed in current AAA FE modeling work. Other authors have also used idealized aneurysm shapes in their attempt to characterize aneurysm geometry. However, realistic AAAs have complex, tortuous, and asymmetric shapes with local changes in surface curvature and regional variations in wall thickness. It is evident that an accurate characterization of the aneurysmal sac shape and its wall thickness distribution need to be accounted for in the assessment of AAA rupture risk. Geometry quantification of AAAs can be used to establish correlations with peak wall stress predictions obtained with FEA and discriminate aneurysm populations as a means for rupture risk assessment. While this study does not provide direct insight into the possible clinical use of such correlations, we believe that it provides the foundation necessary for future efforts in that direction.

APPENDIX

3-D shape indices.

Nomenclature	Name	Equation
IPR	Isoperimetric ratio	$\text{IPR}=\frac{S}{V^{2/3}}$
NFI	Non-fusiform index	$\mathit{\text{NFI}}=\frac{\frac{S}{V^{2/3}}}{\frac{S_{\mathit{\text{fusiform}}}}{V_{\mathit{\text{fusiform}}}^{2/3}}}=\frac{\mathit{\text{IPR}}}{{\mathit{\text{IPR}}}_{\mathit{\text{fusiform}}}}$

Second-order curvature-based indices (calculation described in detail in Martufi et al.⁹)

Nomenclature	Name	Equation
GAA	Area averaged Gaussian curvature	$\mathit{\text{GAA}}=\frac{{\displaystyle {\sum }_{\mathit{\text{all elements}}}{K}_j{S}_j}}{{\displaystyle {\sum }_{\mathit{\text{all elements}}}{S}_j}}$
MAA	Area averaged Mean curvature	$\mathit{\text{MAA}}=\frac{{\displaystyle {\sum }_{\mathit{\text{all elements}}}{M}_j{S}_j}}{{\displaystyle {\sum }_{\mathit{\text{all elements}}}{S}_j}}$
GLN	L2 norm of the Gaussian curvature	$\mathit{\text{GLN}}=\frac{1}{4\pi }\sqrt{{\displaystyle {\sum }_{\mathit{\text{all elements}}}{S}_j}·{\displaystyle {\sum }_{\mathit{\text{all elements}}}\left(K_j^2{S}_j\right)}}$
MLN	L2 norm of the Mean curvature	$\mathit{\text{MLN}}=\frac{1}{4\pi }\sqrt{{\displaystyle {\sum }_{\mathit{\text{all elements}}}\left(M_j^2{S}_j\right)}}$