Summary
In this article we develop a latent class model with class probabilities that depend on subject-specific covariates. One of our major goals is to identify important predictors of latent classes. We consider methodology that allows estimation of latent classes while allowing for variable selection uncertainty. We propose a Bayesian variable selection approach and implement a stochastic search Gibbs sampler for posterior computation to obtain model averaged estimates of quantities of interest such as marginal inclusion probabilities of predictors. Our methods are illustrated through simulation studies and application to data on weight gain during pregnancy, where it is of interest to identify important predictors of latent weight gain classes.
Keywords: Bayesian model averaging, Finite mixture model, Markov chain Monte Carlo, Multinomial logit model, Variable selection
1. Introduction
Latent class models arise naturally in the context of modeling heterogeneity and are particularly suited for data expected to have underlying clusters. It is well-known that a finite mixture of normal densities can characterize densities of widely varying shapes. Hence these models are appealing for both cluster analysis and density estimation. Latent class models and their extensions to more complicated settings such as longitudinal data have gained considerable popularity and have been successfully used for many applied problems. For example, Oh et al. (2003) use latent class logit models for modeling heterogeneity in a target market or population, Elliott et al. (2005) use latent class trajectory models to distinguish patients with depressive symptoms, while Dunson et al. (2008) develop semiparametric Bayesian latent class trajectory models for joint modeling of pregnancy weight gain trajectory clusters and response densities of birth weight.
Bayesian analysis of latent class or Gaussian mixture models poses several challenges such as selecting the number of components and the so-called label switching problem. The Bayes information criterion (BIC) (Schwarz, 1978) and the deviance information criterion (DIC) (Spiegelhalter et al., 2002) are often used to choose the number of classes. For these models, Schwarz's theoretical justification of the BIC as an approximation to the log marginal likelihood does not hold, and the DIC does not have a unique interpretation (Celeux et al., 2006). Full Bayesian analysis of mixtures with an unknown but finite number of components can be carried out using the reversible jump Markov chain Monte Carlo (MCMC) method of Richardson and Green (1997). Their approach treats the number of components as unknown and mixes over all possible values of number of classes. The other alternative is to use semiparametric approaches that avoid specification of a fixed number of classes, for example using Dirichlet process mixtures (Escobar and West, 1995). The non-identifiability of the components poses another hurdle; this happens when the parameters have exchangeable priors and permuting the labels of the parameters produces identical posterior distributions. One solution to this problem is to impose an identifiability constraint on the parameters, for example impose a particular ordering on the class means or precisions. There are other alternatives that define label invariant loss functions and minimize the loss using stochastic optimization; for a detailed review see Jasra et al. (2005) and the references therein.
In this article our focus is on developing latent class models for scenarios where information is available on several covariates, in addition to having a univariate response variable. We let the probability of belonging to a particular class depend on subject-specific covariates through a multinomial logit model. While one alternative is to use probit regression for the underlying class probabilities, epidemiologists find logistic regression models more appealing, because the regression coefficients can be interpreted as the change in the log-odds of the binary response variable for an unit change in the predictors. In particular, it is of considerable interest to determine important predictors of the latent classes. We develop Bayesian variable selection methods for a novel formulation of multinomial logit regression models embedded in latent class models.
If the latent classes were known the problem would boil down to incorporating variable selection uncertainty in logistic regression models for unordered categorical data. Although multinomial probit models have been widely studied and used in Bayesian statistics, especially after the seminal ideas of data augmentation by Albert and Chib (1993), multinomial logit models have not gained so much popularity in spite of the natural interpretability of the design coefficients in terms of odds ratios. This is perhaps because these models are less amenable to Bayesian computation compared to their probit counterparts. Gustafson and Lefebvre (2008) develop Bayesian variable selection methods for multinomial probit models, where the set of relevant predictors is allowed to vary with the class. A recent paper by Holmes and Held (2006) provides a clever representation of Bayesian logistic regression in terms of scale mixture of normal densities. We extend their idea to a mixture model framework, which simultaneously incorporates covariate information and variable selection uncertainty, and propose a joint model for infant birth weight and latent pregnancy weight gain classes. Although our methodology has been motivated by data from a reproductive epidemiologic study, the methods can certainly be used for more general settings.
Section 2 introduces our Bayesian latent class model, then provides a detailed description for choice of prior distributions and outlines a Gibbs sampling algorithm for posterior computation. In Section 3 we validate our approach through simulation studies. In Section 4 we apply our methodology to the motivating application of pregnancy weight gain classes and birth weight. We identify several important predictors of weight gain classes. In addition we compare our latent class model to a commonly used model with pre-determined classes, and show that our model can outperform it. In Section 5 we summarize our key contributions and conclude with a list of possible extensions.
2. A Bayesian Latent Class Model to Include Predictors
We consider the following latent class model with Q classes:
| (1) |
where yi denotes the continuous, univariate response variable for the ith subject, μk and ϕk denote the kth class mean and precision, and wik is the binary latent allocation variable, such that wik = 1 if the ith subject belongs to class k and 0 otherwise. Additional information is available on each subject through a set of p covariates, denoted by xi = (xi1, … xip)′, which we allow to influence the response distribution through the class probabilities.
The latent class indicator variables are assumed to be drawn from a multinomial distribution, whose cell probabilities depend on predictors via a polytomous generalization of the logit link:
| (2) |
where denotes a multinomial distribution with cell probabilities πi = (πi1, …, πiQ)′. Following common practice we set βQ = 0, so that the other coefficients can be interpreted in terms of change in log-odds relative to this baseline category.
2.1 Prior Distributions
Choice of prior distributions is an important aspect of Bayesian analysis. Since it may be unrealistic to assume the availability of strong prior information regarding mixture components in practice, we follow the guidelines of Richardson and Green (1997). We choose weakly informative prior distributions; however, subject matter knowledge can be incorporated in our method whenever available. Our prior distributions are as follows:
| (3) |
where denotes the Gamma distribution with mean g/h and variance g/h2. Without further restrictions, the class labels for k = 1, 2, … Q, are not uniquely determined and a permutation of the labels would lead to the same model. Since our interest lies in inferences on class-specific parameters, the non-identifiability of labels would cause a problem in posterior computation. We adopt a traditional choice and impose restrictions on the class means for identifiability. Henceforth we assume μ1 > μ2 > … μQ.
It is of primary interest to identify important predictors of the latent classes. Moreover, including the full set of predictors will ignore uncertainty and may lead to more error-prone estimates of class probabilities due to inclusion of irrelevant predictors. With that in mind, we formally account for variable selection uncertainty in our prior distribution. We specify a mixture of point mass at zero and a normal distribution for the βk's:
| (4) |
where δ0(.) represents a measure concentrated at 0. Here pkj denotes the exclusion probability of the covariate xj in predicting membership to class k, with respect to the baseline class Q. The above formulation essentially embeds models with all possible combinations of predictors in an all encompassing mixture model. This allows unimportant predictors to automatically drop out of the model via zeroing of the regression coefficients βk. We can use a Gibbs sampling algorithm for posterior computation, which simultaneously explores models and parameters, commonly referred to as the stochastic search variable selection (SSVS) approach (George and McCulloch, 1993).
2.2 Posterior Computation for Multinomial Logit Models
We first briefly review the computational challenges involved in Bayesian logistic regression with two categories. While conditionally conjugate prior distributions are available for linear models and the posterior distribution can be computed in closed form, that is not the case for either probit or logistic models. For normal prior distributions on regression coefficients, the posterior distribution is known only up to a normalizing constant. The data augmentation approach of Albert and Chib (1993) introduces underlying normally distributed latent variables for observed binary response variables in probit models. Marginalizing out the latent variables yields the original likelihood. Conditional on the latent variables, the full-conditional posterior distributions of the regression coefficients are available and Gibbs sampling can be used to draw samples from the joint posterior distribution.
Taking the latent variables to be distributed as a logistic distribution would lead to the logistic likelihood. However this will not lead to a conditionally conjugate form for the regression coefficients. In a recent article, Holmes and Held (2006) develop an innovative scale mixture of normals representation for logistic regression. They introduce an extra layer of latent variables as scale parameters, which yields conditionally conjugate forms. For a binary response variable wi, their specification is as follows:
| (5) |
| (6) |
| (7) |
where zi and λi are latent variables and KS denotes the Kolmogorov Smirnov distribution (Devroye, 1986). As in the probit case, the original logistic regression model is obtained by marginalizing out the latent variables. The above specification leads to normal full conditional distributions for the regression coefficients and truncated normal distributions for zi, as in probit regression. However, it is not straightforward to sample from the full conditional distribution of λi, and the authors outline a rejection sampling method. This method is attractive for its exact representation of the logistic model in terms of scale mixture of normals; however, we have found that it becomes computationally prohibitive for large values of sample size, say a few thousands, as in our application. Hence we adopt an approximation of the logistic density with location parameter μ, by a tν(μ, σ2) distribution (O'Brien and Dunson, 2004), with ν degrees of freedom and location and scale parameters μ and σ2 respectively. They recommend using ν = 7.3 and σ2 = π2(ν − 2)/(3ν), values chosen to have equal variances for the exact and approximating density and to minimize the integrated squared distance between them. To obtain exact inferences, one can use importance sampling to re-weight the samples generated from a Markov chain Monte Carlo (MCMC) output. Kinney and Dunson (2007) illustrate that the above approximation is very close, leading to weights that are close to 1, and hence the weighted and unweighted results are nearly the same. Thus we have refrained from using the importance re-weighting to avoid extra computational overhead. Because a t distribution can be expressed as a scale mixture of normals, this approximation yields normal and Gamma full conditional distributions which are easy to sample from and helps us eliminate the time-consuming rejection sampling step. An approximation of the logistic distribution by a finite scale mixture of normals (Frühwirth-Schnatter and Frühwirth, 2010) may offer another promising alternative to the Holmes and Held (2006) approach.
As it is likely that our latent class model will have more than two classes, we need to extend the above approach to accommodate for an unordered categorical response variable. Suppose there are Q categories and let wik = 1 if subject i belongs to the kth category and 0 otherwise. Holmes and Held (2006) show that the conditional likelihood L(βk|β−k, w) also has the form of a logistic regression in terms of wik for the kth class vs. all the other classes, where β−k = (β1,…,βk−1,βk+1,…,βQ). This is the key idea for extending our latent two-class model to a latent multi-class model, and allows for the construction of a Gibbs sampler, which loops over the parameters of all classes.
2.3 Gibbs Sampling Algorithm for Latent Class Model
We first define auxiliary variables in the context of our latent class model, given by eqn (2).
| (8) |
| (9) |
| (10) |
where i = 1,…n and k = 1,…,Q − 1. We set and as per the recommendations of O'Brien and Dunson (2004). The Gibbs sampling algorithm for posterior computation proceeds by drawing samples from the full conditional distributions:
-
(1)
For k = 1,…Q, μk|(ϕ,w,z,ζ,β,βϕ,y) ~ N(Eμk,Vμk), Vμk = (κ + ϕknk)−1, , with μ1 > μ2 >…μQ.
-
(2)
For k = 1,…Q, , .
-
(3)
For i = 1,…n, wi|(μ,ϕ,β,βϕ,y) ~ MN(Q,θi), θi = (θi1,…,θiQ)′, .
-
(4)
For k = 1,…Q − 1 and for i = 1,…n, , where denotes the logistic distribution with location and scale parameters μ and S2 respectively.
-
(5)
For k = 1,…Q − 1 and i = 1,…n, .
-
(6)
For k = 1,2,…Q − 1, and j = 1,2,…,p, , where β−kj = (βk′j′ : k′ = 1,…,k − 1,k + 1,…,Q − 1; j′ = 1,…,j − 1,j + 1,……p), , ,
-
(7)
βϕ|(z,w,μ,ϕ,β,ζ,y) ~
We have done a block updating for (w, z, ζ) in the above Gibbs sampler. In particular, it is necessary to integrate out z in the full conditional distribution of w, otherwise wik would be a deterministic function of zik.
3. Simulation Study
To evaluate the performance of our method, we simulate 25 datasets with sample size 3,000 and Q = 4 classes. We consider 20 predictors (besides the intercept), generated from independent N(0,1) variables. The true βk's are chosen to be sparse: β1 = (0.8,1,2,0.5,0,…,0), β2 = (0.3,0,…,0,−1,1.7,−2), and β3 = (0.3,1,−2,0.8,0.9,0,…,0). The values are chosen so that the true predictors of classes 1 and 2 are different, and most of those for classes 1 and 3 are overlapping but with different magnitudes and signs. We generate the class labels from a multinomial distribution with cell probabilities as given in eqn (2). To have resemblance with our real data, the true class means and precisions are set close to the posterior means obtained from using a latent class model with 4 classes for the real data. They are (0.58, 0.44, 0.38, 0.20) and (43.49, 78.32, 101.95, 45.71) respectively.
The prior distributions and their hyperparameters are chosen as described in Section 2.1. For class means and precisions, we choose data-dependent hyperparameters, similar to Richardson and Green (1997). In particular, we take ξ as the observed sample mean and 1/κ as the square of the observed range of the data. This leads to a fairly weak prior for the class means. The values of α, g and h are taken as 2, 0.2 and 10/(observed range)2. The prior exclusion probabilities, pkj are set equal to 1/2, which corresponds to an uniform prior over the model space, and , the prior variance of βkj is taken to be 1.
3.1 Selection of the Number of Classes
Our Bayesian variable selection approach assumes that the number of latent classes is fixed. Thus, we first address how to select the number of classes using the pseudo Bayes factor (PSBF) (Geisser and Eddy, 1979). The PSBF is based on the idea of choosing models based on their leave-one-out cross-validation predictive densities. The PSBF for comparing models Mj and Mj′ with j and j′ classes is: where y−i = (y1,…,y(i−1),y(i+1),…yn). Gelfand and Dey (1994) describe how to estimate PSBF from MCMC output. We also calculate the BIC for a simplified log-likelihood ignoring covariates, as it is readily available as part of the R package mclust.
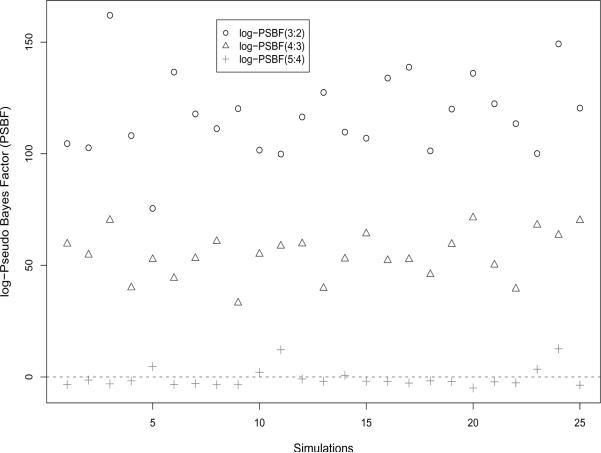
We run the Gibbs sampler described in Section 2.3 under each of 2, 3, 4, and 5 class models for 25,000 iterations, and discard the first 5,000 samples as burn-in. We find that PSBF shows an overwhelming support for the 4 class model versus 2 and 3; however, it does not penalize the 5 class model as much. Interestingly, estimates of true Bayes factors based on path sampling in Scaccia and Green (2003) also show a similar trend: a steady incline and then leveling off for models with more classes. It is likely that there is some inherent problem of identifiability in these models, which is responsible for not penalizing the over-parameterized models enough. PSBF identifies the 4 class model as the true model 19/25 times. BIC fails to identify the true model in all 25 datasets, it almost always chooses the 2 class model. The BIC calculation assumes a typical univariate mixture model without covariates, i.e., , π = (π1,…,πQ)′, i = 1,…n. The poor performance of BIC in this case may be attributed to the over-simplified log-likelihood used instead of the true one.
3.2 Bayesian Variable Selection and Bayesian Lasso
We now study the performance of our Bayesian variable selection (BVS) approach under the 4 class model. We also develop a Bayesian analogue of the Lasso (Tibshirani, 1996), and compare it to BVS. We extend the Bayesian Lasso (BL) of Park and Casella (2008) for linear regression to our latent class model. BL leads to using Laplace priors for the regression coefficients, , in place of the mixture priors described for BVS in eqn (4). A Gibbs sampler can be developed for the latent class model with BL, exploiting the fact that the Laplace distribution can be expressed as a scale mixture of normals. The resulting hierarchical prior is βkj|η ~ N(0, ηkj2), ηkj2 ~ ε(ak2/2), k = 1,…Q−1, j = 1,…p, where ε(α) is the exponential distribution with mean 1/α. This produces tractable full conditional distributions viz. normal for βkj and inverse-Gaussian for 1/ηkj2, leading to a straightforward Gibbs sampler. One option is to put a weak prior on the penalty parameter, ak2, to learn adaptively from the data. However, for our model there is not enough information on this parameter, and putting a prior had adverse effects on MCMC convergence. Hence, we implement BL for several fixed values of ak2: the mean, 25th, 50th, and 75th percentiles of a Gamma prior distribution, , with hyperparameters as in Park and Casella (2008).
The posterior inclusion probability of a predictor xj for predicting membership to class k vs. baseline class Q, is the sum of posterior probabilities of all models with βkj ≠ 0. Its Monte Carlo estimate is the proportion of non-zero βkj's in the MCMC samples. The Bayes factor (BF) for testing the hypothesis that xj is a predictor of class k vs. the hypothesis that it is not, is the ratio of posterior odds to prior odds: {p(βkj ≠ 0|y)/p(βkj = 0|y)}/{p(βkj ≠ 0)/p(βkj = 0)}. For BVS, we flag a covariate as important using two thresholds: BF> 1 and BF> 3.2, using Jeffreys' scale of evidence (Jeffreys, 1961). For BL, a covariate is flagged if the 95% posterior credible interval of the associated regression coefficient does not contain zero.
The summarized results are shown in Web Figures 1–3 and Web Table 1. The rate of classifying subjects to the true class is best for BVS, with a median around 0.8. For variable selection, BVS and BL are comparable in identifying true predictors, while BVS with BF> 3.2 does best overall in controlling false positives. Web Table 3 shows the mean squared error (MSE) in estimating βkj's. BL consistently has a higher MSE than BVS. A cross-validation approach to select ak2 may improve the performance of BL, but will be computationally much more demanding, so we do not consider it here.
4. Application to Data From PIN Study
4.1 Description of Data and Scientific Goals
We use data from the Pregnancy, Infection and Nutrition (PIN) studies (Savitz et al., 1999; Deierlein et al., 2008), which consists of multiple cohorts of pregnant women from central North Carolina. Weight gain during pregnancy has been shown to be associated with various maternal and child health outcomes like mode of delivery, child birth weight, preterm birth, maternal postpartum weight-retention etc. (Viswanathan et al., 2008). The Institute of Medicine (IOM) specifies a recommended weight gain for women based on their pregravid body mass index (BMI) (Institute of Medicine, 1990, 2009). Based on the IOM recommendations, women can be classified into one of the three IOM weight gain classes: inadequate, adequate, and excessive. Since the cut-offs for these classes are often debated and do not take into account any other maternal characteristics apart from pre-pregnancy BMI, we propose an alternative approach in which we let the classes be unknown, and the probability of being allocated to a class depend on covariates.
One of our primary goals is to investigate which additional maternal characteristics such as age, race, diet, etc. are predictive of the mother's weight-gain class. Considering both continuous and categorical variables representing maternal characteristics, we have 21 predictors in all. We develop a Bayesian hierarchical latent class model, with class probabilities depending on subject-specific predictors. In addition we formally account for variable selection uncertainty in the model and obtain posterior estimates of quantities of interest such as log-odds for a particular covariate via Bayesian model averaging (BMA). The idea is that this approach would automatically zero out the unimportant predictors of weight gain class, and thus enable us to identify relevant predictors and possibly improve predictions of health outcomes such as birth weight. We analyze data from 2,660 pregnant women with complete information on outcome and covariates of interest.
4.2 Joint Model for Birth Weight and Weight Gain Class
A simple two-stage approach for modeling birth weight and weight gain class is to: i) first estimate the latent weight gain class using the model in Section 2, and then ii) use the estimated class as a “known” predictor in a linear regression model with child's birth weight as the outcome. This naïve approach has two main drawbacks. First, it ignores uncertainty in estimating latent classes by treating them as observed covariates. Second, the weight gain classes cannot borrow any information from the birth weight distribution, as they are constructed independently of birth weight. Hence, instead of using this approach, we develop a joint model for latent classes and birth weight, such that the classes also depend on birth weight. Moreover, the latent classes used as unknown covariates in the birth weight regression are not fixed for any individual. They are allowed to vary across MCMC iterations, with more probable classes (that receive more weight under the posterior distribution) appearing more frequently. We provide a detailed description of our joint model below.
We choose the first level of our joint model as described in eqn (1) and eqn (2). Here yi represents the weekly weight gain rate for the ith subject, where weekly weight gain rate is calculated as (total weight gain recorded at last visit/gestational age at last visit in days)×7. Let xi = (xi1, … xip)′ denote the p covariates, and wi = (wi1, wi2, … wiQ)′ be the vector of latent class indicators, where wik = 1 if the ith subject belongs to class k and 0 otherwise. We now specify the next hierarchy of the model: birth weight regression given the latent weight gain classes. As birth weight distribution has slightly heavier tails than a normal distribution, we assume that the errors follow a t distribution. Let bwti denote the ith person's birth weight and ui(wi) denote the corresponding r by 1 vector of covariates, which includes indicators of the latent classes and their interactions with indicators of the BMI groups. We include these interactions because weight gain recommendations depend on pregravid BMI, as the implications of varying amounts of weight gain depends on maternal weight status before pregnancy. The resulting model is
| (11) |
where G(a, b) is a Gamma distribution with mean a/b and variance a/b2. This leads to t errors with scale parameter 1/τ and a degrees of freedom (df). In accordance with the belief of epidemiologists, this model assumes that conditional on the latent classes, birth weight is independent of weight gain. In reality, the latent classes are not observed and induce a dependency among birth weight and weight gain, thus making it possible for birth weight to inform the classification.
By examining residual plots we take a = 20 which works reasonably well. For the prior distribution for α to be at least as flat as the likelihood (Clyde and George, 2000) we take t priors with a df and scale parameter 1/τ for α. The prior distribution for τ is p(τ) ∝ 1/τ, 0 < τ < ∞, and those for unknown parameters in eqns (1) and (2), are chosen to be the same as described in Section 2.1.
4.3 Analyses and Results for Classes Based on Weekly Weight Gain Rate
We carry out the analysis for the above model using the Gibbs sampler in Section 2. We run the Gibbs sampler for 100,000 iterations, saving every 10th iterate to reduce autocorrelation and save computer memory. The first 1,000 samples of the thinned chain are discarded as burn-in. Motivated by a desire to have parsimonious and interpretable models, we do not consider models with more than 6 classes. We choose hyperparameters based on the recommendations by Richardson and Green (1997) and calculate the PSBF for models with 2–6 classes. The motivation for using PSBF is to choose models based on leave-one-out cross-validation predictive densities for birth weight. The PSBF for comparing models Mj and Mj′ with j and j′ classes is defined as
where bwt−i =(bwt1, …, bwt(i−1), bwt(i+1), … bwtn). The estimates of PSBF(3:2), PSBF(4:3), PSBF(5:4) and PSBF(6:5) are 2.19 × 1013, 4.64 × 107, 6.06 and 2.13 respectively. While the actual value of PSBF picks the 6 class model, a close scrutiny reveals a similar trend as in the simulation studies in Section 3. There is a sharp rise in PSBF until the 4 class model is reached and then it stabilizes. For the simulation studies this happened exactly after reaching the true class model, so we set the number of classes, Q = 4. For the selected model, we run the Gibbs sampler for a million iterations, saving every 100th sample.
Based on the mean weekly weight gain rate, we shall refer to classes 1, 2, 3 and 4 as very high, high, moderate and low weight gain rate classes. Prior hyperparameters are chosen as in Section 3. The only difference is instead of using data-dependent prior distributions, we now use subject matter knowledge to construct weakly informative priors. It is hypothesized a priori that the range of weight gain in kilograms is [−9, 36], and dividing this by a representative gestational age of 40 weeks, the postulated range for weekly weight gain rate is I = [−0.225, 0.9]. In particular, ξ and 1/κ in eqn (3) are chosen to be the mid-point of I and the square of its range respectively.
We also carry out a separate analysis to compare our results with IOM classes. Here we consider three prespecified weight gain classes (inadequate, adequate and excessive), with cut-offs formed using the IOM recommendations. Thus this involves only the birth weight t regression in eqn (11), with indicators of classes that are completely known.
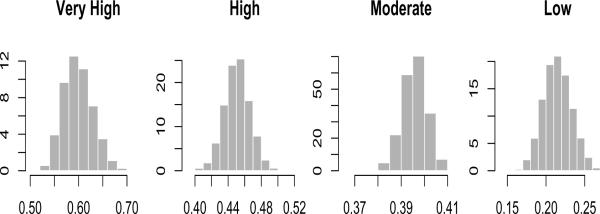
We examined trace plots of all parameters for MCMC convergence and mixing. Web Figure 6 shows agreement of inclusion probabilities from two different runs of the Gibbs sampler, started from dispersed initial values, indicating further empirical evidence of MCMC convergence. The posterior summaries are presented in Figure 2 and Tables 1, 2, 3. Figure 2 shows the posterior densities for mean weekly weight gain rate for all classes. Summarizing the results from Tables 1, 2 and 3, it appears that underweight women tend to be in the moderate class with high probability whereas overweight and obese women tend to be in the low class. This agrees with the fact that the heavier women are expected to gain less weight and vice versa. Black women or those with depressive symptoms are more often in the low class compared to moderate or high. Women who report vomiting naturally belong to the low class vs. moderate or very high. Non-smokers tend to be in the low or moderate class. Some other covariates that were also flagged as important are mother's height, percentage of protein in the diet, physical activity in the 3 months prior to pregnancy, and parity.
Figure 2.
Posterior density (y-axis) plots of mean weekly weight gain rate (x-axis) for very high, high, moderate, and low classes.
Table 1.
Table showing log(odds) of belonging to very high vs. low weekly weight gain rate class for having covariates that are found “interesting” (marginal posterior inclusion probability > 0.75); note that P(β1j ≠ 0) was fixed at 1 for the Intercept
| 95% C.I. | |||
|---|---|---|---|
| Intercept | 0.33 | 1 | (−0.66, 1.24) |
| obese | −2.03 | 1 | (−2.6, −1.51) |
| nulliparous | 0.98 | 1 | (0.53, 1.47) |
| non-smoker | −0.54 | 0.83 | (−1.16, 0) |
| height | 0.35 | 0.9 | (0, 0.62) |
| physical activity | 1.11 | 0.99 | (0.44, 1.73) |
| vomiting | −0.72 | 0.93 | (−1.31, 0) |
Table 2.
Table showing log(odds) of belonging to high vs. low weekly weight gain rate class for having covariates that are found “interesting” (marginal posterior inclusion probability > 0.75); note that P(β1j ≠ 0) was fixed at 1 for the Intercept
| 95% C.I. | |||
|---|---|---|---|
| Intercept | 0.64 | 1 | (−0.78, 1.72) |
| overweight | −1.24 | 0.88 | (−2.6, 0) |
| obese | −1.73 | 0.98 | (−2.64, −0.38) |
| mom race black | −0.88 | 0.88 | (−1.79, 0) |
| depression | −0.9 | 0.89 | (−1.93, 0) |
| protein percent | 0.7 | 1 | (0.34, 1.21) |
| height | 0.97 | 1 | (0.63, 1.38) |
Table 3.
Table showing log(odds) of belonging to moderate vs. low weekly weight gain rate class for having covariates that are found “interesting” (marginal posterior inclusion probability > 0.75); note that P(β1j ≠ 0) was fixed at 1 for the Intercept
| 95% C.I. | |||
|---|---|---|---|
| Intercept | 1.3 | 1 | (0.35, 2.12) |
| underweight | 1.6 | 1 | (0.82, 2.59) |
| obese | −2.94 | 1 | (−3.78, −2.23) |
| mom race black | −0.67 | 0.88 | (−1.39, 0) |
| depression | −0.56 | 0.77 | (−1.32, 0) |
| non-smoker | 0.6 | 0.79 | (0, 1.44) |
| physical activity | 1.13 | 0.99 | (0.51, 1.73) |
| vomiting | −0.61 | 0.88 | (−1.2, 0) |
We next focus on the birth weight regression part of the model. It is evident from Table 4, that obese women have heavier babies than normal weight women. Only one of the interaction terms of weight gain classes with BMI classes is significant, based on the 95% credible intervals. As expected women in the high and very high classes have heavier babies than those in the low class. To get a complete picture we also plot expected birth weight vs. gestational age at delivery, for all possible combinations of weight gain classes and BMI groups in Web Figures 4 and 5. The expectation is calculated for other covariates held constant at their most commonly observed values, viz. non-smoker, nulliparous, white mothers and male babies.
Table 4.
Table showing posterior means and 95% credible intervals for birth weight regression coefficients with indicators of latent weekly weight gain rate classes: very high, high and moderate as covariates
| 95% C.I. | ||
|---|---|---|
| high*underweight | 0.03 | (−0.18, 0.25) |
| high*overweight | 0.38 | (−0.03, 0.84) |
| high*obese | 0.07 | (−0.12, 0.26) |
| moderate*underweight | −0.06 | (−0.24, 0.12) |
| moderate*overweight | 0.23 | (−0.01, 0.44) |
| moderate*obese | −0.04 | (−0.27, 0.28) |
| Intercept | 3.04 | (2.94, 3.15) |
| gestational age | 0.38 | (0.36, 0.4) |
| (gestational age)2 | −0.05 | (−0.07, −0.04) |
| (gestational age)3 | −0.04 | (−0.05, −0.02) |
| non-smoker | 0.17 | (0.12, 0.23) |
| nulliparous | −0.16 | (−0.19, −0.12) |
| male | 0.1 | (0.07, 0.13) |
| mom race black | −0.15 | (−0.2, −0.11) |
| underweight | −0.11 | (−0.41, 0.2) |
| overweight | 0.04 | (−0.11, 0.19) |
| obese | 0.15 | (0.05, 0.25) |
| very high | 0.38 | (0.26, 0.51) |
| high | 0.48 | (0.32, 0.66) |
| moderate | 0.08 | (−0.03, 0.2) |
| very high*underweight | 0.13 | (−0.24, 0.49) |
| very high*overweight | 0.08 | (−0.34, 0.52) |
| very high*obese | 0.06 | (−0.27, 0.37) |
| high*underweight | 0.03 | (−0.19, 0.25) |
| high*overweight | 0.38 | (−0.03, 0.86) |
| high*obese | 0.07 | (−0.12, 0.26) |
| moderate*underweight | −0.06 | (−0.24, 0.12) |
| moderate*overweight | 0.23 | (0.02, 0.43) |
| moderate*obese | −0.05 | (−0.27, 0.25) |
For the IOM class model (results in Web Table 2) none of the BMI classes and their interactions with IOM classes are significant. Interestingly out of the two IOM classes included in the model, only excessive is significant. Web Figure 7 shows observed vs. fitted values of birth weight for latent and IOM class models. We further compare the latent class model with i) Bayesian variable selection (BVS) and ii) Bayesian Lasso (BL) to the iii) IOM class model based on out of sample predictions. We hold out a randomly chosen 10% (266 women) test sample to predict birth weight. We replicate this 10 times and calculate the RMSE (root mean squared error), for each test sample. Web Figure 8 contrasts the RMSE for different methods. BVS has lower RMSE than both BL and IOM in 9 out of 10 test samples. The average RMSE over 10 replicates for IOM and BVS are 416 and 408 grams respectively. BL was run for four different choices of the penalty parameter, as in the simulation study. The minimum average RMSE among these is 410 grams. This suggests that the latent class model (using either BVS or BL) has better predictive power than the IOM class model. A huge gain in predictions is not expected as weight gain class constitutes only one of the many relevant predictors of birth weight. In general, BVS and BL are comparable, with BVS doing slightly better than BL.
5. Discussion
Latent class models have received considerable attention in the literature for their ability to flexibly model data with unknown clusters. In this article we have proposed a new approach to let the latent class probabilities depend on predictors through a multinomial logit link. Instead of choosing the full set or a subset of predictors, we perform Bayesian model averaging over all possible subsets of predictors. The posterior computation can be implemented using a Gibbs sampler, and importance of predictors can be assessed through marginal posterior probabilities of inclusion.
For the application we have used a joint model for birth weight and weight gain during pregnancy. This model has identified several important predictors apart from pre-pregnancy BMI, such as race, parity, smoking status of mother etc. Our model also led to improvement in prediction. This suggests that the IOM guidelines for weight gain during pregnancy in the context of birth weight, could be refined by accounting for additional maternal characteristics. A direct extension of our model is to estimate the latent classes using a more general bivariate distribution of birth weight and weight gain class. An important extension would be to consider latent class trajectory models to include multiple observations on weight gain observed at different time points. The prior distribution on the model space can be extended to a more flexible family of beta-binomial priors (Scott and Berger, 2008).
In this article we have introduced a full Bayesian variable selection approach, conditional on the number of latent classes. We have outlined an approach to select the number of classes, using the pseudo Bayes factor, followed by a visual inspection of its values. As pointed out by one of the referees, the approach for selecting the number of classes is exploratory as it relies on the modeler's judgment. There is extensive literature for Bayesian model selection for the number of classes in typical univariate mixture models. However, none of this is applicable to our model. In our framework the number of parameters change across models with different number of classes, and also within a model with fixed number of classes due to the variable selection component. Scaccia and Green (2003) have implemented reversible jump MCMC (RJMCMC) (Green, 1995) in a model similar to ours, but without the variable selection aspect. Their examples show that in these models RJMCMC can have a very low acceptance rate for split/combine proposals, which are used to move across models with different number of classes. Path sampling (Gelman and Meng, 1998) may offer an attractive option from both theoretical and empirical standpoints. As future work, we intend to use path sampling for Bayesian model selection/averaging for the number of classes.
Supplementary Material
Figure 1.
Pseudo Bayes factors for comparing models with 3 vs. 2, 4 vs. 3, and 5 vs. 4 classes: PSBF(3:2), PSBF(4:3), PSBF(5:4), for the simulation study described in Section 3
Acknowledgments
This research was supported by the National Institutes of Health grants NIH/NIDDK DK61981, NIH/NICHD HD28684, HD37584, HD39373, NIH/NIEHS P30ES10126, and MCHB grant MCHB R40MC08952. The first author was supported by the National Institutes of Health Grant NIH/NIEHS 5T32ES007018. The authors thank Prof. David Dunson for helpful discussions and Dr. Quaker Harmon for help with the data. The authors are thankful to the editor, associate editor, and reviewers for valuable comments and suggestions.
Footnotes
Supplementary Materials Web Tables and Figures, referenced in Sections 3 and 4 are available under the Paper Information link at the Biometrics website http://www.tibs.org/biometrics.
References
- Albert JH, Chib S. Bayesian analysis of binary and polychotomous response data. Journal of the American Statistical Association. 1993;88:669–679. [Google Scholar]
- Celeux G, Forbes F, Robert C, Titterington D. Deviance information criteria for missing data models. Bayesian Analysis. 2006;1:651–674. [Google Scholar]
- Clyde M, George EI. Flexible empirical Bayes estimation for wavelets. Journal of the Royal Statistical Society, Series B. 2000;62:681–698. [Google Scholar]
- Deierlein AL, Siega-Riz AM, Herring A. Dietary energy density but not glycemic load is associated with gestational weight gain. American Journal of Clinical Nutrition. 2008;88:693–699. doi: 10.1093/ajcn/88.3.693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devroye L. Non-uniform random variate generation. Springer-Verlag; New York: 1986. [Google Scholar]
- Dunson DB, Herring AH, Siega-Riz AM. Bayesian inference on changes in response densities over predictor clusters. Journal of the American Statistical Association. 2008;103:1508–1517. doi: 10.1198/016214508000001039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elliott MR, Gallo JJ, Ten Have TR, Bogner HR, Katz IR. Using a Bayesian latent growth curve model to identify trajectories of positive affect and negative events following myocardial infarction. Biostatistics. 2005;6:119–143. doi: 10.1093/biostatistics/kxh022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Escobar MD, West M. Bayesian density estimation and inference using mixtures. Journal of the American Statistical Association. 1995;90:577–588. [Google Scholar]
- Frühwirth-Schnatter S, Frühwirth R. Data augmentation and MCMC for binary and multinomial logit models. In: Kneib T, Tutz G, editors. Statistical Modelling and Regression Structures – Festschrift in Honour of Ludwig Fahrmeir. Physica-Verlag; Heidelberg: 2010. pp. 111–132. [Google Scholar]
- Geisser S, Eddy WF. A predictive approach to model selection (Corr: V75 p765) Journal of the American Statistical Association. 1979;74:153–160. [Google Scholar]
- Gelfand AE, Dey DK. Bayesian model choice: Asymptotics and exact calculations. Journal of the Royal Statistical Society, Series B. 1994;56:501–514. [Google Scholar]
- Gelman A, Meng X-L. Simulating normalizing constants: From importance sampling to bridge sampling to path sampling. Statistical Science. 1998;13:163–185. [Google Scholar]
- George EI, McCulloch RE. Variable selection via Gibbs sampling. Journal of the American Statistical Association. 1993;88:881–889. [Google Scholar]
- Green PJ. Reversible jump Markov chain Monte Carlo computation and Bayesian model determination. Biometrika. 1995;82:711–732. [Google Scholar]
- Gustafson P, Lefebvre G. Bayesian multinomial regression with class-specific predictor selection. The Annals of Applied Statistics. 2008;2:1478–1502. [Google Scholar]
- Holmes CC, Held L. Bayesian auxiliary variable models for binary and multinomial regression. Bayesian Analysis. 2006;1:145–168. [Google Scholar]
- Institute of Medicine . Nutrition during pregnancy. Part I, weight gain. National Academy Press; Washington, DC: 1990. [Google Scholar]
- Institute of Medicine . Weight gain during pregnancy: Reexamining the guidelines. National Academy Press; Washington, DC: 2009. [PubMed] [Google Scholar]
- Jasra A, Holmes CC, Stephens DA. Markov chain Monte Carlo methods and the label switching problem in Bayesian mixture modeling. Statistical Science. 2005;20:50–67. [Google Scholar]
- Jeffreys H. Theory of Probability. Oxford Univ. Press; 1961. [Google Scholar]
- Kinney S, Dunson D. Fixed and random effects selection in linear and logistic models. Biometrics. 2007;63:690–698. doi: 10.1111/j.1541-0420.2007.00771.x. [DOI] [PubMed] [Google Scholar]
- O'Brien SM, Dunson DB. Bayesian multivariate logistic regression. Biometrics. 2004;60:739–746. doi: 10.1111/j.0006-341X.2004.00224.x. [DOI] [PubMed] [Google Scholar]
- Oh M-S, Choi JW, Kim D-G. Bayesian inference and model selection in latent class logit models with parameter constraints: an application to market segmentation. Journal of Applied Statistics. 2003;30:191–204. [Google Scholar]
- Park T, Casella G. The Bayesian lasso. Journal of the American Statistical Association. 2008;103:681–686. [Google Scholar]
- Richardson S, Green PJ. On Bayesian analysis of mixtures with an unknown number of components. Journal of the Royal Statistical Society, Series B. 1997;59:731–792. [Google Scholar]
- Savitz D, Dole N, Williams J, Thorp JJ, McDonald T, Carter C, Eucker B. Study design and determinants of participation in an epidemiologic study of preterm delivery. Paediatric and Perinatal Epidemiology. 1999;13:114–125. doi: 10.1046/j.1365-3016.1999.00156.x. [DOI] [PubMed] [Google Scholar]
- Scaccia L, Green P. Bayesian growth curves using normal mixtures with nonparametric weights. Journal of Computational and Graphical Statistics. 2003;12:308–331. [Google Scholar]
- Schwarz G. Estimating the dimension of a model. Annals of Statistics. 1978;6:461–464. [Google Scholar]
- Scott JG, Berger JO. Bayes and empirical-bayes multiplicity adjustment in the variable-selection problem. Annals of Statistics To appear. 2008 [Google Scholar]
- Spiegelhalter DJ, Best NG, Carlin BP, van der Linde A. Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society, Series B. 2002;64:583–616. [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society, Series B. 1996;58:267–288. [Google Scholar]
- Viswanathan M, Siega-Riz A, Moos M, Deierlein A, Mumford S, Knaack J, Thieda P, Lux L, Lohr K. Outcomes of maternal weight gain. Evidence Report/Technology Assessment. 2008;168:1–223. [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.