Stimulus Compounding in Interval Timing: The Modality-Duration Relationship of the Anchor Durations Results in Qualitatively Different Response Patterns to the Compound Cue

Abstract

We have previously demonstrated that rats trained on a two-duration peak procedure in which 2 different modal signals (i.e., tone and houselight) predicted probabilistic reinforcement availability at 2 different times (10s and 20s), would respond in a scalar manner at a time between the trained durations in response to the simultaneous compound cue (tone + houselight). The present experiments evaluated whether this scalar response pattern would remain with greater relative separation between the anchor durations. Results revealed an effect of the modality-duration relationship, such that scalar responding was seen on compound trials in rats trained that the auditory stimulus signaled the shorter duration, while the visual stimulus signaled the longer duration, but not in the reverse condition. In those rats showing scalar responding on compound trials, post-hoc analyses demonstrated that the peak time of compound responding was most accurately predicted by the reinforcement probability weighted average of anchor peak times. In contrast, rats trained that the visual stimulus signaled the shorter duration, while the auditory stimulus signaled the longer duration, responded in a highly rightward skewed manner. In these subjects, initiation of responding to the compound stimulus appeared to be controlled by the visual stimulus only, while response terminations reflected control by both modal stimuli. These latter data provide evidence of separate determinants of response initiation and termination.

The ability to accurately perceive time in the range of seconds-to-minutes, interval timing, is crucial to the successful performance of everyday behaviors (Gallistel, 1990). Besides providing the important ability to predict when specific events should occur, thereby facilitating the efficient organization of behavior, interval timing may also be essential for the computational processes underlying associative learning (Gallistel & Gibbon, 2000), adaptive foraging (Kacelnik & Bateson, 1996), and rate estimation (Brunner, Kacelnik, & Gibbon, 1992).

While a number of timing studies have examined behavioral control following the presentation of a single stimulus that indicates fixed or variable delays to reinforcement, comparatively little attention has been paid to the temporal control of behavior resulting from the presentation of multiple cues that each indicate a specific, but discrepant, delay until reinforcement. Intriguingly, while animals can be trained to time multiple durations simultaneously and independently (Guilhardi, Keen, MacInnis, & Church, 2005; Meck & Church, 1984), and appear to do so when the cues indicating their onset are asynchronous (Olton, Wenk, Church, & Meck, 1988), they do not appear to accurately time previously trained stimuli when presented as a simultaneous compound. Rather, the available evidence suggests that they somehow combine their temporal expectations for each individual stimulus, responding most frequently at a time between the previously trained durations. In one study, Cheng and Roberts (1991) trained pigeons on a peak procedure in which one spatially distinct visual cue signaled probabilistic reinforcement at 9 sec, and a different spatially distinct visual cue signaled probabilistic reinforcement at 30 sec. On a proportion of trials, the two cues were presented as a simultaneous compound, and responses on these trials were not reinforced. Responding on these compound trials tended to occur at a time between the two criterion durations. However, the response rate on compound trials was extremely low, and it extinguished very rapidly, leading to difficulties drawing firm conclusions regarding the form of responding and the expected time of reinforcement. Nevertheless, in keeping with the vector averaging model developed previously by Cheng (1989) in regards to spatial searching, the authors concluded that the birds were computing a vector average of the criterion durations, and using this average to guide their behavior.

Holland (1998) examined the effects of stimulus compounding in Pavlovian occasion setting, in which one stimulus, the feature, indicated whether a second subsequent stimulus, the target, would predict reinforcement. In this study, rats were trained with two sets of specific feature–target pairs and each pair was associated with a specific feature-target interval. Varying the feature-target interval during test sessions revealed that the rats responded maximally to the target when it followed the feature at the trained interval, thereby demonstrating that they had encoded the feature-target interval. As it relates to the present work, rats were also tested following presentation of the feature stimuli as a simultaneous compound. Like the results of Cheng and Roberts (1991), Holland found that responding to the target was maximal when it occurred at a delay between the two trained feature-target intervals. As such, Holland suggested that the rats were averaging the trained intervals to guide expectation of target onset. Unfortunately, the temporal manipulations in this experiment were examined with a 5 second resolution, thereby preventing an adequate assessment of the form of temporal expectation resulting from the memory mixing. Further, while there was anticipatory responding to presentation of the elemental features alone (i.e., before target presentation), there was no evidence of averaging of anticipatory responding to the features presented as a compound, but rather responding was indistinguishable from that produced in response to the feature stimulus associated with the short feature-target interval.

In addition to these two reports showing limited evidence of temporal memory mixing, we have recently shown that rats, trained on a mixed-modality variant of the procedure used by Cheng and Roberts (1991), will merge their temporal memories when presented with a compound stimulus (Swanton, Gooch, & Matell, 2009). In our work, the animals were first trained on a two-duration peak procedure where one stimulus (tone or houselight) signaled the probabilistic opportunity to earn reward following a 10 sec delay and the other modality stimulus signaled the probabilistic opportunity to earn reward following a 20 sec delay. On test trials, the animals were presented with the simultaneous compound stimulus (tone + light) and were never reinforced for responding. In response to this compound cue, the animals produced a single, robust, scalar peak of responding at a time midway between the obtained peaks for the two anchor durations. Since responding to the compound cue was both Gaussian in shape and scalar (i.e., it superimposed on the normalized peak functions resulting from the anchor cues alone), we concluded that the animals were averaging or integrating their temporal memories associated with the two anchor cues and timing this average in a normal manner as though it were a singular expectation.

Given the novelty of this finding, we sought here to further explore the boundary conditions under which such temporal memory integration occurs. In Experiment 1, we expanded the separation in durations of the component stimuli, using durations of 4 sec and 12 sec as well as 8 sec and 24 sec (1:3 ratios) to assess whether memory synthesis was impacted by either the absolute durations or the relative difference in durations. Our results revealed a substantial qualitative difference in responding to the compound stimulus as a result of the modality-duration relationship of the component stimuli. Therefore, we followed this experiment up with another experiment using a 1:6 duration ratio (Experiment 2) to investigate whether the effect was due to the specific ratio used.

Experiment 1

Method

Subjects and Apparatus

Twenty adult male Sprague-Dawley rats (Rattus norvegicus; Harlan, Indianapolis, IN) approximately 3 months of age at the beginning of the experiment were used. Rats were housed in pairs with a 12 hr light:dark cycle (lights on at 8 a.m.). All behavioral testing was conducted during the light phase. The rats had ad libitum access to drinking water, but were kept on a restricted feeding schedule (Harlan 2019 Rat Diet) to maintain their body weights at 85–90% of free-feeding levels, adjusted for growth. Rodent chow was provided immediately following each daily session.

Training and testing took place in 10 standard operant-conditioning chambers (30.5 × 25.4 × 30.5 cm, Coulbourn Instruments, Allentown, PA). The sides of the chambers were ventilated Plexiglas, and the front and back walls and ceiling were aluminum. The floor was composed of stainless steel bars. A pellet dispenser delivered 45-mg sucrose pellets (Formula F; Noyes Precision, Lancaster, NH) to a food magazine on the front wall of the chamber. Three nosepoke response apertures (2.5 cm opening diameter) with photobeam detection circuits were placed on the back wall of the chamber, and had yellow and green LED cue lights in their interior. The operant chambers were also equipped with an 11 lux houselight on the front wall of the chamber and a seven-tone audio generator which could play 95 dB tones through a speaker on the back wall of the chamber. Stimulus control and data acquisition were achieved using a standard operant-conditioning control program (Graphic State, Coulbourn Instruments), with a temporal resolution of 20 msec.

Procedure

The rats progressed through a sequence of nosepoke training, fixed-interval training with two stimuli/durations, peak-interval training with two stimuli/durations, and compound testing, which was identical to the peak-interval training stage, but with the addition of non-reinforced compound stimulus presentations as a proportion of the probe trials. Subjects were randomly divided into two groups of 10 rats, with the first group reinforced for the short and long cues at 4 sec and 12 sec, while the second group was reinforced at 8 sec and 24 sec. The discriminative stimuli were the houselight and a 4kHz tone, and the modality-duration relationship was counter-balanced in each group (tone short/light long, T_SL_L; light short/tone long, L_ST_L). Rats were run five days per week at the same time each day. Two days before training commenced, rats were given twenty 45mg sucrose pellets in their home cage to acclimate them to the sucrose pellets.

Nosepoke training (5 sessions)

Rats were reinforced with a sucrose pellet on a fixed ratio 1 schedule on the center nosepoke aperture, until 60 reinforcers had been earned or 2 hrs elapsed. Due to the fact that subjects could break the photobeam multiple times in rapid succession (thereby activating the feeder repeatedly and potentially jamming the food delivery port), a 2 second “timeout” was instituted following the delivery of each pellet during this phase of training. Rats were maintained on this training procedure until all of them earned 60 reinforcements on two sequential sessions.

Fixed-interval training (5 sessions)

Trials commenced with the presentation of either the “short” stimulus (either a 4 kHz steady tone or illumination of the houselight; counter-balanced) or the “long” stimulus (the other stimulus). The first nosepoke entry into the center nosepoke aperture after the associated criterion duration elapsed was reinforced and the stimulus terminated. Responses made prior to the criterion duration had no programmed consequence. A variable, uniformly distributed 60–90 sec inter-trial interval (ITI) separated trials. Sessions lasted 2 hrs in this and all subsequent procedures.

Peak-interval training (50 sessions)

Peak-Interval training was identical to Fixed-Interval training, except that non-reinforced probe trials were presented in addition to the reinforced trials. Probe trials were identical to the fixed-interval trials, except that the trials terminated independently of responding at a duration that was 3–4 times the criterion duration for the long signal (i.e., 36–48s, group 1; 72–96s, group 2, uniformly distributed) and no reinforcement was provided. To generate roughly equivalent response rates for the short and long signals, reinforcement probability for the long cue was set at 80%, while reinforcement probability for the short cue was decreased each week from 80% at week 1 of peak training to 20% at week 10, at which point, there was no significant difference in mean response rates across the two durations. Trial type was selected at random with replacement.

Compound testing (5 sessions)

Compound testing was identical to Peak-Interval training, with the addition of compound stimulus probe trials on approximately 20% of all trials. On these compound probes, both the 4 kHz tone and the houselight commenced simultaneously, and then terminated without reinforcement in a response-independent manner at a duration equivalent to the probe length for the long cue.

Analysis

Nosepoke responses were recorded and analyzed as singular, instantaneous, events corresponding to the initial interruption of the photobeam upon head entry into the nosepoke. The detection of a subsequent response only occurred if the subject removed and reinserted its snout into the nosepoke aperture. Previous work from our lab (Gooch, Wiener, Portugal, & Matell, 2007) has demonstrated that training animals with this operant entry contingency results in rapid movements into and out of the nosepoke aperture in a manner analogous to the response pattern seen when levers are used as the operant manipulandum (Matell, Bateson, & Meck, 2006).

Mean functions

The mean response rate as a function of signal duration on probe trials (peak function) was computed using 1 sec bins. The data from each rat were pooled over 5 sessions to obtain sufficient trials to generate peak functions. Due to the skewed pattern of responding sometimes seen on compound trials (see results), rather than use a standard Gaussian to describe the data, we fit (curve fitting package of MATLab, Cambridge, MA) the pooled responses with the dual asymmetric sigmoid function, Y = Y₀ + A * (1/(1+exp(−1*((x-B+C/2)/D)))) * (1-(1/(1+exp(−1*((x-B-C/2)/E))))), [equation from PeakFit; Systat, San Jose, CA]. This function described the asymmetric response data very well (mean R² of fits = 0.99). Y₀ is the baseline, A is a scaling factor, peak time was taken as B, peak spread was taken as C, while D and E are parameters that contribute to the shape of each sigmoidal half. Normalized spread was computed by dividing peak spread by peak time. To determine the degree of skew of the peak function, we computed Pearson’s 2nd skewness coefficient, [3*(mean-median)/standard deviation].

Single trials

Because we could not ensure that the response pattern on compound trials was identical to that seen on component trials in all animals (i.e., a single continuous high rate step between two low rate steps - Cheng & Westwood, 1993; Church, Meck, & Gibbon, 1994), we utilized a simpler analysis to determine the initial onset and terminal offset of high rate responding on each trial. Specifically, we identified the first and last time the local response rate for each pair of sequential responses (computed as two responses divided by their inter-response interval) was greater than the average response rate (total number of responses per trial divided by the probe trial duration). These rate transition times were designated as start times and stop times, respectively. The use of these local rate statistics as indicators of the initiation and termination of high rate responding is preferable to using the first and last response of a trial as they are resistant to the inclusion of a single, temporally uncontrolled response (e.g., a single “exploratory” poke near the end of a probe trial).

Peak times, normalized spreads, and skew coefficients from the mean functions were separately analyzed using a repeated measures analysis of variance (ANOVA), with relative duration (short stimulus; compound stimulus; long stimulus) as a within subject factor, and modality (T_SL_L; L_ST_L) and group (4s/12s; 8s/24s sec) as between subjects factors. To compare across groups, peak times were normalized by the programmed short duration. Either LSD or paired t-tests were used as post-hoc tests to compare responding for individual cues when the omnibus analysis was significant. In cases where sphericity was violated, the Greenhouse-Geiser correction was used for significance testing. The statistics from the single trial analyses were computed in the same manner.

Results

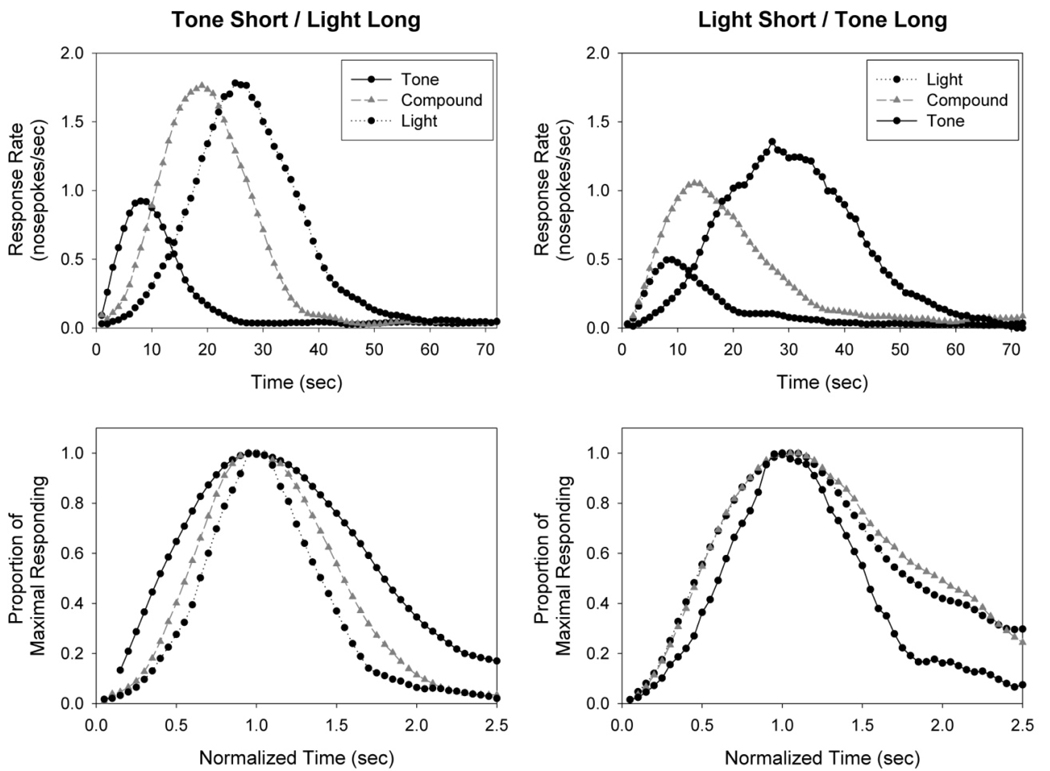
Peak and superimposition functions displayed as a function of stimulus modality are shown in Figure 1 (4s/12s) and Figure 2 (8s/24s). Peaks for the short and long component cues fell at approximately the criterion durations (mean +/− s.d. = 5.3 +/− 0.6 s and 13.1 +/− 1.5 s for 4s/12s group; 8.3 +/− 1.1 s and 26.8 +/− 3.8 s for the 8s/24s group). Mean peak times on compound trials were 9.3 +/− 1.5 s and 15.4 +/− 3.7 s for the 4s/12s and 8s/24s groups, respectively. These compound peak times were significantly different from the component peak times, as demonstrated by a main effect of relative duration, F(2,32) = 300.30, p < .001, and confirmed by pairwise comparisons. However, the compound peak in the L_ST_L rats was significantly earlier than the compound peak of the T_SL_L rats, as demonstrated by the significant interaction between relative duration and modality, F(2,32) = 18.42, p < 0.001, and pairwise comparison. In contrast, the peak time for the long cue was later in L_ST_L rats than T_SL_L rats. In addition, a main effect of group was also found, F(1,16) = 7.32, p < .05, as 4s/12s rats peaked relatively later on both short trials and compound trials than rats in the 8s/24s group.

Figure 1.

Peak functions (top) and superimposition functions (bottom) in rats trained with anchor durations of 4s and 12s, displayed as a function of the stimulus modality-duration relationship.

Figure 2.

Peak functions (top) and superimposition functions (bottom) in rats trained with anchor durations of 8s and 24s displayed as a function of the stimulus modality-duration relationship.

The normalized spreads of the peaks differed as a function of both relative duration and modality, and these differences were further moderated by their significant interaction, F(2,32) = 3.43, p < .05. Specifically, the normalized spread of the compound peak was significantly larger in the L_ST_L groups than the T_SL_L groups, whereas the spread of the component peaks did not differ as a function of modality. Analyzing these data separately for each modality-sub group revealed that the normalized width of the short peak was larger than that of both the compound and long peaks in the T_SL_L groups, whereas both the short peak and compound peak were larger than the long peak in the L_ST_L groups.

Visual inspection of the normalized peak functions revealed that responding to the compound cue in the L_ST_L groups was unusually rightward skewed. This assessment was confirmed by an ANOVA for skew, which revealed a significant main effect of relative duration and a relative duration x modality interaction, F(2,32) = 6.60, p < 0.005. Similar to the analysis of normalized spread, the rightward skew in the compound peak was significantly larger in the L_ST_L groups than the T_SL_L groups. The rightward skew of the compound cue was also greater than that of the component cues in the L_ST_L groups, whereas skew did not vary as a function of cue in the T_SL_L groups.

The distributions of start times and stop times for each relative duration, modality and group are shown in Figures 3 (4s/12s) and 4 (8s/24s). In the T_SL_L groups, the start and stop times on compound trials fell between the times at which responding began and ended on component cue trials. In contrast, in the L_ST_L groups, the start times on compound trials showed substantial overlap with the start times for the short anchor duration, whereas the stop times on compound trials fell between the stop times on component cue trials. For the start times, there was a main effect of relative duration, as well as an interaction between relative duration and modality, F(2,32) = 13.92, p < 0.001. Probing this interaction demonstrated that the start times for the short cue were later in the L_ST_L groups than the T_SL_L groups, while the start times for the compound cue were earlier in the L_ST_L groups than the T_SL_L groups. For the stop times, a main effect of relative duration was seen, which was moderated by an interaction with group, F(2,32) = 4.32, p < 0.05, due to the compound peak being relatively later in the 4s/12s group than the 8s/24s group. In addition, a main effect of modality was seen, F(1,16) = 4.50, p = 0.05, such that peak times were generally later in the L_ST_L groups than the T_SL_L groups.

Figure 3.

Distributions of start times (left) and stop times (right) as a function of the stimulus modality-duration relationship in rats trained with anchor durations of 4s and 12s.

Figure 4.

Distributions of start times (left) and stop times (right) as a function of the stimulus modality-duration relationship in rats trained with anchor durations of 8s and 24s.

Referring back to Figures 3 and 4, it also appeared that the distributions were relatively broader in the L_ST_L groups than in the T_SL_L groups. An examination of the CV of the start times revealed a main effect of relative duration, which was moderated by an interaction with modality, F(2,32) = 7.76, p < 0.01. Post-hoc analyses revealed that the CVs of the compound start times were broader in the L_ST_L rats than the T_SL_L rats. In addition, in the T_SL_L rats, the short CV was broader than both the compound and long CV, which did not differ from one another, whereas in the L_ST_L rats, the short CV was broader than the compound CV, and both were broader than the long CV. An examination of the CVs of the stop time distributions revealed significant main effect for duration, which was moderated by the three-way interaction, with group and modality, F(2,32) = 5.39, p<0.05. Subsequent pairwise comparisons revealed a number of effects. First, like the start times, the compound stop time distributions were broader in L_ST_L rats compared to T_SL_L rats in both groups. In contrast, the width of the stop time distributions for the component cues did not differ as a function of modality in either group. In addition, the short stop CVs were broader than the compound CVs, which were broader than the long stop CV in all groups, except the T_SL_L rats of the 4s/12s group, in which the compound and long CVs did not differ.

Discussion

The results of Experiment 1 demonstrate that when presented with a simultaneous compound of two trained anchor cues, rats will respond vigorously at a time between the trained durations associated with the component cues. However, in contrast to our previous results with a 1:2 duration ratio of the anchor durations (Swanton, et al., 2009), the present results with 1:3 duration ratios revealed a clear difference in the pattern of compound responding as a function of the modality-duration relationship.

Rats in the T_SL_L group responded to the compound cue in an approximately symmetrical and scalar manner, as the compound peak fell between the anchor peaks in the superimposition plots in Figures 1 and 2. The distributions of start and stop times for the compound cue were also roughly symmetrical and fell between the distributions of start and stop times for the two anchor cues. Given the scalar nature of compound responding, these results suggest that the rats in this group were combining in some manner the temporal “memories” signaled by each anchor cue in order to generate a single expectation of the time of reinforcement, and then timing this expectation in a normal manner. One notable aspect of the present results is that responding for the compound cue peaked at a time closer to the long duration peak than the short duration peak, both in the mean functions and in the stop time distributions. This bias may be related to greater control by the light cue than the tone cue, or the higher probability of reinforcement for the long cue than the short cue. We will address this issue in the general discussion.

In contrast to the T_SL_L rats, subjects in the L_ST_L groups responded to the compound cue in a unusually rightward skewed manner, peaking at times that were earlier than those obtained in the T_SL_L groups. This skewed pattern of responding is highly reminiscent of the temporal pattern of responding on constrained variable interval schedules (Brunner, Fairhurst, Stolovitzky, & Gibbon, 1997; Brunner, Kacelnik, & Gibbon, 1996). These authors proposed that animals utilized a minimax model to guide behavior, such that they began responding at a time related to the earliest time at which food had been reliably obtained (minimum), and terminated responding at a time related to the latest time that food had been reliably obtained (maximum). Such response decisions would ensure that opportunities to obtain food would not be missed, which might occur if responding was instead guided by the average reinforcement duration (e.g., as seen in the T_SL_L groups). While the general shape of the mean function, as well as the placement of the start time distribution, is consistent with the minimax model, the times at which subjects terminated responding did not overlap with the stop times for the long duration, suggesting that a minimax approach based solely on obtained reinforcement times is not an accurate account of the present data. Rather, the placement of the stop time distribution, which fell between the stop times obtained for the short and long trials, suggests that the stop decision was based upon a combination of the temporal expectancies from both cues. While these data indicate independence between response initiation and termination, it remains unclear why these processes are based upon different pieces of information (i.e., one versus both temporal memories).

The basis for the difference in response pattern between the T_SL_L and L_ST_L groups is also unclear. One possibility is that the effect results from a modality difference in the ability of the visual versus auditory stimuli to control behavior. The compound peak was closer to the anchor duration associated with the light in all groups, irrespective of whether the light was short or long, consistent with greater control by the light cue. However, in the L_ST_L groups, the light cue dominated control early in the trial, such that responding for the compound overlapped that for the short light cue, whereas in the T_SL_L groups, compound responding did not overlap responding generated by the long light cue late in the trial. In other words, the degree of control exerted by the light cue interacted with the associated duration and/or the amount of time elapsed in the trial. We will return to this issue in the general discussion.

Surprisingly, the behavior in response to the anchor cues in all groups was not consistent with scalar timing, which specifies that the spread of responding for a particular duration scales with the duration being timed (Gibbon, 1977). Rather, in the present data, responding is significantly sharper for the long duration than the short duration. Such a failure could be due to either greater variability in timing processes when timing the shorter cue, while responding for an equivalent relative breadth, or it could be due to a broader breadth of responding for the short cue, but equivalent variability in the times that responding begins and ends. The results of the single trial analyses inform this issue. Specifically, the CVs of the start times in the 8s/24s T_SL_L group, and the stop times in the 4s/12s L_ST_L group, and in both groups in the 8s/24s experiment were significantly greater for the short cues than the long cues. In contrast, the relative spread of responding on individual trials was either equivalent or broader for the long trials compared to the short trials in all groups. Together, these data indicate that the failure of scalar timing is due to greater variability in the timing processes used for the short cue as compared to the long cue, rather than utilization of a more liberal similarity threshold used to guide responding for the short cue. Why this effect occurs remains unclear, although smaller violations in the same direction have recently been reported (Lejeune & Wearden, 2006; Lewis & Miall, 2009). It is possible that the different modalities of the signals specifying the short and long durations may have contributed to these differences, as modality differences in clock speeds, as well as latency to begin timing have been observed previously (Droit-Volet, Meck, & Penney, 2007; Penney, Allan, Meck, & Gibbon, 1998; Penney, Gibbon, & Meck, 2000). However, as the failure of superimposition in the anchor durations is seen for both the T_SL_L groups and the L_ST_L groups, the failure would have to be due to an interaction resulting from the use of two cues, rather than a direct effect of the two modalities contributing different levels of variability themselves. Alternatively, the result may be due to the different reinforcement probabilities used for the short and long cues. It has previously been demonstrated that the lower the ratio of reinforced trials to probe trials, the broader the peak response function (Kaiser, 2008, 2009; Roberts, 1981), although whether this is due to increased variability or increased spread is unclear. Similarly, exposure to extinction trials, or decreased reinforcement probabilities, has sometimes been reported to lead to increased variability (Antonitis, 1951; Boren, Moerschbaecher, & Whyte, 1978; Neuringer, Kornell, & Olufs, 2001), although this effect has not been universally seen (Blough, 1966; Drew, Yang, Ohyama, & Balsam, 2004; Herrnstein, 1961; Machado, 1989).

Experiment 2

The similarities in compound responding across the 4s/12s and 8s/24s groups in Experiment 1 suggested that the absolute durations used as anchors were not important in the patterns of compound responding. While it seemed likely that the differences in the current results using a 1:3 duration ratio as compared to past results using a 1:2 duration ratio were due to the increase in the duration ratio, previous work has suggested that some duration ratios may have special relationships to one another (Crystal, 1999; Kirkpatrick-Steger, Miller, Betti, & Wasserman, 1996). Experiment 2 sought to address this possibility by further separating the relative durations of the anchor cues, using a 1:6 duration ratio.

Method

Subjects and Procedure

The experimental procedures used in this experiment were generally identical to the ones used in Experiment 1, with the following exceptions: Ten Sprague-Dawley rats approximately 3 months of age at the beginning of the experiment were used. A slightly different number of training sessions were utilized: Nosepoke Training (5 sessions), Fixed-Interval Training (6 sessions) and Peak-Interval Training (49 sessions). The anchor durations used were 5 sec and 30 sec, corresponding to a 1:6 duration ratio. The reinforcement probabilities were set at the beginning of peak-interval training to be 75% reinforcement for the long cue and 12.5% reinforcement for the short cue (1/6 that of the long reinforcement percentage to correspond to 1:6 duration ratio). Short trial probe lengths lasted 38–53 sec, while long probe trials, and compound trials, lasted 75–105 sec. The probability of a compound probe was 7% of all trials. Due to the low number of compound and long probe trials, we pooled data over 10 sessions, which provided 291 +/− 48 short trials, 30+/− 7 compound trials, and 16 +/− 5 long trials with responses.

Analysis

The pattern of responding on compound trials in the L_ST_L group showed evidence of bimodality in all rats (see results). As such, the dual asymmetric sigmoidal function used in Experiment 1 was unable to adequately characterize these data. To provide general descriptors of the data, response functions were smoothed with a 5 sec running mean, and the time of maximal responding was used as the peak time, and peak spread was defined as the width at half maximal responding. Due to the bimodal compound peak functions in the L_ST_L group, we sought to analyze these data using each peak separately, as follows. First, the point in each compound response function that was the local minimum between the two peaks was visually identified. The time of each peak’s maximal response rate served as the peak times. Because the dip between peaks was generally not deep enough to allow the width at half maximal responding to be determined for each peak, the width of the entire response function was computed by determining the first time at which the response rate function crossed the early peak’s half maximal response rate and the last time at which the response rate crossed the late peak’s half maximal response rate. This full response function spread was then normalized by dividing by the peak time of the early or late peak. As it seemed likely that the two peaks were based upon different temporal expectancies, we also wished to assess the width of each peak on its own. However, because the local minimum between the peaks was sometimes insufficient to fully separate the peaks, we estimated the width of each peak under the assumption that single duration peaks are roughly symmetric (Church, Miller, Meck, & Gibbon, 1991). As such, the peak spread for each of the bimodal peaks was computed as twice the width of the left half of the early peak or twice the width of the right half of the late peak. Superimposition functions were created separately with the data points and peak times associated with each peak, up to the local minimum that was used to split the peaks. Single trial start and stop times were identified in the same manner as in Experiment 1.

Results

Mean and superimposition functions for the two groups of rats are displayed in Figure 5. Peaks for the short and long compound cues fell at approximately the criterion durations (6.4 +/− 1.2 sec and 32.5 +/− 2.3 sec). As can be seen, in the T_SL_L group, the compound stimulus induced a single peak that fell between the peaks associated with the short and long cues, although it was close in time (29.0 +/− 2.6 sec) to that of the long cue. This compound peak was roughly scalar in nature, as compound responding superimposed with the peaks of the short and long cues. In contrast, in the L_ST_L group, responding for the compound cue was bimodal. All five rats in this group showed evidence of bimodality, although the relative heights of these two peaks varied across rats with three rats showing a larger early peak, and two rats showing a larger late peak. The early peak occurred around the time of the short criterion duration (7.6 +/− 2.3 sec), while the second peak occurred earlier than the long criterion duration (22.4 +/− 5.6 sec).

Figure 5.

Peak functions (top) and superimposition functions (bottom) in rats trained with anchor durations of 5s and 30s, displayed as a function of the stimulus modality-duration relationship.

Due to this bimodality, statistics were computed separately using both sets of obtained peak times. In addition to main effects of relative duration (p < 0.001 using either early or late peak) and modality in one case (p<0.001 early, p = 0.059 late), an interaction between relative duration and modality was found using either the earlier compound peak times, F(2,16) = 98.05, p < 0.001, or the later compound peak times, F(2,16) = 4.21, p < 0.05. Probing this interaction in the T_SL_L group demonstrated that the peak time for compound responding was later than the peak time for the short cue, and earlier than the peak time for the long cue. In contrast, the earlier peak time in the L_ST_L group was not significantly later than the short cue peak time, but it was earlier than the peak time for the long cue. However, the later compound peak time was significantly later than the peak time for the short cue and significantly earlier than the peak time for the long cue. Comparing across groups, the compound peak time of the T_SL_L group was significantly later than both the earlier compound peak time of the L_ST_L group, and the later compound peak time of the L_ST_L group, although this latter comparison was just shy of significance. (p = 0.053).

The relative width of the peak functions varied as a function of both relative duration and modality, and these factors interacted (all p < 0.01). As these results were anticipated given the bimodal nature of the compound peaks in the L_ST_L group, we also computed estimated normalized spreads (see methods) for these rats using the peak width and peak time of each of the bimodal peaks separately. Intriguingly, using either of the early or late peak statistics, a repeated measures ANOVA failed to reveal significant differences in normalized spread as a function of duration, modality, or their interaction. These results suggest that both compound peaks in the L_ST_L group were being timed in a normal, scalar, manner.

Figure 6 shows the distribution of start and stop times for each cue, plotted separately for each modality group. The start times differed as a function of duration, and modality, and these effect were moderated by their interaction, F(2,16) = 8.29, p < 0.005. In the both groups, the median start times on compound trials were between the short and long start times, however, the compound start times in the T_SL_L group were much later than the compound start times in L_ST_L group. In contrast, the compound stop times differed as a function of duration (F,2,16) = 436.37, p < 0.001, but there was no effect of modality, nor an interaction. All comparisons between durations were significant.

Figure 6.

Distributions of start times (left) and stop times (right) as a function of the stimulus modality-duration relationship in rats trained with anchor durations of 5s and 30s.

An analysis of start time CVs demonstrated that the start time variability differed as a function of duration F(2,16) = 5.10, p < 0.05, and modality, F(1,8) = 5.32, p = 0.05. Pairwise comparisons showed that short start CVs were broader than long start CVs, and CVs were larger in the L_ST_L group than the T_SL_L group. Planned comparisons showed that the compound start CV was smaller than the short CV, but statistically indistinguishable from the long CV in the T_SL_L group. This pattern was reversed for the L_ST_L group, such that the compound CV was indistinguishable from the short CV, whereas there was a trend for the compound CV to be larger than the long CV (p = 0.09). For stop CVs, short CVs were larger than compound CVs which were larger than long CVs, as demonstrated by a main effect of duration, F(2,16) = 27.93, p < 0.001, and confirmed by pairwise comparisons. There were no differences as a function of modality, nor an interaction. However, a planned comparison of compound CVs between the groups demonstrated that the stop variability was greater in the L_ST_L group than the T_SL_L group, although this comparison did not reach statistical significance (p = 0.07).

Discussion

The results of Experiment 2 again revealed a difference in the pattern of compound responding as a function of the modality-duration association. As in Experiment 1, rats in the T_SL_L group responded to the compound cue in an approximately scalar manner, as indicated by the general superimposition of compound responding on single cue responding. The timing of the compound peak was close to, though significantly earlier than, the peak from the long anchor duration. Likewise, the distributions of start and stop times in this group were also slightly, but significantly, earlier than the distributions of start and stop times from the long cue. The finding that the compound response function was closer to the long peak function than the short peak function could result from a variety of processes. One possibility is that the compound stimulus leads to retrieval of the long temporal memory by itself, but the simultaneous presence of the short cue results in a faster clock speed than with the long cue alone. As a result, the peak time for the compound would be leftward shifted from the long peak time. Alternatively, both the short and long temporal memories could be retrieved, and a biased, or weighted, average of these memories could be used to time. The bias toward the long light cue could be due to its modality (i.e., light bias) or its increased probability of reinforcement (i.e., incentive bias). To shed light on these possibilities, an examination of compound peak times across experiments will be presented in the general discussion.

In contrast to the skewed, but single peak response functions seen in the L_ST_L groups in Experiment 1, the average response functions in the L_ST_L group were bimodal with an early peak that was around the time of the short anchor duration, and a later peak that was between, and significantly different from, the short and long anchor peaks. Given this bimodality, it is unsurprising that overall responding to the compound cue was not scalar. However, superimposition plots constructed from each compound peak separately showed a surprising degree of overlap with the peaks from the anchor cues. Further, estimates of the normalized spread of each of these compound peaks were not significantly different from those from the anchor trials. These data suggest that the rats were timing two durations in a normal, independent, manner when presented with the compound cue.

The bimodality in the compound peak function in the L_ST_L group could arise from two different processes. One possibility is that subjects utilized different temporal memories on different trials, such that on some trials they would behave as though they were timing the short cue only and peak at a short time, whereas on other trials they would behave as though they were timing an average expectation, and peak only at an intermediate time. Alternatively, subjects may have responded on each trial by responding at a high rate at the early time, slowing or pausing responding for a period of time, and then responding again at a high rate at the intermediate time. The results of the single trial analysis are useful in choosing between these possibilities. Remarkably, there was little evidence of bimodality in the distributions of either start or stop times in the L_ST_L group (the small fluctuations in the stop times in Figure 6 are likely due to the low number of trials available for analysis, as the small peaks do not correspond in time to the bimodal peaks in the mean functions). As such, the data are inconsistent with the first notion of different memories being selected on different trials. Thus, the bimodality in the peak function appears to be the result of bimodality in response rate on individual trials. However, visual inspection of the response patterns on single compound trials did not reveal a clear pause in responding sandwiched between two periods of high rate responding. As such, the dip in the compound peak function appears to be the result of a slight, phasic, decrease in the rate of responding during a broader period of activity, rather than the result of two separate response periods. These data suggest that rats are capable of finer gradations in their response rate decisions than the all-or-none pattern suggested by classic approaches to single trial analysis (Cheng & Westwood, 1993; Church, et al., 1994). A similar conclusion was reached by Meck and Williams (1997) following an analysis of the temporal response patterns of rats given prenatal choline supplementation. While these findings suggest that additional clarity might be derived by the use of a more complex algorithm for single trial analysis (Swanton & Matell, 2009; Taylor, Horvitz, & Balsam, 2007), the complex results from such analyses have not yet been sufficiently investigated in single duration cases, and doing so here is beyond the scope of this report.

General Discussion

Several consistent trends emerged across these experiments. First, in rats in which the short duration was paired with a tone, while the long duration was paired with a light (T_SL_L group), presentation of the compound (tone + light) cue resulted in a single symmetric peak between the anchor durations. After normalization, these compound peaks roughly superimposed on at least one of the anchor peaks, thereby indicating that they were approximately scalar. These results suggest that the rats in this group were temporally controlling their behavior by generating a single temporal expectation and then timing this single expectancy in a normal manner. In contrast, for the rats that had the short duration paired with the light, while the long duration was paired with the tone (L_ST_L group), responding to the compound cue was either highly skewed (Experiment 1) or bimodal (Experiment 2), suggesting the rats were not timing a single temporal expectation. Rather, these latter rats’ behavior was consistent with initiating responding as though they were timing only the short light cue, whereas they terminated responding at a time suggesting combinatorial control by both tone and light cues.

Rats in all of the T_SL_L groups had peak times, as well as start and stop distributions, which were closer to the long duration signaled by the light, than the short duration, which was signaled by the tone. Similarly, rats in the L_ST_L groups had their peak functions and their start distributions, closer to the short duration signaled by the light, than the long duration signaled by the tone. These data are clear in indicating that the visual stimulus is having a stronger impact on temporal control than the auditory stimulus. Modality differences in temporal control have been previously described (Droit-Volet, et al., 2007; Melgire, et al., 2005; Penney, et al., 2000; Wearden, Edwards, Fakhri, & Percival, 1998), and these reports have shown auditory stimuli to generate faster clock speeds and diminished latencies, consistent with enhanced attention to the auditory domain. Why then does the visual cue play a stronger role in the stimulus compound? Several features of the experimental set-up may have contributed to this effect, including the use of albino rats which may have differential sensitivity to light as compared to pigmented rats (Balkema, 1988; Herreros de Tejada, Green, & Munoz Tedo, 1992; Thomas, Aramant, Sadda, & Seiler, 2005), the spatial precision of the houselight compared to the distributed nature of the tone stimulus, and the fact that the houselight was spatially closer to the food magazine than the speaker, which has been shown to facilitate more rapid conditioning (Harrison, Iversen, & Pratt, 1977; Rescorla & Cunningham, 1979). However, pilot work in our lab, in which the relative intensities of the light and tone had been manipulated, had no substantive effects, suggesting that factors related to salience are insufficient to explain the present effects. Alternatively, these data may reflect an inherent bias in rats to more strongly associate positive reinforcement with visual stimuli over auditory stimuli. For example, Weiss and colleagues (1993) trained rats that the presence of a tone-light compound was either hedonically positive or hedonically negative by manipulating response contingencies. Subsequent tests of the elemental stimuli revealed dominance of the auditory stimulus when trained that the compound was hedonically negative, whereas the visual stimulus dominated when the compound was hedonically positive. Nevertheless, a simple modality effect by itself does not explain why the response pattern qualitatively differed across groups (i.e., symmetrical peaks versus asymmetrical peaks). Rather, the present differences indicate an interaction between the modality of the cues and the relative durations timed by the rats (i.e., short versus long). Furthermore, as we did not see strong evidence of a modality effect in our previous work using a 1:2 duration ratio (Swanton, et al., 2009), the ratio of durations is apparently a third interacting factor. Taken together, one possibility is that the incentive value attributed to each cue (which may vary as a function of both relative duration and cue modality) may be a critical factor in generating the different response patterns seen here.

Because of the qualitative differences in compound responding as a function of the modality-duration relationship, we will discuss the results of each group separately. In the T_SL_L group, the single, symmetric and scalar compound peak suggests normal timing of a single temporal expectation. But what is this singular expectation? We hypothesized that compound expectations reflected an average of the two anchor durations. To this end, we asked how well we could predict the compound peak time by computing an average of the obtained peak times of the anchor durations. Specifically, we calculated the three Pythagorean means – arithmetic, geometric and harmonic. An arithmetic mean is suggestive of timing on a linear scale; whereas, a geometric mean is suggestive of timing on a logarithmic scale or a ratio based comparison process operating on a linear time scale (i.e., short duration : compound duration = compound duration : long duration). Finally, a harmonic mean suggests an averaging of rates. For these analyses, we also included our previously reported data using the anchor durations of 10s and 20s (Swanton, et al., 2009) and data from unpublished observations using anchor durations of 5s and 20s. Across the 5 groups (10s/20s, 4s/12s, 8s/24s, 5s/20s, 5s/30s), none of these means did an accurate job of generating the compound peak time. The best predictions were based upon the arithmetic means, which under-predicted the actual compound peak time by 14% +/− 12%. The geometric and harmonic means produce even earlier averages, being early by 25% +/− 15% and 35% +/− 17%, respectively.

These under-predictions are consistent with the fact that the compound peaks were closer to the long duration signaled by the light than the short duration signaled by the tone, and such late peaks may simply reflect greater control by the visual modality. However, in all experiments, we programmed a greater probability of reinforcement for long stimulus trials compared to short stimulus trials, in order to roughly equate response rates. As such, it is possible that these differential reinforcement probabilities bias response timing. To evaluate this possibility, we also calculated a weighted version of each of the above means, in which the relative probability of reinforcement served as the weighting factor. The relative probability of reinforcement was obtained by determining the percentage of reinforced trials for a given stimulus duration (i.e., the proportion of FI to probe trials) and then dividing that by the total percentage of reinforcement for both stimulus durations. For example, if the “short” cue was reinforced on 90% of “short” trials and the “long” cue was reinforced on 30% of “long” trials, then the relative probability of reinforcement would be .75 [0.9 / (0.9 + 0.3)] and .25 [0.3 / (0.9 + 0.3)] for the “short” and “long” cues, respectively. In other words, of the reinforced trials, 75% of them were “short” and 25% of them were “long”. The weighted arithmetic average of the component peaks over-predicted the obtained compound peak by 10% +/− 14%, whereas the weighted harmonic average under-predicted the compound peak by 10% +/− 13%. In contrast, the weighted geometric mean (a weighted average using log scaled times) provided remarkable accuracy, over-predicting the mean by 2% +/− 13%. One sample t-tests evaluating the accuracy of these predictions (comparing proportional differences between predicted and obtained peak times) indicated significant differences for all predicted means (all p < .005) except for the weighted geometric mean, t(24) = .75.

We also tested whether a modality-based “light” bias could explain the data by computing a weighted average using a fixed weighting factor across all experiments. By iterative analysis, the best weighting factor (average error across all rats = −0.0007) occurred at a bias of 21.9% tone, 78.1% light (which happens to exactly coincide with the average relative reinforcement probability of the anchor cues across the 5 experiments). However, the squared deviations were 40% higher in this scenario than what was found when weighted by reinforcement probability. More importantly, in contrast to the non-systematic directional deviations seen when using the reinforcement probability as weights, the errors in this fixed weight analysis were systematic, such that there were over-predictions in the 1:2 ratio group, and under-predictions in the 1:6 ratio group. Such over- and under- predictions are precisely what would be expected if the compound peak was biased by the relative reinforcement probabilities (33% short/ 66% long, 10s/ 20s group, and 14% short/86% long, 5s/30s group).

It is important to note that this cross-experiment analysis is a post-hoc characterization of the data, and as such, will require further experimental support. However, if these findings hold under further experimental tests, the fact that responding was most accurately predicted using reinforcement probability-weighted, logarithmically-scaled durations provides a modicum of support that time is subjectively perceived on a logarithmic scale, rather than a linear scale. The question of linear versus logarithmic timing is a long debated topic (Gibbon, 1977; Staddon & Higa, 1999) and support for both subjective scales has been obtained (Gibbon & Church, 1981; Yi, 2009). One of the most consistent findings related to this debate comes from the temporal bisection task in which the point of subjective equality occurs at the geometric mean (e.g., a 2s vs. 8s bisection yields the point of subjective equality at the geometric mean of 4s) (Allan & Gibbon, 1991; Church & Deluty, 1977). In addition to these bisection data, Meck et al. (1984) used the peak-interval procedure and found that when the time of reinforcement was abruptly switched, subjects would respond maximally at the geometric mean of the two durations. While bisection at the geometric mean could indicate equivalent temporal distance on a logarithmic scale (i.e., 2, 4, 8,…), it could also reflect a ratio based equivalency on a linear time scale (i.e., 2s/x = x/8s; x = 4s), as arithmetic differences on a log scale are computationally equivalent to proportions on a linear scale. Critically, in both of these previous tasks, the probability of reinforcement has been equal for the two trained anchor durations. In contrast, in the stimulus compounding experiments, we used different probabilities of reinforcement for the two durations, and found that using these probabilities as a weighting factor was necessary to accurately predict compound peak times. Intriguingly, it is a relatively simple operation to compute a weighted average on logarithmically scaled peak times, [R_S*D_S + R_L*D_L = D_C], where D corresponds to the duration on a log scale, R corresponds to reinforcement probability, and the subscripts S, L, and C correspond to the short, long, and compound peak times. In contrast, the computationally equivalent operation using durations scaled in a linear manner is [D_S^R_S * D_L^R_L = D_C]. Thus, to the extent that it is easier, and therefore more parsimonious, to imagine a mechanism by which the nervous system could perform operations that are equivalent to addition (as used for a log scale) as compared to operations that are equivalent to exponentiation (as used for a linear scale), the current data provide tentative support for a logarithmic scaling of subjective time.

In contrast, in the L_ST_L group, presentation of the compound cue resulted in a skewed response distribution that began at the short duration, and ended at a time between the short and long peaks across all three groups tested. Examination of the start and stop distributions revealed strong control of the light in the initiation of responding on compound trials. In contrast, the finding that the stop distributions fell between the stop distributions seen on component cue trials suggests that the temporal memories associated with both cues contribute to the decision to stop responding on compound trials. As the compound stop distributions were generally quite broad both in comparison to the anchor stop distributions, and in comparison to the stop distributions in the T_SL_L groups, these data are not easy to reconcile with a single temporal expectation composed of a (weighted) average of the component durations, as such an expectation should result in scalar responding. One possibility is that the stop times in these groups represent an amalgamation in which stops are controlled by a single cue (the short or long) on some trials, whereas they are controlled by a combination of both cues on other trials. However, the lack of multiple modes in the stop distributions is inconsistent with this notion. Alternatively, it is possible that the stop times are based a singular average of the anchor durations, but the presence of both cues results in increased variability in clock speeds and/or response thresholds, leading to greater variability in the stop times. However, such an explanation would require specifying why increased variability would be found in the L_ST_L groups, but not in the T_SL_L groups. Also, given the difference in placement of the stop time distributions between modality conditions, any average would have to have been computed with a different weighting than what was used in the T_SL_L groups.

Irrespective of the precise computation used for terminating responding, the fact that the start distributions on compound trials overlap the start distributions on short trials, whereas the stop distributions do not, provides strong evidence that start and stop times are computed independently. Such independence of start and stop times had been identified previously through inductive reasoning based upon the patterns of correlations seen in single trial analyses (Church, et al., 1994). In contrast, the present data provide direct evidence of different source(s) of temporal information being utilized in initiating and terminating responding. As such, the current data also provide support for the minimax model of Brunner and colleagues (Brunner, et al., 1997; Brunner, et al., 1996), which requires independent control of response behavior. It remains unclear why different sources of information are being used for these two decisions. It also remains unclear why the sources of information used in these decisions should vary as a function of the duration-modality relationship. Additional research will be required to address these questions.

A somewhat similar phenomenon of memory mixing as that reported here has been observed previously by Malapani and colleagues (1998) in Parkinson’s disease patients. In this experiment, patients were both trained and tested while off their dopamine-replacement medication to respond after a visual stimulus had been on for 8s. After a block of testing at this duration, they were trained and tested using the same visual stimulus to time a 21s duration. While responding to the 8s duration was significantly later than 8s, responding for the 21s duration was significantly earlier than 21s. In contrast, when participants were trained and tested on the 21s duration alone (i.e., without experience with the 8s duration), responding was significantly later than 21s. These data suggested that these patients’ 21s reproductions were drawn toward the 8s duration to which they had been previously exposed, a phenomenon referred to as the “migration effect”. In a subsequent study (Malapani, Deweer, & Gibbon, 2002), the authors manipulated whether Parkinson’s patients were trained and/or tested, either on- or off-medication. The results indicated that the migration effect occurred when tested off-medication, irrespective of their medication state during training. In contrast, when tested on-medication, the migration effect was not obtained, irrespective of their medication state during training. These data were interpreted as showing that the diminished dopaminergic tone of these patients when tested off-medication leads to a failure to selectively retrieve the appropriate memory, and that some form of temporal memory synthesis must have occurred, leading to a peak at a time that reflected a combination of both the 8s and 21s durations. While these data are somewhat suggestive of an averaging of the 8s and 21s durations, the altered peak was broader than scalar, which is not immediately consistent with timing a single average duration. Rather, the Parkinson’s data may be, in some respects, similar to the effects seen here in the L_ST_L groups. Unfortunately, single trial analyses were not performed in those experiments, limiting any conclusions regarding the applicability of the present paradigm as an animal model of the migration effect.

In sum, the current work suggests that under certain conditions in which signals with incongruent meaning are presented, rats will compute a weighted average of their temporal memories, and use this average to guide responding in a normal manner. In addition to the synthesis of incongruent temporal information described here, the integration of incongruent information in other domains has also been reported. Vector averaging in spatial searching (Cheng, 1989) has been extensively documented in a number of species, ranging from bees to humans (see Gallistel, 1990 for a review). Vector averaging has also been demonstrated in producing a singular behavior, despite broad tuning curves in cortical activity, within both the motor system (Georgopoulos, Schwartz, & Kettner, 1986) and the visual system (Churchland & Lisberger, 2001; Nichols & Newsome, 2002) . Synthesis has also been demonstrated across different sources of information. For example, Cheng and colleagues (1996) demonstrated averaging between temporal and spatial information, while Gibbon et al. (1997) showed that pigeons would integrate information from a circadian expectation and an interval expectation. Together, these data suggest that averaging may be a standard solution that organisms use in dealing with discrepant information.