A Thermodynamic Approach to the Mechanism of Cell-Penetrating Peptides in Model Membranes

Abstract

We report a first test of the hypothesis that the mechanism of antimicrobial, cytolytic, and amphipathic cell-penetrating peptides in model membranes is determined by the thermodynamics of peptide insertion into the lipid bilayer from the surface-associated state. Three peptides were designed with minimal mutations relative to the sequence of TP10W, the Y3W variant of transportan 10, which is a helical, amphipathic cell-penetrating peptide previously studied. Binding to 1-palmitoyl-2-oleoylphosphatidylcholine (POPC) membranes and dye release from those vesicles were measured by stopped-flow fluorescence, and the secondary structure of the peptides on the membranes was determined by circular dichroism. The Gibbs energy of binding determined experimentally was in excellent agreement with that calculated using the Wimley-White interfacial hydrophobicity scale, taking into account the helical content of the membrane-associated peptide. Dye release from POPC vesicles remained graded, as predicted by the hypothesis. More significantly, as the Gibbs energy of insertion into the bilayer became more unfavorable, which was estimated using the Wimley-White octanol hydrophobicity scale, dye release became slower in quantitative agreement with the prediction.

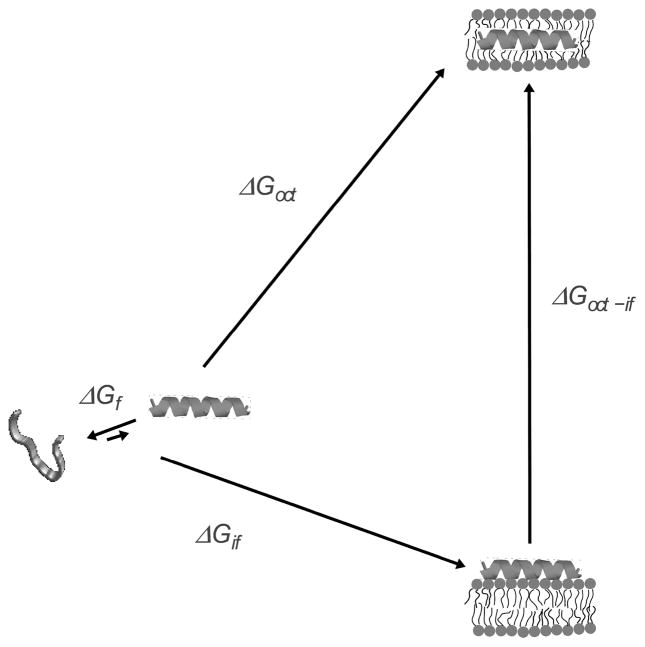
We have proposed the hypothesis that the mechanism of membrane interaction and perturbation by amphipathic, α-helical peptides with antimicrobial, cytolytic, or cell-penetrating properties is determined by the thermodynamics of insertion into the lipid bilayer from the surface-associated state (1). A more precise formulation, which reveals the implications of the hypothesis regarding both the mechanism of membrane interaction and the rates of dye release, requires the definition of some terms. The concept is illustrated in Figure 1. In water, an equilibrium exists between helical and unfolded conformations of the peptide, which favors the unfolded state. Upon binding to the bilayer/water interface, the peptide folds to an α-helix. The Gibbs energy of binding to the interface is $\mathrm{\Delta }{G}_{if}^o$.¹ If we ignore the free energy of folding in water, which is typically small compared to the other terms (1), the Gibbs energy of insertion, from the surface-bound state, should be approximately given by $\mathrm{\Delta }{G}_{\mathit{oct}}^o-\mathrm{\Delta }{G}_{if}^o=\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$, where $\mathrm{\Delta }{G}_{\mathit{oct}}^o$ is the Gibbs energy of transfer from water to octanol. The use of $\mathrm{\Delta }{G}_{\mathit{oct}}^o$ is justified because it provides a reasonable estimate for the transfer of an α-helical polypeptide from water to the bilayer hydrophobic interior (2). Those Gibbs energies can be calculated using the interfacial and the octanol hydrophobicity scales of White and Wimley (3–5). The idea is that $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$ provides a tool for predicting the behavior of the peptides. We found that, for peptides that cause graded dye release, such as δ-lysin, transportan 10 (TP10), mastoparan, and melittin, $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o\approx 20\text{kcal}/\text{mol}$ or less. Further, the kinetic mechanism proposed required translocation of the peptide across the bilayer (6–9). But for peptides that cause all-or-none release, such as cecropin A and magainin 2, $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o>23\text{kcal}/\text{mol}$, and no peptide translocation needed to be included in the kinetic mechanism (10, 11). This seems to indicate that insertion is easier for peptides that cause graded release (1). The correlation observed between $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$ and the kinetic mechanism of dye release suggests a more quantitative formulation of the hypothesis. If $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o\le 20\text{kcal}/\text{mol}$, the peptides can translocate across the bilayer, and cause graded release as a consequence of the transient membrane perturbation that occurs concomitant with translocation. If $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o>23\text{kcal}/\text{mol}$, the energy barrier for translocation is prohibitively large, and the peptides accumulate on the membrane surface until, in a stochastic manner, the membrane yields, releasing the vesicle contents in an all-or-none manner. A “gray zone” may exist for $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$ between about 20–23 kcal/mol, in which either mechanism may prevail (1).

FIGURE 1.

Thermodynamic cycle for peptide binding to the membrane interface and insertion into the bilayer. The folding equilibrium in water lies toward the unstructured state and is determined by $\mathrm{\Delta }{G}_f^o$, which is typically small in comparison with the other terms. The Gibbs energy of binding to the interface ( $\mathrm{\Delta }{G}_{if}^o$) includes contributions from the hydrophobic effect and secondary structure formation. Transfer, as an α-helix, from water to the bilayer interior is approximated by transfer to octanol ( $\mathrm{\Delta }{G}_{\mathit{oct}}^o$). The Gibbs energy of transfer from the surface to the interior of the bilayer is approximately $\mathrm{\Delta }{G}_{\mathit{oct}}^o-\mathrm{\Delta }{G}_{if}^o=\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$. Modified with permission from ref (8). Copyright 2007 Elsevier.

This hypothesis also makes definite predictions regarding the rate of release. If a pore has formed in the membrane, dye release from a large unilamellar vesicle (LUV) is a very fast process, on the order of milliseconds (1). Hence, it appears that the time of release from an LUV mainly reflects formation of this porous, or leaky, state, and not dye diffusion to and through the pore. (This assumption may not be correct for GUVs or cells.) The rate of peptide insertion in the bilayer is determined by the free energy of the transition state, ΔG^‡. The large values of $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$ indicate that insertion of an amphipathic peptide into the bilayer is associated with a high free energy increase. According to the postulate of Hammond (12), as a high free energy state, the inserted peptide should lie close to the transition state in the translocation or pore formation pathway, which corresponds to the greatest perturbation of the bilayer. Therefore, we conjectured that $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o\approx \mathrm{\Delta }{G}^{‡}$ (1). Whereas perturbation of the bilayer by the peptide will most certainly lower those free energies, $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$ provides a quantitative measure of the difficulty of insertion. The hypothesis that the mechanism of dye release is determined by the thermodynamics of peptide insertion from the surface-bound state predicts that the rate constant of dye release (k) should be larger the more negative the binding Gibbs energy ( $\mathrm{\Delta }{G}_{if}^o$) and the smaller the Gibbs energy of insertion ( $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o\approx \mathrm{\Delta }{G}^{‡}$), that is, $k\sim e^{-\mathrm{\Delta }{G}_{if}^o/RT}{e}^{-\mathrm{\Delta }{G}^{‡/RT}}$.

TP10 has been designed as a cell-penetrating peptide (13, 14). Previously, we examined the kinetics of binding to membranes and induced dye release for a few TP10 variants (8, 15). Now, based on TP10W (the Y3W variant of TP10), the mutants TPW-1, TPW-2, and TPW-3 were designed to test some of the predictions of the hypothesis (Table 1). First, if graded release indeed correlates with translocation, then dye release should remain graded because $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o<20\text{kcal}/\text{mol}$ for all these peptides. Second, the better the binding and easier the insertion, the faster the dye release should be. Formation of salt bridges (hydrogen-bonded ion pairs) by the residue side chains favors partitioning into octanol (16). We conjectured they may also form at the membrane interface, improving binding and translocation in a way consistent with the hypothesis (1). In TPW-3, the residue Lys-7 of TP10W was changed to Asp, to allow formation of one intramolecular salt bridge with Lys-11. Salt bridges where Asp is located four residues before Lys are expected to be especially favorable (17). In TPW-1, Lys-11 was also changed to Asp, eliminating the possibility of intramolecular salt bridges. Membrane binding should not differ much from that of TP10W. Finally, if the thermodynamics of binding and insertion is all that matters, the detailed sequence should not change the mechanism of these peptides. TPW-2 was designed to test this idea. With a minimal number of mutations, the sequence was modified to contain only Gly, Ala, Leu, Lys, and Trp, eliminating Asn and Ile from TP10W.

Table 1.

Peptide sequences of TP10W and its mutants. The changes to the sequence of TP10W are underlined.

Peptide	Charge (pH 7)	Length	Sequence
TP10W	+5	21	AGWLLGKINLKALAALAKKIL-amide
TPW-1	+1	21	AGWLLGDINLDALAALAKKIL-amide
TPW-2	+5	21	AGWLLGKLALKALAALAKKLL-amide
TPW-3	+3	21	AGWLLGDINLKALAALAKKIL-amide

Materials and Methods

Chemicals

TPW-1 (purity 98%) was purchased from from Genscript (Scotch Plains, NJ), TPW-2 (95%) from New England Peptide (Gardner, MA), and TPW-3 (95%) from Bachem (Torrance, CA). Their identity was ascertained by mass spectrometry, and the purity was determined by HPLC, both provided by the manufacturer. Stock solutions were prepared by dissolving lyophilized peptide in deionized water or water/ethanol 1:1 (v/v) (AAPER Alcohol and Chemical, Shelbyville, KY). Stock peptide solutions were stored at −80°C, and kept on ice during experiments. 1-Palmitoyl-2-oleoyl-sn-glycero- 3-phosphocholine (POPC), 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphatidylethanolamine (POPE), and 1-palmitoyl-2-oleoyl-sn-glycero-3-[phospho-rac-(1-glycerol)] (POPG), in chloroform solution, were purchased from Avanti Polar Lipids (Alabaster, AL). 7-Methoxycoumarin-3-carboxylic acid (7MC) succinimidyl ester, 8-aminonaphtalene-1,3,6-trisulfonic acid (ANTS) disodium salt, p-xylene-bis-pyridinium bromide (DPX), and carboxyfluorescein (CF) were purchased from Molecular Probes/Invitrogen (Carlsbad, CA). Organic solvents (High performance Liquid Chromatography/American Chemical Society grade) were purchased from Burdick & Jackson (Muskegon, MI). Lipids and fluorophores were tested by thin layer chromatography (TLC) and used without further purification.

Synthesis of Fluorescent Probes

The syntheses of fluorescent probes, using POPE and a fluorophore attached through an amide bond to the amino group of the ethanolamine, were performed as previously described in detail (10, 18, 19), following the method of Vaz and Hallmann (20).

Preparation of Large Unilamellar Vesicles

Large unilamellar vesicles (LUV) were prepared as previously described (7, 10, 11). Lipids were mixed in chloroform in a round-bottom flask, and the solvent was rapidly evaporated in a rotary evaporator (R-3000, Büchi Labortechnik, Flawil, Switzerland) at 60–70°C. The lipid film was placed under vacuum for 4 hours and hydrated by the addition of buffer containing 20 mM MOPS, pH 7.5, 0.1 mM EGTA, 0.02% NaN₃, and 100 mM KCl or appropriately modified as indicated below. In the modified buffers, containing carboxyfluorescein (CF) or ANTS/DPX, the KCl concentration was adjusted to yield the same measured osmolarity as in this buffer. The suspension of multilamellar vesicles that form was subjected to five freeze-thaw cycles and extruded 10 × through two stacked polycarbonate filters of 0.1 μm pore size (Nuclepore, Whatman, Florham, NJ) using a water-jacketed high pressure extruder (Lipex Biomembranes, Vancouver, Canada) at room temperature. For membranes containing 7MC-POPE, the probe was added in chloroform solutions together with the lipids. Lipid concentrations were assayed by the Bartlett phosphate method (21), modified as previously described (6).

Circular Dichroism

Peptide secondary structure was determined by Circular Dichroism (CD). The measurements were performed on a Chirascan circular dichroism spectrometer (Applied Photophysics, Leatherhead, Surrey, UK), in rectangular, 1mm-pathlength quartz spectrophotometer cells (Starna Cells, Inc.), in 1.0 nm steps, 2.0 s/step, from 190–260 nm. CD spectra were obtained in aqueous solution, with 1–5 μM peptide, in 10 mM phosphate buffer, pH 7.5, and in the presence of POPC vesicles, under two types of concentration regimes. At low concentrations, with 5 μM peptide and 300 μM POPC LUV, and at high concentrations, with 20 μM peptide and 5 mM POPC LUV. A lipid baseline spectrum was subtracted from all peptide/lipid spectra. The resulting trace was smoothed while maintaining random residuals, using the Chirascan Pro-Data software. Additionally, in some cases at low concentrations, 2–4 spectra were averaged. The final helicities were obtained from the average of 2 independent samples at high concentrations and 2–6 independent samples at low concentrations.

The use of LUV in CD measurements of amphipathic peptides has been recently discussed in detail and shown to yield results equivalent to those obtained with small unilamellar vesicles (SUV), even at lipid concentrations of 3–7 mM (22). Using low lipid concentrations has several disadvantages. To obtain the helicity of the bound peptide, the helicity in solution and the dissociation constant (K_D) from the membrane are necessary. The helicities in aqueous solution have a significant error because of the small peptide concentrations used, which were chosen to minimize aggregation and to match approximately the peptide concentration in equilibrium with the peptide/lipid samples. The concentration range that can be used in the peptide/lipid samples is also limited by the need to keep the peptide-to-lipid ratio (P/L) sufficiently low to avoid vesicle micellization by the peptide, or the production of lipid/peptide structures that do not correspond to surface-bound peptide. The use of high LUV concentrations (≥ 10 × K_D) has the advantage that all the peptides are bound, and therefore it is not necessary to correct the observed helical content by the fraction of bound peptide. Furthermore, it allows the use of much larger peptide concentrations, which results in CD spectra with higher signal/noise. The determination of helicity on the membrane and the binding affinity are then truly independent. For those reasons, we relied on the determinations at high concentrations for the calculation of peptide helicity on the membrane. However, the two types of determination actually yielded peptide helicities on the membrane that differ only by 5–10% helical content.

The fractional helicity on the membrane (f_H) was calculated according to Luo and Baldwin (23),

$$f_H=\frac{{\theta }_{\mathit{obs}}-{\theta }_C}{{\theta }_H-{\theta }_C}$$ (1)

where θ_H, the ellipticity of the full helix at 222 nm, is given by

$${\theta }_H(T)=\left({\theta }_H(0)+T\frac{d{\theta }_H}{dT}\right)(1-x/N_{\mathit{res}})$$ (2)

in units of deg cm² dmol⁻¹, where T is the temperature in °C, dθ_H/dT = 250, θ_H(0) = −44000, x = 2.5, N_res is the number o residues, and θ_C = 1500 is the ellipticity of the random coil (23).

Membrane binding kinetics

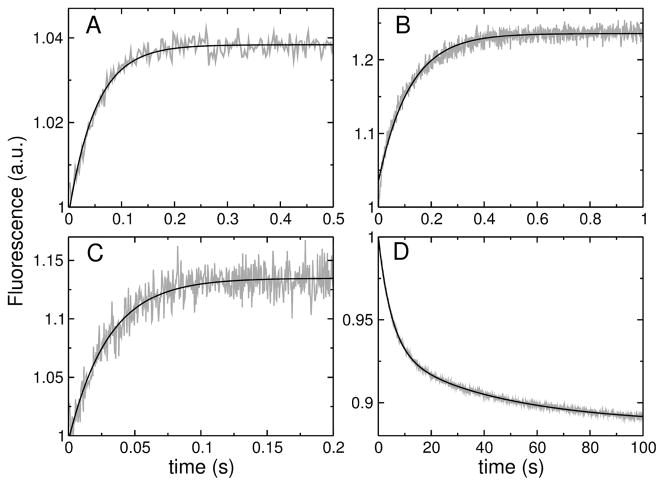
The kinetics of peptide binding to lipid LUV were measured in a stopped-flow fluorimeter (SX.18MV, Applied Photophysics), as previously described (10, 11, 19). The fluorescence signal recorded was the emission of 7MC-POPE incorporated into the bilayer at 1 mole %, upon Förster Resonance Energy Transfer (FRET) from a Trp residue on the peptide. The Trp was excited at 280 nm, and the emission of 7MC (maximum at 396 nm) was measured with a cut-off filter (GG-385, Edmund Industrial Optics, Barrington, NJ). After mixing, the concentration of peptide was 0.5–1 μM and the lipid varied between 25 and 400 μM. The kinetics of peptide binding to membranes were analyzed as previously described in detail (10, 11, 19). Briefly, each kinetic trace (see Figure 3A–C), or the average of several traces from the same sample, was fit with a single exponential rising function of the form

FIGURE 3.

(A–C) Examples of binding kinetics of the peptides (1 μM) to POPC LUV (100 μM lipid): (A) TPW-1, (B) TPW-2, and (C) TPW-3. The signal (gray traces) is the fluorescence emission of the lipid fluorophore 7MC-POPE incorporated in the membrane, which results from FRET, upon excitation of the Trp residue on the peptide. The lines are single exponential fits to the data. (D) Dissociation kinetics of TPW-2 from POPC. TPW-2 (1 μM) was pre-equilibrated with POPC LUV containing 7MC-POPE (donor vesicles, 100 μM lipid), which were mixed in the stopped-flow system with an excess of unlabeled POPC LUV (acceptor vesicles, 1000 μM). After mixing, the concentrations are halved: 0.5 μM peptide, 50 μM donors, and 500 μM acceptors. The signal recorded (gray trace) is the decrease in FRET as the peptide dissociates from the labeled POPC membranes. The black line is a double exponential fit to the data.

$$F(t)=1-exp(-k_{\mathit{app}}t)$$ (3)

where t is time and k_app is the apparent rate constant. This rate constant contains contributions from the on- and off-rate constants, k_app = k_on[L] + k_off , where [L] is the lipid concentration. A linear fit to the plot of k_app as a function of lipid concentration yields k_on from the slope and k_off from the y-intercept.

An additional estimate of k_off was obtained by measuring the kinetics of dissociation more directly, as previously described (10, 11, 19). The peptide was first allowed to bind to donor POPC vesicles labeled with 1 mole % 7MC-POPE, which were then mixed with an excess of unlabeled acceptor POPC vesicles in the stopped-flow instrument. After mixing donors and acceptors in the stopped-flow system, the peptide concentration was 0.5 μM, the donor vesicle concentration varied between 50 and 300 μM, and the acceptor concentration was 500 μM. The decrease observed in the FRET signal, as the peptide dissociates from the donors and associates with the acceptor vesicles, yields the kinetics of dissociation (10, 11). The curves obtained in this experiment are typically double-exponential (see Figure 3D). The apparent k_off was obtained from a weighted average involving the two time constants (τ₁ and τ₂) determined from a double-exponential fit to the experimental curves (10, 11). Two possible averages can be formed, using either the average of the apparent rate constants (1/τ ),

$$k_{\mathit{off}}=\frac{{\alpha }_1}{{\tau }_1}+\frac{{\alpha }_2}{{\tau }_2},$$ (4)

or the average of the time constants,

$$k_{\mathit{off}}=\frac{1}{{\alpha }_1{\tau }_1+{\alpha }_2{\tau }_2},$$ (5)

where the α factors are the amplitudes of the two exponential functions in the fits. Previously, we have used Eq. 5, but this provides only the lower bound on k_off ; the upper bound is provided by Eq. 4. We have now used the average of the two bounds as the best estimate from this method.

ANTS/DPX requenching assay

Steady state fluorescence measurements were performed in a spectrofluorimeter (8100 SLM-Aminco, Urbana, IL) upgraded by ISS (Champaign, IL), as previously done for the original peptides (7–11). In the ANTS/DPX assay (24–26), excitation was at 365 nm (8 nm slitwidth) and emission at 515 nm (16 nm slitwidth). The solution encapsulated in the LUV contained 5 mM ANTS, 10 mM DPX, 20 mM MOPS, pH 7.5, 0.1 mM EGTA, 0.02% NaN₃, and 70 mM KCl. The titrating solution contained 45 mM DPX, 20 mM MOPS, pH 7.5, 0.1 mM EGTA, 0.02% NaN₃, and 30 mM KCl. Following extrusion, the LUVs with encapsulated ANTS and DPX were passed through a Sephadex-G25 column to separate the dye in the external buffer from the vesicles. Typical concentrations were 0.1–2 μM peptide and about 600 μM lipid. The data were analyzed as described in detail by Ladokhin et al. (26). The curve for graded release is given by

$$Q_{in}=\frac{F_i}{F_i^{\mathit{max}}}=\frac{1}{{(1+K_{\mathit{dyn}}{[\text{DPX}]}_0(1-f_{\mathit{out}}))}^{\alpha }){(1+K_{\mathit{sta}}{[\text{DPX}]}_0(1-f_{\mathit{out}}))}^{\alpha })},$$ (6)

where F_i and $F_i^{\mathit{max}}$ are the fluorescence intensities from the vesicle interior with and without quencher (DPX), [DPX]₀ is the initial concentration of DPX encapsulated, f_out is the ANTS fraction outside the vesicles, K_dyn is the dynamic quenching constant, fixed at 50 M⁻¹ in the fits, K_sta is the static quenching constant, and α is the ratio of the rates of release of DPX to ANTS (25, 26).

Carboxyfluorescein release kinetics

Carboxyfluorescein (CF) release kinetics were measured as previously described (7, 8, 10, 11, 19). LUV were prepared by hydration of the lipid film in 20 mM MOPS buffer, pH 7.5, containing 0.1 mM EGTA, 0.02% NaN₃, and 50 mM CF, to give a final lipid concentration of 10 mM. Following extrusion, CF-containing LUV were passed through a Sephadex-G25 column to separate the dye in the external buffer from the vesicles. For fluorescence measurements, the suspension was diluted to the desired lipid concentration in buffer containing 20 mM MOPS, pH 7.5, 100 mM KCl, 0.1 mM EGTA, and 0.02% NaN₃. The kinetics of CF release, measured by the relief of self-quenching of CF fluorescence, were recorded in a stopped-flow fluorimeter (SX.18MV, Applied Photophysics), with excitation at 470 nm and emission recorded through a long-pass filter (OG 530, Edmund Industrial Optics). The peptide concentration was 1 μM after mixing, in all experiments. The fraction of CF released was determined by comparison of the fluorescence with that obtained upon addition of 1% Triton X-100, which releases all the dye. To characterize the efficiency of dye release quantitatively in a model-free way, the average time constant of dye release (τ) was calculated (27, 28),

$$\tau =\frac{\int tf(t)dt}{\int f(t)dt},$$ (7)

where f(t) = d F(t)/d t, the time-derivative of the fractional release as a function of time F(t), behaves as a probability density function (29, 30).

Results

Peptide secondary structure on the membrane

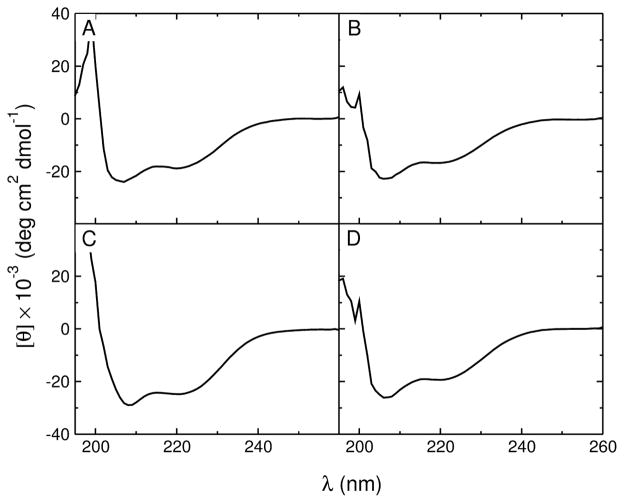
The secondary structure of the peptides in aqueous solution and on the membrane was determined by CD. All peptides were helical in POPC LUV (Figure 2). The percent helicity of the membraneassociated peptides was obtained from the ellipticity at 222 nm, at high lipid concentration (5 mM ≫K_D), so that all peptides were fully bound. The values obtained for TPW-1 and TPW-3 are similar to those of the original TP10W, but TPW-2 is more helical both on the membrane and in solution (Table 2). For comparison, the peptide helicity in solution was also calculated with AGADIR (31–36). The results are in good agreement with experiment for TP10W, TPW-1, and TPW-3 (Table 2). For TPW-2, the experimental helicity in solution has a considerable uncertainty, but is still close to the value from AGADIR within experimental error.

FIGURE 2.

CD spectra of the peptides (20 μM) in 5 mM POPC LUV: (A) TP10W, (B) TPW-1, (C) TPW-2, and (D) TPW-3. Below 200 nm the high LUV concentration has a pronounced effect on the spectra.

Table 2.

Thermodynamic, kinetic, and structural parameters for peptide interaction with POPC bilayers at room temperature. The results for the original TP10W were previously published (15), but are supplemented with new measurements.

	TP10W	TPW-1	TPW-2	TPW-3
% Helicity
Aqueous solution (exp)	28 ± 4	27 ± 2	38 ± 9	28 ± 6
Aqueous solution (AGADIR (31–36))	23	27	27	28
POPC membrane (exp)	57 ± 2	50 ± 4	75 ± 1	57 ± 2
Binding and insertion in POPC
kon (M−1s−1)	(9.4 ± 0.7) × 104	(4.0 ± 0.3) × 104	(1.6 ± 0.6) × 105	(7.8 ± 1.2) × 104
koff s−1	13 ± 1.6	16 ± 0.8	0.37 ± 0.25	25 ± 2.7
KD(μM)	140 ± 20	400 ± 50	2.3 ± 1.5	320 ± 60
$\mathrm{\Delta }{G}_{\mathit{bind}}^o$ (exp) (kcal/mol)	−7.7 ± 0.1	−7.0 ± 0.1	−10.1 ± 0.4	−7.1 ± 0.1
$\mathrm{\Delta }{G}_{if}^o$ (calc) (kcal/mol)	−7.5	−6.5	−9.8	−7.3
$\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$a (kcal/mol)	17.0	18.0	18.7	17.3
Dye release kinetics and mechanism
Release τ (s)b	18.5	220	0.7	3.8
ANTS/DPX mechanism	gradedc	graded	gradedd	graded

^aCalculated using the experimental value $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ for the free energy of binding to the interface.

^bThe values of the mean time of dye release τ have a relative error of about 20%.

^cThe measurement was made with TP10 in POPC/POPS 80:20 (8) instead of TP10W, but the two peptides differ only in the replacement of one Tyr by Trp, and have very similar properties.

^dAll-or-none release in POPC/POPG 80:20.

Peptide binding to POPC membranes

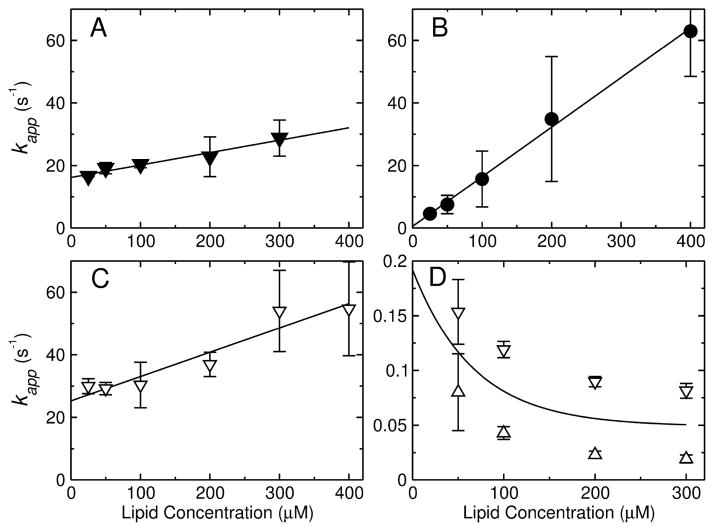
The Gibbs free energy of peptide binding to the membrane surface was estimated by measuring the kinetics of binding to POPC LUV (8–11, 15). The binding kinetics were measured by stopped-flow fluorescence, using the change in FRET from a Trp residue on the peptide to a lipid fluorophore (7MC-POPE) incorporated in the bilayer (Figure 3A–C). These measurements were performed on a very short time frame, to capture only the binding event and not the slower processes associated with membrane perturbation by the peptides. The apparent rate constant for binding, k_app, was determined from a fit of a single exponential function (Eq. 3) to the experimental data, which is the expected functional form (8, 10, 11). The fits are very good for TPW-1 and TPW-3 (Figure 3A,C). For TPW-2 there is a slight deviation from single exponential behavior at the beginning of the trace, but this approximating clearly captures the main component of the kinetics (Figure 3B). This experiment was performed as a function of lipid concentration [L] to yield the on- and off-rate constants, k_on and k_off , from k_app = k_on[L] + k_off. Plots of k_app as a function of [L] are shown in Figure 4A–C for TPW-1, TPW-2, and TPW-3. The equilibrium dissociation constants were calculated from K_D = k_off /k_on. The rate and equilibrium constants obtained are listed in Table 2.

FIGURE 4.

(A–C) Kinetics of peptide binding to POPC LUV. The apparent rate constant (k_app) obtained from binding kinetics is plotted against the lipid concentration for (A) TPW-1, (B) TPW-2, and (C) TPW-3. The points represent mean values and standard deviations from 2–4 independent experiments, and the lines are linear regressions, which yield k_on (slope) and k_off (y-intercept). (D) Kinetics of TPW-2 dissociation from POPC LUV. The k_app for dissociation from POPC LUV is plotted as a function of concentration (after mixing in the stopped-flow) of the donor vesicles. The concentration of the acceptors was constant (500 μM). The upper and lower bounds on k_app are shown (open triangles), which are means and standard deviations from 2 independent experiments. The extrapolation of the mean of the two bounds (solid line) to zero concentration of the donor vesicles provides the best estimate of k_off in the dissociation experiment.

In the case of TPW-2, the value of k_off obtained from the binding kinetics has a considerable uncertainty because the y-intercept occurs very close to the origin (Figure 4B). Therefore, a dissociation kinetics experiment was performed to better determine k_off (Figure 3D). TPW-2 was pre-equilibrated with POPC LUV labeled with 7MC-POPE (donor vesicles), which were then mixed in the stopped-flow system with an excess of unlabeled POPC LUV (acceptor vesicles). As the peptide dissociates from the donors and binds mainly to the acceptors, the FRET signal decreases. In the limit of zero donor concentration, the peptides cannot reassociate with the donors, and the apparent rate constant k_app ≈ k_off (10, 11). These kinetic dissociation curves, however, are generally double-exponential decays. Upper and lower bounds on k_app were calculated from the averages of the rate or time constants (Eqs. 4 and 5). These bounds are are shown in Figure 4D (symbols) together with their mean (line), as a function donor concentration. Extrapolation of the mean to zero donor concentration yields k_off = 0.19 s⁻¹ for TPW-2. This value compares with 0.55 s⁻¹ obtained in the binding kinetics. The average of these two determinations provides our best estimate of k_off = 0.37 s⁻¹, which was used to calculate K_D (Table 2).

In summary, the values of k_on are similar for all TP10W variants, but k_off for TPW-2 is about 2 orders of magnitude smaller than for the other variants. Because of that, TPW-2 binds much better than the other peptides to POPC membranes.

Kinetics of dye release induced by mutant peptides

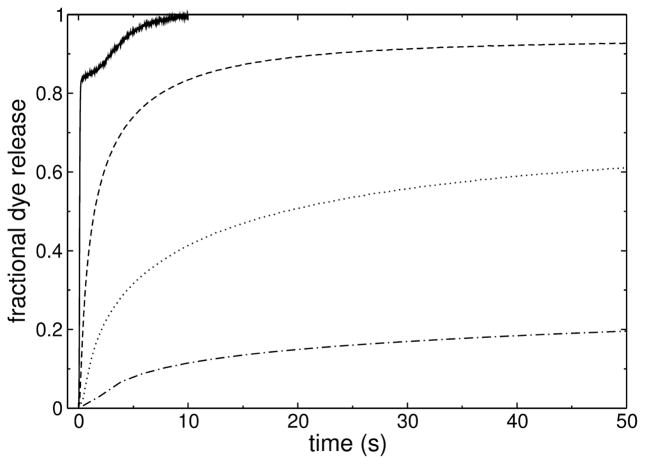
Examples of curves of peptide-induced release of carboxyfluorescein (CF) from POPC vesicles are shown in Figure 5. TPW-1 (dash-dotted line) and TPW-3 (dashed line) are, respectively, less and more efficient that TP10W (dotted line). TPW-2 (solid line) is much more efficient than all the others and the curve has an unusual shape. The efficiency of dye release was quantitatively characterized, in a model-free way, by the average time constants of dye release τ (Eq. 7), which are listed in Table 2.

FIGURE 5.

Kinetics of CF release induced by the peptides (1 μM) from POPC LUV (50 μM): TP10W (dotted line), TPW-1 (dash-dotted), TPW-2 (solid), and TPW-3 (dashed). The curves were acquired for longer times (except for TPW-2), but are shown in the time frame that allows best comparison.

Dye release: graded or all-or-none

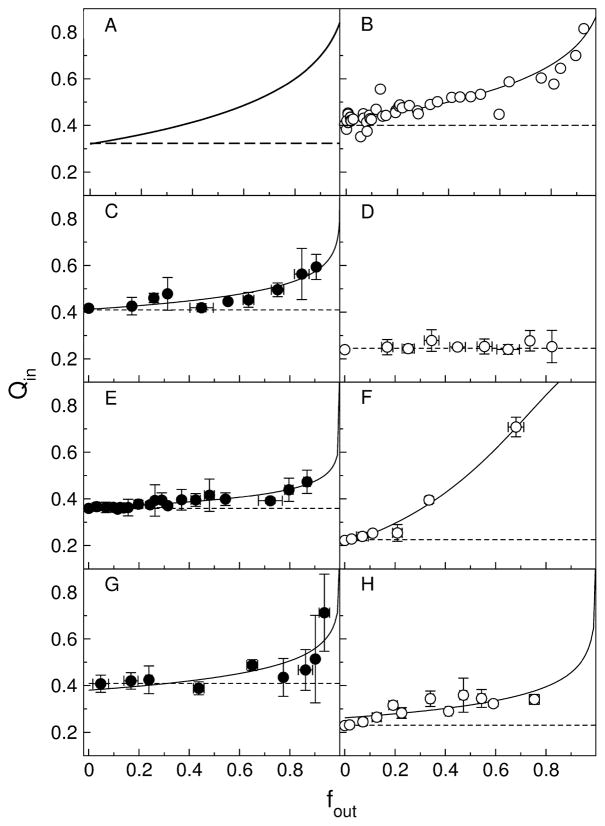
To determine if graded or all-or-none release occurred, the conventional ANTS/DPX requenching assay (24–26) was performed with the mutant peptides, as previously done with the original TP10. Briefly, if release is all-or-none, ANTS fluorescence inside the vesicles does not change. A plot of the fluorescence inside the vesicles against the fraction of ANTS released yields a horizontal line. But if release is graded, the degree of quenching inside the vesicles decreases as DPX (quencher) leaks out, resulting in a rising curve (Figure 6A). The results of the ANTS/DPX assay are shown in Figure 6B–H. The solid lines represent the best fits to the equation for graded release (Eq. 6), and the dashed lines represent all-or-none behavior. The assay for TP10 in POPC/1-palmitoyl-2-oleoylphosphatidylserine (POPS) 80:20 is shown in Figure 6B for comparison (8). All TP10Wvariants cause graded release from POPC vesicles (Figure 6, solid symbols, left). TPW-1 and TPW-3 cause graded release from POPC (Figure 6E,G) and, even more pronounced, from POPC/POPG 80:20 (Figures 6F,H). TPW-2 causes graded release from POPC (Figure 6C) but all-or-none release from POPC/POPG 80:20 (Figure 6D). The shape of the curves in graded release depends especially on the parameter α, which is the ratio of the rates of release of DPX to ANTS. If DPX is released very slowly (α → 0), the curves can look almost like all-or-none release. The results of the fits of Eq. 6 to the data points are shown in Table 3, including those for the original TP10 (8), for comparison. Release of DPX always increases, relative to ANTS, in the presence of POPG, as observed for indolicidin by Ladokhin et al. (37), probably because cationic DPX accumulates at the negatively charged membrane and is released first.

FIGURE 6.

ANTS/DPX requenching assay for the mutant peptides. Experiments in pure POPC LUV are shown on the left side with solid symbols; experiments in POPC/POPG 80:20 are on the right with open symbols. (A) Schematic of typical curves for graded (solid line) and all-or-none (dashed line) behavior; (B) TP10 in POPC/POPS 80:20 (8), (C) and (D) TPW-2, (E) and (F) TPW-1, (G) and (H) TPW-3. The solid lines in panels B–H are fits to equation for graded release (Eq. 6). The fit parameters are listed in Table 3. The dashed horizontal lines represent the behavior expected for all-or-none release.

Table 3.

Parameters for the ANTS/DPX assay, obtained from a fit of Eq. 6 to the data, where α is the ratio of the rates of release of DPX to ANTS, and K_sta (M⁻¹) is the dynamic quenching constant. PC is POPC, PG is POPG, and PS is POPS.

Peptide	Lipid	α	Ksta (M−1)
TP10	PS/PC 20:80	0.548	181
TPW-1	POPC	0.170	84
TPW-1	PG/PC 20:80	1.670	216
TPW-2	POPC	0.241	62
TPW-2	PG/PC 20:80	–a	–
TPW-3	POPC	0.265	75
TPW-3	PG/PC 20:80	0.315	157

^aAll-or-none release.

Gibbs free energy of binding to membranes

The Gibbs free energies of binding to POPC were derived from K_D by $\mathrm{\Delta }{G}_{\mathit{bind}}^o=\mathit{RT}ln{K}_D-\mathit{RT}ln[W]$, where [W] = 55.5 M is the molar concentration of water. The correction term RT ln 55.5 = 2.4 kcal/mol (at room temperature) is necessary to convert K_D to a partition coefficient of the peptide between lipid and water, where the concentrations are expressed in units of mole fraction. These are the units used in the Wimley-White interfacial scale and must be used here for consistency in the calculations (3, 5). The values of $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ obtained are listed in Table 2. Also listed are $\mathrm{\Delta }{G}_{if}^o$, the Gibbs energies of binding calculated with the Wimley-White interfacial scale, extended to different types of amino- and carboxyterminal groups (38), assuming a free energy $\mathrm{\Delta }{G}_{hb}^o=-0.4\text{kcal}/\text{mol}$ for formation of a hydrogen bond between the backbone amide groups in a helix at the membrane interface (39). Calculation of $\mathrm{\Delta }{G}_{if}^o$ requires the helicity of the peptide on the membrane, which was determined by CD. These calculations were performed with the program Membrane Protein Explorer, MPEx (40). As shown in Table 2, the Gibbs energies of binding to the membrane interface determined from experiment ( $\mathrm{\Delta }{G}_{\mathit{bind}}^o$) are in excellent agreement with those calculated from the Wimley-White interfacial scale ( $\mathrm{\Delta }{G}_{if}^o$).

Discussion

We have begun testing the predictions of our hypothesis (1) by examining the effects of a few mutations in the sequence of the cell-penetrating peptide TP10. TP10W, the Y3W variant of TP10, was chosen as the basis for the design of three variants. In TPW-3, a Lys residue was changed to Asp, which would allow formation of an intramolecular salt bridge (Asp-7/Lys-11). In TPW-1, both Lys-7 and Lys-11 were switched to Asp; therefore, no intramolecular salt bridges should form. As such, TPW-1 was expected to bind worse than TP10W, because transfer to the membrane interface is less favorable for Asp than for Lys (3). TPW-3 was expected to bind better than TP10W to POPC membranes if a salt bridge formed on the membrane, but worse if it did not. TPW-2, on the other hand, was designed as a minimalist version of TP10W. The only changes were two Ile residues mutated to Leu, and one Asn to Ala. Those changes are very conservative in terms of the polarity of the residues according to the Wimley-White hydrophobicity scales (3). In all cases, insertion from the membrane interface into the bilayer corresponds to $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o<20\text{kcal}/\text{mol}$, so no changes were expected in the type of release, which should remain graded at least in POPC vesicles.

Binding to POPC membranes

There is excellent agreement between the experimentally determined Gibbs free energies of binding ( $\mathrm{\Delta }{G}_{\mathit{bind}}^o$) and those calculated using the Wimley-White interfacial scale ( $\mathrm{\Delta }{G}_{if}^o$), taking into account the helical contents of the membrane-associated peptides determined by CD (Table 2). As expected, TPW-1 binds worse than TP10W to POPC membranes.² TPW-3 binds as predicted by the Wimley-White scale, indicating that a salt bridge between Asp-7 and Lys-11 either does not form or has no effect on binding. TPW-2 binds to POPC vesicles much better than TP10W, and thus appears to contradict the prediction because the minimal changes in sequence are not sufficient to change the hydrophobicity in any appreciable manner. The reason, however, is that TPW-2 is 75% helical on the membrane whereas the other TP10 variants are only 50–60% helical. This difference alone, which results in the contribution of −0.4 kcal/mol to $\mathrm{\Delta }{G}_{if}^o$ for each additional backbone hydrogen bond (39), quantitatively explains the improved binding of TPW-2 (Table 2).

Relation between dye release mechanism and Gibbs energy of insertion

The type of dye release was determined with the ANTS/DPX requenching assay, and the predictions of our hypothesis were confronted with the results. The calculated values of the Gibbs energy of insertion, estimated by $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$, where the experimental value of $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ was used for the Gibbs energy of binding to the interface, are listed in Table 2. Graded release was previously observed for the original TP10 (8). For TPW-1 and TPW-3 dye release remained graded, as predicted ( $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o<20\text{kcal}/\text{mol}$). TPW-2 induced graded release from POPC, which is according to prediction, but all-or-none release from POPC/POPG 80:20. It is possible that the peptide binds better to POPC/POPG 80:20 because of an electrostatic component, which could render $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ more negative and consequently increase $\mathrm{\Delta }{G}_{\mathit{oct}-if}^o$ beyond the threshold for graded release. If so, TPW-2 is be the most likely of the mutants for this to happen because it has the most negative $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ in POPC. Be it as it may, this result is unexpected because, to our knowledge, this is the first peptide observed to change to all-or-none behavior when negatively charged lipids are incorporated in the membrane. This probably deserves more investigation in the future. In summary, the release results are consistent with the hypothesis regarding the threshold value 20 kcal/mol for graded release in POPC. However, because the type of release did not change, the test is not very stringent, and we do not consider the support to the hypothesis from this experiment to be very strong. An all-or-none result in POPC would have disproved the hypothesis, or at least the conjecture that graded release is indicative of peptide translocation across the bilayer.

Relation between release kinetics, binding, and insertion into the membrane

We now compare the effects of mutations on the rate of dye release. The peptide activity toward model membranes was characterized by the kinetics of CF release from LUV, under similar conditions for all peptides (P/L ≈ 1:50, with peptide and lipid concentrations of 0.5–1 μM and 30–50 μM). The release kinetics were quantified by calculating the average characteristic time constants τ (Table 2). To understand the results in a global way, peptide binding and insertion need to be taken into account together. We assume that the rate-limiting step in dye release is the formation of the leaky state of the membrane, which results from peptide insertion, and not the efflux of the dye through that perturbed state, be it a pore or just a small membrane perturbation. This is the most conservative assumption because diffusion of the dye to the pore is very fast in an LUV and diffusion through the pore is probably fast as well (1). Hence, the apparent rate constant of dye release (k), which is the reciprocal of the mean time constant (τ), should depend on the Gibbs energies of binding ( $\mathrm{\Delta }{G}_{\mathit{bind}}^o$) and insertion in the bilayer (ΔG^‡) through an Arrhenius equation,

$$k=1/\tau =A_o{e}^{-\mathrm{\Delta }{G}_{\mathit{bind}}^o/RT}{e}^{-\mathrm{\Delta }{G}^{‡}/RT}.$$ (8)

The pre-exponential factor A_o depends in general on the lipid and peptide concentrations, and on their ratio, because that determines the peptide concentration on the membrane. However, since all dye release measurements were made under similar conditions, we can consider A_o ≈ Const in this analysis; this is especially true after taking logarithms of Eq. 8. According to the hypothesis, $\mathrm{\Delta }{G}^{‡}\approx \mathrm{\Delta }{G}_{\mathit{oct}-if}^o$ , and since $\mathrm{\Delta }{G}_{\mathit{bind}}^o\simeq \mathrm{\Delta }{G}_{if}^o$ for all these peptides, Eq. 8 simplifies to

$$1/\tau =A_o{e}^{-\mathrm{\Delta }{G}_{\mathit{oct}}^o/RT}.$$ (9)

The prediction embodied in this equation is easy to test.

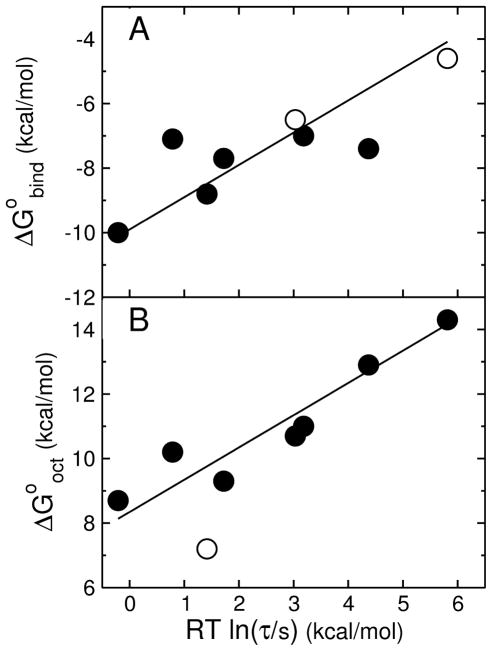
Let us first consider the effect of $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ alone. There is a correlation between $\mathit{RT}ln\mathrm{\Delta }{G}_{\mathit{bind}}^o$ and RT ln τ (Figure 7A), showing that the rate of release increases as binding affinity increases. However, at least four peptides have similar $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ but τ values that differ by orders of magnitude. Thus $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ is not the only important factor in dye release. Taking logarithms of Eq. 9 and multiplying by −RT,

FIGURE 7.

(A) Gibbs energy of binding to the membrane interface determined experimentally ( $\mathrm{\Delta }{G}_{\mathit{bind}}^o$) as a function of the mean characteristic time τ for CF release from POPC LUV. Each point corresponds to a peptide: TP10W and its mutants TPW-1, TPW-2, and TPW-3; TP10, the C-terminal carboxylate versions TP10-COO⁻ and TP10W-COO⁻, and the fluorophore-modified TP10-7MC (8, 15). The solid symbols correspond to entirely experimental data, both for binding and dye release. The open symbols correspond to TP10 and TP10-COO⁻, for which τ is experimental but the binding affinity is calculated with the Wimley-White scale (neither contains Trp). The line is a fit with a slope of 1. (B) Gibbs energy of transfer to octanol calculated with the Wimley-White scale ( $\mathrm{\Delta }{G}_{\mathit{oct}}^o$) as a function of the mean characteristic time τ for CF release from POPC LUV. The points correspond to the same peptides as in (A). The open symbol corresponds to TP10-7MC for which $\mathrm{\Delta }{G}_{\mathit{oct}}^o$ is an estimate assuming a replacement of the modified Lys by Tyr, which gave good agreement with $\mathrm{\Delta }{G}_{\mathit{bind}}^o$ when used to calculate $\mathrm{\Delta }{G}_{if}^o$ for binding using the Wimley-White interfacial scale. The line is a fit with a slope of 1 (excluding the TP10-7MC point).

$$\mathrm{\Delta }{G}_{\mathit{oct}}^o=\mathit{RT}ln\tau +\mathit{Const},$$ (10)

which indicates that a plot of $\mathrm{\Delta }{G}_{\mathit{oct}}^o$ against RT ln τ should yield a straight line with a slope of 1. The data are plotted in Figure 7B according to Eq. 10. The solid line is a linear fit to the TP10 family data (solid circles) with a slope of 1. The good agreement with the data supports the prediction of the hypothesis. Eq. 10 also provides a very simple tool to predict the efficiency of amphipathic peptides on model membranes, because $\mathrm{\Delta }{G}_{\mathit{oct}}^o$ can easily be calculated for any peptide. Thus, both peptide binding and efficiency are entirely accounted for by the thermodynamics of binding to the membrane and solubility in octanol, as a mimic for the membrane interior.

Importance of detailed sequence

Finally, let us consider the importance of detailed sequence in peptide binding and efficiency. The attempt at engineering a salt bridge in TPW-3 failed, suggesting that the structure of even these simple peptides is less malleable than we conceived (or the salt bridge has no effect on binding). In TPW-2, the simplified sequence results in a peptide that binds much better to POPC membranes and is much more efficient in releasing dye from those vesicles. This may appear surprising because the changes to the sequence of TP10W were not such that the thermodynamics of binding and insertion should have changed. Yet, once the increased helical content of this peptide on the membrane is taken into account, both binding and activity are in excellent agreement with the predictions from the Wimley-White scales and our hypothesis. The replacement of Asn, one of the residue types with least helical propensity, by Ala, the residue with greatest helical propensity (31–36), appears to be largely responsible for the increased helical content of TPW-2. It is interesting that Asn is the residue type that has been recently noted to be underrepresented in a library of peptides selected to be active toward lipid vesicles (41), but overrepresented in a library selected for activity against bacteria (42).