Breakthrough in three-dimensional scoliosis diagnosis: significance of horizontal plane view and vertebra vectors

Abstract

Scoliosis is a multifactorial three-dimensional (3D) spinal deformity with integral and directly related vertebral deviations in the coronal, sagittal and horizontal planes. Current classification and diagnostic methods rely on two-dimensional (2D) frontal and lateral X-ray images; no routine methods are available for the visualization and quantitative evaluation of deviations in the horizontal plane. The EOS 2D/3D system presented here is a new, low-dose, orthopedic radiodiagnostic device based on Nobel prize-winning X-ray detection technology with special software for 3D surface reconstruction capabilities that finally led to a breakthrough in scoliosis diagnosis with high-quality, realistic 3D visualization and accurate quantitative parametric analysis. A new concept introducing vertebra vectors and vertebra vector parametric calculations is introduced that furnishes simplified visual and intelligible mathematical information facilitating interpretation of EOS 2D/3D data, especially with regard to the horizontal plane top view images. The concept is demonstrated by a reported scoliotic case that was readily characterized through information derived from vertebra vectors alone, supplemented with the current angulation measurement methods in the coronal and sagittal planes and axial vertebral rotation measurements in the horizontal plane, with a calibrated 3D coordinate system suitable for inter-individual comparisons. The new concept of vertebra vectors may serve as a basis for a truly 3D classification of scoliosis.

Introduction

Scoliosis is a multifactorial three-dimensional (3D) spinal deformity that always involves elemental deformities in the three main planes: lateral curvature in frontal, anteroposterior (mainly lordotic) deviation in sagittal, and (very characteristically) vertebral axial rotation in the horizontal plane. Studies of vertebral rotation, translation and angulation have revealed that a direct nonlinear relationship may exist between these elemental components of spinal deformities, but details of this relationship remain unclear [1].

Vertebral rotation has been demonstrated to play a fundamental role in the pathomechanism of the onset of scoliosis [2]. Even though quantification of the vertebral rotation is important in the planning of surgical corrections and the evaluation of surgical results, current techniques in scoliosis surgery are not based on its accurate measurement and evaluation [3].

The demand for an accurate evaluation of the vertebral rotation detectable in scoliosis is hardly new. Several measurement methods have been published [4–6], all based on assessments of the relative positions of various posterior elements of the vertebrae. Despite use of the Perdriolle torsiometer [6], currently being the most accepted measurement method in clinical practice, its reproducibility is very limited and cannot be quantified precisely [7, 8].

Computer tomography (CT) permits a potentially more precise analysis of the vertebral rotation in the horizontal plane, but is limited to short spinal segments and requires a prohibitively high radiation dose [9, 10]. Expert opinion is divided on the veracity and reproducibility of CT scans for such measurements [11, 12].

In 1994, the Scoliosis Research Society (SRS) Working Group on the 3D Terminology of Spinal Deformity stated the need for a truly 3D diagnostic method that can properly diagnose and evaluate scoliotic deformity in all three planes [13]. Nevertheless, the lack of clinically available tools necessary for accurate direct measurement of axial vertebra rotation, with simultaneous evaluation of the coronal and sagittal curves, meant that this need remained unachieved.

Georges Charpak received the Nobel Prize in Physics in 1992 “for his invention and development of particle detectors, in particular the multiwire proportional chamber” [14, 15]. Since its invention, this type of detector has been extensively used in elementary particle physics and has led to new types of radioimaging devices in biology and medicine that are capable of providing a better image quality with an order-of-magnitude lower radiation dose than those in traditional X-ray radiography [16].

The EOS 2D/3D radioimaging device, constructed from two pairs of units comprising an X-ray tube and a Charpak detector, is capable of biplanar capture of high-quality digital images of an area of 180 × 45 cm within 10–25 s [17, 18]. Precisely perpendicular placement of co-linked X-ray tube-detector pairs allows the simultaneous capturing of spatially calibrated anteroposterior and lateral X-ray images in a weight-bearing standing position, and special software provides a precise 3D reconstruction of the vertebrae, spine and pelvis, complete with automatically generated clinical parameters [19]. From representations of planar projections of an EOS 3D reconstruction, visualization of the spinal geometry in the horizontal view from above (top view) has become a routine daily task in scoliosis surgery.

This publication is aimed at the 3D visualization of spine deformities with the EOS 2D/3D system, with interpretation of the horizontal plane view of 3D deformities and introduction of the concept of vertebra vectors, which permit a truly 3D classification of scoliosis.

Methods

The EOS 2D/3D radiography system (Biospace Med, Paris, France) has been used by our work group for routine clinical orthopedic diagnostic work for the past 2 years. During this period, more than 100 EOS examinations have been carried out on scoliotic patients who then underwent correction surgery at our department.

A representative clinical case of a 15-year-old girl with adolescent idiopathic scoliosis presenting with a right convex major thoracic curve (Lenke type 1A) is demonstrated. She was operated on successfully in March 2008. Pre-operative EOS examination took place 54 days before surgery. Post-operative EOS examination was made on the fifth day following surgery. The curvature was corrected by means of an SCS implant (Scient’X, France) according to the Cotrel–Dubousset principle, using hooks, screws and rods.

Surface 3D reconstructions of the spine by sterEOS 3D software based on the pre- and post-operative EOS X-ray images strictly followed the guidelines of the manufacturer. For a quantitative description of the scoliotic curves in the coronal and sagittal planes, the Cobb’s method was used. Sagittal curves were measured between vertebrae Th₄ and Th₁₂ for thoracic kyphosis and vertebrae L_I and L_V for lumbar lordosis. Instead of measurement of the angulation between lines corresponding to the upper and lower endplates of relevant vertebrae, the angles between the coronal and sagittal projections of a plane defined by the interpedicular axis and the vertebra vector of the corresponding vertebrae were used, i.e., the upper and lower-end vertebrae of the scoliotic curve for the coronal plane (Fig. 2c, f), and vertebrae Th₄–Th₁₂ (for thoracic kyphosis) and L_I–L_V (for lumbar lordosis) in the sagittal plane (Fig. 3c, f).

Fig. 2.

Coronal plane visualizations of the scoliotic spine (a–c) before and (d–f) after correction. Pre-operative and post-operative EOS X-ray images (a, d); images corresponding to pre-operative and post-operative sterEOS 3D reconstructions (b, e); and pre-operative and post-operative full spine vertebra vectors (c, f). Conventional Cobb angulation measurements (shown with red lines) are carried out using lines connecting pedicular centroids as detailed in “Methods”. See Table 1 for measurement values

Fig. 3.

Sagittal plane visualizations of the scoliotic spine (a–c) before and (d–f) after correction. Pre-operative and post-operative EOS X-ray images (a, d); images corresponding to pre-operative and post-operative sterEOS 3D reconstructions (b, e); and pre-operative and post-operative full spine vertebra vectors (c, f). Conventional Cobb angulation measurements (shown with red lines) are carried out using vertebra vectors as detailed in “Methods”. See Table 1 for measurement values

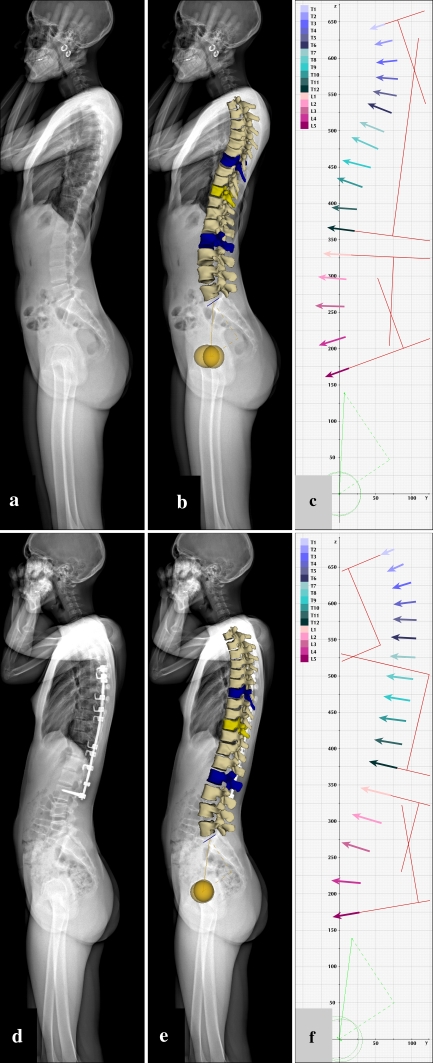
In view of the lack of a definitive and reproducible measurement method for the horizontal plane, the concept of vertebra vectors was introduced. A vertebra vector is a simplified representation of the real vertebra of the spine, and it is based on known vertebral landmarks. Details of this concept and generation of a vertebra vector are illustrated in Fig. 1a–f. Vertebral reference points for the right and left pedicles of each sterEOS 3D reconstructed vertebra were used to obtain both pedicular centroids as the baricenter of the four points corresponding to each pedicle. Initial point A of vector AB is the midpoint of the interpedicular line connecting the two pedicular centroids. A line corresponding to the vertebra vector originating from initial point A is drawn parallel to the upper endplate of the vertebra. Terminal point B of vector AB is determined by the intersection of this line and the ventral surface of the vertebra body. Vertebra vector AB appears in the horizontal plane as a line starting at the midpoint of the interpedicular line forming the axis of the vertebra body in the sagittal median axis of the vertebra. Initial point A is positioned inside the spinal canal, symmetrically dividing the interpedicular distance.

Fig. 1.

Vertebra vector visualization in contour (a–c) and surface mode (d–f) of a sterEOS 3D reconstructed vertebra. Coordinate system and calculation of vertebra vector parameter values in horizontal plane (g, h). a Coronal plane view. A sterEOS 3D reconstructed Th₉ apical vertebra of a right convex scoliotic curve shown in contours mode with colored reference points for vertebral landmark points: right and left pedicles (four yellow dots for each), right and left pedicular centroids (two orange dots), initial point A (black dot) of vertebra vector AB (magenta arrow) as the midpoint of the interpedicular line (orange) connecting the two pedicular centroids. b Sagittal plane view. Vertebra vector AB (magenta arrow) is parallel to the upper endplate of the vertebra body (upper thin black line). Terminal point B of the vector (black dot on the left) shown as the intersection of the vector line and the ventral surface of the vertebra body (green contour line). cHorizontal plane view. Vertebra vector AB (magenta arrow) appears as a line starting at the midpoint of the interpedicular line (orange) forming the symmetry axis of the vertebra body. d–f A sterEOS 3D reconstructed vertebra (same as in a–c) shown in Surface mode with its vertebra vector (magenta arrow), in coronal, sagittal and horizontal planes, respectively. gHorizontal plane view of the coordinate system used for vertebra vectors. The x axis of the coordinate system is the interacetabular line connecting the centers (green dots) of each acetabulum (green circles). The y axis is a line perpendicular to the coronal plane and the interacetabular line with the origin at its midpoint. A value of 100 is assigned to the distance between the origin and either of the acetabular centers on the x axis. The calibration scale is identical for the y axis. A sterEOS 3D reconstructed L_II apical vertebra of a left convex scoliotic curve in Contours mode with its vertebra vector is also shown (colored markings identical to those in c above). h Illustration for the calculation of vector parameter values for the same vertebra vector shown in g above

Following the creation of the vertebra vectors of the spine, vectors were placed in a coordinate system to determine the x, y and z coordinates of their initial and terminal points. This coordinate system was created utilizing principles described by the SRS Working Group on the 3D Terminology of Spinal Deformity [13] and detailed in Fig. 1g. Center points of each acetabulum in the horizontal plane top view images were determined. A line connecting the two acetabular centers is the x axis of the coordinate system. A line perpendicular to the coronal plane and the interacetabular line with the origin at its midpoint is the y axis. The z axis is a perpendicular to the horizontal plane and the x axis at the origin (not shown in Fig. 1g).

Calibration scale of the coordinate system is based on the interacetabular distance in horizontal plane view. A value of 100 is assigned to the distance between the origin and either of the acetabular centers. Thus, the full value of the interacetabular distance equals 200 units. The calibration scale is identical for the y and z axes. The interacetabular distance in 3D was also determined in millimeters with sterEOS 3D.

After vertebra vectors are placed inside this calibrated coordinate system, the coordinates of each vector point can be determined in all three planes by using basic vector algebra. This is demonstrated for a single vector of an apical vertebra L_II of a scoliotic curve in the horizontal plane view in Fig. 1h. Coordinates of initial point A and terminal point B of vector AB in the horizontal plane are A (A_x; A_y), B (B_x; B_y). Coordinates of vector AB are therefore

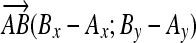These coordinates are used directly to determine lateral translation B_x from the y axis, while the projected length of vector AB in the horizontal plane is calculated as

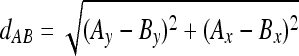and the vector angle α relative to the y axis is calculated by using a tangent function

Only measurement values obtained and calculated in the horizontal plane of this coordinate system will be discussed in detail below, although they were calculated similarly to the coronal and sagittal planes, as well.

Results

The patient presented a typical right convex major thoracic curve (Lenke type 1A) between vertebra Th₇ and L_II, with apical vertebra Th₁₀. Corrective surgery was performed with posterolateral fusion between vertebra Th₅ and L_III. Pre- and post-operative EOS X-ray images, images of sterEOS 3D surface reconstructions and full spine vertebra vectors in the frontal and sagittal plane views are shown in Figs. 2 and 3, respectively. Pre- and post-operative EOS 3D reconstructions and vertebra vectors for the full spine in the horizontal plane view are depicted in Fig. 4. Corresponding angulation measurement values and vertebra vector coordinate and parameter values are shown in Tables 1 and 2, respectively.

Fig. 4.

Horizontal plane visualizations of the scoliotic spine (a, b) before and (c, d) after correction. Pre- and post-operative top view sterEOS 3D reconstructions of the spine are shown in a and c, respectively. The pelvis (semi-transparent), acetabulums (yellow spheres) and interacetabular axis (yellow line) are also visible. Pre-operative axial rotation of apical vertebra Th₁₀ (yellow in a) was measured by sterEOS 3D software as 21°. Post-operative axial rotation of the apical vertebra Th₁₀ (yellow in c) decreased to 13°. b Pre-operative and d post-operative full spine vertebra vectors in the horizontal plane. See Table 2 for vertebra vector coordinate and parameter values

Table 1.

Pre- and post-operative parameters of the scoliotic curve Th₇–L_II

	Cobb (°)	ΔCobb (°)
Pre-operative
Th7–LII curve	49	–
Th4–Th12 kyphosis	23	–
LI–LV lordosis	31	–
Post-operative
Th7–LII curve	8	−41
Th4–Th12 kyphosis	33	+10
LI–LV lordosis	31	0

Cobb angle measurement values were obtained as detailed in “Methods”

Table 2.

Horizontal plane coordinate values and calculated vector parameters for pre- and post-operative vertebra vectors of the scoliotic curve Th₇–L_II

	A (x; y)	B (x; y)	AB (x; y)	tgα	α	Δα
Pre-operative
Th7 UEV	−50.79; 61.42	−53.81; 27.80	−3.02; −33.62	0.08983	5.13°	–
Th10 APV	−68.89; 31.68	−80.10; −4.53	−11.21; 36.21	0.28197	17.20°	–
LII LEV	−25.21; 9.69	−27.65; −29.10	−2.44; −38.79	0.0629	3.60°	–
Post-operative
Th7 UEV	−7.18; 104.6	−10.05; 69.54	−2.87; −35.06	0.08186	4.68°	−0.45°
Th10 APV	−5.89; 92.53	−13.65; 54.31	−7.76; −38.22	0.20304	11.48°	−5.72°
LII LEV	8.05; 57.33	8.34; 16.67	0.29; −40.66	0.00713	0.41°	−3.19°

UEV upper-end vertebra; APV apical vertebra; LEV lower-end vertebra

Discussion

The etiology and nature of idiopathic scoliosis and the mode of progression of the structural deformity are still unknown. The primary deformity, however, has been linked to vertebral rotation that causes sagittal instability and imbalance in the coronal plane [20]. It is widely accepted that, after the initial deformity has developed, idiopathic scoliosis progresses through a self-sustaining biomechanical process within the period of fast growth in adolescent life.

The clinical diagnosis of scoliosis is commonly based on biplanar X-ray images. Various methods have been reported for determination of the axial rotation of the vertebrae through the use of 2D X-rays [13, 14, 17], but all of them have been shown to be rather unreliable because such images provide inadequate quantitative or qualitative information on the anatomical landmarks needed to determine the axial rotation [7, 21]. Significant progress and fundamentally new knowledge were attained when it became possible to measure axial rotation in 3D reconstructions from digitized biplanar X-ray images. This method was shown to be more accurate than any other method of axial rotation measurement [22]. Moreover, this 3D reconstruction allows the segmental quantitative analysis of rotational deformities [22, 23]. For the highest possible accuracy and reliability of 3D reconstruction-based measurements, the precisely orthogonal acquisition of biplanar X-rays and correct patient positioning are of critical importance [23].

The most accurate measurement of vertebral axial rotation has been claimed to be achieved in axial CT images [9, 10]. However, the use of CT in routine scoliosis diagnostics is limited, due to its very high radiation dose and the supine position during imaging, which has been shown to alter the coronal and sagittal scoliotic curves significantly relative to an upright position [24]. Another problem is related to the level of rotation measurement within the vertebral body, since the value for rotation can vary significantly, due to vertebral torsion, when measured at the lower and upper endplates of the same vertebra [1]. To achieve a standardized and reasonably accurate visualization of the vertebrae in the horizontal plane, axial rotation should be measured in a segment that is either at an equal distance from the endplates, or through which the mean difference in variable rotation of the lower and upper endplates can be represented.

The new EOS 2D/3D radioimaging device with its sterEOS 3D reconstruction software has given rise to a breakthrough in the visualization of the scoliotic spine, allowing the simultaneous capture of orthogonal, coronal and lateral X-ray images with an ultra-low radiation dose in an upright standing position, in a spatially calibrated system resulting in highly accurate 3D surface reconstructions [17–19]. The high-quality images provided by EOS permit accurate and reproducible detection of the landmarks required for 3D clinical parameters for the spine, including vertebral rotation. This is the first routine clinical diagnostic tool that allows simultaneous visualization of spinal deformities in an upright standing position in all three planes, with unique insight into the deformities present in the horizontal plane.

EOS 3D surface reconstructions produce complex, full-detailed, very realistic-looking images containing a significant amount of information. This is especially true for the horizontal plane top view images, which afford possibilities unrivalled by any clinical diagnostic tool available in scoliosis today.

A simplified and easy-to-understand interpretation of these images is promoted by the concept of vertebra vectors. The positioning of the vector neutralizes the variance in axial rotation due to vertebral body torsion, since the relative distance of the vector from the upper endplate is constant for each vertebra. A vertebra vector defined in this way is least prone to be affected by scoliotic vertebral shape changes.

In the horizontal plane, the vector orientation always corresponds to the axis of the vertebra body. The size of the vector is determined by the vertebra body size, accurately modelling the size changes of the vertebrae from the cervical to the lumbar region.

The coordinates of vertebra vectors can be determined in the coordinate system based on the interacetabular axis (x), the sagittal median axis (y) and the axis perpendicular to the intersection of the x and y axes (z), providing a mathematical description of the position, orientation and rotation of each vertebra vector.

A vertebra vector therefore furnishes complete and accurate information concerning the size, position, orientation and rotation of the vertebra in all three planes. A combined series of vertebra vectors of the full spine fully reflect spinal 3D deformation processes in a simple and straightforward manner.

Since the y axis of the coordinate system used in our concept corresponds to the sagittal median axis of the body, and the vertebra vector corresponds to the vertebral symmetry axis in the horizontal plane, the vector angle α relative to the y axis is identical to the vertebral rotation in the horizontal plane. Vertebral axial rotation can therefore be determined directly through the use of vertebra vectors, without involving any of the known auxiliary methods.

Relative inter-individual variations of the spino-pelvic skeletal system inside this coordinate system (for example, total height of the vertebral column versus pelvic diameter represented by the value of interacetabular distance) make it very important to have a calibrated scale that allows direct inter-individual comparison of measurement values and through that could form a basis for a classification. The calibration method used with this concept employs an individually specific, relative calibration scale with the additional possibility to calculate any absolute derivative value from a true-to-reality sterEOS 3D value of the interacetabular distance.

The angulation measurement methods currently used for scoliotic curves can be preserved with very slight modifications when using vertebra vectors. Coronal plane deviations are characterized with the Cobb method, but angles between the lines corresponding to the interpedicular axes of the relevant vertebrae are used. The sagittal plane curves of the spine are also measured with the Cobb method, but lines corresponding to the sagittal projections of the vectors for vertebrae Th₄–Th₁₂ (for thoracic kyphosis) and L_I–L_V (for lumbar lordosis) are used for its angulation measurement.

The reported scoliotic case was completely characterized by the addition of vertebral axial rotations to the angulations in the coronal and sagittal planes, all of which information was obtained from vertebra vectors alone.

The vertebra vector concept provides a solid basis for a truly 3D scoliosis classification without the introduction of an abstract, difficult-to-understand, continually changing, extraspinal auxiliary plane [25].

In summary, vertebra vectors afford simple and intelligible means of visualizing and quantifying the essential features of the complex information provided by the EOS 2D/3D system concerning the scoliotic spine. The analysis of vertebra vector data may lead to a better understanding of spinal deformities and promote development of a truly 3D scoliosis classification as a basis for new concepts in therapeutic procedures.