Ontogeny of lift and drag production in ground birds

Abstract

The juvenile period is often a crucial interval for selective pressure on locomotor ability. Although flight is central to avian biology, little is known about factors that limit flight performance during development. To improve understanding of flight ontogeny, we used a propeller (revolving wing) model to test how wing shape and feather structure influence aerodynamic performance during development in the precocial chukar partridge (Alectoris chukar, 4 to >100 days post hatching). We spun wings in mid-downstroke posture and measured lift (L) and drag (D) using a force plate upon which the propeller assembly was mounted. Our findings demonstrate a clear relationship between feather morphology and aerodynamic performance. Independent of size and velocity, older wings with stiffer and more asymmetrical feathers, high numbers of barbicels and a high degree of overlap between barbules generate greater L and L:D ratios than younger wings with flexible, relatively symmetrical and less cohesive feathers. The gradual transition from immature feathers and drag-based performance to more mature feathers and lift-based performance appears to coincide with ontogenetic transitions in locomotor capacity. Younger birds engage in behaviors that require little aerodynamic force and that allow D to contribute to weight support, whereas older birds may expand their behavioral repertoire by flapping with higher tip velocities and generating greater L. Incipient wings are, therefore, uniquely but immediately functional and provide flight-incapable juveniles with access to three-dimensional environments and refugia. Such access may have conferred selective advantages to theropods with protowings during the evolution of avian flight.

INTRODUCTION

Aerodynamic capacity is a crucial component of locomotor performance among extant birds, from fledging through adulthood. Prior to becoming flight capable, immature birds often engage their forelimbs in flapping behaviors that do not require full weight support by the wings. For example, in the precocial chukar partridge (Alectoris chukar Gray 1830, hereafter ‘chukar’), young birds 6–8 days post hatching (d.p.h.) are capable of supporting ∼5–10% of their body weight by flapping (Tobalske and Dial, 2007) and rely on their wings for wing-assisted incline running (WAIR) and controlled flapping descent. Adults, in contrast, are capable of a broader array of flapping behaviors, generating 60% of their body weight during WAIR on a 65 deg incline and >100% body weight during active flight (Tobalske and Dial, 2007). Thus aerodynamic capacity is not an all-or-none phenomenon in precocial birds, and it increases through ontogeny.

Aerodynamic performance in developing birds may be limited by a number of factors, including neural control, muscular output and wing or feather morphology, but the relative contributions of these factors are not well understood (Tobalske and Dial, 2007). Compared with adults, immature birds are often characterized by inconsistent or asymmetric flight strokes (Jackson et al., 2009), small pectoral muscles (e.g. Hohtola and Visser, 1998) and wings with strikingly different feather morphologies and arrangements (Dial et al., 2006). Although ontogenetic improvements in aerodynamic capacity are most likely the result of a developmental interplay between such factors, we undertook the present study to test for an effect of wing shape and feather structure. Feather structure (particularly the degree of vane symmetry) has long been assumed to influence lift (L) and drag (D) production (e.g. Norberg, 1985). In contrast, many studies using propeller models of insect and bird wings suggest that aerodynamic performance is largely unaffected by changes in wing shape (Usherwood and Ellington, 2002a; Usherwood and Ellington, 2002b; Usherwood, 2009), though leading edge morphology and camber were found to affect the performance of hummingbird wing models (Altshuler et al., 2004). Examining the roles of L, D, wing shape and feather structure during locomotor development may address some of these differences and improve our understanding of flight ontogeny.

Ontogenetic transitions in feather structure are particularly intriguing because they appear to mimic evolutionary transitions among feathered theropod dinosaurs. Younger birds and more basal theropods often have distally branched and/or symmetrical flight feathers, whereas older birds and more derived theropods tend to have fully vaned asymmetrical feathers (e.g. Prum and Brush, 2002; Dial et al., 2006). Clarifying the contributions of feather structure to the production of L and D among extant birds can, therefore, enhance our understanding of both the development and evolution of avian flight. Ultimately, the timing of developmental transitions in locomotor capacity may relate to life history strategy, ecological preference and adult locomotor habit.

We chose to examine precocial chukars because they have a relatively long period of morphological development (∼100 days) and because transitions in locomotor capacity are well documented for this species (e.g. Jackson et al., 2009) (Table 1). Pin feathers begin to emerge at approximately 4 d.p.h.; at this age chukars will use their wings to crawl up slopes. By 6 d.p.h., flight feathers have begun to unfurl and birds start to engage in WAIR through inconsistent, asymmetrical flapping. Flapping becomes more rhythmic and more symmetrical by 8 d.p.h., although flight feathers remain unfurled only distally until 10–12 d.p.h. Sustained level flight is possible by 20 d.p.h. By 50 d.p.h., birds are capable of accelerating flights, although pectoral musculature is not fully developed until nearly 100 d.p.h. Throughout this time period, wing area and tip velocity increase. In the precocial chukar, ontogenetic improvements in aerodynamic capacity thus occur in conjunction with morphological changes in wing area and feather structure, and with increases in tip velocity and Reynolds number (Re).

Table 1.

Developmental transitions in behavior and wing kinematics in chukar (from Jackson et al., 2009)

MATERIALS AND METHODS

To measure L and D in developing chukar wings, we adapted the methods of Usherwood and Ellington (Usherwood and Ellington, 2002a; Usherwood and Ellington, 2002b) and Usherwood (Usherwood, 2009). Dried, spread wings were spun by a propeller apparatus that was mounted on a force plate. This experimental setup is designed to mimic flapping at very low advance ratios (e.g. WAIR, standing take-off, hovering, vertical ascent or slow forward flight), where local air velocity at the wing tip greatly exceeds that at the wing base. We spun all wings at in vivo angular velocities and calculated coefficients of lift and drag (C_L and C_D, respectively) to control for the contribution of wing size to absolute levels of wingtip velocity and force production. To control for changing fluid dynamics as a function of size, we also spun the wings at equivalent Re. Re values were calculated using mean wing chord lengths and tip velocities, as in Ellington (Ellington, 1984b).

Animals and wing preparation

All birds, from commercially purchased eggs, were incubated and raised post hatching in indoor pens at the Field Research Station at Fort Missoula, University of Montana, Missoula, MT, USA, and transferred at 40 d.p.h. to outdoor aviaries. Upon hatching all animals received food and water ad libitum. The University of Montana Institutional Animal Care and Use Committee approved all protocols.

We studied the right wings of chukars aged 4, 6, 8, 10, 20, 49 and ≥100 d.p.h. (N=2 birds per age class, except at 4 d.p.h. where N=1). After chukars were killed, we removed a wing at the glenoid, stretched it into a mid-downstroke posture as verified using high-speed three-dimensional video (Jackson et al., 2009) and dried it in a low-temperature oven (25°C). To mount the wing and to provide a counterweight, we inserted a small-diameter (2 mm) brass rod into the head of the humerus and soldered it to a larger brass rod (4 mm diameter) that was oriented parallel to the leading edge of the wing and that extended approximately the length of the wing.

Propeller model

The wing and counterbalancing brass rod were attached upside-down to a custom-made Bertec force plate (15×15 cm platform, 200 Hz resonant frequency; Bertec Corp., Columbus, OH, USA) via a NEMA 23 brushless DC motor (model BLWR232S-36V-4000, Anaheim Automation, Inc., Anaheim, CA, USA) or NEMA 23 stepper motor (23W108D-LW8, Anaheim Automation, Inc.), which were controlled by a Luminary Micro LM3S8971 BLDC Motor controller (Stellaris Group, Texas Instruments, Austin, TX, USA) or an Arcus Technology ACE-SDE controller (Arcus Technology Inc., Livermore, CA, USA), respectively. The force plate was shielded from airflow using a cardboard cowling. To mimic in vivo conditions, each wing was spun at the mid-downstroke angular velocity previously recorded from live birds performing WAIR up 65 deg slopes (Table 1) (Jackson et al., 2009). This was the only locomotor style available to all age classes.

To explore possible effects of Re and to bracket potential performance of extinct theropods, we then spun the wings at angular velocities that yielded a Re characteristic of a 10 d.p.h. bird engaged in 65 deg WAIR, and at Re values estimated for theropod fossils (supplemental material Table S1) (A.M.H., unpublished).

Each wing was positioned at active (aerodynamically loaded) angles of attack (α) ranging from –10 to 80 deg, in 10 deg increments for in vivo modeling, and from 15 to 60 deg, in 15 deg increments for equivalent Re modeling. Adult (≥100 d.p.h.) wings were never measured at α>60 deg because of limitations of the force plate apparatus. To measure α, each wing was marked with reflective tape on the leading edge near the wrist, and on the trailing edge at a position creating a line perpendicular to the leading edge and parallel to the chord of the wing. The marked wings were viewed using Photron Fastcam Viewer v3.1.3 software and a Photron 1024 PCI camera sampling at 500 Hz (shutter speed 1/2000 s; Photron USA Inc., San Diego, CA, USA). Wings were spun three times per α, and values of L and D were averaged among the three trials. We measured an ‘inactive’ α before and after each trial to ensure that the wing did not slip or permanently deform during the trial.

Aerodynamic measurements using a force plate

Forces generated by the spinning wings were measured using the Bertec force plate, digitally amplified (Bertec AM6800), and recorded at 500 Hz using Chart software v4.5 (ADInstruments, Inc., Colorado Springs, CO, USA) and a Powerlab 8SP A/D converter (ADInstruments Inc.). Signals were low-pass filtered at 11 Hz. Forces generated by brass rods doubled in length but otherwise identical to the counterbalancing rod of each wing were also measured, to account for forces generated by the counterbalancing rods rather than the wings.

Vertical force (F_V) was measured directly along the z-axis of the Bertec force plate, whereas horizontal force (F_H) was derived from torque (Q, Nm) about the z-axis. We used equations developed by Usherwood and Ellington (Usherwood and Ellington, 2002a) to convert these measures to force coefficients. In brief, the coefficient of vertical force (C_V) was calculated as:

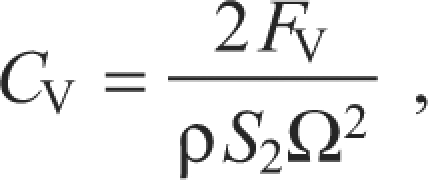(1)

where ρ is air density (1.07 kg m^–3 in Missoula, MT, USA), S₂ is the second moment of area (m⁴) and Ω is the angular velocity of the wing (rad s^–1). The coefficient of horizontal force (C_H) was calculated as:

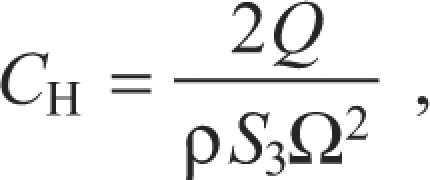(2)

where S₃ is the third moment of area (m⁵). When necessary for subsequent analyses, an absolute measure of horizontal force (F_H) was then computed by substituting into Eqn 1 C_H for C_V and F_H for F_V. We computed resultant force as the vector sum of F_H and F_V.

C_V and C_H were converted into coefficients of lift (C_L) and drag (C_D). C_L and C_D are expressed relative to the velocity of air at a wing element given predicted effects of induced downwash upon the effective angle of attack:

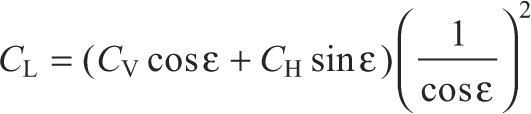(3)

and

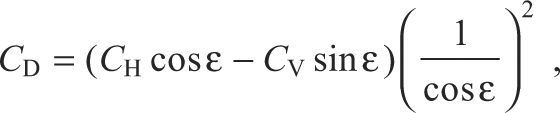(4)

where ϵ is the downwash angle. We modeled induced downwash velocity assuming a Rankine–Froude momentum jet and a triangular distribution for local induced downwash along the wing; see Usherwood and Ellington (Usherwood and Ellington, 2002a) for further explanation.

C_L and C_D were averaged for each age class. Using IGOR Pro v6.12 (Wavementrics Inc., Portland, OR, USA), C_L and C_D for both wings (except in the case of 4 d.p.h.) were plotted against α and averaged with a 100-point spline interpolation curve (supplemental material Fig. S1).

Particle image velocimetry

Due to small signal magnitude, our force plate could not be used to resolve aerodynamic forces for the smallest wings (4 and 6 d.p.h.). Consequently, we used particle image velocimetry (PIV) to measure the wake dynamics and calculate F_V of the propeller model for these two age classes. We extended the PIV sampling to all wings to compare force plate and PIV techniques.

For PIV, we used a LaVision GmBH system with DaVis 7.1 software (Goettingen, Germany), a Flowmaster 1376×1040 pixel digital camera (Goettingen, Germany) sampling at 5 Hz and a 50 mJ dual-cavity pulsed NdYAG laser (New Wave Research Inc., Fremont, CA, USA). We seeded the air with particles of olive oil (<1 μm in diameter) generated at a rate of 7×10¹⁰ particles s^–1 using a vaporizer fitted with a Laskin nozzle. We placed the camera perpendicular to the planar (∼3 mm thick) illumination field.

To calculate particle velocity, we used cross-correlation of paired images with an elapsed time between images (Δt) of 250–400 μs to give ∼10 pixel particle separation in the regions of greatest velocity. We employed an adaptive multipass with an initial interrogation area of 64×64 pixels and final area of 16×16 pixels with 50% overlap. Vector fields were post-processed using a median filter (strong removal if difference relative to average >2× the r.m.s. of neighbors and iterative reinsertion if <3× the r.m.s. of neighbors), removal of groups with <5 vectors, fill of all empty spaces by interpolation and one pass of 3×3 smoothing. We estimated minimum error in velocity measurements to be 5.0±0.5% including contributions due to a correlation peak of 0.1 pixels, optical distortion and particle–fluid infidelity (Spedding et al., 2003a).

We calculated F_V using the Rankine–Froude axial momentum theory, treating the propeller as an actuator disc (Ellington, 1984a) and sampling a horizontal, mid-wake transect of vertical velocity (v) averaged from 50 PIV images:

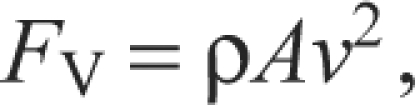(5)

where A is the cross-sectional area of the wake at the level of the wake transect. Transects were taken at 1.5 chord lengths from the root of the wing.

Morphological measurements

Wings of all birds were photographed in dorsal view, and gross morphology [length, surface area (S) and moments of area (S₂ and S₃)] was measured using ImageJ software (v. 1.43u, National Institutes of Health, Bethesda, MD, USA). Camber (dimensionless) was measured at the wrist using a ruler, as the maximum wing depth divided by the chord length at that point. Wing porosity was calculated as:

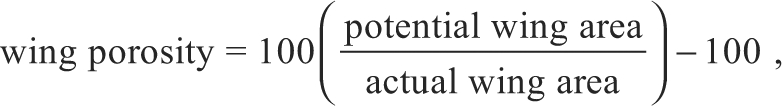(6)

where potential wing area is the area outlined by the leading edge of the wing and the tips of the primary and secondary feathers. A wing with no gaps between its feathers would have a porosity of 0, whereas a wing with many gaps between its feathers would have a porosity exceeding 0.

Primary and secondary feathers from two additional birds of each age class were scanned using an HP Photosmart scanner (Palo Alto, CA, USA) at a resolution of 236 pixels cm^–1. Feather length, degree of unfurling, degree of asymmetry and rachis width were measured from these scans using ImageJ. Asymmetry measurements were taken on the two most distal primary feathers at distances 25 and 50% down the rachis shaft from the feather tip, and were calculated as the width of the trailing (inner) vane divided by the width of the leading (outer) vane of the feather:

(7)

such that 1 would represent a perfectly symmetrical feather. Averages of the two distances (25, 50%) and two feathers are reported. For distal primary feathers (7th primary for 8–20 d.p.h., 8th primary for 49–100 d.p.h., N=2 per age class), flexural stiffness was also measured, based on the technique outlined by Combes and Daniel (Combes and Daniel, 2003):

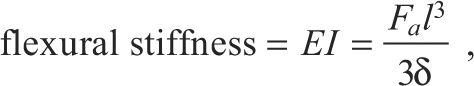(8)

where E is Young's modulus, I is the second moment of area, F_a is the applied force, l is the effective beam length (70% of feather length) and δ is feather displacement (<10% of l) (for details, see Combes and Daniel, 2003). Finally, the seventh primary feathers of 8, 49 and 100 d.p.h. birds were scanned using a Hitachi S-4700 cold field emission SEM (Hitachi High Technologies America Inc., Pleasanton, CA, USA). Feather samples were coated with gold palladium sputter using a Pelco Sputter coater (Ted Pella Inc., Redding, CA, USA) and attached to aluminum stubs via carbon sticky tabs. SEM scans were analyzed in ImageJ for barbicel density and barbule overlap. The seventh primary feather was chosen because it forms the leading edge of the wing in immature birds and a substantial portion of the leading edge in adults.

RESULTS

Aerodynamic performance at in vivo Re

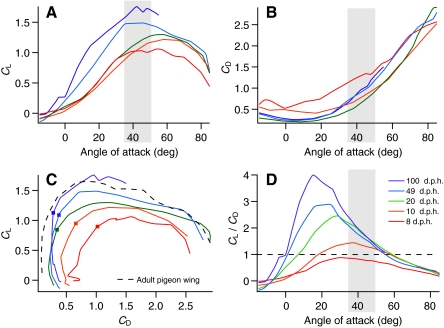
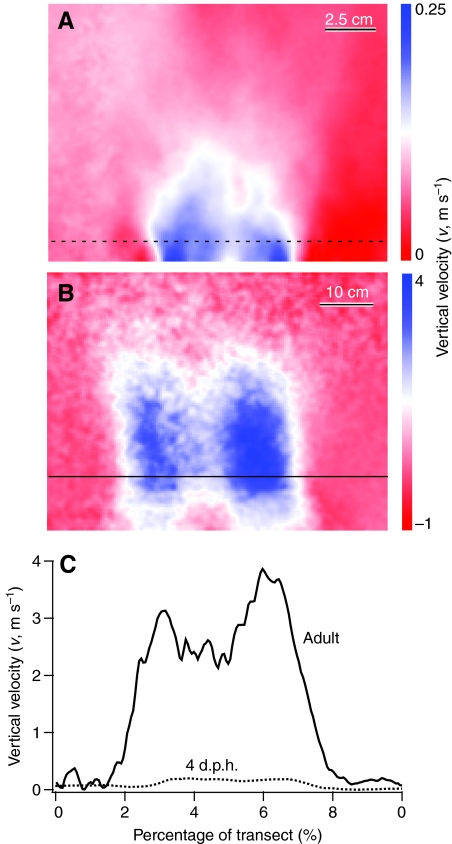
Absolute magnitudes of L and D produced by wings increased throughout ontogeny. The C_D at a given angle of attack (α) was relatively high at 8 d.p.h. but was fairly similar across older age classes (Fig. 1B). The C_L consistently improved with age (Fig. 1A). Consequently, at most α, L:D ratios also increased with age (Fig. 1C,D); adult wings generated forces very similar to previously published results for pigeons (Usherwood, 2009) (Fig. 1C). Maximum L:D ratios increased from 0.88 at 8 d.p.h. to 4.00 in adults, with maximum L:D ratios tending to occur at progressively lower α as age increased (31, 38, 28, 24 and 15 deg). Even the youngest bird wings, however, produced detectable amounts of vertical force. As resolved using PIV, these levels were <1% of body weight (Figs 2, 3).

Fig. 1.

Ontogenetic trends in chukar wing performance at in vivo Reynolds numbers: (A) coefficient of lift (C_L) versus angle of attack (α); (B) coefficient of drag (C_D) versus α; (C) C_L versus C_D; and (D) C_L/C_D versus α. In vivo angles of attack (α) are indicated by shaded areas; maximum L:D ratios are indicated by squares (in C). Pigeon wing (4 Hz) (Usherwood, 2009) is included in C for comparison. d.p.h.: days post hatching.

Fig. 2.

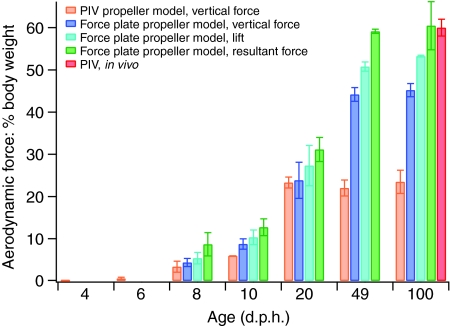
Mass-specific aerodynamic force at α=45 deg. Values represent means ± s.d.

Fig. 3.

Average vertical velocity induced in the wake of propeller models by chukar wings, as measured using particle image velocimetry (PIV). (A) 4 d.p.h., α=15 deg, (B) adult (100 d.p.h.), α=30 deg and (C) transect profiles of vertical velocity in the wake, sampled 1.5 chord lengths from the wing root.

For 8–100 d.p.h. wings, PIV yielded estimates of vertically directed forces that were 76±16% (mean ± s.d.) of those measured using the force plate (α=15–60 deg). At in vivo α, PIV estimates were 81% of force plate measurements for 8–20 d.p.h. wings but were only 51% for 49–100 d.p.h. wings (Fig. 2). PIV may underestimate induced velocities for 49 and 100 d.p.h. wings because of rapid self-convection of the wake away from the sampling plane (Spedding et al., 2003b). For example, PIV measurements for 49 and 100 d.p.h. wings were 77% of force plate measurements when force production was lower (α=15–30 deg).

Resultant forces seem to be required to balance force plate measurements with the in vivo measurements of Tobalske and Dial (Tobalske and Dial, 2007) for adult birds. Resultant forces produced by 8 and 10 d.p.h. bird wings were between 8 and 13% body weight compared with 31, 59 and 60% produced by 20, 49 and 100 d.p.h. wings, respectively (Fig. 2).

Aerodynamic performance at equivalent Re

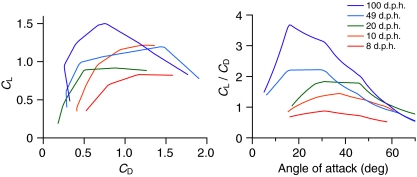
Across a range of other Re values, ontogenetic trends in aerodynamic performance were similar to those observed at in vivo Re. With increasing age, the C_L tended to increase and the C_D tended to decrease (Fig. 4, supplemental material Fig. S2). The L:D ratio also improved with age, particularly at biologically relevant α (<50 deg) (Jackson et al., 2009). Maximum L:D ratios generally occurred at lower α in older bird wings, as with in vivo Re.

Fig. 4.

Ontogenetic trends in chukar wing performance at 10 d.p.h. equivalent Reynolds numbers (Re=12,893).

Younger bird wings (8 d.p.h.) tended to perform best at lower Re and lower tip velocities, whereas older bird wings (20, 49 and 100 d.p.h.) tended to perform best at higher Re and higher tip velocities (supplemental material Fig. S3). Generally, as Re increased, peak L:D ratios occurred at lower α.

Deformation of the wings during spinning

For all ages, wings tended to deform more at higher α and at higher Re and tip velocities. At in vivo Re, for α<30 deg, 8, 10 and 20 d.p.h. wings deformed by ∼0–2 deg whereas 49 and 100 d.p.h. wings deformed by ∼1–6 deg. For α>30 deg, 8 and 10 d.p.h. wings deformed by up to ∼3 deg, and 20, 49 and 100 d.p.h. wings deformed by up to ∼10 deg; deformation tended to increase with increasing α (supplemental material Fig. S4A). Wing deformation also increased with increasing Re. For α=15–60 deg, 8 and 10 d.p.h. wings deformed, on average, by <2.1 deg at Re<13,000 and by 4.5–6 deg at Re=19,000–23,000. For the same α, 20–100 d.p.h. wings deformed by <2 deg at Re<31,000 and 3.7–5.4 deg at Re>63,000 (supplemental material Fig. S4B). At a given Re, younger wings tended to deform more than older wings. For example, at Re=12,893, 8, 10, 20, 49 and 100 d.p.h. wings deformed by 2.1, 1.5, 1.0, 0.7 and 0.4 deg, respectively (supplemental material Fig. S4B).

Resultant orientation at in vivo angles of attack

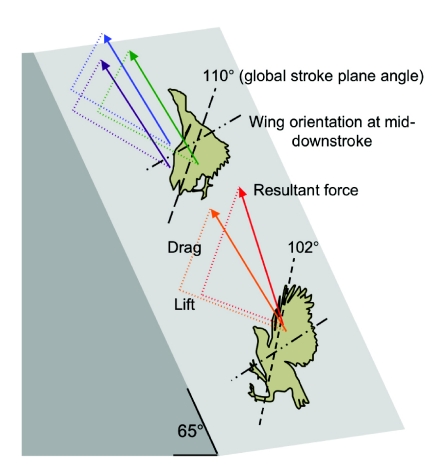
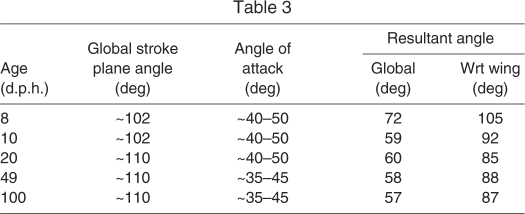
During WAIR at inclines of 65 deg, young chukars tend to flap their wings in more vertically aligned stroke planes (∼102 deg) and at higher α (∼40–50 deg) than more mature chukars (∼110 deg, ∼35–45 deg) (Jackson et al., 2009). In vivo α roughly coincided with peak L:D ratios in 8 and 10 d.p.h. bird wings, and with peak C_L in 49 and 100 d.p.h. wings (Fig. 1). Although α employed during 65 deg WAIR did not coincide with peak L:D ratios in older birds, 20, 49 and 100 d.p.h. wings still generated higher ratios than 8 and 10 d.p.h. wings at in vivo α. Despite a twofold variation in L:D ratios at in vivo angles (0.78–1.96), all wings (especially 10–100 d.p.h. wings) generated similarly directed resultant forces, approximately perpendicular to the wing (Table 3, Fig. 5). Such similarity in resultant orientation is consistent with previous research (Tobalske and Dial, 2007), and seems to be due to slight age-dependent differences in α and stroke plane angle.

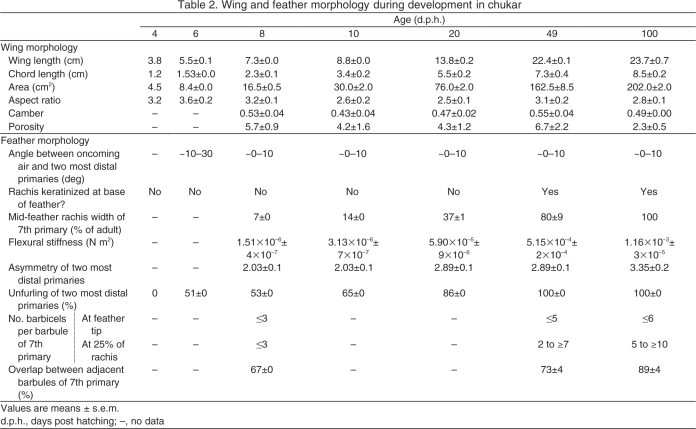
Table 2.

Wing and feather morphology during development in chukar

Fig. 5.

Orientation of resultant forces during 65 deg wing-assisted incline running in chukar. Bird ages are represented by differently colored arrows: 8 d.p.h. (red), 10 d.p.h. (orange), 20 d.p.h. (green), 49 d.p.h. (blue), ≥100 d.p.h. (purple).

Morphological development

Ontogenetic improvements in aerodynamic performance occurred in conjunction with changes in wing shape and feather structure. Although aspect ratio and camber showed no obvious ontogenetic trends and varied between 2.5–3.6 and 0.43–0.55, respectively [Table 2; correlation (r_S) with peak C_L≤|0.20|], wing area increased substantially. Nevertheless, C_L and C_D account for wing area, so other morphological attributes must be responsible for observed differences in aerodynamic performance.

Table 3.

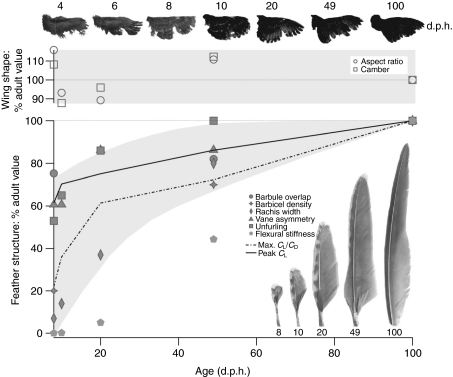
Between 4 d.p.h. and adulthood, primary feathers became oriented more perpendicular to airflow. Primary feathers also became less flexible, more unfurled and more asymmetrical, with more barbicels per barbule and greater overlap between barbules of adjacent barbs (Table 2, Fig. 6). These changes in feather structure closely tracked ontogenetic improvements in aerodynamic performance [Fig. 7; correlation (r_S) with peak C_L>0.95 for all metrics of feather morphology]. Although feather unfurling contributed to reduced wing porosity between 4 and 10 d.p.h., by 10 d.p.h. there was enough overlap between remiges and coverts such that wing porosity did not correlate strongly with peak C_L between 8 d.p.h. and adulthood (r_S=–0.30).

Fig. 6.

Ontogeny of chukar feather micromorphology. All images magnified at ×500.

Fig. 7.

Ontogenetic trends in wing shape, feather structure and aerodynamic performance in chukar.

DISCUSSION

Our study of wing and feather ontogeny demonstrates a clear relationship between morphology and aerodynamic performance. At in vivo angular velocities and at most angles of attack (α), older bird wings generate greater coefficients of lift (C_L) and greater lift per unit drag (L:D) than younger bird wings (Fig. 1). This general trend holds across a range of flow conditions (Reynolds numbers), with peak C_L and peak L:D ratios improving with age (Fig. 4, supplemental material Fig. S2). Collectively, such findings indicate that developmental changes in wing shape and/or feather structure contribute substantially to ontogenetic improvements in aerodynamic performance. These results may seem surprising given that previous work using similar models showed that aerodynamic performance is largely unaltered by dramatic changes in aspect ratio, camber, twist and leading edge morphology (Usherwood and Ellington, 2002a; Usherwood and Ellington, 2002b; Usherwood, 2009) (cf. Altshuler et al., 2004). However, previous studies focused on gross morphology of the wing, and our present investigation of a developmental series introduces, for the first time, the effects of feather structure (Fig. 7).

Although (unloaded) wing shape remains fairly constant during development (Table 2, Fig. 7), feather structure changes dramatically and, therefore, appears to affect production of lift (L) and drag (D). As developing feathers unfurl, lengthen and keratinize, they become less flexible and more asymmetrical (Table 2, Fig. 7). Because the number of barbicels per barbule and the overlap between barbules of adjacent barbs both increase towards the rachis base and following first molt (∼30–60 d.p.h.) (Fig. 6), feathers also become more structurally cohesive (and presumably less transmissive) as they unfurl and are replaced by adult feathers. Therefore, a major hypothesis that emerges from our results is that the porosity or transmissivity (Müller and Patone, 1998) of wings and feathers dramatically affects aerodynamic performance. Ellington (Ellington, 2006) briefly explored porosity in relation to wing aerodynamics and predicted that the transmissivity of adult bird feathers would offer higher L:D ratios than those generated by insects. Ellington's prediction may hold true for the feathers of adult birds when compared with insects. However, the extreme porosity of young chukar wings and feathers, due to incomplete feather unfurling, low numbers of barbicels and low barbule overlap (Figs 6, 7), was associated with low C_L and low L:D ratios. Feather unfurling and increases in feather stiffness, asymmetry, barbicel density and barbule overlap appear to improve structural integrity and reduce porosity during ontogeny, contributing to higher L:D ratios at most α and suggesting that feather morphology strongly affects aerodynamic performance in developing birds.

Ontogenetic trends in wing kinematics may be tuned to feather development. Between 8 d.p.h. and adulthood, wing angular velocities decrease slightly, whereas tip velocities increase because of increases in wing length (Tables 1 and 2). When examined across a range of tip velocities (Re), wings with stiffer, more asymmetrical and more cohesive feathers (20, 49 and 100 d.p.h.) appear to perform best at higher velocities. In contrast, wings with more flexible, more symmetrical and less cohesive feathers (8 d.p.h.) appear to perform best at lower velocities (supplemental material Fig. S3). Given that wing deformation increases with increasing Re and tip velocity (supplemental material Fig. S4B), older wings may require the deformation associated with high tip velocities to function at their full potential, whereas younger wings may deform excessively and perform poorly under such conditions. Thus feather structure could also influence L and D production by affecting the three-dimensional shape of aerodynamically loaded wings. Although beyond the scope of this study, instantaneous wing shape almost certainly has important functional consequences (Daniel and Combes, 2002). Previous work on locusts and hawkmoths indeed suggests that aeroelasticity is an important component of aerodynamic performance (Young et al., 2009; Mountcastle and Daniel, 2009). In short, feather morphology and tip velocity may influence aerodynamic performance by affecting instantaneous loaded wing shape, and may be developmentally ‘tuned’ to one another, with increases in tip velocity tracking improvements in feather structure.

Feather development could also play a fundamental role in the ontogeny of flapping behavior. As immature chukars grow and acquire the ability to fly, L:D ratios not only improve but also peak at lower α (Fig. 1C,D). During 65 deg WAIR, older birds nevertheless employ relatively high α that correspond with peak L and higher resultant forces, rather than peak L:D ratios. This suggests that during WAIR, efficacy is more important than efficiency; this may be a general pattern for escape behavior. Further, because birds flap their wings at relatively low advance ratios (translational velocity/flapping velocity) during WAIR, and because oncoming airflow is aligned relatively vertically (global stroke plane angle=102–110 deg), drag-based forces contribute substantially to weight support (Table 3, Fig. 5). Although higher L:D ratios may generally be necessary for level, long distance or gliding flight in birds (e.g. L:D=10.5 in gliding Harris hawk, Parabuteo unicinctus) (Tucker, 1991), incipient wings that produce roughly equal amounts of L and D are effective during WAIR. Thus the ontogenetic acquisition of flight capacity seems to involve: (1) a morphological transition from ‘draggy’ wings with relatively flexible, symmetrical and loose feather morphologies to wings with stiffer, asymmetrical and cohesive feathers capable of producing higher C_L, and (2) a corresponding behavioral transition, from drag-based to lift-based performance. This unique but immediate aerodynamic capacity of immature wings plays a crucial role during development. Incipient wings allow non-volant juveniles to flap-run up slopes or across water (Anseriforms; Common Mergansers (Mergus merganser), Mallards (Anas platyrhynchos), A.M.H., personal observation), control falling descents and even swim [hoatzins (Opisthocomus hoazin) (Thomas, 1996)], thereby providing access to elevated habitats or refugia (e.g. Dial et al., 2006).

Access to three-dimensional environments and refugia might also have conferred selective advantages to feathered theropods during the evolution of avian flight. Ontogenetic trends in feather morphology in many ways mimic evolutionary trends in feather appearance. Both younger birds and more basal feathered theropods may have primary feathers that are distally branched or unfurled [e.g. Beipiaosaurus (Xu et al., 1999), Similicaudipteryx (STM4-1) (Xu et al., 2010); 6–8 d.p.h. chukars], relatively symmetrical [e.g. Caudipteryx (Qiang et al., 1998), Similicaudipteryx (Xu et al., 2010); 6–14 d.p.h. chukars] and oriented obliquely to airflow [e.g. Caudipteryx (Qiang et al., 1998); 6 d.p.h. chukars]. Older birds and more derived feathered theropods tend to have completely unfurled, asymmetrical feathers [e.g. Microraptor (Xu et al., 2003), Archaeopteryx (e.g. Prum and Brush, 2002); 49 to ≥100 d.p.h. chukars]. Ontogenetic improvements in aerodynamic performance may, therefore, provide insight into the evolutionary acquisition of avian flight. Chukars at 8 d.p.h. rely on drag-based flapping behaviors, driven by wings with relatively symmetrical and structurally diffuse feathers, that elicit relatively little aerodynamic force (<10% body weight; Fig. 2) (Tobalske and Dial, 2007), and that are often supplemented by hindlimb support. Mature chukars expand their behavioral repertoire by generating larger aerodynamic forces (often exceeding body weight) while vigorously flapping wings composed of asymmetrical and cohesive feathers. Given similar patterns between feather ontogeny and feather evolution, evolutionary trajectories in flight capacity may have paralleled these developmental trajectories in aerodynamic performance and flapping behavior (A.M.H., unpublished). By examining the ontogeny of aerodynamic performance, we therefore gain insight into both the development and evolution of avian flight. By examining transitions in form, function and behavior, we may also improve our understanding of life history strategies, ecological preferences and adult locomotor habits.

Conclusions and future directions

Our analysis suggests that feather structure influences aerodynamic performance in developing birds. Older wings with stiffer and more asymmetrical feathers, high numbers of barbicels and a high degree of overlap between barbules generate greater C_L and L:D ratios than younger wings with flexible, relatively symmetrical and less cohesive feathers. Developmental changes in feather structure may effect developmental changes in lift and drag production by influencing wing transmissivity and aeroelasticity. Although our metrics of unloaded wing shape (aspect ratio, camber) did not correlate with peak C_L, the shape of aerodynamically loaded wings almost certainly contributes to aerodynamic performance. Thus the relationship between feather structure, aeroelasticity and instantaneous loaded wing shape (which we did not attempt to quantify) warrants further study.

Feather morphology and flapping behavior may be developmentally ‘tuned’ to one another in the precocial chukar. Younger birds with less effective wing and feather morphologies engage in behaviors that require relatively little aerodynamic force and that allow D to contribute to weight support, whereas older birds may expand their behavioral repertoire by flapping with higher tip velocities and generating greater amounts of L. Incipient wings are, therefore, uniquely but immediately functional. Comparing these findings with a developmental series of wing shape, feather structure, aerodynamic performance and flapping behavior in an altricial species and in a bat (which lacks feathers) could further illuminate flight ontogeny. Likewise, using incipient wings of extant birds to model aerodynamic performance of extinct theropods with protowings could elucidate flight evolution (A.M.H., unpublished).

Finally, resultant forces recorded by our propeller model match in vivo measurements for adult birds (Fig. 2). This suggests that the wake of live birds is a product of all forces operating on the surface of the wing (vector sum of L and D). Although the orientations of resultant forces in the present study (57–72 deg; Table 3, Fig. 5) do not agree with those recorded in vivo (∼45±6 deg, mean ± s.d.) (Tobalske and Dial, 2007), this could be due to a variety of reasons. For example, the complicated nature of wake rollup (Spedding et al., 2003a), the fact that this study sampled only mid-downstroke postures [whereas the stroke plane in live birds is more vertical early in the stroke (Jackson et al., 2009)] and possible effects of the tail and/or substrate could all contribute to the observed difference in resultant orientation between the propeller apparatus and in vivo recordings. Regardless, the relationship between near wake forces and far wake vorticity merits further consideration.

LIST OF SYMBOLS AND ABBREVIATIONS

A

cross-sectional area of the wake

C_D

coefficient of profile drag

C_H

coefficient of horizontal force

C_L

coefficient of lift

C_V

coefficient of vertical force

d.p.h.

days post hatching

D

profile drag

E

Young's modulus

EI

flexural stiffness

F_a

applied force

F_H

horizontal force

F_V

vertical force

I

second moment of area

l

effective beam length

L

lift

PIV

particle image velocimetry

Q

torque

Re

Reynolds number

S

surface area

S₂

second moment of area

S₃

third moment of area

v

vertical velocity

α

active (aerodynamically loaded) angle of attack

δ

feather displacement at point of force application

ϵ

downwash angle

ρ

air density

Ω

angular velocity of wing