Biomechanics of hair cell kinocilia: experimental measurement of kinocilium shaft stiffness and base rotational stiffness with Euler–Bernoulli and Timoshenko beam analysis

Abstract

Vestibular hair cell bundles in the inner ear contain a single kinocilium composed of a 9+2 microtubule structure. Kinocilia play a crucial role in transmitting movement of the overlying mass, otoconial membrane or cupula to the mechanotransducing portion of the hair cell bundle. Little is known regarding the mechanical deformation properties of the kinocilium. Using a force-deflection technique, we measured two important mechanical properties of kinocilia in the utricle of a turtle, Trachemys (Pseudemys) scripta elegans. First, we measured the stiffness of kinocilia with different heights. These kinocilia were assumed to be homogenous cylindrical rods and were modeled as both isotropic Euler–Bernoulli beams and transversely isotropic Timoshenko beams. Two mechanical properties of the kinocilia were derived from the beam analysis: flexural rigidity (EI) and shear rigidity (kGA). The Timoshenko model produced a better fit to the experimental data, predicting EI=10,400 pN μm² and kGA=247 pN. Assuming a homogenous rod, the shear modulus (G=1.9 kPa) was four orders of magnitude less than Young's modulus (E=14.1 MPa), indicating that significant shear deformation occurs within deflected kinocilia. When analyzed as an Euler–Bernoulli beam, which neglects translational shear, EI increased linearly with kinocilium height, giving underestimates of EI for shorter kinocilia. Second, we measured the rotational stiffness of the kinocilium insertion (κ) into the hair cell's apical surface. Following BAPTA treatment to break the kinocilial links, the kinocilia remained upright, and κ was measured as 177±47 pN μm rad^–1. The mechanical parameters we quantified are important for understanding how forces arising from head movement are transduced and encoded by hair cells.

INTRODUCTION

Vestibular hair cells are the mechanoreceptors in vestibular organs of the inner ear that detect head accelerations. Their mechanosensitive receptor is the hair cell bundle, a collection of actin-based stereocilia arranged in rows of increasing height with a single microtubule-based kinocilium at the tall edge of the bundle. Several types of interciliary links connect the stereocilia to each other and to the kinocilium. Tip links run in a uniform direction from the tips of stereocilia to the sides of their taller neighbor in the adjacent row. Deflection of these stereocilia towards the kinocilium produces tensioning in the tip links, which is thought to increase the open probability of mechanically gated transduction channels. Conversely, deflection of stereocilia away from the kinocilium reduces tip link tension and decreases the open probability of the transduction channels. In the otolith organs of the vestibular system (utricle, saccule and lagena), head movements result in deflection of the otoconial layer (OL) to which kinocilia tips attach directly (Fig. 1B,C) or indirectly. Kinocilia thus act as mechanical links that transfer movements of the OL to the stereocilia, whose resulting deflections modulate mechanotransduction by the hair cell. Given the kinocilium's role in transducing head movements, it is crucial to quantify its mechanical properties to examine how head movements are encoded by vestibular hair cells.

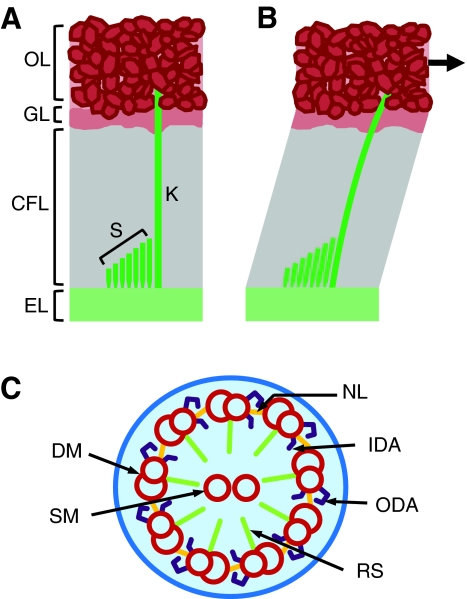
Fig. 1.

(A,B) In medial extrastriolar hair bundles from the turtle Trachemys scripta elegans utricle, the kinocilia (K) are much taller than the stereocilia (S). The kinocilia project from basal bodies in the epithelial layer (EL) through the gelatinous column filament (CFL) and gel (GL) layers, and embed in the otoconial layer (OL). Movement of the OL, deflection indicated by the arrow, produces shearing of the CFL and GL. The kinocilium deflects in response to movement of the OL, which in turn deflects the stereocilia, resulting in signal transduction. (C) A cross-section of the classic 9+2 axoneme of cilia shows nine peripheral doublet microtubules (DM) surrounding two single microtubules (SM). The peripheral doublets connect to each other through nexin links (NL) and to the central tubules through radial spokes (RS). Inner (IDA) and outer dynein arms (ODA) interact with neighboring peripheral tubules. Kinocilia posses this 9+2 microtubule structure, but have been shown to lack IDA (Kikuchi et al., 1989).

This is especially true for hair cells in which the kinocilium is much taller than the tallest stereocilia. In this configuration, the kinocilium dominates the bundle mechanics. Such hair cells are found in the extrastriola of the turtle utricle (Xue and Peterson, 2006) and are widespread in the otoconial organs of other vertebrates (Lewis et al., 1985). The kinocilium stiffness, which decreases with an increase in the height of an applied force, dictates how much of the OL movement is transmitted to the mechanotransducing part of the hair bundle. Previous computational studies have shown that the tall and compliant kinocilia of extrastriolar bundles increase the hair cells' operating range (range of deflections over which vestibular sensory cell can encode) to several microns compared with that of striolar bundles, which is ∼0.1 μm (Nam et al., 2005). Knowing the mechanical properties of the kinocilium will further our understanding of how these hair cells operate.

Kinocilia are composed of a microtubular core, a 9+2 axoneme, composed of nine peripheral doublet microtubules encircling two central single tubules. This configuration is common to motile cilia and eukaryotic flagella (Fig. 1A) but, despite their common structure, kinocilia are thought to be non-motile, unlike flagella, as they lack the inner arms of the motor protein dynein, which are essential for motility (Kikuchi et al., 1989). A limited number of spontaneous flagella-like oscillations have been observed in ampullary kinocilia but were limited in number and suggested to result from tissue degradation (Flock et al., 1977; Rüsch and Thurm, 1986; Rüsch and Thurm, 1990).

Flexural rigidity (EI) is a measure of a beam's ability to resist bending based on material composition and geometry. It has been measured for non-kinocilial structures with a 9+2 axoneme, including compound cilia (Baba, 1972) and echinoderm sperm flagella (Okuno and Hiramoto, 1979; Okuno, 1980; Ishijima and Hiramoto, 1994; Pelle et al., 2009). In these studies, the EI was measured based on the Euler–Bernoulli beam theory and assumptions that these 9+2 microtubular structures behave as homogenous, linearly elastic and isotropic beams (Okuno and Hiramoto, 1979; Okuno, 1980; Ishijima and Hiramoto, 1994). Shear deformation due to the sliding of adjacent doublets was only considered in one study of passive sea sperm flagella (Pelle et al., 2009). The reported values for echinoderm sperm flagella EI ranged from 300 to 15,000 pN μm² and varied with a number of factors, including immobilization with CO₂ (Okuno and Hiramoto, 1979; Ishijima and Hiramoto, 1994) and exposure to ATP and vanadate (Okuno and Hiramoto, 1979; Okuno, 1980; Ishijima and Hiramoto, 1994; Pelle et al., 2009), and a 12- to 14-fold difference in EI was found when it was measured within and perpendicular to the beating plane (Ishijima and Hiramoto, 1994). The only reported value of kinocilium EI (2400 pN μm²) was measured from the superficial neuromasts of the zebrafish lateral line (McHenry and van Netten, 2007). This value was cleverly inferred from the number of kinocilia and the overall EI of the neuromast cupula.

Single microtubules (MTs) have also been analyzed using elastic beam theories to quantify their mechanical properties. Experimental measurements suggest that the EI of microtubules is height dependent, such that shorter microtubules have lower values of EI (Kurachi et al., 1995; Takasone et al., 2002; Pampaloni et al., 2006), but this height dependence is not expected for an isotropic Euler–Bernoulli beam, demonstrating that the MT is not accurately modeled as such. Indeed, atomic force microscopy shows that MTs are highly anisotropic because the longitudinal bond strength between tubulin dimers along the protofilaments is greater than the lateral bond strength between protofilaments (Kis et al., 2002). Computational studies in which the MT was modeled as a two-dimensional orthotropic shell or a one-dimensional Timoshenko beam predict a length dependence of EI that results from an extremely low shear modulus relative to the longitudinal Young's modulus (E) (Li et al., 2006; Pampaloni et al., 2006; Shi et al., 2008). Use of the Euler–Bernoulli model, which does not account for shear deformation, leads to an underestimate of EI for shorter MTs (Li et al., 2006). The Timoshenko beam theory, which can account for shear deformation, was applied to MTs, yielding results comparable to that of the more complicated orthotropic shell model, which includes transverse shearing (Gu et al., 2009). These findings regarding MTs are relevant to the study of kinocilium mechanical properties in two ways. First, microtubules are the building blocks and main structural elements of the kinocilium's 9+2 axoneme, contributing an inherent anisotropy to the microtubular structure. Second, there is potential for sliding between doublet microtubules during bending, further disposing them to translational shearing. Both reasons suggest that a shear-deformable Timoshenko beam may be a more accurate model for a kinocilium than an Euler–Bernoulli beam.

This study experimentally measures the stiffness of the kinocilium shaft in bending. Stiffness was measured using a force-deflection technique by applying a force to the tip of individual kinocilia of differing heights. The measurements of kinocilia stiffness are analyzed using two mechanical beam theories, the Euler–Bernoulli and the Timoshenko beam theories, to determine EI, E, shear rigidity (kGA) and shear modulus (G). We asked which model produces results that most accurately reflect our experimental data: an isotropic model, which ignores shear deformation (the Euler–Bernoulli model), or an anisotropic model, which includes shear deformation (the Timoshenko model).

In addition, the rotational stiffness (κ) of the kinocilium's insertion into the apical surface of the hair cell was measured. The kinocilium remains upright when the links between it and neighboring stereocilia are broken, and a kinocilium separated from the stereocilia and pinned to the epithelial surface returns to an upright position within seconds of release (Hudspeth and Jacobs, 1979). Both behaviors indicate that the insertion of the kinocilium possesses an inherent rotational stiffness, which is quantified here for the first time.

MATERIALS AND METHODS

Modeling the kinocilium as a cantilevered beam

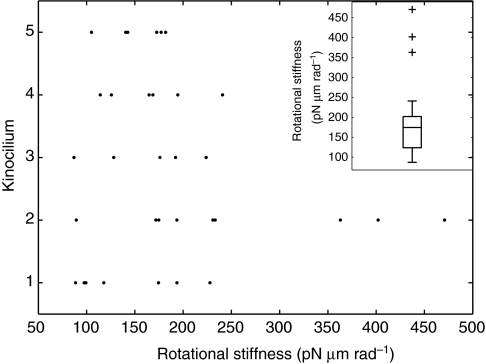
The kinocilium was modeled as a vertically oriented cantilever beam with elastic properties using the Euler–Bernoulli and Timoshenko beam theories (Fig. 2A). The Euler–Bernoulli theory is the simpler of the two because it omits the effect of transverse shear deformation. It assumes that, during bending, the transverse cross-sections of the beam remain planar and perpendicular to the bending axis. For this case, the kinocilium was assumed to be homogenous and isotropic, meaning the mechanical properties are the same in all directions, and there are two independent mechanical parameters, E and Poisson's ratio (ʋ). For a Euler cantilever beam with a point load at the tip, the transverse deflection (δ_E) at the free end is given by:

(1)

where F is the force applied at the free end, L is the length of the beam, I is the second moment of inertia and EI is the flexural rigidity.

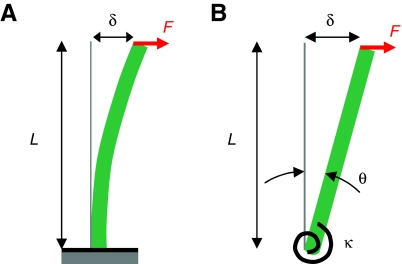
Fig. 2.

(A) The kinocilium was modeled as a vertically oriented cantilevered beam. A force (F) applied at the tip of a kinocilium of height L induces a deflection (δ). (B) To determine rotational stiffness of the kinocilium's insertion, the kinocilium was modeled as a flexible beam with a rotational spring of stiffness κ at the insertion. For small angles of deflection (θ), κ can be determined from L, F, δ and curve-fit predictions of flexural rigidity (EI) and shear rigidity (kGA).

The Timoshenko beam theory accounts for transverse shear by assuming that, during bending, the cross-sections remain planar but are not restrained to be perpendicular to the bending axis. The structure of the kinocilium, with its longitudinally aligned microtubules, is loosely analogous to a composite beam reinforced by unidirectional longitudinally oriented fibers. For this reason, the kinocilium was modeled as a transversely isotropic material, meaning the transverse cross-sections are considered isotropic and the material properties in the transverse direction differ from those in the longitudinal direction. The deflection at the free end of a Timoshenko cantilever beam (δ_T) with a point load at the tip is the sum of the deflection due to bending (Eqn 1) and the deflection due to shear, and is given by (Wang et al., 2000; Kollar and Springer, 2003):

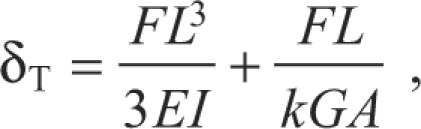(2)

where E is now specific to the longitudinal Young's modulus, k is a shear correction factor equal to 3/4 for a cylindrical beam (Boresi and Schmidt, 2003), G is the transverse shear modulus and A is the cross-sectional area.

The beam analysis employed here assumes that kinocilia are homogenous beams, meaning their composition and elastic properties are the same at every point. Even though kinocilia are not homogenous because of their microtubular structure, this assumption is necessary for the type of simplified beam analysis presented here and is made in previous studies of kinocilia and flagella mechanics (McHenry and van Netten, 2007; Okuno and Hiramoto, 1979; Okuno, 1980; Ishijima and Hiramoto, 1994). In consequence, the determined values of EI and kGA serve as effective values, meaning that the kinocilia effectively function (or can be effectively modeled) as homogenous beams with these properties. Throughout this paper, EI, kGA, E and G of the kinocilium refer to the effective values.

Accuracy of small-deflection beam theory

The application of both the Euler–Bernoulli and Timoshenko beam analyses used here is based on small-deflection beam theory. The accuracy of this small-deflection formulation is dependent on the force loading condition. To determine accuracy, we compared results from small-deflection theory with those from large- or finite-deflection theory in which nonlinearities in the deflection gradient are taken into account (Timoshenko and Gere, 1972). Comparison showed that the small-deflection theory, for the force-deflection method that uses a point load at the top of the kinocilium, has an accuracy that is better than 1.3% for δ/L<0.1, where δ is deflection at beam length L (the error increases to 10% with δ/L<0.3). All our δ/L values are well below 0.1, with a maximum δ/L of 0.07. Thus, the application of the small-deflection beam theory to our kinocilia measurements has better than 1.3% accuracy.

Rotational stiffness

The rotation stiffness κ of a torsional spring is related to its angular rotation θ due to an applied moment M as M=κθ. Fig. 2B illustrates a rigid bar pivoting about a rotational spring. For small angular deflections, the angle of rotation is approximately equivalent to the deflection at the tip of the bar δ_R divided by its length L: θ≈sinθ=δ_R/L. Defining the applied moment as M=FL, where F is the force applied at distance L from the spring pivot, the rotational stiffness relationship becomes:

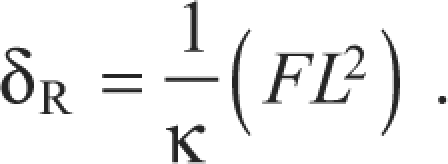(3)

This approach has previously been used to determine the κ of intact hair bundles where the kinocilium was approximately the same height as the tallest stereocilia (Crawford and Fettiplace, 1985; Howard and Ashmore, 1986). Here, the insertion of the kinocilium is modeled as a rotational spring and the tall kinocilium shaft as a flexible beam.

To measure the κ of kinocilia, the filamentous links connecting the kinocilia to their adjacent stereocilia were broken (see Experimental preparation). A force applied to the tip of a kinocilium that is disconnected from the adjacent stereocilia induces both rotation about the insertion and bending of the shaft. In the experiment, the total deflection at the tip of the kinocilium δ includes the sum of the rotational deflection δ_R (Eqn 3) and the bending deflection δ_T for a Timoshenko beam (Eqn 2):

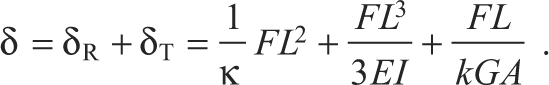(4)

Experimental preparation

Experiments were performed on hair cell bundles in isolated utricles from turtles Trachemys (Pseudemys) scripta elegans (Wied-Neuwied 1839). Turtles were killed following guidelines of the Virginia Tech Institutional Animal Care and Use Committee. Utricles were removed and maintained at room temperature in Hanks' balanced salt solution (HBSS; 1.26 mmol l^–1 CaCl₂, 0.493 mmol l^–1 MgCl₂, 0.407 mmol l^–1 MgSO₄, 5.33 mmol l^–1 KCl, 0.441 mmol l^–1 KH₂PO₄, 4.17 mmol l^–1 NaHCO₃, 137.93 mmol l^–1 NaCl, 0.338 mmol l^–1 Na₂HPO₄, 5.56 mmol l^–1 d-glucose; pH 7.2, 300 mOsm) with 10 mmol l^–1 Hepes [4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid] added as a buffering agent. The utricles were folded along a medial to lateral transect and securely pinned in an experimental chamber. The otoconial membrane was peeled away using an eyelash. Bundles along the folded edge were viewed from the side using a Zeiss Axioskop with a differential interference contrast 100× water immersion objective, 10× oculars and an oil immersion substage condenser (Jena, Germany). Experiments were performed on a vibration isolation table. Measurements of the kinocilia's properties were made from hair bundles located in the medial extrastriola of the turtle utricle. The kinocilia in this region are very tall (10 to >40 μm) and the stereocilia are short (2–5 μm).

To measure the stiffness of the kinocilium shaft (N=27), the portion of the kinocilium projecting above the tallest stereocilia was examined. The base of the kinocilium was backed up with a rigid glass probe, mechanically fixing it between the stereocilia and the probe (Fig. 3A,B). The supporting probe was fabricated from a solid pipette pulled and trimmed to have a flat end 5 μm in diameter. The supporting probe was trimmed while under tension to produce a smooth flat surface. The glass probe was positioned with its top edge at the height of the tallest stereocilia so that when the kinocilium was deflected in the excitatory direction, the exposed portion bent in flexure (Fig. 3B). This produced a single stiffness measurement for each of 27 kinocilia.

Fig. 3.

(A) For stiffness measurements of the kinocilium shaft in bending, bundles were backed up with a supporting probe to fix the kinocilium at the height of the tallest stereocilia. When pushed in the excitatory direction with a flexible glass fiber, the kinocilium bent in flexure. (B) Measurements of applied force (F), tip deflection (δ_tip) and height projecting above the supporting probe (h) were used to calculate EI and kGA. (C) Exposure to BAPTA broke the kinocilial links connecting the kinocilia with their neighboring stereocilia. This photograph of a large deflection shows there was complete separation. (D) Following BAPTA treatment, κ was determined from the force applied through a flexible glass fiber and measurements of the kinocilium's δ_tip, L and values of EI and kGA determined from the Timoshenko analysis.

For measurements of κ, the kinocilium was detached from the adjacent stereocilia in five hair cells (Fig. 3C,D) by using the calcium chelator BAPTA [1,2-bis(2-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid tetrasodium salt, Sigma-Aldrich]. BAPTA has been shown to sever kinocilial links in chick utricular bundles (Goodyear and Richardson, 2003). A 5 mmol l^–1 solution of BAPTA was prepared in Ca²⁺- and Mg²⁺-free HBSS (5.33 mmol l^–1 KCl, 0.441 mmol l^–1 KH₂PO₄, 4.17 mmol l^–1 NaHCO₃, 137.93 mmol l^–1 NaCl, 0.338 mmol l^–1 Na₂HPO₄, 5.56 mmol l^–1 d-glucose; pH 7.2, 300 mOsm) with 0.9 mmol l^–1 MgCl₂ and 10 mmol l^–1 Hepes added. A peristaltic pump was used to exchange the fluid in the experimental chamber with the BAPTA solution. Measurements of κ were begun after at least 10 min of BAPTA exposure. It is assumed that the BAPTA treatment did not otherwise damage the kinocilia or the epithelium at the apical insertions. Fig. 3C demonstrates a kinocilium that is fully detached and rotated about its insertion for a large deflection. It is important to note that the deflections of the kinocilia during actual measurements were much smaller (<1 μm) than the deflection shown in the photograph. The angular deflections (≤0.09 rad) during experiments complied with the small angle approximation applied in Eqns 3 and 4.

Force-deflection technique

A force-deflection technique was used to measure both the stiffness of the kinocilium shaft in bending, from which EI and kGA were determined, and the rotational stiffness of the kinocilium insertion. Kinocilia were deflected in their excitatory directions with flexible glass fibers positioned at their tips (Fig. 3B,D). The fibers were made from solid borosilicate glass pipettes using a microforge. The fibers were drawn perpendicular to the shank of the rod by quickly retracting a platinum heating element. The fibers had tip diameters of 2.9–4.2 μm, were trimmed to lengths of 2.8–3.5 mm and were sputter coated with 200 Å gold to improve their optical contrast. The stiffness of the fibers was determined by measuring the deflection of a horizontally positioned fiber when microbeads of 30–100 μm in diameter were statically attached to the free end. From the bead properties, fiber length and vertical deflection, the stiffness was determined using a cantilever beam equation. The fibers used had stiffness values of 6–47 pN μm^–1.

The free end of a flexible glass fiber was brought into contact with the tip of the kinocilium such that their shafts were parallel. The base of the fiber was displaced sinusoidally (see below) using a piezoelectric linear actuator, and the base movement was measured using a fiber optic displacement sensor known as an extrinsic Fabry-Perot interferometer (Luna Innovations, Blacksburg, VA, USA). Deflections at the tip of the glass fiber, in contact with the kinocilium, were measured using a dual array of photodiodes housed at the camera port of the microscope (Fig. 4A). The rectangular photodiodes were located side-by-side and the gap separating them was aligned with the projected image of the fiber. As the magnified image of the fiber passed between the two diodes, their differential output voltage was proportional to the fiber position (Fig. 4B). The force applied to the kinocilium by the glass fiber can be quantified by multiplying the fiber stiffness by the deflection of the glass fiber (i.e. the difference between the fiber's base and tip deflections). The stiffness of the kinocilium shaft is equal to the applied force divided by the tip deflection.

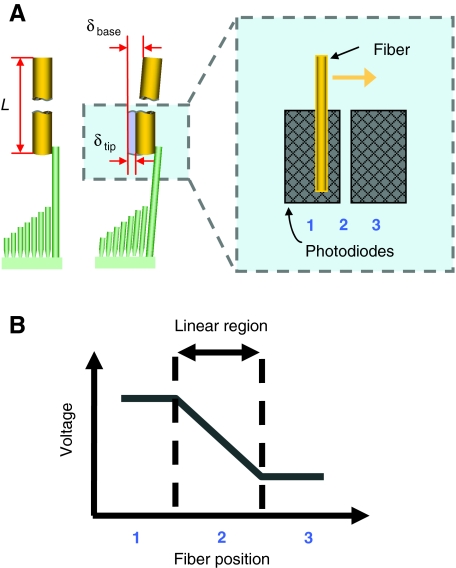
Fig. 4.

(A) A flexible glass fiber deflects the tip of a kinocilium. The magnified image of the tip of the fiber is projected onto a dual array of photodiodes, positioned at the camera port of the microscope. Movement of the glass fiber changes the distribution of light on the photodiodes. (B) As the fiber passes between the two diodes, the diode output voltage is linearly related to fiber position (plot is an illustration).

With the fiber contacting the kinocilium's tip, the base of the glass fiber was sinusoidally oscillated a peak-to-peak distance of 1 μm at 0.5 Hz. Testing at various frequencies demonstrated that movement of the fiber tip in fluid was not impaired at 0.5 Hz and thus drag on the fiber was negligible. Signals from the displacement sensor and photodiodes were recorded in 30 s trials at a sampling frequency of 1 kHz with LabVIEW 7.0 (National Instruments, Austin, TX, USA). The photodiodes were calibrated at the end of each trial by positioning the oscillating fiber just above the kinocilium in the same horizontal plane. Again, the displacement sensor and photodiode outputs were recorded in 30 s trials. This yielded a calibration factor relating photodiode output voltage to deflections of the fiber tip. The stiffness of the kinocilium was determined from the peak-to-peak base and tip deflections of each oscillation, averaged over the trial. The reported stiffness measurements of individual kinocilia are the means of at least four trials.

Kinocilium heights were measured from high-resolution digital photographs using Image J software (NIH, Bethesda, MD, USA). To determine EI and kGA, the height of the kinocilium projecting above the supporting probe was measured. The total length of the kinocilium was measured to determine the rotational stiffness (Fig. 3B,D).

Values of EI and kGA were determined for both the Euler–Bernoulli and Timoshenko beam theories using two approaches. In the first approach, the shaft stiffnesses of 27 kinocilia having different heights were measured. The resulting 27 data points were curve-fit to the Euler–Bernoulli and Timoshenko beam equations – Eqns 1 and 2 rewritten to solve for stiffness (F/δ) – to obtain best-fit predictions of EI and kGA. Nonlinear least squares curve fits were performed with Matlab Curve Fitting Toolbox using the Trust-region algorithm and the Bisquare weights robust regression method to reduce the impact of outliers on the fit. This approach yields single values of EI and kGA based on the stiffness values of the 27 kinocilia we measured.

The second approach determined EI and kGA for each individual kinocilium measured. For the Euler–Bernoulli theory, EI was calculated directly from Eqn 1 using the kinocilium's measured values of stiffness (F/δ) and kinocilia height projecting above the supporting probe. For the Timoshenko beam theory, both EI and kGA are unknown (Eqn 2), so the curve-fit predicted value of kGA (from approach 1) was used in combination with the measured values to calculate EI of individual kinocilia. Similarly, the predicted EI (from approach 1) was used to calculate kGA of individual kinocilia.

Rotational stiffness was calculated (Eqn 4) from measured values of tip deflection, applied force, total kinocilium height and EI and kGA values predicted from the Timoshenko beam curve fit. We chose to use the Timoshenko rather than the Euler–Bernoulli EI and kGA because the Timoshenko analysis produced a better fit to our experimental stiffness data.

The effects of different contact conditions between the kinocilium and the glass whisker (i.e. point load vs distributed load) were examined using a finite element model. This analysis showed that the contact could be treated as a point load at the end of the glass whisker with negligible error. Consequently, we chose to incorporate a point loading condition for the beam analysis.

Error analysis

To assess the error in the force-deflection measurements, seven borosilicate glass fibers were made. Stiffness of these fibers was measured using: (1) microbeads (as previously described in this section) and (2) the force-deflection technique, where a stationary glass fiber was positioned opposite the forcing fiber. The seven fibers (with a stiffness range of 7.6–1107 μN m^–1) were paired 17 ways with ratios of forcing fiber to stationary fiber stiffness (k_f/k_s) ranging from 0.01 to 22.11. The percent difference between the photodiode system and bead-calibrated stiffness measurements depended on the k_f/k_s ratio. For k_f/k_s>0.17, the percent difference was 10% or less. Below 0.17, the percent difference steadily increased from 30 to 90% as the k_f/k_s decreased. In the present study, the ratio of fiber stiffness to kinocilium stiffness for all measurements ranged from 0.4 to 14, indicating that the error, measured as the percent difference between the force-deflection and bead-calibrated results, ranged between 0 and 10%.

Additionally, we determined the uncertainty in EI calculations due to propagation of the uncertainty of each individually measured value: kinocilium height, fiber base deflection, fiber tip deflection and fiber stiffness. The uncertainty in each measured value was assumed to be independent and random. It was quantified as the standard deviation of the mean (σ_m) of each measured value, which is the standard deviation of repeated measurements divided by the square root of the number of measurements. For equations where the measured values are multiplied and/or divided, as in Eqn 1, the total uncertainty is equal to the square root of the sum of the squared fractional uncertainties, where fractional uncertainty is σ_m divided by the absolute value of the mean (Taylor, 1982). Following this approach, the error in the force-deflection measurements was determined to have a maximum value of 9%. The measurements of fiber stiffness using the bead-calibration method yielded the largest fractional uncertainties of all measured values.

RESULTS

Properties of the kinocilium shaft

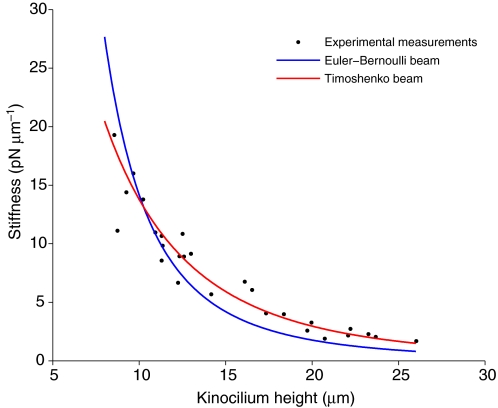
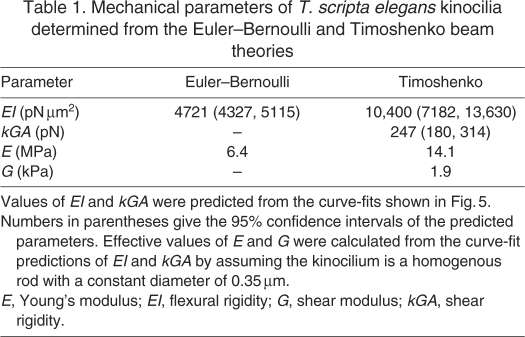
Using the force-deflection technique, we took a stiffness measurement from 27 kinocilia of differing heights located in the medial extrastriolar region of the turtle utricle. These results are plotted in Fig. 5. The stiffness values ranged from 2 to 19 pN μm^–1 for kinocilia with heights projecting above the tallest stereocilia of 8.5–26.0 μm. Kinocilium stiffness decreased with height, as expected from both the Euler–Bernoulli and Timoshenko beam theories: Eqns 1 and 2 for both beam theories show that stiffness (F/δ) is inversely proportional to the height cubed. Values of EI and kGA were determined in two ways. In one technique, the stiffness measurements from all 27 kinocilia were curve-fit using the Timoshenko and Euler–Bernoulli beam equations (Eqns 1 and 2) to predict single values of EI (for both) and kGA (for the Timoshenko equation only) for the whole data set. The Timoshenko beam model produced a better fit to the experimental data than the Euler–Bernoulli model with R² values of 0.94 and 0.83, respectively. The predicted curve-fit values and their 95% confidence intervals are given in Table 1.

Fig. 5.

Stiffness of 27 T. scripta elegans kinocilia of different heights. Each point represents the experimentally measured stiffness of a single kinocilium versus its height above the tallest stereocilia. These stiffness measurements are curve-fit with the Euler–Bernoulli and Timoshenko beam theories.

Table 1.

Mechanical parameters of T. scripta elegans kinocilia determined from the Euler–Bernoulli and Timoshenko beam theories

Using a second technique, values of EI and kGA were determined for each of the 27 kinocilia measured. From the Euler–Bernoulli beam equation, the EI of an individual kinocilium can be calculated based on measured values of its stiffness and kinocilium height. EI calculated in this way demonstrates a dependence on kinocilium height, increasing by ∼6000 pN μm² as the height increases by ∼17 μm (Fig. 6A). Regression analysis demonstrates a significant (P<0.0001) linear dependence of Euler EI on height and gives the relationship EI=346L+1148 with R²=0.71.

Fig. 6.

(A) Using the Euler–Bernoulli beam equation (Eqn 1), the EI of 27 T. scripta elegans kinocilia was calculated directly from measured values of stiffness and height projecting above the tallest stereocilia. A linear regression demonstrates that the Euler–Bernoulli EI is significantly dependent on kinocilium height. (B) The EI of individual kinocilia was calculated from the Timoshenko beam equation (Eqn 2) using the measured values of stiffness and kinocilium height and the Timoshenko curve-fit prediction of kGA=247 pN. A linear regression showed no significant relationship between the Timoshenko EI and kinocilium height. (C) The kGA of individual kinocilia was determined from the Timoshenko beam equation (Eqn 2), measured values of stiffness and kinocilium height, and the Timoshenko EI curve-fit prediction of 10,400 pN μm². A linear regression using bisquare weights was performed to reduce the impact of outliers. The regression showed that there is not a significant dependence of kGA on kinocilium height.

Using the Timoshenko beam theory, EI cannot be directly calculated from our measured values of stiffness and kinocilium length because of the additionally unknown kGA term. For this reason, the curve-fit predicted value of kGA was used in combination with the measured values to calculate the EI of individual kinocilia; conversely, the predicted EI was used to calculate the kGA of individual kinocilia (Fig. 6B,C). Using the curve-fit values introduces any error associated with the curve-fit parameters. This is probably the reason the Timoshenko EI values determined in this way demonstrate more scatter than the Euler EI calculations (cf. Fig. 6A and Fig. 6B). Linear regression analysis of these data shows no significant EI dependence on kinocilium height (P=0.29). Determining kGA in this way resulted in several extreme outliers (Fig. 6C). We found that calculated values of kGA are extremely sensitive to variation in kinocilium height. In one case, a change in kinocilium height of only 0.2 μm produced a 700 pN change in the kGA calculation. The resolution of the digital images from which kinocilium height was measured is ∼0.1 μm pixel^–1, so it is very likely that small errors in the measurements of kinocilia height are responsible for the extreme outliers and the increased variation in kGA observed for taller kinocilia. In addition, it is difficult to find tall kinocilia that lie perfectly in the focal plane, which may also decrease the accuracy of their height measurements. A linear regression was performed using the Bisquare weights robust method, which lessens the impact of outliers (MATLAB Curve Fitting Toolbox, MathWorks, Natick, MA, USA). The regression produces the line kGA=8.7L+132 (R²=0.72). The 95% confidence intervals for both the slope and intercept include zero, showing that they are not significantly different from zero and thus that kGA is not significantly dependent on height.

Effective values of Young's modulus (E) and the shear modulus (G) in Table 1 were determined from the curve-fit values of EI and kGA, assuming a constant kinocilium diameter of 0.35 μm (Silber et al., 2004) and a shear correction factor for a circular cross-section (k) of 3/4 (Boresi and Schmidt, 2003). Based on the Timoshenko fit, the shear modulus is four orders of magnitude less than the Young's modulus, indicating that kinocilia will experience shear deformation during bending.

It is worth noting that an occasional kinking behavior was observed for large deflections of the kinocilium. When large deflections were applied to a kinocilium several microns from its tip, the kinocilium sometimes buckled or kinked at a point near its center so that the upper section was almost parallel to the epithelium. Once released while in this configuration, the upper portion remained horizontal but shortened as the kink propagated to the tip of the kinocilium. During the occasional kinking, the tip of the kinocilium did not traverse a radial arc as the shaft returned to equilibrium as normally observed. Any kinocilium that exhibited this behavior was not used in experimental measurements.

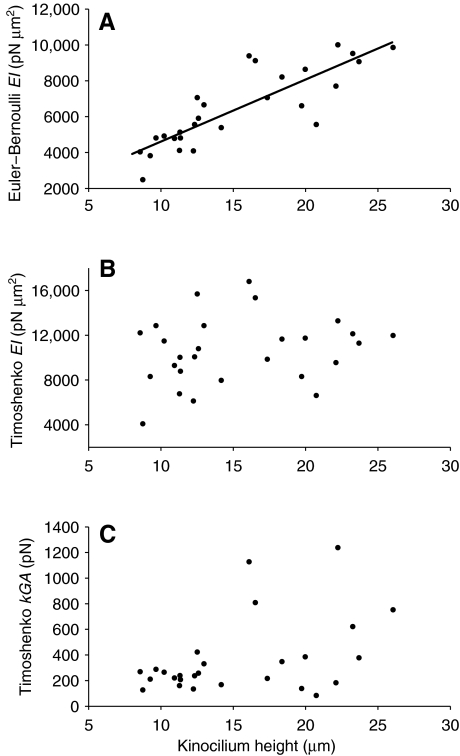
Rotational stiffness of the insertion

With kinocilium links broken following BAPTA treatment, kinocilia remained vertical and snapped back to an upright position following large deflections. This behavior demonstrates that the kinocilia possess an inherent rotational stiffness about their apical insertion. The rotational stiffness was measured for a total of five kinocilia. Multiple trials were performed for each kinocilium, and the results are plotted in Fig. 7 and summarized in the inset. Except for three outliers from the second kinocilium, the measured rotational stiffness ranged from 86 to 240 pN μm rad^–1. The mean rotational stiffness and standard deviation for all measurements is 177±47 pN μm rad^–1. A Kruskal–Wallis ranked sum test demonstrates that there is not a significant difference between the rotational stiffness of the five kinocilia measured (P>0.18). The three outlying measurements occurred for the same kinocilium, suggesting that there was something unusual about the arrangement of that particular bundle. For example, it is possible that the deflecting fiber was contacting a neighboring kinocilium during the three outlying trials, giving a rotational stiffness approximately two to three times greater than normal.

Fig. 7.

The rotational stiffness of kinocilia about their apical insertion was measured for five T. scripta elegans kinocilia. Multiple measurements (black points) were made of each kinocilium. The inset box plot summarizes all the measurements showing the mean (line through the box), interquartile range (box), 1.5 times the interquartile range (whiskers) and three outliers (plus signs).

Fig. 3C shows a kinocilium following BAPTA treatment to break the kinocilium links. The deflection shown is extremely large compared with the deflections used during testing and little bending of the kinocilium shaft is apparent. The amount of kinocilium tip deflection due to rotation and bending was determined using Eqn 4. The results showed that, on average, bending contributed 12% to the total tip deflection.

DISCUSSION

This work quantifies the shaft stiffness of individual kinocilia of various heights and the rotational stiffness of the kinocilium's insertion for the first time. Comparisons were made of the kinocilium modeled as an isotropic Euler–Bernoulli and a transversely isotropic Timoshenko beam. The results show that the kinocilium is better modeled as a shear deformable Timoshenko beam, indicating that the kinocilium behaves as a transversely isotropic material.

Euler–Bernoulli vs Timoshenko beam analysis

Curve-fitting experimental measurements of kinocilia shaft stiffness demonstrated that the Timoshenko beam is a more accurate model of the kinocilium than the Euler–Bernoulli model; the goodness-of-fit, i.e. the R² value, is higher for the Timoshenko model (0.94 compared with 0.83). In addition, when EI is calculated for individual kinocilia directly from measured stiffness using the Euler–Bernoulli theory, the EI shows a linear dependence on height. This observed height dependence is not consistent with the Euler–Bernoulli theory. For a homogenous isotropic beam with a constant cross section, the EI is expected to be constant regardless of length. EI is the product of the Young's modulus and the area moment of inertia, and it seems reasonable to assume that both these quantities do not change with kinocilium height given the consistent 9+2 structure along the kinocilium shaft. The observed EI length dependence indicates that the isotropic Euler beam is not an appropriate model for the kinocilium.

Similar results have been observed for MTs. Measurements of MTs have shown that EI is length dependent (Kurachi et al., 1995; Takasone et al., 2002; Pampaloni et al., 2006), and modeling MTs as an Euler–Bernoulli beam leads to underestimates of EI for shorter MTs (Li et al., 2006). A Timoshenko beam model of an MT predicts an EI length dependence that matches experimental results, provided the shear modulus is five to six orders of magnitude lower than the longitudinal Young's modulus (Shi et al., 2008). Our results for the kinocilia differ from those of MTs in that a significant EI length dependence was not observed using the Timoshenko analysis. However, our results show that the effective shear modulus for kinocilia is only four orders of magnitude less than the effective Young's modulus. Also, the MT analysis examined a much wider range of heights (100 μm) compared with the range of kinocilia heights examined (17.5 μm).

The curve-fit predicted value of EI is more than two times greater for the Timoshenko compared with the Euler–Bernoulli analysis (10,400 compared with 4700 pN μm²). We conclude that the Euler–Bernoulli theory underestimates the EI of kinocilia because it does not account for shear deformation. For any shear-deformable beam, the impact of shear deformation during bending will be more evident in beams with shorter lengths. Because the Euler–Bernoulli theory does not account for shear, all the deflection at the tip of the kinocilium is attributed to bending, which results in an underestimate of EI for shorter kinocilia. A critical height must exist beyond which the differences in a Timoshenko and Euler–Bernoulli beam are insignificant. From the current data set, we were not able to determine that height. Kinocilia in the turtle utricle can reach heights of >40 μm (Fontilla and Peterson, 2000; Xue and Peterson, 2006), but because of limitations of our measurement system the tallest kinocilia we could accurately measure was 26 μm. Measurements were attempted for three kinocilia with heights of ∼33 μm, but the measurements were discarded due to imprecision (s.d.=30–50% of the measured value).

The deflection of the OL in the utricle is proportional to head acceleration. The kinocilia are the links that transfer OL deflection to the mechanotransducing portion of the hair cell bundle. Hair cell bundles in the turtle have a spectrum of bundle morphologies that systematically vary with epithelium location (Xue and Peterson, 2006). In the striolar region, the heights of tallest stereocilia are approximately the same as those of the kinocilia (10 μm). In addition, the height at which the kinocilia insert into the otoconial layer is also ∼10 μm (Xue and Peterson, 2002). At the other end of the spectrum, the heights of the tallest stereocilia in the medial extrastriolar region are much less (3–4 μm), and the kinocilia insert into the otoconial layer at heights of 13–14 μm (Xue and Peterson, 2002). Thus, in the medial extrastriolar region, there is a ∼10 μm portion of the kinocilium that can bend in response to otoconial layer deflections. Bending of the kinocilium in the extrastriola hair cells enable the hair cell bundles to respond to larger deflections of the OL.

We examined the bending deformation profile of the kinocilium in a medial extrastriolar bundle using a computational model in which the kinocilium was modeled as a cantilever beam (14 μm tall) and the stereocilia portion (4 μm tall) was represented by its deflection stiffness. The kinocilium was modeled as both Euler–Bernoulli and Timoshenko beams with an EI of 10,400 pN μm² (for both cases) and a kGA of 247 pN (for the Timoshenko case). A stiffness of the stereociliary bundle of 400 pN μm^–1 was utilized for the bundle model. This computational model showed that a smaller percentage of the tip deflection was transferred to the stereocilia bundle when the kinocilium was modeled as a Timoshenko (2.8%) versus a Euler–Bernoulli (8.0%) beam. For example, a 3 μm deflection at the tip of the kinocilium produces a deflection at the height of the tallest stereocilia of 84 and 240 nm for the Timoshenko and Euler–Bernoulli models, respectively. The shear deformation present in the kinocilium reduces the deflection of the stereocilia bundle in this medial extrastriolar region. This reduced deflection of the stereocilia extends the operating rage of these bundles so they can transduce accelerations of a much broader range. These results suggest that the physiological importance of shear deformation in the kinocilium is to extend the range of OL deflections that the bundle can detect before saturating the hair cell transduction.

Comparison with literature

Although there are no direct kinocilium stiffness measurements in the literature, there are studies that quantify the EI of kinocilia and flagella with which our data can be compared. The only reported value of kinocilium EI was derived from the superficial neuromast in the lateral line of zebrafish (McHenry and vanNetten, 2007). The superficial neuromast is a structure that contains hair cells with tall kinocilia embedded in an elongated cupula. Its function is to detect water flow across the surface of the lateral line of fish. In this study, McHenry and van Netten (McHenry and van Netten, 2007) modeled the neuromast's entire cupular structure as a Euler–Bernoulli beam, and its EI was measured using a force-deflection technique. A linear relationship was observed between the cupula EI and the number of kinocilia per cupula. The slope of this linear relationship gave the EI of a single kinocilium as 2400 pN μm². This value is less than the EI we measured for vestibular kinocilia of the same height. The majority of kinocilia heights in the neuromasts cupula were reported to range between 16 and 24 μm. Using the Euler–Bernoulli theory to directly calculate EI from stiffness measurements (Fig. 6A) yields EI values of 5500–10,000 pN μm² for kinocilia within this same height range, which is approximately two to four times greater than calculated values for neuromast kinocilia. The difference from Timoshenko curve-fit prediction was approximately four times greater than the EI measured for the neuromast's kinocilia. The discrepancy between EI measurements of vestibular and neuromast kinocilia may result from differences between the kinocilia of different neurosensory systems, differences between species and/or differences between measurement techniques.

One difference in technique is that the present study sought to determine the properties of individual kinocilia, and force was applied directly to the tip of freestanding kinocilia. The neuromast study examined a more complex structure (McHenry and vanNetten, 2007). The kinocilia EI was inferred from EI measurements of the cupula as a whole, and force was applied to the edge of the cupula. This loading condition could cause relative deflection between the kinocilia and the cupular matrix or local deflection of the soft cupular matrix at the site of force application. If either condition occurred, it would lead to underestimates of the kinocilium EI.

The literature also contains information regarding the EI of flagella, which can be compared with the kinocilia. Though kinocilia and flagella are not identical in composition (kinocilia lack inner dynein arms), both derive structural integrity from a 9+2 microtubular core. The echinoderm sperm flagellum provides a good comparison for kinocilia because they lack coarse fibers that are observed in other flagella (e.g. bull sperm flagellum), which likely influence the stiffness (Okuno and Hiramoto, 1979). Experimental measurements from echinoderm sperm flagella suggest that dynein cross-bridging greatly influences EI, presumably by preventing sliding between microtubule doublets. In the absence of ATP, demembranated flagella acquire a state of rigor attributed to stable dynein cross-bridges (Okuno, 1980). In this rigor state, the EI ranges from 11,000 to 15,000 pN μm² (Okuno and Hiramoto, 1979; Okuno, 1980; Ishijima and Hiramoto, 1994), which overlaps the 95% confidence interval of kinocilia EI determined through the Timoshenko analysis (7200–13,600 pN μm²). When exposed to Mg-ATP in addition to vanadate (NaVO₃), a compound that disables the dynein motors, demembranated flagella assume a relaxed state and EI is greatly reduced to 600–900 pN μm² (Okuno, 1980; Pelle et al., 2009). Comparing the EI of kinocilia with that of demembranated flagella in states of rigor and relaxation suggests that cross-bridging contributes greatly to the stiffness of the kinocilium. Because the inner dynein arms are absent in the kinocilium, the results suggest that cross-bridging of the outer arms contributes to kinocilia stiffness.

A theoretical study determined the EI of a 9+2 axoneme based on detailed calculation of its moment of inertia (Schoutens, 1994). Assuming no connections between the microtubules, a lower EI value of 680 pN μm² was determined, which is in remarkable agreement with measured values of the relaxed flagellum. For the case where the doublet and central microtubules are rigidly bound and therefore not permitted to slide, an EI of 74,000 pN μm² was calculated. This upper value is greater than five times the EI of the kinocilium and the flagellum in a state of rigor, suggesting that even with cross-bridging the microtubules are not rigidly bound. These findings are additional evidence that microtubule sliding occurs during kinocilium bending and supports our conclusion that a beam theory, such as the Timoshenko theory, that incorporates shear deformation should be used to model the kinocilium.

LIST OF SYMBOLS AND ABBREVIATIONS

A

cross-sectional area

D

diameter of cylinder

E

Young's modulus

EI

flexural rigidity

F

applied force

G

shear modulus

HBSS

Hanks' balanced salt solution

I

second moment of inertia

k

shear correction factor

kGA

shear rigidity

L

kinocilium/beam length

M

moment

MT

microtubule

OL

otoconial layer

δ

deflection

δE

deflection due to bending for a Euler–Bernoulli beam

δR

deflection due to rotation

δT

deflection due to bending for a Timoshenko beam

κ

rotational stiffness

θ

angle of rotation

σm

standard deviation of the mean

ʋ

Poisson's ratio