The utility of geometrical and chemical restraint information extracted from predicted ligand binding sites in protein structure refinement

Abstract

Exhaustive exploration of molecular interactions at the level of complete proteomes requires efficient and reliable computational approaches to protein function inference. Ligand docking and ranking techniques show considerable promise in their ability to quantify the interactions between proteins and small molecules. Despite the advances in the development of docking approaches and scoring functions, the genome-wide application of many ligand docking/screening algorithms is limited by the quality of the binding sites in theoretical receptor models constructed by protein structure prediction. In this study, we describe a new template-based method for the local refinement of ligand-binding regions in protein models using remotely related templates identified by threading. We designed a Support Vector Regression (SVR) model that selects correct binding site geometries in a large ensemble of multiple receptor conformations. The SVR model employs several scoring functions that impose geometrical restraints on the Cα positions, account for the specific chemical environment within a binding site and optimize the interactions with putative ligands. The SVR score is well correlated with the RMSD from the native structure; in 47% (70%) of the cases, the Pearson’s correlation coefficient is >0.5 (>0.3). When applied to weakly homologous models, the average heavy atom, local RMSD from the native structure of the top-ranked (best of top five) binding site geometries is 3.1 Å (2.9 Å) for roughly half of the targets; this represents a 0.1 (0.3) Å average improvement over the original predicted structure. Focusing on the subset of strongly conserved residues, the average heavy atom RMSD is 2.6 Å (2.3 Å). Furthermore, we estimate the upper bound of template-based binding site refinement using only weakly related proteins to be ~2.6 Å RMSD. This value also corresponds to the plasticity of the ligand-binding regions in distant homologues. The Binding Site Refinement (BSR) approach is available to the scientific community as a web server that can be accessed at http://cssb.biology.gatech.edu/bsr/.

1. Introduction

With the rapid accumulation of protein sequences generated by the now numerous genome-sequencing projects (Aury et al., 2008; Tettelin and Feldblyum, 2009; Wheeler et al., 2008), the key challenge in biological sciences has shifted from the study of single molecules to the exhaustive exploration of molecular interactions and biological processes at the level of complete proteomes (Butcher et al., 2004; You, 2004). To achieve the ambitious goal of characterizing and understanding the molecular function of all gene products in a given proteome, a number of structure-based approaches to protein function inference have been developed (Juncker et al., 2009; Loewenstein et al., 2009; Rost et al., 2003). Contemporary methods for binding site detection are fairly insensitive to the overall quality of the target structures (Brylinski and Skolnick, 2008a) and facilitate the selection of correctly predicted models in protein structure prediction (Chelliah and Taylor, 2008). Approximate protein models can be routinely generated by the state-of-the-art structure prediction techniques for the majority of gene products in a given proteome (Fiser, 2004; Gopal et al., 2001; Yura et al., 2006; Zhang and Skolnick, 2004a); this opens up the possibility of using low-to-moderate resolution models for genome-wide function annotation.

Qualitative protein function annotation using Enzyme Commission (EC) numbers or Gene Ontology (Ashburner et al., 2000)terms is typically followed by a comprehensive functional characterization at the molecular level. The studies of interactions between proteins and other molecular species in a cell are routinely supported by computations involving docking of DNA (Gao and Skolnick, 2009; van Dijk and Bonvin, 2008), other protein partners (Lyskov and Gray, 2008; Wiehe et al., 2008)and small ligands (Goodsell et al., 1996; Moustakas et al., 2006). In the latter case, the docking of specific ligands can be extended to large-scale virtual screening of combinatorial libraries in order to discover novel bioactive compounds (Rajamani and Good, 2007; Seifert et al., 2007). Notwithstanding the advances in the development of docking approaches and scoring functions, the application of many ligand docking/screening algorithms to protein models is limited by the quality of the binding site in the target structure; mean structure rearrangements greater than 1.5 Å may cause the loss of even 90% of the docking accuracy (Erickson et al., 2004). Many other benchmark studies report a notable drop off in the docking accuracy when non-native structures are used as the target receptors (Murray et al., 1999; Sutherland et al., 2007; Wu et al., 2003).

Despite progress in protein structure prediction (Kryshtafovych et al., 2005), theoretical models, particularly those modeled using remote homology, still have significant structural inaccuracies in ligand binding sites (DeWeese-Scott and Moult, 2004; Piedra et al., 2008); this has stimulated the development of methods for the local refinement of binding pocket residues prior to ligand docking. The local refinement of ligand-binding regions is complicated by many factors. The conformational changes triggered by ligand binding may require side chain geometries (Heringa and Argos, 1999) absent in standard rotamer libraries (Dunbrack and Karplus, 1993; Koehl and Delarue, 1994). Moreover, it has been demonstrated that there is no correlation between the backbone movement of a residue upon binding and the flexibility of its side chain (Najmanovich et al., 2000). To tackle the difficult problem of binding site modeling, Kauffman and colleagues incorporated information on the residues involved in ligand binding in constructing the target-template alignments and observed an improvement in the overall quality of the modeled ligand-binding regions (Kauffman et al., 2008). In principle, ligand molecules could also be explicitly used to model the binding sites. However, due to imperfections of available all-atom force fields, inclusion of protein flexibility in ligand docking against non-native receptor structures typically does not the improveroot-mean-square deviation, RMSD of thebinding pocketresidues from the native structure (Davis and Baker, 2009). A slightly different approach, MOBILE, includes information about bioactive molecules as spatial knowledge-based restraints in the iterative refinement of protein models constructed using close homology (Evers et al., 2003). The issue is what happens when no closely related homologous structures are solved for the protein target of interest.

In this study, we describe a new template-based approach to the local refinement of ligand-binding regions in protein models that exploits the information provided by remotely related templates. We begin with an analysis of the plasticity of ligand-binding regions in distant homologues which provides an estimate of what would be the upper bound for the template-based refinement accuracy using only weakly related binding pockets. This also provides interesting insights into how structurally degenerate are similar/identical binding geometries in nature. Building on the resulting insights, we propose a new ligand binding site refinement procedure that consists of the following: First, a large ensemble of multiple receptor conformations is generated. Then, a fitness function is applied to rank the structurally diverse set of constructed binding site geometries. This function comprises four scoring terms, whose parameters are derived from weakly related templates identified by threading (Jones and Hadley, 2000). The individual terms provide geometrical restraints on the Cα positions and Cα-Cα distances, account for a specific chemical environment within a binding site and optimize the interactions with putative ligands. The scoring functions are used to train a Support Vector Regression model to rank multiple receptor conformations. Here, for a large benchmark set, we apply this model to refine ligand-binding regions in proteins that are weakly homologous to their closest template whose structure is known and show that the SVR-based ranking selects fairly good binding site geometries. The Binding Site Refinement (BSR) approach presented in this paper is available to the scientific community as a web server that can be accessed at http://cssb.biology.gatech.edu/bsr/.

2. Materials and Methods

2.1. Dataset

Protein-ligand complexes used in this study were taken from the Protein-Small-Molecule Database (PSMDB) (Wallach and Lilien, 2009), a non-redundant repository of small molecule complexes for protein-ligand interaction studies. We selected proteins up to 200 residues in length, for which at least 3 weakly homologous (<35% sequence identity) template structures can be identified by threading (Skolnick and Kihara, 2001; Skolnick et al., 2004; Zhou and Zhou, 2004; Zhou and Zhou, 2005). Furthermore, we excluded those proteins that bind very small (<6 heavy atoms) as well as very big (>100 heavy atoms) ligands. The total number of complexes in the dataset is 904. Finally, we used only those targets for which the binding site center of mass can be predicted by FINDSITE within a distance of 6 Å. Since the accuracy of binding site prediction depends on the quality of the target structure, the number of proteins used for binding site refinement ranges from 662 for crystal structures to 440 for the most distorted models with an average RMSD (root-mean-square deviation) from the crystal structure of 9Å; see additional details below. The PDB identifiers for the dataset proteins are provided in Supplementary Materials, SI Table 1. Moreover, the entire dataset as well as the modeling results are available from http://cssb.biology.gatech.edu/bsr/.

2.2. All-atom RMSD of similar binding pockets

Due to significant sequence variability in remotely related proteins, the RMSD is typically calculated over Cα atoms. Here, we develop a simple method to calculate the heavy atom RMSD of similar, but not identical pockets extracted from weakly homologous template complexes. Residue equivalences are obtained from global structure alignments by fr-TMalign (Pandit and Skolnick, 2008; Zhang and Skolnick, 2005a), whereas the equivalent atoms in residue side chains are calculated by SMSD (Small Molecule Subgraph Detector) (Rahman et al., 2009). SMSD is a graph-based algorithm developed to identify the exact atom-bond equivalence between the query and target organic molecules in chemical similarity searches. Here, we apply SMSD to match the heavy atoms of different residue side chains. The all-atom RMSD calculated over the atoms matched for all binding residue pairs within a common pocket is denoted as RMSD^res. For a given pocket, ligand-binding residues can be divided into three groups, depending on the conservation of their binding patterns in evolutionarily related proteins. Strongly, moderately and weakly conserved binding residues are defined based on the fraction of templates that have a residue in an equivalent position in contact with a ligand: >0.75, 0.50–0.75, and 0.25–0.50, respectively. RMSD^res values calculated over strongly, moderately and weakly conserved binding residues are denoted as ${\mathit{RMSD}}_{0.75}^{\mathit{res}},{\mathit{RMSD}}_{0.50}^{\mathit{res}}$ and ${\mathit{RMSD}}_{0.25}^{\mathit{res}}$, respectively. In the RMSD calculations for the ligand-binding regions, we can also include the coordinates of bound ligands. Again, we use SMSD to establish the atom equivalences in ligand structures; the combined RMSD calculated over the heavy atoms of both protein residues and ligands is denoted as RMSD^res+lig.

2.3. Proteinstructure modeling

For each protein, we have constructed several models with different accuracy in terms of their RMSD and TM-score (Zhang and Skolnick, 2004b) from the native structure. In addition to the crystal structures, we use three sets of uniformly distorted structures with an average RMSD of 3, 6 and 9 Å from native. The distorted structures were generated starting from the crystal structures by a simple Monte Carlo procedure that deforms protein structures to a desired deviation from native (Bindewald and Skolnick, 2005). Furthermore, we have constructed weakly homologous protein models using a state-of-the-art template-based structure prediction algorithm. First, for each target protein, weakly homologous template structures (<35% sequence identity to the target) were identified in a non-redundant PDB library by our meta-threading procedure that employs the SP3 (Zhou and Zhou, 2005), SPARKS2 (Zhou and Zhou, 2004) and PROSPECTOR_3 (Skolnick and Kihara, 2001; Skolnick et al., 2004) algorithms. Subsequently, full-length models were assembled and refined by chunk-TASSER (Zhou and Skolnick, 2007). Finally, all-atom models from the top ranked chunk-TASSER structure were constructed by Pulchra (Rotkiewicz and Skolnick, 2008).

2.4. Binding site identification

Ligand-binding residues are identified in the target structures using FINDSITE, a structure/evolution-based approach to binding site prediction and molecularfunction inference (Brylinski and Skolnick, 2008a; Brylinski and Skolnick, 2009a; Skolnick and Brylinski, 2009). FINDSITE detects common ligand binding sites in a set of evolutionarily related proteins. Here, we used only those templates that were identified by meta-threading with a Z-score of ≥4 reported by at least one threading method. All templates have <35% sequence identity to the target. FINDSITE typically identifies multiple ligand-binding sites and ranks them by the fraction of templates that have binding sites in similar locations. As the targets for local refinement, we used the best of top five binding sites predicted within 6 Å from the geometrical center of a bound ligand in the native crystal structures.

2.5. Compound ranking

In addition to the binding site location, FINDSITE also provides information on the chemical identity of molecules that likely occupy the predicted pockets. This is done by simple ligand-based virtual screening using consensus molecular fingerprints and a modified Tanimoto coefficient calculated using the template-bound ligands (Brylinski and Skolnick, 2009b; Tanimoto, 1958; Xue et al., 2003). Compound selection is assessed based on the rank assigned to the native ligand in a random library. As background compounds, we used a non-redundant subset of 68,109 molecules selected from the ZINC8 library (Irwin and Shoichet, 2005). The non-redundant subset, compiled using the SUBSET 1.0 program (Voigt et al., 2001) and a Tanimoto coefficient threshold of 0.7, is available from http://cssb.biology.gatech.edu/findsite/ (ZINC8 non-redundant, Tanimoto<0.7).

2.6. Binding site refinement

Binding site refinement consists of two steps: First, for a given target protein structure, an ensemble of 50 non-redundant all-atom conformations is generated. Then, the conformations are ranked using an empirical fitness function that employs both geometric as well as chemical scoring terms. The construction of a conformational ensemble, the development of the scoring function and the ranking procedure are described in the following sections.

2.7. Construction of the conformational ensemble

For each target protein structure, we generated an ensemble of multiple conformations as follows: Starting from the initial, unrefined structure (crystal structure, 3, 6, 9Å RMSD from the native structure or chunk-TASSER model), 50 nearby conformations with a Cα RMSD of 2Å to the intial structure were generated using a Monte Carlo sampling procedure described above(Bindewald and Skolnick, 2005). Subsequently, these conformations are subject to a clustering procedure in order to compile a set of 10 diverse structures. We used a k-way clustering method by repeated bisections with global optimization implemented in the clustering package CLUTO 2.1.2 (Karypis, 2003). Next, Modeller 9v8 (Sali and Blundell, 1993) was used to generate 2,000 conformations using Cα restraints extracted from these 10 structures. This procedure improves the structural diversity and results in a set of structurally distinct models compared to a standard procedure for the ensemble generation from a single structure using self-restraints. In addition, we provide Modeller with a set of auxiliary distance restraints imposed on the predicted binding residues. These restraints are included as Cα-Cα average distances calculated from the ligand-bound template structures using target-template structural alignments generated by fr-TMalign (Pandit and Skolnick, 2008; Zhang and Skolnick, 2005a). Finally, the number of conformations in the ensemble was reduced to 50 by a clustering procedure using CLUTO (Karypis, 2003). Here, we cluster the ensemble conformations using the pairwise all-atom RMSD of the ligand-binding regions to compile a non-redundant set of 50 pocket geometries.

2.8. Geometrical restraints

A fitness function was developed to rank the conformations in the non-redundant ensemble constructed for each protein target structure. This section describes the geometric-based function components.

The first scoring component is a weighted RMSD (Damm and Carlson, 2006) term calculated using the average Cα positions of the residues in the threading templates in equivalent positions to the binding residues reported by FINDSITE. The average positions are calculated upon the global structure alignment by fr-TMalign (Pandit and Skolnick, 2008; Zhang and Skolnick, 2005a) of the templates onto the input target structure (which may be a model or an experimental structure):

$$\mathit{wRMSD}=\sqrt{\frac{1}{n}\sum _{i=1}^n{w}_i{d}_i^2}$$ Eq. 1

where n is the number of binding residues, d is the deviation of a binding residue Cα atom from its average position and w is a weight factor that corresponds to the ligand-binding probability calculated by FINDSITE (Brylinski and Skolnick, 2008a). The binding probability is the fraction of templates that have a residue in an equivalent position in contact with the ligand. Here, we only use residues with a binding probability of ≥0.25.

Next, we use single Gaussian restraints imposed on the binding residue Cα-Cα distances (Sali and Blundell, 1993):

$${\mathit{restr}}^{C\alpha -C\alpha }=\frac{1}{n}\sum _{i=1}^{n}0.5{\left(\frac{r-\langle r\rangle }{\sigma }\right)}^2-ln\frac{1}{\sigma \sqrt{2\pi }}$$ Eq. 2

where n is the number of binding residue pairs i–j separated in sequence by at least four other residues, r is the distance between Cα atoms of residues i and j in the ensemble conformation, 〈r〉 is the average distance between residues equivalent to i and j in the threading templates and σ is its standard deviation. Both geometric restraint terms are strongly shape-dependent; wRMSD also depends on the global position in the target structure with respect to the center of mass.

2.9. Chemical restraints

In addition to the geometrical restraints that enforce the native-like conformation of the backbone Cα atoms, we use chemical restraints to facilitate the correct orientation of the residue side chains within the binding pocket. Since only weakly homologous template structures are used in this study, we derive the chemical constraints for the functional groups of the side chains rather than their heavy atoms. Here, we use 8 different chemical groups present in amino acid side chains: aromatic rings, hydroxyl, thiol, carboxyl, aliphatic carbon atoms, amine, amide and guanidine. The definition of chemical groups is provided in Supplementary Materials, SI_Table 2. First, all functional groups are detected in the superimposed set of threading templates identified by FINDSITE to share a common binding site. Next, the centers of mass of the chemicalgroups of particular type are used to calculate its probability density function using a standard kernel density approximation technique:

$${\widehat{f}}_h^j(x,y,z)=\frac{1}{nh}\sum _{i=1}^n{K}_h^{\mathit{gauss}}$$ Eq. 3

where n is the number of functional groups of type j in the side chains of the template residues, $K_h^{\mathit{gauss}}$ is a three-dimensional Gaussian kernel and h is a smoothing parameter (bandwidth) that needs to be optimized. The bandwidth optimization is described in the next section.

The three-dimensional Gaussian kernel function with a bandwidth h is given by:

$$K_h^{\mathit{gauss}}=\frac{1}{\sqrt{2\pi }}exp\left(-\frac{x^2+y^2+z^2}{2h^2}\right)$$ Eq. 4

The final score is calculated over all chemical groups in the binding residues of a target structure candidate in the ensemble:

$$\mathit{KDE}=\frac{1}{n}\sum _{i=1}^n{\widehat{f}}_h^{i,j}$$ Eq. 5

where n is the number of chemical groups in the binding residues of the target pocket and j is the type of a functional group i. For the center of mass of each functional group i in a structure candidate, the probability is calculated using Eq. 3. The KDE score is the average probability over all chemical groups.

The second scoring function that contributes to the chemical restraints is a pocket-specific potential calculated against the representative set of compounds that contain the anchor functional groups. The pocket-specific potential is a knowledge-based potential derived from evolutionarily related ligand-bound threading templates that is primarily used in ligand docking and scoring, as described in (Brylinski and Skolnick, 2008b; Brylinski and Skolnick, 2009c). The set of anchor-containing ligands is a non-redundant collection of compounds extracted from the holo template structures bearing the common molecular substructures that are highly conserved across the evolutionarily related family. Their detailed description is provided in (Brylinski and Skolnick, 2009b). Briefly, small organic compounds are extracted from the template structures and clustered using the SIMCOMP chemical matching algorithm (Hattori et al., 2003). For each cluster, a representative compound is selected and decomposed into functional groups. Here we use a set of 17 functional groups described in (Brylinski and Skolnick, 2008b). The conservation of each functional group in the anchor-containing molecule corresponds to the fraction of cluster compounds that have a similar functional group matched by SIMCOMP. Typically, the positions of the anchor functional groups tend to be strongly conserved across the set of template-bound ligands with very high conservation of their chemical properties.

For a given target binding pocket and an anchor-containing compound A, the pocket-specific potential is calculated over all binding residues and functional groups present in A:

$$E_{\mathit{specific}}^A=\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^m{w}_j\sum _{k=1}^{17}{u}_k{CP}_{\mathit{specific}}^{i,k}$$ Eq. 6

where n is the number of binding residues, m is the number of functional groups in the anchor compound A, w_j is the fraction of similar compounds extracted from those threading templates that have a functional group in the equivalent position, u_k is the fraction of compounds in which the functional group in equivalent position is of type k, and ${CP}_{\mathit{specific}}^{i,k}$ is the pocket-specific contact potential between the residue i and a functional group of type k. The low-resolution contacts between the geometric centers of the residue side chains and functional groups are calculated using cutoff distances optimized to mimic all-atom contacts (Brylinski and Skolnick, 2008b).

Finally, for a given binding site conformation, the specific protein-ligand interactions are calculated using all identified anchor-containing compounds:

$$\mathit{PSP}=\sum _{i=1}^n{w}_i{E}_{\mathit{specific}}^i$$ Eq. 7

where n is the total number of the anchor molecules, w_i is the fraction of threading templates that bind a ligand similar to i (a member of its cluster) and $E_{\mathit{specific}}^i$ is the pocket-specific potential calculated against the anchor compound i.

2.10. Kernel bandwidth optimization

In our method, the chemical environment formed by a binding site is approximated by a kernel density estimation using a set of similar sites extracted from weakly related template structures. The free parameter of a kernel, the bandwidth, is optimized using an objective function that maximizes the probability difference between finding a functional group of a particular type in locations occupied by similar functional groups in evolutionarily related pockets and those locations that are occupied bychemically different functional groups:

$$\mathrm{\Delta }\mathit{KDE}=\frac{1}{n}\sum _{i=1}^n\left({\mathit{KDE}}^i-\frac{1}{n-1}\sum _{j\ne i}^{n-1}{\mathit{KDE}}^j\right)$$ Eq. 8

where n is the number of different chemical groups and KDE is the average kernel density for a given chemical group of type i and j, where j≠i.

The grid search for the optimal bandwidth was carried out for the crystal structures of the target proteins. The kernel densities for all chemical groups were calculated from the set of superimposed threading templates. The KDE scores (Eq. 5) were calculated for the crystal side chain geometries of the binding residues and the bandwidth varying from 1 to 5 Å. The bandwidth value that maximizes ΔKDE was used in further calculations.

2.11. Binding site ranking by machine learning

The scoring function designed to select native-like binding site geometries from the conformational ensemble consists of four terms: wRMSD, restr^Cα-Cα, KDE and PSP. Since these component scores have different units and value ranges, we constructed a simple SVM-based regression model to combine them into a single fitness function. To avoid the memorization of the dataset, we used a 2-fold cross validation protocol. The complete dataset of the target complexes was randomly divided into two subsets with < 40% sequence identity between any two proteins that belong to different subsets (see SI Table 1). Subsequently, each subset was used to train the model and the predictions were made for the remaining targets, excluded from the training procedure. We used libSVM 2.9 (Chang and Lin, 2001) to build a standard, epsilon-SVR model with the radial basis function. As described above, for each target protein, an ensemble of 2,000 conformations was generated. These were subsequently partitioned into 50 clusters. The constructed SVR model employs a set of 11 features calculated for each cluster. wRMSD, restr^Cα-Cα, KDE and PSP are included as the average value for each cluster and the standard deviation. In addition, we use the cluster fraction and the average all-atom RMSD within the cluster as well as its standard deviation. The optimal values for the model parameters, a cost function (c), a gamma parameter of the kernel (g) and an epsilon in the loss function (p) were determined by an exhaustive grid search using 10 samples of 5,000 values each, that were randomly withdrawn from the dataset. The determined set of parameters was consistent across the random samples; c=8.0, g=1.0 and p=0.5 minimize the MSE (mean squared error) of the estimator to an average value of 0.573.

Table 1.

Dataset of protein models used in this study for binding site refinement.

Structural form	Number of proteins	TM-score	Binding pocket RMSDa [Å]	Number of binding residues	Pockets at rank 1b
Crystal	662	1.00±0.00	0.00 ±0.00	14	78.7%
3Å RMSD	632	0.76±0.04	1.93 ±0.70	15	81.0%
6Å RMSD	544	0.61±0.06	2.81 ±1.20	15	81.7%
9Å RMSD	440	0.53±0.06	3.15 ±1.27	15	77.3%
chunk- TASSER	557	0.74±0.12	3.25±1.23	14	77.8%

^aall – atom RMSD,

^bpercentage of targets for which the best pocket is at rank 1

3. Results and discussion

3.1. Plasticity of weakly homologous binding sites

For any prediction approach, it is important to know what is the regime that it can be successfully applied to and to estimate what is the upper bound for its accuracy. Here, we discuss what would be the theoretical limit for the accuracy of template-based binding site refinement using the structural information extracted from weakly related template structures. Essentially, this limit can be estimated from the analysis of the plasticity of similar binding sites found in distantly related proteins.

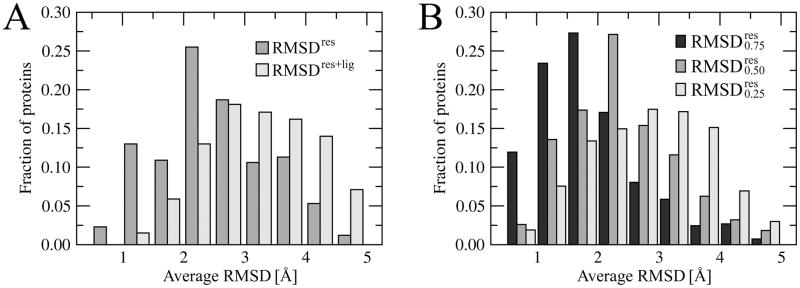
In protein structure prediction, the requirement of a RMSD close to 0 Å is clearly not physical since crystal structures of the same protein solved by different groups or in different conditions show a deviation in the backbone coordinates of ~0.5Å (Chothia and Lesk, 1986). Moreover, the differences in side chain positions typically depend on their solvent-exposed surface area and vary from 1.0Å to 1.5Å RMSD (Levitt et al., 1997). Modeled protein structures, particularly those that are weakly homologous to their templates, are considered to be correctly predicted when their Cα RMSD is below 4–6Å (Kryshtafovych et al., 2005; Moult et al., 2009; Moult et al., 2007). To address the issue of the maximum accuracy for template-based binding site refinement, we calculated the average heavy atom RMSD^res of the common ligand binding regions between the target crystal structures and their weakly homologous (<35% sequence identity) templates. For different side chains found in the corresponding positions in the template structures, the atom equivalences were obtained by a graph-based chemical matching algorithm, commonly used in Cheminformatics (Rahman et al., 2009). The distribution of RMSD^res/RMSD^res+lig values is presented in Figure 1A. The average plasticity of weakly homologous ligand-binding regions, expressed as the mean RMSD^res, is 2.6 Å with a standard deviation of 1.0 Å. When the ligand atoms are also included, the mean RMSD^res+lig is 3.4 ±1.1 Å. Furthermore, we find that the conformation of residues whose binding pattern is strongly conserved in evolutionarily related proteins, is also conserved. This is shown in Figure 1B; here, the mean ${\mathit{RMSD}}_{0.75}^{\mathit{res}},{\mathit{RMSD}}_{0.50}^{\mathit{res}}$ and ${\mathit{RMSD}}_{0.25}^{\mathit{res}}$ is 2.0, 2.6 and 3.0 Å, respectively. Below, we examine the performance of our template-based approach to binding site refinement and demonstrate that it appears to be fairly close to the theoretical upper limit for this type of method.

Figure 1.

Histogram of the average RMSD for similar binding sites extracted from weakly related proteins. A – RMSD calculated over protein (RMSD^res) as well as protein and ligand heavy atoms (RMSD^res+lig). B – RMSD^res for strongly (0.75), moderately (0.50) and weakly (0.25) conserved binding residues.

3.2. Accuracy of binding site prediction and virtual screening

The set of protein models was used by FINDSITE for binding site prediction and ligand virtual screening. FINDSITE employs structure alignments of the threading templates generated by fr-TMalign to transfer template-bound ligands to the target (Brylinski and Skolnick, 2008a). Subsequently, a clustering procedure applied to the center of mass of the transferred ligands identifies putative ligand-binding locations on the target protein surface. The accuracy of binding site prediction can be assessed by the distance between the predicted pocket center and the center of mass of a bound ligand in the crystal structure of the complex. In this study, we use only those targets for which the pocket center can be predicted within a distance of 6 Å. As we mentioned before, the number of such targets is different when the crystal structures, distorted models and chunk-TASSER models are used by FINDSITE. The structural distortions may slightly shift the alignments generated by fr-TMalign and move thepredicted binding pocket center beyond the threshold of 6 Å. We exclude such cases because the geometrical and chemical restraints derived for less accurately predicted pockets do not sufficiently overlap with the true ligand-binding regions.

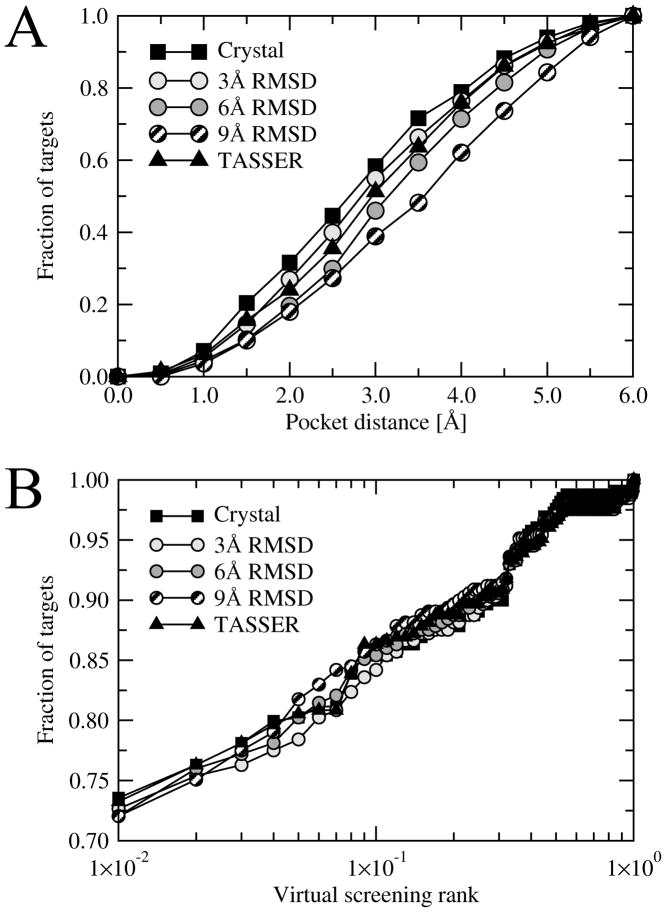
The number of protein targets used for binding site refinement is given in Table 1. Using crystal structures, structures distorted to a 3 Å, 6 Å and 9 Å RMSD from native, and chunk-TASSER models, the fraction of targets whose pocket center is predicted within a distance of 6 Å is 73%, 70%, 60%, 49% and 62%, respectively. We focus on this subset as monitoring improvement from models whose RMSD from native is close to random would yield meaningless results. It is only in the regime where the models at least loosely resemble the binding site of the native structure can one assess if the improvements are meaningful. On average, 14–15 residues per target were identified as ligand binding, with the best pockets assigned with rank 1 in ~80% of the cases. Local geometries of ligand-binding regions in chunk-TASSER models tend to be more deformed than those in the distorted protein structures with a 3 Å RMSD, 6 Å RMSD and 9 Å RMSD. The explanation to this is simple; the distorted structures were constructed starting from the crystal all-atom structures and the native protein conformations were deformed to a desired RMSD. Structure prediction by chunk-TASSER is carried out as low-resolution simulations, using Cα atoms and side chain centers of mass only. In the last step, all-atom models are rebuilt from their Cα coordinates by Pulchra. Therefore, despite a better mean TM-score, for models at 6 Å and 9 Å RMSD, the all-atom RMSD values calculated over the rebuilt conformations of binding residues are higher than the distorted ones. The accuracy of binding site prediction by FINDSITE is presented in Figure 2A. Using crystal structures, structures distorted to 3 Å, 6 Å and 9 Å RMSD, and chunk-TASSER models, the average binding site accuracy is 2.78, 2.96, 3.20, 3.46 and 3.02 Å, respectively. The high accuracy of binding site prediction was accompanied by a highly effective ligand ranking using consensus molecular fingerprints constructed using ligands extracted from the threading templates. Figure 2B shows that the native ligand is ranked within the top 1% of the screening library of 68,109 non-redundant compounds in 65–70% of the cases on average. As we will demonstrate in the following sections, both the pocket prediction accuracy as well as the effective ligand ranking are very important for successful refinement of ligand-binding regions in protein models.

Figure 2.

Accuracy of ligand binding site prediction by FINDSITE (A) and ligand-based virtual screening (B). A – the cumulative fraction of proteins with a distance between the center of mass of a ligand in the native complex and the center of the best of top five predicted binding sites displayed on the x-axis. B – the cumulative fraction of proteins, whose native ligand was ranked within the fraction of the screening library displayed on the x-axis.

3.4. Kernel bandwidth optimization

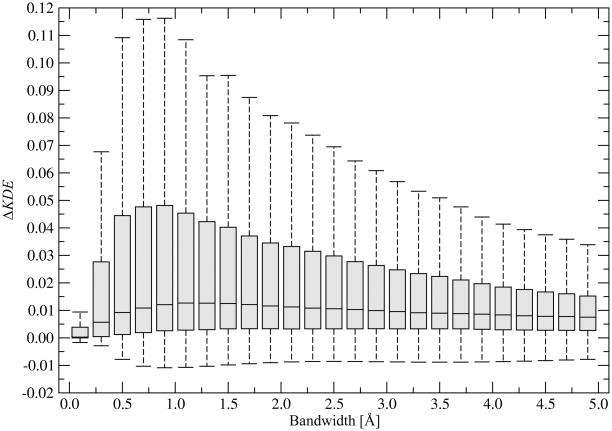
The approximate positions of the binding residue side chains are calculated using a kernel density estimation technique, also known as a Parzen window method (Parzen, 1962). This information is subsequently incorporated as chemical restraints into the fitness function developed for ligand binding site refinement. There is one free parameter of the kernel function, a bandwidth, which needs to be optimized. Many methods have been developed to support the selection of the correct bandwidth for kernel density estimation (Berwin; Jones et al., 1996). Here, we employ an empirical bandwidth optimization. Namely, we try to maximize the probability of finding a chemical group of a particular type in locations occupied by similar groups in threading templates that have similar binding sites and minimize the corresponding probability of finding it in locations occupied by chemically different functional groups. In binding site refinement, we will search for the target binding site conformation that fits the chemical group densities calculated from the template binding sites. Here, we keep the target binding site geometry fixed in its crystal form and change the kernel bandwidth, h, to obtain the maximum overlap with the superposed evolutionarily related pockets. The results in terms of ΔKDE (defined in Equation 8) are presented in Figure 3. The optimal bandwidth length for the Gaussian kernel used in the chemical density estimation is 1 Å. Smaller values cause undersmoothing and result in a noisy function. Larger values of h clearly smudge the structure data. In further binding site refinement simulations, a bandwidth of 1 Å is used.

Figure 3.

Optimization of the kernel bandwidth on the target crystal structures. ΔKDE is defined in Equation 8. Boxes end at the quartiles Q₁ and Q₃; a horizontal line in a box is the median. “Whiskers” point at the farthest points that are within 3/2 times the interquartile range.

3.5. Binding site ranking by SVR

Support Vector Machines (SVM) is a supervised machine learning technique used for classification and regression (Cortes and Vapnik, 1995; Drucker et al., 1997). In this study, we developed a regression model (SVR) to estimate the heavy atom RMSD from native for a given binding site conformation. The performance of our SVR model is assessed using 2-fold cross validation. As a set of features, we use the geometrical and chemical restraint information extracted from ligand-binding sites in weakly homologous template structures. In Figure 4, we assess the accuracy of the regression model in terms of the correlation between the observed and predicted RMSD from native for a non-redundant set of binding site geometries extracted from the ensemble of target conformations. In most ofthe cases, a positive correlation is found. Using the crystal structures, the Pearson’s correlation coefficient (CC) of >0.5 (>0.3) between the observed and predicted RMSD is observed for 70% (88%) of the target binding sites. For protein models constructed by chunk-TASSER, a CC of >0.5 (>0.3) is found in 47% (70%) of the cases, respectively.

Figure 4.

Cumulative fraction of targets with a Pearson’s correlation coefficient calculated between the true binding site RMSD and that predicted by machine learning plotted on the x-axis. For each target, the correlation coefficient is calculated over the ensemble of 50 representative conformations.

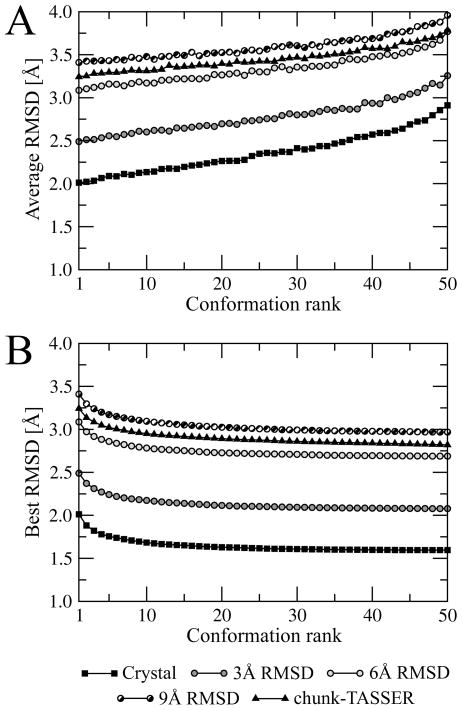
As we describe in Materials and Methods, for each target structure, an ensemble of 2,000 conformations generated using Modeller is subject to the clustering procedure to construct a non-redundant set of 50 conformations. The binding sites extracted form these structures are ranked by the RMSD to native predicted by the SVR model. The average as well as the best RMSD for conformations ≤ the specified rank is presented in Figure 5. Clearly, the binding site ranking by the expected RMSD calculated by machine learning using geometrical and chemical restraints is very effective not only for the crystal structures but also for the distorted and modeled protein conformations. Figure 5A shows that the average RMSD to native calculated over the heavy atoms of the binding residues is the lowest for the top-ranked pockets. Similarly, the best geometries are typically assigned with high (best=rank 1) ranks; there is only a minor improvement if lower ranks are considered. This is shown in Figure 5B, where the best RMSD values for at or above ranks lower than 10 are rather constant.

Figure 5.

Average (A) binding site heavy atom RMSD at a given rank and (B) best RMSD for conformations ≤ the specified rank for the ensemble conformations constructed from structures initially distorted to 3, 6 and 9 Å Cα RMSD as well as from chunk-TASSER models. Binding site conformations are ranked by SVR.

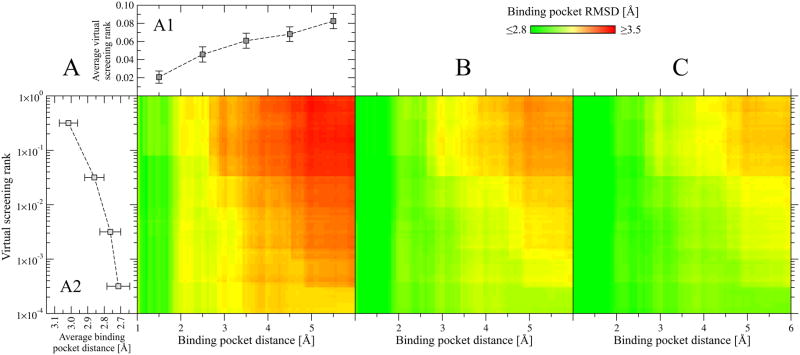
Next, we analyze what are the features of the predicted binding sites that make the local refinement successful. Two factors affect the final outcome: the accuracy of the pocket location prediction and the similarity of template-bound ligands to a ligand that binds to the target pocket in the crystal structure. Figure 6 shows how these factors affect the results considering the top-ranked pocket, the better of top 2 and the best top 3 pockets. We find that the quality of the geometrical restraints used as a part of the fitness function correlates well with the predicted pocket distance. The closer the predicted pocket center is to the real one, the better are the restraints and the more accurate is the refined geometry of the binding regions; this is shown in Figure 6. Moreover, if the anchor-containing molecules are chemically similar to the native ligand, one can expect their local chemical environment to be also similar. The similarity of template-bound ligands to the native molecule can be assessed by the native ligand rank in the random library that is calculated using molecular fingerprints constructed from the template ligands. Figure 6 also demonstrates that a better rank of the native ligand typically results in more accurately refined local geometries of the binding regions. Both features, the predicted pocket location and the rank of a native ligand, are also well correlated with each other. This is shown in Figure 6A (lean-to plots A1 and A2). In the case of very accurately predicted pockets, the majority of native ligands are at very low (better) ranks; this results in the vertical green stripes in Figure 6A, B and C that correspond to the all-atom RMSD of ≤2.8 Å for binding pockets predicted within ≤2, ≤2.5 and ≤3 Å, respectively. Similarly, correctly ranked native ligands tend to be predicted closer to the real pocket center than those at higher ranks (Figure 6, A2). In Table 2, the average performance using the top five ranked ligand-binding sites is shown for all chunk-TASSER models as well as for the subset of models for which the binding site was predicted within 3 Å and the native ligand was ranked within the top 1% of the screening library. The dataset coverage remains relatively high; both criteria are satisfied for roughly half of the targets. Considering the top (the best of top five) binding sites, the average RMSD from the native pocket geometry drops to ~3.1 Å (~2.9 Å). Focusing on the comparison to the original chunk-TASSER models, we observe a 0.1 (0.3) Å average improvement over that in the original predicted structure (see Table 1).

Figure 6.

Dependence of the binding site refinement outcome on the accuracy of pocket detection and virtual screening for chunk-TASSER models. Heat maps in A, B and Cshow the average all-atom RMSD calculated for the top-ranked, the better of top two and the best of top three binding site conformations ranked by SVR, respectively. The accuracy of pocket detection is expressed as the distance from the real binding pocket center, which is ≤ the value displayed on the x axis, whereas the performance of virtual screening is measured by a native ligand rank, which is ≤ the value displayed on the y axis. Lean-to plots in A show (A1) the average virtual screening rank ±SEM forpockets predicted within a distance displayed on the x axis and (A2) the average binding pocket distance ±SEM for native ligands ranked higher that the value displayed on the y axis.

Table 2.

All-atom RMSD in Å from the nativestructurecalculated for top-ranked binding sitesofchunk-TASSER models.

Set of binding pockets	Binding pocket ranka
	1	2	3	4	5
All binding pockets (557 targets)	3.24	3.14	3.09	3.05	3.02
Pocket center ≤3 Å, ligand rank ≤1% (232 targets)	3.09	2.99	2.94	2.89	2.86

^aranking by SVR in 2-fold cross-validation, the best RMSD of top n pockets is reported.

In addition, we analyze the accuracy of refined binding sites in terms of all-atom RMSD calculated separately for strongly, moderately and weakly conserved binding residues. As explained in Materials and Methods, the conservation of a binding residue corresponds to the fraction of templates that have a residue in equivalent position in contact with a ligand. Table 3 shows that particularly strongly, but also moderately, conserved residues are modeled to a higher accuracy than the weakly conserved ones. Indeed the top (best of 5) models as a RMSD of 2.6 (2.2) Å for the strongly structural conserved binding residues. These results are consistent with the analysis of the plasticity of ligand-binding regions in weakly related pockets, which reveals that highly conserved residues tend to adopt similar conformations.

Table 3.

All-atom RMSD in Å from the nativestructurecalculated over strongly, moderately and weakly conserved binding residuesfor the top-ranked binding sitesof chunk-TASSER models.

Binding residue conservationa	Binding pocket rankb
	1	2	3	4	5
strong	2.58 ±1.13	2.39 ±1.10	2.30 ±1.10	2.25 ±1.08	2.20 ±1.07
moderate	2.97 ±1.18	2.82 ±1.16	2.75 ±1.17	2.70 ±1.16	2.66 ±1.16
weak	3.41 ±1.45	3.25 ±1.45	3.18 ±1.45	3.14 ±1.45	3.09 ±1.44

^astrong: p ≥ 0.75, moderate: 0.50 ≤ p < 0.75, weak: 0.25 ≤ p < 0.50, where p corresponds to the fraction of templates that have a residue in equivalent position in contact with a ligand;

^branking by SVR in 2-fold cross-validation, the best RMSD of top n pockets is reported. Conservation here refers to the set of residues that are structurally conserved and bind to similar ligand positions.

3.6. Example: Immunophilin FKBP12

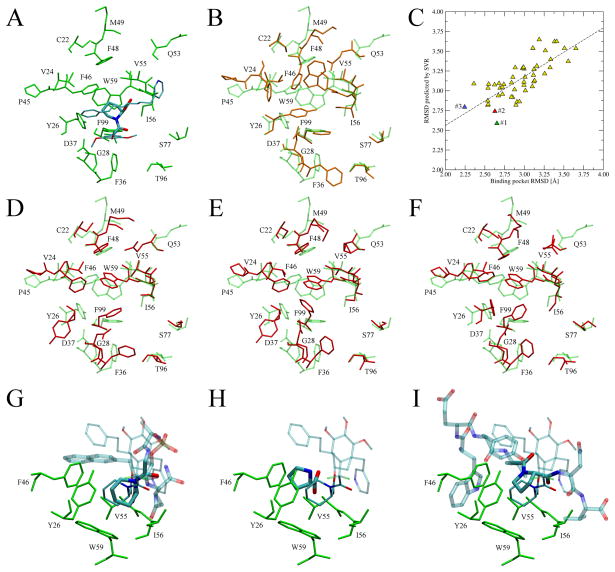
FK506-binding proteins, FKBPs, are peptidyl-prolyl cis-trans isomerases that catalyze the interconversion of peptidylprolyl imide bonds in peptides and other proteins (Galat, 1993). Here, we describe the application of the Binding Site Refinement approach to immunophilin FKBP12, whose crystal structure in complex with a high affinity pipecolate ligand, FKB-001, is available in the PDB (ID: 1j4r) (Dubowchik et al., 2001). The pipecolate or proline ring of FKBP12 ligands is located inside a largely hydrophobic pocket and forms interactions with several residues including Y26, V55, I56 and W59 (Figure 7A). In the predicted structure of FKBP12, the binding pocket is modeled to an accuracy of 3.11 Å RMSD from the native structure, with significant deviations from the crystallographic positions of side-chains, particularly for Y26, F36, F48, F46 and W59 (Figure 7B). Such distortions may cause a considerable deteriorationin the performance of many ligand docking approaches. In Figure 7C, we assess the accuracy of the SVR model in terms of the correlation between the observed and predicted RMSD from native for a non-redundant set of 50 binding site geometries constructed for FKBP12. Here, the Pearson’s correlation coefficient is 0.76, with the best binding site conformation (2.24 Å RMSD) at rank 3. The all-atom RMSD for the conformations at rank 1 and 2 is 2.65 Å and 2.63 Å, respectively. These top-ranked pocket geometries modeled by BSR are shown in Figure 7D-F. Compared to the chunk-TASSER model (Figure 7B), the side-chain orientations of many key residues, e.g. F36, F46, F48 and W59, are significantly improved. Many high affinity FKBP12 ligands are pipecolyl and prolyl ketoamides (Armistead et al., 1995). Interestingly, proline and pipecolate moieties were identified as highly conserved anchor substructures in several weakly homologous templates detected by threading. Moreover, their binding mode is strongly conserved across a set of distantly related proteins; this is shown in Figure 7G,H and I for peptidyl-prolyl cis-trans isomerase NIMA-interacting 1 (PDB IDs: 2itk and 1pin) and chaperone surA (PDB ID: 2pv1), whose sequence identity (TM-score) to FKBP12 is 15% (0.56) and 18% (0.49), respectively where we apply FINDSITE/FINDSITE^LHM to identify the putative ligand binding pose and conserved anchor region geometries. As we discuss above, correctly predicted binding ligands are very important for successful refinement of binding pockets in protein models.

Figure 7.

Binding site refinement for immunophilin FKBP12. (A) Binding pose of the FKB-001 ligand in the crystal structure of FKBP12 (PDB ID: 1j4r). FKB-001 is colored by atom type with the pipecolate moiety represented by thick sticks. (B) Binding pocket conformation in the structure modeled by chunk-TASSER (orange, solid) superposed onto the crystal structure (green, transparent). (C) Correlation between the observed and predicted RMSD from native for a non-redundant set of 50 binding site geometries constructed for FKBP12. Conformations at rank 1, 2 and 3 are colored in green, red and blue, respectively. (D, E and F) Top-ranked conformations (rank 1, 2 and 3, respectively) modeled by the BSR approach (red, solid) superimposed onto the crystal structure (green, transparent). (G, H and I) Ligands extracted from weakly related templates (PDB IDs: 2itk, 1pin and 2pv1, respectively) that contain conserved proline and pipecolate moieties (thick sticks colored by atom type) upon superposition of the template onto the target crystal structure. The anchor region is solid whereas the remaining part of the molecule is transparent. Thick (thin lines) indicate the ligand binding pose in the model (crystal structure). Selected interacting residues are shown in green.

4. Concluding remarks

In this work, we present a new method for the template-based refinement of ligand-binding regions in weakly homologous protein models. Low-resolution information about the interactions between evolutionarily related proteins and their ligands is converted into a set of geometrical and chemical restraints. The use of sensitive sequence-profile driven threading (Jones and Hadley, 2000) to identify template complexes is critical in that it efficiently eliminates structurally similar, yet functionally unrelated, proteins. It has already been shown that threading greatly reduces the false positive rate in the detection of template structures for functional annotation (Brylinski and Skolnick, 2009a). The presented method performs satisfactorily even when no closely related templates are used. Thus, it can be included in the large-scale structure modeling of complete proteomes, where the typical coverage of the gene products by weakly related structures from the PDB (Berman et al., 2000)is 50–70% (O’Toole et al., 2003; Xie and Bourne, 2005; Zhang and Skolnick, 2004a; Zhang and Skolnick, 2005b).

Machine learning that uses the developed scoring functions is demonstrated to efficiently rank the diverse conformations of the ligand-binding regions. This is of practical use in ligand docking and screening against an ensemble of receptor models, a commonly used technique that accounts for the receptor flexibility (Teodoro and Kavraki, 2003). Using the method developed in this study, the number of possible geometries of the binding pockets could be dramatically reduced to the most probable ones. This would reduce the computational expense of the ensemble docking approaches. Recent benchmarks show that using multiple homology models in virtual screening can significantly improve the enrichment in bioactive compounds (Fan et al., 2009).

A key feature of this model is that it employs low-resolution restraints in the form of the approximate Cα positions and Cα-Cα distances as well as functional groups instead of the heavy atoms to describe the local chemical environment and interactions with small molecules. Such a description allows for the accommodation of structural variations observed in corresponding ligand-binding regions in distantly related homologues (Liang et al., 1998; Panjkovich and Daura; Pils et al., 2005; Weisel et al., 2009). On the other hand, such variations roughly concur with the maximum accuracy, estimated to be ~2.6 Å RMSD for the heavy atoms, which is in good agreement with the previous studies (Mendes et al., 2001; Wilson et al., 1993). As in protein structure prediction, where low-resolution template-based approaches are able to construct approximate backbone geometries that require further all-atom refinement, e.g. using physics-based force fields (Fan and Mark, 2004; Kmiecik et al., 2007; Wroblewska et al., 2008), the roughly correct geometries of the ligand-binding regions modeled in this study from weakly related templates may require additional refinement at the atomic level (Huang et al., 2006; Pencheva et al., 2008). Alternatively, approximately correct side chain orientations predicted to ~2.9 Å RMSD from native should be of sufficient accuracy for low-resolution ligand docking that tolerates to some extent the structural distortions of ligand-binding regions (Bindewald and Skolnick, 2005; Brylinski and Skolnick, 2008b; Brylinski and Skolnick, 2009c; Vakser, 1996; Wojciechowski and Skolnick, 2002). Considering the significant coverage of proteomes by remotely related templates, the binding site refinement described in this study should be of practical use in structure-based drug design applied at the proteome level.