Determination of Sample Sizes for Demonstrating Efficacy of Radiation Countermeasures

SUMMARY

In response to the ever increasing threat of radiological and nuclear terrorism, active development of non-toxic new drugs and other countermeasures to protect against and/or mitigate adverse health effects of radiation is ongoing. Although the classical LD₅₀ study used for many decades as a first step in preclinical toxicity testing of new drugs has been largely replaced by experiments that use fewer animals, the need to evaluate the radioprotective efficacy of new drugs necessitates the conduct of traditional LD₅₀ comparative studies (FDA, 2002). There is, however, no readily available method to determine the number of animals needed for establishing efficacy in these comparative potency studies. This paper presents a sample-size formula based on Student’s t for comparative potency testing. It is motivated by FDA’s requirements for robust efficacy data in the testing of response modifiers in total body irradiation experiments where human studies are not ethical or feasible. Monte Carlo simulation demonstrated the formula’s performance for Student’s t, Wald, and Likelihood Ratio tests in both logistic and probit models. Importantly, the results showed clear potential for justifying the use of substantially fewer animals than are customarily used in these studies. The present paper may thus initiate a dialogue among researchers who use animals for radioprotection survival studies, institutional animal care and use committees, and drug regulatory bodies to reach a consensus on the number of animals needed to achieve statistically robust results for demonstrating efficacy of radioprotective drugs.

1. Introduction

The development of drugs and biological products for treating human illnesses relies heavily on animal studies. There is a long history of the use of lethality data from acute toxicity studies as the initial step in the development of preclinical safety and toxicological profiles of potential drugs and biologic products prior to clinical testing (Casarett and Doull, 1975). The principal purpose of the acute lethality study is the estimation of an LD₅₀, a dose that corresponds to 50% lethality, as first proposed by Trevan (1927). The “classical” LD₅₀ experiment involves a large number of animals; e.g., 10 doses with 10 animals per dose (usually rats or mice) (Walum, 1998). Over the past several decades there has been movement away from traditional LD₅₀ studies in favor of studies that use fewer animals, such as the fixed-dose procedure (British Toxicology Society Working Group, 1984) and the up-and-down procedure (Bruce, 1985; OECD, 2001). In 1988, the US Food and Drug Administration published a policy statement supporting efforts to eliminate conduct of the classical LD₅₀ experiment in acute toxicity testing (FDA, 1988). Recently, a working group representing 18 European pharmaceutical companies concluded that acute toxicity studies are not needed prior to first clinical trials in humans (Robinson et al., 2008).

Although the classical LD₅₀ estimation study has fallen out of common use for preliminary assessment of toxicity in drug development, there is still a need for comparative LD₅₀ studies for testing the efficacy of drugs designed as countermeasures to agent-induced lethality. This is especially true in the case of radiation-induced lethality, where there is a critical need to develop countermeasures to serious health threats posed by radiological and nuclear terrorism (Mettler and Voelz, 2002; Stone et al., 2004; Waselenko et al., 2004; Pellmar and Rockwell, 2005; Hauer-Jensen et al., 2008; Kumar, Ghosh, and Hauer-Jensen, 2008). Hence, relative potency testing, including traditional acute toxicity testing in animals, is still a regulatory requirement for establishing the efficacy of new drugs and biologic products used to reduce or prevent radiological or other toxicity when human efficacy studies are not ethical or feasible (FDA, 2002). Because acute toxicity studies focus on enhancing survival, lethality studies are necessary. From an animal-welfare perspective, use of an appropriate number of animals (neither too many nor too few) to demonstrate the effect is paramount, especially considering that more than one animal species is generally required (FDA, 2002). Although relative potency testing has been done for decades (Finney, 1978), there does not appear to be a readily available formula for calculating the sample sizes of dose groups needed to achieve a specified statistical power for demonstrating a significant effect in a comparative potency study. The purpose of this paper is to present such a formula and to validate its application.

2. Method

In relative potency testing of toxic substances, there are typically two groups to compare: a standard treatment group and a test treatment group (Finney, 1978). Commonly, animals are randomly chosen to be exposed to one of two different agents; within each agent, animals are further subdivided into several dose groups. Alternatively, groups of animals may each be exposed to the same agent at several doses, with half the animals also being exposed to a drug as a countermeasure and the other half to a vehicle control. For the specific intent of this paper, the latter experimental setting applies, with radiation as the toxic agent; the radioprotectant drug group is referred to as the modified (or test) treatment group and the vehicle control group as the unmodified (or standard) treatment group. The term treatment may refer to either prophylactic (pre-irradiation) or therapeutic (post-irradiation) treatment. The objective is to test whether the radiation LD₅₀ of the modified treatment group is significantly greater than that of the unmodified treatment group. A statistically significantly larger LD₅₀ for the drug group compared to the vehicle group establishes the drug’s efficacy as a countermeasure for reducing the potency of the radiation toxicity; larger relative differences in LD₅₀s imply greater efficacy.

Probit analysis and logit analysis (Finney, 1978) are common tools for studying the relative potency of a test treatment to a standard treatment. The equivalent-deviate transformation is

$$Y=F^{-1}(P)={\beta }_0+{\beta }_1{log}_{10}D,$$ (1)

where P is the lethality proportion for subjects exposed to dose D of a substance (radiation in the present setting). For probit analysis, F is the normal (Gaussian) cumulative distribution function (cdf) and for logit analysis F is the logistic cdf, where β₀ and β₁ are intercept and slope parameters, respectively. The term ‘logit’ is used here to describe the latter transformation and analysis while the term ‘logistic’ is used to describe the corresponding model; the term ‘probit’ is used in all instances to describe the former transformation, analysis and model. Base-10 logarithmic transformation of dose is commonly used in this setting. Finney (1978) discusses estimation of relative potency (efficacy) on the basis of parallel probit log-dose regression lines. Relative potency estimation using logistic log-dose regression is similar. Define LD_100P as the lethal dose for 100P% of a population of test animals. Let ρ denote the relative potency of the unmodified (U) to modified (M) treatment, that is, the factor by which an equivalent-effect dose of M is greater than or less than the corresponding dose of U. Thus, in general,

$${\rho }_{100P}={LD}_{100P}(M)/{LD}_{100P}(U).$$ (2)

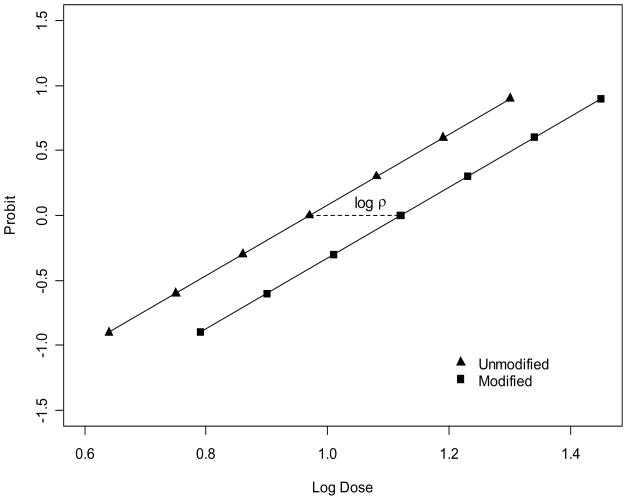
Given that the probit (logistic) log-dose regression lines are parallel, ρ_100P = ρ for any value of P such that 0<P<1, so that logρ is the horizontal distance between the lines for unmodified and modified treatment groups (Figure 1). It is common to choose P = 0.50 and to express logρ as the difference between the log LD₅₀s of the two treatment groups. Then, for future reference,

Figure 1.

Illustration of parallel probit log-dose regression lines for an unmodified treatment (▲) and a modified treatment (■). The horizontal distance between the lines is the logarithm of the relative potency, i.e., the difference in logLD₅₀s.

$$log\rho =log\{{LD}_{50}(M)\}-log\{{LD}_{50}(U)\}.$$ (3)

Although the ratio may be taken either way, ρ as defined in (2) is the relative potency of U to M. In this discussion, it will be assumed that M is at most as potent as U, i.e., ρ = 1 or ρ > 1. Hence, for the experimental setting that motivates this discussion, ρ is commonly referred to as a dose reduction factor (DRF), the factor by which the modifying substance, the drug, reduces the potency of the radiation dose; DRF is used here interchangeably with ‘relative potency’. The objective here is to test whether LD₅₀(M) is significantly greater than LD₅₀(U); i.e., whether ρ (alternatively logρ) is significantly greater than 1(0). The null and alternative hypotheses are:

$$\begin{array}{l}{H}_0:\rho =1(log\rho =0)\\ H_1:\rho ={\rho }_1>1(log\rho =log{\rho }_1>0).\end{array}$$ (4)

Brown (1966) discusses estimation of logρ, giving guidance for determining sample sizes needed to achieve a specified precision of the estimate, but he does not discuss sample-size determination for testing. Finney (1978) also discusses estimation, but not testing, of relative potency. However, Finney’s discussion of fiducial-intervals for logρ provides a basis for devising a t-test to use for sample-size determination for testing. For notational convenience, let θ = log ρ. Then, by Finney’s definition,

$$\theta =({\beta }_{0U}-{\beta }_{0M})/{\beta }_1,$$ (5)

where β_0U and β_0M are the respective intercepts for U and M, and β₁ is the common slope. Thus,

$$\widehat{\theta }=({\widehat{\beta }}_{0U}-{\widehat{\beta }}_{0M})/{\widehat{\beta }}_1,$$ (6)

where ^ indicates an estimate of a parameter. Equivalently,

$$\widehat{\theta }=({\overline{x}}_M-{\overline{x}}_U)-({\overline{y}}_M-{\overline{y}}_U)/b,$$ (7)

where b = β̂₁, x̄_M and x̄_U are weighted averages of the log doses for M and U, respectively, and ȳ_M and ȳ_U are weighted averages of the probits (logits) for M and U based on the maximum likelihood estimates of β_0U, β_0M and β₁. An expression for the variance of θ̂ may be obtained using the delta method, under the assumption that the numerator and denominator of θ̂ are independent random variables. That is, the variance is estimated by

$$\widehat{V}(\widehat{\theta })\cong s^2(1/b^2)[\sum _{U,M}(1/\sum _i{w}_i{n}_i)+\{{({\overline{y}}_M-{\overline{y}}_U)}^2/b^2\}\{1/\sum _{U,M}\sum _i{w}_i{n}_i{(x_i-\overline{x})}^2\}],$$ (8)

where n_i is the number of animals in the i^th dose group of M or U and w_i is a weight related to the lethality proportion, P_i. For the probit transformation w_i is [φ{Φ¹(P_i)}]²/{P_i(1−P_i)}, with φ(*) and Φ(*) being the standard normal probability density function (pdf) and cdf, respectively. For the logit transformation, w_i is P_i(1−P_i). The summations with index i in (8) are taken over the dose groups of M and U. In (8) s² is an estimate of the variance among the probits (logits). Finney calls s² a heterogeneity factor; he says to use s² only when there are significant deviations from linearity, and otherwise to use the expected variance of unity (Finney, 1978, Chapter 17). Here, we treat s² as unity in deriving the sample size, but when testing, we use the deviance from the probit (logistic) regression divided by the deviance’s degrees of freedom, f, to have a valid t test.

The statistic for testing H₀ against H₁ in (4) is given by

$$T=\widehat{\theta }/{\{\widehat{V}(\widehat{\theta })\}}^{1/2},$$ (9)

which has a central t distribution with f degrees of freedom under H₀. To derive the sample size needed to test H₀ with a significance level α and power 1−β, one solves

$$1-\beta =Pr(T>t_{f,\alpha }\mid H_1)$$ (10)

for n_i, where t_f,α is a Student’s-t variate with f degrees of freedom having α probability to its right. Although the test statistic under H₁ has a non-central t distribution with the noncentrality parameter involving the sample size, the central t distribution can be used to approximate the power in order to obtain a closed-form solution for the sample size (Kraemer and Paik, 1979). That is, one uses Pr(T_f > t_f,α − δ) to approximate Pr(T_f,δ > t_f,α ) where δ is the noncentrality parameter; this works very well for powers of 80% and higher. Taking s² = 1 in (8) gives

$$1-\beta \cong Pr\left[T_f>t_{f,\alpha }-{\theta }_1/{\{\widehat{V}(\widehat{\theta })\}}^{1/2}\right],$$ (11)

where θ₁ = log ρ₁, from which it follows that

$$-t_{f,\beta }\cong t_{f,\alpha }-{\theta }_1/{\{\widehat{V}(\widehat{\theta })\}}^{1/2}.$$ (12)

The value of f in (12) is the total number of doses for M and U minus 3, since three parameters (β_0M, β_0U, and β₁) are estimated. Thus, although the variance per observation is taken to be unity in (12), f represents the degrees of freedom of an estimate of the variance based on the sum of squared deviations of mean responses from the fitted regression line.

Solving for the required sample size per dose group requires some additional simplifying conditions and assumptions. First, let all dose groups have the same sample size; i.e., n_i = n for all dose groups of both M and U, which is a common design feature. Next, let ${\displaystyle \sum _{i=1}^g}{w}_i$ be the same for both M and U; this is satisfied if both M and U have the same number of dose groups, g, and if the lethality responses at respective, but different, doses are comparable (e.g., M and U each have a 5%-response dose, a 50%-response dose, etc.) (Figure 1). Then,

$$n\cong \frac{{(t_{f,\alpha }+t_{f,\beta })}^2[(2/{\displaystyle \sum _i}{w}_i)+{\{({\overline{y}}_M-{\overline{y}}_U)/b\}}^2\{1/{\displaystyle \sum _{U,M}}{\displaystyle \sum _i}{w}_i{(x_i-\overline{x})}^2\}]}{b^2{(log{\rho }_1)}^2}.$$ (13)

As a final simplification, assume that the second term in braces in the numerator in (13) is negligible relative to the first term in braces. This is tantamount to assuming that ȳ_M is equal to ȳ_U, as it is in expectation under the above condition of equal lethality targets. Thus,

$$n\cong \frac{{(t_{f,\alpha }+t_{f,\beta })}^2(2/{\displaystyle \sum _{i=1}^g}{w}_i)}{{b_j}^2{(log{\rho }_1)}^2},$$ (14)

where α is the significance level, 1−β is the power, w_i is the probit or logit weight for the i^th of g groups, ρ₁ is the relative potency to be detected under the alternative hypothesis, and b_j is an a priori estimate of the common slope, j=p for probit and j=l for logit. A non-integer value of n obtained from (14) is raised to the next higher integer.

To make expression (14) specific, let there be g = 5 dose groups for each of M and U. Further, let the targeted lethality responses be 5%, 27.5%, 50%, 72.5% and 95% for each treatment. The corresponding probit weights are 0.22394, 0.55843, 0.63662, 0.55843 and 0.22394, and the corresponding logit weights are 0.04750, 0.19938, 0.25, 0.19938 and 0.04750. Thus, ${\displaystyle \sum _{i=1}^g}{w}_i=2.20136$ for the probit transformation and 0.74376 for the logit transformation. The value of f will be 2(5)−3=7. If α =0.05 and β=0.20 (power = 0.80), then t_{7, 0.05} = 1.895 and t_7,0.20 = 0.896. For the probit model,

$$n_p={(1.895+0.896)}^2(2/2.201)/\{{b_p}^2{(\text{log}{\rho }_1)}^2\}=7.1/\{{b_p}^2{(\text{log}{\rho }_1)}^2\}$$ (15)

and for the logistic model,

$$n_l={(1.895+0.896)}^2(2/0.744)/\{{b_l}^2{(\text{log}{\rho }_1)}^2\}=20.9/\{{b_l}^2{(\text{log}{\rho }_1)}^2\},$$ (16)

where b_p and b_l are the a priori estimates of the probit and logistic slopes, respectively.

For a five-dose experiment with the specified lethality targets, equating n_p and n_l in (15) and (16) results in b_l = (2.201/0.744)^0.5b_p ≅ 1.720b_p. An approximate probit-to-logistic slope factor is $F={({\displaystyle \sum _{i=1}^g}{w}_{ip}/{\displaystyle \sum _{i=1}^g}{w}_{il})}^{1/2}$. F is 1.720 in this case; in general, it will depend on g and the specified lethality targets. F is a useful quantity for relating the probit and logistic slopes, especially when quantifying the effect size to be detected in the logistic context, which is not as natural as the probit context. For the probit model, since b_p is the reciprocal of the estimated standard deviation of the log-normal distribution of dose, b_plogρ₁ is the effect size, i.e., the estimated size of the DRF (relative potency) that can be detected relative to the underlying standard deviation, with the specified power. In the logistic context, (b_l/F)(logρ₁) is the approximate effect size in standard-deviation units. When performing power analyses in designing experiments, power curves are very useful, with power plotted as a function of the detectable effect size for a fixed sample size, or of the sample size for a fixed effect size.

3. Monte Carlo Simulation Study

3.1 Background

A Monte Carlo simulation study was conducted to validate the applicability of the sample-size formula with various statistical tests, in terms of achieving a specified power while maintaining a specified size (significance level). Four sets of radiation lethality data generated in one of our laboratories were modeled to select parameters for the simulation study. Three datasets consisted of 10-day lethality data, each with a vehicle control (standard) group and a radioprotectant treated (test) group, and one dataset consisted of 30-day lethality data for a vehicle group and radioprotectant group. While all the reported experiments involved total body irradiation and thus caused injury in all organ systems, 10-day lethality is generally considered to have a substantial component of gastrointestinal injury while 30-day lethality is primarily reflective of damage to the hematopoietic system. Table 1 presents a representative set of 10-day lethality data, with selected analytical results given in the table’s footnote.

Table 1.

Data from a 10-day lethality study in mice. Unmodified and modified treatments were each represented by five dose groups exposed to radiation at the given dose levels. The modified group was treated with drug X as a countermeasure, resulting in reduced lethality after radiation exposure.^*

Dose (Gy)	Unmodified			Modified
	n	r	%	n	r	%
7	8	0	0	8	0	0
8	8	1	12.5	8	0	0
9	8	3	37.5	8	0	0
10	8	8	100	8	4	50
11	8	8	100	8	5	62.5

^*n is the sample size, r is the number that died, % is 100r/n. β̂₁ (logistic) = 48.96, β̂₁ (probit) = 28.51, ρ̂ = 1.16, estimated effect size: 1.9 standard deviations, t-test p-value < 10⁻⁶.

To develop parameters for the simulation study, logistic and probit models were fitted to the four lethality data sets using SAS Version 9.1.3 (SAS, 2004), first with the untransformed dose as the dose metric and then with log₁₀-dose as the dose metric. Ratios of slopes (vehicle to drug) were calculated and averaged. For the logistic model, the average ratio for the untransformed dose was 1.14 (individual ratios: 0.82, 0.96, 1.19, 1.59) while the average ratio for log₁₀-dose was 1.02 (individual ratios: 0.79, 0.86, 1.05, 1.40), where the first three values are from 10-day lethality data and the last value is from 30-day data. Comparable results were obtained for the probit model. Based on these limited data, it appears that using either the untransformed dose or log-dose as the dose metric can satisfy the assumption of parallelism of the logistic (and probit) lines. Following Finney (1978), we adopt the log-dose metric. (Log_e-dose gives the same result as log₁₀-dose.)

3.2 Study Design and Implementation

Although the sample-size formula (14) has been derived primarily from Finney’s discussion of the probit log₁₀-dose model, popular use of the logistic model (Morgan, 1992; Hosmer and Lemeshow, 2000) suggests expressing the simulation parameters in terms of the latter model. Using either the probit or logit slope with associated weights gives the same sample size for the conditions simulated, because corresponding slopes are chosen based on the probit-to-logistic slope factor. Based on a logistic log₁₀-dose model, a slope of 40 is simulated, along with an intercept of −40 for the unmodified group, to be representative of the observed 10-day and 30-day lethality data. The intercept parameter determines the vertical location of the dose-response, but has no effect on the relative potency comparison. In addition to the above parameters for a steep dose-response relationship, the insulin example of Finney (1978, Chapter 18) was used to select parameters for a shallow dose-response. This gave a slope of 5 and an intercept of 2.7 for the unmodified group based on a logistic log₁₀-dose model.

A comparative potency (efficacy) experiment with two treatment groups, unmodified and modified, was simulated. The essential parameters of the study are given in Table 2. Two different experimental designs were investigated: five doses per treatment with lethality targets of P=0.05, 0.275, 0.50, 0.725 and 0.95; and seven doses per treatment with lethality targets of P=0.05, 0.20, 0.35, 0.50, 0.65, 0.80 and 0.95. There were no zero-dose controls. The intercept for the modified group was determined by the slope and intercept of the unmodified group, along with the relative potency. For the steep dose-response, relative potencies (DRFs) of ρ = 1.0 (no effect), 1.10 (1 standard deviation (sd) effect size) and 1.16 (1.5 sd effect size) were simulated. For the shallow dose-response, DRFs of ρ = 1.0, 2.20 (1 sd) and 3.26 (1.5 sd) were simulated. The number of animals per dose group, n, was determined by expression (14) for powers of 1 − β = 0.8 and 0.9, with a significance level (size) of α = 0.05 (Table 2). Although the sample sizes were the same for the steep and shallow dose-responses for equivalent effect sizes, the simulated dose-response data were very different, thus allowing investigation of the robustness of the sample-size formula’s performance with respect to different levels of variability in the data.

Table 2.

Parameters of Monte Carlo simulation study.

Lethality Targets (P)	Logistic β1	Probit β1	ρ	Pr(Reject H0)	n*
0.05, 0.275, 0.5, 0.725, 0.95 (5 doses)	40	23.25	1.1	1−β = 0.9	11
				1−β = 0.8	8
			1	α = 0.05	8, 11
			1.16	1−β = 0.9	5
				1−β = 0.8	4
			1	α = 0.05	4, 5
	5	2.91	2.2	1−β = 0.9	11
				1−β = 0.8	8
			1	α = 0.05	8, 11
			3.26	1−β = 0.9	5
				1−β = 0.8	4
			1	α = 0.05	4, 5
0.05, 0.2, 0.35, 0.5, 0.65, 0.8 0.95 (7 doses)	40	23.41	1.1	1−β = 0.9	7
				1−β = 0.8	5
			1	α = 0.05	5, 7
			1.16	1−β = 0.9	3
				1−β = 0.8	2
			1	α = 0.05	2, 3
	5	2.93	2.2	1−β = 0.9	7
				1−β = 0.8	5
			1	α = 0.05	5, 7
			3.26	1−β = 0.9	3
				1−β = 0.8	2
			1	α = 0.05	2, 3

^*n is calculated from formula (14) based on the set of P, β₁, ρ, and power (size) settings. For each presented n, 10000 datasets were generated and analyzed. Estimated power and size results are presented in Figures 2 and 3 in a similar arrangement as this table.

For each configuration, 10000 simulations were run. Dose levels were determined by log₁₀(dose_i) = {F⁻¹(P)−β_0i}/β₁, where F is the logistic cdf, and i = U or M. Note: F⁻¹(P) = log_e{P/(1−P)}. Binomial samples were drawn randomly from Bin(n_l, P), where P=F{β_0i+ β₁·log₁₀(dose_i)}. For dose groups with 0% or 100% responses, the data were handled two ways: unadjusted and adjusted, where the adjusted data had 0.01 substituted for P when there were no simulated deaths (0%) and 0.99 substituted for P when all simulated observations were deaths (100%). The adjustment was included mainly to determine if it had a stabilizing influence on the dose-response models and/or the statistical tests, considering that many proportions of 0 and 1 can occur with small samples, especially at extreme targets like 5% and 95%. Both log-logistic and log-probit models were fitted to each generated data set. The t-test (9) of H₀: ρ = 1 vs. H₁: ρ = ρ₁ > 1 was conducted. Although the sample-size calculation is based on the t-test, the model Wald test and Likelihood Ratio test of the treatment effect (H₀: β_0U − β_0M = 0 vs. H₁: β_0U − β_0M > 0) were also conducted, since these two tests are commonly provided by statistical packages for logistic and probit models, and correspond to the desired test of ρ in this common-slope setting. The size and power of each test statistic were calculated as the proportion of rejections of the one-sided, 0.05-level tests among the 10000 runs. The simulation was conducted in R Version 2.6.0 (R Development Core Team, 2007).

3.3 Study Results

The results of the simulation study are presented in Figures 2a,b and 3a,b for the 5-dose and 7-dose cases, respectively. Results for both the logistic (left side) and probit (right side) models are given, with the value of the corresponding slope, β₁, indicated for each. The sample size of each dose group, n, is shown for each indicated value of ρ, where the first value of n above each panel corresponds to 80% power and the second value to 90% power. Simulated powers and sizes for each test are plotted in each panel and connected by straight lines for ease of visualization. The upper power line is for the 90% power target and the lower line for 80%. Two values of the size of each test are plotted for the two targeted powers.

Figure 2.

Simulated powers and sizes of Student’s t (t, t*), Wald (Wald, Wald*) and Likelihood Ratio (LR, LR*) tests based on logistic and probit models for 5-dose studies having steep (2a) and shallow (2b) dose-responses with slope β. Asterisks indicate tests performed on adjusted 0–1 response data. Upper and lower pairs of panels correspond to 1.0 and 1.5 sd effect sizes, respectively, represented by indicated values of ρ. The smaller value of n in each pair is for targeted power of 80% (▲) and the larger value is for 90% (■), with test sizes similarly shown at the bottom of each panel.

Figure 3.

Simulated powers and sizes of Student’s t (t, t*), Wald (Wald, Wald*) and Likelihood Ratio (LR, LR*) tests based on logistic and probit models for 7-dose studies having steep (3a) and shallow (3b) dose-responses with slope β. Asterisks indicate tests performed on adjusted 0–1 response date. Upper and lower pairs of panels correspond to 1.0 and 1.5 sd effect sizes, respectively, represented by the indicated values of ρ. The smaller value of n in each pair is for targeted power of 80% (▲) and the larger value is for 90% (■), with test sizes similarly shown at the bottom of each panel.

From Figures 2a and 2b it can be seen that the logistic and probit models gave very similar results for the 5-dose experiment in both steep and shallow cases. All statistical tests had simulated powers that equaled or exceeded the targets, while maintaining size close to nominal. The Likelihood Ratio test on the unadjusted 0–1 response data (LR) had the highest power of the six tests for all configurations. However, its size exceeded the 5% nominal level in all cases (range: 0.0515–0.0613). The Likelihood Ratio test on the adjusted 0–1 response data (LR*) had slightly reduced power compared to the unadjusted LR test, but better size (range: 0.0458–0.0531). The power of the Wald test tended to slightly exceed that of the t-test for the 1 sd effect size, while the reverse was true for the 1.5 sd effect size. This happened for both the unadjusted 0–1 versions (Wald and t) and adjusted 0–1 versions (Wald* and t*). The size ranges were 0.0376–0.0505 for the t test, 0.0355–0.0463 for the t* test, 0.0441–0.0546 for the Wald test, and 0.0412–0.0502 for the Wald* test.

For the 7-dose experiment, there was more variation in estimated power among the tests in both steep and shallow cases, as shown in Figures 3a and 3b. The main difference between the logistic and probit models occurred for the Wald and Wald* tests for 80% power, with the logistic model having slightly lower power than the probit. For the 1 sd effect size, all six tests achieved simulated power that equaled or exceeded the 80% and 90% targets except for the Wald* test which missed the target slightly in the steep case (79%). The primary differences occurred for the 1.5 sd effect size, where the sample sizes generated by (14) were n=2 and n=3 for 80% and 90% power, respectively. The sample size of n=2 led to substantial underachievement of power for Wald (range: 0.6762–0.7121) and Wald* (range: 0.6613–0.0.7003) and moderate underachievement for LR (range: 0.7564–0.7647) and LR* (range: 0.7364–0.7476). The sample size of n=3 led to moderate underachievement of power for Wald (range: 0.8508–0.8662) and Wald* (range: 0.8420–0.8562), and slight underachievement for LR (range: 0.8799–0.8835) and LR* (0.8698–0.8732). In these cases, the t-tests performed well, giving simulated powers only slightly less than nominal. For n=2 the t-test’s power ranged from 0.7807 to 0.7940, and the t*-test’s power ranged from 0.7819 to 0.7934. For n=3, the power ranges were 0.8960–0.8981 and 0.8937–0.8942 for t and t*, respectively. The test sizes were higher for the 7-dose experiment than for the 5-dose experiment. The size ranges were 0.0415–0.0638 for the t test, 0.0371–0.0578 for the t* test, 0.0425–0.0557 for the Wald test, 0.0399–0.0483 for the Wald* test, 0.0517–0.0692 for the LR test, and 0.0460–0.0576 for the LR* test.

In order to summarize the simulation results, estimated test sizes and powers were further analyzed with a five-factor analysis of variance (ANOVA), allowing up to three-way interactions. Separate analyses were conducted for the logistic and probit models. The factors were Slope (shallow or steep); #Doses (5 or 7 per treatment); Effect size (1 sd or 1.5 sd); Power (projected 0.8 or 0.9); and Test (t, t*, Wald, Wald*, LR, and LR*). For the test-size analysis, ρ=1, so Effect size represented the different sample sizes rather than different values of ρ; this factor was nested within levels of Slope, #Doses, and Power.

The ANOVA for size showed strong evidence of a Test effect for both the logistic and probit models, with no evidence of any two- or three-way interactions. In the power ANOVA, there were some two- and three-way interactions with the Test factor involving #Doses, Effect-size and Power. However, because these interactions represent simply more extreme results for certain factor levels (7 doses, 1.5 sd, 80% power) than others, but not crossing of effects at different levels, they do not preclude averaging the simulated powers across these effects to get representative powers for each test under each model. Table 3 presents the estimated test sizes and powers for each statistical Test averaged over the levels of the other factors. In keeping with Figures 2 and 3, Table 3 indicates that the size of only the LR test consistently exceeded the nominal size of 5% on average, although the 95% upper confidence limit on the mean was less than 6%. Table 3 indicates that, on average, the tests achieved the targeted power, the only exception being the Wald and Wald* tests for the 80% target. The t and LR tests had very similar powers on average, but the t test maintained size better than the LR test. Web-based Appendix A gives complete details of the ANOVA of size and power.

Table 3.

Estimated Sizes and Powers of Tests averaged over factors Slope, #Doses, Effect size, and projected Power, for the nominal Sizes and Powers indicated.^*

Model	Test	Nominal Size = 0.05	Nominal Power = 0.8	Nominal Power = 0.9
Logistic	t	0.047 (0.045, 0.049)	0.834 (0.830, 0.837)	0.919 (0.915, 0.922)
	t*	0.043 (0.041, 0.046)	0.831 (0.827, 0.835)	0.916 (0.912, 0.920)
	Wald	0.049 (0.047, 0.051)	0.794 (0.790, 0.798)	0.903 (0.899, 0.907)
	Wald*	0.045 (0.043, 0.047)	0.780 (0.777, 0.784)	0.898 (0.894, 0.901)
	LR	0.057 (0.055, 0.059)	0.834 (0.831, 0.838)	0.920 (0.916, 0.924)
	LR*	0.051 (0.049, 0.053)	0.820 (0.817, 0.824)	0.914 (0.910, 0.917)
Probit	t	0.048 (0.046, 0.049)	0.832 (0.829, 0.835)	0.917 (0.914, 0.920)
	t*	0.042 (0.041, 0.044)	0.828 (0.825, 0.831)	0.915 (0.912, 0.918)
	Wald	0.052 (0.050, 0.053)	0.807 (0.804, 0.810)	0.910 (0.907, 0.913)
	Wald*	0.046 (0.044, 0.047)	0.796 (0.793, 0.799)	0.903 (0.900, 0.906)
	LR	0.057 (0.055, 0.058)	0.830 (0.827, 0.833)	0.918 (0.915, 0.921)
	LR*	0.049 (0.048, 0.051)	0.817 (0.815, 0.820)	0.912 (0.909, 0.915)

^*First entry in each triplet is the average. Values in parentheses are upper and lower 95% confidence limits.

4. Discussion

The DRF, ρ, is an important measure of the efficacy of a putative radioprotective drug. As represented by the designs of the experiments simulated in Section 3, establishing efficacy of such a drug by demonstrating a statistically significant DRF is generally accomplished using 5–7 radiation doses with the lowest dose giving mortality near 0% and the highest dose giving mortality near 100% (Singh et al., 2005). Since the promulgation of the New Animal Rule (FDA, 2002), it is imperative that these efficacy determinations be robust because the final tests are done only in animals; human efficacy studies are not ethical or feasible. Generally, an initial efficacy study at the LD₅₀ radiation dose for a given species is done prior to a full dose-response study, with efficacy determined by log-rank survival analysis. In addition to establishing initial efficacy of a radioprotectant drug, this study is used to set the radiation doses for specific lethality targets in the dose-response study. Because there does not appear to be a readily available formula for determining sample sizes for LD₅₀ comparative dose-response studies of efficacy, this investigation was undertaken to derive such a formula. The results of the Monte Carlo simulation study conducted to evaluate size and power showed that the derived formula (14) gave correct sample sizes under the usual conditions of linearity and parallelism. Considering that the initial DRF studies provide a fairly good profile of the survival-efficacy pattern of a candidate radioprotectant drug, a single DRF comparative dose-response study with the number of animals calculated by (14) should be sufficient to satisfy the robustness required by the FDA. If, on the other hand, divergence is observed between the initial efficacy studies and the subsequent DRF comparative study, the latter may need to be repeated. Given that the derived sample sizes tended to be smaller than those customarily used in classical LD₅₀ comparisons, use of the sample-size formula can contribute to the goal of reducing the number of animals used for experimentation in lethality studies of efficacy.

Several approximations and simplifying assumptions have led to a closed-form solution for the sample size that can be easily used by statisticians and radiobiologists alike, without having to implement specialized software. These approximations and assumptions have led to very little cost in accuracy, as is borne out by the simulation study results. As mentioned in Section 2, the central t approximation to the noncentral t distribution works very well for the power range of common interest, 80% and higher. However, in order not to depend on this approximation to the exact power, one could calculate a sample size from (10) based on inverting the non-central t distribution; alternatively, one could verify the power associated with the sample size calculated from (14) with a small simulation study. The assumption that the “regression” component of expression (13) could be ignored in the sample-size derivation was confirmed by the reported power simulations as well as by a small comparison of powers with and without the term (results not included). In the Monte Carlo study, the unmodified and modified groups being compared were simulated to have comparable lethalities at corresponding dose levels, consistent with the latter assumption. Additional evaluation of the sample-size formula for different sets of lethality targets, both between and within treatments, is planned. Meanwhile, the formula can be used confidently when conditions like those simulated are expected to prevail. Expression (14) is not restricted to lethality studies, but applies to any quantal-response assay conducted to compare two treatments. It can be used even when the underlying slope is unknown, simply by specifying the desired size of the effect to be detected in standard-deviation units. The t-statistic (9) may also be used to determine sample sizes for estimating DRFs with specified precision as is shown in Web-based Appendix B.

The sample-size formula was evaluated on the basis of two models and six statistical tests. Although the derived sample sizes gave adequate powers in most cases, there were some exceptions for specific tests. Most notably, the Wald and Wald* tests exhibited powers substantially below the targeted level for sample sizes of 2 and 3 in the 7-dose case, and the LR and LR* tests showed powers moderately below nominal. However, these tests are asymptotic tests, and should not necessarily be expected to perform well for such small sample sizes. Moreover, the sample sizes were not derived in consideration of alternatives for the Wald and LR tests, but rather for the t-test, which performed well even for such small samples. These results suggest that if samples sizes of 2 or 3 are derived from the t-test-based formula for use with either the Wald or LR test, then imposing a minimum sample size of, say, 3 or 4 per group may be prudent. That is, just as care should be taken not to use too many animals in lethality studies, care should also be taken not to use too few animals. On the other hand, the results indicate that sample sizes derived from (14), even small sample sizes, can be used with confidence in designing experiments as long as the corresponding t-test is used for analysis.

There was little difference between the logistic and probit models, indicating that either can be used with confidence in conjunction with the sample-size formula. Of course, one would use the probit slope and weights when designing a study for probit analysis and the logit slope and weights when designing a study for logit analysis. The popular and powerful LR test exhibited slight, but consistent, anti-conservatism. The version of that test applied to adjusted 0–1 responses, LR*, appeared to control size better without sacrificing nominal power. The t test appeared to have the best performance overall, maintaining size at or below the nominal 5% level on average, while achieving power rivaling the LR test in most cases, and exceeding it for small sample sizes.

For completeness, it is noted that Hsieh, Bloch and Larsen (1998) present a formula for determining the sample size needed for testing the significance of a binary independent variable in a logistic regression model with one or more covariates. They show it to be competitive with a related formula developed previously from the work of Whittemore (1981) and implemented in SSIZE (Hsieh, 1991) and nQuery (Elashoff, 1996). To adapt the formula of Hsieh et al. (1998) to the present setting as closely as possible, consider the treatment, U or M, as a binary independent variable and log₁₀-dose as a single covariate (common slope). Based on representative lethality proportions for the two treatments calculated at the average value of log₁₀-dose over all groups of both treatments, PASS (Power Analysis and Sample Size system) (Hintze, 2005) was used to implement Hsieh’s formula to derive a total sample size to be divided equally among either 5 or 7 dose groups per treatment in the steep-slope scenarios of the simulation study of Section 3. For 90% power in a one-sided 5% test, PASS gave total sample sizes of 61 and 32 for ρ = 1.1 and 1.16, respectively, for a 5-dose experiment. Dividing by ten and raising the result to the next highest integer gives 7 and 4 animals per dose group, respectively, which may be compared to the values of 11 and 5 derived from this paper’s formula (14) (Figure 2a). In a similar calculation for a 7-dose experiment, sample sizes from PASS were adjusted upward to 5 and 3 per dose group, respectively, for detecting ρ = 1.1 and 1.16 with 90% power. These numbers may be compared to the values of 7 and 3 derived from formula (14) (Figure 3a). The formula of Hsieh et al. (1998) is not designed to take into account the lethality-targeting, discrete-dose nature of the comparative potency experimental design, and thus should not necessarily be expected to provide adequate sample sizes for the present setting. However, as the number of dose groups increases, there may be a tendency for formula (14) to give smaller sample sizes that approach those from Hsieh’s formula, in which case the latter formula might be a viable alternative to (14).