Determining under- and oversampling of individual particle distributions in microfluidic electrophoresis with orthogonal laser-induced fluorescence detection

Abstract

This report investigates the effects of sample size on the separation and analysis of individual biological particles using microfluidic devices equipped with an orthogonal LIF detector. A detection limit of 17 ± 1 molecules of fluorophore is obtained using this orthogonal LIF detector under a constant flow of fluorescein, which is a significant improvement over epifluorescence, the most common LIF detection scheme used with microfluidic devices. Mitochondria from rat liver tissue and cultured 143B osteosarcoma cells are used as model biological particles. Quantile–quantile (q–q) plots were used to investigate changes in the distributions. When the number of detected mitochondrial events became too large (>72 for rat liver and >98 for 143B mitochondria), oversampling occurs. Statistical overlap theory is used to suggest that the cause of oversampling is that separation power of the microfluidic device presented is not enough to adequately separate large numbers of individual mitochondrial events. Fortunately, q–q plots make it possible to identify and exclude these distributions from data analysis. Additionally, when the number of detected events became too small (<55 for rat liver and <81 for 143B mitochondria) there were not enough events to obtain a statistically relevant mobility distribution, but these distributions can be combined to obtain a statistically relevant electrophoretic mobility distribution.

1 Introduction

The analysis of individual subcellular particles is an important area of study to help elucidate the more complex function of cells, and microfluidic devices appear to be an ideally suited technique for this purpose due to their ability to handle, manipulate, and analyze small volumes and their very short analysis times. Historically speaking, flow cytometry was the first technique to analyze individual subcellular particles [1], so it is not surprising that many of the first analyses of large populations of individual microparticles [2–7], cells [8, 9], and subcellular particles [10] on microfluidic devices also used flow cytometry. Electrophoretic separation schemes have also been used since the first glass microfluidic devices were described by Manz et al. [11] and Harrison et al. [12, 13] and they continue to be quite popular due to ease of application. IEF [14] and electrophoresis [15] on microfluidic devices have been used to determine mitochondrial pI and electrophoretic mobility, respectively, both of which can be used to evaluate differences in the surface characteristics of biological particles [14, 16]. Of these analysis schemes presented, only electrophoresis allows for the analysis of individual subcellular particles and separation of the particles based on their surface chemistry.

Mitochondria are usually the foremost sample for initial subcellular particle analyses because of their importance to cellular function and health as well as their abundance within the cell. Previous reports by this laboratory have suggested that the number of detected particles and interactions with the fused silica surface play a critical role in the electrophoretic mobility distributions of mitochondria in CE [17]. It is reasonable to assume that separations of mitochondria on glass microfluidic devices will behave in a similar fashion.

Due to the small amount of detectable analyte in most biological particles, detection schemes like LIF are required because of their high sensitivity and ability to detect ymol quantities of fluorophores [18, 19]. LIF was used in the first microfluidic devices [11–13] because its power as a detection scheme made it an ideal match for the small sample quantities and, typically, pL-sized detection volumes. Ocvirk et al. [20] later pioneered the use of epifluorescence in microfluidics, which focuses the laser and collects the fluorescence through the same objective, and achieved a zmol LOD. Epifluorescence quickly became very popular because of the simplicity of the epifluorescence design and the availability of commercial microscopes designed with epifluorescence capability. Currently, it is quite common to find microfluidic epifluorescence with LODs of zmol or better [21–24]. However, these detectors may not be fully adequate in mitochondrial analyses in which there are a significant number of events occurring very close to the LOD [25, 26]. Improved LIF detectors, with LODs similar to CE with post-column sheath flow LIF, should be used when analyzing isolated individual mitochondrial events via LIF. Fu et al. [27] reported an improved detector in which the laser focusing objective and collection objective are in an orthogonal arrangement, producing less laser light scattering than epifluorescence. This report utilizes a similar orthogonal arrangement to obtain LODs superior to those obtained utilizing epifluorescence.

Estimation of LOD values has been based on either fixed injections or continuous delivery of known amounts of a fluorophore to the LIF detector [20]. The latter is a more accurate description of a detector’s ability to analyze particles because it represents how many fluorophores need to be present within the detector volume to obtain a detectable signal. This stems from the fact that the fluorophores are bound and do not diffuse away from the body of the particle, causing the particles become “packets” of fluorophores that travel through the detector. An LOD determination based upon a fixed injection of a known amount of a fluorophore is less suitable for particle analysis because the fluorophore undergoes diffusional broadening, forming a zone much wider than the detector’s width.

This report analyzes the mitochondrial mobility distributions obtained on a commercially available glass microfluidic device for their dependence on the number of detected events. Quantile–quantile (q–q) plots were used to identify unbiased distributions and those associated with under- and oversampling. The two types of mitochondria chosen for analysis in this report were isolated from rat liver tissue and cultured 143B cells, an osteosarcoma cell line. Rat liver mitochondria were chosen because they represent a difficult separation in CE due to their high degree of adsorption to the fused-silica surface [28], while mitochondria from 143B cells were chosen because the dependence of their electrophoretic mobility distribution on sample size has not yet been studied.

2 Materials and methods

2.1 Microfluidic devices

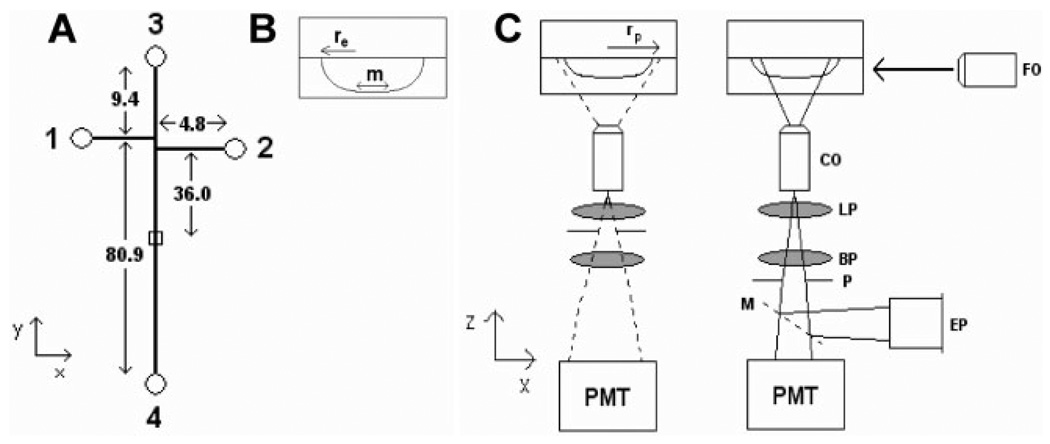
Glass microfluidic chips were purchased from Micralyne (MC-BF4-TT100, Edmonton, Alberta, Canada). The chips contained 20 µm deep and 50 µm wide channels (i.e., 10 µm mask width with a 20 µm chemical etch) with a 100 µm Twin-T injection scheme (Fig. 1). Sample and sample waste reservoirs (reservoirs 1 and 2, respectively) were 4.8 mm from the Twin-T. Buffer and buffer waste reservoirs (reservoirs 3 and 4, respectively) were 9.4 and 80.9 mm from the Twin-T, respectively. The detection zone was 36.0 mm from the Twin-T. The tops of plastic disposable pipette tips were glued to the reservoirs using Loctite quick set epoxy (Avon, OH) to increase the reservoir capacity to roughly 250 µL.

Figure 1.

Schematic diagram of microfluidic devices and orthogonal fluorescence detection scheme. (A) 1, 2, 3, and 4 represent the sample, sample waste, buffer, and buffer waste reservoirs, respectively, with a detection zone 36.0 mm from the channel intersection. All distances are given in mm. (B) Channel dimensions as defined by the etch depth (r_e = 20 µm) and the mask width (m = 10 µm). (C) Laser light is focused onto the microfluidic device with a 6.3× objective (FO), fluorescence is collected with a 60× long working distance objective (CO), passed through a 505 nm long pass filter (LP), a 535 ± 17 nm bandbass filter (BP), and a pinhole (P) before being detected by the photo-multiplier tube (PMT). The pinhole produces a collection zone (r_p) defined by the position of the pinhole in the detector. Alternately, a mirror (M) could redirect the fluorescence to an eyepiece (EP) for rough alignment. The pinhole is placed at either 47 or 66 mm from the back of the collection objective so that light is collected from a zone on the device with a radius of either 27.8 or 19.8 µm.

2.2 Orthogonal LIF detection

A homebuilt microfluidics instrument was used with an orthogonal detection scheme (Fig. 1C). The detector collected fluorescence with a 60× long working distance objective (MO-0060LWD, Universe Kogaku America, Oyster Bay, NY), and filtered it through a 505 nm long pass filter (505 AELP) to minimize scattering and a 535 ± 17 nm bandpass filter (535DF35) to select the desired wavelength (Omega Optical, Brattleboro, VT). The collection objective was imaged onto a 980 µm diameter pinhole placed inside the detector either 47.0 or 66.0 mm from the collection objective, and since the pinhole was not placed 160 mm from the collection objective, this resulted in an effective magnification of 18× and 25× and detection zones with a calculated radius of 27.8 or 19.8 µm (r_p), respectively. A mirror reflected the image from the collection objective to a 10× eyepiece (04 EHR 004, Melles Griot, Irvine, CA) to allow a rough alignment of the detector onto the microfluidic device. The pinhole was not in place during the rough alignment. During data collection, a photomultiplayer tube (PMT; R1477, Hamamatsu, Hamamatsu City, Japan) biased at 1000 V was used to collect the signal. Two translational stages (423 series, Newport, Irvine, CA) allowed the detector to be manipulated along the x- and z-axes.

Microfluidic chips were suspended above the detector by a plastic stage. The 488 nm line from an air-cooled Arion laser (2211-20SL, JDS Uniphase, Milpitas, CA) was brought in from the side of the chip and detection occurred underneath the chip. The laser was focused through a 2.0 mm pinhole and 6.3× objective (04OAS008, Melles Griot) onto the detection zone within the chip. The focusing objective was placed on a translational stage and a multiaxis lens positioner (P100-A, Newport) to allow for fine manipulation of the laser beam size and location on the y- and z-axes.

2.3 Data analysis

Output from the PMT was electronically filtered (RC = 0.01 s) and digitized at 200 Hz using a PCI-6034E data acquisition card from National Instruments operated by Labview 5.1 software. The data were stored in a binary format and analyzed via Igor Pro software (Wavemetrics, Lake Oswego, OR). First, a four-point binomial smoothing algorithm available in Igor Pro was used to smooth out the noise present in the data. Then, in-house written Igor Pro procedures were used to select peaks whose height exceeded a threshold of five times the SD of the baseline noise. Igor Pro then tabulated the migration time, peak height, and peak width (at 10% of the peak height) for the selected peaks. The integrals used to find the detection volumes were performed by Mathematica 5.2 software (Wolfram, Champaign, IL).

2.4 Reagents

Poly(vinyl alcohol) (PVA), 99% hydrolyzed and MW 31–50 kDa, and HEPES were purchased from Aldrich (Milwaukee, WI). EDTA, minimum essential medium Eagle modified, and d-mannitol along with CE-grade sucrose were from Sigma (St. Louis, MO). Fluorescein, and 10-N-nonyl acridine orange (NAO) were from Invitrogen (Eugene, OR). Electrophoresis grade sodium tetraborate was from EM Science (Gibbstown, NJ). Reagent grade potassium hydroxide, sodium hydroxide, methanol, and hydrochloric acid along with CE grade SDS were obtained from Mallinkrodt (Paris, KT). DMSO was purchased from Burdick&Jackson (Muskegon, MI). Ethanol (95%) was from Pharmco (Brookfield, CT). Borate/SDS buffer was made with 10 mM borate and 10 mM SDS adjusted to pH 9.4 with sodium hydroxide. PVA dynamic coating buffer was made by dissolving 0.2% w/w PVA at 60°C (to speed dissolution) into a solution of 10 mM HEPES and 250 mM sucrose adjusted to pH 7.4 with potassium hydroxide. Mitochondria isolation buffer was 210 mM d-mannitol, 70 mM sucrose, 5 mM EDTA, 5 mM HEPES, and pH 7.4 adjusted with potassium hydroxide. All buffers were made with deionized water filtered through a 0.2 µm filter. Stock solutions of 1 mM fluorescein and NAO were made in ethanol and DMSO, respectively, and stored at −20°C. Samples from these stocks were serially diluted in PVA buffer immediately prior to use.

2.5 Mitochondrial preparation

Rat liver cells were obtained from surgically removed and homogenized livers of Fischer 344 rats and suspended in mitochondria isolation buffer. 143B cells, a bone marrow osteosarcoma cell line, were cultured at 37°C and 5%CO₂ in 90% α-modified minimum essential medium (Eagle) with 10% fetal bovine serum. Biosafety level 1 was observed at all times. Prior to isolation, the 143B cell suspension was enriched by pelleting at 600× g for 10 min and resuspending in mitochondria isolation buffer. A differential centrifugation protocol based on procedures from Howell et al. [29] and Bogenhagen and Clayton [30] was followed to isolate mitochondria of both types from cellular suspension in mitochondria isolation buffer. Briefly, cells were washed three times with cold mitochondria isolation buffer and counted using a Fuchs–Rosenthal hemocytometer (Hausser Scientific, Horsham, PA). Cell disruption was 100% by using 30 strokes in a Potter–Elvehjem homogenizer with a clearance of 0.004–0.006 inches (Kontes, Dusseldorf, Germany). Nuclei and large cell debris were pelleted and removed from the suspension by centrifugation at 1400× g for 5 min and discarding the pellet. This centrifugation step was repeated three times. The remaining mitochondrial fraction was then frozen and stored in liquid nitrogen as described previously [28].

All mitochondrial samples were removed from liquid nitrogen and placed in a −20°C freezer for 5 min before being thawed out at room temperature and then stored on ice. The samples were prepared for CE analysis by pelleting out debris caused by the freeze–thaw process at 600× g for 6 min. The supernatant was removed, stored on ice, and incubated in 10 µM NAO, a fluorescent mitochondrion-selective probe [31], for 10 min. The mitochondrial suspension was then washed with PVA buffer by pelleting the mitochondria twice at 16 100× g for 10 min and resuspending in PVA buffer.

2.6 Microfluidic preparation

The microfluidic devices were prepared by attaching a house vacuum line to the reservoir 4 and filling the other reservoirs with conditioning solutions as follows: 0.5 M potassium hydroxide for 30 min, water for 15 min, and PVA buffer for 15 min. After conditioning, PVA buffer was placed in reservoirs 3 and 4, the mitochondrial suspension in reservoir 1, and 1 nM fluorescein in reservoir 2. The size of the laser beam was adjusted to ~75 µm by redirecting the collected light to an eyepiece with a mirror and visually comparing the width of the laser to the channel width through the eyepiece with the pinhole removed (Fig. 1C). Alignment was performed using a −400 V/cm electric field to create a continuous flow of 1 nM fluorescein. The positions of the detector and focusing objective were adjusted until the maximal fluorescence response was obtained using the PMT.

2.7 Microfluidic electrophoresis

Mitochondrial separations were carried out in PVA buffer with a −400 V/cm electric field between reservoirs 3 and 4 and a pullback voltage of −225 V at reservoirs 1 and 2 to prevent leakage into the separation channel. Injections were performed with a −400 V/cm electric field between reservoirs 1 and 2 for 20 s and holding reservoirs 3 and 4 at ground. EOF was measured using fluorescein as a reference. The electrophoretic mobility of fluorescein was obtained via CE (µ_CE = −2.8 × 10⁻⁴ cm²V⁻¹s⁻¹) using PVA buffer and compared to the apparent electrophoretic mobility obtained in the microfluidic devices (µ_T).

$$\text{EOF}={\mathrm{\mu }}_{\mathrm{T}}-{\mathrm{\mu }}_{\text{CE}}$$ (1)

The actual electrophoretic mobility (µ_p) of a mitochondrial event can then be obtained by adjusting its apparent mobility to account for the EOP.

$${\mathrm{\mu }}_{\mathrm{p}}={\mathrm{\mu }}_{\mathrm{T}}-\text{EOF}$$ (2)

Electric potentials were generated by Glassman high voltage power supplies (PS/MJ30N0400-11, High Bridge, NJ), delivered to the reservoirs by platinum wire electrodes, and controlled by a Labview 5.1 program written in-house through a PCI-6713 card (National Instruments, Austin, TX). A series of electronic relays (S05LTA345, Kilovac, Santa Barbara, CA) were used to switch the state of the electrodes between the separation and injection conditions described above, and were automated using the same Labview 5.1 program.

The reproducibility of the detector was evaluated with multiple injections of 0.5 µm latex microspheres (Invitrogen). The RSD of the microsphere peak heights was 15%, which is comparable to data obtained by other groups analyzing microspheres on microfluidic devices [15].

3 Results and discussion

3.1 Detection volume

The detection volume is an intersection of the laser beam, the detection zone, and the channel (Fig. 1C). Though the detection zone is actually a cone, assuming that the change in its radius is insignificant across the channel allows the zone to be approximated as a cylinder. Keeping the laser beam diameter large (~75 µm) allows the assumption that the entire detection volume is illuminated. The detection volume (V_D) can then be defined by the intersection of the detection zone and the channel

$$V_{\mathrm{D}}=4\left(r_{\mathrm{e}}{\displaystyle \underset{0}{\overset{m/2}{\int }}\sqrt{r_{\mathrm{p}}^2-x^2}\mathit{\text{dx}}+{\displaystyle \underset{m/2}{\overset{r_{\mathrm{p}}}{\int }}\sqrt{r_p^2-x^2}\sqrt{r_{\mathrm{e}}^2-{(x-\frac{m}{2})}^2}\mathit{\text{dx}}}}\right)$$ (3)

where r_p is the radius of the detection zone, r_e is the radius of the channel sides defined by the etch depth (20 µm), and m is the width of the mask used during the photolithography stage of creating the device (10 µm). The solution to Eq. (3) is 22.8 and 33.5 pL when the detection zone has a radius of 19.8 and 27.8 µm, respectively. A detailed derivation of Eq. (3) is given in the Supporting Information for this manuscript.

3.2 LOD

The method described by Ocvirk et al. [20] was used to determine the mass LOD of this orthognal LIF system. Briefly, a solution containing 1 nM fluorescein is continuously introduced into the separation channel. The increase in the baseline caused by the fluorescein (the signal) was divided by the SD of the baseline before the fluorescein was introduced into the separation channel (the noise). Since the detection volume can be calculated using Eq. (3), it is possible to back calculate the number of fluorescein molecules that are necessary to generate an S/N of 3, which is taken as the LOD.

Table 1 shows that the best fluorescein LOD obtained with this microfluidic device was 17 ± 1 molecules using multiple, sequential LOD determinations with 10⁻⁹ M fluorescein in borate-SDS running buffer. A t-test shows us that there is no statistical difference in LODs when the concentration of fluorescein is 5 × 10⁻¹¹ M (p = 0.05). PVA buffer was also tested since it is the buffer of choice for mitochondrial analysis, and an LOD of 59 ± 7 molecules was obtained. Increasing the detection zone to include the channel walls (27.8 µm) caused the LOD to worsen by about a factor of three. This is most likely due to increased laser scattering at the curved sides of the channel wall and the decrease in the effective numerical aperture, which results from positioning the objective farther away from the detection volume to obtain a detection zone radius of 27.8 µm (cf. Section 2.2).

Table 1.

LIF LOD on microfluidic devices^a)

	n	Pinhole image (µm)	Fluorescein (M)	LOD (ymol)	SD	RSD (%)	Molecular LOD
Borate/SDS	6	19.8	1 × 10−9	27.9	1.9	7	17
Borate/SDS	5	19.8	5 × 10−11	32.3	4.8	15	19
PVA	5	19.8	1 × 10−9	97.8	12	12	59
Borate/SDS	5	27.8	1 × 10−9	86.9	9.3	11	52

^a)n is the number of multiple, sequential LOD determinations.

While this is the lowest mass LOD reported for a microfluidic device, the authors recognize that Fu et al. [27] developed a superior detection scheme. Briefly, Fu et al. found that the optimal configuration involved introducing the laser along the flat portion of the channel wall, and adjusting the angle of their detector to be both orthogonal and 45° off axis. In Fig. 1, this would correspond to introducing the laser above the chip along the z-axis and placing the detector on the xy-plane at a 45° angle to both the x- and y-axes. A 14 molecule LOD can be calculated using estimates from their report, which is better than the LOD reported here. Unfortunately, their detector required the manufacture of special microfluidic devices, and cannot be used on commercially obtained microfluidic devices, such as the devices from Micralyne (http://www.micralyne.com/markets/lifesciences.html).

3.3 Identifying sampling effects on mitochondrial distributions

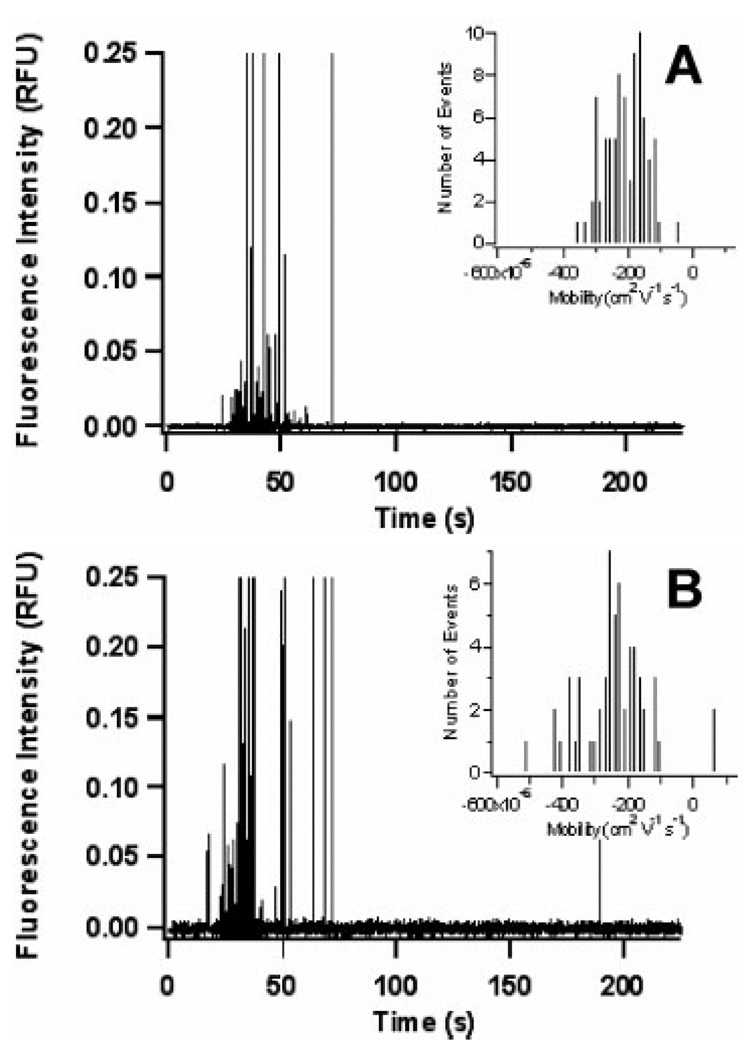
Electropherograms of individual mitochondria are presented in Fig. 2, which resembles the electropherograms of individual mitochondrial previously obtained on CE [17, 28] and microfluidic devices [15]. In order to prevent unwanted adsorption to the glass microfluidic device, a buffer containing 0.2% w/w PVA was used. This PVA dynamic coating has allowed for separation of mitochondria on both capillaries [17] and glass microchips [15]. In addition, this coating reduces strong adsorption of mitochondria, thereby reducing the number of events that were the result of carryover from a previous sample. The carryover in rat liver and 143B mitochondria was determined to be 7 ± 6 and 4 ± 5 events, respectively, which translates into 7.5 ± 3.9% and 5.4 ± 5.8% carryover. A complete description of carryover analysis is provided in the Supporting Information.

Figure 2.

Electropherogram of mitochondrial events separated on a glass microfluidic device with PVA dynamic coating buffer. (A) 55 rat liver mitochondrial events and (B) 82 143B mitochondrial events. Insets are a histogram of the electrophoretic mobilities of the events in each figure

As reported previously, there is a large variation in fluorescence intensities (cf. Fig. 2), which is due to the size heterogeneity of mitochondrial particles and the presence of some mitochondrial fragments and aggregates in the sample [32]. Fortunately, particles that are similar in size to mitochondria have been shown to have electrophoretic mobilities independent of size [33].

While the electrophoretic mobility histograms also appear similar to the previous CE reports [17, 28], it can be difficult to make a detailed comparison of a large number of distributions using histograms, particularly when these distributions cannot be easily mathematically described. Thus, a better method for comparing mobility distributions was developed for this purpose. q–q plots are a very effective means of comparing the differences in location, shape, and skew of a large number of electrophoretic mobility distributions [17]. A quantile is defined as the value at a given fraction of a distribution (i.e., the 0.5 quantile is the median). A q–q plot is generated by plotting the mobility quantiles of a distribution of interest as the y-axis data with the corresponding quantiles from a reference distribution as the x-axis data [17]. The resulting data points are displayed with a 45° line of identity that bisects the graph. This line of identity graphically represents the reference distribution. Thus, if a distribution of interest is similar to the reference distribution, the data points will fall along the line of identity. Deviations from the line of identity correspond to differences between the distribution of interest and the reference distribution.

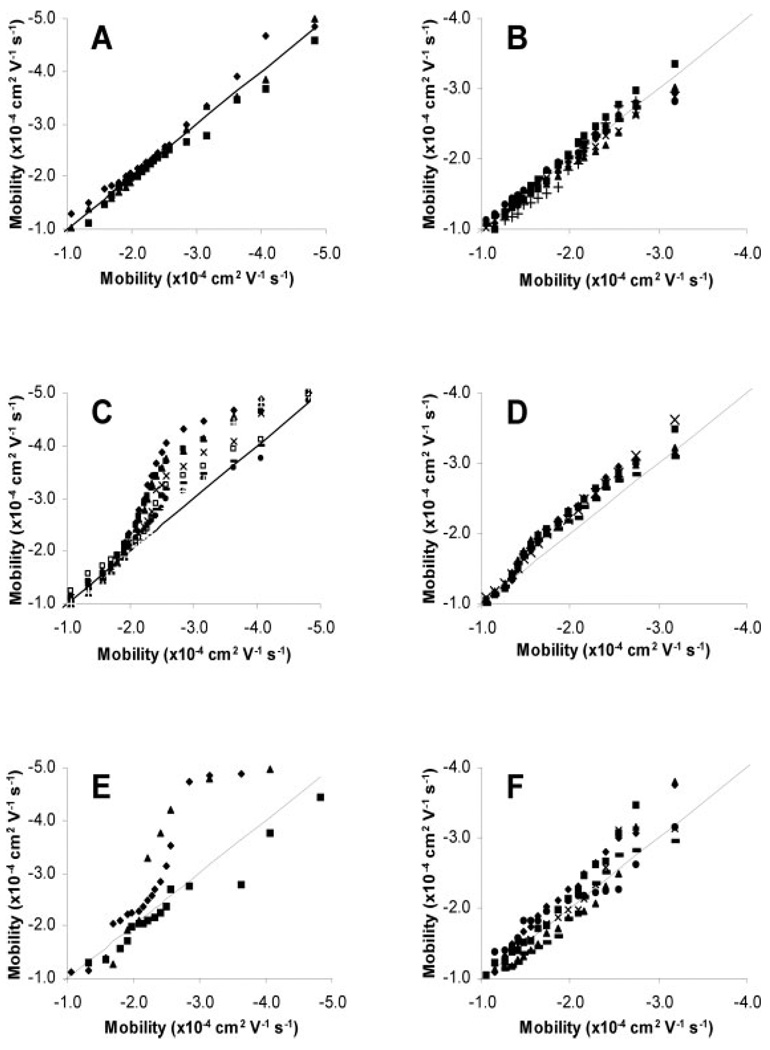
Figure 3 is a series of q–q plots showing how the mobility distributions appear significantly altered as the number of detected events changes when compared to a reference distribution that is the average of all the distributions whose mobilities are unbiased by sample size. Figures 3A and B show that unbiased distributions produce q–q plots very close to the line of identity, indicating little difference between the distributions. When the number of detected events becomes too large, the distributions take on a characteristic shape (Figs. 3C and D). This condition is called oversampling and the threshold above which this occurs is the oversampling threshold (N_OT). Likewise, when the number of detected events becomes too small, the distributions become much more erratic than the unbiased distributions (Figs. 3E and F). This condition is called undersampling and the threshold below which this occurs is the undersampling threshold (N_UT). Such comparisons using histograms would be cumbersome and extremely difficult to do with accuracy, showing the power of the q–q plot.

Figure 3.

q–q plots of mitochondrial distributions versus the average of the quantiles from the unbiased distributions. (A) Unbiased rat liver, (B) unbiased 143B, (C) oversampled rat liver, (D) oversampled 143B, (E) undersampled rat liver, and (F) undersampled 143B.

In oversampled distributions, early events (i.e., events with less negative mobilities) are tightly grouped around the line of identity, while later events are skewed above the line of identity (Figs. 3C and D). A distribution can be identified as oversampled if its later quantiles show a significant deviation from the line of identity. The N_OT will be defined by the last distribution whose 0.75 quantile is within 1.5 SDs of the averaged, unbiased 0.75 quantiles (Table 2). By this definition, the N_OT is 72 and 98 for rat liver and 143B mitochondria, respectively.

Table 2.

Average mobility quantiles for unbiased, undersampled, and oversampled distributions^a)

	Rat liver							143B
	nb)	0.25 Quantile		0.50 Quantile		0.75 Quantile		nb)	0.25 Quantile		0.50 Quantile		0.75 Quantile
		Mean	SD	Mean	SD	Mean	SD		Mean	SD	Mean	SD	Mean	SD
Unbiased	3	−1.80	0.09	−2.23	0.07	−2.57	0.06	6	−1.35	0.06	−1.74	0.08	−2.29	0.12
Undersampled	3	−1.75	0.30	−2.61	0.60	−3.47	0.76	6	−1.34	0.14	−1.78	0.19	−2.38	0.23
Oversampled	8	−1.84	0.12	−2.57	0.28	−3.40	0.42	5	−1.41	0.04	−2.03	0.04	−2.58	0.06
CE	5	−1.97	0.09	−2.25	0.06	−2.48	0.10

^a)All mobility data are × 10⁻⁴ cm²V⁻¹s⁻¹.

^b)n is the number of multiple, sequential injections of individual mitochondria samples.

Undersampling occurs when there are not enough events to statistically recreate the true mobility distribution from the data [17]. Undersampled distributions are characterized by large SDs in the quantiles and abnormally broad distributions, which are represented on a q–q plot as highly erratic quantile behavior. Figures 3E and F present the q–q plots of undersampled distributions, and indeed their quantiles appear higly erratic compared to the larger, unbiased distributions (Figs. 3A and B). Additionally, Table 2 shows large differences in the SDs of the 0.25, 0.50, and 0.75 quantiles from undersampled distributions. An F-test shows that the variances for these quantiles are significantly different from the unbiased distributions (p = 0.10), further supporting the claim that these distributions are undersampled. In this study, the N_UT is 55 and 81 for rat liver and 143B mitochondria, respectively.

3.4 Oversampling

The most likely explanation for oversampling is insufficient separating power. Since electrophoretic mobility is inversely proportional to time, a small change in time represents a large range of electrophoretic mobilities early in an electropherogram and a smaller range of electrophoretic mobilities later in the electropherogram. Therefore, events will first start to overlap during early portions of the electropherogram. If the overlapping becomes so severe that two or more events appear as only one peak, then the data analysis program will consider this multiple component peak to be a single event. When multiple component peaks occur early in the electropherogram, the actual number of events will be undercounted and the distributions will be underrepresented at more negative electrophoretic mobilities (i.e., early migration times). This will be characterized by the later quantiles in a q–q plot being skewed above the line of identity. Table 2 shows that the 0.50 and 0.75 quantiles are significantly skewed when the number of detected events exceeds the N_OT. The deviation from the line of identity is also expected to get larger as the number of detected events increases since the number of multiple component peaks also increases. This effect is clearly shown in Fig. 3C, though it is also occurring in Fig. 3D despite being difficult to observe visually.

Davis and Giddings [34–36] developed a means to calculate the probability that a peak in chromatography is the result of more than one component, called statistical overlap theory (SOT). This theory was later adopted for CE by Ahmadzadeh et al. [37] and utilized to evaluate the peak overlap in an electropherogram of latex microparticles. The basis of SOT centers around the following equation [35]:

$$n=\overline{m}{\mathrm{e}}^{-\mathrm{\alpha }}$$ (4)

where n is the number of observed peaks, m̄ is the expected number of events/particles, and α is the saturation factor of the electropherogram. e^−α defines the probability that the peak from one event will not overlap with the peak from the next event. α is defined as:

$$\mathrm{\alpha }=\frac{\overline{m}}{n_{\mathrm{c}}}$$ (5)

where n_c is the peak capacity of the electropherogram, which is defined as the maximum number of peaks that could be resolved in an electropherogram. n_c can be calculated using

$$n_{\mathrm{c}}=\frac{X}{x_0}$$ (6)

where x₀ is the minimum amount of space on the electropherogram needed to resolve a peak and X is the total amount of space in the electropherogram. Given the definition of e^−α the probability that a peak from one event will not overlap with either the event before it or the event after it is given by [37]

$$p_{\text{SCP}}=({\mathrm{e}}^{-\mathrm{\alpha }})({\mathrm{e}}^{-\mathrm{\alpha }})={\mathrm{e}}^{-2\mathrm{\alpha }}$$ (7)

where p_SCP is the probability that any one peak is the result of a single component, or event. The number of single component peaks is then given by

$$n_{\text{SCP}}=\overline{m}{\mathrm{e}}^{-2\mathrm{\alpha }}$$ (8)

Equations (4)–(8) show that as the number of particles separated via CE increases, the probability of two peaks overlapping also increases. While a few overlapping events may be tolerable, if the number of overlapping events becomes too large it can significantly affect the characteristics of the distribution.

Unfortunately, SOT assumes that the distribution of events is random [35, 36], and as Fig. 2 suggests, the distribution of events is not random throughout the electropherogram. However, it should be possible to assume that the distribution of events is random within a small portion of the electropherogram, if that portion is sufficiently small. A 2-s window around the median mobility should be small enough to consider the distribution of events as random while keeping the number of detected events large. For example, rat liver mitochondria, whose average median mobility is −2.28 × 10⁻⁴ cm²V⁻¹s⁻¹, will have a window from 33.63 to 35.63 s. Averaging the number of events unbiased distributions have within this 2-s window shows that 17 ± 2% and 9 ± 2% of the total number of events occur within this window for unbiased rat liver and 143B mitochondria samples, respectively. Therefore, a distribution with 67 events, such as the one presented in Fig. 2A, is expected to have ten events within the 2 s window.

The value of x₀ was determined to be equal to the smallest peak widths regularly observed in these experiments, which was 0.030 ms. In nearly every case, peaks with a peak width of 0.030 ms were barely observable as an individual peak from a neighboring peak, suggesting that if the peak maxima are not separated by at least 0.030 ms they will appear as a single peak.

Using the SOT procedure developed previously [37], the probability that any individual peak will actually be composed of multiple events in the 2 s window is 28% (three overlapping peaks) and 24% (two overlapping peaks) when the number of events equals the N_OT for rat liver and 143B mitochondria, respectively. Considering that this is only a 2 s portion of the electropherogram, this shows that the number of multiple component peaks is a major concern in analysis of individual mitochondrial events in microfluidic devices.

There are four suggestions for overcoming oversampling in microfluidic devices. First, increase the separation distance, which would, unfortunately, increase analysis time. Second, use a narrow slit instead of a pinhole. Peak width is defined by the time a particle takes to travel through the detection zone. A slit could be designed to block most of the scattering from the channel walls, include most of the channel cross-section, and minimize the time a particle spends in the detection zone. Alternately, a cylindrical lens could be used to achieve the same effect as a slit, similar to the work described by Huang et al. [38]. Decreasing the time in the detection zone by increasing the separation voltage is not a good alternative. Mouse liver mitochondria undergo significant electroporation in the presence of an 8 kV/cm pulse that lasts only a few milliseconds [39], suggesting that to maintain mitochondrial membrane integrity in a constant electric field, like during electrophoresis, the voltage should be significantly smaller. Third, a cooled CCD camera could be utilized to help spatially separate mitochondrial events that may travel through the detection zone simultaneously but at different locations within the separation channel. Such a system would have significantly enhanced resolving power, reducing the number of overlapping peaks. Finally, oversampling could be overcome by splitting the sample into several parallel separation channels and detecting each channel individually, similar to the device created by Shen et al. [40].

3.5 Undersampling

The N_UT values obtained in these microfluidic experiments were 55 and 81 for rat liver and 143B mitochondria respectively, which is similar to the N_UT of 78 obtained on CE using rat liver and mouse liver mitochondria [17]. This similarity helps support the hypothesis that the N_UT is indeed statistical in origin. Additionally, the data here supports the previous claim that undersampling can be overcome if a minimum of 78 events is observed.

Our previous studies indicated that rat liver mitochondria undergo adsorption at the surface of the capillary in CE, even in the presence of a PVA dynamic coating [17], causing a significant alteration in electrophoretic mobility and an increase in the N_UT. Fortunately, neither the N_UT nor the mobility distributions appear to be significantly altered by any adsorption effects in microfluidic devices.

3.6 Unbiased distributions

Unbiased distributions obtained on microfluidic devices should show a strong correlation to unbiased distributions obtained on CE. Table 2 compares the average 0.25, 0.50, and 0.75 quantiles for the unbiased microfluidic distributions and CE distributions of rat liver mitochondria separated under identical conditions [28]. A t-test shows that these quantiles are not statistically different (p = 0.05), suggesting that microfluidic devices are comparable to CE for the determination of mitochondrial electrophoretic mobility distributions, if oversampling and undersampling can be avoided.

A major advantage of microfluidic devices is their short analysis times. Figure 2 shows a typical unbiased electropherogram for rat liver and 143B mitochondria, and it is apparent that a run time of 200 s should detect nearly all of the events. Using the same buffer conditions and electric field, a typical CE would take 30 min to complete the same analysis [28], representing a nine-fold improvement in analysis time.

Unfortunately, the range in which the number of detected events is unbiased for both rat liver and 143B mitochondria is very small (17 events). This may appear to be a troubling observation because it can be difficult to obtain an injection of mitochondria with an exact number of detected events. Fortunately, the shorter analysis times make it feasible to rapidly analyze a distribution and identify it as unbiased, undersampled, or oversampled. Oversampled distributions will need to be excluded from data analysis, but undersampled distributions can be combined with other undersampled distributions to create a distribution that statistically has enough events to recreate the distribution, as shown previously [17].

4 Concluding remarks

This report is the first evidence that a commercial microfluidic device with an orthogonal detection scheme compares well with capillary electrophoresis when analyzing individual mitochondrial particles. The nine-fold reduction in analysis time is one of the advantages of the microfluidic device over conventional capillary electrophoretic analyses.

Studying the effects of sample size on mitochondrial mobility distributions using q–q plots made it possible to identify a range of sample sizes where the mobility distributions are not biased by sampling effects. The undersampling thresholds obtained in this report were similar to the thresholds obtained previously for CE, supporting the hypothesis that the undersampling threshold is statistical in origin and not dependent on sample type or instrumentation. Oversampling was detected in this report and is expected to result from a lack of resolving power caused by the short separation distance in the microfluidic device. Calculations using statistical overlap theory support this hypothesis. Since oversampling causes underestimation of the number of mitochondrial events and skewed the electrophoretic mobility distributions, q–q plot analysis makes it possible to identify and exclude these distributions from the data analysis. When undersampled distributions are identified, they can be combined to create statistically relevant data. Ultimately, further development of microfluidic devices designed to avoid oversampling may prove useful to expand the current range between the undersampling and oversampling of the current microfluidic design.

Abbreviations

NAO

10-N-nonyl acridine orange

PMT

photo-multiplier tube

q–q

quantile–quantile

SOT

statistical overlap theory