Abstract
The brain-to-skull conductivity ratio (BSCR) is an important parameter in EEG source imaging and localization. Misspecification of this value may introduce localization errors in the estimation of brain electrical activity. However, the effect of this ratio has not been well understood despite many investigations. In the present study, we conducted a series of computer simulations to investigate the relationship between BSCR and EEG source localization accuracy. Furthermore, we have attempted to correlate the localization accuracy of epileptogenic regions with the BSCR in epilepsy patients. Our results indicate that the dipole localization errors ranged from 10 to 20 mm. The localization accuracy resulting when the conductivity ratio used in the inverse calculation was set at 20 was better than those resulting when the ratio was set at 80 in epilepsy patients with a deep tumor. Future work is needed to validate this finding by experimental investigations in a large patient population.
I. INTRODUCTION
The electroencephalogram (EEG) measures the scalp electrical field propagated from the neuronal synaptic activity through the head volume conductor. A number of efforts have been made to reconstruct brain electrical activity from the scalp EEG measurements by solving the so-called EEG inverse problem [1]. In most of the EEG source localization methods, a piecewise homogeneous head model is used to represent the physical properties of the head. This model usually consists of three compartments (brain, skull and scalp), which are segmented from the MR images and equivalent conductivity values are assigned to each compartment [2]. These conductivity values play a critical role in obtaining the accurate source localization results. In such head model, the scalp is commonly assumed to have the same conductivity as that of the brain while the skull has a much lower conductivity. In addition, only the relative conductivity values would matter for source localization. Thus it is important to specify the brain-to-skull conductivity ratio (BSCR) in EEG source localization.
Many efforts have been made to estimate the BSCR. Rush and Driscoll showed that the ratio was 80 by employing an electrolytic tank to measure the impedance of the human skull [3]. In the past decades, this value has been widely accepted and used. Later, Oostendorp et al. [4] conducted in vivo and in vitro experiments which suggested a different BSCR of 15. Recently, Lai et al. [5] employed cortical imaging technique and estimated the human BSCR as 24.8±6.6 from 5 epilepsy patients. Another study conducted by Zhang et al. [2] in two epilepsy patients suggested the ratio to be 18.7±2.1 using simultaneous intra- and extra-cranial recordings and accurate finite element modeling. Awada et al. [6] presented a sensitivity study of EEG source localization using a two-dimensional finite element model and indicated that conductivity uncertainty may result in large source location errors. Although various conductivity ratios have been explored and used in EEG inverse problem, no systematic study has been reported to elaborate the effect of conductivity uncertainties on EEG source localization accuracy.
The aim of this paper is to investigate the relationship between BSCR and EEG source localization accuracy. We conducted a computer simulation study to explore this problem using a single equivalent current dipole (ECD) model [7] in a realistically shaped head volume conductor [8]. Furthermore, because it has been demonstrated that epileptogenic regions are found near structural lesions [9], [10], the border of the structural lesion may be regarded as a reference for defining the EEG source location. Thus, we have attempted to correlate the localization accuracy of epileptogenic regions with the BSCR in epilepsy patients.
II. METHODS AND MATERIALS
In the computer simulation, a boundary element method (BEM) head model was constructed, which contains three compartments (brain, skull and scalp). The surfaces (skin layer, outer skull layer and inner skull layer) separating the three compartments were segmented from a set of high-resolution T1-weighted magnetic resonance (MR) images of a human subject (256 slices, a field of view of 256 mm, matrix size: 256×256, voxel size: 1×1×1 mm3) using CURRY software (V6, Compumedics, Charlotte, NC). Conductivity values were assigned to each of the compartments to build a three-shell realistically shaped piece-wise homogeneous head volume conductor [8]. A 31-electrode setting was simulated based on the clinical electrode configuration.
We employed four widely used BSCRs: 15, 20, 25 and 80. The simulation can be separated to three steps as follows. (1) Simulate the EEG measurements: The single dipole sources were used to represent the cortical neural activity. Around 8000 current dipoles were evenly placed over the folded cortical surface reconstructed from the MRI images and the orientation of each dipole was assumed to be perpendicular to the local cortical patch [11], [12]. For each of the dipoles on the folded cortical surface, four scalp potentials were generated using the BEM-based forward calculation [8] by assigning the conductivity ratio as 15, 20, 25 and 80, respectively. Ten trails of Gaussian white noise with 10dB signal-to-noise ratio (SNR) was added to the generated scalp potentials to simulate the noise-contaminated EEG measurements. (2) EEG source localization: for each of the simulated EEG distribution, an ECD fitting [7] was performed to solve the inverse problem. In the inverse calculation, we also used the BEM model and assigned the conductivity ratio as 15, 20, 25 and 80 separately. (3) Calculation of localization errors: The localization error is defined as the 3-D distance between the simulated source location and the estimated source location. For each of the cortical dipole sources, a localization error was obtained by averaging over the 10 trails. This can effectively reduce the uncertainty and bias of localization error, which results from adding Gaussian white noise to the scalp potentials.
Two patients with medically intractable partial epilepsy were studied using a protocol approved by the Institutional Review Boards of the University of Minnesota and Mayo Clinic. Each patient was admitted to the Mayo Clinic epilepsy monitoring unit for presurgical evaluation. The scalp EEG data were recorded from 31 scalp electrodes, placed according to the modified 10–20 system, with Cz electrode as reference. The differential amplifiers with bandpass filters between 1Hz and 35Hz were used to minimize the effects of high frequency noise and low frequency artifacts. The sampling rate of the signals was 200Hz. The anatomical MR images (256 slices, a field of view of 256 mm, matrix size: 256×256, voxel size: 1×1×1 mm3) were acquired on a 1.5-T GE Signa using a SPGR sequence (TR = 24 ms, TE = 5.4 ms). For the coregistration of EEG data and MR images, the scalp electrode locations and the locations of three fiducial points on the head (nasion, left and right preauricular points) were digitized using a hand-held magnetic digitizer (Polhemus Inc., Colchester, VT). One of two patients was injected with 99Tcm-ECD during the patient’s habitual seizures. The single photon emission computerized tomography (SPECT) images were acquired after injection using a Helix systems (Elscint Inc.) gamma camera. The pathological site for this patient was determined from SPECT images. Another patient has the clear visible lesion from the structure MRI.
In analysis of epilepsy patients, we also employed the BEM model. The scalp and skull were segmented on the MR images using Curry software (V6, Compumedics, Charlotte, NC) for each subject. Then, the subject-specific BEM models were constructed by the segmentation results. The coregistration of EEG data and MR images, i.e. the transformation of electrode positions and MR images into the same coordinate system, was achieved based on matching the digitized positions of three fiducial points (nasion, left and right preauricular points) with the locations of these points from the MR images.
The overall EEG records were reviewed to identify the interictal spikes which were the artifact-free pre-operative scalp EEG epochs of 2s duration. The experienced epileptologists performed this task via the visual inspection of the recorded data. Then, the EEG data were modified to use a common average reference montage and the global field power (GFP) peak was marked for further analysis. Baseline-correction was based on the scalp EEG data from 300 to 100 ms before the GFP peak of the interictal discharge.
In order to evaluate the effect of different BSCR on EEG source localization in epilepsy patients, the ECD fitting was performed at one time point corresponding to the GFP peak. We used two BSCRs: 20 and 80. The tissue in a spherical shell around the lesion is considered most likely to be the epileptogenic area [9], [10]. Thus, the localization error was evaluated by the shortest distance between the estimated dipole and the border of the MRI lesion or pathological site. Finally, we calculated the localization error for each patient according to different conductivity ratios.
III. RESULTS
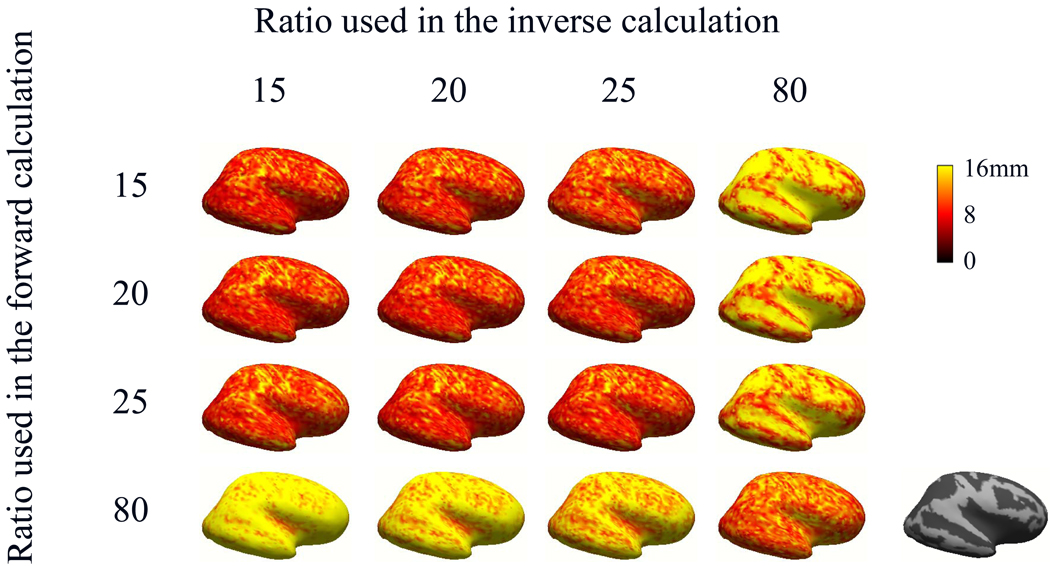
Fig. 1 illustrates the distribution of localization errors of the cortical dipole sources with different settings of conductivity ratios used in the forward and inverse calculations. Each row of the figure corresponds to a specific conductivity ratio used in forward calculation. Each column corresponds to a value of the ratio used in the inverse calculation. The magnitude of the localization errors were color-coded and plotted over the inflated cortical surface. The depth of the dipoles was defined as the shortest distance between a single dipole source and the inner skull layer in the BEM head model. For the inflated cortex displayed on the far right of Fig. 1, dark color denotes deep dipole sources (i.e. the depth of dipole is greater than 10 mm) and grey color denotes shallow dipole sources (i.e. the depth of dipole is less than 10 mm). Note that the localization errors of deep sources were higher than that of shallow sources for the fourth column, which could result from the deep dipoles being located closer to the skull boundary. The localization errors of deep sources were lower than that of shallow sources for the fourth row, probably deriving from the shallow dipoles being located deeper. When the conductivity ratios in the forward and inverse calculation were 15, 20 and 25, the simulation results were similar because the used ratios were close.
Fig. 1.
Distribution of dipole localization errors shown on an inflated cortical surface when 10dB noise was considered. Rows correspond to different conductivity ratios used in the forward calculation and columns correspond to different conductivity ratios used in the inverse calculation. The inflated cortex displayed on the far right denotes deep dipole sources (dark color) and shallow dipole sources (grey color).
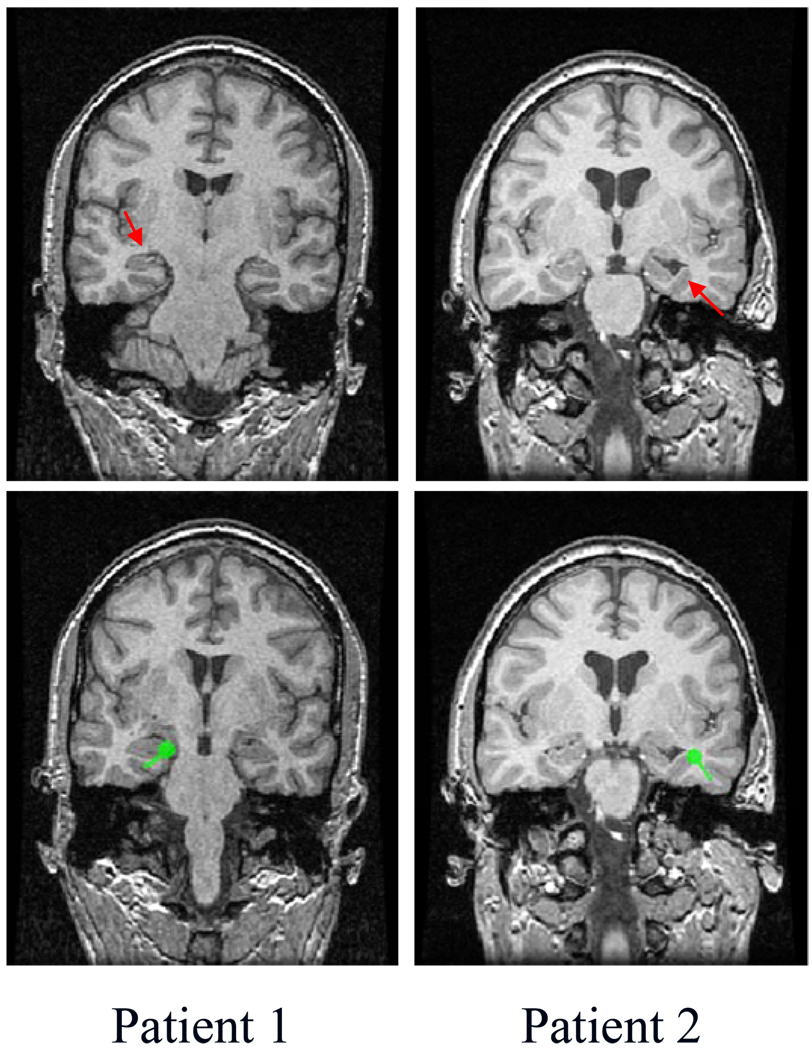
For patient #1, the pre-operative long-term scalp EEG monitoring suggested the presence of epilepsy foci in the left temporal region. The SPECT scan was performed on this patient and indicated that this patient had left mesial temporal epilepsy (the left of first row of Fig. 2). The neurosurgical resection of the left temporal lobectomy made the patient seizure free. Four interictal spikes were chosen for the ECD fitting analysis. A typical example of the ECD fitting results is illustrated in the left of second row of Fig. 2 (interictal spike 3 from TABLE I). As shown in this figure, the location of the estimated dipole source is consistent with the pathological site of this patient from SPECT images. The localization errors of the dipole sources obtained from interictal spikes relative to the pathological site are summarized in Table I when the conductivity ratios used in the inverse calculation were set at 20 and 80.
Fig. 2.
MRI images and illustrations of the interictal analysis for two patients. The MRI lesion or pathological site is marked with red arrows (first row). A typical example of the ECD fitting results is marked with green points (second row, spike 3 form TABLE 1 and spike 1 from TABLE II
TABLE I.
Localization errors (MM) from the interictal analysis of patient #1
| Interictal Spike |
Brain-to-skull Conductivity Ratio |
|
|---|---|---|
| 20 | 80 | |
| 1 | 10.07 | 22.86 |
| 2 | 4.85 | 23.16 |
| 3 | 2.81 | 11.06 |
| 4 | 14.82 | 22 |
| Mean ± SD | 8.14 ± 5.40 | 19.77 ±± 5.83 |
The pre-operative long-term scalp EEG monitoring showed that patient #2 had a right temporal epileptic focus. The anatomical MR images revealed that this patient had dilated ventricle from the loss of right hippocampal volume (the right of first row in Fig. 2). The patient remained seizure free since the right temporal lobectomy. Ten interictal spikes were chosen and the ECD fitting was performed on each spike. A typical example is shown in the right of second row of Fig. 2 (interictal spike 1 from TABLE II). It can be shown that the location of the estimated dipole source is consistent with the MRI lesion location. The localization errors of the dipole sources identified from these interictal spikes relative to the MRI lesion are summarized in Table II when the conductivity ratios used in the inverse calculation were set at 20 and 80.
TABLE II.
Localization errors (MM) from the interictal analysis of patient #2
| Interictal Spike |
Brain-to-skull Conductivity Ratio |
|
|---|---|---|
| 20 | 80 | |
| 1 | 8.31 | 19.34 |
| 2 | 11.10 | 22.44 |
| 3 | 9.64 | 16.03 |
| 4 | 16.41 | 22.49 |
| 5 | 9.83 | 20.73 |
| 6 | 12.51 | 21.92 |
| 7 | 17.01 | 18.31 |
| 8 | 9.94 | 21.59 |
| 9 | 10.36 | 21.22 |
| 10 | 15.18 | 19.18 |
| Mean ± SD | 12.03 ± 3.10 | 20.32 ± 2.08 |
IV. DISSCUSSION
The present study provided a computer simulation to elaborate the effect of different BSCR on EEG source localization using a realistically shaped head volume model. The results indicated that the localization accuracy is sensitive to the BSCR in EEG source reconstruction. When 10dB noise was considered (Fig. 1), the localization errors ranged from 10 to 20 mm in spite of the conductivity ratio used in the forward calculation. From the analysis of epilepsy patients, it can be shown that the localization errors were also between 10 and 20 mm when the conductivity ratios used in the inverse calculation were set at 20 and 80. On the other hand, the localization accuracy resulting when the conductivity ratio used in the inverse calculation was set at 20 was better than those resulting when the ratio was set at 80 in epilepsy patients. Note that these human results are for sources located in deep portion of the brain (see Fig. 2), as defined by MRI and SPECT results. Future investigations should be performed to evaluate sources in other portion of the brain and in a larger population of subjects, in order to draw statistically significant conclusions. Also note that the present results are obtained using a clinical electrode configuration (31 electrodes). The effects of the scalp electrode number on source localization accuracy should also be examined.
ACKNOWLEDGMENT
The authors would like to thank Zhongming Liu for useful discussion, and Cindy Nelson for technical assistance in data collection.
Contributor Information
Gang Wang, Department of Biomedical Engineering at the University of Minnesota, 7-105 NHH, 312 Church Street SE, Minneapolis, MN 55455 USA (wang1490@umn.edu).
Lin Yang, Department of Biomedical Engineering at the University of Minnesota, 7-105 NHH, 312 Church Street SE, Minneapolis, MN 55455 USA.
Gregory Worrell, Department of Neurology at the Mayo Clinic, 200 First Street SW, Rochester, MN 55905 USA.
Bin He, Department of Biomedical Engineering at the University of Minnesota, 7-105 NHH, 312 Church Street SE, Minneapolis, MN 55455 USA.
REFERENCES
- 1.He B, Lian J. In: Neural Engineering. He B, editor. Kluwer Academic/Plenum Publishers; 2005. pp. 221–262. [Google Scholar]
- 2.Zhang Y, van Drongelen W, He B. Estimation of in vivo brain-to-skull conductivity ratio in humans. Applied Physics Letters. 2006 Dec;vol. 89(no. 22):223903. doi: 10.1063/1.2398883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Rush S, Driscoll DA. EEG electrode sensitivity--an application of reciprocity. IEEE transactions on biomedical engineering. 1969 Jan;vol. 16(no. 1):15. doi: 10.1109/tbme.1969.4502598. [DOI] [PubMed] [Google Scholar]
- 4.Oostendorp TF, Delbeke J, Stegeman DF. The conductivity of the human skull: results of in vivo and in vitro measurements. IEEE transactions on biomedical engineering. 2000 Nov;vol. 47(no. 11):1487–1492. doi: 10.1109/TBME.2000.880100. [DOI] [PubMed] [Google Scholar]
- 5.Lai Y, van Drongelen W, Ding L, et al. Estimation of in vivo human brain-to-skull conductivity ratio from simultaneous extra- and intra-cranial electrical potential recordings. Clinical Neurophysiology. 2005 Aug;vol. 116(no. 2):456–465. doi: 10.1016/j.clinph.2004.08.017. [DOI] [PubMed] [Google Scholar]
- 6.Awada K, Jackson D, Baumann S, et al. Effect of conductivity uncertainties and modeling errors on EEG source localization using a 2-D model. IEEE Trans Biomed Eng. 1998 Sep;vol. 45(no. 9):1135–1145. doi: 10.1109/10.709557. [DOI] [PubMed] [Google Scholar]
- 7.He B, Musha T, Okamoto Y, Homma S, Nakajima Y, Sato T. Electric dipole tracing in the brain by means of the boundary element method and its accuracy. IEEE Transactions on Biomedical Engineering, BME-34. 1987:406–414. doi: 10.1109/tbme.1987.326056. [DOI] [PubMed] [Google Scholar]
- 8.Hämäläinen M, Sarvas J. Realistic conductivity geometry model of the human head for interpretation of neuromagnetic data. IEEE transactions on biomedical engineering. 1989 Feb;vol. 36(no. 2):165–171. doi: 10.1109/10.16463. [DOI] [PubMed] [Google Scholar]
- 9.Boon PA, Williamson PD, Fried I, et al. Intracranial, intraaxial, space-occupying lesions in patients with intractable partial seizures: an anatomoclinical, neuropsychological, and surgical correlation. Epilepsia. 1991 Jul–Aug;vol. 32(no. 4):467. doi: 10.1111/j.1528-1157.1991.tb04679.x. [DOI] [PubMed] [Google Scholar]
- 10.Krings T, Chiappa KH, Cuffin BN, et al. Accuracy of electroencephalographic dipole localization of epileptiform activities associated with focal brain lesions. Annals of Neurology. 1998 Jul;vol. 44(no. 1):76. doi: 10.1002/ana.410440114. [DOI] [PubMed] [Google Scholar]
- 11.Dale A, Sereno M. Improved localizadon of cortical activity by combining eeg and meg with mri cortical surface reconstruction: A linear approach. Journal of Cognitive Neuroscience. 1993;vol. 5(no. 2):162–176. doi: 10.1162/jocn.1993.5.2.162. [DOI] [PubMed] [Google Scholar]
- 12.Liu Z, He B. fMRI-EEG integrated cortical source imaging by use of time-variant spatial constraints. NeuroImage. 2008 Feb;vol. 39(no. 3):1198–1214. doi: 10.1016/j.neuroimage.2007.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]