Nonlinear simulations of solid tumor growth using a mixture model: invasion and branching

Abstract

We develop a thermodynamically consistent mixture model for avascular solid tumor growth which takes into account the effects of cell-to-cell adhesion, and taxis inducing chemical and molecular species. The mixture model is well-posed and the governing equations are of Cahn–Hilliard type. When there are only two phases, our asymptotic analysis shows that earlier single-phase models may be recovered as limiting cases of a two-phase model. To solve the governing equations, we develop a numerical algorithm based on an adaptive Cartesian block-structured mesh refinement scheme. A centered-difference approximation is used for the space discretization so that the scheme is second order accurate in space. An implicit discretization in time is used which results in nonlinear equations at implicit time levels. We further employ a gradient stable discretization scheme so that the nonlinear equations are solvable for very large time steps. To solve those equations we use a nonlinear multilevel/multigrid method which is of an optimal order O (N) where N is the number of grid points. Spherically symmetric and fully two dimensional nonlinear numerical simulations are performed. We investigate tumor evolution in nutrient-rich and nutrient-poor tissues. A number of important results have been uncovered. For example, we demonstrate that the tumor may suffer from taxis-driven fingering instabilities which are most dramatic when cell proliferation is low, as predicted by linear stability theory. This is also observed in experiments. This work shows that taxis may play a role in tumor invasion and that when nutrient plays the role of a chemoattractant, the diffusional instability is exacerbated by nutrient gradients. Accordingly, we believe this model is capable of describing complex invasive patterns observed in experiments.

1 Introduction

The uncontrolled growth of abnormal cells often results in cancer. Cancer is an enormous societal problem. For example, cancer is newly diagnosed at a rate of every thirty seconds in the United States and is currently the second leading cause of death for adults (after heart disease). In the past 35 years, tremendous resources have been spent in understanding and identifying the root causes of cancer and to develop effective treatment strategies. While much progress has been made—roughly 2/3 of people diagnosed with cancer typically live for more than 5 years—there is much more work to be done to prevent, treat and control or eliminate this complex disease.

In the past several years, the body of research on mathematical models of cancer growth has increased dramatically. See for example the review papers [1,7,17,42,59,60,63]. Most models fall into two categories: discrete cell-based models and continuum models. In discrete modeling, individual cells are tracked and updated according to a specific set of biophysical rules. Examples include cellular automaton modeling (e.g., see [2,13,30,47,49,66]), hybrid continuum-discrete models (e.g., [4,41,55]), and agent-based models (e.g., [12,46,56]). These approaches are particularly useful for studying carcinogenesis, natural selection, genetic instability, and interactions of individual cells with each other and the microenvironment. On the other hand, these methods can be difficult to study analytically, and the computational cost increases rapidly with the number of cells modeled.

In larger-scale systems where the cancer cell population is on the order of 1,000,000 or more, continuum methods provide a good modeling alternative. The governing equations are typically of reaction-diffusion type. Early work (e.g., [19,20,43]), used ordinary differential equations to model cancer as a homogeneous population, as well as partial differential equation models restricted to spherical tumor growth geometries. Linear and weakly nonlinear analysis have been performed to assess the stability of spherical tumors to asymmetric perturbations (e.g., [16,18–20,22,29,40,51]) as a means to characterize the degree of aggression. Reaction-diffusion equations have been successfully used to model brain tumors (e.g., glioma, see [45,48,63]). Further, various interactions of the tumor with the microenvironment have also been studied (e.g., [8–10,26,27,61]).

Very recently, nonlinear modeling has been performed to study the effects of shape instabilities on avascular, vascular and angiogenic solid tumor growth. Cristini et al. [29] performed the first fully nonlinear simulations of a continuum model of avascular and vascularized tumor growth in 2d that accounts for cell-to-cell and cell-to-matrix adhesion. Using a boundary integral method, it was found that instability provides a mechanism for tumor invasion that does not require an external nutrient source such as would occur from a developing neovasculature during angiogenesis. Li et al. [51] extended this model to 3d using an adaptive boundary integral method. Zheng et al. [70] also extended this model to include a hybrid continuum discrete model of angiogenesis (based on earlier work of Anderson and Chaplain [5]) and investigated the nonlinear coupling between growth and angiogenesis in 2d using finite element/level-set method. Recently, Hogea et al. [44] used a level-set method to investigate tumor progression in a homogeneous, isotropic growth environment and employed a continuous model of angiogenesis.

Using the model developed by Zheng et al., Cristini et al. [28] and Frieboes et al. [38] examined the competition between heterogeneous cell proliferation, caused by spatial diffusion gradients, and stabilizing mechanical forces, e.g., cell-to-cell and cell-to-matrix adhesion. In particular, it is shown that microenvironmental substrate gradients may drive morphologic instability with separation of cell clusters from the tumor edge and infiltration into surrounding normal tissue. Local regions of hypoxia are observed to increase the instability. Similar results were also obtained using a hybrid continuum discrete model by Anderson et al. [6] who also considered the effect of the microenvironment on mutations and the selection of tumor cell phenotypes. Macklin and Lowengrub [52–54] developed a highly accurate level-set/ghost fluid method to further investigate the long-time dynamics and the effect of microenvironmental inhomogeneities on tumor growth in 2d. Very recently, Frieboes et al. [37,67] simulated tumor growth and angiogenesis in 3d using a diffuse interface, multiphase mixture model.

Most of the previous modeling has considered single-phase tumors. Recently, multiphase mixture models have been developed to account for heterogeneities in cell-type and in the mechanical response of the cellular and liquid tumor phases (e.g., [3,9,10,14,21,23,25,34–37,67]). In these models, the multicell spheroid is described as a saturated porous medium, comprising of at least a solid phase and a liquid phase, and can be generalized to incorporate any number of additional phases, as needed to describe solid tumors containing multiple cell types. The governing equations consist of mass and momentum balance equations for each phase, interphase mass and momentum exchange, and appropriate constitutive laws to close the model equations. The multiphase approach represents a more general, and natural modelling framework for studying solid tumor growth and it gives a more detailed account of the biophysical process of tumor growth than that in single-phase models. However, due to the complexity of the models, most of the analyses and numerical simulations are one-dimensional or radially symmetric. Recently, two-dimensional simulations of a mixture model were performed to study the development of tumor cords and the formation of fibrosis [58]. As mentioned above, diffuse-interface, mixture models have also been used to study 3d tumor growth and angiogenesis [37,67].

In this work, we develop, analyze and simulate numerically a thermodynamically consistent mixture model for avascular solid tumor growth which takes into account the nonlinear effects of cell-to-cell adhesion, and taxis inducing chemical and molecular species. Cell-to-cell adhesion has also been investigated in previous mixture models (e.g., [3,23]), however these older models behave like backward parabolic equations when the cellular fraction is within a certain range and thus are ill-posed. More recently, well-posed continuum models of adhesion have been considered by [11] and by [37,67] in the context of diffuse-interface, mixture models. Here, we follow [37,67], and develop a well-posed mixture model. The governing equations are of Cahn–Hilliard type and can be viewed as a regularization of previous mixture models. Unlike [37,67] where a direct approach was taken to determine the cell-velocity via energy variation, here we pose momentum equations for each component with momentum exchange terms that are determined in a thermodynamically consistent way. When there are only two phases, our asymptotic analysis shows that single-phase models of the type used in [29,51] may be recovered as limiting cases of a two-phase model.

To solve the governing equations, we have developed a numerical algorithm based on an adaptive Cartesian block-structured mesh refinement scheme which is ideal for nonlinear multigrid methods. The basis of our algorithm is the algorithm developed by Wise et al. [68] for anisotropic Cahn–Hilliard equations. A centered-difference approximation is used for the space discretization so that the scheme is second order accurate in space. An implicit discretization in time is used which results in nonlinear equations at implicit time levels. We further employ a gradient stable discretization scheme (see [32,33]) so that the nonlinear equations are solvable for very large time steps. To solve those equations we use a nonlinear multilevel/multigrid method which is of an optimal order O (N) where N is the number of grid points.

Spherically symmetric and fully two dimensional nonlinear numerical simulations are performed using our adaptive multigrid/finite-difference scheme. We investigate tumor evolution in nutrient-rich and nutrient-poor tissues. A number of important results have been uncovered. For example, we demonstrate that taxis of tumor cells up nutrient gradients (nutrient-taxis) may drive fingering instabilities which are most dramatic when cell proliferation is low, as predicted by linear stability theory. This is also observed in experiments. Indeed, experimental evidence suggests that nutrient deprivation can importantly contribute to increase the invasive behavior of a tumor. In some situations, the tumor may even develop branched tubular structures (e.g., [57]) where premetastatic clusters of tumor cells invade the host tissue [39]. This work shows that nutrient-taxis may play a role in tumor invasion and that the diffusional instability is exacerbated by nutrient gradients. Accordingly, we believe this model is capable of describing complex invasive patterns observed in experiments.

The paper is organized as follows. The general tumor mixture model is formulated in Sect. 2. An example of two component mixture model is given in Sect. 3. We present the gradient stable nonlinear multigrid/finite-difference scheme used to solve the Cahn–Hilliard type system of equations in Sect. 4. The nonlinear simulations are presented in Sect. 5. We conclude this paper in Sect. 6 with a summary and a brief description of future work. In the Appendix, we demonstrate the thermodynamic consistency of the constituent relations.

2 The general tumor mixture model

2.1 The mass equation

Define the volume fractions of the water and cellular (solid) components to be ϕ_k for k = 0, 1,..., N – 1. In the following, without loss of generality, we assume that component 0 identifies the water component. The remaining components are solid phases. Arguing that the tissue is saturated, we have the following constraint

$$\sum _{k=0}^{N-1}{\varphi }_k(\mathbf{x},t)=1.$$ (1)

Assuming that the densities of the components ρ_k are constant, the equations for the volume fractions are:

$${\partial }_t{\varphi }_k+\nabla \cdot \left({\varphi }_k{\mathbf{v}}_k\right)=({\Gamma }_k-\nabla \cdot J_k)∕{\rho }_k,$$ (2)

where v_k are the component velocities, Γ_k is the mass exchange term and J_k is the component flux.

The mixture density and velocity, respectively, are defined by $\rho ={\sum }_{k=0}^{N-1}{\rho }_k{\varphi }_k$ and $\mathbf{v}=\frac{1}{\rho }{\sum }_{k=0}^{N-1}{\rho }_k{\varphi }_k{\mathbf{v}}_k$. The mixture density is conserved, i.e., ∂_t ρ ∇ · (ρv) 0. This implies that the fluxes, the mass-exchange terms and the component velocities are constrained to satisfy

$$\sum _{k=0}^{N-1}{J}_k=0,\sum _{k=0}^{N-1}{\Gamma }_k=0,\sum _{k=0}^{N-1}\nabla \cdot \left({\varphi }_k{\mathbf{v}}_k\right)=\sum _{k=0}^{N-1}{\Gamma }_k∕{\rho }_k.$$ (3)

If the densities are matched, ρ_k = ρ, then the mixture velocity is incompressible, i.e.,

$$\nabla \cdot \left(\sum _{k=0}^{N-1}{\varphi }_k{\mathbf{v}}_k\right)=0.$$ (4)

The constitutive equations for J_k and v_k that are consistent with the second law of thermodynamics are derived in Appendix A and are given in Sect. 2.3. The biophysically consistent constitutive equations for Γ_k are also given in Sect. 2.3.

2.2 The momentum equation

For each component, the balance of linear momentum is

$$0=\nabla \cdot {\sigma }_k+{\rho }_k{\varphi }_k{\mathbf{F}}_k+{\pi }_k,$$ (5)

where we have neglected inertial forces. In Eq. (5), σ_k is the stress tensor, F_k are external forces per unit mass acting on the system and π_k are the forces per unit volume due to interactions with other components. Arguing that the linear momentum for the mixture satisfies

$$\nabla \cdot \sigma =\rho \mathbf{F},\text{where}\sigma =\sum _{k=0}^{N-1}{\sigma }_k,\rho \mathbf{F}=\sum _{k=0}^{N-1}{\rho }_k{\varphi }_k{\mathbf{F}}_k,$$ (6)

gives the constraint on the interaction forces

$$\sum _{i=0}^{N-1}{\pi }_i=0.$$ (7)

The constitutive relations for the momentum interaction forces π_k consistent with the second law of thermodynamics are derived in Appendix A and are given in Sect. 2.3.

2.3 Constitutive relations

For simplicity, we consider isothermal systems here. Introduce Ψ_k to be the Helmholtz free energy per unit volume of the kth component. Note that the free energy may also depend on the concentrations of chemical species whose presence may induce the taxis of cells (e.g., chemotaxis, haptotaxis, etc.). Then, suppose that the (generalized) Helmholtz free energy takes the following form:

$${\Psi }_k={\Psi }_k({\varphi }_0,\dots ,{\varphi }_{N-1},\nabla {\varphi }_0,\dots ,\nabla {\varphi }_{N-1}).$$ (8)

The dependence of Ψ_k upon the gradients of volume fraction arises naturally through the expansion of a nonlocal interaction potential among the phases (see for example Cahn and Hilliard [24], Davis and Scriven [31], Wise et al. [67]) and represent the effects of weakly nonlocal interactions. We also note that a nonlocal model of cell interaction (and adhesion) has been recently considered by Armstrong et al. [11].

In this paper, we assume the tumor cells behave like a viscous fluid. Extensions to include viscoelasticity of the components can be incorporated following the framework of Yue et al. [69]. The inclusion of elastic effects and residual stress can be incorporated following Araujo and McElwain [9] and Bowen [15]. From Appendix A, a thermodynamic analysis reveals that the stress tensor and interaction forces may be taken to be

$${\sigma }_k=\left({\Psi }_k-{\varphi }_k\sum _{j=0}^{N-1}{\mu }_{jk}-{\rho }_k{\varphi }_{k}p\right)\mathbf{I}-\sum _{j=0}^{N-1}\nabla {\varphi }_j\otimes \frac{\partial {\Psi }_k}{\partial \nabla {\varphi }_j}+{\mathcal{L}}_k\left(\nabla {\mathbf{v}}_k+\nabla {\mathbf{v}}_k^T\right),$$ (9)

$${\pi }_k=p{\rho }_0\nabla {\varphi }_k+\sum _{j=0}^{N-1}({\mu }_{jk}\nabla {\varphi }_k-{\mu }_{kj}\nabla {\varphi }_j)-{\alpha }_k({\mathbf{v}}_k-{\mathbf{v}}_0),\text{for}k\ne 0,$$ (10)

$${\pi }_0=-\sum _{k=1}^{N-1}{\pi }_k,$$ (11)

$$J_k=-\sum _{j=0}^{N-1}{M}_{jk}\nabla {\mu }_{jk}∕{\rho }_k,\text{for}k\ne 0,$$ (12)

$$J_0=-\sum _{k=1}^{N-1}{J}_k,$$ (13)

where p is the pressure and μ_jk is the species chemical potential:

$${\mu }_{jk}=\frac{\partial {\Psi }_j}{\partial {\varphi }_k}-p({\rho }_j-{\rho }_0){\delta }_{jk}-\nabla \cdot \frac{\partial {\Psi }_j}{\partial \nabla {\varphi }_k},$$ (14)

M_jk is the flux mobility, ${\mathcal{L}}_k$ is a symmetric, positive definite tensor, α_k in Eq. (10) is a symmetric, positive definite matrix, and δ_jk = 1 if j = k and δ_jk = 0 otherwise. Assuming isotropy,

$${\mathcal{L}}_k\left(\nabla {\mathbf{v}}_k+\nabla {\mathbf{v}}_k^T\right)={\eta }_k\left(\nabla {\mathbf{v}}_k+\nabla {\mathbf{v}}_k^T\right)+{\nu }_k(\nabla \cdot {\mathbf{v}}_k)\mathbf{I},$$ (15)

where η_k and ν_k are viscosity coefficients. More generally, ${\mathcal{L}}_k$ could depend on the orientation of fibers in the tissue. The first term on the right of the interaction forces in Eq. (10) represents the contribution due to pressure, the second term on the right represents the contribution due to the chemical potential and the third term on the right represents the contribution due to interphase drag.

In the liquid phase, it makes sense to assume that the liquid is inviscid (e.g., Byrne and Preziosi [23]). We further neglect body forces. Then, the momentum equation (5) in the liquid (k = 0)

$$0=\nabla \cdot {\sigma }_0+{\pi }_0$$ (16)

becomes a multicomponent Darcy's law:

$${\varphi }_0\nabla p^{\prime }=\sum _{k=0}^{N-1}{\alpha }_k({\mathbf{v}}_k-{\mathbf{v}}_0),$$ (17)

where p′ is a modified pressure

$$p^{\prime }={\rho }_{0}p+\sum _{j=0}^{N-1}{\mu }_{j0}.$$ (18)

Thus, the interaction forces among the solid components influence the motion of the liquid through the modified pressure and the drag velocities α_k (v_k – v₀).

We further consider the following form of the Helmholtz free energy:

$${\Psi }_k({\varphi }_0,\dots ,{\varphi }_{N-1},\nabla {\varphi }_0,\dots ,\nabla {\varphi }_{N-1})={\tilde{\Psi }}_k({\varphi }_0,\dots ,{\varphi }_{N-1})+{\varphi }_k\sum _{l=1}^L{\chi }_{kl}{c}_l+\sum _{j=0}^{N-1}\frac{{∊}_{kj}^2}{2}{\mid \nabla {\varphi }_j\mid }^2,$$ (19)

where c₁,..., c_L are the concentration of taxis inducing chemical and molecular species, χ_kl are taxis coefficients and ∈_kj measures the strength of component–component interactions (Wise et al. [67]). Assuming ∈_kj is constant, we then obtain

$$\frac{\partial {\Psi }_k}{\partial \nabla {\varphi }_j}={∊}_{kj}^2\nabla {\varphi }_j,$$ (20)

and thus the momentum balance equation (5) for the solid components becomes

$${\alpha }_k({\mathbf{v}}_k-{\mathbf{v}}_0)=-\frac{{\rho }_k}{{\rho }_0}{\varphi }_k\nabla (p^{\prime }+{\tilde{\mu }}_k)+\nabla \cdot \left({\mathcal{L}}_k\left(\nabla {\mathbf{v}}_k+\nabla {\mathbf{v}}_k^T\right)\right),k>0,$$ (21)

where ${\tilde{\mu }}_k$ is the modified chemical potential

$${\tilde{\mu }}_k=\frac{{\rho }_0}{{\rho }_k}\sum _{j=0}^{N-1}{\mu }_{jk}-\sum _{j=0}^{N-1}{\mu }_{j0}.$$ (22)

Using Eq. (19), ${\tilde{\mu }}_k$ reduces to

$${\tilde{\mu }}_k=\frac{{\rho }_0}{{\rho }_k}\sum _{j=0}^{N-1}\left(\frac{\partial {\tilde{\Psi }}_j}{\partial {\varphi }_k}-\frac{\partial {\tilde{\Psi }}_j}{\partial {\varphi }_0}\right)+\frac{{\rho }_0}{{\partial }_k}\sum _{l=1}^L({\chi }_{kl}-{\chi }_{0l})c_l-p^{\prime }\left(1-\frac{{\rho }_0}{{\rho }_k}\right)-\frac{{\rho }_0}{{\rho }_k}\sum _{j=0}^{N-1}\left({∊}_{jk}^2\Delta {\varphi }_k-{∊}_{j0}^2\Delta {\varphi }_0\right).$$ (23)

Equations (21) and (23) together with the generalized Darcy's law (17) for the liquid component, the incompressibility condition

$$\sum _{k=0}^{N-1}{\rho }_k\nabla \cdot \left({\varphi }_k{\mathbf{v}}_k\right)=0,$$ (24)

and the volume fraction equation

$$\frac{\partial {\varphi }_k}{\partial t}+\nabla \cdot \left({\varphi }_k{\mathbf{v}}_k\right)=({\Gamma }_k-\nabla \cdot J_k)∕{\rho }_k$$ (25)

completes the system of equations governing the tumor mixture. Note that the biophysical processes arise in the mechanics through the chemical potential (23) and the mass exchange terms Γ_k. Equations governing the chemical species c₁,..., c_L must be posed in addition to this system (see Sect. 3.2 for an example).

3 Examples of tumor mixtures

3.1 Two component mixtures: tissue and water

Let us now specialize to the case of mixtures containing solid matter (e.g., tissue, extracellular matrix, etc.) and water. An example of a three component mixture model is given in [50]. In this case N = 2 and we also assume that the densities are matched ρ₀ = ρ₁ = ρ, there are no body forces F_k = 0 and that there are no component fluxes J_k = 0 (i.e., M_jk = 0). We further assume that the nutrient plays the role of a chemoattractant. Taking ∈_jk = ∈/2, then the system of Eqs. (17), (21), (24) and (25) reduces to

$${\varphi }_0\nabla p^{\prime }={\alpha }_1({\mathbf{v}}_1-{\mathbf{v}}_0),$$ (26)

$$-{\varphi }_1\nabla (p^{\prime }+{\tilde{\mu }}_1)+\nabla \cdot \left({\mathcal{L}}_1\left(\nabla {\mathbf{v}}_1+\nabla {\mathbf{v}}_1^T\right)\right)={\alpha }_1({\mathbf{v}}_1-{\mathbf{v}}_0),$$ (27)

$$\nabla \cdot ({\varphi }_0{\mathbf{v}}_0+{\varphi }_1{\mathbf{v}}_1)=0,$$ (28)

$$\frac{\partial {\varphi }_k}{\partial t}+\nabla \cdot \left({\varphi }_k{\mathbf{v}}_k\right)=({\Gamma }_k-\nabla \cdot J_k)∕\rho ,\text{for}\mathrm{k}=0,1.$$ (29)

The modified chemical potential ${\tilde{\mu }}_1$ is given by

$${\tilde{\mu }}_1=\sum _{j=0}^1\left(\frac{\partial {\tilde{\Psi }}_j}{\partial {\varphi }_1}-\frac{\partial {\tilde{\Psi }}_j}{\partial {\varphi }_0}\right)-{∊}^2\Delta {\varphi }_1+({\chi }_{11}-{\chi }_{01})\sigma ,$$ (30)

where σ is the concentration of a vital nutrient (e.g., oxygen or glucose). The incompressibility condition (28) and the viscosity term ${\mathcal{L}}_1$ make the system nonlocal. In the following, we discuss a simplification in which the system is localized but the viscosity term may be kept. We will then consider the fully nonlocal model.

A local model

The solution to the incompressibility condition (28) can be written as

$${\mathbf{v}}_0=-\frac{{\varphi }_1}{{\varphi }_0}{\mathbf{v}}_1+\frac{1}{{\varphi }_0}\nabla \times \zeta .$$ (31)

Then,

$${\mathbf{v}}_1-{\mathbf{v}}_0=\frac{1}{{\varphi }_0}{\mathbf{v}}_1-\frac{1}{{\varphi }_0}\nabla \times \zeta .$$ (32)

Using Eq. (32) in Eq. (27), we get

$$-{\varphi }_1\nabla (p^{\prime }+{\tilde{\mu }}_1)+\nabla \cdot \left({\mathcal{L}}_1\left(\nabla {\mathbf{v}}_1+\nabla {\mathbf{v}}_1^T\right)\right)=\frac{{\alpha }_1}{{\varphi }_0}{\mathbf{v}}_1-\frac{{\alpha }_1}{{\varphi }_0}\nabla \times \zeta ,$$ (33)

The local model is obtained by taking p′ and ζ constant, and dropping Eq. (26) since the velocity in the liquid is determined uniquely (under these assumptions) by ϕ₁ and v₁. In this case, Eq. (33) becomes

$$\left(I-(1-{\varphi }_1){\alpha }_1^{-1}\nabla \cdot {\mathcal{L}}_1\left(\nabla +{\nabla }^T\right)\right){\mathbf{v}}_1=-(1-{\varphi }_1){\varphi }_1{\alpha }_1^{-1}\nabla {\tilde{\mu }}_1,$$ (34)

where we have used ϕ₀ = 1 – ϕ₁. Assuming zero viscosity, ${\mathcal{L}}_1=0$, and

$${\alpha }_1=(1-{\varphi }_1)M^{-1},$$ (35)

where M is a permeability, then Eq. (34) becomes a generalized Darcy's law:

$${\mathbf{v}}_1=-M{\varphi }_1\nabla {\tilde{\mu }}_1.$$ (36)

In general, including viscous terms, we get an elliptic equation for v₁:

$$\left(I-M\nabla \cdot {\mathcal{L}}_1\left(\nabla +{\nabla }^T\right)\right){\mathbf{v}}_1=-M{\varphi }_1\nabla {\tilde{\mu }}_1.$$ (37)

Using Eq. (37) in Eq. (25) gives the generalized, nonlocal Cahn–Hilliard equation

$$\frac{\partial {\varphi }_1}{\partial t}=\nabla \cdot \left({\varphi }_1{\left(I-M{\tilde{\mathcal{L}}}_1\right)}^{-1}(M{\varphi }_1\nabla {\tilde{\mu }}_1)\right)+{\Gamma }_1∕\rho ,$$ (38)

where

$${\tilde{\mathcal{L}}}_1\left({\mathbf{v}}_1\right)=\nabla \cdot \left({\mathcal{L}}_1\left(\nabla {\mathbf{v}}_1+\nabla {\mathbf{v}}_1^T\right)\right).$$ (39)

We remark that this equation is analogous to the nonlocal equation derived in Byrne and Preziosi [23] except that the ${\tilde{\mu }}_1$ contains high order derivative terms due to ∈ (weakly nonlocal interactions).

If the viscosity is equal to zero, using Eq. (36) in Eq. (29) gives a local Cahn–Hilliard equation with variable mobility:

$$\frac{\partial {\varphi }_1}{\partial t}=\nabla \cdot \left(M{\varphi }_1^2\nabla {\tilde{\mu }}_1\right)+{\Gamma }_1∕\rho ,$$ (40)

$${\tilde{\mu }}_1=\sum _{j=0}^1\left(\frac{\partial {\tilde{\Psi }}_j}{\partial {\varphi }_1}-\frac{\partial {\tilde{\Psi }}_j}{\partial {\varphi }_0}\right)-{∊}^2\Delta {\varphi }_1+({\chi }_{11}-{\chi }_{01})\sigma .$$ (41)

This system is similar to the cell-to-cell interaction model described in Ambrosi and Preziosi [3], except that ${\tilde{\mu }}_1$ contains high order derivatives.

The full nonlocal system

In this case, we deal directly with Eqs. (26) and (27). Using Eq. (26) in Eq. (27), we get the Stokes system

$$-\nabla p^{\prime }+\nabla \cdot \left({\mathcal{L}}_1\left(\nabla {\mathbf{v}}_1+\nabla {\mathbf{v}}_1^T\right)\right)={\varphi }_1\nabla {\tilde{\mu }}_1.$$ (42)

In Sect. 3.4, a matched asymptotic analysis shows that the term on the right-hand side of Eq. (42) mimics surface tension-like cell-adhesion forces in a certain limit. Further by taking

$${\alpha }_1={\varphi }_0^2{M}^{-1},$$ (43)

where M is a permeability matrix, then Eq. (26) becomes

$${\mathbf{v}}_0={\mathbf{v}}_1-\frac{1}{{\varphi }_0}M\nabla p^{\prime },$$ (44)

Next, from the incompressibility condition (28) and Eq. (44), we obtain

$$\nabla \cdot ({\mathbf{v}}_1-M\nabla p^{\prime })=0.$$ (45)

Putting together all the equations, we get a system entirely involving ϕ₁, p′ and v₁:

$$-\nabla p^{\prime }+\nabla \cdot \left({\mathcal{L}}_1\left(\nabla {\mathbf{v}}_1+\nabla {\mathbf{v}}_1^T\right)\right)={\varphi }_1\nabla {\tilde{\mu }}_1,$$ (46)

$$\nabla \cdot ({\mathbf{v}}_1-M\nabla p^{\prime })=0,$$ (47)

$$\frac{\partial {\varphi }_1}{\partial t}+\nabla \cdot \left({\varphi }_1{\mathbf{v}}_1\right)={\Gamma }_1∕\rho .$$ (48)

This is an interesting system for a variety of reasons. First, if ${\mathcal{L}}_1=0$, that is the solid phase is inviscid, then this system has no solution in two or more dimensions because of the presence of the nongradient term on the right-hand side of Eq. (46). The viscous terms are needed to balance the nongradient part of the cell-adhesion forces. In addition, the system (46)–(47) is equivalent to a pressure-stabilized form of the incompressible Stokes Equations with an additional force (${\varphi }_1\nabla {\tilde{\mu }}_1$) (see Shen [62]).

In spherical coordinates, the system (46)–(48) can be reduced to the generalized nonlocal Cahn–Hilliard equation

$$\frac{\partial {\varphi }_1}{\partial t}=\frac{1}{r^2}{\partial }_r\left(r^2{\varphi }_1{\left(I-M{\tilde{\mathcal{L}}}_1\right)}^{-1}\left(M{\varphi }_1{\partial }_r{\tilde{\mu }}_1\right)\right)+{\Gamma }_1∕\rho ,$$ (49)

$${\tilde{\mu }}_1=\sum _{j=0}^1\left(\frac{\partial {\tilde{\Psi }}_j}{\partial {\varphi }_1}-\frac{\partial {\tilde{\Psi }}_j}{\partial {\varphi }_0}\right)-{∊}^2\frac{1}{r^2}{\partial }_r\left(r^2{\partial }_r{\varphi }_1\right)+({\chi }_{11}-{\chi }_{01})\sigma .$$ (50)

Note that this equation is very similar to that obtained using the local approximation (cf. Eqs. (38), (41)). In the spherical geometry, the viscosity may be set to zero because the right-hand side of Eq. (46) becomes a perfect derivative.

To summarize, our two component mixture model comprises Eqs. (26–30). To close the model we must specify an equation for the nutrient and provide the constitutive equations for the Helmholtz free energy and the mass exchange term. In addition, boundary and initial conditions must be posed. A complete model formulation is given in the next section. It should be noted that both local and nonlocal models are well posed.

3.2 A complete model formulation

For the rest of the paper, we shall consider a special case of the mixture model developed in the previous section, i.e., two component mixtures consisting of tumor tissue and water. Furthermore, we focus on the local model of two component mixtures described in the previous section. The governing equations are given by

$$\frac{\partial {\varphi }_1}{\partial t}=\nabla \cdot \left(M{\varphi }_1^2\nabla {\tilde{\mu }}_1\right)+{\Gamma }_1∕\rho ,$$ (51)

$${\tilde{\mu }}_1=\sum _{j=0}^1\left(\frac{\partial {\tilde{\Psi }}_j}{\partial {\varphi }_1}-\frac{\partial {\tilde{\Psi }}_j}{\partial {\varphi }_0}\right)-{∊}^2\Delta {\varphi }_1+({\chi }_{11}-{\chi }_{01})\sigma .$$ (52)

We pose Eqs. (51), (52) in a domain Ω. On ∂Ω, we impose the Neumann boundary conditions:

$$\frac{\partial {\varphi }_1}{\partial \mathbf{n}}=\frac{\partial {\tilde{\mu }}_1}{\partial \mathbf{n}}=0,$$ (53)

where n is the unit normal vector.

The initial condition ϕ₁(·, 0) is given. For simplicity of notation, in the remainder of the paper, we replace ϕ₁ by ϕ, ${\tilde{\mu }}_1$ by μ, and Γ₁ by Γ. Note that ϕ₀ = 1 – ϕ₁.

Following previous models, a biologically consistent mass exchange given Γ is given by

$$\Gamma ={\lambda }_p\sigma \rho \varphi -{\lambda }_A\rho \varphi ,$$ (54)

where the first term represents cell-mitosis with a rate proportional to the nutrient concentration. The second term represents the mass converted to the fluid phase due to cell death (apoptosis). The parameter λ_p is the proliferation rate per unit mass concentration, and λ_A is the apoptosis rate per unit mass.

Next, we consider the Helmholtz free energy. Using that ϕ₀ = 1 – ϕ₁, we define:

$$f^{\prime }\left(\varphi \right)=\sum _{j=0}^1\left(\frac{\partial {\tilde{\Psi }}_j}{\partial {\varphi }_1}-\frac{\partial {\tilde{\Psi }}_j}{\partial {\varphi }_0}\right),$$ (55)

and we take

$$f\left(\varphi \right)=f_e\left(\varphi \right)-f_c\left(\varphi \right)$$ (56)

to be a double-well potential, where f_e and f_c are convex functions. The former, f_e, represents repulsive forces among the cells while the latter, f_c, accounts for adhesive forces.

To describe the contribution from taxis, i.e., third term in Eq. (52), we suppose χ₀₁ = 0. That is, there is no taxis of the liquid component. To simplify notation, define χ_σ = χ₁₁. Putting these results together gives the chemical potential:

$$\mu =f^{\prime }\left(\varphi \right)-{∊}^2\Delta \varphi -{\chi }_{\sigma }\sigma .$$ (57)

The nutrient evolution equation is an advection–diffusion equation. We assume the consumption of the nutrient to be proportional to the local nutrient concentration and cellular fraction. This gives:

$${\sigma }_t+\nabla \cdot \left(\sigma {\mathbf{v}}_0\right)-\nabla \cdot (D_{\sigma }\nabla \sigma )=-{\lambda }_{\sigma }\sigma \varphi ,$$ (58)

where D_σ is the nutrient diffusion coefficient and λ_σ is the nutrient uptake rate. The far field boundary condition for nutrient is given by

$${\left(\sigma \right)}_{\partial \Omega }={\sigma }_{\infty },$$ (59)

where σ_∞ is the nutrient concentration in the far field tissue, assumed to be uniform.

Combining Eqs. (51), (54), (57) and (58), the governing equations are as follows:

$${\varphi }_t=\nabla \cdot (M{\varphi }^2\nabla \mu )+{\lambda }_p\sigma \varphi -{\lambda }_A\varphi \text{in}\Omega ,$$ (60)

$$\mu =f^{\prime }\left(\varphi \right)-{∊}^2\Delta \varphi -{\chi }_{\sigma }\sigma \text{in}\Omega ,$$ (61)

$${\sigma }_t=-\nabla \cdot \left(\sigma {\mathbf{v}}_0\right)+\nabla \cdot (D_{\sigma }\nabla \sigma )-{\lambda }_{\sigma }\sigma \varphi \text{in}\Omega ,$$ (62)

with boundary conditions:

$$\nabla \varphi \cdot \mathbf{n}=\nabla \mu \cdot \mathbf{n}=0\text{on}\partial \Omega ,$$ (63)

$$\sigma ={\sigma }_{\infty }\text{on}\partial \Omega .$$ (64)

As pointed out earlier, this model is similar to those of Ambrosi and Preziosi [3] and Byrne and Preziosi [23], however their models behave like backward parabolic equations when the cellular fraction is within a certain range and thus are ill-posed. In contrast, our mixture model is well-posed and the governing equations are of Cahn–Hilliard type. We will further show that the two component mixture model converges to the classical sharp interface limit given in [29] in Sect. 3.4.

3.3 Nondimensionalization

Before analyzing the complete two component mixture model described in the previous section, it is convenient to recast the model in dimensionless form, and thereby identify the key dimensionless parameter groups. We define

$${\varphi }^{\prime }=\frac{\varphi }{{\varphi }_T},{\sigma }^{\prime }=\frac{\sigma }{{\sigma }_{\infty }},{\chi }_{\sigma }^{\prime }=\frac{{\chi }_{\sigma }}{{\stackrel{‒}{\chi }}_{\sigma }},\tilde{f}=\frac{f}{\stackrel{‒}{f}},D^{\prime }=\frac{D_{\sigma }}{D_T},$$ (65)

where ϕ_T is the characteristic solid tumor volume fraction, ${\stackrel{‒}{\chi }}_{\sigma }$ is a characteristic taxis coefficient, f̄ is a characteristic interaction energy, and we assume

$$D_{\sigma }=D_T\varphi +D_H(1-\varphi ),$$ (66)

where D_T and D_H are the diffusion coefficients for tumor and health tissue respectively.

Introduce the intrinsic taxis time scale ${\lambda }_{\chi }^{-1}$ corresponding to the rate ${\lambda }_{\chi }=M{\stackrel{‒}{\chi }}_{\sigma }{\sigma }_{\infty }{\varphi }_T∕l^2$, and the diffusional length $l=\sqrt{D_T∕{\lambda }_{\sigma }{\varphi }_T}$. We may then define the following nondimensional parameters:

$${∊}^{\prime }=\frac{∊}{l\sqrt{\stackrel{‒}{f}∕{\varphi }_T}},\mathcal{G}=\frac{l{\stackrel{‒}{\chi }}_{\sigma }{\sigma }_{\infty }}{∊\sqrt{\stackrel{‒}{f}{\varphi }_T}},\mathcal{P}=\frac{{\lambda }_p{\sigma }_{\infty }}{{\lambda }_{\chi }},\mathcal{A}=\frac{{\lambda }_A}{{\lambda }_{\chi }},\alpha =\frac{l^2{\lambda }_{\chi }}{D_T},$$ (67)

where ∈′ represents the relative strength of intermixing to interaction energy, $\mathcal{G}$ represents the relative strength of cell–cell interactions (adhesion), $\mathcal{P}$ represents the relative rate of cell mitosis to taxis, $\mathcal{A}$ represents the relative rate of cell apoptosis to taxis, and α represents the relative rate of taxis to nutrient uptake.

Since diffusion occurs more slowly than taxis (e.g., minutes vs. hours), we have α ≪ 1. Therefore, we can approximate the nutrient equation by a quasi-steady diffusion-reaction equation.

Dropping the primes, replacing f̃ by f, the dimensionless system is:

$${\varphi }_t=\nabla \cdot \left(\frac{1}{∊}{\varphi }^2\nabla \mu \right)+\mathcal{P}\sigma \varphi -\mathcal{A}\varphi ,$$ (68)

$$\mu ={\mathcal{G}}^{-1}(f^{\prime }\left(\varphi \right)-{∊}^2\Delta \varphi )-∊{\chi }_{\sigma }\sigma ,$$ (69)

$$0=\nabla \cdot (D\left(\varphi \right)\nabla \sigma )-\sigma \varphi ,$$ (70)

where

$$D\left(\varphi \right)=\varphi +\mathcal{D}(1-\varphi ),$$ (71)

and $\mathcal{D}=D_H∕D_T$, i.e., the diffusion constant outside the tumor is $\mathcal{D}$ times larger than that inside.

The boundary conditions are given by:

$$\nabla \varphi \cdot \mathbf{n}=\nabla \mu \cdot \mathbf{n}=0\text{on}\partial \Omega ,$$ (72)

$$\sigma =1\text{on}\partial \Omega .$$ (73)

3.4 Matched asymptotic expansions

In this section, we briefly present a matched asymptotic analysis to show that the two component mixture model converges to the classical sharp interface limit equations given in [29].

Suppose there is a single smooth transition layer of width ∈ separating the tumor Ω_T and host Ω_H domains. Let Σ be a curve (the analysis may easily be extended to surfaces) centered in the transition layer. Away from Σ, we suppose that the solutions may be written as a regular expansion in the parameter ∈:

$$\varphi (x,y,t)={\varphi }^{\left(0\right)}(x,y,t)+∊{\varphi }^{\left(1\right)}(x,y,t)+{∊}^2{\varphi }^{\left(2\right)}(x,y,t)+\cdots .$$ (74)

Near Σ, we introduce a local normal-tangential coordinate system with respect to the curve Σ. Let Σ = (X (s, t), Y (s, t)) where s is arclength and t is time. Let r be defined as the signed distance along the normal from a point (x, y) to Σ. Then, introduce a local coordinate transformation from (x, y) to (r, s). The orientation of Σ is chosen so that Ω_T lies on the left of Σ if the curve is traversed along the direction of increasing s, which means the normal n = (∂Y/∂s, – ∂X/∂s) points into the region Ω_H. Near Σ, we assume that in the stretched local coordinate system z = r/∈, the solutions have a regular expansion

$$\varphi (x,y,t)=\widehat{\varphi }(z,s,t)={\widehat{\varphi }}^{\left(0\right)}(z,s,t)+∊{\widehat{\varphi }}^{\left(1\right)}(z,s,t)+{∊}^2{\widehat{\varphi }}^{\left(2\right)}(z,s,t)+\cdots .$$ (75)

In a region of overlap, where both the outer and inner expansions are valid, the representation must match:

$$\left({\varphi }^{\left(0\right)}+∊{\varphi }^{\left(1\right)}+\cdots \right)(∊z,s,t)=\left({\widehat{\varphi }}^{\left(0\right)}+∊{\widehat{\varphi }}^{\left(1\right)}+\cdots \right)(z,s,t).$$ (76)

Expanding and equating equal powers of ∈ gives the matching conditions:

$$\underset{r\to 0\pm }{\text{lim}}{\varphi }^{\left(0\right)}(r,s,t)=\underset{z\to \pm \infty }{\text{lim}}{\widehat{\varphi }}^{\left(0\right)}(z,s,t),$$ (77)

$$\underset{r\to 0\pm }{\text{lim}}\mathbf{n}\cdot \nabla {\varphi }^{\left(0\right)}(r,s,t)=\underset{z\to \pm \infty }{\text{lim}}{\partial }_z{\widehat{\varphi }}^{\left(1\right)}(z,s,t),\dots$$ (78)

Expansions and matching conditions for σ and μ may be similarly identified.

Substituting the outer and inner expansions into Eqs. (68–70) and matching powers of ∈ using appropriate local coordinate transformations in the inner region, and the matching conditions, one obtains the sharp interface equations which are given as follows. At leading order, the nutrient satisfies the quasi-steady diffusion equation:

$${\nabla }^2\sigma =\sigma \text{in}{\Omega }_T,$$ (79)

$$\nabla \cdot (D\left(\varphi \right)\nabla \sigma )=0\text{in}{\Omega }_H,$$ (80)

where σ = σ⁽⁰⁾ and ϕ = ϕ⁽⁰⁾, are the leading order terms in the outer expansions. Further, we obtain ϕ⁽⁰⁾ = 1 in Ω_T and ϕ⁽⁰⁾ = 0 in Ω_H.

By matching the inner and outer expansions near Σ, we obtain the boundary conditions for nutrient and its flux at leading order

$$\left[\sigma \right]=0,[\mathbf{n}\cdot D\left(\varphi \right)\nabla \sigma ]=0\text{on}\Sigma ,$$ (81)

where [·] denotes jump of the quantity across the interface.

The far field boundary condition for nutrient is given by:

$${\left(\sigma \right)}_{\partial \Omega }=1.$$ (82)

We define the bulk velocity u via Darcy's law:

$$\mathbf{u}=-\nabla p+{\chi }_{\sigma }\nabla \sigma ,$$ (83)

where p = μ⁽¹⁾ + χ_σσ⁽⁰⁾ is the modified pressure (and μ⁽¹⁾ = f″(ϕ⁽⁰⁾)ϕ⁽¹⁾ – χ_σσ⁽⁰⁾). We note that from outer expansions we obtain that μ⁽⁰⁾ is a constant (μ⁽⁰⁾ = 0), so p is defined in terms of μ⁽¹⁾. Also from outer expansions we arrive at the continuity equation for velocity field:

$$\nabla \cdot \mathbf{u}=\mathcal{P}\sigma -\mathcal{A}\text{in}{\Omega }_T.$$ (84)

The normal velocity at the tumor interface is given by:

$$V=-\mathbf{n}\cdot {(\nabla p)}_{\Sigma }+{\chi }_{\sigma }\mathbf{n}\cdot {(\nabla \sigma )}_{\Sigma }.$$ (85)

By matching the inner and outer expansions near Σ, we obtain the boundary condition for the modified pressure p:

$${\left(p\right)}_{\Sigma }={\tilde{\mathcal{G}}}^{-1}\kappa ,$$ (86)

where ${\tilde{\mathcal{G}}}^{-1}={\mathcal{G}}^{-1}\tau$, and $\tau ={\int }_0^1\sqrt{2f\left(\varphi \right)}d\varphi$, is the cell-cell adhesion parameter, κ is the local total curvature.

It should be noted that the sharp interface limit is an extension (inclusion of taxis) of previous single phase models.

3.5 Linear analysis

In this section, we perform a linear stability analysis of the sharp interface limit equations (79–86) we obtained in the preceding section. In [29,51], Cristini et al. and Li et al. analyzed the linear stability of perturbed radially symmetric and spherically symmetric tumors. Here, we extend their results to take into account taxis due to nutrient.

We consider a perturbation of a radially symmetric tumor interface Σ [29,51]:

$$r(\theta ,\varphi ,t)=\{\begin{array}{cc}R\left(t\right)+\delta \left(t\right)\text{cos}l\theta \hfill & 2\mathrm{d},\hfill \\ R\left(t\right)+\delta \left(t\right)Y_{l,m}(\theta ,\varphi )\hfill & 3\mathrm{d},\hfill \end{array}\phantom{\}}$$ (87)

where r is the radius of the perturbed sphere, R is the radius of the underlying sphere, δ is the dimensionless perturbation size and Y_l,m is a spherical harmonic, l and θ are the polar wavenumber and angle, and m and ϕ are the azimuthal wavenumber and angle.

We assume that the nutrient diffuses from the surface of a sphere of radius R₀, where R₀ >> R, and the nutrient at R₀ is assumed to be 1. It can be shown that the evolution equation for the tumor radius R is given by:

$$\frac{dR}{dt}=V=\{\begin{array}{cc}{C}_2\mathcal{P}-\mathcal{A}R∕2\hfill & 2\mathrm{d},\hfill \\ C_3\mathcal{P}-\mathcal{A}R∕3\hfill & 3\mathrm{d},\hfill \end{array}\phantom{\}}$$ (88)

where $C_2=\frac{\mathcal{D}\frac{I_1\left(R\right)}{I_0\left(R\right)}}{\mathcal{D}+R\text{log}\frac{R_0}{R}\frac{I_1\left(R\right)}{I_0\left(R\right)}}$, and $C_3=\frac{\mathcal{D}(\frac{1}{\text{tanh}\left(R\right)}-\frac{1}{R})}{\mathcal{D}+R\frac{R_0-R}{R_0}(\frac{1}{\text{tanh}\left(R\right)}-\frac{1}{R})}$. We note that the radial velocity is independent of χ_σ.

The equation for the shape perturbation δ/R is given by:

$${\left(\frac{\delta }{R}\right)}^{-1}\frac{d\left(\frac{\delta }{R}\right)}{dt}=\{\begin{array}{cc}-{\tilde{\mathcal{G}}}^{-1}\frac{l(l^2-1)}{R^3}+l\frac{\mathcal{A}}{2}-\frac{(l+2\mathcal{D})\mathcal{P}-l{\chi }_{\sigma }}{\mathcal{D}R}{C}_2\hfill & \hfill \\ +\frac{(1+\mathcal{D})l\mathcal{P}-l{\chi }_{\sigma }}{R\left(\frac{(1+\mathcal{D})l}{R}+\frac{I_{l+1}\left(R\right)}{I_l\left(R\right)}\right)}{C}_2\left[\frac{I_0\left(R\right)}{I_1\left(R\right)}+\frac{1-\mathcal{D}}{\mathcal{D}}\left(\frac{l}{R}+\frac{I_{l+1}\left(R\right)}{I_l\left(R\right)}\right)\right]\hfill & 2\mathrm{d},\hfill \\ -{\tilde{\mathcal{G}}}^{-1}\frac{l(l+2)(l-1)}{R^3}+l\frac{\mathcal{A}}{3}-\frac{(l+3\mathcal{D})\mathcal{P}-l{\chi }_{\sigma }}{\mathcal{D}R}{C}_3\hfill & \hfill \\ +\frac{((1+\mathcal{D})l+\mathcal{D})\mathcal{P}-l{\chi }_{\sigma }}{R\left(\frac{(1+\mathcal{D})l+\mathcal{D}}{R}+\frac{I_{l+\frac{3}{2}}\left(R\right)}{I_{l+\frac{1}{2}}\left(R\right)}\right)}{C}_3\left[\frac{1}{\frac{1}{\text{tanh}\left(R\right)}-\frac{1}{R}}+\frac{1-\mathcal{D}}{\mathcal{D}}\left(\frac{l}{R}+\frac{I_{l+\frac{3}{2}}\left(R\right)}{I_{l+\frac{1}{2}}\left(R\right)}\right)\right]\hfill & 3\mathrm{d},\hfill \end{array}\phantom{\}}$$ (89)

where $I_{l+\frac{3}{2}}\left(R\right)$ and $I_{l+\frac{1}{2}}\left(R\right)$ are the modified Bessel functions of the first kind. A complete derivation is given in [50].

At the level of linear theory, perturbations consisting of different spherical harmonics are superpositions of the above solutions. Observe that in 3d the shape perturbation depends on l but not on m.

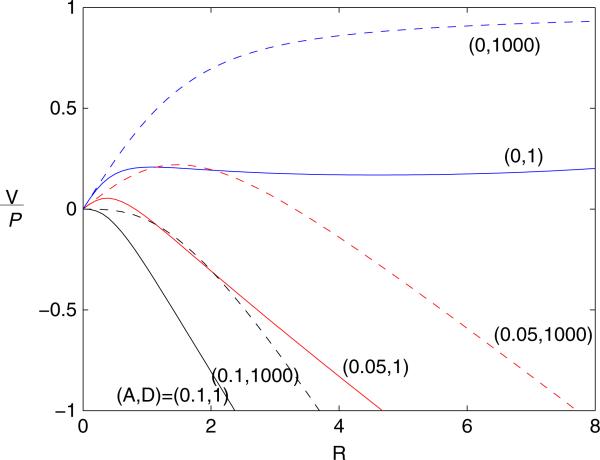
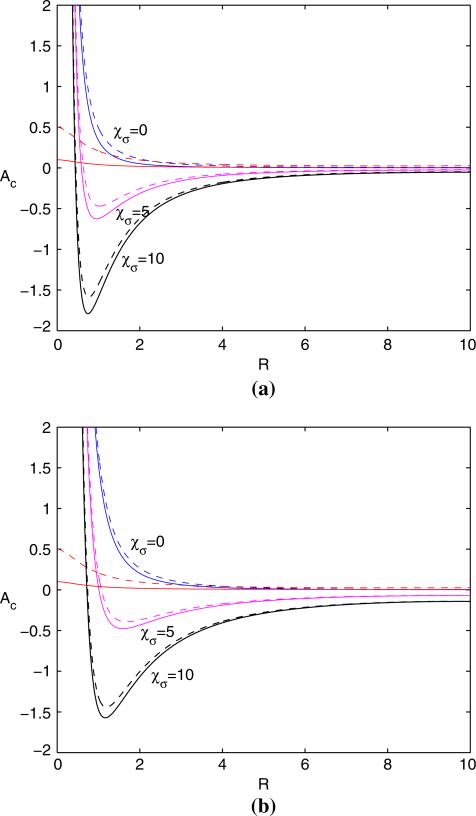
Figure 1 shows the rescaled rate of growth $V∕\mathcal{P}$ as a function of unperturbed tumor radius R in 2d. For a given $\mathcal{A}$ and diffusion constant D, evolution from initial condition R(0) occurs along the corresponding curve. Note that for 3d, the results are qualitatively similar. Figure 2a characterizes the stability region by keeping $\mathcal{P}$ constant and varying $\mathcal{A}$ as a function of the unperturbed radius R such that d(δ/R)/dt = 0:

$${\mathcal{A}}_c=\{\begin{array}{cc}{\mathcal{G}}^{-1}\tau \frac{2(l^2-1)}{R^3}+2\frac{\left(1+\frac{2\mathcal{D}}{l}\right)\mathcal{P}-{\chi }_{\sigma }}{\mathcal{D}R}{C}_2\hfill & \hfill \\ -2\frac{(1+\mathcal{D})\mathcal{P}-{\chi }_{\sigma }}{R\left(\frac{(1+\mathcal{D})l}{R}+\frac{I_{l+1}\left(R\right)}{I_l\left(R\right)}\right)}{C}_2\left[\frac{I_0\left(R\right)}{I_1\left(R\right)}+\frac{1-\mathcal{D}}{\mathcal{D}}\left(\frac{l}{R}+\frac{I_{l+1}\left(R\right)}{I_l\left(R\right)}\right)\right]\hfill & 2\mathrm{d},\hfill \\ {\mathcal{G}}^{-1}\tau \frac{3(l+2)(l-1)}{R^3}+3\frac{\left(1+\frac{3\mathcal{D}}{l}\right)\mathcal{P}-{\chi }_{\sigma }}{\mathcal{D}R}{C}_3\hfill & \hfill \\ -3\frac{((1+\mathcal{D})+\frac{\mathcal{D}}{l})\mathcal{P}-{\chi }_{\sigma }}{R\left(\frac{(1+\mathcal{D})l+\mathcal{D}}{R}+\frac{I_{l+\frac{3}{2}}\left(R\right)}{I_{l+\frac{1}{2}}\left(R\right)}\right)}{C}_3\left[\frac{1}{\frac{1}{\text{tanh}\left(R\right)}-\frac{1}{R}}+\frac{1-\mathcal{D}}{\mathcal{D}}\left(\frac{l}{R}+\frac{I_{l+\frac{3}{2}}\left(R\right)}{I_{l+\frac{1}{2}}\left(R\right)}\right)\right]\hfill & 3\mathrm{d},\hfill \end{array}\phantom{\}}$$ (90)

where ${\mathcal{A}}_c$ is the critical value which divides the plot into regions of stable growth (the region $\mathcal{A}<{\mathcal{A}}_c$ (i.e., below the curve)) and regions of unstable growth (the region $\mathcal{A}>{\mathcal{A}}_c$) for a given mode l. We focus on the parameter $\mathcal{G}=20\tau$ such that ${\mathcal{G}}^{-1}\tau =0.05$ which matches the surface tension as in [29]. In the figure, only the 2d result is shown (3d is qualitatively similar). In Fig. 2a, we plot ${\mathcal{A}}_c$ as a function of R, l = 2, $\mathcal{P}=0.1$ (solid), $\mathcal{P}=0.5$ (dashed), and χ_σ labeled. The figure reveals that the taxis destabilizes the tumor evolution and the curves are pulled downward when $\mathcal{P}$ is smaller. Figure 2b shows a similar result for l = 4. The result illustrates that when l is larger, the curves shift to the right and hence mode l = 4 is more stable for this set of parameters.

Fig. 1.

Two dimensional tumor growth, $\mathcal{P}=0.1$. Rescaled rate of growth $V∕\mathcal{P}$ as a function of unperturbed radius tumor radius R, $\mathcal{A}$ and $\mathcal{D}$ labeled

Fig. 2.

Spherically symmetric tumor growth. Apoptosis parameter ${\mathcal{A}}_c$ as a function of unperturbed radius R from condition (90) in 2d, R₀ = 13, $\mathcal{D}=1$, and χ_σ labeled. Solid: $\mathcal{P}=0.1$; Dashed: $\mathcal{P}=0.5$. The two curves that intersect the y-axis correspond to the relation between $\mathcal{A}$ and the stationary radius for $\mathcal{P}=0.1$ and 0.5. a l = 2. b l = 4

It should be noted that when the taxis is absent and the diffusion constant outside the tumor is large, we recover the linear stability analysis in [29,51].

4 Numerical method

In this section we describe the nonlinear multigrid method used to solve Eqs. (68)–(73). The basis of our approach is the solver developed by Wise et al. [68] for sixth-order strongly anisotropic Cahn–Hilliard equations. In our work, the governing equation is of Cahn–Hilliard type, which is a fourth-order nonlinear parabolic partial differential equation, augmented with a diffusion equation for the nutrient. A centered-difference approximation is used for the space discretization so that the scheme is second order accurate in space. If an explicit time discretization method were used, a time step restriction of the order Δt ≤ Ch⁴, where h is the grid size and C is a constant, would be required. To overcome the time step restrictions, an implicit discretization in time is used here that results in nonlinear equations at implicit time levels. However, most implicit schemes for Cahn–Hilliard equations have time step restrictions due to solvability conditions. To overcome the solvability restrictions, we further employ a gradient stable discretization scheme (see [32,33]) so that the nonlinear equations arising from the discretization of the Cahn–Hilliard part are solvable for very large time steps and that the system energy (in the absence of mass exchange terms) is nonincreasing for any time step.

To solve the nonlinear equations at the implicit time level we use a nonlinear multilevel/multigrid method whose complexity is optimal, i.e., the number of operations to solve the equations is O(N), where N is the number of unknowns. We use block-structured Cartesian mesh refinement, which is ideal for the nonlinear multigrid algorithm. The details of the adaptive nonlinear multigrid algorithm can be found in the work by Wise et al. [68].

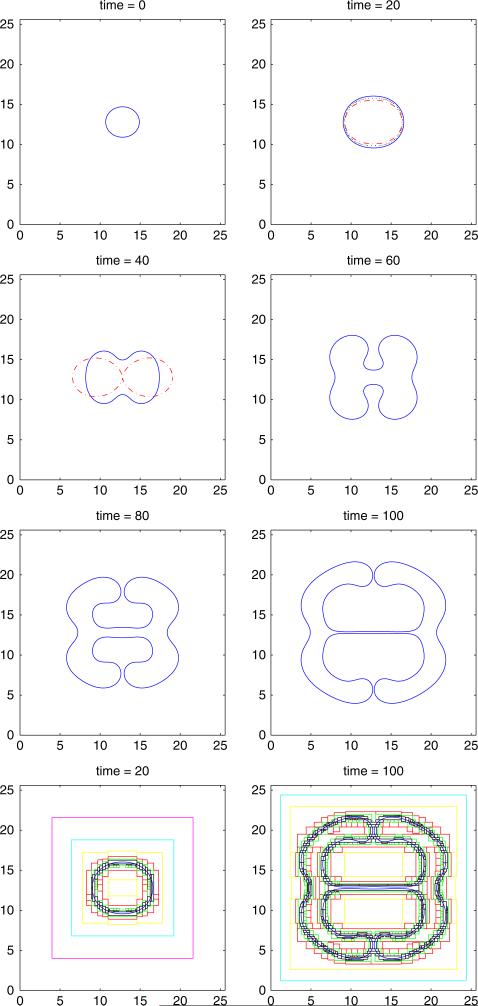
To perform mesh refinement, we first start with a multilevel, block-structured mesh, then we refine the mesh by constructing new multilevel, block-structured mesh based on the undivided gradient test (Wise et al. [68]). This test first finds the set of grid cells where the finite differences of the cell volume fraction are large, then the set is expanded by buffering and a new, refined Cartesian mesh is placed over the tagged regions. After the new grids have been constructed, the field variables are transferred from the old grid to the new grid by interpolation [68]. Accordingly, the mesh will be refined in the diffuse interface region where the cell volume fraction exhibits a sharp transition. We then solve the problem on the refined mesh using the adaptive version of the FAS Multigrid method [64]. Figure 6 (last row) shows the boundaries of the locally refined Cartesian mesh patches (each nested mesh has one-half the mesh size of the parent mesh) at two times during the evolution. More details of the adaptive mesh refinement can be found in Wise et al. [68].

Fig. 6.

Evolution of the tumor surface (2d), $\mathcal{P}=1$, $\mathcal{A}=0.5$, $\mathcal{D}=100$, ∈ = 0.005, χ_σ = 0, and initial tumor surface as in Eq. (92). The ϕ = 0.5 contour is shown, where in the interior of the shape ϕ ≈ 1 and in the exterior ϕ ≈ 0. Solid: nonlinear simulation; Dash-dotted: solution from linear analysis. Dotted: ∈ = 0.002, the coarsest level is 32 × 32 and the finest level has the equivalent resolution a uniform 4096 × 4096 mesh. The last row shows the boundaries of the locally refined Cartesian mesh patches (each nested mesh has one-half the mesh size of the parent mesh) at times t = 20 and 100

5 Numerical results

Here, we investigate the nonlinear evolution of a tumor proliferating into surrounding tissue. We focus on the parameter $\mathcal{G}=1$. We use the double-well potential f (ϕ) = 0.18ϕ²(ϕ – 1)²/4, and so the convex functions f_e and f_c can be chosen as f_e(ϕ) = 0.18 (4 (ϕ – 1/2)⁴ + 1/4) / 16 and f_c(ϕ) = 0.18 (ϕ – 1/2)² /8. We note that with this choice of f (ϕ), $\tilde{\mathcal{G}}=20$ in Eq. (86) which matches the surface tension in [29,51]. We present a spherically symmetric tumor growth in Sect. 5.1, then two-dimensional tumor growth showing invasion and the development of branched tubular structures in Sect. 5.2.

5.1 Spherically symmetric tumor growth

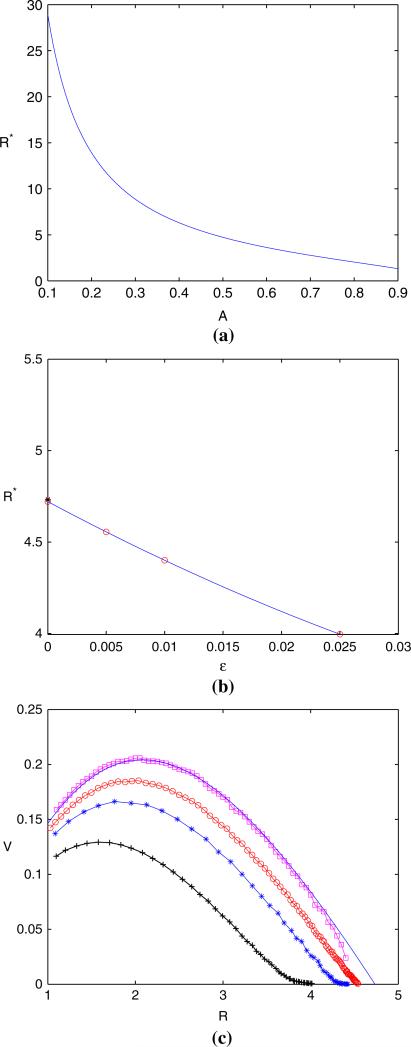
We begin by comparing results from the sharp interface model (79–82) to the mixture model in spherical geometries. In spherical geometry, the tumor velocity is given by Eq. (88). The steady-state occurs at the point R* where V (R*) = 0. Note, if $\mathcal{A}=0$, there is no steady-state. By setting V = 0 identically in Eq. (88) and using Newton's method, we find R* as a function of $\mathcal{A}$ as shown in Fig. 3a.

Fig. 3.

Spherical symmetric tumor growth, $\mathcal{P}=1$, $\mathcal{A}=0.5$, $\mathcal{D}=1000$, and χ_σ = 0. a Steady-state radius as a function of A by setting V (R*) = 0 in Eq. (88). b Convergence of steady state interface position with respect to ∈. Circle: nonlinear simulations of steady state interface positions for ∈ = 0.005, ∈ = 0.01 and ∈ = 0.025, the interface position at ∈ = 0 is the least-square fit of those at ∈ = 0.025, ∈ = 0.01 and ∈ = 0.005; Star: interface position predicted by sharp interface model. c Convergence of tumor interface velocity with respect to ∈. $\mathcal{P}$, $\mathcal{D}$ and χ_σ are the same as (a). Circle: ∈ = 0.005; Star: ∈ = 0.01; Plus: ∈ = 0.025; Square: Linear extrapolation of ∈ = 0.01 and ∈ = 0.005; Solid: Sharp interface model given in Eq. (88)

Next, we investigate the nonlinear evolution of spherically symmetric tumors using the model (68–73). We focus on the parameters the $\mathcal{P}=1$, $\mathcal{A}=0.5$, $\mathcal{D}=1000$ (i.e., the diffusion constant outside the tumor is 1000 times larger than that inside) for our nonlinear simulations. The initial shape of the tumor is given by:

$$\{\begin{array}{cc}\varphi \left(r\right)=1\hfill & 0\le r\le 1,\hfill \\ \varphi \left(r\right)=0\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$ (91)

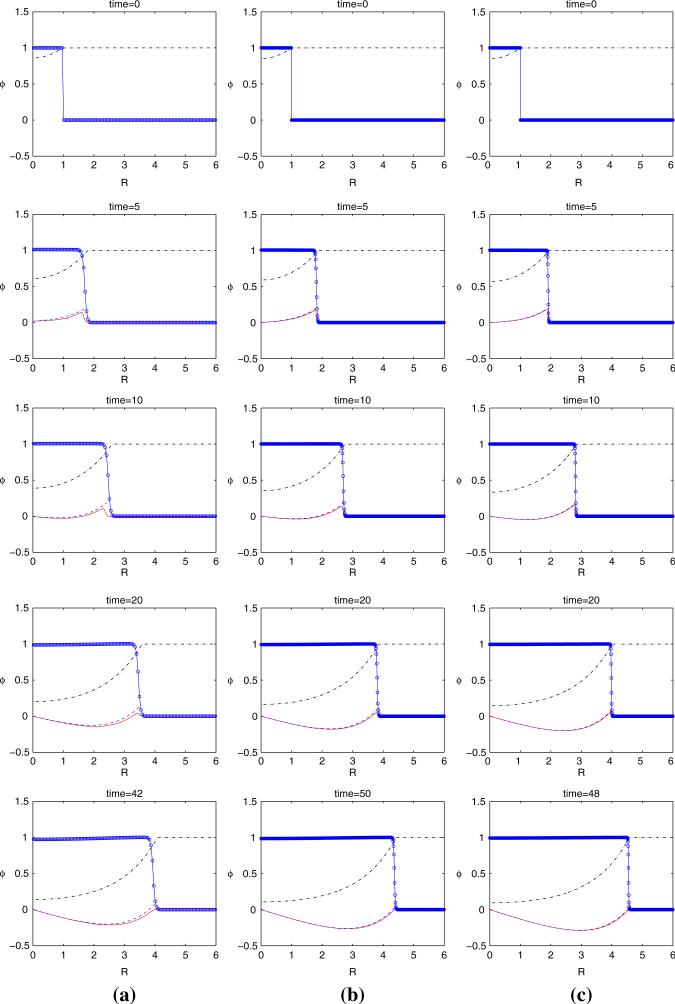
In Fig. 3b, we show the convergence of steady state tumor interface positions generated from nonlinear simulations with three values of ∈. The steady-state radii (circles) are generated from three numerical simulations: ((i) ∈ = 0.025, N = 128, (ii) ∈ = 0.01, N = 512 and (iii) ∈ = 0.005, N = 1024), where N denotes the number of mesh points in the simulation. The interface position (circles) at ∈ = 0 is the least-square fit using the data of (i), (ii), and (iii). The result agrees very well with the steady state tumor interface position predicted by sharp interface limit (star). The corresponding velocities at the tumor interface during evolution in time for the above three numerical simulations is depicted in Fig. 3c. The squared curve represents the linear extrapolated velocity at ∈ = 0 using the data of (ii) and (iii). The solid curve represents the tumor velocities at the tumor interface predicted by sharp interface limit. We see that as ∈ becomes smaller, the numerical results of the mixture model approaches that from the sharp interface limit.

In Fig. 4, the tumor evolution generated from the nonlinear simulations described previously in Fig. 3 is shown. In (a), ∈ = 0.025 while ∈ = 0.01 in (b) and ∈ = 0.005 in (c). The dash-dotted curve shows the nutrient concentration profile. The circled curve shows ϕ, (the circle stands for the position of a mesh point). The solid curve shows the tumor velocity of the mixture model and the dashed curve corresponds to the tumor velocity of the sharp interface limit. Initially, the tumor grows rapidly with all tumor cells moving outward as the velocity is positive for the whole tumor (corresponding to the plot at t = 1 and t = 5). As the tumor grows larger, cell death in center due to apoptosis overcomes proliferation because nutrient is low (which implies a low proliferation rate). As a consequence, the tumor forms a low pressure near the center so that the tumor cells are driven towards the center (corresponding to the figure at t = 20, water is correspondingly fluxed outward). Finally, the tumor reaches steady-state around time t = 42 with the cell proliferation balanced by apoptosis. We see that as ∈ becomes smaller, the tumor interface becomes sharper, and the tumor velocity of the mixture model becomes closer to that from the sharp interface limit.

Fig. 4.

Details of the evolution of the tumor interface in time corresponding to the numerical simulation in Fig. 3. a ∈ = 0.025, b ∈ = 0.01, c ∈ = 0.005. Dash-dotted: nutrient concentration profile; Dashed: tumor velocity predicted by the sharp interface limit given in Eqs. (79–81); Solid: the tumor velocity of mixture model. The tumors reach steady state by the end of the simulations

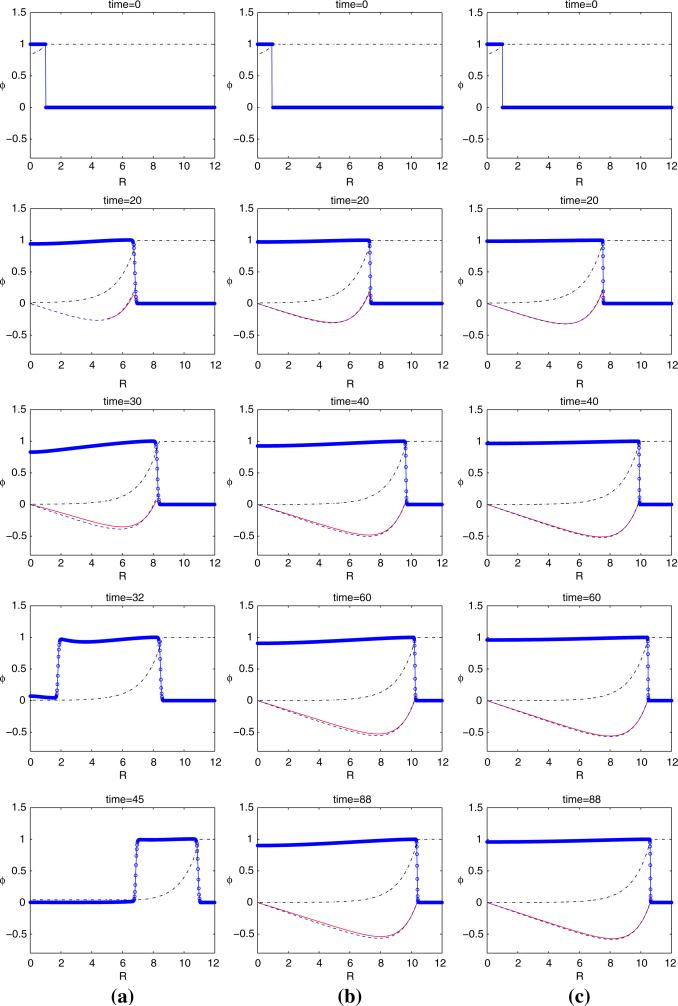
Next, we investigate the effect of a smaller apoptosis rate on tumor evolution. We set $\mathcal{A}=0.25$, all other parameters are same as the previous study. We note that when $\mathcal{A}=0.25$, R* = 10.899 which is significantly larger than the critical radius R* = 4.7333 for $\mathcal{A}=0.5$. In Fig. 5, we show the tumor evolution generated from the nonlinear simulations for $\mathcal{A}=0.25$. In (a), ∈ = 0.025 while ∈ = 0.01 in (b) and ∈ = 0.005 in (c). In (a), we observe that at t = 30, cell death in center due to apoptosis overcomes proliferation because nutrient is low. Indeed, the nutrient concentration level near the center is almost 0 and the tumor cells are starved of nutrient. As a result, the tumor volume fraction near the center drops to about 0.8 because the tumor cells generated near the tumor/host interface are not able to replenish the center. At t = 32, the tumor volume fraction near the center drops below the spinodal point (the point where d² f/d²ϕ changes sign), the tumor cells are not able to support the structure so that it collapses, and it tends to form a ring due to cell-cell adhesion that pulls the cells from the inner region toward the more dense periphery. There is no steady state solution and the ring then travels towards the right boundary. If we compare this simulation to the case with $\mathcal{A}=0.5$, we see that for $\mathcal{A}=0.5$, the steady state radius is much smaller and the tumor cells are therefore able to replenish the center. Therefore, the tumor does not form a ring. In (b) and (c), smaller ∈ implies a larger cell mobility via Eq. (68). Thus more tumor cells are able to reach the center, the tumor volume fraction near the center is higher than that for smaller cell mobility, and the tumor avoids the formation of a ring. Indeed, the tumor reaches steady state at the time as labeled.

Fig. 5.

The evolution of the tumor interface in time for $\mathcal{A}=0.25$. a ∈ = 0.025, b ∈ = 0.01, c ∈ = 0.005. Dash-dotted: nutrient concentration profile; Dashed: tumor velocity predicted by the sharp interface limit given in Eqs. (79–81); Solid: the tumor velocity of mixture model. The tumors reach steady state by the end of the simulations for (b) and (c)

5.2 2D tumor growth

We first investigate tumor growth into a nutrient-rich microenvironment with a large proliferation rate. We focus on the parameters $\mathcal{P}=1$, $\mathcal{A}=0.5$, $\mathcal{D}=100$, and χ_σ = 0, i.e., there is no taxis. We note that this choice of parameters is consistent with that given in [29,54,70].

In Fig. 6, the morphological evolution of a tumor without taxis is shown from the initial radius:

$$(x\left(\alpha \right)-12.8,y\left(\alpha \right)-12.8)=(2+0.1\text{cos}2\alpha )(\text{cos}\alpha ,\text{sin}\alpha ),$$ (92)

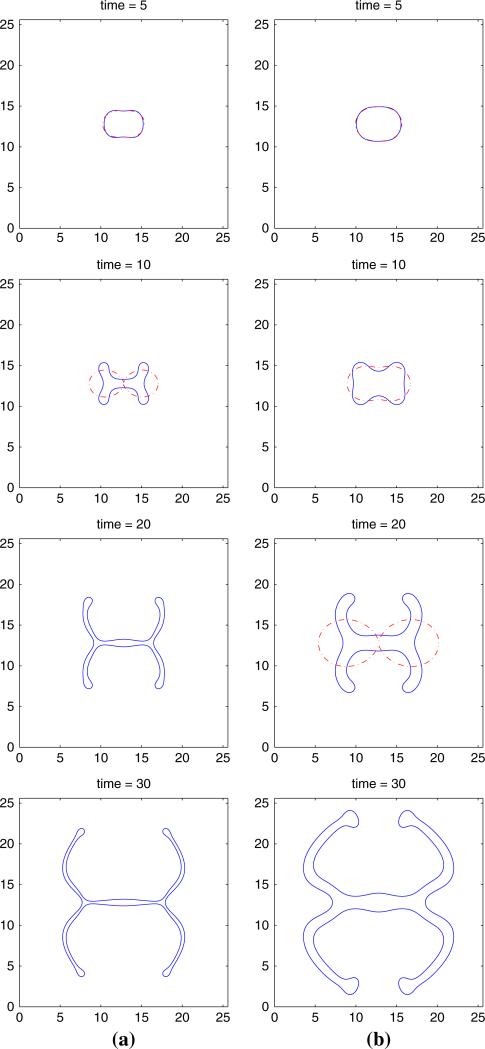
with ∈ = 0.005, and χ_σ = 0. The computational domain is Ω = [0, 25.6] × [0, 25.6]. The coarsest mesh level is 32 × 32 and the finest level has equivalent resolution of a uniform 2048 × 2048 mesh. We note that for this mesh resolution, there are about six mesh points across the tumor interface, and our empirical study shows that the interface can be well resolved by placing about six points across the interface. At early times, the perturbation size increases slowly and the tumor becomes ellipse-like, good agreement is obtained with the results of the linear stability analysis (dash-dotted) and nonlinear simulations (solid) and is improved as ∈ → 0 (the dotted curve shows the nonlinear result at smaller ∈). As the tumor continues to grow, a shape instability develops and necks form around time t = 40. The tumor develops large buds and the buds tend to bend inward around time t = 60 in a manner similar to that seen in [29]. We note that while the numerical result in [29] illustrates that the large buds would reconnect in the end, our numerical result shows that at larger time, though the large buds tend to advance toward each other, they never reach each other. Instead, the tumor continues to spread out into the surrounding tissue. The last row shows the boundaries of the locally refined Cartesian mesh patches (each nested mesh has one-half the mesh size of the parent mesh) at two times during the evolution.

We next investigate tumor growth into a nutrient-poor microenvironment with low proliferation rate. In this regime, cell apoptosis rate is small, so we set $\mathcal{A}=0$ in the simulation, i.e., we neglect tumor apoptosis. We focus on the parameters $∊=0.005$ and $\mathcal{D}=1$. We further use an adaptive mesh where the coarsest level is 32 × 32 and the finest level has the equivalent resolution of a uniform 2048 × 2048 mesh.

We investigate the effects of the nutrient-taxis. It has been observed in experiments that nutrient deprivation can importantly contribute to increase the invasive behavior of a tumor. In some situations, the tumor may even develop branched tubular structures (e.g., [57]). We show below that nutrient taxis in hypoxic and low-proliferating cells environment produces branched invasive structures.

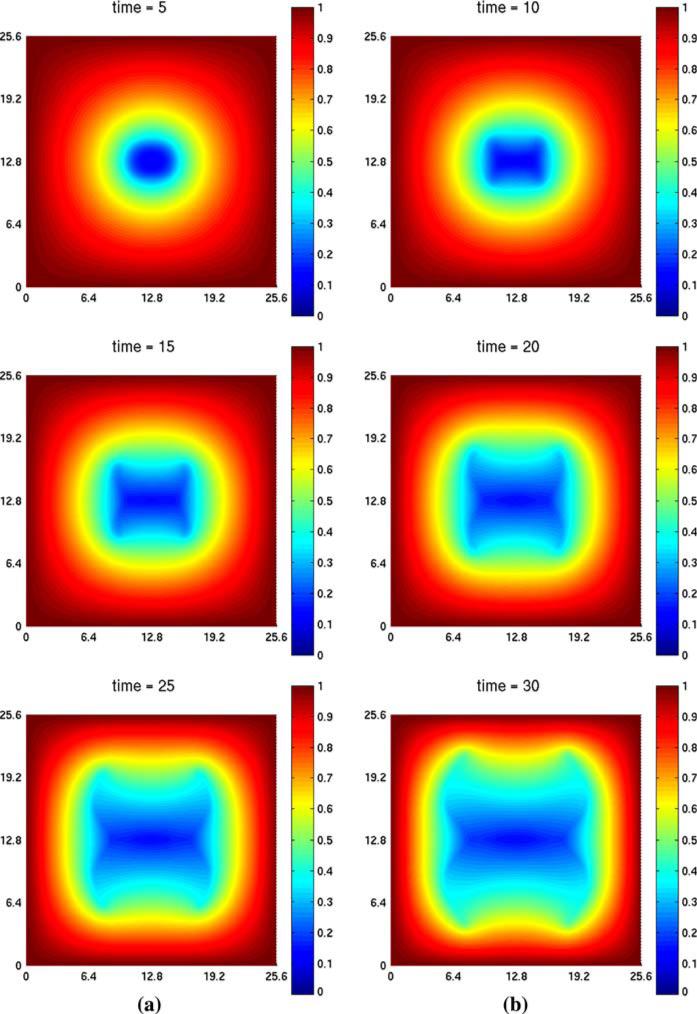
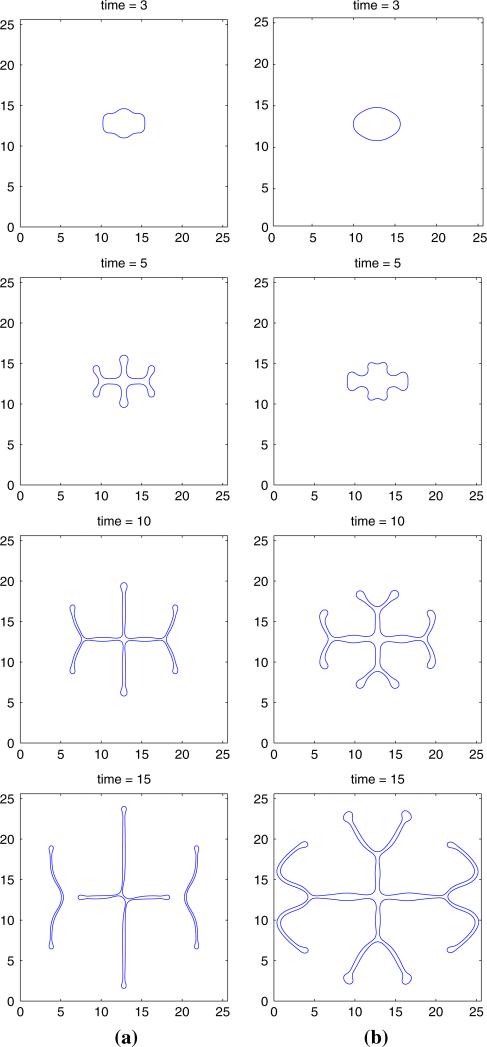
In Fig. 7a, the tumor evolution for $\mathcal{P}=0.1$, and χ_σ = 5 is shown (we note that if χ_σ = 0, i.e., when there is no taxis, the evolution is stable). The solid curve represents the tumor interface and dash-dotted curve represents the linear results for the sharp interface model. The figure illustrates that fingers develop around time t = 10 and get stretched out at time t = 20, forming long, slim and invasive fingers, thereby increasing the surface area of the tumor and allowing better access to nutrient. At later times, the fingers continue to stretch and the fingers tend to bend inward (as in the case with linear $\mathcal{P}=1$, χ_σ = 0 considered previously). There is good agreement between the and nonlinear results at early times although there is significant deviation at later times due to strong nonlinearity. Figure 7b shows similar simulations of tumor evolution for $\mathcal{P}=0.5$. All other parameters are the same as Fig. 7a. We observe that the fingers are thicker for $\mathcal{P}=0.5$ than those for $\mathcal{P}=0.1$, and the spread of the fingers into the surrounding tissue for $\mathcal{P}=0.1$ is more pronounced at early times. As before, there is good agreement between the linear and nonlinear results at early times before nonlinear effects dominate the evolution. Finally, in Fig. 8, contour plots of the nutrient concentration are shown. We observe that the nutrient level decreases from the outer boundary towards the center of the tumor with the most rapid decrease occuring in the region near the tumor/host interface. This provides the driving force for the taxis of tumor cells.

Fig. 7.

Evolution of the tumor surface, with $\mathcal{A}=0$, $\mathcal{D}=1$, ∈ = 0.005, χ_σ = 5, and the initial tumor surface as in Eq. (92). The ϕ = 0.5 contour is shown, where in the interior of the shape ϕ ≈ 1 and in the exterior ϕ ≈ 0. a $\mathcal{P}=0.1$; b $\mathcal{P}=0.5$. Solid: nonlinear simulation; Dash-dotted: linear results

Fig. 8.

Contour plots of nutrient concentration evolution corresponding to the simulation in Fig. 7a

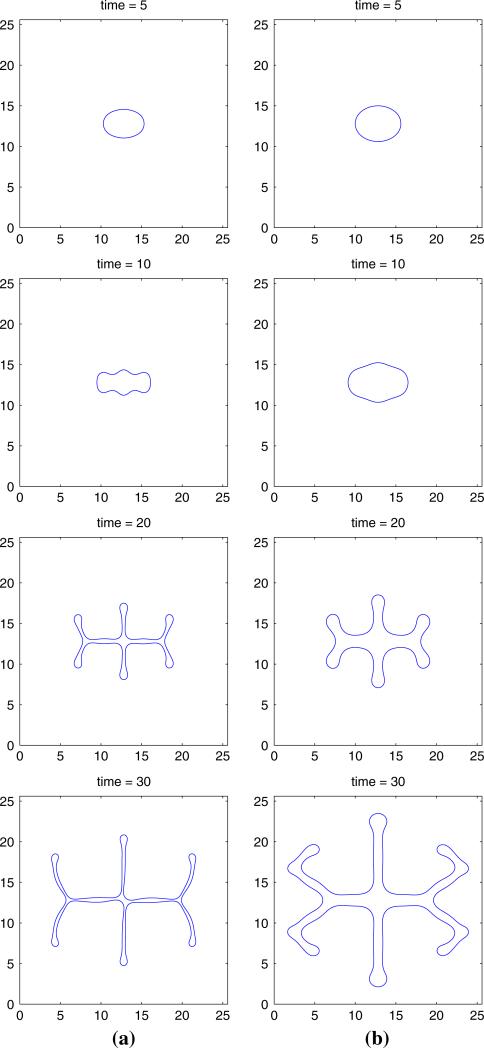
In Fig. 9, we show the morphological evolution of tumors with larger taxis coefficient χ_σ = 10. As before, there is good agreement between the linear and nonlinear results at early times. When χ_σ is larger, the instability is more pronounced, forming slimer, more invasive fingers, and we observe that the tumor pinches off and forms a small satellite tumor near the center at time t = 15 in Fig. 9a. The numerical results therefore reveal that the tumor may suffer from nutrient-taxis-driven fingering instabilities which are most dramatic when cell proliferation is low. This suggests that nutrient-taxis may play a role in tumor invasion and that the diffusional instability is exacerbated by nutrient gradients.

Fig. 9.

Evolution of the tumor surface for $\mathcal{A}=0$, $\mathcal{D}=1$, ∈ = 0.005, χ_σ = 10, and the initial tumor surface as in Eq. (92). The ϕ = 0.5 contour is shown, where in the interior of the shape ϕ ≈ 1 and in the exterior ϕ ≈ 0. a $\mathcal{P}=0.1$; b $\mathcal{P}=0.5$. Solid: nonlinear simulation; Dash-dotted: linear results

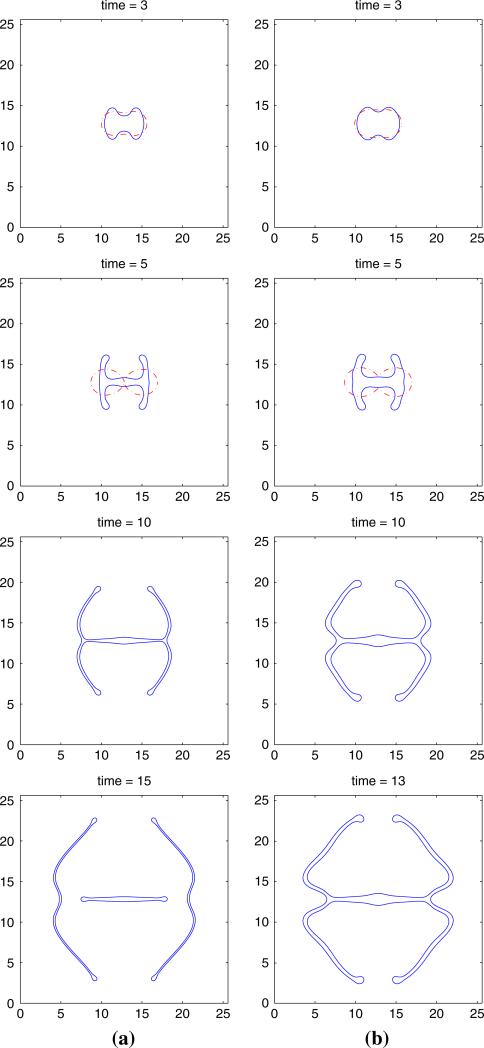
In Figs. 10 and 11, the morphological evolution is shown of tumors evolving from a different initial condition:

$${\left(\frac{x-12.8}{2.1}\right)}^2+{\left(\frac{y-12.8}{1.9}\right)}^2=1.$$ (93)

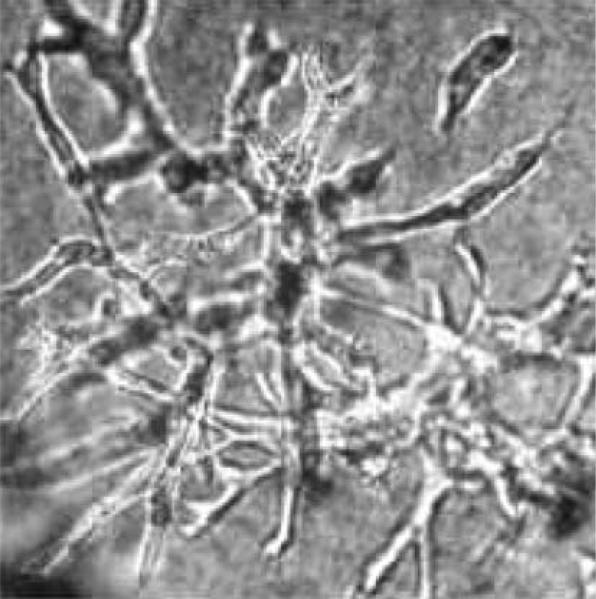
As before, the morphological evolution is shown for two values of χ_σ (χ_σ = 5 for Fig. 10 and χ_σ = 10 for Fig. 11) and $\mathcal{P}=0.1,0.5$. Qualitatively, the evolution is similar to that obtained for the initial radius given in Eq. (92). (Here, however the tumor with $\mathcal{P}=0.5$ bends away from the boundary of computational domain in order to more up nutrient gradients). We observe that the tumor exhibits a more branched tubular structure. This reminiscent of the in vitro experimental observations in [57] where tumor spheroids were embedded into a collagen gel in hypoxic conditions. After 24 h, cell colonies were analyzed by microscopy and representative spheroids photographed. A typical branching morphology from the experiment is shown in Fig. 12.

Fig. 10.

Evolution of the tumor surface, with $\mathcal{A}=0$, $\mathcal{D}=1$, ∈ = 0.005, χ_σ = 5, and the initial tumor surface as in Eq. (93). The ϕ = 0.5 contour is shown, where in the interior of the shape ϕ ≈ 1 and in the exterior ϕ ≈ 0. a $\mathcal{P}=0.1$; b $\mathcal{P}=0.5$

Fig. 11.

Evolution of the tumor surface, with $\mathcal{A}=0$, $\mathcal{D}=1$, ∈ = 0.005, χ_σ = 10, and the initial tumor surface as in Eq. (93). The ϕ = 0.5 contour is shown, where in the interior of the shape ϕ ≈ 1 and in the exterior ϕ ≈ 0. a $\mathcal{P}=0.1$; b $\mathcal{P}=0.5$

Fig. 12.

In vitro experimental evidence. Hypoxia-induced invasive growth with a branched tubular structure from the study by Pennacchietti et al. [57]

6 Conclusion

In this work, we have developed, analyzed and simulated numerically a thermodynamically consistent mixture model for avascular tumor growth. The derivation of governing equations relied on mass and momentum balance equations and thermodynamic consistent constitutive laws are employed to supplement those equations. We then reduced the model to a special case which is similar to the closure models of Ambrosi and Preziosi [3]. The mixture model takes into account the effects of cell-to-cell adhesion, and taxis inducing chemical and molecular species. Cell-to-cell adhesion was also investigated in previous works (e.g., [3,23]), however their models behave like backward parabolic equations when the cellular fraction is within a certain range and thus are ill-posed. In contrast, our mixture model is well-posed and the governing equations are of Cahn–Hilliard type. When there are only two phases, an asymptotic analysis showed that single-phase models of the type used in [29,51] can be recovered as limiting cases of a two-phase model.

To solve the governing equations, we developed a numerical algorithm based on an adaptive Cartesian block-structured mesh refinement scheme. A centered-difference approximation was used for the space discretization so that the scheme was second order accurate in space. An implicit discretization in time was used which resulted in nonlinear equations at implicit time levels. We further employed a gradient stable discretization scheme (see [32,33]) so that the nonlinear equations were solvable for very large time steps. To solve these equations we used a nonlinear multilevel/multigrid method which was of an optimal order O (N) where N was the number of grid points.

Spherically symmetric and fully two dimensional nonlinear numerical simulations were performed using our adaptive multigrid/finite-difference scheme. We investigated tumor evolution in nutrient-rich and nutrient-poor tissues. A number of important results have been uncovered. For example, we demonstrated that taxis of tumor cells up nutrient gradients (nutrient-taxis) may drive fingering instabilities which are most dramatic when cell proliferation is low, as predicted by linear stability theory. This is also observed in experiments. Indeed, experimental evidence suggests that nutrient deprivation can importantly contribute to increase the invasive behavior of a tumor. In some situations, the tumor may even develop branched tubular structures (e.g., [57]) where premetastatic clusters of tumor cells invade the host tissue [39]. This work showed that nutrient-taxis may play a role in tumor invasion and that the diffusional instability is exacerbated by taxis up nutrient gradients. Accordingly, we believe this model is capable of describing complex invasive patterns observed in experiments. Further development of the model to incorporate more realistic biophysical processes such as necrosis, angiogenesis and soft tissue mechanics is underway.

Appendix A: Derivation of the interaction terms

In this Appendix, we demonstrate the thermodynamic consistency of the constituent laws (9), (10) and (12) given in Sect. 2.3. See Bowen [15] and Araujo and McElwain [9] for additional insight on the theory of mixtures.

A.1 The energy equation

Let u_k be the internal energy of the kth component and let internal energy of the mixture be $u=\frac{1}{\rho }{\sum }_{k=0}^{N-1}{\varphi }_k{\rho }_k{u}_k$. Now, let Ω be an arbitrary fixed domain. For simplicity, we consider here the case in which the system is isothermal. Then, the integral form of the mixture energy balance equation is

$$\frac{d}{dt}{\int }_{\Omega }\rho ud\Omega =\sum _{k=0}^{N-1}{\int }_{\partial \Omega }\left(({\sigma }_k\mathbf{n}-{\varphi }_k{\rho }_k{u}_k\mathbf{n})\cdot {\mathbf{v}}_k+\sum _{j=0}^{N-1}{\mathbf{t}}_{kj}\cdot \mathbf{n}\frac{D^k{\varphi }_j}{Dt}\right)d\Sigma +{\int }_{\Omega }\left(\rho r+\sum _{l=1}^L{z}_{kl}\frac{D^k{c}_l}{Dt}+\sum _{k=0}^{N-1}{\rho }_k{\varphi }_k{\mathbf{F}}_k\cdot {\mathbf{v}}_k\right)d\Omega ,$$ (94)

where n is the outward normal to ∂Ω, $\frac{D^k}{Dt}={\partial }_t+{\mathbf{v}}_k\cdot \nabla$ is the advective derivative with respect to the velocity v_k, t_kj are generalized forces that arise due to nonlocality (i.e., dependence of free energy on a nonlocal adhesion potential), z_kl are generalized forces that arise due to taxis, r is the mass-averaged rate of heat supply $r=\frac{1}{\rho }{\sum }_{k=0}^{N-1}{\varphi }_k{\rho }_k{r}_k$ and r_k is the heat added to each phase to keep the mixture isothermal. In Eq. (94), the first term on the right represents the traction and the internal energy fluxes, the second term on the right represents the generalized force due to the presence of gradients of volume fraction or nonlocality in the internal energy, the fourth term represents the generalized forces due to the variation of chemical factors and the fifth represents the energy change due to applied body forces.

Correspondingly, the local energy balance equation is given by

$${\rho }_k{\varphi }_k\frac{D^k{u}_k}{Dt}={\sigma }_k:\nabla {\mathbf{v}}_k+{\rho }_k{\varphi }_k{r}_k+\nabla \cdot \left(\sum _{j=0}^{N-1}{\mathbf{t}}_{kj}\frac{D^k{\varphi }_j}{Dt}\right)+\sum _{l=1}^L{z}_{kl}\frac{D^k{c}_l}{Dt}+{∊}_k,$$ (95)

where ∈_k are energy interaction terms that satisfy

$$\sum _{k=0}^{N-1}({∊}_k+{\Gamma }_k{u}_k-{\pi }_k\cdot {\mathbf{v}}_k)=0.$$ (96)

To make further progress, we turn to the second law of thermodynamics.

A.2 Thermodynamics

Define η_k to be the entropy of each component. Accordingly, the mass-averaged entropy of the mixture is $\eta =\frac{1}{\rho }{\sum }_{k=0}^{N-1}{\varphi }_k{\rho }_k{\eta }_k$. Define the temperature of the mixture to be θ (which is constant because we are dealing with isothermal mixtures). The second law for the mixture, in the form of the Clausius-Duhem inequality [65], is

$$\rho \frac{D\eta }{Dt}+\nabla \cdot \mathcal{J}-\rho r∕\theta \ge 0,$$ (97)

where $\frac{D}{Dt}={\partial }_t+\mathbf{v}\cdot \nabla$ and $\mathcal{J}$ is the diffusion flux. In terms of components, the Clausius-Duhem inequality is

$$\sum _{k=0}^{N-1}\left({\varphi }_k{\rho }_k\frac{D^k{\eta }_k}{Dt}+{\Gamma }_k{\eta }_k-{\varphi }_k{\rho }_k{r}_k∕\theta +\nabla \cdot ({\mathcal{J}}_k-{\varphi }_k{\rho }_k{\eta }_k{\mathbf{w}}_k)\right)\ge 0,$$ (98)

where ${\mathcal{J}}_k$ is the entropy flux for each component and $\mathcal{J}={\sum }_{k=0}^{N-1}{\mathcal{J}}_k$ and w_k = v_k – v is the diffusion velocity.

Since the system is isothermal, it is useful to use the Helmholtz free energy rather than the internal energy. The Helmholtz free energy per unit mass ψ_i of each component is

$${\psi }_k=u_k-\theta {\eta }_k.$$ (99)

In addition, define Ψ_k = ρ_kϕ_kψ_k to be Helmholtz free energy per unit volume.

Next, we take into account that the mixture components are incompressible, that is the densities ρ_k are constant. This implies that the terms in Eq. (95) involving ∇v_k and v_k are not independent. Let p be a scalar function (e.g., Lagrange multiplier). Then,

$$\sum _{k=0}^{N-1}{\rho }_k{\varphi }_{k}p\mathbf{I}:\nabla {\mathbf{v}}_k=-\sum _{k=0}^{N-1}p({\rho }_k-{\rho }_0)\frac{D^k{\varphi }_k}{Dt}-p{\rho }_0\sum _{k=0}^{N-1}{\mathbf{v}}_k\cdot \nabla {\varphi }_k,$$ (100)

where we have used the volume fraction equation (2) together with the conservation of mass (3). Next, observe that only relative velocities are important. Without loss of generality, let us measure velocities relative to that of component 0 (the liquid phase). For example,

$$\sum _{k=0}^{N-1}{\mathbf{v}}_k\cdot \nabla {\varphi }_k=\sum _{k=0}^{N-1}({\mathbf{v}}_k-{\mathbf{v}}_0)\cdot \nabla {\varphi }_k,\sum _{k=0}^{N-1}{\pi }_k\cdot {\mathbf{v}}_k=\sum _{k=0}^{N-1}{\pi }_k\cdot ({\mathbf{v}}_k-{\mathbf{v}}_0).$$ (101)

Using Eqs. (100), (101) and (96), Eq. (95) may be re-written, upon summing over k, as the following equation for the entropy components:

$$\sum _{k=0}^{N-1}\left({\rho }_k{\varphi }_k\frac{D^k{\eta }_k}{Dt}+{\Gamma }_k{\eta }_k-{\varphi }_k{\rho }_k{r}_k∕\theta \right)=-\frac{1}{\theta }\sum _{k=0}^{N-1}\left(\frac{D^k{\Psi }_k}{Dt}-\sum _{l=1}^L{z}_{kl}\frac{D^k{c}_l}{Dt}-({\sigma }_k-({\Psi }_k-{\rho }_k{\varphi }_{k}p)\mathbf{I}):\nabla {\mathbf{v}}_k-\sum _{j=0}^{N-1}(\nabla \cdot {\mathbf{t}}_{kj}+p({\rho }_k-{\rho }_0){\delta }_{kj})\frac{D^k{\varphi }_j}{Dt}-({\pi }_k+p{\rho }_0\nabla {\varphi }_k)\cdot ({\mathbf{v}}_k-{\mathbf{v}}_0)-\sum _{j=0}^{N-1}{\mathbf{t}}_{kj}\cdot \nabla \frac{D^k{\varphi }_j}{Dt}\right),$$ (102)

where δ_jk = 1 if j = k and is zero otherwise.

A.3 Justification of constitutive relations

We next demonstrate that the constitutive relations (9), (10) and (12) posed in Sect. 2.2 are consistent with the second law of thermodynamics (98). We begin with the free energy. Let us take

$${\Psi }_k={\Psi }_k({\varphi }_1,\dots ,{\varphi }_N,\nabla {\varphi }_1,\dots ,\nabla {\varphi }_N,c_1{\varphi }_k,\dots ,c_L{\varphi }_k),$$ (103)

where c_l, l = 1,..., L are chemical factors that may induce taxis. Note that the dependence of Ψ_k on c_l's in Eq. (8) is suppressed [e.g., Eq. (19)]. From Eq. (103) we get

$$\frac{D^k{\Psi }_k}{Dt}=\sum _{j=0}^{N-1}\left(\frac{\partial {\Psi }_k}{\partial {\varphi }_j}\frac{D^k{\varphi }_j}{Dt}+\frac{\partial {\Psi }_k}{\partial \nabla {\varphi }_j}\cdot \frac{D^k(\nabla {\varphi }_j)}{Dt}\right)+\sum _{l=1}^L\frac{\partial {\Psi }_k}{\partial \left(c_l{\varphi }_k\right)}\frac{D^k\left(c_l{\varphi }_k\right)}{Dt}.$$ (104)

Using the identities

$$\frac{D^k}{Dt}\nabla {\varphi }_j=\nabla \frac{D^k{\varphi }_j}{Dt}-\nabla {\mathbf{v}}_k\cdot \nabla {\varphi }_j,$$ (105)

$$\frac{D^k{\varphi }_j}{Dt}=-{\varphi }_j\nabla \cdot {\mathbf{v}}_j+({\Gamma }_j+\nabla \cdot J_j)∕{\rho }_j+({\mathbf{v}}_k-{\mathbf{v}}_j)\cdot \nabla {\varphi }_j,$$ (106)

the total derivative of the Helmholtz free energy for the kth component is given by

$$\frac{D^k{\Psi }_k}{Dt}=\sum _{j=0}^{N-1}{\mu }_{kj}\frac{D^k{\varphi }_j}{Dt}+p({\rho }_k-{\rho }_1)\frac{D^k{\varphi }_k}{Dt}+\sum _{j=0}^{N-1}\nabla \cdot t_{kj}\frac{D^k{\varphi }_j}{Dt}+\sum _{j=0}^{N-1}\frac{\partial {\Psi }_k}{\partial \nabla {\varphi }_j}\cdot \left(\nabla \frac{D^k{\varphi }_j}{Dt}-\nabla {\mathbf{v}}_k\cdot \nabla {\varphi }_j\right).$$ (107)

Using Eqs. (103), (2), the definition of the chemical potential

$${\mu }_{kj}=\frac{\partial {\Psi }_k}{\partial {\varphi }_j}+\left(\sum _{l=1}^L\frac{\partial {\Psi }_k}{\partial \left(c_l{\varphi }_k\right)}{c}_l-p({\rho }_k-{\rho }_0)\right){\delta }_{kj}-\nabla \cdot {\mathbf{t}}_{kj},$$ (108)

in Eq. (102) we obtain

$$\sum _{k=0}^{N-1}\left({\rho }_k{\varphi }_k\frac{D^k{\eta }_k}{Dt}+{\Gamma }_k{\eta }_k-{\varphi }_k{\rho }_k{r}_k∕\theta \right)=\frac{1}{\theta }\sum _{k=0}^{N-1}\left(\left({\sigma }_k-\left({\Psi }_k-\sum _{j=0}^{N-1}{\varphi }_k{\mu }_{jk}-{\rho }_k{\varphi }_{k}p\right)\mathbf{I}+\sum _{j=0}^{N-1}\nabla {\varphi }_j\otimes \frac{\partial {\Psi }_k}{\partial \nabla {\varphi }_j}\right):\nabla {\mathbf{v}}_k+\sum _{j=0}^{N-1}\left({\mathbf{t}}_{kj}-\frac{\partial {\Psi }_k}{\partial \nabla {\varphi }_j}\right)\cdot \nabla \frac{D^k{\varphi }_j}{Dt}+\sum _{l=1}^L\left(z_{kl}-\frac{\partial {\Psi }_k}{\partial \left(c_l{\varphi }_k\right)}{\varphi }_k\right)\frac{D^k{c}_l}{Dt}+\left({\pi }_k+p{\rho }_0\nabla {\varphi }_k+\sum _{j=0}^{N-1}({\mu }_{jk}\nabla {\varphi }_k-{\mu }_{kj}\nabla {\varphi }_j)\right)\cdot ({\mathbf{v}}_k-{\mathbf{v}}_0)-\sum _{j=0}^{N-1}{\mu }_{jk}{\Gamma }_k∕{\rho }_k-\sum _{j=0}^{N-1}{\mu }_{jk}\nabla \cdot J_k∕{\rho }_k\right).$$ (109)

Using the constitutive relations given in Sect. 2.2 together with

$${\mathbf{t}}_{kj}=\frac{\partial {\Psi }_k}{\partial \nabla {\varphi }_j},z_{kl}=\frac{\partial {\Psi }_k}{\partial \left(c_l{\varphi }_k\right)}{\varphi }_k,$$ (110)

then Eq. (109) becomes

$$\sum _{k=0}^{N-1}\left({\rho }_k{\varphi }_k\frac{D^k{\eta }_k}{Dt}+{\Gamma }_k{\eta }_k-{\varphi }_k{\rho }_k{r}_k∕\theta +\nabla \cdot ({\mathcal{J}}_k-{\varphi }_k{\rho }_k{\eta }_k{\mathbf{w}}_k)\right)=\frac{1}{\theta }\sum _{k=0}^{N-1}\left(({\mathbf{v}}_k-{\mathbf{v}}_0)\cdot {\alpha }_k({\mathbf{v}}_k-{\mathbf{v}}_0)+\frac{1}{2}\left(\nabla {\mathbf{v}}_k+\nabla {\mathbf{v}}_k^T\right):{\mathcal{L}}_k\left(\nabla {\mathbf{v}}_k+\nabla {\mathbf{v}}_k^T\right)-{\Gamma }_k∕{\rho }_k\sum _{j=0}^{N-1}{\mu }_{jk}+\sum _{j=0}^{N-1}\nabla {\mu }_{jk}{J}_k∕{\rho }_k\right),$$ (111)

where ${\mathcal{J}}_k={\varphi }_k{\rho }_k{\eta }_k{\mathbf{w}}_k+{\sum }_{j=0}^{N-1}{\mu }_{jk}{J}_k∕\left({\rho }_k\theta \right)$. Thermodynamic consistency then requires the right-hand side of Eq. (111) be nonnegative which is the case for the constitutive relations in Eqs. (9), (10) and (12) if Γ_k = 0. In principle, one may also choose Γ_k such that the right-hand side is positive using Arrhenius kinetics, for example.