Phase-field modeling of the dynamics of multicomponent vesicles: Spinodal decomposition, coarsening, budding, and fission

Abstract

We develop a thermodynamically consistent phase-field model to simulate the dynamics of multicomponent vesicles. The model accounts for bending stiffness, spontaneous curvature, excess (surface) energy, and a line tension between the coexisting surface phases. Our approach is similar to that recently used by Wang and Du [J. Math. Biol. 56, 347 (2008)] with a key difference. Here, we concentrate on the dynamic evolution and solve the surface mass conservation equation explicitly; this equation was not considered by Wang and Du. The resulting fourth-order strongly coupled system of nonlinear nonlocal equations are solved numerically using an adaptive finite element numerical method. Although the system is valid for three dimensions, we limit our studies here to two dimensions where the vesicle is a curve. Differences between the spontaneous curvatures and the bending rigidities of the surface phases are found numerically to lead to the formation of buds, asymmetric vesicle shapes and vesicle fission even in two dimensions. In addition, simulations of configurations far from equilibrium indicate that phase separation via spinodal decomposition and coarsening not only affect the vesicle shape but also that the vesicle shape affects the phase separation dynamics, especially the coarsening and may lead to lower energy states than might be achieved by evolving initially phase-separated configurations.

I. Introduction

Biomembranes form the basic structural units for compartmentalizing biological systems. Biomembranes are complex structures whose fundamental components include lipids, proteins, and cholesterol. The morphology and structure of membranes play an important role in their biological function [1]. Vesicles are closed biomembranes consisting of different types of lipids and cholesterol and serve as important, but simplified models of more complex cell membranes [2]. Vesicles are liquidlike yet exhibit bending resistance, e.g., Refs. [2,3]. When several types of lipid and choletesterol are present, phase transformations may occur on the membrane leading to the formation of domains or rafts. From a biological point of view, rafts may play significant roles in regulating protein activity since particular proteins may concentrate at or near rafts [4]. This may, in turn, affect signaling and trafficking [5,6]. Rafts may also play a role in the budding and fission processes during endocytosis and exocytosis [7] as well as in membrane adhesion and fusion [8].

Recent experiments on giant unilamellar vesicles containing ternary mixtures of lipid components and cholesterol have provided evidence of phase separation under a variety of different driving mechanisms such as temperature and magnetic fields, light, polymer anchorage, osmotic pressures, and chemical variations. See, for example, Refs. [9–19]. The different phases coexist in the membrane (e.g., liquid-ordered and/or liquid-disordered phases) forming domains rich in one phase and poor in the other. Spinodal decomposition, coarsening, viscous fingering, vesicle budding, and fission are observed with concomitant changes in membrane morphology.

By exploiting the scale difference between the bilayer thickness (nm range) and the vesicle size (μm range), mathematical models have been developed in which the vesicle is treated as an elastic surface [20]. While there have been many theoretical and numerical studies of homogeneous vesicles using discrete and continuum models (e.g., see the reviews [3,21–24], the recent papers [25–36] and the references therein), there are far fewer studies of inhomogeneous systems although there has been an increasing focus on the inhomogeneous vesicles in the past ten years.

Phase separation is a well-studied process in bulk phases. However, the dynamics of spinodal decomposition into separated phases and their subsequent coarsening in multicomponent vesicles is much richer than its materials science counterpart in alloys. In vesicles, the phase separation process is strongly coupled to the shape dynamics and curvature effects can dynamically influence the phase separation and vice versa. Using discrete approaches such as Monte Carlo methods, dissipative particle dynamics, and molecular dynamics, the dynamics of phase separation and domain formation, vesicle fission and fusion have been simulated numerically. See, for example, Refs. [37–48]. Such atomistic simulations however are limited by computational cost in the length and time scales they are able to achieve.

Continuum methods provide a good modeling alternative to reach larger length and time scales. Continuum models are also easier to analyze and parametrize. Phase separation processes in the bulk have been successfully studied by continuum models. The continuum approach is based on the generalized bending energy proposed by Helfrich [20] supplemented by a line energy associated with the energy cost for the domain boundaries on the vesicle, see Lipowsky [49], Seifert [50], and Julicher and Lipowsky [51,52]. In the continuum description, budding and vesicle fission can be understood as a mechanism to reduce the line energy of a multicomponent vesicle. Until recently, studies of multicomponent vesicles have been limited to equilibrium investigations (e.g., Refs. [18,50,52–61]) or dynamical simulations limited to small deformations or special shapes (e.g., [62–66]) due to the difficulty in coupling phase separation and domain formation to highly nonlinear surface evolution.

Very recently, phase-field models developed for single-component vesicles (e.g., see [25–32]) have been extended to the multicomponent case [67,68]. In this approach, which we follow here, the vesicle is defined implicitly as the level set of an auxiliary phase field variable that varies smoothly, but rapidly, across the membrane. Accordingly, the membrane has a small but finite thickness and thus this is also known as a diffuse-interface method. The generalized Helfrich bending energy and the line tension are reformulated using a phase-field approximation. Evolution equations for the phase-field variable follow, roughly speaking, from gradient descent of this energy. This approach eliminates the need for introducing and evolving a surface mesh for the vesicle. Further, topological transitions such as vessel fission or fusion are straightforwardly captured via changes in the level set topology. However, further work is needed to interpret such changes since the details of vesicle fission or fusion go beyond the level of description contained in the Helfrich model.

In the context of multicomponent vesicles, Campelo and Hernandez-Machado [67,69] developed a phase-field framework to simulate pearling instabilities driven by polymers anchored to a tubular membrane. Accordingly a local polymer density is introduced and is coupled to the spontaneous curvature. However, only homogeneous polymer distributions were used.

A fuller coupling of membrane and surface phases was recently developed by Wang and Du [68] in order to simulate equilibrium states. In this work, a pair of phase-field variables were introduced such that one variable characterizes the vesicle (via a level set) while the other describes the distribution of the surface phases. The bending stiffness and spontaneous curvatures may depend on the surface phase distribution. Equations for both phase-field variables follow from a gradient descent algorithm where penalty terms are added to the system energy to enforce the conservation of the surface phase masses (which is sufficient for finding equilibrium states), surface area conservation and the conservation of the volume enclosed by the vesicle. The three-dimensional results obtained demonstrate the effectiveness of using phase-field methods to simulate highly complex vesicle and surface phase equilibrium morphologies that are qualitatively consistent with experiments.

In this paper, we develop a thermodynamically consistent phase-field model to simulate the dynamics of multicomponent vesicles. The model accounts for bending stiffness, spontaneous curvature, excess (surface) energy, and a line tension between the coexisting surface phases. Our approach is similar to that used by Wang and Du [68] with a key difference. Here, we solve the surface mass conservation equation explicitly. This equation was not considered in [68]. The equation for the vesicle phase-field variable follows from an energy dissipation principle (second law of thermodynamics [70]) while taking into account the mass conservation equation for the surface phases. This results in a fourth-order strongly coupled system of nonlinear nonlocal equations. Although the system is valid for three dimensions, we limit our studies here to two dimensions where the vesicle is a curve. The equations are solved numerically using an adaptive finite element numerical method, implemented using the adaptive finite element method (FEM) toolbox AMDiS [71], together with a semi-implicit time-stepping algorithm which removes high-order time step constraints. We perform a study of the dynamics of two-dimensional vesicles containing two surface phases (i.e., liquid-ordered and liquid-disordered phases). We find that differences between the spontaneous curvatures and the bending rigidities of the surface phases may lead to the formation of buds, asymmetric vesicle shapes, and vesicle fission even in two dimensions. In addition, simulations of configurations far from equilibrium indicate that phase decomposition via spinodal decomposition and coarsening not only affect the vesicle shape but also that the vesicle shape affects the phase-separation dynamics and may lead to lower energy states than might be achieved by evolving initially phase-separated configurations.

The paper is organized as follows. We first review the sharp-interface framework. We then derive the thermodynamically consistent phase-field model. The adaptive finite element method is briefly presented, followed by numerical results that demonstrate the strong coupling between surface phase composition and the vesicle shape during evolution. Finally, conclusions are discussed together with plans for future work. An appendix provides some details regarding the sharp-interface energy variations.

II. Energy and Dynamic Evolution: Sharp-Interface Framework

The starting point for membrane modeling in the sharp interface context has traditionally been the generalized bending energy proposed by Helfrich [20] in the single component case and by Lipowsky [49], Seifert [50], and Julicher and Lipowsky [51,52] for phase-separated multicomponent membranes. When the phases are not separated, a more general energy may be formulated, e.g., see [62–64,72] for special cases with limited phenomenological coupling between the surface phases and the membrane geometry and parameters. Here, we briefly summarize a general sharp-interface formulation [73] as it provides a motivation and guide for the phase-field model considered in the next section.

Consider a two-component system with mass density ρ_A and ρ_B for components A and B, respectively. The concentration variable is defined as u = (ρ_A − ρ_B)/(ρ_A + ρ_B). Note that in most examples, the two components correspond to liquid-ordered and liquid-disordered surface phases, e.g., Refs. [10,11,74]. Assuming that the membrane parameters depend on u, the energy to be minimized is the sum of the following contributions:

1. The normal bending energy

   $$E_B=\frac{1}{2}{\int }_{\mathrm{\Gamma }}{b}_N(u){[H-H_0(u)]}^{2}dA,$$

2. the Gaussian bending energy

   $$E_G={\int }_{\mathrm{\Gamma }}{b}_G(u)\mathit{\text{KdA}},$$

3. the excess energy associated with the presence of the membrane

   $$E_S={\int }_{\mathrm{\Gamma }}\gamma (u)dA,$$

4. the line energy

   $$E_T=\sigma {\int }_{\mathrm{\Gamma }}\left(\frac{\delta }{2}{\Vert {\nabla }_{\mathrm{\Gamma }}u\Vert }^2+{\delta }^{-1}W(u)\right)dA,$$

where Γ is the membrane surface (assumed to have zero thickness), H is the total curvature (twice the mean curvature), H₀(u) is the spontaneous curvature, K the Gaussian curvature, b_N(u) is the normal bending stiffness, b_G(u) is the Gaussian bending stiffness, and γ(u) is the surface tension (excess energy associated with the membrane surface). Further, σ is the line tension, W(u) = 1/4(1 − u)²(1 + u)² is a double well potential that describes the tendency of the two surface components to phase separate and δ is a small parameter that effectively describes the thickness of the transition layer on the membrane that separates the A and B components. Hereafter, we will take σ = 1 which corresponds to rescaling all the energies by the line tension.

For constant b_G the Gaussian bending energy is proportional to the Euler characteristic of the membrane (Gauss-Bonnet theorem, e.g., Ref. [75]) and so changes in shape, which preserve the topology, do not change the energy. The Gauss modulus, however, influences membrane processes that change topology such as vesicle fission or fusion. Further, recent work [18,60,76] suggests that differences in the Gauss moduli of coexisting surface phases may explain the vesicle shape and surface phase distribution in experiments, especially in the neighborhood of a neck. Here, for simplicity, we will omit the possible dependency of b_G on u, thus we will not consider contributions of the Gaussian bending energy. These will be incorporated in a future work.

In [73] a thermodynamically consistent sharp-interface model for the evolution of a multicomponent vesicle is derived from the total energy E[Γ, u] = E_B + E_S + E_T. Taking the time derivative of the energy we obtain

$$\frac{d}{dt}E={\int }_{\mathrm{\Gamma }}{\partial }_{t}u\frac{\delta E}{\delta u}d\mathrm{\Gamma }+{\int }_{\mathrm{\Gamma }}\mathbf{\text{v}}\cdot \frac{\delta E}{\delta \mathrm{\Gamma }}d\mathrm{\Gamma },$$ (1)

where δE/δu and δE/δΓ are the variational derivatives of the total energy E[Γ, u] with respect to Γ and u, respectively. Further, v is the velocity of Γ. For completeness, the variational derivatives are defined in the Appendix. Note that we have implicitly assumed that u is extended off Γ such that the derivative in the normal direction ∂u/∂n = 0 in the neighborhood of Γ [73].

The surface mass conservation equation for u is

$${\partial }_{t}u+{\mathbf{\nabla }}_{\mathrm{\Gamma }}\cdot (\mathbf{\text{T}}u)+\mathit{\text{uVH}}=-{\mathbf{\nabla }}_{\mathrm{\Gamma }}\cdot \mathbf{\text{q}},$$ (2)

where v = Vn + T and q is a surface mass flux. The simplest thermodynamically consistent system of equations for u and Γ, without constraints on the volume or the surface area (e.g., required for conservation of these quantities), is obtained by taking $\mathbf{\text{q}}=-{\xi }_u\frac{\delta E}{\delta u}-u\mathbf{\text{T}}$ to yield [73]

$${\partial }_{t}u+\mathit{\text{uVH}}={\mathbf{\nabla }}_{\mathrm{\Gamma }}\cdot \left({\xi }_u{\mathbf{\nabla }}_{\mathrm{\Gamma }}\frac{\delta E}{\delta u}\right),$$ (3)

$$V=-{\xi }_V\left(\mathbf{\text{n}}\cdot \frac{\delta E}{\delta \mathbf{\text{Γ}}}-uH\frac{\delta E}{\delta u}\right),$$ (4)

$$\mathbf{\text{T}}=-{\xi }_T\left((\mathbf{\text{I}}-\mathbf{\text{n}}\otimes \mathbf{\text{n}})\frac{\delta E}{\delta \mathbf{\text{Γ}}}\right),$$ (5)

where n is the unit outward normal to Γ and ξ_u, ξ_V, and ξ_T are non-negative mobility coefficients. The incorporation of constraints on the volume and surface area for conservation can easily be done using Lagrange multipliers or by adding penalty terms to the total energy. The first equation is a Cahn-Hilliard type equation on an evolving surface, the second equation accounts for the evolution of the surface in normal direction is related to the Willmore flow problem, and the third equation models the tangential movement. For more details on the model we refer to [73].

III. Phase-Field Approximation

Next we derive a thermodynamically consistent phase-field model which approximates the sharp-interface description of vesicle evolution described in the previous section. Our approach is similar to that used by Wang and Du [68] with the key difference being how we treat the surface phase concentration u which we point out below. In this approach, the vesicle membrane is defined implicitly through a phase-field variable ϕ such that ϕ = 1 inside the vesicle, ϕ = 0 outside the vesicle with a smooth, but rapid transition across the vesicle Γ = {x ∈ Ω: ϕ(x) = 1/2}, where Ω ⊂ ℝ^2,3 is a volume domain with Γ(t) ⊂ Ω for t ∈ [0, T]. The membrane is characterized by a diffuse transition layer with a small but finite thickness ε. This eliminates the need for introducing and evolving a surface mesh for the membrane. Further, topological transitions such as vessel fission are straightforwardly captured via changes in the ϕ = 1/2 level set topology. The evolution equations are extended off the membrane Γ and the phase-field equations are solved in Ω. Accordingly, the phase concentration u is now interpreted as an extended variable which is defined not only on Γ but also in Ω.

A. Model derivation

The phase-field equations are derived using an energy variation approach together with a surface mass conservation equation for u. The free energy functional of the system is defined to be F[ϕ, u]. We defer the specific definition of F until later in this section when we consider the different constituent components, e.g., the bending and surface energies, line tension, etc.

To satisfy energy dissipation, and hence the second law of thermodynamics (assuming a constant temperature) [70], we require

$$\frac{d}{dt}F[\phi ,u]={\int }_{\mathrm{\Omega }}{\partial }_t\phi \frac{\delta F}{\delta \phi }+{\partial }_{t}u\frac{\delta F}{\delta u}dx\le 0,$$ (6)

where $\frac{\delta F}{\delta \phi }$ and $\frac{\delta F}{\delta u}$ denote variational derivatives of F with respect to ϕ and u, respectively. To make further progress, we derive and use the mass conservation equation for u in Eq. (6).

In the phase-field framework, it can be shown that if G(ϕ) is a double-well potential, i.e., G(ϕ) = 36ϕ²(1 − ϕ)², and ε is a small parameter, i.e., the interface thickness, then

$$\frac{\varepsilon }{2}{\left|\nabla \phi \right|}^2+{\varepsilon }^{-1}G(\phi )\to C{\delta }_{\mathrm{\Gamma }}\text{as}\varepsilon \to 0,$$ (7)

where C is a constant that depends on the specific form of G (equal to 1 for the specific choice of G given above) and δ_Γ is the surface δ function. See [25,71,77,78] for example. We note that there are other diffuse-interface approximations of the surface δ function. Since −1 ≤ u ≤ 1, we may define the total mass difference between the surface phases in an arbitrary domain Ω_a ⊂ Ω as

$$M(\phi ,u)≔{\int }_{{\mathrm{\Omega }}_a}\left(\frac{\varepsilon }{2}{\left|\nabla \phi \right|}^2+{\varepsilon }^{-1}G(\phi )\right)\mathit{\text{udx}},$$ (8)

i.e., M ≈ M_A − M_B, where M_A and M_B are the masses of the A and B phases in Ω_a. Then, conservation of mass follows from

$$\begin{array}{cc}\frac{d}{dt}M(\phi ,u)\hfill & =\frac{d}{dt}\left[{\int }_{{\mathrm{\Omega }}_a}\left(\frac{\varepsilon }{2}{\left|\nabla \phi \right|}^2+{\varepsilon }^{-1}G(\phi )\right)\mathit{\text{udx}}\right]\hfill \\ \hfill & =-{\int }_{\partial {\mathrm{\Omega }}_a}\mathbf{\text{j}}.\mathbf{\text{m}}dA,\hfill \end{array}$$

where Ω_a is assumed to be independent of time with boundary ∂Ω_a. We may also assume that Ω_a ∩ Γ(t) ≠ ∅. The flux j denotes the net flux of mass and m the normal on ∂Ω_a. Arguing that this equation holds for arbitrary Ω_a, we thus obtain the local mass conservation equation

$$\left(\frac{\varepsilon }{2}{\left|\nabla \phi \right|}^2+{\varepsilon }^{-1}G(\phi )\right){\partial }_{t}u+\varepsilon u\mathbf{\nabla }\phi \cdot \mathbf{\nabla }{\partial }_t\phi +{\varepsilon }^{-1}u{G}^{\prime }(\phi ){\partial }_t\phi =-\mathbf{\nabla }\cdot \mathbf{\text{j}}.$$ (9)

Multiplying by μ, with μ defined by

$$\left(\frac{\varepsilon }{2}{\left|\nabla \phi \right|}^2+{\varepsilon }^{-1}G(\phi )\right)\mu =\frac{\delta F}{\delta u},$$ (10)

we obtain

$${\partial }_{t}u\frac{\delta F}{\delta u}+\varepsilon \mu u\mathbf{\nabla }\phi \cdot \mathbf{\nabla }{\partial }_t\phi +{\varepsilon }^{-1}\mu uG\prime (\phi ){\partial }_t\phi =-\mu \mathbf{\nabla }\cdot \mathbf{\text{j}}.$$ (11)

It remains now to determine the flux mass flux j consistent with the decrease of the free energy. Using Eq. (11) in Eq. (6), we obtain

$$\begin{array}{cc}\frac{d}{dt}F[\phi ,u]\hfill & ={\int }_{\mathrm{\Omega }}{\partial }_t\phi \frac{\delta F}{\delta \phi }+{\partial }_{t}u\frac{\delta F}{\delta u}dx\hfill \\ \hfill & ={\int }_{\mathrm{\Omega }}{\partial }_t\phi \frac{\delta F}{\delta \phi }-\varepsilon \mu u\mathbf{\nabla }\phi \cdot \mathbf{\nabla }{\partial }_t\phi -{\varepsilon }^{-1}\mu uG\prime (\phi ){\partial }_t\phi -\mu \mathbf{\nabla }\cdot \mathbf{\text{j}}dx\hfill \\ \hfill & ={\int }_{\mathrm{\Omega }}{\partial }_t\phi \left(\frac{\delta F}{\delta \phi }+\varepsilon \mu \mathbf{\nabla }\cdot (u\mathbf{\nabla }\phi )-{\varepsilon }^{-1}\mu uG\prime (\phi )\right)-\mu \mathbf{\nabla }\cdot (\mathbf{\text{j}}+\varepsilon u{\partial }_t\phi \mathbf{\nabla }\phi )dx.\hfill \end{array}$$

If we now define

$$\varepsilon {\partial }_t\phi =-{\beta }_{\phi }\left(\frac{\delta F}{\delta \phi }+\varepsilon \mu \mathbf{\nabla }\cdot (u\mathbf{\nabla }\phi )-{\varepsilon }^{-1}\mu uG\prime (\phi )\right),$$ (12)

$$\mathbf{\text{j}}=-{\varepsilon }^{-1}{\beta }_{u}B(\phi )\mathbf{\nabla }\mu -\varepsilon u{\partial }_t\phi \mathbf{\nabla }\phi ,$$ (13)

where B(ϕ) is a non-negative mobility function that is localized near the interface, e.g., B(ϕ) = 36ϕ²(1 − ϕ)², which is introduced to ensure that the mass flux is localized near the interface. Further, β_u and β_ϕ are non-negative mobility coefficients and the scaling in ε is chosen such that the equations are consistent with the sharp interface limit as ε → 0. With these choices, we obtain

$$\frac{d}{dt}F[\phi ,u]=-{\int }_{\mathrm{\Omega }}\frac{{\beta }_{\phi }}{\varepsilon }{\left(\frac{\delta F}{\delta \phi }+\varepsilon \mu \mathbf{\nabla }\cdot (u\mathbf{\nabla }\phi )-{\varepsilon }^{-1}\mu uG\prime (\phi )\right)}^{2}dx-{\int }_{\mathrm{\Omega }}\frac{{\beta }_u}{\varepsilon }B(\phi ){\left|\nabla \mu \right|}^{2}dx,$$ (14)

where we have assumed the natural boundary condition ∇μ · n = 0 holds on ∂Ω. Finally, using the identity εu∇ϕ · ∇∂_tϕ − ε∇ · (u∂_tϕ∇ϕ) = −ε∇ · (u∇ϕ)∂_tϕ and the definition of j from Eq. (13) in Eq. (9), the governing equations can be written as

$$\varepsilon {\partial }_t\phi +{\beta }_{\phi }\left(\frac{\delta F}{\delta \phi }+[\varepsilon \mathbf{\nabla }\cdot (u\mathbf{\nabla }\phi )-{\varepsilon }^{-1}uG\prime (\phi )]\mu \right)=0,$$ (15)

$$\left(\frac{\varepsilon }{2}{\left|\nabla \phi \right|}^2+{\varepsilon }^{-1}G(\phi )\right)\mu =\frac{\delta F}{\delta u},$$ (16)

$$\left(\frac{\varepsilon }{2}{\left|\nabla \phi \right|}^2+{\varepsilon }^{-1}G(\phi )\right){\partial }_{t}u+[-\varepsilon \mathbf{\nabla }\cdot (u\mathbf{\nabla }\phi )+{\varepsilon }^{-1}uG\prime (\phi )]{\partial }_t\phi ={\varepsilon }^{-1}\mathbf{\nabla }\cdot [{\beta }_{u}B(\phi )\mathbf{\nabla }\mu ].$$ (17)

At this point, several remarks are in order. This system differs from that considered by Wang and Du [68] in that Eq. (17) follows from mass conservation and energy dissipation whereas in Ref. [68] both the ϕ and u equations were derived by energy variation only. In Ref. [68], mass conservation of the surface phase was only approximately enforced by introducing a corresponding penalty term in the system energy and the surface phase conservation equation was not considered.

In the region near the membrane, an asymptotic analysis of the equations (not shown) would roughly speaking give ∂_tϕ ∼ −V/ε and ε⁻¹G′(ϕ) − εΔϕ ∼ H. From these results, it can be seen that the structure of Eqs. (15)–(17) is analogous to the sharp interface model in Eqs. (3)–(5). We note that a general treatment of partial differential equations on surfaces within a phase field approximation is discussed in [79,80].

We next present the specific form of the free energy F[ϕ, u] by considering the phase-field representation of the normal bending energy, the excess (surface) energy associated with the membrane and the line energy associated with the presence of different surface phases.

B. Phase-field representation of energy terms

1. Normal bending energy

Consider the phase-field approximation of the sharp-interface normal bending energy E_B. If b_N(u) = 1 and H₀(u) = 0 the problem reduces to the classical Willmore energy, for which phase-field approximations are known. In one approach [29,30,32], the curvature of the vesicle is obtained directly by H ∼ ∇ · (∇ϕ/|∇ϕ|) and |∇ϕ| is used to approximate the surface δ function. Thus, the phase-field approximation of the bending energy (in the absence of spontaneous curvature) is the integral of the product of these functions. This approach is easily generalized to nonzero spontaneous curvature. An alternative approach [81–83], which we follow here, is related to a conjecture of DiGiorgi [77,83]. The corresponding phase-field bending energy is

$$F_B[\phi ]=\frac{1}{2}{\int }_{\mathrm{\Omega }}{\varepsilon }^{-1}{[\varepsilon \mathrm{\Delta }\phi -{\varepsilon }^{-1}G\prime (\phi )]}^{2}dx$$

with G(ϕ) = 36ϕ²(1 − ϕ)² being the double well potential. The variational derivative δF_B/δϕ is

$$\begin{array}{c}\hfill \frac{\delta F_B}{\delta \phi }=\mathrm{\Delta }\omega -{\varepsilon }^{-2}\omega G″(\phi ),\hfill \\ \hfill \omega =\varepsilon \mathrm{\Delta }\phi -{\varepsilon }^{-1}G\prime (\phi ).\hfill \end{array}$$

In the more general case the energy is [25]

$$F_B[\phi ,u]=\frac{1}{2}{\int }_{\mathrm{\Omega }}{\varepsilon }^{-1}{b}_N(u){[\varepsilon \mathrm{\Delta }\phi -{\varepsilon }^{-1}G\prime (\phi )+6\phi (1-\phi )H_0(u)]}^{2}dx,$$

and the variational derivative becomes

$$\begin{array}{l}\frac{\delta F_B}{\delta \phi }=\mathrm{\Delta }\omega -{\varepsilon }^{-2}G″(\phi )\omega +{\varepsilon }^{-1}{H}_0(u)6(1-2\phi )\omega ,\hfill \\ \frac{\delta F_B}{\delta u}=\frac{b_N^{\prime }(u)}{2\varepsilon b_N(u)}{\omega }^2+{\varepsilon }^{-1}\omega b_N(u)6\phi (1-\phi )H_0^{\prime }(u),\hfill \\ \omega =b_N(u)[\varepsilon \mathrm{\Delta }\phi -{\varepsilon }^{-1}G\prime (\phi )+6\phi (1-\phi )H_0(u)].\hfill \end{array}$$

Note that for b_N = 1 and H₀ = 0 both the free energy and the variational derivatives reduce to the special case mentioned above.

2. Excess energy

Consider the phase-field approximation of the sharp-interface excess (surface) energy E_S. If γ(u) = 1 the phase-field approximation is also well known [84,85] and is given by

$$F_S[\phi ]={\int }_{\mathrm{\Omega }}\left(\frac{\varepsilon }{2}{\left|\nabla \phi \right|}^2+{\varepsilon }^{-1}G(\phi )\right)dx.$$

The variational derivative is

$$\frac{\delta F_S}{\delta \phi }=-\varepsilon \mathrm{\Delta }\phi +{\varepsilon }^{-1}G\prime (\phi ).$$

With γ(u) the energy was extended in [80] to

$$F_S[\phi ,u]={\int }_{\mathrm{\Omega }}\left(\frac{\varepsilon }{2}{\left|\nabla \phi \right|}^2+{\varepsilon }^{-1}G(\phi )\right)\gamma (u)dx,$$

which yields the variational derivatives

$$\begin{array}{c}\hfill \frac{\delta F_S}{\delta \phi }=-\varepsilon \mathbf{\nabla }\cdot [\gamma (u)\mathbf{\nabla }\phi ]+{\varepsilon }^{-1}G\prime (\phi )\gamma (u),\hfill \\ \hfill \frac{\delta F_S}{\delta u}=\left(\frac{\varepsilon }{2}{\left|\nabla \phi \right|}^2+{\varepsilon }^{-1}G(\phi )\right)\gamma \prime (u).\hfill \end{array}$$

Again if γ = 1 both the free energy and the variational derivatives reduce to the classical results.

3. Line energy

Consider next the phase-field approximation of the sharp-interface line energy E_L. An appropriate energy was introduced in [79] and was used later by Wang and Du [68]. The phase-field energy is given by

$$F_L[\phi ,u]={\int }_{\mathrm{\Omega }}\left(\frac{\varepsilon }{2}{\left|\nabla \phi \right|}^2+{\varepsilon }^{-1}G(\phi )\right)\left(\frac{\delta }{2}{\left|\nabla u\right|}^2+{\delta }^{-1}W(u)\right)dx,$$

with the variational derivatives given by

$$\begin{array}{c}\frac{\delta F_L}{\delta \phi }=-\varepsilon \mathbf{\nabla }\cdot \left[\left(\frac{\delta }{2}{\left|\nabla u\right|}^2+{\delta }^{-1}W(u)\right)\mathbf{\nabla }\phi \right]+{\varepsilon }^{-1}G\prime (\phi )\left(\frac{\delta }{2}{\left|\nabla u\right|}^2+{\delta }^{-1}W(u)\right),\hfill \\ \frac{\delta F_L}{\delta u}=-\delta \mathbf{\nabla }\cdot \left[\left(\frac{\varepsilon }{2}{\left|\nabla \phi \right|}^2+{\varepsilon }^{-1}G(\phi )\right)\mathbf{\nabla }u\right]+{\delta }^{-1}{W}^{\prime }(u)\left(\frac{\varepsilon }{2}{\left|\nabla \phi \right|}^2+{\varepsilon }^{-1}G(\phi )\right).\hfill \end{array}$$

4. Volume and surface area constraints

Following [25,68], we introduce penalty terms to enforce volume and surface area conservation for evolving vesicles. Alternatively, we note that Lagrange multipliers could be used to conserve volume and total vesicle surface area [25,26] or local surface area [29–31]. The use of Lagrange multipliers in our approach is straightforward and is currently under study. Here, we use the following phase-field approximation of the volume of the vesicle:

$$V[\phi ]≔{\int }_{\mathrm{\Omega }}\phi dx,$$ (18)

and introduce the penalty term

$$F_V[\phi ]≔\frac{M_V}{2}{(V[\phi ]-V_0)}^2,$$ (19)

where V₀ is a prescribed volume and M_V is a large positive constant. The functional derivative δF_V/δϕ is

$$\frac{\delta F_V}{\delta \phi }=M_V(V[\phi ]-V_0).$$ (20)

Similarly, we consider the phase-field approximation of the surface area

$$A[\phi ]={\int }_{\mathrm{\Omega }}\left(\frac{\varepsilon }{2}{\left|\nabla \phi \right|}^2+{\varepsilon }^{-1}G(\phi )\right)dx$$ (21)

and the corresponding penalty functional

$$F_A[\phi ]≔\frac{M_A}{2}{(A[\phi ]-A_0)}^2,$$ (22)

where A₀ is the prescribed area and M_A is a large positive constant. The corresponding function derivative is

$$\frac{\delta F_A}{\delta \phi }=M_A(A[\phi ]-A_0)[\varepsilon \mathrm{\Delta }\phi -{\varepsilon }^{-1}{G}^{\prime }(\phi )].$$ (23)

Note that the functional derivatives in Eq. (20) and Eq. (23) lead to nonlocal terms in the evolution equations.

5. Total energy

The total energy free energy F[ϕ, u] of the vesicle model consists of the sum of all the effects considered,

$$F[\phi ,u]≔F_B[\phi ,u]+F_S[\phi ,u]+F_L[\phi ,u]+F_V[\phi ]+F_A[\phi ].$$ (24)

Correspondingly, the functional derivatives with respect to ϕ and u sum up to

$$\frac{\delta F}{\delta \phi }=\frac{\delta F_B}{\delta \phi }+\frac{\delta F_S}{\delta \phi }+\frac{\delta F_L}{\delta \phi }+\frac{\delta F_V}{\delta \phi }+\frac{\delta F_A}{\delta \phi }$$

and

$$\frac{\delta F}{\delta u}=\frac{\delta F_B}{\delta u}+\frac{\delta F_S}{\delta u}+\frac{\delta F_L}{\delta u}.$$

Note that $\frac{\delta F_V}{\delta u}=\frac{\delta F_A}{\delta u}=0$. Incorporating these functional derivatives in the evolution equations (15)–(17) yields a fourth-order strongly coupled system of nonlinear nonlocal equations.

We note that in the system considered by Wang and Du [68], an additional penalty term was added to enforce ∇u · ∇ϕ ≈ 0 (i.e., the normal derivative ∂u/∂n ≈ 0). This was not found to be necessary here because this condition is automatically enforced by having u satisfy the mass conservation equation (17). For example, it can be seen that the leading term in an asymptotic expansion near the vesicle membrane arises from the line tension term δF_L/δu and implies that ∂u/∂n = 0 to leading order.

IV. Finite Element Discretization

In this section we briefly describe the finite element discretization for the fourth-order system of nonlinear nonlocal equations (15)–(17) implemented using the adaptive FEM toolbox AMDiS [71]. First, we consider the time discretization, where we split the time interval [0, T] into discrete time increments 0 = t₀ < t₁ < … and associated time steps Δt_k ≔ t_k+1 − t_k, with k = 0, 1, …. To discretize the equations in time, we use a semi-implicit algorithm in which only the nonlocal terms V[ϕ] and A[ϕ] are treated explicitly. This allows us to overcome the severe time step restrictions (Δt_k ∼ Δx⁴, where Δx is the smallest mesh spacing) required for stability by explicit methods and the high costs associated with solving coupled nonlinear systems that arise from fully implicit time discretizations.

To discretize in space, let ${\mathcal{\text{T}}}_h^m$ be a conforming triangulation of Ω at time t = t_m. Denote the set of polynomials of degree 1 by ℙ¹ and define the finite element space of globally continuous, piecewise linear elements by ${\mathbb{\text{V}}}_h^m=\{v_h\in X:v_{h|T}\in {\mathbb{P}}^1\forall T\in {\mathcal{\text{T}}}_h^m\}$, where X is an appropriate function space. Let (ψ_i)_i be the standard nodal basis of ${\mathbb{\text{V}}}_h^m$ and take ${\phi }_h^{(m+1)}={\sum }_i{\mathrm{\Phi }}_i^{(m+1)}{\psi }_i$, ${\omega }_h^{(m+1)}={\sum }_i{W}_i^{(m+1)}{\psi }_i$, $u_h^{(m+1)}={\sum }_i{U}_i^{(m+1)}{\psi }_i$ and ${\mu }_h^{(m+1)}={\sum }_i{M}_i^{(m+1)}{\psi }_i$. Then, taking the inner product of Eqs. (15)–(17) with ψ_k, we obtain a linear system of equations for ${\mathrm{\Phi }}_i^{(m+1)}$, $W_i^{(m+1)}$, $U_i^{(m+1)}$, and $M_i^{(m+1)}$.

In order to reduce the computational cost the mesh is locally adapted using a bisection algorithm (see [71] and references therein) such that a fine mesh is used near the vesicle membrane and a coarse mesh is used elsewhere. For local mesh adaptation, we use an L²-like error indicator based on a jump residual [71,86] for the phase-field variable ϕ; see Fig. 1 for an example of an adaptively refined mesh. The number of elements in the simulations is in the order of 100 000. Within the diffuse interface we use approximately five grid points. Furthermore a simple strategy of time adaptivity is used, where the time step is inversely proportional to the maximum of the normal or intrinsic normal velocity of the interfaces, leading to time steps Δt_k ∈ [10⁻⁵, 10⁻⁴].

FIG. 1.

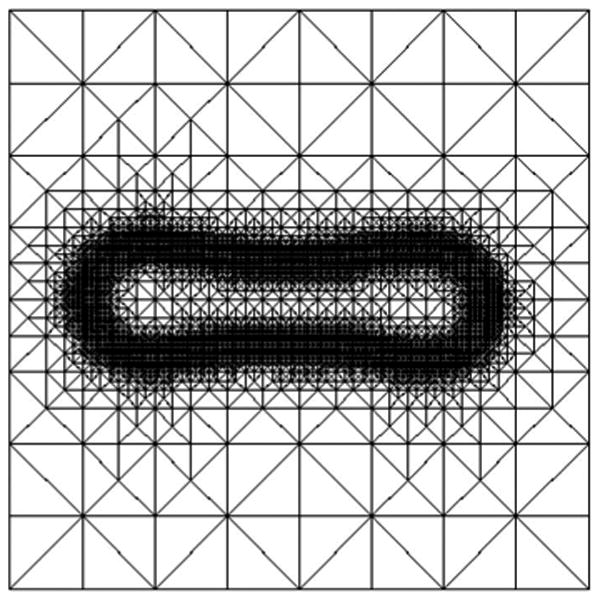
Typical adaptively refined mesh. The mesh corresponds to the simulation of spinodal decomposition at t = 0.0406 shown in Fig. 9.

V. Numerical Results

Next, we consider the application of the model and numerical algorithm to simulate the dynamics of multicomponent lipid membranes in two dimensions. Take, for example, ternary lipid mixtures which involve cholesterol long-chain and short-chain lipids as studied in [11,60]. The long-chain lipids enrich a liquid-ordered L₀ phase while the short-chain lipids enrich a liquid-disordered L_d phase. The concentration u thus represents the rescaled relative concentration of the two phases.

An accurate determination of all the material parameters involved is a challenging problem. In principle, the parameters can be estimated by matching experimentally measured membrane and computed shapes, e.g., see [52] for single-component membranes and [18,60,76] for ternary liquid ordered and/or disordered systems, although this approach may not yield a unique set of parameters.

For membranes containing coexisting surface phases only values for selected average compositions are known [11]. According to Ref. [14] no attempts have been made to measure the normal elastic rigidity in phase-separated membranes. Measurements of the line tension can be found in [14,16] and are found to strongly depend on cholesterol concentration.

Here, we present a study in which we examine the influence of the spontaneous curvature H₀ and the normal bending stiffness b_N. We do not consider the effects of a variable surface energy γ as this is deferred to future work. Recall that the energy is rescaled by the line tension and thus this parameter is fixed. The kinetic coefficients β_u and β_ϕ are also fixed and set to 1. This is the simplest possible situation. More complicated choices, e.g., a functional dependency of β_u on u, clearly will influence the dynamics. Indeed, in [87], the dynamics was found to strongly depend on the cholesterol concentration. However, little is known about the magnitude and functional dependence of these kinetic parameters which is why we focus on the other parameters here and defer a more detailed study of β_u to a future study.

In order to demonstrate the effect of the dependency of H₀, b_N, and γ upon u, we assume a generic function h (i.e., h = H₀, b_N, γ)

$$h=h(u)=\{\begin{array}{ccc}{h}_{-1}\hfill & \hfill & \text{for}u<-1,\hfill \\ h_{-1}\hfill & +\hfill & \frac{1}{16}(h_1-h_{-1})(8+15u-10u^3+3u^5)\hfill \\ \hfill & \hfill & \text{for}-1\le u\le -1,\hfill \\ h_1\hfill & \multicolumn{2}{c}{\text{for}u>1,}\end{array}$$

where h₋₁ and h₁ are the values for constant composition. Note that because the polynomial energy W(u) is used, u may fall slightly outside the range of −1 to 1 by an amount that is O(δ). In addition, this higher order interpolation is needed in order to assign values of the parameters, within the diffuse interface that separates the surface domains, in an appropriate way. In particular, a higher order interpolation yields more accurate results as the difference between h₋₁ and h₁ increases.

In addition, we consider the domain Ω ≔ (−1, 1)² and use periodic boundary conditions. For all the simulations presented here, we took the penalty parameters to be M_V = 10⁴ and M_A = 10³ which were found by numerical experimentation to give good results for volume and surface area conservation. The widths of the diffuse interfaces separating the interior and exterior of the vesicle (e.g., diffuse membrane) and separating the surface phase domains are controlled by the parameters ε and δ which are set to be 0.1 and 0.01, respectively; these choices are also a result of numerical experimentation and are similar to the parameters used in [79] in which a Cahn-Hilliard equation is solved on implicitly described surfaces. We use the same parameter set for all simulations. We note that with these parameters, our simulations indicate that all structure remains tangential to the interface and no structure forms normal to the interface within the diffuse layer. Furthermore, we introduce a parameter ε_B > 0 in order to regularize the degenerate mobility function B ⇝ ε_B + B (see also [79,88]), and we use ε_B = 10⁻⁴ here. Finally, in all the simulations, the initial vesicle shape is an ellipse. In particular, the level-set {x∣ϕ(x, 0) = 1/2} is an ellipse and the initial phase-field variable ϕ(x, 0) = ϕ₀ is given by

$${\phi }_0(x)=1/2\{1-tanh[3r_h(x)/\varepsilon ]\}$$

where r_h(x) is a discrete approximation of the signed distance function of an ellipse.

A. Symmetric shapes

We begin by considering the effect of only the line tension. In particular, we take the spontaneous curvature H₀(u) = 3.25 and the normal bending rigidity b_N(u) = 1 to be constant as well as γ(u) = 0. The initial concentration u₀ is symmetrically distributed with u₀ = −1 (blue) on the left half of the initial ellipse and u₀ = 1 on the right half (red), as seen in Fig. 2. Away from the ellipse, u₀ tends smoothly, and rapidly to 0. Note that other smooth extensions away from the interface could be used. The diffuse interface separating the two surface domains is clearly seen. In the figure, u is plotted on the isocontours of ϕ from ϕ = 0.4 to ϕ = 0.6. Note that the membrane is characterized by the level-set {x∣ϕ(x, t) = 1/2}.

FIG. 2.

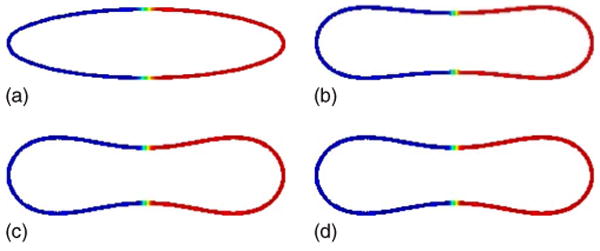
(Color online) Evolution of the concentration u on the isocontours of ϕ from ϕ = 0.4 to ϕ = 0.6 is shown at times t = 0 (a), t = 0.0006 (b), t = 0.0024 (c), and t = 0.0120 (d); H₀(−1) = H₀(1) = 3.25, b_N(−1) = b_N(1) = 1.

As the vesicle relaxes to reduce its energy, buds form at the vessel tips and a neck of negative curvature develops at the vesicle center. This reflects the competition between the tendency to reduce the bending energy and decrease the vesicle curvature while at the same time maintaining constant vesicle volume and surface area. The resulting discocyte shape is a common shape for homogeneous vesicles. Here, because the bending rigidity and spontaneous curvature are independent of u, the surface phases evolve symmetrically with the transition between the two confined being confined to the vesicle center. The line tension tends to reinforce the discocyte shape, although since the simulation is two dimensional there is not a significant advantage, as there would be for axisymmetric and three-dimensional vesicles, for having the transition between the two surface phases occurring at the minimum neck radius.

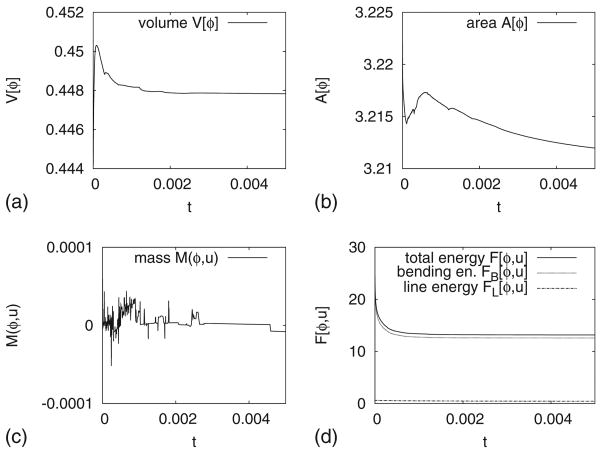
In Fig. 3 we present the evolution of the volume V[ϕ], the surface area A[ϕ], the mass difference M(ϕ, u), and the total energy F[ϕ, u] and its components, the bending energy F_B, and the line tension F_L, throughout the simulation. The maximal relative deviation of the volume compared to its initial value is ≈0.2%. For the surface area, the relative deviation is ≈0.07%, and for the mass difference, the absolute deviation is ≈5 × 10⁻⁵. The bending energy (dotted) dominates the total energy (solid) and thus the decrease in total energy is due primarily to the reduction in bending energy. The line energy (dotted-dashed line) is approximately constant throughout the simulation since the interface layers separating the two surface phases are nearly equilibrated.

FIG. 3.

(a) The volume, (b) surface area, (c) mass, and (d) the total energy F[ϕ, u] (solid), the bending energy F_B[ϕ, u] (dotted), and the line energy F_L[ϕ, u] (dotted-dashed line) for the simulation shown in Fig. 2.

B. Asymmetric shapes

We next consider the effects of differences in spontaneous curvatures and bending energies between the two phases. We also consider asymmetric initial surface phase distributions.

1. Asymmetric spontaneous curvature

We begin with a case such that the two phases have different spontaneous curvatures: H(−1) = 2 and H(1) = 5. For simplicity, we take a constant normal bending rigidity b_N(u) = 1 and we take a symmetric initial concentration u₀. The evolution towards an asymmetric discocyte vesicle shape is shown in Fig. 4. As the vesicle relaxes to equilibrium, the curvature of the u = 1 phase decreases while that of the u = −1 phase increases. This occurs because in each surface phase, the vesicle curvature tends toward the appropriate spontaneous curvature. Correspondingly, the surface phase concentration also becomes asymmetric. Not only are the u = −1 and u = 1 phases located at the corresponding vesicle ends but the u = −1 phase also nearly covers the neck region. This is a consequence of volume, surface area, and mass conservation. A check of these theoretically conserved quantities indicates that deviations from their initial values in the simulation are similar to that described previously for the symmetric vesicle. Indeed, this is the case for all the simulations presented hereafter.

FIG. 4.

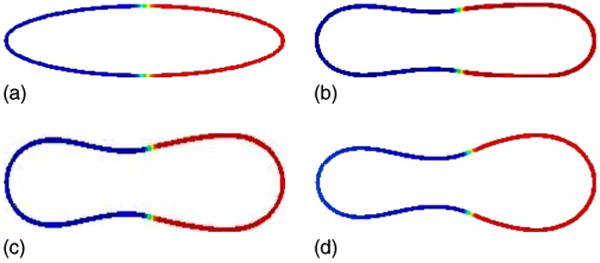
(Color online) Evolution of the concentration u on the isocontours of ϕ from ϕ = 0.4 to ϕ = 0.6 is shown at times t = 0 (a), t = 0.0005 (b), t = 0.001 (c), and t = 0.02 (d); H₀(−1) = 2, H₀(1) = 5, b_N(−1) = b_N(1) = 1.

As an additional comparison, we repeat the previous simulation using an asymmetric initial surface phase distribution. In particular, there is now more u = −1 phase. The simulation is shown in Fig. 5. Not surprisingly, the results are similar and the u = −1 phase now fully covers the neck region of the asymmetric discocyte.

FIG. 5.

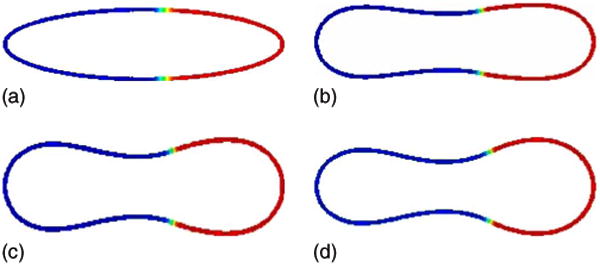
(Color online) Evolution of an asymmetric concentration u on the isocontours of ϕ from ϕ = 0.4 to ϕ = 0.6 is shown at times t = 0 (a), t = 0.0005 (b), t = 0.001 (c), and t = 0.02 (d); H₀(−1) = 2, H₀(1) = 5, b_N(−1) = b_N(1) = 1.

2. Asymmetric normal bending rigidity

We next consider a case in which the normal bending rigidities are different in the two surface phases. We correspondingly take b_N(−1) = 1/2 and b_N(1) = 5. For simplicity, a constant spontaneous curvature H₀(u) = 3.25 is used and the initial surface phase distribution is symmetric. The results are shown in Fig. 6. As the vesicle relaxes towards equilibrium, a large nearly circular bud develops in the u = 1 phase in response to the large bending rigidity. The u = −1 phase is pulled entirely through the neck region and a much smaller bud forms in the u = −1 phase. Because of the large difference between the bending rigidities, b_N(1)/b_N(−1) = 10, the discocyte shape is highly distorted.

FIG. 6.

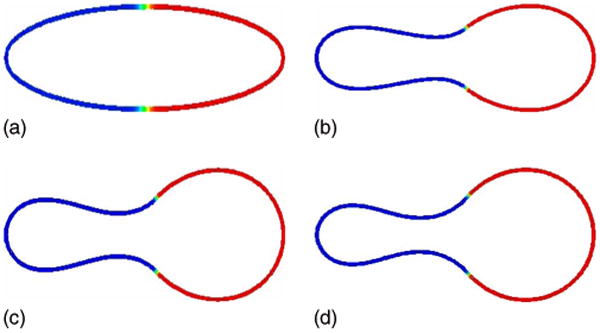
(Color online) Evolution of the concentration u on the isocontours of ϕ from ϕ = 0.4 to ϕ = 0.6 is shown at times t = 0 (a), t = 0.0005 (b), t = 0.0010 (c), and t = 0.0100 (d); H₀(−1) = H₀(1) = 3.25, b_N(−1) = 1/2, b_N(1) = 5.

In Fig. 7, we now repeat the above simulation but with the initially asymmetric surface phase, used previously in Fig. 5 such that there is more u = −1 phase present. In this case, there is not enough u = 1 phase to form a large bud. Instead, a large bud forms in the plentiful u = −1 phase which is attached to a small bud in the u = 1 phase by a narrow neck. As the evolution proceeds, the neck narrows leading to vesicle fission which results in the formation of a large vesicle consisting mostly of the u = −1 phase and a u = 1 rich small vesicle. Because the u = 1 phase spans the neck region before pinchoff, the large vesicle has a small region rich in the u = 1 phase while the small vesicle contains essentially no u = −1 phase.

FIG. 7.

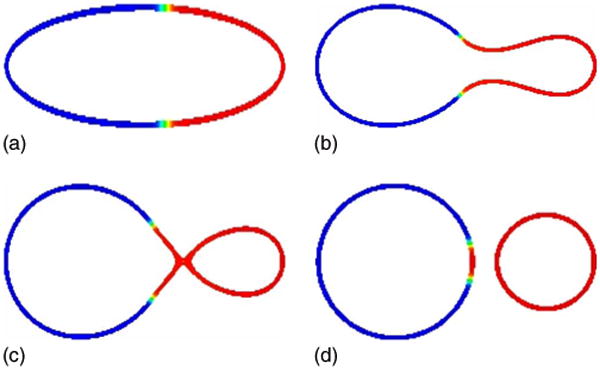
(Color online) Fission of a vesicle. The evolution of the asymmetric concentration u on the isocontours of ϕ from ϕ = 0.4 to ϕ = 0.6 is shown at times t = 0 (a), t = 0.0010 (b), t = 0.0020 (c), and t = 0.0161 (d); H₀(−1) = H₀(1) = 3.25, b_N(−1) = 1/2, b_N(1) = 5.

It is important to note that the neck of a vesicle in three dimensions has a different character than that of the vesicle simulated here since in a two-dimensional vesicle in three dimensions, the mean curvature may be very small in magnitude because the two principle curvatures have opposite signs. Here, the one-dimensional vesicle in two dimensions has large curvature in the neck. In addition, in three dimensions, the line tension strongly favors fission. Thus, it is interesting that we obtain fission even in two dimensions.

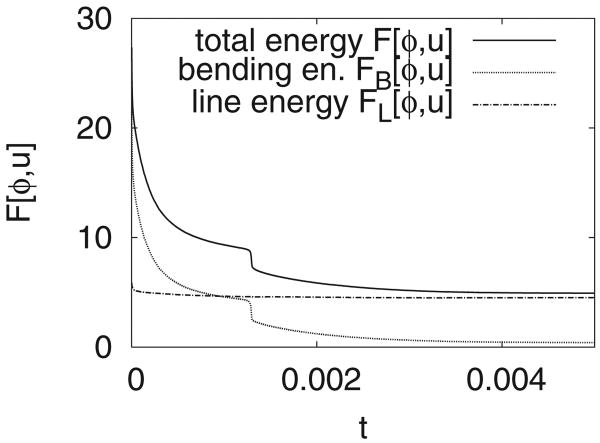
The corresponding total F[ϕ, u] (solid), bending F_B[ϕ, u] (dotted), and line F[ϕ, u] (dotted-dashed line) energies are shown in Fig. 8. At early times, the total energy is dominated by the bending energy which decreases to the level of the line energy. As these effects compete, the vesicle fissions and there is a rapid drop in the bending energy with a concomitant drop in the total energy. The line energy slightly decreases at early times associated with the equilibration of the interface layers separating the surface phases. After this initial decrease, the line energy becomes roughly constant as the structure of the interface layers equilibrates.

FIG 8.

The total energy F[ϕ, u] (solid), the bending energy F_B[ϕ, u] (dotted), and the line energy F_L[ϕ, u] (dotted-dashed line) for the simulation shown in Fig. 7.

C. Spinodal decomposition and coarsening

To further investigate the coupling between the motion of the interface—given by the phase-field variable ϕ—with the evolution of the lipid concentration u, we take an initial surface phase distribution far from equilibrium. We let u₀ take random values around u = 0 in [−1, 1]. The corresponding initial mass is M[ϕ, u] (t = 0) = −0.029 997 3.

The initial condition and subsequent spinodal decomposition and surface phase coarsening is shown in Fig. 9. The parameters are listed in the figure caption. As can be seen in the figure, not only does the surface phase affect the shape of the interface but the shape of the interface affects the spinodal decomposition and coarsening. In particular, observe that the u = 1 phase, which is associated with a larger spontaneous curvature, forms preferentially in regions of large curvature.

FIG. 9.

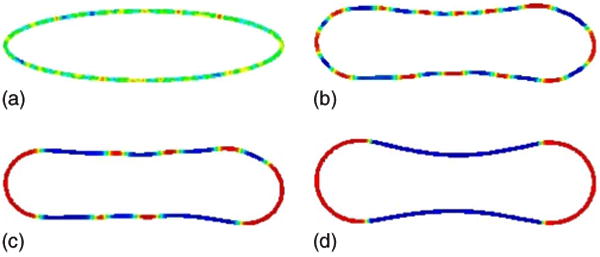
(Color online) Spinodal decomposition. The evolution of the concentration u(x, t) on the isocontours of ϕ from ϕ = 0.4 to ϕ = 0.6 is shown at times t = 0 (a), t = 0.001 (b), t = 0.01 (c), and t = 0.04 (d), H₀(−1) = 2, H₀(1) = 5, b_N(−1) = b_N(1) = 1.

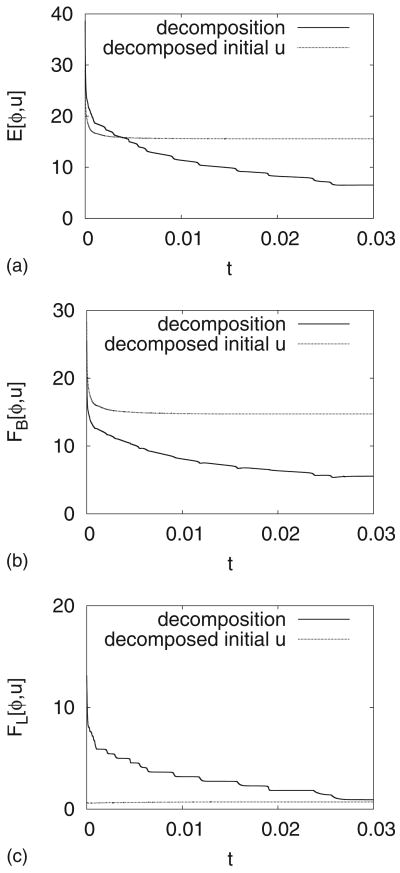
Interestingly, the nearly equilibrium configuration shown in Fig. 9(d) is quite different than that obtained when the initial condition is already decomposed into large regions of u = −1 and u = 1 phases. Recalling Fig. 4, we note that when the vesicle is divided into two surface phases, u = −1 and u = 1, buds form on the corresponding sides of the vesicle. In contrast, when the decomposition occurs freely as in Fig. 9, the u = 1 phases comprise the large curvature regions while the u = −1 phases are located in regions of small curvature. This is an energetically more favorable configuration as seen in Figs. 10(a)–10(c). We observe that while both the bending [Fig. 10(b)] and line [Fig. 10(c)] energies decrease in time, the line energy for the simulation in Fig. 9 is strictly larger than that for the simulation in Fig. 4 because in Fig. 9 there are ultimately four interface layers that separate the surface domains while in Fig. 4 there are only two such interface layers. It is thus the large reduction in bending energy, associated with having the u = 1 and u = −1 phases in the regions of large and small curvature, respectively, that is responsible for the fact that the total energy [Fig. 10(a)] is smaller for the configuration from Fig. 9(d) than that from Fig. 4(d). Thus, phase separation via spinodal decomposition and coarsening not only affects the vesicle shape but also the vesicle shape affects the phase separation dynamics.

FIG. 10.

A comparison of the total energies (a), the bending energies (b), and the line energies (c) for the simulations in Fig. 4 (labeled “decomposed initial u”) and Fig. 9 (labeled “decomposition”).

VI. Discussion

We have developed a phase-field model to simulate the dynamics of multicomponent vesicles. The model is derived using an energy variation approach together with the conservation of the masses of the surface phases and accounts for bending stiffness, spontaneous curvature, excess (surface) energy, and a line tension between the coexisting surface phases. The phase-field model extends the sharp-interface description of the vesicle dynamics, eliminates the need for introducing a surface mesh to track the membrane, and allows topology changes, such as vesicle fission, to occur smoothly.

The model consists of a coupled system of fourth-order nonlinear nonlocal equations for a variable ϕ that characterizes the vesicle membrane (as a level set of ϕ) and a variable u that describes the concentration of the surface phases. The constraints of volume and surface area conservation are implemented using a penalty approach which is the source of the nonlocal terms in the system. The model is closely related to the phase-field model recently introduced by Wang and Du [68] for simulating equilibrium states with the key difference being that in [68] surface mass conservation was only approximately enforced using a penalty approach and the surface mass conservation equation was not considered; this equation plays an essential role in our model. Although the system is valid for three dimensions, we limited our studies here to two dimensions where the vesicle is a curve.

To solve the model equations efficiently and accurately, an adaptive finite element method is utilized together with a semi-implicit time discretization which removes high order time step constraints. We then performed a study of the dynamics of two-dimensional vesicles containing two surface phases (i.e., liquid-ordered and liquid-disordered phases). We found that differences between the spontaneous curvatures and the bending rigidities of the surface phases led to the formation of buds and asymmetric vesicle shapes. We also presented an example of asymmetric spontaneous curvature-induced vesicle fission. In this example, two asymmetric daughter vesicles are produced with each daughter vesicle being rich in one of the surface phases. However, we observe that asymmetries in the neck region before fission takes place can create a small domain of the other phase in a daughter vesicle. Finally, we considered a configuration far from equilibrium and observed that not only does the spinodal decomposition and coarsening of the surface phases affect the vesicle shape but also that the vesicle shape affects spinodal decomposition. In particular, for the parameters used here, it is energetically more favorable for the surface phase with smaller spontaneous curvature to form in the neck regions of the vesicle even though this configuration has a larger line energy than if the surface phase boundaries were at the neck (i.e., four interface layers in Fig. 9 versus two interface layers in Fig. 4).

The phase-field approach and the associated numerical method described here provides a general framework for studying the dynamics of multicomponent vesicles and biomembranes. Although they were not considered in this work, the effects of surface energy and Gaussian bending stiffness differences between the surface phases will be incorporated in a future work. Recent studies have shown, for example, that differences in the Gaussian bending stiffness may play an important role in the vesicle dynamics and equilibrium shapes [18,60]. While the techniques described in [89,90] can be used for calculating the Gaussian curvature in phase-field models, there may be other more straightforward approaches.

The model presented here can be straightforwardly extended to systems with more surface components and more realistic thermodynamics, e.g., Refs. [13,91,92] and to vesicles in three dimensions. The presence of a fluid flow may also induce surface-phase separation, budding, and vesicle fission, e.g., Ref. [47], and can be incorporated within this framework by coupling the phase-field model with the Stokes or Navier-Stokes equations for fluid flow, e.g., see [27,29,30,32] for such coupling for homogeneous vesicles. The presence of membrane proteins within the phases can also have an important influence on the vesicle shape and surface phase distribution, e.g., Refs. [52,93], and can be modeled by incorporating the concentration(s) of membrane proteins in the phase-field model described here via an additional protein energy and introducing coupling between the protein and the bending rigidity and spontaneous curvature, e.g., see [94–96]. Vesicle-vesicle and vesicle-substrate adhesion can also be modeled by introducing adhesion potentials in the phase-field framework, e.g., Refs. [97,98].

After reviewing we became aware of another approach in which adaptive finite elements are used to solve a phase-field model of vesicle deformation [99], in which a one-component model is used.

Appendix: Sharp-Interface Energy Variation

The total energy in the sharp-interface model presented in Sec. II is E[Γ, u] = E_B + E_S + E_T. The variational derivatives $\frac{\delta E}{\delta \mathrm{\Gamma }}$ and $\frac{\delta E}{\delta u}$ are given by

$$\begin{array}{l}\frac{\delta E}{\delta \mathrm{\Gamma }}=\frac{\delta E_B}{\delta \mathrm{\Gamma }}+\frac{\delta E_S}{\delta \mathrm{\Gamma }}+\frac{\delta E_T}{\delta \mathrm{\Gamma }},\\ \frac{\delta E}{\delta u}=\frac{\delta E_B}{\delta u}+\frac{\delta E_S}{\delta u}+\frac{\delta E_T}{\delta u},\end{array}$$

where [73]

$$\begin{array}{c}\frac{\delta E_B}{\delta \mathbf{\text{Γ}}}=-\left({\mathbf{\text{Δ}}}_{\mathrm{\Gamma }}\{b_n(u)[H-H_0(u)]\}+\frac{b_n}{2}(H-H_0)[H(H+H_0)-4K]\right)\mathbf{\text{n}},\frac{\delta E_S}{\delta \mathbf{\text{Γ}}}=\gamma H\mathbf{\text{n}},\\ \frac{\delta E_T}{\delta \mathbf{\text{Γ}}}=\left({\delta }^{-1}W(u)+\frac{\delta }{2}{\left|{\nabla }_{\mathrm{\Gamma }}u\right|}^2\right)H\mathbf{\text{n}}+\delta {\mathbf{\nabla }}_{\mathrm{\Gamma }}{\mathbf{\nabla }}_{\mathrm{\Gamma }}u\cdot {\mathbf{\nabla }}_{\mathrm{\Gamma }}u,\end{array}$$

K is the Gaussian curvature, and

$$\begin{array}{c}\hfill \frac{\delta E_B}{\delta u}=\frac{1}{2}{b}^{\prime }(u){[H-H_0(u)]}^2-b(u)[H-H_0(u)]H_0^{\prime }(u),\hfill \\ \hfill \frac{\delta E_S}{\delta u}={\gamma }^{\prime }(u),\hfill \\ \hfill \frac{\delta E_T}{\delta u}=\frac{1}{\delta }W\prime (u)-\delta {\mathrm{\Delta }}_{\mathrm{\Gamma }}u.\hfill \end{array}$$