Bayesian symmetrical EEG/fMRI fusion with spatially adaptive priors

Abstract

In this paper, we propose a novel symmetrical EEG/fMRI fusion method which combines EEG and fMRI by means of a common generative model. We use a total variation (TV) prior to model the spatial distribution of the cortical current responses and hemodynamic response functions, and utilize spatially adaptive temporal priors to model their temporal shapes. The spatial adaptivity of the prior model allows for adaptation to the local characteristics of the estimated responses and leads to high estimation performance for the cortical current distribution and the hemodynamic response functions. We utilize a Bayesian formulation with a variational Bayesian framework and obtain a fully automatic fusion algorithm. Simulations with synthetic data and experiments with real data from a multimodal study on face perception demonstrate the performance of the proposed method.

Introduction

Electroencephalography (EEG) is one of the most widely used functional brain mapping methods. A main advantage of EEG is that it provides a direct measure of electrical activity in the brain via voltage sensors on the scalp and thus can achieve a high temporal resolution. However, locating the sources of activity in the brain from the EEG measurements is a difficult problem as there is an indefinite number of source configurations which give rise to the same measurements. The same problem is also encountered in magnetoencephalography (MEG), where the electrical activity in the brain is measured using magnetic field sensors. Due to the problem that the same measurements can be generated by an indefinite number of source configurations, EEG and MEG source localization are referred to as ill-posed inverse problems (Hämäläinen et al., 1993).

In the last two decades a large number of EEG and MEG source localization methods have been proposed in the literature. Due to the similarity of the inverse problems most methods are applicable to either modality and can be divided into two groups. The first group assumes that there is a small number (typically 1–5) of sources, each modeled by an equivalent current dipole (ECD) (Scherg and Von Cramon, 1986). The locations of the dipoles are found by performing a nonlinear optimization which minimizes the discrepancy to the data with respect to the dipole locations. While ECD methods are popular in practice, they have some major limitations: First, the number of dipoles has to be specified by the user and second, the optimization algorithm can get trapped in a local minimum and thus might not be able to find the optimal dipole locations. In fact, ECD methods are known to be unreliable when more than one dipole is used (Yao and Dewald, 2005). The second, and more recently proposed group of methods is referred to as distributed methods (Hämäläinen et al., 1993). Methods in this group assume a large number, typically several thousands, of dipoles with fixed locations which are distributed over the cortical surface. Source localization then amounts to finding the current amplitudes for all dipoles simultaneously, which is still an ill-posed problem since the number of dipoles is much larger than the number of sensors. However, the use of dipoles with fixed locations means that the forward problem is linear and source localization can be regarded as solving an underdetermined linear system of equations, which is similar to problems encountered in signal and image processing.

In order to find a unique solution, it is necessary to make assumptions about the solution. Such assumptions can be formulated as deterministic regularization terms, such as in the minimum norm method (Hämäläinen and Ilmoniemi, 1994), which finds the source configuration with minimal energy or in the low resolution electromagnetic tomography (LORETA) method (Pascual-Marqui et al., 1994), where a regularization term based on a spatial Laplacian is used to enforce a smooth solution.

The source localization problem can also be formulated as a Bayesian inference problem (Baillet and Garnero, 1997), which allows for an elegant way to include a priori information about the solution in the form of priors, such as spatial and temporal smoothness priors (Baillet and Garnero, 1997). The priors can be either fixed or can be automatically selected from a set of candidate priors, by means of Bayesian model selection. Examples of methods using fixed priors are ℓ₂-norm methods (Baillet et al., 2001), ℓ₁-norm methods (Uutela et al., 1999; Huang et al., 2006), as well as, the Bayesian formulation of the LORETA method (Pascual-Marqui et al., 1994). As stated in Wipf and Nagarajan (2009) there is a number of methods which attempt to perform Bayesian model selection. Examples of methods which automatically select priors using Bayesian model selection are methods which use a Gaussian prior with a linear combination of covariance components (Phillips et al., 2005; Mattout et al., 2006; Friston et al., 2006, 2008). These methods employ an empirical Bayesian scheme to estimate the hyperparameters controlling the contribution of each component. This formulation is very flexible and allows for the combination of priors such as spatial Laplacian, minimum norm, and depth constraints. Methods which use automatic relevance determination (ARD) (MacKay, 1992; Tipping, 2001; Ramírez, 2005; Wipf, 2006; Wipf et al., 2010) are based on similar ideas, i.e., the estimation of covariance components, but are more effective when the number of components is large. Typically, a separate hyperparameter is used for every diagonal element of the covariance matrix, which leads to a sparse solution, i.e., a solution with a small number of active dipoles, similar to ℓ₁-norm regularization. Many existing M/EEG source localization methods can be formulated in a unified Bayesian framework; we refer to Wipf and Nagarajan (2009) where the framework is introduced for a more thorough review of Bayesian M/EEG source localization methods.

The Bayesian treatment of M/EEG source localization offers advantages other than the automatic determination of relevant priors. The Bayesian formulation offers a formal way to include information from other functional neuroimaging modalities, such as functional magnetic resonance imaging (fMRI), into the source localization problem.

In recent years, fMRI has become a prominent neuroimaging method as it offers a very high spatial resolution. On the other hand, the temporal resolution is limited by technical and physical constraints, which limit the repetition time (TR) to be in the order of seconds, as well as, by the indirect mechanism fMRI uses to measure neuronal activity, i.e., the so-called blood oxygen level dependent (BOLD) contrast (Ogawa et al., 1990; Frahm et al., 1992), which depends on slow hemodynamic processes. However, the complementary advantages of EEG and fMRI and the fact that they can be acquired simultaneously (Laufs et al., 2008) make the modalities attractive candidates to be combined, or “fused”, with the goal of obtaining functional neuroimaging data with high spatial and temporal resolution.

A number of methods have been proposed for combining M/EEG and fMRI for source localization. They are all based on the assumption that a subset of the neuronal activity is detectable by both modalities (Pflieger and Greenblatt, 2001), thus fMRI data can be used to inform the source localization method about the location of the sources. In terms of ECD methods, it is possible to constrain the location of the dipoles to be within fMRI active areas (George et al., 1995) or to use them as starting points for the optimization algorithm (dipole seeding) (Hillyard et al., 1997). More recently, an ECD method using a Bayesian formulation with an fMRI location prior and Markov Chain Monte Carlo sampling has been proposed (Jun et al., 2008). In the distributed formulation, fMRI active areas can be assigned different weights when using a weighted minimum norm method (Liu et al., 1998), or principal component analysis (PCA) and independent component analysis (ICA) can be used to obtain basis signals which can explain both the EEG and fMRI observations (Brookings et al., 2009). Another method is based on an adaptive Wiener filter where it is assumed that the energy of the electrical activity at every location on the cortex is proportional to the magnitude of the BOLD response at the same location (Liu and He, 2008). It can also be assumed that the cortical activity is sparse, i.e., there are a small but unknown number of active dipoles, which are often located in fMRI active areas. This assumption can be formulated in a Bayesian framework using an ARD prior with different hyperparameters for fMRI active areas (Sato et al., 2004). Another approach is to employ a Bayesian EEG source localization method which can automatically select priors from a set of candidate priors (Phillips et al., 2005; Mattout et al., 2006). When using such a method for EEG/fMRI fusion, location priors can be derived from fMRI activation maps (Mattout et al., 2006). An advantage of this formulation is the possibility to include every fMRI active cluster as a separate location prior (Henson et al., 2010). Doing so enables the method to automatically adjust the relative prior weights by means of model evidence maximization, which is very powerful since it allows the method to emphasize valid fMRI priors (Henson et al., 2010).

All these methods are considered asymmetric since the fMRI data set is analyzed separately and location priors for source localization are derived from the obtained fMRI activation maps. Since some neuronal activity may only be visible in one modality, the introduction of a fixed fMRI based prior can cause an estimation bias which strongly depends on the way the fMRI prior is introduced (Mattout et al., 2006).

Symmetrical EEG/fMRI fusion methods, which analyze the EEG and fMRI jointly and do not use an explicit fMRI prior are believed to be more robust against possible discrepancies between EEG and fMRI. Recently, a method which combines EEG and fMRI symmetrically by means of a common generative model has been proposed (Daunizeau et al., 2007). The method links the modalities by means of a time invariant spatial profile and uses temporal smoothness priors for the cortical currents and the hemodynamic response functions, as well as, a spatial smoothness prior based on a spatial Laplacian, which is also used in the LORETA method (Pascual-Marqui et al., 1994). By using a fully Bayesian formulation and variational Bayesian (VB) inference (Jordan et al., 1999; Attias, 2000) the method can estimate all parameters from the data and does not depend on any user defined parameters. Recently, a method with a similar generative model structure has been proposed (Ou et al., 2010). A key difference is that the generative model is not fully symmetric since the hemodynamic response function for each voxel is treated as an input to the algorithm. Together with a gradient descent based optimization method, this leads to advantages in terms of computational efficiency. Another difference lies in the prior model, the method uses a spatially adaptive Laplacian spatial smoothness prior and does not use temporal smoothness priors.

In this paper, we propose a symmetrical EEG/fMRI fusion method which uses a common generative model and spatially adaptive priors. We extend the method by Daunizeau et al. (2007) in several directions and achieve a higher source localization performance. Specifically, we assume that the spatial profile can contain sharp boundaries between active and inactive regions. We model this by means of a total variation (TV) prior (Rudin et al., 1992) for the spatial profile of cortical activity. In contrast to LORETA-type, i.e., spatial Laplacian, priors (Pascual-Marqui et al., 1994), which are commonly employed in existing methods, the TV prior is spatially adaptive, that is, the degree of spatial smoothness imposed by the prior varies depending on the location. Our generative model can therefore explain abrupt changes in cortical activity, which typically occur at the boundaries of brain regions involved in event related processing, while simultaneously enforcing smoothness in the solution (we refer to Strong and Chan (2003) for a thorough analysis of the properties of the TV prior). A fundamental difference between the spatially adaptive Laplacian prior used in Ou et al. (2010) and the TV prior is that the former can only adapt the degree of spatial smoothness on a per-region basis while the TV prior can do so on a per-vertex basis. The spatially adaptive Laplacian prior therefore depends on an a priori segmentation of the cortex and changes in the degree of spatial smoothness can only occur at region boundaries. The TV prior on the other hand does not depend on such a segmentation and can explain changes in the degree of smoothness at arbitrary locations on the cortex. The TV prior was used in Adde et al. (2005) as a deterministic regularization term for the spatial current distribution at a single time instant. The use of the TV prior in this paper in the context of Bayesian inference is fundamentally different and also requires a different discretization. The proposed method also utilizes spatially adaptive temporal priors, allowing for adaptation of the amount of temporal smoothness according to the estimated activity in different brain regions. We use a fully Bayesian formulation and estimate all parameters from the data. Due to the form of the TV prior, it is not possible to directly apply standard variational Bayesian methods to estimate the posterior distribution. Therefore, in order to draw inference, we resort to a majorization method recently proposed in Babacan et al. (2008). The method employs a Gaussian approximation to the TV prior, which renders variational distribution approximation possible, but retains the spatial adaptivity of the TV prior.

We demonstrate the effectiveness of the proposed method using both simulation experiments with synthetic EEG and fMRI data and real data from a multimodal study on face perception. We also include comparisons with existing source localization algorithms and show that the proposed method provides higher performance than existing methods in terms of estimation of the spatio-temporal cortical current distribution. Due to the novel prior model, the proposed method also estimates the hemodynamic response functions more accurately than previous symmetrical fusion methods.

Organization of this paper

This paper consists of 5 sections. In the first section we model the EEG/fMRI fusion problem using the Bayesian paradigm and introduce new realistic prior distributions for the spatio-temporal cortical current distribution and the hemodynamic response functions. The Bayesian inference scheme is introduced in the second section. In the third section we report on experiments with simulated data and in the fourth section we apply the proposed method to real data from a multimodal study on face perception. The paper is discussed and conclusions are drawn in the last section. Appendices with a description of the anatomical parceling, a definition of the signal to noise ratio, an explanation of the quality metrics used, and a detailed derivation of the calculated posterior distributions using the variational framework complete the paper.

Notation

We use the following notation throughout this paper: A_ij and A_i,j denote the element at the i-th row and j-th column of matrix A, while the i-th element of a vector a is denoted as a_i. A_i. denotes a row vector containing the elements of the i-th row of A, while A._i is a column vector containing the elements of the i-th column of A. The operator diag(A) extracts the main diagonal of A as a column vector, whereas Diag(a) a is a diagonal matrix with a as its diagonal. The operator vec (A) vectorizes A by stacking its columns, tr(A) denotes the trace of matrix A, and ⊗ denotes the Kronecker product.

Hierarchical Bayesian modeling

In this section we define the hierarchical generative model which forms the basis of the proposed method. In the first part we model the process which gives rise to the observed EEG and fMRI data when the current distribution on the cortex and the hemodynamic response function at every location are known. This constitutes the observation model which corresponds to the lowest level of the hierarchical model. In the second part we describe the spatio-temporal decomposition, which divides the cortex into a number of temporally coherent regions and establishes a connection between EEG and fMRI by means of an unknown time invariant spatial profile. We proceed by describing the spatio-temporal prior model, where we introduce the TV spatial prior, as well as, temporal priors which model varying degrees of temporal smoothness across the surface of the cortex. Following a fully Bayesian formulation, prior distributions for all hyperparameters of the model are defined next. At the end of this section, we combine the introduced probability density functions (pdf) to obtain a joint pdf over the observed data and all parameters of the model, which will enable us to obtain the Bayesian inference procedure defined in the next section.

Observation model

In the following we assume that the data is only related to a single event type. For EEG this means that the raw data is averaged over trials for the same event type in order to obtain event related potentials (ERPs) and for fMRI the event onset times for a single event type are used.

Using the distributed source framework (Hämäläinen et al., 1993) the EEG data is modeled as

$$\mathbf{M}=\mathbf{LS}+{\mathrm{\eta }}_1,$$ (1)

where M is an m×t₁ matrix containing the EEG recordings with duration t₁ obtained from m electrodes placed on the scalp, S is an unknown n×t₁ matrix representing the responses of n normal-oriented current dipoles distributed on the cortical surface, i.e., a spatio-temporal cortical current distribution, L is a known m×n forward operator, also known as lead-field matrix, which can be calculated from the head geometry and tissue conductivities, and η₁ is an m×t₁ matrix representing noise.

We model the noise η₁ for EEG as zero-mean, independent and identically distributed (i.i.d.) Gaussian, resulting in

$$\mathrm{p}(\mathbf{M}\mid \mathbf{S},{\mathrm{\alpha }}_1)=\prod _{i=1}^{t_1}𝒩\left({\mathbf{M}}_{\cdot i}\mid {\mathbf{LS}}_{\cdot i},{\mathrm{\alpha }}_1^{-1}{\mathbf{I}}_m\right),$$ (2)

where α₁ is the hyperparameter corresponding to the EEG noise precision.

In order to model the fMRI observations it is assumed that there is a linear relationship between the stimulus and the BOLD response, which leads to the following observation model (Marrelec et al., 2002)

$$\mathbf{Y}=\mathbf{BH}+{\mathrm{\eta }}_2,$$ (3)

where Y is the t₂ × n matrix containing the fMRI measurements at n voxels on the cortical surface (we assume here that the locations of the voxels coincide with the locations of the EEG current dipoles), H is an unknown k × n matrix representing the hemodynamic response function (HRF) of length k for each voxel, and η₂ is the t₂ × n matrix with additive noise. The t₂ × k matrix B is different from the design matrix in classical fMRI analysis (Friston et al., 1995). The matrix used here implements a convolution and is given by

$$\mathbf{B}=\left[\begin{array}{cccc}\hfill x_1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill x_2\hfill & \hfill x_1\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill x_{t_2-k+1}\hfill & \hfill x_{t_2-k}\hfill & \hfill \cdots \hfill & \hfill x_{t_2-2k+1}\hfill \\ \hfill 0\hfill & \hfill x_{t_2-k+1}\hfill & \hfill \cdots \hfill & \hfill x_{t_2-2k+2}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill x_{t_2-k+1}\hfill \end{array}\right],$$ (4)

where the experimental time course (x_i)_{1≤i≤t2−k+1} is a discrete time series in which the i-th element encodes an event onset during the i-th fMRI acquisition, i.e., the time series is all zero except at indices corresponding to event onsets where we use x_i=1 to encode the onset. From Eq. (3) and the structure of B in Eq. (4) it can be seen that the acquired fMRI time series of the j-th voxel is modeled as a convolution of the HRF with the experimental time course x plus additive noise, i.e.,

$${\mathbf{Y}}_{\cdot j}=\mathbf{x}\ast {\mathbf{H}}_{\cdot j}+{\left({\mathrm{\eta }}_2\right)}_{\cdot j},$$ (5)

where * denotes the (discrete) convolution operator.

For the fMRI noise we also assume that the noise is zero-mean, i.i.d. Gaussian, resulting in

$$\mathrm{p}(\mathbf{Y}\mid \mathbf{H},{\mathrm{\alpha }}_2)=\prod _{i=1}^n𝒩\left({\mathbf{Y}}_{\cdot i}\mid {\mathbf{BH}}_{\cdot i},{\mathrm{\alpha }}_2^{-1}{\mathbf{I}}_{t_2}\right),$$ (6)

where α₂ is the hyperparameter corresponding to the fMRI noise precision.

Spatio-temporal decomposition model

In this section we introduce the spatio-temporal decomposition model, which allows us to link EEG and fMRI by means of a common time invariant spatial profile. We adopt the model proposed in Daunizeau et al. (2007) as it provides an elegant way to combine EEG and fMRI. The model utilizes a hierarchical description of the cortical current distribution and the hemodynamic response functions. In order to obtain the hierarchical description, it is assumed that the cortical activity can be described by a set of regions where the responses within a region have similar temporal characteristics, i.e., the responses within a region are temporally coherent. In order to introduce the spatio-temporal decomposition, let us first define a fixed segmentation of the cortex into q regions, or parcels, which we encode using a fixed n × q segmentation matrix C defined as

$${\mathbf{C}}_{\mathit{ij}}=\{\begin{array}{cc}1\hfill & \text{if}i-\text{th vertex is in the}j-\text{th parcel},\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$ (7)

In this work the matrix C is obtained by a segmentation procedure which uses a region growing algorithm; the procedure is described in Appendix A. However, we note that the segmentation procedure itself is not an integral part of the proposed EEG/fMRI fusion method. By assuming that the electrical responses within each region have the same shape with different scales, the coherency assumption for EEG is formalized by

$$\mathbf{S}=\mathrm{Diag}\left({\mathbf{w}}^{\mathrm{EEG}}\right)\mathbf{CX}+{\mathrm{\rho }}_1,$$ (8)

where w^EEG is a n × 1 vector representing the unknown spatial profile of the cortical currents, X is a q × t₁ matrix with the unknown temporal shape of the currents for each region, and ρ₁ is a n × t₁ matrix representing residual activity which cannot be explained by the model. From Eqs. (7) and (8) it can be seen that if the i-th dipole lies within the j-th parcel, the current waveform of the dipole is modeled as the waveform of the j-th parcel X_j. scaled by the scaling variable for the i-dipole $w_i^{\mathrm{EEG}}$, i.e.,

$${\mathbf{S}}_{i\cdot }=w_i^{\mathrm{EEG}}{\mathbf{X}}_{j\cdot }+{\left({\mathrm{\rho }}_1\right)}_i..$$ (9)

We assume that all the residuals in ρ₁ are zero-mean, i.i.d. Gaussian distributed and obtain the following hierarchical prior for the cortical currents

$$\mathrm{p}(\mathbf{S}\mid \mathbf{X},{\mathbf{w}}^{\mathrm{EEG}},{∊}_1)=\prod _{i=1}^{t_1}𝒩\left({\mathbf{S}}_{\cdot i}\mid \mathrm{Diag}\left({\mathbf{w}}^{\mathrm{EEG}}\right){\mathbf{CX}}_{\cdot i},{∊}_1^{-1}{\mathbf{I}}_n\right).$$ (10)

Utilizing the same coherency assumption for the HRFs leads to

$${\mathbf{H}}^T=\mathrm{Diag}\left({\mathbf{w}}^{\mathrm{fMRI}}\right)\mathbf{CZ}+{\mathrm{\rho }}_2,$$ (11)

where Z is a q × k matrix containing the unknown HRFs of the parcels, w^fMRI is a n × 1 vector describing the spatial profile, and ρ₂ is a n × k matrix representing the modeling residual. Note that we use H^T instead of H in Eq. (11) since H^T and S have the same spatio-temporal structure, i.e., the rows correspond to waveforms at different locations on the cortex. Therefore, by using H^T in Eq. (11) the equation has the same form as Eq. (8).

As for EEG, we assume that ρ₂ is zero-mean, i.i.d., Gaussian and obtain the following hierarchical prior for the HRFs

$$\mathrm{p}({\mathbf{H}}^T\mid \mathbf{Z},{\mathbf{w}}^{\mathrm{fMRI}},{∊}_2)=\prod _{i=1}^k𝒩\left({\left({\mathbf{H}}^T\right)}_{\cdot i}\mid \mathrm{Diag}\left({\mathbf{w}}^{\mathrm{fMRI}}\right){\mathbf{CZ}}_{\cdot i},{∊}_2^{-1}{\mathbf{I}}_n\right).$$ (12)

In order to establish a connection between the imaging modalities, a common spatial profile is assumed, i.e.,

$${\mathbf{w}}^{\mathrm{EEG}}={\mathbf{w}}^{\mathrm{fMRI}}=\mathbf{w}.$$ (13)

Note how the temporal characteristics of EEG and fMRI are modeled by X and Z, respectively, while the time invariant spatial profile w is responsible for the scale. Therefore, the hierarchical generative model represents a spatio-temporal decomposition and no assumptions are made about the relationship between the temporal shapes of the HRFs and cortical currents. The spatio-temporal decomposition is illustrated in Fig. 1 where the cortical currents and HRFs are shown for two parcels.

Fig. 1.

Illustration of the spatio-temporal decomposition model. The cortical currents and the HRFs within a parcel are assumed to be temporally coherent, i.e., the temporal shape is the same but with different scales, which are modeled by the time invariant spatial profile w. The spatial profile links the EEG and fMRI modalities since w_i controls the scale of the current response as well as the scale of the HRF at the i-th vertex. This is illustrated here for two parcels and three waveforms per parcel; the waveforms belonging to the same vertex are drawn with the same color.

Spatial prior model

It is widely known that event related processing in the brain occurs in a number of specialized brain regions. Based on this, we assume that the spatial profile w contains sharp boundaries between active and inactive regions. In this work, this a priori knowledge is incorporated by utilizing a total variation (TV) prior, given by

$$\mathrm{p}(\mathbf{w}\mid \mathrm{\gamma })=\frac{1}{\mathrm{Z}\left(\mathrm{\gamma }\right)}\exp (-\mathrm{\gamma }\mathrm{TV}\left(\mathbf{w}\right)),$$ (14)

where Z(γ) is the partition function and TV(·) is a discrete version of the total variation integral, which is given by

$${\mathrm{TV}}_{\text{integral}}\left(f\right)={\int }_{\mathrm{\Omega }}\parallel \nabla f\left(\mathbf{x}\right)\parallel d\mathbf{x},$$ (15)

where Ω denotes the domain over which f(·) is defined and ∥▽f(·)∥ denotes the magnitude of the gradient of f(·). The hyperparameter γ is similar to the precision (inverse variance) parameter of a Gaussian prior, i.e., it controls the strength of the prior. As will be shown later, following a fully Bayesian approach γ will be treated as unknown and estimated from the data. Total variation priors have been used with great success in a number of inverse problems, such as image denoising and restoration (Rudin et al., 1992; Babacan et al., 2008). A property of the TV prior is that it promotes piecewise smooth solutions, which matches well with our assumption that the spatial profile contains sharp boundaries between smooth regions. An intuitive explanation for the promotion of piecewise smooth solutions can be obtained by thinking of TV regularization as ℓ₁-norm regularization of the magnitude of the gradient. While regular ℓ₁-norm regularization leads to a sparse solution, i.e., a solution where few entries are non-zero, TV regularization leads to a solution where only few locations have non-zero gradient magnitudes, which corresponds to a piecewise smooth solution.

There are two main difficulties in utilizing a TV-prior on the spatial profile w. First, the spatial profile w is defined on the folded surface of the cortex, such that the calculation of the gradient is not straightforward as in image processing applications where the image is defined on a rectangular 2-D lattice. The second difficulty is that the partition function Z(γ) in Eq. (14) is intractable. Both these difficulties are addressed below.

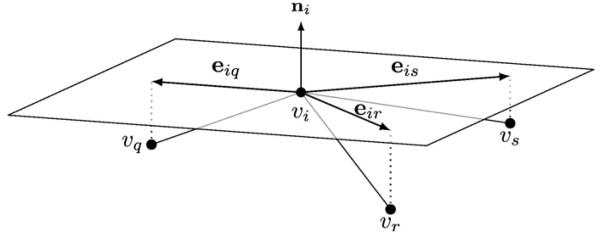
We address the first problem by defining the gradient of the spatial profile on a differentiable 2-manifold representing the cortical surface embedded in ℝ³. In practice, the geometry of the manifold is approximated by a triangular mesh denoted by M=(V,E), where V= {v₁,v₂, …, v_n} is the set of n vertices, and E denotes the set of edges each connecting a pair of vertices. Let us denote ▽_Mw_i the gradient of w at vertex v_i. This gradient ▽_Mw_i is the result of discretizing the gradient on a 2-manifold, i.e., the gradient is in the tangent space of M at v_i, which is a Euclidean space in ℝ² orthogonal to the surface normal vector at v_i. As the surface normal vector at a vertex we utilize the angle-weighted average of the surface normal vectors of the adjacent triangles (Thürmer and Wuthrich, 1998). In order to calculate the gradient, we project the neighboring vertices v_j∀j∈𝒩_i onto the tangent space at v_i, where 𝒩_i denotes the ordered set of neighborhood vertex indices defined as 𝒩_i =(j|(v_i v_j)∈E). By doing so we obtain for every neighbor a vector e_ij in ℝ² which points from vertex v_i to the projected location of v_j, as depicted in Fig. 2. To calculate the gradient, note that the gradient can be used to obtain a first order approximation, i.e.,

$$w_i+{\mathbf{e}}_{\mathit{ij}}^T{\nabla }_M{w}_i=w_j+r\forall j\in {𝒩}_i,$$ (16)

where r denotes the residual error. By using all neighbors and rewriting Eq. (16) in matrix form we obtain

$$\mathbf{r}=\underset{{\mathbf{E}}_i}{\underbrace{\left[\begin{array}{c}\hfill {\mathbf{e}}_{i{𝒩}_i\left(1\right)}^T\hfill \\ \hfill {\mathbf{e}}_{i{𝒩}_i\left(2\right)}^T\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{e}}_{i{𝒩}_i\left(\left|{𝒩}_i\right|\right)}^T\hfill \end{array}\right]}}{\nabla }_M{W}_i-\underset{{\mathbf{d}}_i}{\underbrace{\left[\begin{array}{c}\hfill W_{{𝒩}_i\left(1\right)}-W_i\hfill \\ \hfill W_{{𝒩}_i\left(2\right)}-W_i\hfill \\ \hfill ⋮\hfill \\ \hfill W_{{𝒩}_i\left(\left|{𝒩}_i\right|\right)}-W_i\hfill \end{array}\right]}},$$ (17)

which enables us to estimate the gradient by minimizing the residual ∥r∥₂, resulting in

$${\nabla }_M{w}_i={\left({\mathbf{E}}_i^T{\mathbf{E}}_i\right)}^{-1}{\mathbf{E}}_i^T{\mathbf{d}}_i={\mathbf{G}}_i{\mathbf{d}}_i.$$ (18)

Fig. 2.

Illustration of the tangent plane at vertex v_i, which is assumed to have three neighbors 𝒩_i = (q, r, s). The tangent plane is a Euclidean space in ℝ² oriented orthogonal to the vertex normal n_i. By projecting the neighboring vertices {v_q, v_r, v_s} onto the tangent plane the vectors e_iq, e_ir, and e_is in ℝ² are obtained. The vectors are utilized for calculating the gradient operator matrix at vertex v_i.

Note that since the 2×|𝒩_i| gradient matrix G_i for vertex v_i solely depends on the geometry of the mesh, the gradient matrices for all vertices of the mesh have to be computed only once.

We also note that

$${\mathbf{d}}_i=\left[\begin{array}{c}\hfill w_{{𝒩}_i\left(1\right)}-w_i\hfill \\ \hfill w_{{𝒩}_i\left(2\right)}-w_i\hfill \\ \hfill ⋮\hfill \\ \hfill w_{{𝒩}_i\left(\left|{𝒩}_i\right|\right)}-w_i\hfill \end{array}\right]={\mathrm{\Delta }}_i\mathbf{w}$$ (19)

where Δ_i is a |𝒩_i×n matrix whose j-th row consists of zeros except at the columns i and 𝒩_i(j) where it has the values −1 and 1, respectively.

Finally, the discrete version of the total variation integral in Eq. (14) can be expressed as

$$\mathrm{TV}\left(\mathbf{w}\right)=\underset{i=1}{\overset{n}{\Sigma }}{\parallel {\nabla }_M{w}_i\parallel }_2=\underset{i=1}{\overset{n}{\Sigma }}\sqrt{{\mathbf{w}}^T{\mathrm{\Delta }}_i^T{\mathbf{G}}_i^T{\mathbf{G}}_i{\mathrm{\Delta }}_i\mathbf{w}}.$$ (20)

A second difficulty arising from the use of a TV prior is that the partition function Z(γ) in Eq. (14) has to be calculated as

$$\mathrm{Z}\left(\mathrm{\gamma }\right)=\int \exp (-\mathrm{\gamma }\mathrm{TV}\left(\mathbf{w}\right))d\mathbf{w},$$ (21)

which is intractable since the integral cannot be calculated analytically. Note that we cannot resort to numerical methods, such as Monte Carlo integration, to calculate the partition function as it would require drawing samples from p(w|γ) and there is no known method for this task. To address this difficulty, we use the following method to approximate the partition function. We can express the gradient at the i-th vertex as g = [g₁g₂]^T = G_iΔ_iw and thus ${\mathbf{g}}^T\mathbf{g}=g_1^2+g_2^2$. Using this we can calculate the partition function for a single vertex as follows

$${\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\exp \left(-\mathrm{\gamma }\sqrt{g_1^2+g_2^2}\right){\mathit{dg}}_1{\mathit{dg}}_2=\frac{2\pi }{{\mathrm{\gamma }}^2}.$$ (22)

By combining the partition functions of all n vertices of the mesh we use this to approximate p(w|γ) in Eq. (14) as

$$\mathrm{p}(\mathbf{w}\mid \mathrm{\gamma })=c{\mathrm{\gamma }}^{\phi n}\exp (-\mathrm{\gamma }\mathrm{TV}\left(\mathbf{w}\right)),$$ (23)

where c is a constant and φ is a parameter with a value of φ=2.0 if the gradient at every vertex is assumed to be independent from the gradients at all other vertices. Due to the dependency between the gradient values, we empirically found that using φ=1.0 improves the performance of the algorithm and we therefore used this value throughout the rest of this paper.

Temporal prior model

We also make the assumption that the HRFs and the cortical currents are smooth in the temporal dimension. This assumption can be expressed by a Gaussian prior which penalizes the second order temporal derivative; a prior of this form was also used in Marrelec et al. (2002) and Daunizeau et al. (2007). In contrast to previous work, we assume that the degree of temporal smoothness varies across the surface of the cortex. We model this by utilizing a separate Gaussian prior for every parcel, i.e., for the temporal shapes of the cortical currents we use

$$\mathrm{p}(\mathbf{X}\mid {\mathrm{\beta }}_1)\propto \prod _{i=1}^q\exp \left(-\frac{{\left({\mathrm{\beta }}_1\right)}_i}{2}\left({\mathbf{X}}_{i\cdot }\right){\mathbf{T}}_1^T{\mathbf{T}}_1{\left({\mathbf{X}}_{i\cdot }\right)}^T\right),$$ (24)

where T₁ is a t₁ × t₁ matrix given by

$${\left({\mathbf{T}}_1\right)}_{\mathit{ij}}=\{\begin{array}{cc}-2\hfill & \text{if}i=j,\hfill \\ 1\hfill & \text{if}j=i\pm 1,\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}$$ (25)

and β₁ is a q×1 vector with per-parcel precision hyperparameters, each controlling the smoothness and scale of the cortical current waveform of a parcel. The use of separate hyperparameters allows for spatially adaptive temporal smoothness of the cortical currents, i.e., the model can reduce the degree of temporal smoothness in active regions while enforcing a higher degree of smoothness in inactive regions.

For the temporal shape of the hemodynamic response functions we use

$$\mathrm{p}(\mathbf{Z}\mid {\mathrm{\beta }}_2)\propto \prod _{i=1}^q\exp \left(-\frac{{\left({\mathrm{\beta }}_2\right)}_i}{2}\left({\mathbf{Z}}_{i\cdot }\right){\mathbf{T}}_2^T{\mathbf{T}}_2{\left({\mathbf{Z}}_{i\cdot }\right)}^T\right),$$ (26)

where T₂ is a k × k matrix that is defined analogously to T₁ and β₂ is a q × 1 vector with per-parcel precision hyperparameters. As with the cortical currents, the use of separate hyperparameters allows for spatially adaptive temporal smoothness of the HRF.

Hyperparameter prior model

Following the Bayesian approach we proceed by defining priors for all hyperparameters of the model. In order to obtain priors for the EEG and fMRI noise precisions, we obtain pre-stimulus data segments M⁰ for EEG and Y⁰ for fMRI containing only noise with sizes $m\times t_1^0$ and $t_2^0\times n$, respectively. From the Gaussian noise assumption it follows that p(α₁|M⁰ and p(α₂|Y⁰) are gamma distributed (Daunizeau et al., 2007), which motivates the use of the following prior distribution for the EEG noise precision hyperparameter

$$\begin{array}{cc}\hfill & \mathrm{p}\left({\mathrm{\alpha }}_1\right)=\mathrm{p}\left({\mathrm{\alpha }}_1\mid {\mathbf{M}}^0\right)=\mathrm{\Gamma }\left({\mathrm{\alpha }}_1\mid a_{{\mathrm{\alpha }}_1}^0,b_{{\mathrm{\alpha }}_1}^0\right),\hfill \\ \hfill & a_{{\mathrm{\alpha }}_1}^0=\frac{{\mathit{mt}}_1^0}{2},b_{{\mathrm{\alpha }}_1}^0=\frac{\mathrm{tr}\left({\mathbf{M}}^{0^T}{\mathrm{M}}^0\right)}{2}.\hfill \end{array}$$ (27)

The gamma distribution is defined as

$$\mathrm{\Gamma }(x\mid a,b)=\frac{b^a}{\mathrm{\Gamma }\left(a\right)}{x}^{a-1}\exp (-\mathit{bx}),$$ (28)

where a > 0 and b > 0 are the shape and inverse scale parameters, respectively. Similarly, we use the following prior distribution for the fMRI noise precision hyperparameter

$$\begin{array}{cc}\hfill & \mathrm{p}\left({\mathrm{\alpha }}_2\right)=\mathrm{p}\left({\mathrm{\alpha }}_2\mid {\mathbf{Y}}^0\right)=\mathrm{\Gamma }\left({\mathrm{\alpha }}_2\mid a_{{\mathrm{\alpha }}_2}^0,b_{{\mathrm{\alpha }}_2}^0\right),\hfill \\ \hfill & a_{{\mathrm{\alpha }}_2}^0=\frac{{\mathit{nt}}_2^0}{2},b_{{\mathrm{\alpha }}_2}^0=\frac{\mathrm{tr}\left({\mathbf{Y}}^{0^T}{\mathrm{Y}}^0\right)}{2}.\hfill \end{array}$$ (29)

Note that the prior distributions become more sharply peaked as the lengths of the pre-stimulus segments increase. Longer pre-stimulus segments cause the fusion algorithm to rely more on the initial noise estimates, i.e., the noise estimated by the algorithm becomes almost entirely decided by the initial estimates. On the other hand, as the length of the pre-stimulus segments goes towards zero, the prior distributions become flat and the noise precision is estimated solely by the fusion algorithm.

For the precision parameter vectors β₁ and β₂, which control the per-parcel temporal smoothness and scale of the cortical currents and hemodynamic response functions, respectively, we use a hyperparameter prior model which allows us to control the degree of spatial adaptivity. In order to do so, we use gamma priors as follows

$$\mathrm{p}({\mathrm{\beta }}_1\mid {\mathrm{\delta }}_1)=\prod _{i=1}^q\mathrm{\Gamma }\left({\left({\mathrm{\beta }}_1\right)}_i\mid a_{{\mathrm{\beta }}_1}^0,{\mathrm{\delta }}_1,\right)$$ (30)

$$\mathrm{p}({\mathrm{\beta }}_2\mid {\mathrm{\delta }}_2)=\prod _{i=1}^q\mathrm{\Gamma }\left({\left({\mathrm{\beta }}_2\right)}_i\mid a_{{\mathrm{\beta }}_2}^0,{\mathrm{\delta }}_2,\right)$$ (31)

where $a_{{\beta }_1}^0$ and $a_{{\beta }_2}^0$ are fixed shape parameters and the unknown inverse scale parameters are denoted by δ₁ and δ₂. The use of fixed shape parameters allows us to control the degree of spatial adaptivity. As will become clear after the derivation of the approximate posterior distribution in the next section, by using a value close to zero for $a_{{\beta }_1}^0$ the posterior distributions of (β₁)_i, …,(β₁)_q can be drastically different. Hence, the model is fully spatially adaptive. On the other hand, when $a_{{\beta }_1}^0$ is very large, all posterior distributions will be almost identical and the prior model is not spatially adaptive, which is similar to the temporal prior model in Daunizeau et al. (2007). We empirically find that the proposed method performs best when the degree of spatial adaptivity for the EEG side is limited by using $a_{{\beta }_1}^0=100$ while using a higher degree of spatial adaptivity for the fMRI side with $a_{{\beta }_2}^0={10}^{-3}$. These values are used throughout the rest of this paper. We note here that the proposed method is not very sensitive to the exact values of the shape parameters, i.e., a value in the range 10, …, 200 works well for $a_{{\beta }_1}^0$ while any value close to 0 works well for $a_{{\beta }_2}^0$.

We make no assumptions about the remaining hyperparameters and consequently use noninformative Jeffreys priors given by

$$\mathrm{p}\left({\mathrm{\theta }}_i\right)=\mathrm{\Gamma }({\mathrm{\theta }}_i\mid 0,0)\propto {\left({\mathrm{\theta }}_i\right)}^{-1}\forall {\mathrm{\theta }}_i\in \mathrm{\theta },$$ (32)

where θ ={δ₁, δ₂, ε₁, ε₂, γ}, to define

$$\mathrm{p}\left(\theta \right)=\prod _{{\mathrm{\theta }}_i\in \mathrm{\theta }}\mathrm{p}\left({\mathrm{\theta }}_i\right).$$ (33)

We note here that an important reason for selecting gamma distributions as priors for the hyperparameters is that the gamma distribution is the conjugate prior for the precision of a Gaussian distribution, as well as, for the inverse scale parameter of the gamma distribution, which simplifies the Bayesian inference since the posterior distributions of the hyperparameters will also be gamma distributions. As will be shown in the next section, in order to draw inference we employ a quadratic approximation to the energy of the TV prior in the form of a Gaussian distribution and consequently the conjugate prior for γ is a gamma distribution.

Global modeling

By combining all distributions introduced above, we obtain the joint probability density function as follows

$$\begin{array}{cc}\hfill \mathrm{p}(\mathbf{\Theta },\mathbf{M},\mathbf{Y})=& \mathrm{p}(\mathbf{M}\mid \mathbf{S},{\mathrm{\alpha }}_1)\mathrm{p}(\mathbf{S}\mid \mathbf{X},\mathbf{w},{∊}_1)\mathrm{p}(\mathbf{X}\mid {\mathrm{\beta }}_1)\hfill \\ \hfill & \times \mathrm{p}(\mathbf{Y}\mid \mathbf{H},{\mathrm{\alpha }}_2)\mathrm{p}(\mathbf{H}\mid \mathbf{Z},\mathbf{w},{∊}_2)\mathrm{p}(\mathbf{Z}\mid {\mathrm{\beta }}_2)\mathrm{p}(\mathbf{w}\mid \mathrm{\gamma })\hfill \\ \hfill & \times \mathrm{p}\left({\mathrm{\alpha }}_1\right)\mathrm{p}\left({\mathrm{\alpha }}_2\right)\mathrm{p}({\mathrm{\beta }}_1\mid {\mathrm{\delta }}_1)\mathrm{p}({\mathrm{\beta }}_2\mid {\mathrm{\delta }}_2)\mathrm{p}\left(\theta \right),\hfill \end{array}$$ (34)

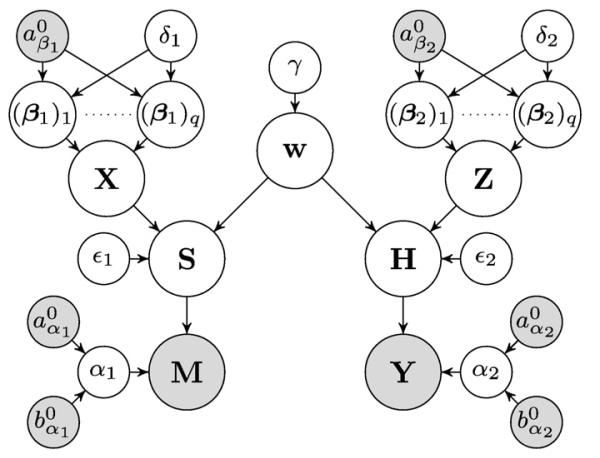
where Θ = {S, H, w, X, Z, α₁, α₂, β₁, β₂,}∪θ is the set of all unknowns. The dependencies between the variables in the joint pdf are illustrated as a directed acyclic graphical model in Fig. 3.

Fig. 3.

Directed acyclic graphical model describing the joint pdf (gray: known, white: unknown).

The joint pdf allows us to derive a fusion algorithm using Bayesian inference, which is described in the next section.

Bayesian inference

Inference is based on the posterior distribution

$$\mathrm{p}(\mathbf{\Theta }\mid \mathbf{M},\mathbf{Y})=\frac{\mathrm{p}(\mathbf{\Theta }\mid \mathbf{M},\mathbf{Y})}{\mathrm{p}(\mathbf{M},\mathbf{Y})}.$$ (35)

However, the posterior p(Θ|M, Y) is intractable since

$$\mathrm{p}(\mathbf{M},\mathbf{Y})=\int \mathrm{p}(\mathbf{M},\mathbf{Y},\mathbf{\Theta })d\mathbf{\Theta }$$ (36)

cannot be calculated analytically. Therefore, we utilize an approximation to the posterior. In this work, we employ the Variational Bayesian (VB) method using the mean field approximation (Jordan et al., 1999; Attias, 2000), i.e., we approximate the true posterior by a distribution which factorizes over the nodes of the graphical model

$$\begin{array}{cc}\hfill \mathrm{q}\left(\mathbf{\Theta }\right)=& \mathrm{q}\left(\mathbf{S}\right)\mathrm{q}\left(\mathbf{H}\right)\mathrm{q}\left(\mathbf{X}\right)\mathrm{q}\left(\mathbf{Z}\right)\mathrm{q}\left(\mathbf{w}\right)\mathrm{q}\left({\mathrm{\alpha }}_1\right)\mathrm{q}\left({\mathrm{\alpha }}_2\right)\hfill \\ \hfill & \times \left(\prod _{i=1}^q\mathrm{q}\left({\left({\mathrm{\beta }}_1\right)}_i\right)\right)\left(\prod _{i=1}^q\mathrm{q}\left({\left({\mathrm{\beta }}_2\right)}_i\right)\right)\hfill \\ \hfill & \times \mathrm{q}\left({\mathrm{\delta }}_1\right)\mathrm{q}\left({\mathrm{\delta }}_2\right)\mathrm{q}\left({\mathrm{∊}}_1\right)\mathrm{q}\left({\mathrm{∊}}_2\right)\mathrm{q}\left(\mathrm{\gamma }\right).\hfill \end{array}$$ (37)

As stated in Jaakkola and Jordan (1998), mean field theory (Parisi, 1998) provides an intuitive explanation of the mean field approximation. That is, in a dense graph each node is influenced by many other nodes such that the influence from each other node is weak and the total influence is approximately additive. Hence, each node can be characterized by its mean value, which is unknown and related to the mean values of all other nodes. The task then becomes finding the relation between the mean values and designing an algorithm which can find a consistent assignment of mean values. This is exactly what we will do in the following. First, we will find a distribution for each node in the graphical model shown in Fig. 3. The distributions describe the relation to all other nodes in the model and allow us to obtain an inference algorithm in which we iteratively update the distribution of each node leading to a consistent assignment of distributions.

The posterior approximation q(Θ) is found by performing a variational minimization of the Kullback–Leibler (KL) divergence, which is given by

$$\begin{array}{cc}\hfill & C_{\mathit{KL}}(\mathrm{q}\left(\mathbf{\Theta }\right)\parallel \mathrm{p}(\mathbf{\Theta }\mid \mathbf{M},\mathbf{Y}))\hfill \\ \hfill & =\int \mathrm{q}\left(\mathbf{\Theta }\right)\log \left(\frac{\mathrm{q}\left(\mathbf{\Theta }\right)}{\mathrm{p}(\mathbf{\Theta }\mid \mathbf{M},\mathbf{Y})}\right)d\mathbf{\Theta }\hfill \\ \hfill & =\int \mathrm{q}\left(\mathbf{\Theta }\right)\log \left(\frac{\mathrm{q}\left(\mathbf{\Theta }\right)}{\mathrm{p}(\mathbf{\Theta }\mid \mathbf{M},\mathbf{Y})}\right)d\mathbf{\Theta }+\mathrm{const}\hfill \\ \hfill & =𝒦\left(\mathrm{q}\left(\mathbf{\Theta }\right)\right)+\mathrm{const},\hfill \end{array}$$ (38)

and is non-negative and equal to zero only if q(Θ) = p(Θ|M, Y). In variational Bayesian analysis, the optimal q(Θ) is found by

$$\begin{array}{cc}\hfill \mathrm{q}\left(\mathbf{\Theta }\right)& =\underset{\mathrm{q}\left(\mathbf{\Theta }\right)}{\text{arg min}}{C}_{\mathit{KL}}(\mathrm{q}\left(\mathbf{\Theta }\right)\parallel \mathrm{p}(\mathbf{\Theta }\mid \mathbf{M},\mathbf{Y}))\hfill \\ \hfill & =\underset{\mathrm{q}\left(\mathbf{\Theta }\right)}{\text{arg min}}𝒦\left(\mathrm{q}\left(\mathbf{\Theta }\right)\right).\hfill \end{array}$$ (39)

Using a standard result from variational Bayesian analysis (Bishop, 2006), for each variable the distribution which minimizes Eq. (38) is given by

$$\mathrm{q}\left({\mathbf{\Theta }}_i\right)\propto \exp \left({𝔼}_{\mathrm{\Theta }\backslash {\mathrm{\Theta }}_i}\left[\ln \mathrm{p}(\mathbf{\Theta },\mathbf{M},\mathbf{Y})\right]\right),$$ (40)

where 𝔼_Θ\Θi[·] denotes the expectation with respect to all variables except the variable of interest.

Unfortunately, the form of the TV prior prevents us from calculating the expectation in Eq. (40) and thus from finding an analytical form of q(Θ). Therefore, we resort to a majorization method which approximates 𝒦(q(Θ)) by upper-bounding functionals which render the calculation of the expectation tractable (Babacan et al., 2008). First, let us consider the geometric–arithmetic mean inequality (Hardy et al., 1988) which states that for two positive numbers a ≥ 0 and b > 0

$$\sqrt{\mathit{ab}}\le \frac{a+b}{2}\Rightarrow \sqrt{a}\le \frac{a+b}{2\sqrt{b}}.$$ (41)

We proceed by defining for w, γ, and an n × 1 vector u∈(ℝ⁺)ⁿ following functional:

$$\mathrm{F}(\mathbf{w},\mathbf{u},\mathrm{\gamma })=c{\mathrm{\gamma }}^{\phi n}\exp \left(-\frac{\mathrm{\gamma }}{2}\underset{i=1}{\overset{n}{\Sigma }}\frac{{\mathbf{w}}^T{\mathrm{\Delta }}_i^T{\mathbf{G}}_i^T{\mathbf{G}}_i{\mathrm{\Delta }}_i\mathbf{w}+u_i}{\sqrt{u_i}}\right).$$ (42)

Using inequality Eq. (41) in Eq. (23) with $a={\mathbf{w}}^T{\mathrm{\Delta }}_i^T{\mathbf{G}}_i^T{\mathbf{G}}_i{\mathrm{\Delta }}_i\mathbf{w}$ and b = u_i, and comparing with Eq. (42), we obtain

$$\mathrm{p}(\mathbf{w}\mid \mathrm{\gamma })\ge \mathrm{F}(\mathbf{w},\mathbf{u},\mathrm{\gamma }).$$ (43)

The auxiliary variable u is related to the spatial smoothness in w and needs to be updated by the inference algorithm, as will be shown later. Using Eq. (43) in Eq. (34), we obtain a lower bound of the joint probability density function, i.e.,

$$\begin{array}{cc}\hfill \mathrm{p}(\mathbf{\Theta },\mathbf{M},\mathbf{Y})\ge & \mathrm{p}(\mathbf{M}\mid \mathbf{S},{\mathrm{\alpha }}_1)\mathrm{p}(\mathbf{S}\mid \mathbf{X},\mathbf{w},{\mathrm{∊}}_1)\mathrm{p}(\mathbf{X}\mid {\mathrm{\beta }}_1)\hfill \\ \hfill & \times \mathrm{p}(\mathbf{Y}\mid \mathbf{H},{\mathrm{\alpha }}_2)\mathrm{p}(\mathbf{H}\mid \mathbf{Z},\mathbf{w},{\mathrm{∊}}_2)\mathrm{p}(\mathbf{Z}\mid {\mathrm{\beta }}_2)\hfill \\ \hfill & \times \mathrm{p}\left({\mathrm{\alpha }}_1\right)\mathrm{p}\left({\mathrm{\alpha }}_2\right)\mathrm{p}({\mathrm{\beta }}_1\mid {\mathrm{\delta }}_1)\mathrm{p}({\mathrm{\beta }}_2\mid {\mathrm{\delta }}_2)\hfill \\ \hfill & \times \mathrm{p}\left(\mathrm{\theta }\right)\mathrm{F}(\mathbf{w},\mathbf{u},\mathrm{\gamma })\hfill \\ \hfill =& \mathrm{F}(\mathbf{\Theta },\mathbf{u},\mathbf{M},\mathbf{Y}),\hfill \end{array}$$ (44)

which allows us to derive an inference procedure, as will be shown below. It should be noted that the proposed method therefore does not employ the TV prior directly; doing so would not lead to a tractable inference. Instead, the proposed method uses the lower bound F(w, u, γ) to the TV prior, which retains many of its desirable characteristics, i.e., the ability to model sharp boundaries, and allows for a tractable inference.

To derive the inference procedure, let us now define

$$\widetilde{𝒦}(\mathrm{q}\left(\mathrm{\Theta }\right),\mathbf{u})=\int \mathrm{q}\left(\mathrm{\Theta }\right)\log \left(\frac{\mathrm{q}\left(\mathrm{\Theta }\right)}{\mathrm{F}(\mathrm{\Theta },\mathbf{u},\mathbf{M},\mathbf{Y})}\right)d\mathrm{\Theta },$$ (45)

which is the KL divergence between q(Θ) and F(Θ, u, M, Y). By using Eqs. (38) and (44), we obtain

$$𝒦\left(\mathrm{q}\left(\mathrm{\Theta }\right)\right)\le \underset{\mathbf{u}}{\min }\widetilde{𝒦}(\mathrm{q}\left(\mathrm{\Theta }\right),\mathbf{u}).$$ (46)

Therefore we can obtain a sequence of distributions {q(Θ)} which monotonically decreases 𝒦̃(q(ϴ), u) for a fixed u. From Eq. (46) it can be seen that this leads to a monotonically decreasing upper bound to C_KL(q(Θ)∥p(Θ|M, Y)) and therefore leads to an approximation of the true posterior distribution. Moreover, we can minimize 𝒦̃(q(ϴ), u) with respect to u for each distribution q(Θ), which tightens the upper bound to the KL divergence and thus leads to a more accurate distribution approximation. The two interleaved minimization steps naturally lead to the iterative distribution estimation algorithm. During each iteration the algorithm first minimizes the functional 𝒦̃(q(ϴ), u) with respect to q(Θ); the distribution approximation which minimizes this functional has the same form as in standard VB analysis (see Eq. (40)) and the distribution approximation of the node Θ_i∈Θ is given by

$$\mathrm{q}\left({\mathrm{\Theta }}_i\right)\propto \exp \left({𝔼}_{\mathrm{\Theta }\backslash {\mathrm{\Theta }}_i}\left[\ln \mathrm{F}(\mathrm{\Theta },\mathbf{u},\mathbf{M},\mathbf{Y})\right]\right).$$ (47)

Using Eq. (47) we obtain a distribution for every node of the graphical model. The distributions of the nodes S, H, X, Z, and w are found to be Gaussian while the hyperparameter distributions are found to be gamma distributions (since conjugate priors were used). The form of the distributions obtained by applying Eq. (47) is given in Table 1 and the corresponding derivations are shown in Appendix D. In order to update the distributions and therefore to minimize 𝒦̃(q(ϴ), u) in the first step of the algorithm, the algorithm updates the parameters of the distributions in Table 1 using the most recently updated parameters, i.e., either from the previous or from the current iteration. The distributions are updated in the following order: q(S), q(α₁), q(X), q(ε₁), q((β₁)₁), …, q((β₁)_q), q(δ₁), q(H),q(α₂), q(Z),q(ε₂), q((β₂)₁), …, q((β₂)_q), q(δ₂), and q(w).

Table 1.

Distributions for the nodes of the graphical model obtained using Eq. (47). Derivations are shown in Appendix D, where matrices Q, P₁, P₂, and W(u) and the cov(·) operator are defined. The matrix R_{(k, q)} is a kq × kq permutation matrix with the property R_{(k, q)}vec(Z^T)=vec(Z) (the matrix R_{(t1, q)} is defined analogously).

Functional form	Parameters
q(S) = 𝒩(vec(S)|vec(〈S〉),It1⊗ΣS)	〈S〉 = ΣS(〈α1〉LTM + 〈∊1〉Diag(〈w〉)C〈X〉)
	ΣS = (〈α1〉LTL + 〈∊1〉In)−1
q(H) = 𝒩(vec(H)|vec(〈H〉),In⊗ΣH)	〈H〉 = ΣH(〈α2〉BTY + 〈∊2〉〈Z〉TCTDiag (〈w〉))
	ΣH = (〈α2〉BTB + 〈∊2〉Ik)−1
q(X)= 𝒩(vec(X)|vec(〈X〉), Σx)	vec(〈X〉) = 〈∊1〉 Σx(It1⊗CTDiag(〈w〉))vec(〈S〉)
	${\Sigma }_{\mathbf{X}}={\left(\langle {∊}_1\rangle ({\mathbf{I}}_{t_1}\otimes \mathbf{Q})+{\mathbf{R}}_{(t_1,q)}^T\left(\text{Diag}\left(\langle {\mathrm{\beta }}_1\rangle \right)\otimes {\mathbf{T}}_1^T{\mathbf{T}}_1\right){\mathbf{R}}_{(t_1,q)}\right)}^{-1}$
q(Z) = 𝒩(vec(Z) | vec(〈Z〉), ΣZ)	vec(〈Z〉) = 〈∊2〉 ΣZ(Ik⊗CTDiag(〈w〉))vec(〈H〉T)
	${\Sigma }_{\mathbf{Z}}={\left(\langle {∊}_2\rangle ({\mathbf{I}}_k\otimes \mathbf{Q})+{\mathbf{R}}_{(k,q)}^T\left(\text{Diag}\left(\langle {\mathrm{\beta }}_2\rangle \right)\otimes {\mathbf{T}}_2^T{\mathbf{T}}_2\right){\mathbf{R}}_{(k,q)}\right)}^{-1}$
q(w) = 𝒩(w | 〈w〉, Σw)	〈w〉 = Σwdiag(〈∊1〉 〈S〉 〈X〉TCT + 〈∊2〉〈H〉T 〈Z〉TCT)
	Σw = (〈∊1〉 P1 + 〈∊2〉 P2 + 〈γ〉W(u))−1
q(α1)= Γ(α1|aα1, bα1)	$a_{{\alpha }_1}=\frac{{\mathit{mt}}_1}{2}+a_{{\alpha }_1}^0$
	$b_{{\alpha }_1}=\frac{1}{2}\mathrm{tr}\left({(\mathbf{M}-\mathbf{L}\langle \mathbf{S}\rangle )}^T(\mathbf{M}-\mathbf{L}\langle \mathbf{S}\rangle )\right)+\frac{t_1}{2}\mathrm{tr}\left({\Sigma }_{\mathbf{S}}{\mathbf{L}}^T\mathbf{L}\right)+b_{{\alpha }_1}^0$
q(α2) = Γ(α2 | aα2, bα2)	$a_{{\alpha }_2}=\frac{{\mathit{nt}}_2}{2}+a_{{\alpha }_2}^0$
	$b_{{\alpha }_2}=\frac{1}{2}\mathrm{tr}\left({(\mathbf{Y}-\mathbf{B}\langle \mathbf{H}\rangle )}^T(\mathbf{Y}-\mathbf{B}\langle \mathbf{H}\rangle )\right)+\frac{n}{2}\mathrm{tr}\left({\Sigma }_{\mathbf{H}}{\mathbf{B}}^T\mathbf{B}\right)+b_{{\alpha }_2}^0$
q(∊1) = Γ(∊1|a∊1, b∊1)	$a_{{∊}_1}=\frac{t_{1}n}{2}$
	$b_{{∊}_1}=\frac{1}{2}\left[\mathrm{tr}\left({\langle \mathbf{S}\rangle }^T\langle \mathbf{S}\rangle -2{\langle \mathbf{S}\rangle }^T\text{Diag}\left(\langle \mathbf{w}\rangle \right)\mathbf{C}\langle \mathbf{X}\rangle +{\langle \mathbf{X}\rangle }^T\mathbf{Q}\langle \mathbf{X}\rangle \right)+t_1\mathrm{tr}\left({\Sigma }_{\mathbf{S}}\right)+\mathrm{tr}\left({\Sigma }_{\mathbf{X}}({\mathbf{I}}_{t_1}\otimes \mathbf{Q})\right)\right]$
q(∊2) = Γ(∊2|a∊1, b∊1)	$a_{{∊}_2}=\frac{\mathit{kn}}{2}$
	$b_{{∊}_2}=\frac{1}{2}\left[\mathrm{tr}\left(\langle \mathbf{H}\rangle {\langle \mathbf{H}\rangle }^T-2\langle \mathbf{H}\rangle \text{Diag}\left(\langle \mathbf{w}\rangle \right)\mathbf{C}\langle \mathbf{Z}\rangle +{\langle \mathbf{Z}\rangle }^T\mathbf{Q}\langle \mathbf{Z}\rangle \right)+n\mathrm{tr}\left({\Sigma }_{\mathbf{H}}\right)+\mathrm{tr}\left({\Sigma }_{\mathbf{Z}}({\mathbf{I}}_k\otimes \mathbf{Q})\right)\right]$
q((β1)i) = Γ((β1)i|(aβ1)i, (bβ1)i)	$\left({\mathbf{a}}_{{\mathrm{\beta }}_1}\right)=\frac{t_1}{2}+a_{{\mathrm{\beta }}_1}^0$
	${\left({\mathbf{b}}_{{\mathrm{\beta }}_1}\right)}_i=\frac{1}{2}\langle {\mathbf{X}}_i.\rangle {\mathbf{T}}_1^T{\mathbf{T}}_1{\langle {\mathbf{X}}_i.\rangle }^T+\frac{1}{2}\mathrm{tr}\left({\mathbf{T}}_1^T{\mathbf{T}}_1\mathrm{cov}\left({({\mathbf{X}}_i.)}^T\right)\right)+\langle {\mathrm{\delta }}_1\rangle$
q((β2)i) = Γ((β2)i|(aβ2)i, (bβ2)i)	${\left({\mathbf{a}}_{{\mathrm{\beta }}_2}\right)}_i=\frac{k}{2}+a_{{\mathrm{\beta }}_2}^0$
	${\left({\mathbf{b}}_{{\mathrm{\beta }}_2}\right)}_i=\frac{1}{2}\langle {\mathbf{Z}}_i.\rangle {\mathbf{T}}_2^T{\mathbf{T}}_2{\langle {\mathbf{Z}}_i.\rangle }^T+\frac{1}{2}\mathrm{tr}\left({\mathbf{T}}_2^T{\mathbf{T}}_2\mathrm{cov}\left({({\mathbf{Z}}_i.)}^T\right)\right)+\langle {\mathrm{\delta }}_2\rangle$
q(δ1) = Γ(δ1|aδ1, bδ1)	aδ1 = aβ10q
	$b_{{\mathrm{\delta }}_1}={\Sigma }_{i=1}^q\langle {\left({\mathrm{\beta }}_1\right)}_i\rangle$
q(δ2)= Γ(δ2|aδ2, bδ2)	aδ2 = aβ20q
	$b_{{\mathrm{\delta }}_2}={\Sigma }_{i=1}^q\langle {\left({\mathrm{\beta }}_2\right)}_i\rangle$
q(γ) = Γ(γ|aγ, bγ)	aγ = φn
	$b_{\mathrm{\gamma }}={\Sigma }_{i=1}^n\sqrt{u_i}$

After updating q(Θ) in the first step of an iteration of the algorithm, the algorithm minimizes the functional 𝒦̃(q(ϴ), u) with respect to u in the second step of an iteration, which is equivalent to

$$\mathbf{u}=\underset{\mathbf{u}}{\text{arg min}}\underset{i=1}{\overset{n}{\Sigma }}\frac{𝔼\left[{\mathbf{w}}^T{\mathrm{\Delta }}_i^T{\mathbf{G}}_i^T{\mathbf{G}}_i{\mathrm{\Delta }}_i\mathbf{w}\right]+u_i}{\sqrt{u_i}}.$$ (48)

Since Eq. (48) is a linear combination of n functions where the i-th function is convex with respect to u_i, the minimizer is found by calculating the derivative with respect to u_i and equating to zero, which results in the following update

$$\begin{array}{cc}\hfill u_i& =𝔼\left[{\mathbf{w}}^T{\mathrm{\Delta }}_i^T{\mathbf{G}}_i^T{\mathbf{G}}_i{\mathrm{\Delta }}_i\mathbf{w}\right]\hfill \\ \hfill & =\mathrm{tr}\left[{\mathrm{\Delta }}_i^T{\mathbf{G}}_i^T{\mathbf{G}}_i{\mathrm{\Delta }}_i\left({\Sigma }_{\mathbf{w}}+\langle \mathbf{w}\rangle {\langle \mathbf{w}\rangle }^T\right)\right],\hfill \end{array}$$ (49)

for i = 1, …, n. It is clear from Eq. (49) that the auxiliary vector u is related to the gradient of the estimated spatial profile w. Moreover, as can be seen from q(w) (shown in Table 1), the vector u introduces spatially adaptive smoothing through the matrix W(u) into the estimation process (see Appendix D). This matrix controls the amount of smoothing at each vertex depending on the local variation of the spatial profile.

Computational complexity

To conclude this section we discuss the per-iteration computational complexity of the proposed method. Note that this does not take into account the computational cost of obtaining the parcellation of the cortex and the cost of computing the gradient projection matrices, as these operations only have to be performed once for a given cortical mesh. Excluding these operations from the discussion is also justified by the fact that the time required to perform them is typically shorter than the time required for one iteration of the proposed method. The per-iteration computational complexity of the proposed method is governed by the complexity of the matrix inversions needed to compute the covariance matrices in Table 1. For many applications it is possible to avoid the explicit inversion of matrices by employing efficient linear system solvers, such as the conjugate gradient method. Unfortunately, this is not possible in fully Bayesian methods, such as the one proposed in this work, since the covariance matrices are required for the computation of hyperparameters. By assuming that the inversion of an N × N matrix has complexity O(N³) and by taking into account the sizes of the covariance matrices in Table 1, the per-iteration complexity of the proposed method is found to be $O(n^3+q^3(t_1^3+k^3))$. From this one can see how the number of parcels q, which is in the range [1, n], affects the computational complexity. Ideally one would like to use a large number of parcels, such that parcels are small and the probability of having multiple sources in the same parcel is low. However, doing so can lead to prohibitively high computational demands and one has to chose q ≪ n in order to satisfy the constraints imposed by the computational resources available.

Simulations

In this section we evaluate the proposed method using simulations with synthetic EEG and fMRI data. The use of synthetic data enables us to compare the proposed method and existing methods by means of objective quality metrics.

At the end of this section we evaluate the results and compare the proposed method to several existing methods. Two EEG/fMRI fusion methods are used for the comparison. The first method is the symmetrical BASTERF method (Daunizeau et al., 2007), which is similar to the proposed method but uses a different prior model. The second method is the fMRI weighted minimum norm method (fWMN) (Liu et al., 1998), which can be considered one of the simplest methods for asymmetrical EEG/fMRI fusion. As an additional reference we include several EEG-only source localization methods in the comparison. The MSP method (Friston et al., 2008) is a recently proposed method that uses multiple sparse priors (256 per hemisphere are used here) with an empirical Bayesian modeling and can be considered a state of the art EEG source localization method. We also include two classic EEG source localization methods, namely the LORETA method (Pascual-Marqui et al., 1994), and the minimum norm method (MNE) with Tikhonov noise regularization (Dale and Sereno, 1993).

EEG forward model

The lead field matrix L used for the simulations was calculated as follows. First, the template cortical mesh included in SPM8 (http://www.fil.ion.ucl.ac.uk/spm) with a total of 8196 vertices was down-sampled to n = 1000 vertices. While the coarser mesh provides a less accurate geometrical description of the cortex, it significantly reduces the computational requirements. The lead field matrix was then computed using the BEM method from FieldTrip (http://fieldtrip.fcdonders.nl) with standard sensor locations for a 64 channel montage and canonical scalp, outer skull, and inner skull meshes, which are included in SPM8.

Simulated EEG and fMRI data

In order to simulate a range of source configurations and various degrees of agreement between EEG and fMRI a total of 5 different simulation scenarios are used in our evaluation. In the first simulation scenario we use a complex source configuration with more widespread sources, such sources are for example known to occur in children (Friedrich and Friederici, 2004; Sanders et al., 2006). We denote the scenario CPX and use a total of 4 sources, among which 2 are more widespread. All sources are hemodynamically, as well as, electrically active. Due to the complexity of source configuration, it can be expected that EEG/fMRI fusion methods have a significant advantage over EEG-only methods for this scenario. The remaining simulation scenarios use simpler source configurations with only 2 sources and are used to depict situations where some sources can be detectable by either only one modality or both (a similar experiment was presented in Daunizeau et al. (2007)). In practice such situations can for example occur when a source is active for a short time and can be detected by EEG but does not generate a BOLD response strong enough to be detectable by fMRI. On the other hand, it is possible that a source is far from the surface of the scalp, and thus generates a weak EEG signal while having a strong BOLD response. The scenarios are denoted as MM for the scenario with 2 multimodal, i.e., electrically and hemodynamically active, sources, ME for the scenario with one multimodal source and another source that only exhibits electrical activity, MH with one multimodal source and another source that is only hemodynamically active, and EH where one source is electrically active and the other is hemodynamically active. The EH scenario is included for completeness and it should be noted that it fundamentally violates the assumption which motivates fusion of EEG and fMRI, that is, the assumption that a subset of the neuronal activity is detectable by either modality. An overview of the simulation scenarios is given in Table 2. For each scenario, two sources each with a spatial extent of either 8 or 16 vertices are placed at random, non-overlapping locations on the cortical surface. Note that we assume no knowledge about the parcellation used by our algorithm when placing the sources on the cortex. It is therefore possible that the sources overlap parcel boundaries or that multiple sources are within the same parcel.

Table 2.

Simulation scenarios used in the empirical evaluation. A multimodal source is denoted as “M” while sources which are only electrically or hemodynamically active are denoted as “E” and “H”, respectively. The numbers indicate the spatial extent in vertices of the source, e.g., M(16) denotes a multimodal source with a spatial extent of 16 vertices. The source waveforms of the various sources are depicted in Fig. 4.

Scenario	Source 1	Source 2	Source 3	Source 4
CPX	M(8)	M(8)	M(16)	M(16)
MM	M(8)	M(8)
ME	M(8)	E(8)
MH	M(8)	H(8)
EH	E(8)	H(8)

To simulate source waveforms, we use sinusoids with different starting points and frequencies as the current waveforms of electrically active sources and a shifted canonical HRF from SPM8 with a positive peak at 5 s and a smaller negative peak at 12 s for hemodynamically active sources. The source waveforms of the sources, as well as, an example of the source distribution on the cortex for the MM scenario are illustrated in Fig. 4. The rest of the simulation parameters are as follows. For EEG we use m = 64 sensors, t₁ = 75 (we assume a sampling rate of 1 kHz), and signal to noise ratios (SNRs) of 15 dB, 20 dB and 25 dB (refer to Appendix B for a definition of the SNR). For fMRI we use t₂ = 1000, k = 30 with 30 random occurrences of the event of interest, and an SNR of 5 dB. We use q = 32 anatomical parcels which are obtained using the procedure described in Appendix A. Note that we use the same parceling for the proposed method and for the BASTERF method. A summary of all parameters used for the simulations is shown in Table 3.

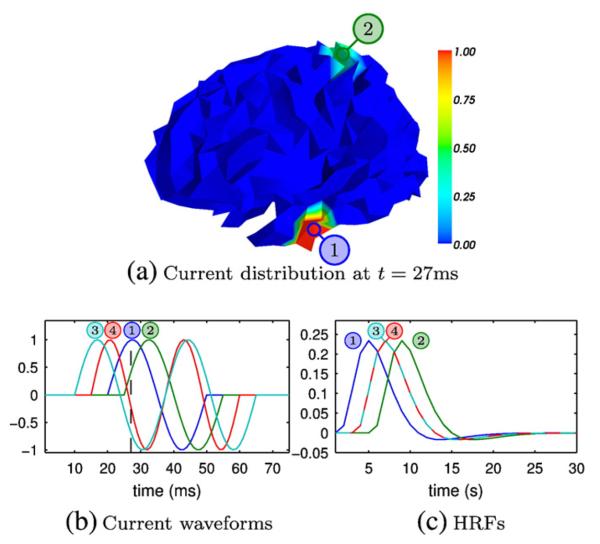
Fig. 4.

Source configurations used for simulations. The upper panel illustrates an example current distribution of a simulation with the MM scenario (two multimodal sources); the lower panels show the current waveforms and HRFs used for the simulations. The numbers refer to the source numbers in Table 2.

Table 3.

Summary of simulation parameters.

Common
Size cortical mesh			n = 1000
Number of parcels			q =32
EEG		fMRI
Number of sensors	m = 64	Length HRF	k =30
Time points	t1 = 75	Time points	t2 = 1000
Sampling rate	1 kHz	Sampling rate	1 Hz
SNR	15 dB, 20 dB, 25 dB	SNR	5 dB

We perform 25 simulations per scenario and SNR configuration for each algorithm. For all algorithms the same random source configurations and noise manifestations are used in order to provide a fair comparison.

Initialization

In order to start the iterative inference procedure we initialize the parameters of the proposed method as follows. For the EEG noise precision we assume that the noise only data window M⁰ is one third of the length of M, i.e., 25 columns, anduse $a_{{\alpha }_1}=a_{{\alpha }_1}^0=25m∕2$, $b_{{\alpha }_1}=b_{{\alpha }_1}^0=a_{{\alpha }_1}{\sigma }_{\mathrm{EEG}}^2$, where ${\sigma }_{\mathrm{EEG}}^2$ is the EEG noise variance. Similarly, we use for the fMRI noise precision hyperparameters $a_{{\alpha }_2}=a_{{\alpha }_2}^0=250n∕2$, $b_{{\alpha }_2}={b_{{\alpha }_2}}^0=a_{{\alpha }_2}{\sigma }_{\mathrm{fMRI}}^2$. The expectations of the remaining hyperparameters and the vector u are initialized with small values of 10⁻³. The variables 〈Z〉, 〈X〉, and 〈w〉 and their covariance matrices are initialized with all zero values, while minimum norm estimates are used for 〈S〉 and 〈H〉 together with all zero covariance matrices. After the initialization the algorithm is started and the variables are updated in the order given in the previous section. While we do not provide a detailed analysis of the convergence properties of the proposed method, we note here that we find that the method is insensitive to parameter initialization, which agrees with earlier work where the same inference scheme is used (Babacan et al., 2008). For example, the proposed method typically converges to the same solution when it is initialized using the method stated above as when it is initialized with the solution found by the BASTERF method.

Results

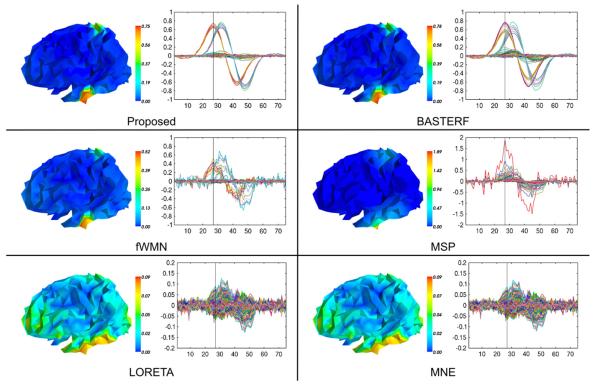
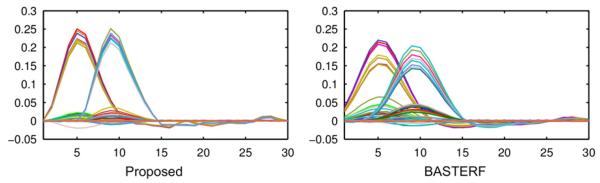
Estimated cortical current waveforms and their spatial distribution on the cortex in one simulation for scenario MM where both sources are electrically and hemodynamically active are shown in Fig. 5. The currents estimated by the proposed method are closer to the ground truth than those estimated by existing methods, i.e., the spatial distribution of the currents contains sharper transitions between active and inactive regions and the temporal waveforms have an appropriate degree of temporal smoothness. While currents estimated by the BASTERF method are both spatially and temporally smooth, the method fails to recover the sharp transitions at the boundaries of the sources and therefore provides a lower localization performance than the proposed method. This behavior can be explained by the fact that the BASTERF method uses LORETA-type spatial prior which is not spatially adaptive. Due to the lack of spatial smoothness priors the current distribution obtained by the fWMN method is more widespread than the distribution obtained by the proposed and the BASTERF methods. Considering the simplicity of the fWMN method, the results obtained by the fWMN method are surprisingly good. It should be noted however that in our evaluation the fWMN method has an unfair advantage over the symmetrical fusion methods (proposed and BASTERF) since the true locations of the hemodynamically active sources are used to obtain the weights for the fWMN method. Among the EEG-only methods, the MSP method clearly outperforms the other methods (LORETA and MNE) but due to the lack of fMRI information does not recover the spatio-temporal source distribution as well as the evaluated EEG/fMRI fusion methods. The advantage of spatially adaptive priors can also be seen when comparing the HRFs estimated by the proposed method and the BASTERF method, as shown in Fig. 6. As with the cortical currents, spatial adaptivity enables the proposed method to obtain estimates which are closer to the ground truth with sharper transitions between active and inactive regions and a more accurate degree of temporal smoothness.

Fig. 5.

Butterfly plots of the estimated currents (Ŝ) and their projection onto the cortical mesh at t=27 ms for one simulation of the scenario MM (SNR EEG=20 dB). The ground truth for this simulation is depicted in Fig. 4. Note that the color scales are adjusted for each method to show the full range of the source distribution and that the y-axis of the butterfly plots for the MSP, LORETA, and MNE methods has been adjusted to allow for a clear depiction of the estimated current waveforms.

Fig. 6.

Estimated HRFs (Ĥ) by the proposed method and the BASTERF method for one simulation of the scenario MM (SNR EEG=20 dB). The ground truth for this simulation is depicted in Fig. 4 (hemodynamic sources 1 and 2 are active).

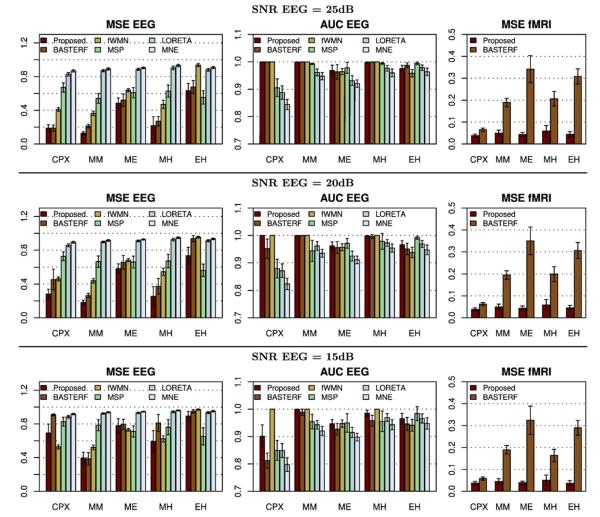
Objective quality metric scores from all simulations are shown in Fig. 7. To evaluate the reconstruction of the current distribution we use the mean squared error (MSE), denoted MSE EEG, as well as, the area under the ROC curve (AUC EEG). For fMRI we evaluate the reconstruction of the HRFs using the MSE, which we denote MSE fMRI. Refer to Appendix C for the definition of the quality metrics used.

Fig. 7.

Objective quality metric scores for different simulation scenarios. The mean squared error scores for the estimated currents and hemodynamic response functions are denoted as MSE EEG and MSE fMRI, respectively. The area under the ROC curve for EEG is denoted as AUC EEG. For mean squared error scores lower values are better while a value of 1.0 indicates the best performance in terms of AUC EEG. The error bars indicate the 95% confidence intervals.

We observe that the proposed method clearly outperforms the other evaluated methods for medium and high EEG SNRs (20 dB and 25 dB), except for the EH scenario where the MSP method performs better. Note, however, that such a result is not unexpected since the EH scenario, which uses one source that is only electrically active and another source that is only hemodynamically active, fundamentally violates the assumption which motivates EEG/fMRI fusion, i.e., that a subset of activity is detectable by both modalities. A method which does not use fMRI information has an advantage in this case since it does not have a bias towards fMRI active locations. From the results for scenario EH it can also be seen that the proposed method is more robust against disagreements between EEG and fMRI than the other EEG/fMRI fusion methods (BASTERF and fWMN). Also note that whenever there is a strong agreement between EEG and fMRI (scenarios CPX and MM), the fusion methods (proposed, BASTERF and fWMN) clearly outperform the EEG-only methods (MSP, LORETA and MNE). It is also interesting to note that the performance for all fusion algorithms is worse when there are current sources which are hemodynamically inactive (scenario ME) than when there are spurious hemodynamic sources (scenario MH), which is in agreement with previously reported results (Liu et al., 1998; Ahlfors and Simpson, 2004; Daunizeau et al., 2005; Daunizeau et al., 2007). As expected, the performance of all evaluated methods degrades when lowering the EEG SNR to 15 dB. It should be noted that the performance of some methods degrades more than that of others, e.g., the advantage of the proposed method over the BASTERF method typically becomes clearer when lowering SNR. A surprising result is that the fWMN method performs better than the other fusion methods for the CPX scenario at a low SNR. However, the same is not true for the other simulation scenarios. Potentially, this is again due to the fact that the fWMN has an unfair advantage over the other methods since the true source locations are used to obtain the weights used in the method. From Fig. 7 it can also be seen that the proposed method clearly outperforms the BASTERF method in terms of MSE of the hemodynamic response function, which can mainly be attributed to the use of spatially adaptive temporal smoothness priors in the proposed method. Another observation is that the reconstruction of the HRFs is largely unaffected by the EEG SNR and the agreement between EEG and fMRI and mainly depends on the number of hemodynamically active sources (CPX: 4 sources, MM,MH: 2 sources, ME,EH: 1 source). This result is not unexpected since unlike the estimation of S, the estimation of H does not amount to a localization problem, i.e., it is not possible to use a source configuration with different source locations and obtain the same observation (assuming no noise). Hence, it can be concluded that for realistic fMRI SNRs the estimation of theHRFsdoesnot benefit from the EEG information.

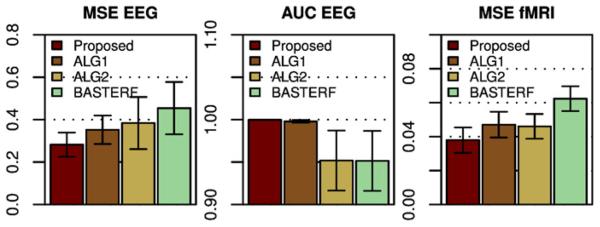
The advantage of the proposed method comes from the improved prior model, consisting of a spatially adaptive TV prior for the spatial profile and spatially adaptive temporal priors for the estimated currents and HRFs. An interesting question is how is the estimation performance affected by each prior? We try to answer this question by repeating the simulations of the CPX scenario with two modified versions of the proposed method, where one prior is replaced with the prior used in the BASTERF method. More specifically, the first method (denoted by ALG1) adopts the spatial Laplacian prior from BASTERF to model w and employs spatially adaptive temporal priors to model X and Z, while the second method (denoted by ALG2) uses a TV prior together with the temporal priors from BASTERF, which are not spatially adaptive. As can be seen from the results in Fig. 8, both additional priors contribute to the improved performance in terms of MSE EEG and MSE HRF. An interesting observation is that for the area under the ROC curve (AUC EEG), methods that use spatially adaptive temporal priors (proposed and ALG1) have higher scores than methods that use temporal priors without spatial adaptivity (ALG2 and BASTERF). While we only show results for the CPX scenario, these results are typical and correspond well with our observations that both parts (spatial and temporal) of the improved prior model contribute to the higher performance of the proposed method.

Fig. 8.

Results for the CPX scenario (SNR EEG=20 dB) for the proposed method, the BASTERF method, and intermediate methods, denoted by ALG1 and ALG2. The method ALG1 uses a Laplacian spatial prior (as in BASTERF) together with spatially adaptive temporal priors (as in the proposed method) and ALG2 uses a TV prior (as in the proposed method) together with temporal priors that are not spatially adaptive (as in BASTERF). It can be seen that the improved spatial prior as well as the improved temporal priors contribute to the higher performance of the proposed method. The error bars indicate the 95% confidence intervals.

To conclude this evaluation, we also mention run times and convergence properties of the evaluated algorithms. Naturally, while using a more complex symmetrical model, as with the proposed and the BASTERF methods, allows for higher performance, doing so comes at the cost of higher computational complexity. For the simulations used in this evaluation, all methods except the proposed method and the BASTERF method require less than 1 s to perform one simulation. The symmetrical fusion methods (proposed and BASTERF) are significantly more complex and both require about 10 s for one iteration (on a standard 2.6 GHz PC). Note that the time required for one iteration is about the same since the computationally most expensive operations are matrix inversions and both methods perform matrix inversions of the same order during each iteration, i.e., the proposed method and the BASTERF method have the same per-iteration time complexity. The time required for one simulation is in the order of 1 h, as both methods typically require several hundred iterations to reach convergence.

Application to real data

In this section, we demonstrate the performance of the proposed method in a real data set. The EEG and fMRI data was acquired for a multimodal study on face perception; details of the experimental paradigm can be found in Henson et al. (2003) and the data is available at http://www.fil.ion.ucl.ac.uk/spm/data/mmfaces/. The experiment involved the subjects making symmetry judgments for pictures of familiar faces, unfamiliar faces, and scrambled faces. In the following, familiar and unfamiliar faces are combined to create the face condition (F) whereas scrambled faces form the scrambled face condition (S). The data set available contains the data for one subject (male, 33 years old, neurologically healthy).

EEG data

The EEG data was collected using a 128-channel BioSemi ActiveTwo system with two additional electrodes, one on each earlobe, and a sampling rate of 2048 Hz. Faces and scrambled faces were presented in random order for 600 ms, every 3600 ms. Data was collected in two (identical) sessions; 86 faces and 86 scrambled faces were presented in each session. The EEG data was downsampled to 200 Hz, referenced to the average across all channels, and epoched from −100 ms to 600 ms. Trials for which the voltage exceeded 120 μV at any channel were rejected, leaving a total of 136 trials for faces and 134 trials for scrambled faces. The remaining trials were baseline corrected from −100 ms to 0 ms and averaged to create one ERP for the face condition and one ERP for the scrambled face condition.

EEG forward model

The EEG forward operator G was calculated using a BEM method implemented in FieldTrip (http://fieldtrip.fcdonders.nl). Subject specific meshes were used for the calculation; the cortex mesh was obtained from a high resolution T1-weighted structural MRI (1 mm³ resolution) of the subject using BrainVisa 3.2 (http://brainvisa.info). The high resolution cortex mesh obtained by BrainVisa was downsampled to 5998 vertices. The remaining meshes needed for the BEM calculation, namely the scalp, outer skull, and inner skull meshes, were obtained as follows. A nonlinear inverse normalization transform using the T1-weighted structural MRI of the subject was calculated using SPM8 (http://www.fil.ion.ucl.ac.uk/spm/). The transform was used to warp template scalp, outer skull, inner skull, and cortex meshes from a standard space into a subject specific space (the template meshes are included in SPM8). The meshes were then used together with electrode locations, which were obtained using a Polhemus Isotrak digitizer, as inputs to the BEM method.

fMRI data

The fMRI data was collected in 2 sessions; 64 faces and 86 scrambled faces were presented in each session. The experimental paradigm was slightly different from that used for EEG, i.e., the stimuli were presented for 600 ms but the time between trials was randomly distributed between 3 s and 18 s to allow for an estimation of the HRF. The data was acquired using a gradient-echo EPI sequence on a 3 T Siemens TIM Trio scanner with 32 slices, voxel size 3×3×3 mm (skip 0.75 mm), and a TR of 2 s. For each session 390 volumes were obtained. The fMRI data was preprocessed using SPM8, which involved the following steps: Slice timing correction to account for descending slice order, realignment for motion correction using 4-th degree b-spline interpolation, co-registration with the T1-weighted structural MRI of the subject, and spatial smoothing using a symmetric Gaussian kernel with a full width at half maximum (FWHM) of 8 mm. In order to be able to use fMRI data as input to the fusion algorithm, the volumetric data has to be interpolated onto the cortical surface, i.e., the cortical mesh of 5998 vertices which was also used for the EEG BEM model. We use the method proposed in Grova et al. (2006) to perform the interpolation. The method uses a binary gray matter mask to construct a 3D geodesic Voronoi diagram with one Voronoi cell for each vertex of the mesh. The interpolated value at a given vertex is then obtained by averaging the voxels belonging to the Voronoi cell which is associated with the vertex. Compared to simplistic interpolation methods, such as integrating over a sphere around each vertex, this interpolation method has the advantage that each gray matter voxel is associated with exactly one vertex. Therefore no signal mixing occurs between neighboring vertices and no signal is lost due to gray matter voxels being too far away from the closest vertex. Here, the gray matter mask was obtained from the T1-weighted structural MRI using BrainVisa 3.2. After interpolation of the fMRI data for each session onto the cortical mesh, low frequency drifts were removed by fitting and subtracting a third order polynomial to the fMRI waveform of each vertex. The interpolated data from the two sessions were then concatenated and upsampled by a factor of 2 to obtain a pseudo TR of 1 s resulting in an fMRI data matrix Y of size 1560×5998.

Noise estimates

The proposed method uses two noise-only data segments M⁰ and Y⁰, for EEG and fMRI, respectively, to obtain noise precision hyperparameters using Eqs. (27) and (29). The pre-stimulus time window from −100 ms to −5 ms was used to obtain an EEG noise matrix M⁰ of size 128×20. For fMRI, ideally the data segment Y⁰ is obtained from a sufficiently long time window during which no event onsets occurred, i.e., it can be assumed that the data segment only contains noise (consisting of measurement noise from the MRI scanner and noise from other sources such as spontaneous brain activity). Unfortunately, the fMRI data provided in the dataset does not contain data from a long period during which no event onsets occurred. In order to obtain an initial noise estimate, first note that the SNR for fMRI is very low and only a small number of brain regions exhibit significant task induced hemodynamic activity. Therefore, calculated across the whole brain and over a long time window, the power of the event related signal is negligible compared to the noise power. Hence, we simply used data from the first 30 s of the experiment, i.e., the first 30 rows in Y, as Y⁰. Due to the above arguments the noise parameter $b_{{\alpha }_2}^0$ is quite accurate but may be slightly larger than the “true” $b_{{\alpha }_2}^0$ due to event onsets during the first 30 s of the experiment. It can be expected that this inaccuracy does not affect the result since the noise precision is mostly estimated by the fusion algorithm itself.

Application of the fusion algorithm

The preprocessed EEG and fMRI data were used as inputs to the proposed EEG/fMRI fusion method, as well as, to the BASTERF method (Daunizeau et al., 2007), which was included for comparison purposes. The fusion methods were applied for each condition (face and scrambled face) separately. Prior to applying the algorithms, the cortical mesh was parcellated into 48 regions using the procedure described in Appendix A; the parcellation is illustrated in Fig. 9. The size EEG data matrix M was 128×61 corresponding to a time window from 0 ms to 300 ms after event onset. The length of the HRF for fMRI was chosen to 20 s, resulting in a design matrix B of size 1560×20. The design matrix was obtained using Eq. (4) with an experimental time course which was zero everywhere except at locations corresponding to the onset times of the condition of interest, where the value of the time course was set equal to 1.

Fig. 9.

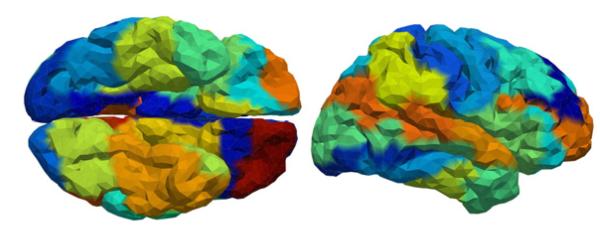
Ventral (left) and right lateral (right) views of the cortical mesh showing the parcellation of 5998 vertices into 48 regions.

Results

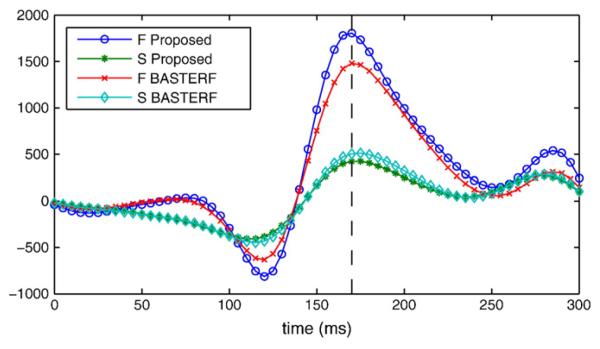
Previous EEG studies (Henson et al., 2003) have shown that the difference between the face (F) and scrambled face (S) conditions is apparent in the negative component of the right occipito-temporal channels at 170 ms after event onset, which is known as N170. This effect is clearly visible in the estimated current waveforms of the dipoles in the right fusiform region, as illustrated in Fig. 10. Notice that the difference between the F and the S condition is larger for the proposed method than for the BASTERF method. The difference between the methods can be attributed to the spatial adaptivity of the proposed method which allows for more focal sources with adaptive temporal smoothness.

Fig. 10.

Estimated current waveforms for a dipole in the right fusiform region. The dipole was selected as the dipole with the maximum current magnitude over all time instants for the face condition and the proposed method. The difference between the face (F) and the scrambled face (S) condition at t=170 ms is clearly visible. Note that the difference is larger for the proposed method than for the BASTERF method.

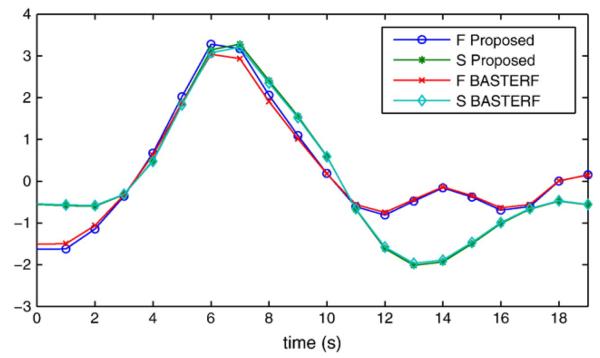
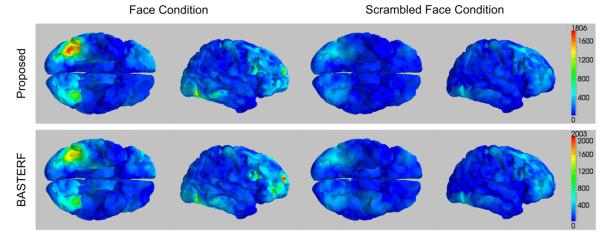
The hemodynamic response functions estimated by both methods look mostly similar as shown in Fig. 11. The similarity between the methods indicates that for this particular example the improved prior model has little influence on the estimates. An explanation for this is that there is a large amount of fMRI data available (86 event onsets for each condition) for the estimation of the HRFs. Hence, the Bayesian methods reduce the weight of the priors and the particular type of prior used has less influence on the estimate. The distributions of the current magnitudes for the F and S conditions at 170 ms are shown in Fig. 12. The results for both, the proposed and the BASTERF methods, are generally consistent with previously reported EEG source localization results for the same data (Trujillo-Barreto et al., 2008; Friston et al., 2008). There is bilateral activity in the fusiform region with emphasis on the right side, as well as, activity in the right superior temporal sulcus and the right middle frontal gyrus. Compared to previously reported results, the current sources, especially the ones in the bilateral fusiform regions, are more clearly separated from inactive regions. This is clear from the sharp boundaries between active and inactive regions shown in Fig. 12. This effect can be explained by the fact that the evaluated EEG/fMRI fusion methods use fMRI information, which allows for more accurate source localization and estimation of the spatial extent of the sources. While the current distributions estimated by the proposed method and the BASTERF method are quite similar, notice that the proposed method obtains sharper boundaries and therefore a better localization of the brain activity. Both methods also find some activity in the medial superior frontal region, which is inconsistent with previous EEG source localization results (Trujillo-Barreto et al., 2008; Friston et al., 2008). Notice that for the BASTERF method, the dipole with the largest magnitude at 170 ms is located in the medial superior frontal region and not in the right fusiform region. More recent MEG results (Henson et al., 2007) show some activity in the medial superior frontal region for some subjects, which suggests that it is possible that previous EEG source localization studies did not report this activity since the employed source localization methods simply failed to detect the activity in the medial superior frontal region. On the other hand, activity in the medial superior frontal region for fMRI and positivity in the frontocentral electrodes for EEG at 550 ms has been reported to be related to the familiarity of faces (Henson et al., 2003). While not shown here, both fusion methods find some hemodynamic medial superior frontal activity. This activity is much weaker than the activity in the fusiform region but may in fact be related to electrical activity that occurs at 550 ms, i.e., outside the EEG time window used in our analysis. The currents in the medial superior frontal regions found by the fusion algorithms may therefore be spurious estimates caused by hemodynamic activity which is related to electrical activity outside the time window of interest. This behavior illustrates a possible shortcoming of EEG/fMRI fusion methods: As the estimated hemodynamic response function is much longer than the EEG time window of interest, information about cortical activity occurring after 300 ms is included into the fusion process, which causes invalid fMRI location priors in the time invariant spatial profile w. While both the proposed method and the BASTERF method have some robustness against spurious hemodynamic sources, the current estimates are still biased towards regions with hemodynamic activity and the currents in the medial superior frontal region at 170 ms may in fact be spurious current estimates caused by invalid fMRI location priors.

Fig. 11.

Estimated hemodynamic response functions for a vertex in the right fusiform region corresponding to the location of the dipole used in Fig. 10.

Fig. 12.

Distributions of the current magnitudes at t=170 ms for the multimodal face data. Results obtained by the proposed method are shown in the top panel while the bottom panel shows the results obtained by the BASTERF method. The color maps are scaled to the range of the current magnitudes for the face condition for each algorithm.

Conclusions

In this paper we proposed a novel symmetrical EEG/fMRI fusion method. The method utilizes a hierarchical generative model with symmetrical structure which explains both EEG and fMRI observations. In contrast to previous symmetrical fusion methods, the proposed method uses spatially adaptive signal priors, leading to an improved performance. Specifically, the use of a total variation (TV) prior allows sharp boundaries between active and inactive brain regions. Unlike LORETA-type (Pascual-Marqui et al., 1994) spatial priors, the TV prior is spatially adaptive, such that it not only imposes spatial smoothness but also allows for abrupt changes in brain activity at the boundaries of active regions. We also assume that although each response is temporally smooth, the degree of smoothness varies from one spatial location to another, which is incorporated by utilizing a spatially adaptive temporal smoothness prior. We use a fully Bayesian formulation with a variational Bayesian inference method. The method utilizes a spatially adaptive bound to the TV prior which makes the calculation of the variational posterior distribution approximation possible.

We used simulations with synthetic EEG and fMRI data and objective quality metrics to evaluate the proposed method and to compare it to existing methods. In terms of estimation of the spatio-temporal cortical current distribution, our results show that the proposed method outperforms existing methods for simulation scenarios with high agreement between EEG and fMRI, i.e., scenarios where the sources of cortical activity are detectable by either modality. In situations where there is a strong disagreement between EEG and fMRI, the performance of the proposed method was slightly lower than that of the EEG-only MSP method but higher than the performance of other fusion methods, suggesting that the proposed method is more robust against disagreement between EEG and fMRI. In terms of estimation of the hemodynamic response function, the proposed method consistently outperformed the BASTERF method (Daunizeau et al., 2007), which can be attributed to the improved prior model.

We also demonstrated the performance of the proposed method using a multimodal EEG/fMRI dataset from an experiment with face evoked responses (Henson et al., 2003). For comparison purposes, we also applied the BASTERF method to the same data. The results of both methods generally agree with previously reported results for the same data (Trujillo-Barreto et al., 2008; Friston et al., 2008), i.e., 170 ms after event onset the cortical current distribution exhibits clusters of activity in the bilateral fusiform region, as well as, activity in the right superior temporal sulcus and in the right middle frontal gyrus. Compared to previously reported results and to the current distribution obtained by the BASTERF method, the proposed method delineates the clusters in the bilateral fusiform more clearly. The proposed method also obtains a larger difference in terms of current amplitudes between the conditions than the BASTERF method. This can be attributed to the use of the spatially adaptive prior model in the proposed method, which allows for sharp transitions in the cortical current density and for adaptation of the degree of temporal smoothness.

Appendix A. Anatomical parceling

In this work we assume a fixed cortical parceling, which is encoded by the matrix C. Since there has been no published method to obtain a functional parceling jointly based on EEG and fMRI data, we resort to parceling based on anatomical information. We empirically find that the proposed method, as well as the BASTERF method (Daunizeau et al., 2007), performs better when all parcels are approximately equal in size. Therefore, we use a simple parcellation procedure which tries to segment the cortical mesh in a number of compact parcels with equal size. The parcellation procedure is similar to that in Daunizeau et al. (2007), i.e., the cortical mesh is first down-sampled to obtain a number of seed vertices and then a region growing algorithm is used to obtain the final parcellation. More specifically, in order to obtain a parcellation with q parcels of a cortical mesh M=(V, E) with n vertices, we first down-sample the mesh of each hemisphere to a mesh with q/2 vertices using the Matlab function “reducepatch”. Note that we require that q is an even number. The down-sampled meshes are then combined to obtain a mesh M_D=(V_D, E_D) with a total of q vertices. The vertices in V_D are used as initial labels for the region growing algorithm. In order to start the algorithm we define a label assignment map L_init of length n as

$$L_{\mathrm{init}}\left(i\right)=\{\begin{array}{cc}j\hfill & \text{if}{v}_i=v_j\in V,v_j\in V_D,\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}$$ (A.1)

where v_i∈V and v_j∈V_D denote the i-th and j-th vertices of the meshes, M and M_D, respectively. The map L_init and the mesh M are then used as inputs to the region growing algorithm in Fig. A.13. The algorithm keeps a map F which indicates if a parcel cannot be grown any further. During each iteration, the algorithm first selects the smallest parcel which can still be grown. In a second step, the neighboring vertex with the largest number of edges connecting the vertex to the selected parcel is added to the parcel. Finally, the algorithm terminates when all vertices have been assigned to a parcel. The n×q parcellation matrix C used in the proposed method is then obtained from L as follows

$${\mathbf{C}}_{\mathit{ij}}=\{\begin{array}{cc}1\hfill & \text{if}L\left(i\right)=j,\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$ (A.2)

Appendix B. Definition of the SNR

Throughout this paper we use the following definition for the EEG signal to noise ratio

$${\mathrm{SNR}}_{\mathrm{EEG}}=10{\log }_{10}\frac{{\parallel \mathrm{vec}\left(\mathbf{LS}\right)\parallel }_{\mathrm{\infty }}^2}{{\mathrm{\sigma }}_1^2},$$ (B.1)

where ∥·∥_∞ denotes the infinity norm; i.e., the largest absolute value of the vector, and ${\sigma }_1^2$ is the noise variance. This definition corresponds to the peak signal to noise ratio and has the advantage that it is not affected by the length of silent periods before and after the evoked responses (a similar definition is used in Lapalme et al. (2006)). Similarly, we use the following definition for the fMRI signal to noise ratio

$${\mathrm{SNR}}_{\mathrm{fMRI}}=10{\log }_{10}\frac{{\parallel \mathrm{vec}\left(\mathbf{BH}\right)\parallel }_{\mathrm{\infty }}^2}{{\mathrm{\sigma }}_2^2},$$ (B.2)

where ${\sigma }_2^2$ denotes the noise variance. One advantage of this definition of the SNR is that the signal power, and thus the SNR, is not affected by the number of voxels for which we assume no hemodynamic response.

Fig. A.13.

Region growing algorithm used to obtain a parcellation of the cortical mesh.

Appendix C. Quality metrics

The following objective quality metrics are used in the evaluation. The mean squared error (MSE) score for EEG measures the deviation of the estimated currents Ŝ from the true currents S and is defined as

$$\mathrm{MSE}\mathrm{EEG}=\frac{{\parallel \widehat{\mathbf{S}}-\mathbf{S}\parallel }_F^2}{{\parallel \mathbf{S}\parallel }_F^2},$$ (C.1)

where ∥·∥_F denotes the Frobenius norm. In addition to the MSE, we use the area under the ROC curve, denoted as EEG AUC, to evaluate the EEG source localization performance. In order to calculate the AUC we calculate the power map P_S (Daunizeau et al., 2007) of size n×1 from the estimated currents Ŝ as follows

$${\left({\mathbf{P}}_S\right)}_i={\widehat{\mathbf{S}}}_{i\cdot }{\widehat{\mathbf{S}}}_{i\cdot }^T,$$ (C.2)

i.e., (P_S)_i contains the power of the estimated source waveform of the i-th dipole. The AUC is then calculated from (P_S)_i and a binary mask encoding the true locations of vertices belonging to electrically active sources. Unlike the MSE, the AUC does not measure the quality of the estimation based on the spatio-temporal shape of the estimated currents but measures the ability of a method to correctly classify dipoles as either active or inactive based on the energy of the estimated source waveforms. The AUC lies in the range [0, 1] where 1 corresponds to perfect classification performance. To evaluate the quality of the estimation of the HRFs we use the MSE, which is analogously defined to the EEG side, i.e.,

$$\mathrm{MSE}\mathrm{fMRI}=\frac{{\parallel \widehat{\mathbf{H}}-\mathbf{H}\parallel }_F^2}{{\parallel \mathbf{H}\parallel }_F^2},$$ (C.3)

with Ĥ and H being the estimated and the true HRFs, respectively.

Appendix D. Derivation of the approximate posterior distribution

In this appendix we show the derivations to obtain the approximate posterior distribution shown in Table 1.

To obtain q(S), we use Eq. (47) and write

$$\ln \mathrm{q}\left(\mathbf{S}\right)={𝔼}_{\mathrm{ϴ}\backslash \mathbf{S}}[\ln \mathrm{p}(\mathbf{M}\mid \mathbf{S},{\mathrm{\alpha }}_1)+\mathrm{lnp}(\mathbf{S}\mid \mathbf{X},\mathbf{w},{∊}_1)]+c,$$ (D.1)

where all terms that do not depend on S have been absorbed into the additive normalization constant c.¹ To perform the calculations it is more convenient to rewrite both p(M|S, α₁) and p(S|X, w, ε₁) in vector form. They are given by

$$\mathrm{vec}{\left(\mathbf{M}\right)}_{(m\cdot t_1)\times 1}=\left({\mathbf{I}}_{t_1}\otimes {\mathbf{L}}_{m\times n}\right)\mathrm{vec}{\left(\mathbf{S}\right)}_{(n\cdot t_1)\times 1}+\mathrm{vec}{\left({\mathrm{\eta }}_1\right)}_{(m\cdot t_1)\times 1},$$ (D.2)

$$\mathrm{vec}{\left({\mathrm{\eta }}_1\right)}_{(m\cdot t_1)\times 1}~𝒩\left(0,{\mathrm{\alpha }}_1^{-1}{\mathbf{I}}_{m\cdot t_1}\right),$$ (D.3)

and

$$\mathrm{vec}{\left(\mathbf{S}\right)}_{(n\cdot t_1)\times 1}=\left({\mathbf{I}}_{t_1}\otimes \mathrm{Diag}{\left(\mathbf{w}\right)}_{n\times n}{\mathbf{C}}_{n\times q}\right)\mathrm{vec}{\left(\mathbf{X}\right)}_{(q\cdot t_1)\times 1}+\mathrm{vec}{\left(\mathrm{\rho }\right)}_{(n\cdot t_1)\times 1},$$ (D.4)

$$\mathrm{vec}{\left({\mathrm{\rho }}_1\right)}_{(n\cdot t_1)\times 1}~𝒩\left(0,{∊}_1^{-1}{\mathbf{I}}_{n\cdot t_1}\right),$$ (D.5)

respectively. Note that we include the sizes of the matrices and vectors in the subscripts as a reference. Using these equations we can write Eq. (D.1) as

$$\ln \mathrm{q}\left(\mathbf{S}\right)={𝔼}_{\mathrm{ϴ}\backslash \mathbf{S}}\left[-\frac{{\mathrm{\alpha }}_1}{2}{\left(\mathrm{vec}\left(\mathbf{M}\right)-\left({\mathbf{I}}_{t_1}\otimes \mathbf{L}\right)\mathrm{vec}\left(\mathbf{S}\right)\right)}^T\times \left(\mathrm{vec}\left(\mathbf{M}\right)-\left({\mathbf{I}}_{t_1}\otimes \mathbf{L}\right)\mathrm{vec}\left(\mathbf{S}\right)\right)-\frac{{∊}_1}{2}{\left(\mathrm{vec}\left(\mathbf{S}\right)-\left({\mathbf{I}}_{t_1}\otimes \mathrm{Diag}\left(\mathbf{w}\right)\mathbf{C}\right)\mathrm{vec}\left(\mathbf{X}\right)\right)}^T\times \left(\mathrm{vec}\left(\mathbf{S}\right)-\left({\mathbf{I}}_{t_1}\otimes \mathrm{Diag}\left(\mathbf{w}\right)\mathbf{C}\right)\mathrm{vec}\left(\mathbf{X}\right)\right)\right]+c.$$ (D.6)

Due to the conjugacy of the priors (Gaussian for the mean and gamma for the precision) we know that q(S) will be Gaussian as well and we can find vec(〈S〉) by taking the derivative with respect to vec(S), equating to zero, and calculating the expectation; by doing so we obtain

$$\mathrm{vec}\left(\langle \mathbf{S}\rangle \right)={\left(\langle {\mathrm{\alpha }}_1\rangle \left({\mathbf{I}}_{t_1}\otimes {\mathbf{L}}^T\mathbf{L}\right)+\langle {∊}_1\rangle {\mathbf{I}}_{n\cdot t_1}\right)}^{-1}\times \left(\langle {\mathrm{\alpha }}_1\rangle \left({\mathbf{I}}_{t_1}\otimes {\mathbf{L}}^T\right)\mathrm{vec}\left(\mathbf{M}\right)+\langle {∊}_1\rangle \left({\mathbf{I}}_{t_1}\otimes \mathrm{Diag}\left(\langle \mathbf{w}\rangle \right)\mathbf{C}\right)\mathrm{vec}\left(\langle \mathbf{X}\rangle \right)\right),$$ (D.7)

where we can see by inspection that the first part corresponds to the covariance matrix. The covariance matrix can also be obtained by calculating the second derivative of Eq. (D.6) with respect to vec(S), equating to zero, and calculating the expectation. Using the properties of the Kronecker product and vec(·) operators, Eq. (D.7) can also be written as

$$\begin{array}{cc}\hfill \langle \mathbf{S}\rangle =& \underset{={\Sigma }_{\mathbf{S}}}{\underbrace{{\left(\langle {\mathrm{\alpha }}_1\rangle {\mathbf{L}}^T\mathbf{L}+\langle {∊}_1\rangle {\mathbf{I}}_n\right)}^{-1}}}\hfill \\ \hfill & \times \left(\langle {\mathrm{\alpha }}_1\rangle {\mathbf{L}}^T\mathbf{M}+\langle {∊}_1\rangle \mathrm{Diag}\left(\langle \mathbf{w}\rangle \right)\mathbf{C}\langle \mathbf{X}\rangle \right),\hfill \end{array}$$ (D.8)

which is the form given in Table 1.

To obtain the distribution q(H) we use the same procedure, i.e., we first write

$$\ln \mathrm{q}\left(\mathbf{H}\right)={𝔼}_{\mathrm{ϴ}\backslash \mathbf{H}}[\ln \mathrm{p}(\mathbf{Y}\mid \mathbf{H},{\mathrm{\alpha }}_2)+\ln \mathrm{p}(\mathbf{H}\mid \mathbf{Z},\mathbf{w},{∊}_2)]+c$$ (D.9)

and use vector notation to obtain

$$\ln \mathrm{q}\left(\mathbf{H}\right)={𝔼}_{\mathrm{ϴ}\backslash \mathbf{H}}\left[-\frac{{\mathrm{\alpha }}_2}{2}{(\mathrm{vec}\left(\mathbf{Y}\right)-({\mathbf{I}}_n\otimes \mathbf{B})\mathrm{vec}\left(\mathbf{H}\right))}^T\times (\mathrm{vec}\left(\mathbf{Y}\right)-({\mathbf{I}}_n\otimes \mathbf{B})\mathrm{vec}\left(\mathbf{H}\right))-\frac{{∊}_2}{2}{\left(\mathrm{vec}\left(\mathbf{H}\right)-\left({\mathbf{C}}^T\mathrm{Diag}\left(\mathbf{w}\right)\otimes {\mathbf{I}}_k\right)\mathrm{vec}\left({\mathbf{Z}}^T\right)\right)}^T\times \left(\mathrm{vec}\left(\mathbf{H}\right)-\left({\mathbf{C}}^T\mathrm{Diag}\left(\mathbf{w}\right)\otimes {\mathbf{I}}_k\right)\mathrm{vec}\left({\mathbf{Z}}^T\right)\right)\right]+c.$$ (D.10)

Since q(H) is Gaussian, we can obtain the mean by calculating the derivative with respect to vec(H) and equating to zero. By doing so and by using the properties of the Kronecker product and vec(·) operators we get

$$\begin{array}{cc}\hfill \langle \mathbf{H}\rangle =& \underset{={\Sigma }_{\mathbf{H}}}{\underbrace{{\left(\langle {\mathrm{\alpha }}_2\rangle {\mathbf{B}}^T\mathbf{B}+\langle {∊}_2\rangle {\mathbf{I}}_k\right)}^{-1}}}\hfill \\ \hfill & \times \left(\langle {\mathrm{\alpha }}_2\rangle {\mathbf{B}}^T\langle \mathbf{Y}\rangle +\langle {∊}_2\rangle {\langle \mathbf{Z}\rangle }^T{\mathbf{C}}^T\mathrm{Diag}\left(\langle \mathbf{w}\rangle \right)\right).\hfill \end{array}$$ (D.11)

The distribution q(X) is obtained similarly, i.e., we collect all terms that depend on X and write

$$\ln \mathrm{q}\left(\mathbf{X}\right)={𝔼}_{\mathrm{ϴ}\backslash \mathbf{X}}[\ln \mathrm{p}(\mathbf{S}\mid \mathbf{X},\mathbf{w},{∊}_1)+\ln \mathrm{p}(\mathbf{X}\mid {\mathrm{\beta }}_1)]+c.$$ (D.12)

Next we rewrite p(X|β₁) in vector form as

$$\mathrm{vec}{\left({\mathbf{X}}^T\right)}_{(t_1\cdot q)\times 1}=0+\mathrm{vec}{\left({\nu }_1\right)}_{(t_1\cdot q)\times 1},$$ (D.13)

$$\mathrm{vec}{\left({\nu }_1\right)}_{(t_1\cdot q)\tilde{n}1}~𝒩\left(0,{\left(\mathrm{Diag}{\left({\mathrm{\beta }}_1\right)}_{q\times q}\otimes {\left({\mathbf{T}}_1^T{\mathbf{T}}_1\right)}_{t_1\times t_1}\right)}^{-1}\right).$$ (D.14)

Using this we can write Eq. (D.12) as

$$\ln \mathrm{q}\left(\mathbf{X}\right)={𝔼}_{\mathrm{ϴ}\backslash \mathbf{X}}\left[-\frac{{∊}_1}{2}{\left(\mathrm{vec}\left(\mathbf{S}\right)-\left({\mathbf{I}}_{t_1}\otimes \mathrm{Diag}\left(\mathbf{w}\right)\mathbf{C}\right)\mathrm{vec}(\mathbf{X})\right)}^T\times \left(\mathrm{vec}\left(\mathbf{S}\right)-\left({\mathbf{I}}_{t_1}\otimes \mathrm{Diag}\left(\mathbf{w}\right)\mathbf{C}\right)\mathrm{vec}\left(\mathbf{X}\right)\right)-\frac{1}{2}\mathrm{vec}{\left({\mathbf{X}}^T\right)}^T\left(\mathrm{Diag}\left({\mathrm{\beta }}_1\right)\otimes {\mathbf{T}}_1^T{\mathbf{T}}_1\right)\mathrm{vec}\left({\mathbf{X}}^T\right)\right]+c.$$ (D.15)

Since the prior used for X is conjugate, we know that q(X) is Gaussian. In order to be able to calculate the derivative with respect to vec(X), we define the t₁·q×t₁·q permutation matrix R_(t1,q) with the property

$${\mathbf{R}}_{(t_1,q)}\mathrm{vec}\left({\mathbf{X}}^T\right)=\mathrm{vec}\left(\mathbf{X}\right),$$ (D.16)

which allows us to rewrite Eq. (D.15) as

$$\ln \mathrm{q}\left(\mathbf{X}\right)={𝔼}_{\mathrm{ϴ}\backslash \mathbf{X}}\left[-\frac{{∊}_1}{2}{\left(\mathrm{vec}\left(\mathbf{S}\right)-\left({\mathbf{I}}_{t_1}\otimes \mathrm{Diag}\left(\mathbf{w}\right)\mathbf{C}\right)\mathrm{vec}(\mathbf{X})\right)}^T\times \left(\mathrm{vec}\left(\mathbf{S}\right)-\left({\mathbf{I}}_{t_1}\otimes \mathrm{Diag}\left(\mathbf{w}\right)\mathbf{C}\right)\mathrm{vec}\left(\mathbf{X}\right)\right)-\frac{1}{2}\mathrm{vec}{\left(\mathbf{X}\right)}^T{\mathbf{R}}_{(t_1,q)}^T\left(\mathrm{Diag}\left({\mathrm{\beta }}_1\right)\otimes {\mathbf{T}}_1^T{\mathbf{T}}_1\right){\mathbf{R}}_{(t_1,q)}\mathrm{vec}\left(\mathbf{X}\right)\right]+c.$$ (D.17)

By taking the derivative with respect to vec(X), equating to zero, and calculating the expectation we obtain

$$\begin{array}{cc}\hfill \mathrm{vec}\left(\langle \mathbf{X}\rangle \right)=& \underset{={\Sigma }_{\mathbf{X}}}{\underbrace{{\left(\langle {∊}_1\rangle \left({\mathbf{I}}_{t_1}\otimes \mathbf{Q}\right)+{\mathbf{R}}_{(t_1,q)}^T\left(\mathrm{Diag}\left(\langle {\mathrm{\beta }}_1\rangle \right)\otimes {\mathbf{T}}_1^T{\mathbf{T}}_1\right)R_{(t_1,q)}\right)}^{-1}}}\hfill \\ \hfill & \times \langle {∊}_1\rangle \left({\mathbf{I}}_{t_1}\otimes {\mathbf{C}}^T\mathrm{Diag}\left(\langle \mathbf{w}\rangle \right)\right)\mathrm{vec}\left(\langle \mathbf{S}\rangle \right),\hfill \end{array}$$ (D.18)

where

$$\begin{array}{cc}\hfill \mathbf{Q}& =𝔼\left[{\mathbf{C}}^T\mathrm{Diag}{\left(\mathbf{w}\right)}^T\mathrm{Diag}\left(\mathbf{w}\right)\mathbf{C}\right],\hfill \\ \hfill & ={\mathbf{C}}^T\left(\mathrm{Diag}{\left(\langle \mathbf{w}\rangle \right)}^T\mathrm{Diag}\left(\langle \mathbf{w}\rangle \right)+\mathrm{Diag}\left(\mathrm{diag}\left({\Sigma }_{\mathbf{w}}\right)\right)\right)\mathbf{C}.\hfill \end{array}$$ (D.19)

To derive q(Z) we write

$$\ln \mathrm{q}\left(\mathbf{Z}\right)={𝔼}_{\mathrm{ϴ}\backslash \mathbf{Z}}[\ln \mathrm{p}({\mathbf{H}}^T\mid \mathbf{Z},\mathbf{w},{∊}_2)+\ln \mathrm{p}(\mathbf{Z}\mid {\mathrm{\beta }}_2)]+c.$$ (D.20)

By comparing the distributions in Eq. (D.20) with those in Eq. (D.12) we see that the distributions have the same form and consequently q(Z) has the same form as qX. Therefore, by applying the same steps that we used for the EEG side we obtain

$$\begin{array}{cc}\hfill \mathrm{vec}\left(\langle \mathbf{Z}\rangle \right)=& \underset{={\Sigma }_{\mathbf{Z}}}{\underbrace{{\left(\langle {∊}_2\rangle \left({\mathbf{I}}_k\otimes \mathbf{Q}\right)+{\mathbf{R}}_{(k,q)}^T\left(\mathrm{Diag}\left(\langle {\mathrm{\beta }}_2\rangle \right)\otimes {\mathbf{T}}_2^T{\mathbf{T}}_2\right)R_{(k,q)}\right)}^{-1}}}\hfill \\ \hfill & \times \langle {∊}_2\rangle \left({\mathbf{I}}_k\otimes {\mathbf{C}}^T\mathrm{Diag}\left(\langle \mathbf{w}\rangle \right)\right)\mathrm{vec}\left({\langle \mathbf{H}\rangle }^T\right),\hfill \end{array}$$ (D.21)

To obtain the distribution q(w) for the spatial profile, we collect all the terms depending on w, which results in

$$\ln \mathrm{q}\left(\mathbf{w}\right)={𝔼}_{\mathrm{ϴ}\backslash \mathbf{w}}\left[\ln \mathrm{p}(\mathbf{S}\mid \mathbf{X},\mathbf{w},{∊}_1)+\ln \mathrm{p}\left({\mathbf{H}}^T\mid \mathbf{Z},\mathbf{w},{∊}_2\right)+\mathrm{lnm}(\mathbf{w},\mathbf{u},\mathbf{\gamma })\right]+c.$$ (D.22)

This can be rewritten as

$$\ln \mathrm{q}\left(\mathbf{w}\right)={𝔼}_{\mathrm{ϴ}\backslash \mathbf{w}}\left[-\frac{{∊}_1}{2}\mathrm{tr}\left({(\mathbf{S}-\mathrm{Diag}\left(\mathbf{w}\right)\mathbf{CX})}^T(\mathbf{S}-\mathrm{Diag}\left(\mathbf{w}\right)\mathbf{CX})\right)-\frac{{∊}_2}{2}\mathrm{tr}\left({\left({\mathbf{H}}^T-\mathrm{Diag}\left(\mathbf{w}\right)\mathbf{CZ}\right)}^T\left({\mathbf{H}}^T-\mathrm{Diag}\left(\mathbf{w}\right)\mathbf{CZ}\right)\right)-\frac{\mathbf{\gamma }}{2}\underset{i=1}{\overset{n}{\Sigma }}\frac{{\mathbf{w}}^T{\mathrm{\Delta }}_i^T{\mathbf{G}}_i^T{\mathbf{G}}_i{\mathrm{\Delta }}_i\mathbf{w}+u_i}{\sqrt{u_i}}\right]+c.$$ (D.23)

Note that there are several terms which do not depend on w. By absorbing all of them into the additive normalization constant and rewriting the remaining terms using w instead of Diag(w) we obtain

$$\ln \mathrm{q}={𝔼}_{\mathrm{ϴ}\backslash \mathbf{w}}\left[{∊}_1{\mathbf{w}}^T\mathrm{diag}\left({\mathbf{SX}}^T{\mathbf{C}}^T\right)-\frac{{∊}_1}{2}{\mathbf{w}}^T\mathrm{Diag}\left(\mathrm{diag}\left({\mathbf{CXX}}^T{\mathbf{C}}^T\right)\right)\mathbf{w}+{∊}_2{\mathbf{w}}^T\mathrm{diag}\left({\mathbf{H}}^T{\mathbf{Z}}^T{\mathbf{C}}^T\right)-\frac{{∊}_2}{2}{\mathbf{w}}^T\mathrm{Diag}\left(\mathrm{diag}\left({\mathbf{CZZ}}^T{\mathbf{C}}^T\right)\right)\mathbf{w}-\frac{\mathbf{\gamma }}{2}{\mathbf{w}}^T\left(\underset{i=1}{\overset{n}{\Sigma }}\frac{{\mathrm{\Delta }}_i^T{\mathbf{G}}_i^T{\mathbf{G}}_i{\mathrm{\Delta }}_i}{\sqrt{u_i}}\right)\mathbf{w}\right]+c,$$ (D.24)

which has the form of a multivariate Gaussian distribution. We find the mean of the distribution by setting the derivative with respect to w to zero, resulting in

$$\begin{array}{cc}\hfill \langle \mathbf{w}\rangle =& \underset{{\Sigma }_{\mathbf{w}}}{\underbrace{{(\langle {∊}_1\rangle {\mathbf{P}}_1+\langle {∊}_2\rangle {\mathbf{P}}_2+\langle \mathbf{\gamma }\rangle W\left(\mathbf{u}\right))}^{-1}}}\hfill \\ \hfill & \times \mathrm{diag}\left(\langle {∊}_1\rangle \langle \mathbf{S}\rangle {\langle \mathbf{X}\rangle }^T{\mathbf{C}}^T+\langle {∊}_2\rangle {\langle \mathbf{H}\rangle }^T{\langle \mathbf{Z}\rangle }^T{\mathbf{C}}^T\right),\hfill \end{array}$$ (D.25)

where P₁ and P₂ are given by

$${\mathbf{P}}_1=𝔼\left[\mathrm{Diag}\left(\mathrm{diag}\left({\mathbf{CXX}}^T{\mathbf{C}}^T\right)\right)\right]=\mathrm{Diag}\left(\mathrm{diag}\left(\mathbf{C}\left[\langle \mathbf{X}\rangle {\langle \mathbf{X}\rangle }^T+\underset{i=1}{\overset{t_1}{\Sigma }}{\Sigma }_{\mathbf{X}}^{\left[i\right]}\right]{\mathbf{C}}^T\right)\right),$$ (D.26)

$${\mathbf{P}}_2=𝔼\left[\mathrm{Diag}\left(\mathrm{diag}\left({\mathbf{CZZ}}^T{\mathbf{C}}^T\right)\right)\right]=\mathrm{Diag}\left(\mathrm{diag}\left(\mathbf{C}\left[\langle \mathbf{Z}\rangle {\langle \mathbf{Z}\rangle }^T+\underset{i=1}{\overset{k}{\Sigma }}{\Sigma }_{\mathbf{Z}}^{\left[i\right]}\right]{\mathbf{C}}^T\right)\right),$$ (D.27)

where ${\Sigma }_{\mathbf{X}}^{\left[i\right]}$ and ${\Sigma }_{\mathbf{Z}}^{\left[i\right]}$ denote the i-th block of size q×q on the main diagonal of the corresponding covariance matrix. The n×n matrix W(u) is defined as

$$W\left(\mathbf{u}\right)=\underset{i=1}{\overset{n}{\Sigma }}\frac{{\mathrm{\Delta }}_i^T{\mathbf{G}}_i^T{\mathbf{G}}_i{\mathrm{\Delta }}_i}{\sqrt{u_i}}.$$ (D.28)

Distributions for hyperparameters

Next, we show the derivations of the approximate posterior distributions for the hyperparameters. To obtain the distribution for the EEG noise precision we write

$$\ln \mathrm{q}\left({\mathrm{\alpha }}_1\right)={𝔼}_{\mathrm{ϴ}\backslash {\mathrm{\alpha }}_1}\left[\ln \mathrm{p}(\mathbf{M}\mid \mathbf{S},{\mathrm{\alpha }}_1)+\ln \mathrm{p}\left({\mathrm{\alpha }}_1\mid a_{{\mathrm{\alpha }}_1}^0,b_{{\mathrm{\alpha }}_1}^0\right)\right]+c.$$ (D.29)

By using vector notation, calculating the logarithms, absorbing constant parts into the constant c, and rearranging, we obtain

$$\ln \mathrm{q}\left({\mathrm{\alpha }}_1\right)={𝔼}_{\mathrm{ϴ}\backslash {\mathrm{\alpha }}_1}\left[\left(\frac{{\mathit{mt}}_1}{2}+a_{{\mathrm{\alpha }}_1}^0-1\right)\ln \left({\mathrm{\alpha }}_1\right)-\frac{{\mathrm{\alpha }}_1}{2}{\left(\mathrm{vec}\left(\mathbf{M}\right)-\left({\mathbf{I}}_{t_1}\otimes \mathbf{L}\right)\mathrm{vec}\left(\mathbf{S}\right)\right)}^T\times \left(\mathrm{vec}\left(\mathbf{M}\right)-\left({\mathbf{I}}_{t_1}\otimes \mathbf{L}\right)\mathrm{vec}\left(\mathbf{S}\right)\right)-b_{{\mathrm{\alpha }}_1}^0{\mathrm{\alpha }}_1\right]+c.$$ (D.30)

By comparing this with the functional form of a gamma distribution, i.e.,

$$\mathrm{p}(x\mid a,b)=\frac{b^a}{\mathrm{\Gamma }\left(a\right)}{x}^{a-1}{\mathrm{e}}^{-\mathit{bx}},$$ (D.31)

where Γ(·) denotes the gamma function, we see that q(α₁) is gamma distributed with parameters

$$a_{{\mathrm{\alpha }}_1}=\frac{{\mathit{mt}}_1}{2}+a_{{\mathrm{\alpha }}_1}^0,$$ (D.32)

$$b_{{\mathrm{\alpha }}_1}=\frac{1}{2}\mathrm{tr}\left({(\mathbf{M}-\mathbf{L}\langle \mathbf{S}\rangle )}^T(\mathbf{M}-\mathbf{L}\langle \mathbf{S}\rangle )\right)+\frac{t_1}{2}\mathrm{tr}\left({\Sigma }_{\mathbf{S}}{\mathbf{L}}^T\mathbf{L}\right)+b_{{\mathrm{\alpha }}_1}^0,$$ (D.33)

where we have used the properties of the vec(·) and Kronecker product operators to write b_α1 in a compact form using the trace operator. The term t₁tr(Σ_SL^TL) comes from the term that is quadratic with respect to S in Eq.(D.30), i.e.,

$$\begin{array}{cc}\hfill 𝔼& \left[\mathrm{vec}{\left(\mathbf{S}\right)}^T\left({\mathbf{I}}_{t_1}\otimes {\mathbf{L}}^T\mathbf{L}\right)\mathrm{vec}\left(\mathbf{S}\right)\right]=\mathrm{vec}{\left(\langle \mathbf{S}\rangle \right)}^T\left({\mathbf{I}}_{t_1}\otimes {\mathbf{L}}^T\mathbf{L}\right)\mathrm{vec}\left(\langle \mathbf{S}\rangle \right)\hfill \\ \hfill & +\mathrm{tr}\left(\left({\mathbf{I}}_{t_1}\otimes {\Sigma }_{\mathbf{S}}\right)\left({\mathbf{I}}_{t_1}\otimes {\mathbf{L}}^T\mathbf{L}\right)\right)=\mathrm{tr}\left({\langle \mathbf{S}\rangle }^T{\mathbf{L}}^T\mathbf{L}\langle \mathbf{S}\rangle \right)+t_1\mathrm{tr}\left({\Sigma }_{\mathbf{S}}{\mathbf{L}}^T\mathbf{L}\right).\hfill \end{array}$$ (D.34)

To obtain the distribution for the noise precision of the fMRI side we collect all the terms depending on α₂ and obtain

$$\ln \mathrm{q}\left({\mathrm{\alpha }}_2\right)={𝔼}_{\mathrm{ϴ}\backslash {\mathrm{\alpha }}_2}\left[\ln \mathrm{p}(\mathbf{Y}\mid \mathbf{H},{\mathrm{\alpha }}_2)+\ln \mathrm{p}\left({\mathrm{\alpha }}_2\mid a_{{\mathrm{\alpha }}_2}^0,b_{{\mathrm{\alpha }}_2}^0\right)\right]+c.$$ (D.35)

Clearly, since the distributions in Eq. (D.29) have exactly the same form as the distributions in Eq. (D.35), q(α₂) is gamma distributed with parameters that have the same form as the parameters of q(α₁); they are given by

$$a_{{\mathrm{\alpha }}_2}=\frac{{\mathit{nt}}_2}{2}+a_{{\mathrm{\alpha }}_2}^0,$$ (D.36)

$$b_{{\mathrm{\alpha }}_2}=\frac{1}{2}\mathrm{tr}\left({(\mathbf{Y}-\mathbf{B}\langle \mathbf{H}\rangle )}^T(\mathbf{Y}-\mathbf{B}\langle \mathbf{H}\rangle )\right)+\frac{n}{2}\mathrm{tr}\left({\Sigma }_{\mathbf{H}}{\mathbf{B}}^T\mathbf{B}\right)+b_{{\mathrm{\alpha }}_2}^0.$$ (D.37)

The distribution of the hyperparameter ε₁, which controls the strength of the hierarchical prior obtained from the spatio-temporal decomposition model on the EEG side, is obtained by

$$\ln \mathrm{q}\left({∊}_1\right)={𝔼}_{\mathrm{ϴ}\backslash {∊}_1}[\ln \mathrm{p}(\mathbf{S}\mid \mathbf{X},\mathbf{w},{∊}_1)+\mathrm{p}\left({∊}_1\right)]+c,$$ (D.38)

which we can write as

$$\ln \mathrm{q}\left({∊}_1\right)={𝔼}_{\mathrm{ϴ}\backslash {∊}_1}\left[\left(\frac{t_{1}n}{2}-1\right)\ln \left({∊}_1\right)-\frac{{∊}_1}{2}{\left(\mathrm{vec}\left(\mathbf{S}\right)-\left({\mathbf{I}}_{t_1}\otimes \mathrm{Diag}\left(\mathbf{w}\right)\mathbf{C}\right)\mathrm{vec}\left(\mathbf{X}\right)\right)}^T\times \left(\mathrm{vec}\left(\mathbf{S}\right)-\left({\mathbf{I}}_{t_1}\otimes \mathrm{Diag}\left(\mathbf{w}\right)\mathbf{C}\right)\mathrm{vec}\left(\mathbf{X}\right)\right)\right]+c.$$ (D.39)

Like for the previous hyperparameter distributions, we can see by inspection that q(ε₁) is gamma distributed with a shape parameter a_ε1=t₁n/2. In order to obtain the parameter b_ε1 we have to calculate the expectation of the second term in Eq. (D.39). We break the calculation of the expectation into several parts. The calculation of 𝔼[vec(S)^Tvec(S)] is similar to Eq. (D.34), i.e.,

$$\begin{array}{cc}\hfill 𝔼& \left[\mathrm{vec}{\left(\mathbf{S}\right)}^T\mathrm{vec}\left(\mathbf{S}\right)\right]=\mathrm{vec}{\left(\langle \mathbf{S}\rangle \right)}^T\mathrm{vec}\left(\langle \mathbf{S}\rangle \right)+\mathrm{tr}\left(\left({\mathbf{I}}_{t_1}\otimes {\Sigma }_{\mathbf{S}}\right)\right)\hfill \\ \hfill & =\mathrm{tr}\left({\langle \mathbf{S}\rangle }^T\langle \mathbf{S}\rangle \right)+t_1\mathrm{tr}\left({\Sigma }_{\mathbf{S}}\right).\hfill \end{array}$$ (D.40)

The expectation of the second quadratic term is calculated as follows

$$\begin{array}{cc}\hfill 𝔼& \left[\mathrm{vec}{\left(\mathbf{X}\right)}^T\left({\mathbf{I}}_{t_1}\otimes {\mathbf{C}}^T\mathrm{Diag}{\left(\mathbf{w}\right)}^T\mathrm{Diag}\left(\mathbf{w}\right)\mathbf{C}\right)\mathrm{vec}\left(\mathbf{X}\right)\right]=𝔼\left[\mathrm{vec}{\left(\mathbf{X}\right)}^T\left({\mathbf{I}}_{t_1}\otimes \mathbf{Q}\right)\mathrm{vec}\left(\mathbf{X}\right)\right]\hfill \\ \hfill & =\mathrm{tr}\left({\langle \mathbf{X}\rangle }^T\mathbf{Q}\langle \mathbf{X}\rangle \right)+\mathrm{tr}\left({\Sigma }_{\mathbf{X}}\left({\mathbf{I}}_{t_1}\otimes \mathbf{Q}\right)\right).\hfill \end{array}$$ (D.41)

By combining Eqs. (D.40) and (D.41) and by also including 𝔼[vec(S)^T(I_t1⊗Diag(w)C)vec(X)] we obtain

$$b_{{∊}_1}=\frac{1}{2}\left[\mathrm{tr}\left({\langle \mathbf{S}\rangle }^T\langle \mathbf{S}\rangle -2{\langle \mathbf{S}\rangle }^T\mathrm{Diag}\left(\langle \mathbf{w}\rangle \right)\mathbf{C}\langle \mathbf{X}\rangle +{\langle \mathbf{X}\rangle }^T\mathbf{Q}\langle \mathbf{X}\rangle \right)+t_1\mathrm{tr}\left({\Sigma }_{\mathbf{S}}\right)+\mathrm{tr}\left({\Sigma }_{\mathbf{X}}\left({\mathbf{I}}_{t_1}\otimes \mathbf{Q}\right)\right)\right].$$ (D.42)

To obtain the distribution q(ε₂) we again make use of the symmetry of the model by realizing that the distributions in

$$\ln \mathrm{q}\left({∊}_2\right)={𝔼}_{\mathrm{ϴ}\backslash {∊}_2}\left[\ln \mathrm{p}\left({\mathbf{H}}^T\mid \mathbf{Z},\mathbf{w},{∊}_2\right)+\mathrm{p}\left({∊}_2\right)\right]+c$$ (D.43)

have the same form as the distributions in Eq. (D.38). Therefore, q(ε₂) is gamma distributed with parameters

$$a_{{∊}_2}=\frac{\mathit{kn}}{2}$$ (D.44)

$$b_{{∊}_2}=\frac{1}{2}\left[\mathrm{tr}\left(\langle \mathbf{H}\rangle {\langle \mathbf{H}\rangle }^T-2\langle \mathbf{H}\rangle \mathrm{Diag}\left(\langle \mathbf{w}\rangle \right)\mathbf{C}\langle \mathbf{Z}\rangle +{\langle \mathbf{Z}\rangle }^T\mathbf{Q}\langle \mathbf{Z}\rangle \right)+n\mathrm{tr}\left({\Sigma }_{\mathbf{H}}\right)+\mathrm{tr}\left({\Sigma }_{\mathbf{Z}}\left({\mathbf{I}}_k\otimes \mathbf{Q}\right)\right)\right].$$ (D.45)

Next, we show the derivation of q((β₁)_i), i.e., the distribution of the hyperparameter (β₁)_i which controls the degree of temporal smoothness and scale of the current waveforms in the i-th parcel. As before, we only need to keep distributions depending on (β₁)_i when applying Eq. (47), resulting in

$$\ln \mathrm{q}\left({\left({\mathrm{\beta }}_1\right)}_i\right)={𝔼}_{\mathrm{ϴ}\backslash {\left({\mathrm{\beta }}_1\right)}_i}[\ln \mathrm{p}(\mathbf{X}\mid {\mathrm{\beta }}_1)+\ln \mathrm{p}({\mathrm{\beta }}_1\mid {\mathrm{\delta }}_1)]+c.$$ (D.46)

Note that we can assign all parts of p(X|β₁) and p(β₁|δ₁) which are independent of (β₁)_i to the additive normalization constant, which allows us to write

$$\ln \mathrm{q}\left({\left({\mathrm{\beta }}_1\right)}_i\right)={𝔼}_{\mathrm{ϴ}\backslash {\left({\mathrm{\beta }}_1\right)}_i}\left[\ln \mathit{det}{\left(2\mathrm{\pi }\left({\left({\mathrm{\beta }}_1\right)}_i{\mathbf{T}}_1^T{\mathbf{T}}_1\right)\right)}^{\frac{1}{2}}-\frac{{\left({\mathrm{\beta }}_1\right)}_i}{2}{\mathbf{X}}_{i\cdot }{\mathbf{T}}_1^T{\mathbf{T}}_1{\mathbf{X}}_{i\cdot }^T-{\mathrm{\delta }}_1{\left({\mathrm{\beta }}_1\right)}_i+\ln \left({\left({\mathrm{\beta }}_1\right)}_i\right)\left(a_{{\mathrm{\beta }}_1}^0-1\right)\right]+c,$$ (D.47)

where det(·) denotes the determinant. By using the properties of the determinant and the logarithm, calculating the expectation, and rearranging we obtain

$$\begin{array}{cc}\hfill \ln \mathrm{q}\left({\left({\mathrm{\beta }}_1\right)}_i\right)=& -\frac{{\left({\mathrm{\beta }}_1\right)}_i}{2}\left(\langle {\mathbf{X}}_{i\cdot }\rangle {\mathbf{T}}_1^T{\mathbf{T}}_1{\langle {\mathbf{X}}_{i\cdot }\rangle }^T+\mathrm{tr}\left({\mathbf{T}}_1^T{\mathbf{T}}_1\mathrm{cov}\left({\left({\mathbf{X}}_{i\cdot }\right)}^T\right)\right)\right)\hfill \\ \hfill & -{\left({\mathrm{\beta }}_1\right)}_i\langle {\mathrm{\delta }}_i\rangle +\ln \left({\left({\mathrm{\beta }}_1\right)}_i\right)\left(\frac{t_1}{2}+a_{{\mathrm{\beta }}_1}^0-1\right)+c,\hfill \end{array}$$ (D.48)

where cov((X_i·)^T) denotes the t₁×t₁ covariance matrix of the i-th row of X; it can be extracted from Σ_X as follows

$$\mathrm{cov}{\left({\left({\mathbf{X}}_{i\cdot }\right)}^T\right)}_{r,c}={\left({\Sigma }_{\mathbf{X}}\right)}_{i+(r-1)q,i+(c-1)q}.$$ (D.49)

By comparing Eq. (D.48) with the functional form of a gamma distribution (Eq. (D.31)) we see that q((β₁)_i) is gamma distributed with parameters

$${\left({\mathbf{a}}_{{\mathrm{\beta }}_1}\right)}_i=\frac{t_1}{2}+a_{{\mathrm{\beta }}_1}^0,$$ (D.50)

$${\left({\mathbf{b}}_{{\mathrm{\beta }}_1}\right)}_i=\frac{1}{2}\left[\langle {\mathbf{X}}_{i\cdot }\rangle {\mathbf{T}}_1^T{\mathbf{T}}_1{\langle {\mathbf{X}}_{i\cdot }\rangle }^T+\mathrm{tr}\left({\mathbf{T}}_1^T{\mathbf{T}}_1\mathrm{cov}\left({\left({\mathbf{X}}_{i\cdot }\right)}^T\right)\right)\right]+\langle {\mathrm{\delta }}_1\rangle .$$ (D.51)

To obtain q((β₂)_i), we write

$$\ln \mathrm{q}\left({({\mathrm{\beta }}_2)}_i\right)={𝔼}_{\mathrm{ϴ}\backslash {\left({\mathrm{\beta }}_2\right)}_i}[\ln \mathrm{p}(\mathbf{Z}\mid {\mathrm{\beta }}_2)+\ln \mathrm{p}({\mathrm{\beta }}_2\mid {\mathrm{\delta }}_2)]+c$$ (D.52)

and again notice that due to the symmetry of the model the distributions have the exact same form as the distributions in Eq. (D.46). Thus, by following the same procedure that we used to obtain q((β₁)_i) we find that q((β₂)_i) is gamma distributed with parameters

$${\left({\mathbf{a}}_{{\mathrm{\beta }}_2}\right)}_i=\frac{k}{2}+a_{{\mathrm{\beta }}_2}^0,$$ (D.53)

$${\left({\mathbf{b}}_{{\mathrm{\beta }}_2}\right)}_i=\frac{1}{2}\left[\langle {\mathbf{Z}}_{i\cdot }\rangle {\mathbf{T}}_2^T{\mathbf{T}}_2{\langle {\mathbf{Z}}_{i\cdot }\rangle }^T+\mathrm{tr}\left({\mathbf{T}}_2^T{\mathbf{T}}_2\mathrm{cov}\left({\left({\mathbf{Z}}_{i\cdot }\right)}^T\right)\right)\right]+\langle {\mathrm{\delta }}_2\rangle .$$ (D.54)

The distribution q(δ₁) is obtained by calculating

$$\ln \mathrm{q}({\mathrm{\delta }}_1)={𝔼}_{\mathrm{ϴ}\backslash {\mathrm{\delta }}_1}[\ln \mathrm{p}({\mathrm{\beta }}_1\mid {\mathrm{\delta }}_1)+\ln \mathrm{p}\left({\mathrm{\delta }}_1\right)]+c,$$ (D.55)

which, by absorbing terms into c, can be written as

$$\ln \mathrm{q}({\mathrm{\delta }}_1)={𝔼}_{\mathrm{ϴ}\backslash {\mathrm{\delta }}_1}\left[-{\mathrm{\delta }}_1\underset{i=1}{\overset{q}{\Sigma }}{\left({\mathrm{\beta }}_1\right)}_i+\ln \left({\mathrm{\delta }}_1\right)\left({\mathit{qa}}_{{\mathrm{\beta }}_1}^0-1\right)\right]+c.$$ (D.56)

From this it can be seen that q(δ₁) is gamma distributed with parameters

$$a_{{\mathrm{\delta }}_1}={\mathit{qa}}_{{\mathrm{\beta }}_1}^0,b_{{\mathrm{\delta }}_1}=\underset{i=1}{\overset{q}{\Sigma }}\langle {\left({\mathrm{\beta }}_1\right)}_i\rangle .$$ (D.57)

Similarly, we find that q(δ₂) is gamma distributed with parameters

$$a_{{\mathrm{\delta }}_2}={\mathit{qa}}_{{\mathrm{\beta }}_2}^0,b_{{\mathrm{\delta }}_2}=\underset{i=1}{\overset{q}{\Sigma }}\langle {\left({\mathrm{\beta }}_2\right)}_i\rangle ,$$ (D.58)

by calculating

$$\ln \mathrm{q}\left({\mathrm{\delta }}_2\right)={𝔼}_{\mathrm{ϴ}\backslash {\mathrm{\delta }}_2}[\ln \mathrm{p}({\mathrm{\beta }}_2\mid {\mathrm{\delta }}_2)+\ln \mathrm{p}\left({\mathrm{\delta }}_2\right)]+c.$$ (D.59)

Finally, we show the derivation of q(γ), i.e., the distribution of the hyperparameter which controls the strength of the TV prior. By collecting all terms that depend on γ and absorbing independent parts into the additive constant we obtain

$$\ln \mathrm{q}\left(\mathbf{\gamma }\right)={𝔼}_{\mathrm{ϴ}\backslash \mathbf{\gamma }}[\ln \mathrm{F}(\mathbf{w},\mathbf{u},\mathbf{\gamma })+\ln \mathrm{p}\left(\mathbf{\gamma }\right)]+c.$$ (D.60)

By calculating the logarithm and absorbing parts independent of γ into c we obtain

$$\ln \mathrm{q}\left(\mathbf{\gamma }\right)={𝔼}_{\mathrm{ϴ}\backslash \mathbf{\gamma }}\left[\ln \left(\mathbf{\gamma }\right)(\mathrm{\phi }n-1)-\frac{\mathbf{\gamma }}{2}\underset{i=1}{\overset{n}{\Sigma }}\frac{{\mathbf{w}}^T{\mathrm{\Delta }}_i^T{\mathbf{G}}_i^T{\mathbf{G}}_i{\mathrm{\Delta }}_i\mathbf{w}+u_i}{\sqrt{u_i}}\right]+c.$$ (D.61)

From which we can see that q(γ) is gamma distributed and that the shape parameter is given by a_γ=φn. To calculate b_γ we use Eq. (49) to obtain

$$b_{\mathbf{\gamma }}=\frac{1}{2}{𝔼}_{\mathrm{ϴ}\backslash \mathbf{\gamma }}\left[\underset{i=1}{\overset{n}{\Sigma }}\frac{{\mathbf{w}}^T{\mathrm{\Delta }}_i^T{\mathbf{G}}_i^T{\mathbf{G}}_i{\mathrm{\Delta }}_i\mathbf{w}+u_i}{\sqrt{u_i}}\right]=\underset{i=1}{\overset{n}{\Sigma }}\sqrt{u_i}.$$ (D.62)