Abstract
Cell spreading is regulated by signaling from the integrin receptors that activate intracellular signaling pathways to control actin filament regulatory proteins. We developed a hybrid model of whole-cell spreading in which we modeled the integrin signaling network as ordinary differential equations in multiple compartments, and cell spreading as a three-dimensional stochastic model. The computed activity of the signaling network, represented as time-dependent activity levels of the actin filament regulatory proteins, is used to drive the filament dynamics. We analyzed the hybrid model to understand the role of signaling during the isotropic phase of fibroblasts spreading on fibronectin-coated surfaces. Simulations showed that the isotropic phase of spreading depends on integrin signaling to initiate spreading but not to maintain the spreading dynamics. Simulations predicted that signal flow in the absence of Cdc42 or WASP would reduce the spreading rate but would not affect the shape evolution of the spreading cell. These predictions were verified experimentally. Computational analyses showed that the rate of spreading and the evolution of cell shape are largely controlled by the membrane surface load and membrane bending rigidity, and changing information flow through the integrin signaling network has little effect. Overall, the plasma membrane acts as a damper such that only ∼5% of the actin dynamics capability is needed for isotropic spreading. Thus, the biophysical properties of the plasma membrane can condense varying levels of signaling network activities into a single cohesive macroscopic cellular behavior.
Introduction
Cell motility is a complex process that involves multiple levels of regulation (1). On a two-dimensional substrate, motility is usually described as being composed of separate steps of protrusion, adhesion, traction at the front, and retraction/deadhesion at the rear (2). Spreading of fibroblasts on substrate-coated surfaces allows us to quantitatively study each of these steps (3,4). In phase 0 of spreading, which lasts ∼1 min, the cell makes its initial contacts with the substrate and focal contacts are formed. These contact sites are based on binding of the integrin receptors to extracellular matrix components, such as fibronectin. Integrin interaction with fibronectin triggers the assembly and activation of tyrosine kinases and then Rho-GTPases to control the activity of actin cytoskeleton modulating proteins (3,4). In phase 1, the fast isotropic spreading phase, which lasts 5–10 min, the fibroblasts start protrusion of their actin filament-rich lamellipodial region and spread in a mostly circular shape, with leading-edge velocities reaching up to 15 μm·min−1 (5,6). During this phase, the adhesion dynamics and myosin do not appear to play a significant role (7,8). The cell then stops the rapid spreading and enters phase 2, where a contractile process involving myosin motors accompanies further spreading. During phase 2, protrusion slows down and the cell shape becomes critically dependent on the adhesion contacts (4). The second phase lasts 15–25 min. Together, the different spreading processes take ∼30 min.
Computational models of cell motility can help us understand the mechanisms of actin remodeling and the interaction of biochemical reactions and physical forces. Previous studies using the Brownian ratchet model and the elastic Brownian ratchet model identified the relationships between the elongating actin filament and the load offered by the plasma membrane (9,10). The models developed by Schaus et al. (11,12) provided insights into the steady-state patterns of actin filament networks in the presence of membrane load and bending rigidity using stochastic simulations. Building on those previous studies, we developed a stochastic three-dimensional model of isotropic spreading of the whole cell based on quantitative macroscopic parameters from spreading experiments using total internal reflection fluorescence microscopy (13). From these simulations, we found that a balance between the biochemical reactions that underlie actin cytoskeleton remodeling and the biophysical properties of the plasma membrane is required for regulating the size and shape of the spreading cell during the isotropic phase (13). Most computational models of cell motility, including ours, focus on the actin polymerization machinery, assuming that the actin filament modulators, such as Arp2/3, and capping protein are present in sufficient amounts to enable branching and growing of filaments (10–16). Signaling proteins regulate the activity of Arp2/3 and capping protein (17,18). Integrins binding to substrate, such as fibronectin, leads to the activation of numerous signaling proteins, including tyrosine kinases and phosphatases, and RhoGTPases. This leads to several downstream events, including the stimulation of phospholipid synthesis (19–21). Integrins can interact with the actin cytoskeleton in two ways: by activating the polymerization machinery, and by physically linking actin to the adhesion sites (17). A complex signaling network emanates from integrins. Many components of this network, such as FAK, Src, and Cdc42, regulate but are not critical for cell spreading (see the Supporting Material).
The experimental observations raise several questions: Does the isotropic phase of cell spreading require the integrin signaling network, and does the integrin signaling network control the dynamics of the isotropic spreading phase? How are the dynamics of the signaling network integrated with the physical forces at the plasma membrane to control the spreading process? To address these questions at a systems level, where signaling network function is considered in the context of whole-cell spreading, we need to construct computational models that can simulate and analyze both the signaling network dynamics and cytoskeletal dynamics. To that end, we developed a hybrid deterministic-stochastic model. We used this model to determine whether the dynamics of the integrin signaling network can affect the spreading behavior of a cell by controlling the activity levels of regulators for the reactions that underlie spreading.
Materials and Methods
Construction of the signaling network
We constructed an integrin-signaling network from known components and interactions from the experimental literature, as described in detail in Table S1. The network was then used to construct a dynamical model. A multicompartmental ordinary differential equation model of the integrin signaling network was constructed in Virtual Cell (22). The rate constants and initial conditions are described in the Supporting Material.
Assumptions in the development of the hybrid model
To develop a hybrid model that would be computationally tractable, we had to make several assumptions, as listed below. The assumptions were made with the proviso that if the output from the integrated model did not agree with experimental observations of spreading, the assumption would be reexamined and the model modified.
-
1.
Integrin clustering, mechanotransduction, and formation of nascent adhesions were not included in the signaling model. Instead, integrins were treated as receptors for signal transduction from fibronectin to the actin filament modulatory proteins.
-
2.
The concentration of the biochemical species was assumed to be spatially uniform in the spreading model because we are only tracking the changes at the nanometer scale in the lamellipodium width (∼200 nm).
-
3.
The hybrid model is unidirectional, in that there is no effect of the spreading dynamics on the signaling model. It is likely that the membrane-imposed load can affect the integrin signaling. In building a unidirectional model, we made the assumption that the changes to the signaling dynamics caused by the changing cell size and shape are not likely to be critically important. As we conducted the numerical simulations, tests of the experimental predictions and comparisons between experiments and simulations indicated that our simplifying assumption was valid.
Detailed explanations for the basis of these assumptions are provided in the Supporting Material.
Development of the hybrid integrated model
The compartmental ordinary differential equation model of the integrin signaling network was coupled with a three-dimensional stochastic model of cell spreading (13) to obtain an integrated model of whole-cell spreading regulated by signaling (Fig. 1 C).
Figure 1.
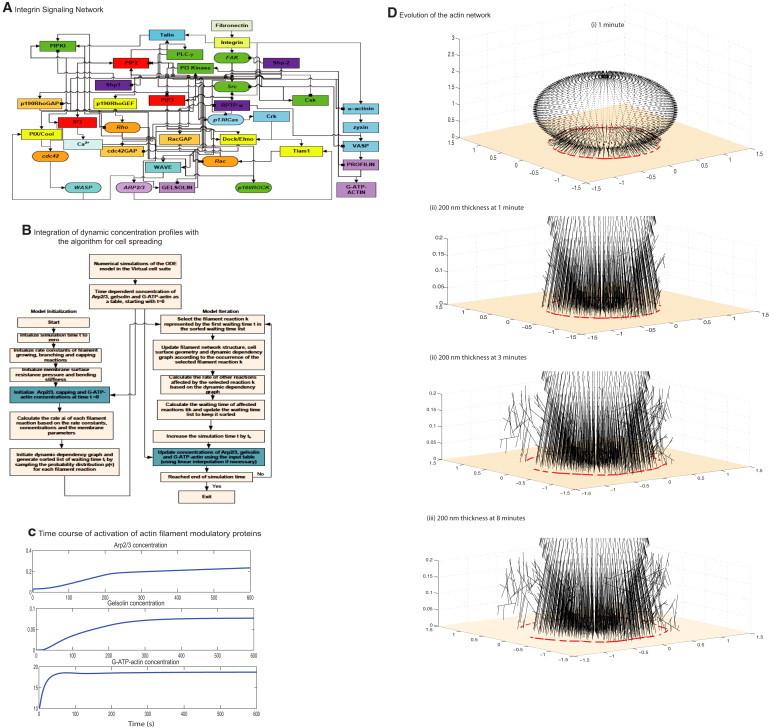
Hybrid model of cell spreading regulated by integrin signaling. (A) The signaling network shows the flow of biochemical information from the binding of fibronectin to integrin to the activation of Arp2/3, gelsolin, and G-ATP-actin. (B) The algorithm from the stochastic spatiotemporal spreading model was modified to accept a text file with the temporal concentration profile as input. At every time step in the iteration, the concentration is updated from the text file. In most cases, the time step calculated from the Gillespie's algorithm is not a direct match with the regular intervals in the concentration profile, so the algorithm interpolates the concentration of Arp2/3, gelsolin, and G-ATP-actin at that time step. (C) Concentration profiles of Arp2/3, G-ATP-actin, and gelsolin from the compartmental deterministic signaling model. These profiles are used as input to the stochastic spatiotemporal spreading model. The concentration of Arp2/3 affects the filament branching reaction, G-ATP-actin affects the elongation reaction, and gelsolin concentration affects the capping reaction. (D) Evolution of the actin filament network and the resultant shape profiles at different times in a single simulation in response to dynamic input of the varying levels of actin regulatory proteins profiles computed by the signaling network. (i) Three-dimensional view of the full network at 1 min. (ii–iv) Magnified view of the 200 nm thick region at (ii) 1 min, (iii) 3 min, and (iv) 8 min. The surface z = 0 is shown by the tan color. Note that the filaments that protrude from outside the radius are not on the surface z = 0.
The whole-cell spreading model is a stochastic spatiotemporal model of cell spreading that consists of actin filament elongation, branching, and capping reactions. The plasma membrane physical properties are represented by the surface load (p, pN·μm−2) and bending rigidity (Kb, pN·μm). The net energy required to move an area dA of the membrane forward by a distance δ, where δ is the length of an actin monomer, is the sum of energy changes associated with the membrane surface being pushed forward (ΔEsurface) and the energy required to change the local curvature of the membrane (ΔEbending; Eq. 1). The elastic Brownian ratchet model (23) is used to describe the relationship between kinetic parameters and the membrane energy requirements (Eq. 2). The detailed calculations are described in the Supporting Material.
| (1) |
| (2) |
The model is implemented in C++ with the use of discrete differential geometry methods (24).
The output from the integrin signaling network ODE model is saved as a text file with concentrations of activated Arp2/3, gelsolin, and G-ATP-actin as a function of time (Fig. 1 C). The stochastic whole-cell spreading model takes in model parameters, reactions, and concentrations as input files and runs the Gillespie algorithm for the filament actin, branching, and capping reactions. This stochastic model was modified to access a look-up table that was generated by the text file containing the dynamics of activated Arp2/3, gelsolin, and G-ATP-actin at every time step of the computation (using linear interpolation when necessary). The flowchart for the process is outlined in Fig. 1 B. When the spreading model is initialized, it uses the parameters file to initialize the number of filaments (4000), the allowed reactions, the kinetic parameters, and the membrane parameters (Table S3). Once this is initialized, the model uses the Gillespie algorithm to compute the reaction rates and corresponding wait times. As the iterations proceed, the main modification to the spreading model is that at the end of every iteration, the concentrations of the actin filament regulatory proteins are updated on the basis of the text file (Fig. 1 B and Fig. S5). The spreading model interpolates the concentrations linearly to obtain the concentration at the exact time step for the Gillespie algorithm. Details of the model development and implementation are presented in the Supporting Material.
Cell-spreading experiments
For the spreading assays, we used immortalized mouse embryonic fibroblasts RPTP α+/+ on fibronectin-coated coverslips. Details of the culture conditions and preparation of the coverglass can be found in Giannone et al. (25). We tested the dependence of spreading on Arp2/3 concentration by using wiskostatin (Calbiochem) (26). We also used Cdc42 dominant negative obtained through electroporation in a wild-type background (n = 5–7). For experiments using wiskostatin, we used a concentration of 20 μM (n = 6). To measure cell spreading, we used a differential interference contrast microscope with a 20× air objective. We recorded the spreading state every 5 s with a charge-coupled device camera.
Results
Comparing the hybrid model with whole-cell spreading experiments
The dynamics of Arp2/3, gelsolin activation, and G-ATP-actin levels are shown in Fig. 1 C. As expected, in response to a stimulus from integrins binding fibronectin, Arp2/3 activation increased. There is an early burst followed by two different slopes of activation. The initial activity comes from the early Cdc42 activation and the PI(4,5)P2 that is already present in the system activating WASP and therefore Arp2/3. The Rac/WAVE pathway also contributes to the early activation of Arp2/3. As more PI(4,5)P2 is synthesized and Cdc42 is activated over the course of the signaling events, the concentration of Arp2/3 increases. The concentration of Arp2/3 active is in the range of 0.2–0.3 μM. Gelsolin activation is slower because it depends on the calcium release from the endoplasmic reticulum. The concentration of gelsolin active plateaus to ∼0.08 μM. G-actin is present in large quantities in the cell (∼10–100 μM), and in the dynamic model the initial concentration of G-ADP-actin is 10 μM (Table S2). In response to activation by profilin, the G-ADP-actin is converted to G-ATP-actin at a fast rate and plateaus at ∼19 μM (Fig. 1 C). The instantaneous concentrations of Arp2/3, gelsolin, and G-ATP-actin were used as inputs to the stochastic spreading model. The evolution of the actin filament network from a single simulation is shown in Fig. 1 D for different times. In response to the dynamic concentrations of the regulators, the actin filament network evolves over time. The radius of the spreading cell is traced from the filaments that are changing at the surface (z = 0; Fig. 1 D).
The average spreading behavior from the integrated model shows that the simulations are able to capture isotropic spreading behavior (Fig. 2). At early times, the radius of the spreading cell is uniform, indicating circular spreading (Fig. 2 A ii). At later times, toward the end of phase 1 spreading, the simulated cell starts exhibiting finger-like projections along the periphery. These projections correspond to the change in spreading velocity, which goes from being uniform along the periphery to regions of zero spreading velocity at later times (Fig. 2 A iii). The radius and velocity maps capture the essential characteristics of isotropic cell spreading observed experimentally (5,13). The total number of filaments increases during isotropic spreading (Fig. 2 A i). To make a direct comparison between experiments and simulations, we calculated the fold change in the radius and the circularity of the spreading cell. The comparison of the fold change in radius shows a reasonable agreement between experiment and simulation (Fig. 2 B). In the simulations, the evolution of the fold change in radius shows a sharp increase at the onset of spreading for approximately the first minute, and then the rate of spreading decreases. This can be explained by the initially high rate of polymerization and high compliance factor. As the number of filaments increases, the rates of spreading and polymerization slow down. In experiments, the circularity is a relatively constant value during spreading in the isotropic phase (Fig. 2 B ii). Note that the overall level of circularity is lower in the experiments due to the fragmentation algorithm that extracts the cell contour. This noise is inherent to the resolution of the images of the experimental assays (13,27). From the simulations, we see that starting from a circle, we are able to maintain the circular shape for the 8 min of phase 1 spreading. These results indicate that in response to the dynamic signal input, we were able to obtain isotropic cell spreading from our model.
Figure 2.

Comparison of the simulated and experimental spreading behaviors based on the dynamic profile of actin modulators. The output from the signaling model from the control case is used as input for the spreading model. (A) Spreading behavior averaged over 24 simulations. (i) Total number of filaments. (ii) Radius map. (iii) Velocity map. (B) Comparison with experimental data using the (i) fold change in radius and (ii) circularity. The experiments were conducted with fibroblasts spreading on fibronectin-coated surfaces (see Materials and Methods).
Effects of Cdc42 and WASP
Cdc42 is a direct activator of N-WASP. When no Cdc42 is present, Arp2/3 activation is limited (Fig. S6). Arp2/3 activation also occurs by Rac activation of WAVE, which is unaffected by the absence of Cdc42. Gelsolin and G-ATP-actin dynamics are not affected. The absence of Cdc42 results in a decrease in Arp2/3 activation by ∼10-fold compared with control; however, this is residual activation due to the Rac pathway (Fig. S6).
In the simulation, the dynamics of Cdc42 knockout or WASP inhibition are similar and the net effect on Arp2/3 is the same. In the absence of Cdc42, the spreading size is decreased but circularity does not change. Experiments with Cdc42DN or wiskostatin-mediated inhibition of WASP showed similar results, in that isotropic spreading was not affected (Fig. 3 A i). The change in spreading radius was small in the Cdc42DN and wiskostatin treatment, and the decrease was not statistically significant (Fig. 3 A ii). The cell-shape evolution did not change in the simulations in response to removal of Cdc42 or WASP (Fig. 3 B i), and this observation was verified experimentally (Fig. 3 B ii).
Figure 3.

Simulations of spreading behavior in the absence of Cdc42 and WASP; comparison with experiment. Simulations using concentration profiles for Arp2/3, gelsolin, and G-ATP-actin in the case in which Cdc42 and WASP initial concentrations were set to zero are compared with spreading experiments performed with Cdc42DN fibroblasts and wiskostatin inhibition of WASP. Panels A and B show the fold change in radius in these cases compared with control; there is a small reduction in the spreading radius. Panels C and D compare the circularity profiles in these cases. Simulations predict no change in cell shape during spreading in the absence of Cdc42 or WASP, and experiments (D) agree with this prediction.
Membrane control of the polymerization rate: analysis of the rate of polymerization and signaling dynamics
We analyzed the effect of the active concentrations of the actin filament regulatory proteins on the rate of polymerization, which is a direct measure of F-actin concentration in the system and an indirect measure of the spread cell area and hence the cell size. In this model, the actin reactions are treated as irreversible and the reaction rates are written as mass-action laws.
The elongation reaction and the corresponding reaction rate are given by
The branching reaction results in the addition of a new filament along the side of an existing filament. Two G-ATP-actin monomers and one Arp2/3 molecule participate in this reaction:
The capping reaction results in the capping of a filament, and only existing filaments and the capping protein participate in this reaction:
The net rate of polymerization is now given by
This can be written as
The above relationships hold in an environment where no resistance is imposed by the plasma membrane on the growing filaments, and the system can be assumed to be well-mixed and spatially uniform, and represents the average rate of polymerization. We denote the above rate as Rfree.
In the presence of the plasma membrane, each reaction experiences resistance offered by the plasma membrane by a combination of surface load and bending rigidity (Eqs. 1 and 2) (13). The observed average rate of polymerization is now given by
The first observation is that the concentration of F-actin is influenced mainly by the amount of G-ATP-actin present. The sensitivity of the time evolution of F-actin to Arp2/3 concentration (ΦF-actin/Arp2/3=d(ln[F-actin])/d[Arp2/3]) is independent of Arp2/3 concentration and depends on G-actin concentration alone. The sensitivity coefficient is defined as (28):
Similarly, the sensitivity of the temporal evolution of F-actin to gelsolin concentration (ΦF-actin/Gelsolin = d(ln[F-actin])/d[gelsolin]) is a constant:
These relationships highlight the fact that although Arp2/3 and gelsolin are required for the maintenance of filament branching and polymerization, within a reasonable concentration range, the actual value of Arp2/3 and gelsolin are less important than the amount of monomeric actin present for polymerization to proceed. The results of varying kcapping and the initial concentration of G-ATP-actin on F-actin concentration are shown in Fig. S7 and Fig. S8, respectively. The size of the spreading cell is directly proportional to the amount of G-ATP-actin present (Fig. S8) and inversely proportional to the capping rate (Fig. S7). Cell shape does not show a strong dependence on either of these parameters.
The exponential term is called the compliance factor. The ratio of Robserved/Rfree is a measure of the average compliance factor. The evolving filament network needs to overcome the energy barrier imposed by the plasma membrane (ΔE (13)) to push the membrane forward. When no membrane resistance is imposed on the system of growing filaments, this term has a value of one, allowing Rfree = Robserved. When the membrane opposes free growth of the filament network, the compliance factor is <1 (Fig. 4 A). In a well-mixed system with no spatial dependence, every filament will experience the same resistance and therefore, Robserved will still be spatially uniform. This means that the imposition of membrane properties will decrease the rate of spreading, but the spreading shape will not deviate from a circle.
Figure 4.
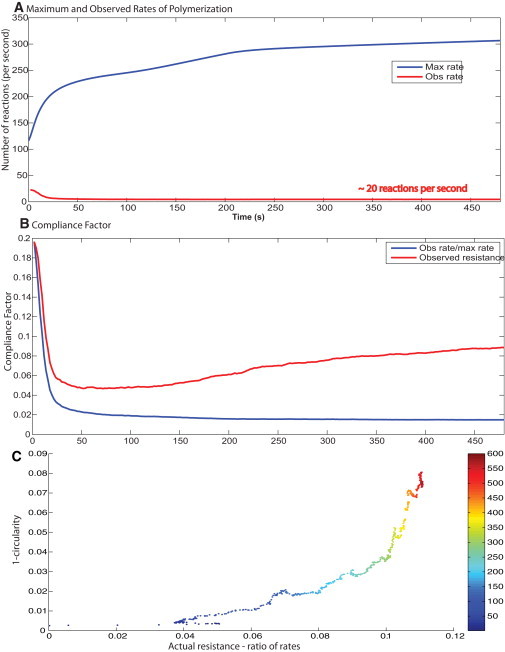
Rate of actin polymerization and membrane control of spreading dynamics. (A) The free rate of polymerization is obtained from the concentration profiles from the deterministic signaling model. The observed rate of polymerization is calculated from the spreading model. (B) The compliance factor from the simulations is compared with the ratio of Rfree/Robserved. At early times, there is a good match, but as the cell begins to deviate from a circular shape, the ratio of Rfree/Robserved and the actual compliance factor deviate from each other. (C) The changing shape over time (1-circularity) correlates well with the difference in the actual compliance factor calculated from the spreading model and the ratio of the observed to free polymerization rates. The color map on the plot shows the time point.
However, actin filament reactions are stochastic and not spatially uniform. Therefore, we need to consider the effect of spatial deviation in reaction rates' impact on spreading dynamics. From the simulations, we get the average rate of polymerization over the spreading space. This is compared with the average rate of polymerization from the deterministic model. The ratio of these two rates is the average compliance factor. At early times, we see that the ratio of observed to free rates correlates very well with the observed compliance factor. At later times, the calculated and actual compliance factors deviate from each other (Fig. 4 B). This deviation corresponds to the changing shape of the cell. Fig. 4 C shows that over time, as the cell deviates from a perfect circle (1-circularity), the difference between the calculated and observed compliance factors deviates accordingly. Thus, the deviation at later times is indicative of the changing shape. Correlating the circularity of the spreading cell with the differences in the two rates shows a strong positive correlation over time.
Effect of varying the surface load and bending rigidity
Using various combinations of surface load and bending rigidity coefficients, we sought to determine what role the biophysical properties of the plasma membrane play in spreading behavior.
In the absence of any membrane control, the spreading behavior is that of a system of free filaments with no resistance imposed on them. The resulting spreading behavior shows a large deviation from observed experimental behavior in terms of both the spreading size and the shape dynamics. The rate of polymerization is high and the compliance factor is equal to one at all times. Initially, the observed rate of polymerization is the same as the free rate of polymerization. The deviation at later times is indicative of the noncircular spreading model (Fig. 5).
Figure 5.
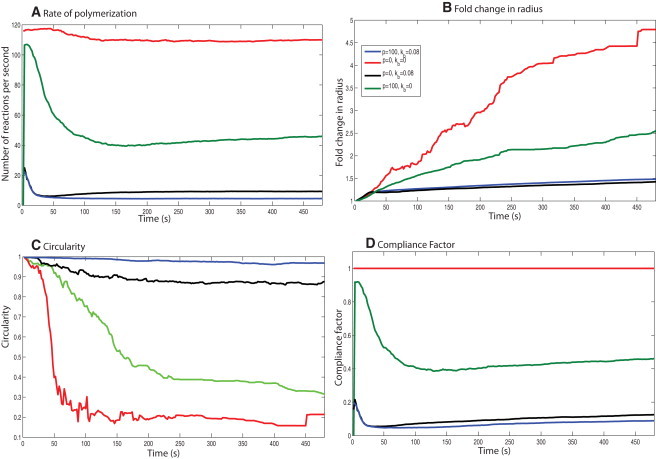
Effects of the physical properties of the membrane on the cell-spreading dynamics. Varying the plasma membrane's biophysical properties for the same signaling input shows that its physical properties affect the spreading dynamics. (A) Rate of polymerization. (B) Fold change in radius. (C) Circularity. (D) Compliance factor for different membrane physical parameters. A change in the membrane properties results in loss of shape control during spreading for the same concentration dynamics.
When we introduce the surface load alone, the membrane is modeled as an infinitely flexible surface. The spreading rate decreases and the spreading is more circular than in the case with no membrane control. The compliance factor is higher than that of the control, but lower than the case with no membrane control (Fig. 5). However, the presence of membrane surface resistance alone is not sufficient to correct the spreading shape dynamics.
This condition represents the case of a bendable plasma membrane that does not offer any resistance to being pushed forward. When the bending rigidity term is used without the membrane resistance, the spreading behavior is closer to control spreading (Fig. 5). However, the spreading size and compliance factor are lower than control. When we compare the F-actin and filament evolution, we see that the bending rigidity contribution is larger than the surface resistance contribution toward maintaining the cell shape. However, p is necessary to maintain the rate of polymerization.
As shown in Fig. 2 B, the spreading behavior generated in this case matches both the size and the shape evolution observed in experiments. The cell shape is the closest to a circle in this case (Fig. 5 B), indicating that both surface load and membrane bending rigidity are necessary to maintain the shape evolution that is experimentally observed. The number of filament reactions per second is slightly larger than the case in which only Kb is present, indicating that having surface load is important for maintaining a favorable rate of polymerization (Fig. 5 C).
Varying signaling input to the spreading model
To computationally test the roles played by various signaling components in isotropic spreading, we generated signaling outputs from the multicompartment model by setting the initial condition of the various components to zero. The components studied included FAK, Src, PIP kinase type I γ, and PLC-γ , among others (Fig. S9, Fig. S10, Fig. S11, Fig. S12, Fig. S13, Fig. S14, Fig. S15, Fig. S16, and Fig. S17; see Supporting Material for complete details). The resulting rates of polymerization show that the various components of the signaling network are important for maintaining the rate of the filament reactions (Fig. 6 A). However, when these various dynamic concentration profiles are input to the spreading model, the resulting spreading behavior is similar in terms of spreading size (Fig. 6 B) and spreading shape (Fig. 6 C). Thus, although the lack of certain components in the signaling network can affect the dynamics of the actin regulatory proteins, these changes have no observable effect on the spreading dynamics at the whole-cell level.
Figure 6.
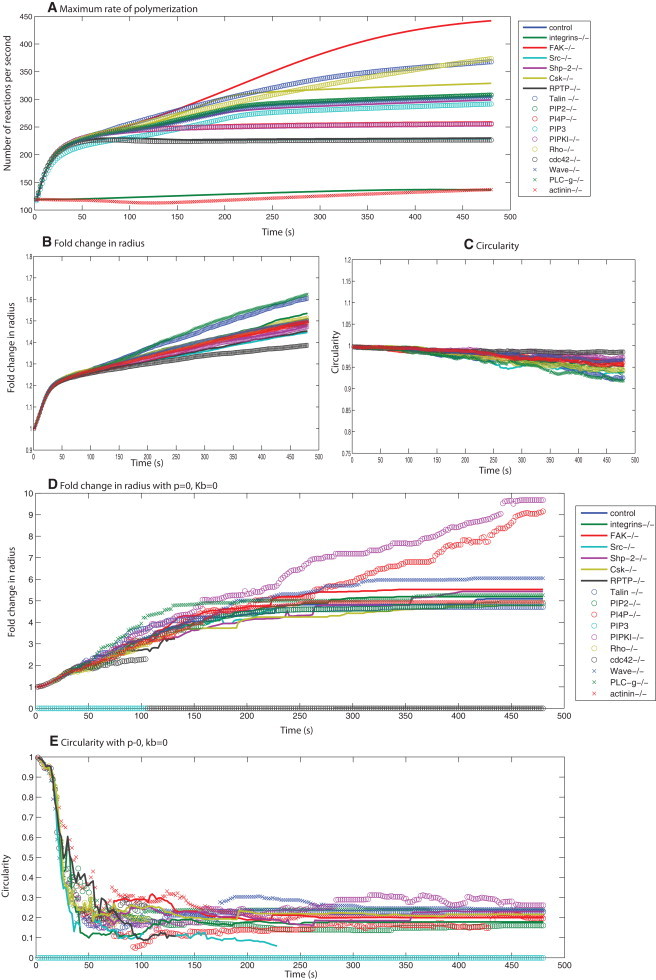
Summary of simulated spreading behavior for knockouts of different signaling components. (A) Free rates of polymerization as calculated from the deterministic signaling model for 17 different signaling conditions. (B and C) The fold change in spreading radius and circularity for these different conditions shows a narrow range of spreading behaviors for a wide range of signaling profiles, suggesting that the plasma membrane acts as a low-pass filter. Panels D and E show the spreading behavior for the case with no membrane, under the 17 conditions for signaling shown in panel A. (D) The fold change in radius is different for different signaling profiles. (E) The cell shape is extremely noncircular.
Because the dynamics of the actin remodeling events are limited by the membrane-imposed load, in the absence of any membrane parameters there should be a correspondence between the different signaling dynamics and the size and shape evolution of freely polymerizing actin filaments. We repeated the simulations with the conditions p = 0 and Kb = 0 and compared the spreading behavior. This situation is comparable to that of a freely polymerizing population of actin filaments rather than the cellular environment.
The simulations (Fig. 6, D and E) show that in the absence of membrane parameter controls, different knockouts of the signaling components exhibit different dynamics of size evolution. Because there is no control for shape, the circularity comparisons show that the filaments are growing in a spatially unregulated pattern in an extremely noncircular manner. This result supports our hypothesis that the effective rate of polymerization is controlled by the biophysical properties of the plasma membrane. Therefore, the plasma membrane controls shape evolution and also acts as a damper by taking a wide range of possible regulatory behaviors of the signaling network and condensing them to a single type of spreading dynamics (Fig. 6).
We varied the membrane parameters (p = 0, 100, and 500 pN·μm−2) and bending rigidity (Kb = 0, 0.08, 0.2 pN·μm), and followed the spreading dynamics for different signaling dynamics. In Fig. S18, we show the fold change in radius and circularity at 8 min, toward the end of isotropic spreading from the simulations. In the absence of membrane bending (Fig. S18 A), the response to different signaling dynamics results in noncircular spreading. Increasing p compensates for the absence of Kb to some extent, but the spreading shape is never circular in the absence of Kb. When Kb is included in the model, the spreading shape is almost always circular (Fig. S18 B). Increasing Kb to 0.2 pN·μm makes the cells spread in a circle and at the same time reduces the spreading size (Fig. S18 C).
Discussion
Biophysical properties of the plasma membrane control isotropic cell spreading
The actin filament motility machinery is complex and regulated by multiple cell signaling components (1). Many of these components are also important for cell survival and proliferation, and share their information processing capability with other signaling pathways. The focus of this study was to elucidate the role of the integrin signaling network in isotropic spreading at the whole-cell level. We found that the spreading that occurs during the isotropic phase is robust and not influenced by the changes in the dynamics of the signaling network. This is surprising, until we look at the balance between the biochemical reactions and biophysical properties in controlling isotropic spreading. The physical properties of the plasma membrane reduced the actual rate of polymerization to ∼5% of the maximum achievable rate of polymerization if the biochemical reactions were unconstrained by the plasma membrane-derived physical forces. This result suggests that activation of small fractions of the actin cytoskeleton regulatory proteins are sufficient to drive isotropic cell spreading. Nolen et al. (29) found that the use of an inhibitor of Arp2/3 did not stop keratocyte motility, and suggested that a small quantity of Arp2/3 (∼500 nM) might be sufficient to maintain motility behavior at the leading edge. The actin cytoskeletal system has been studied in vitro in the absence of signaling components, and the essential dynamics of filament polymerization and force generation to push the leading edge forward can be observed in such minimally reconstituted systems (30). Taken together, our observations from the simulations and the in vitro reconstitution experiments suggest that the actin cytoskeleton is a self-organizing system that may only require a triggering event to start the process.
In a recent study using electron tomography, Urban et al. (31) showed that the actin filaments at the leading edge may also be unbranched. This suggests that there may be multiple mechanisms of actin remodeling at the leading edge, resulting in different configurations of actin filaments and possibly generating robust isotropic spreading. However, further experimental work in this area is needed before we can develop useful computational models.
Role of the integrin signaling network in isotropic cell spreading
Previous in vitro reconstitution experiments in which filament polymerization was studied in the absence of membrane constraints showed that the polymerization kinetics of actin filaments correlated with the levels of Cdc42-GTP, WASP, Arp2/3 complex, or capping protein added to the system (32–35). We were able to mimic those experiments in our simulations by setting the plasma membrane biophysical parameters to zero. Other experiments on cell spreading behavior indicated that although PLC-γ, Talin, Src, FAK, RPTP regulate spreading (8,36–38), none of these components are essential for spreading. Knocking out signaling components modifies spreading behavior, but the term “modified spreading behavior” has not been quantified in a dynamic sense. Because the final spread area is often measured 30 min to 1 h after initiation of spreading, it is not possible to compare the dynamics of isotropic spreading, which lasts for 5–10 min, with these longer-term effects. Presumably, during this longer time range the cells undergo multiple stages of spreading, including contractile phase and then retraction.
Our prediction that the absence of Cdc42 and WASP would not affect spreading during the isotropic phase was confirmed by experiments using Cdc42 dominant negative and wiskostatin inhibition of WASP. In a previous study, Cuvelier et al. (39) analyzed the dynamics of cell spreading using hydrodynamic models and found that cells with Cdc42DN showed the same spreading dynamics as wild-type cells. These researchers concluded that cell spreading in the early stages is driven more by effective filament polymerization and filament network-membrane interaction than by signaling. We arrived at the same conclusion in our model and identified the mechanisms by which the physical properties of the plasma membrane control the effects of the signaling network in regulating the actin cytoskeleton dynamics. Our simulations predicted that disrupting the physical properties of the plasma membrane would affect the isotropic spreading behavior. A comparison of p = 500 pN·μm−2, Kb = 0.2 pN·μm with p = 100 pN·μm−2, Kb = 0.08 pN·μm shows that fluidizing the membrane or reducing the load offered by the membrane increases the spreading rate (Fig. S18, green bars versus red bars). This phenomenon was previously observed in studies in which deoxycholate was used to increase membrane fluidity, resulting in a decrease in membrane tension and hence an increase in spreading velocity (40,41).
Our hybrid model shows that isotropic spreading is robust against changes in signaling and depends on the signaling network only for the initiation of spreading. The mechanism for this robustness arises from membrane-imposed control of the rate of polymerization of the growing actin network. The physical forces from the plasma membrane reduce the rate of polymerization to ∼5% of what is possible in a free system of actin filaments. Therefore, to obtain robust spreading behavior, small amounts of Arp2/3 and gelsolin are sufficient. The plasma membrane acts as a filter to distill a large range of possible Arp2/3 and gelsolin dynamics into a cohesive spreading behavior.
Assumptions and simplifications
In this work, we assume spatially homogeneous concentrations of the components at the leading edge. The spatial distribution of the actin regulatory proteins need not be uniform throughout the cell. However, since the cell-spreading experiments are done with total internal reflection fluorescence microscopy, we explicitly model only 200 nm of the juxtamembrane region, and within this space this assumption appears valid. Future models will have to consider the dynamic inhomogeneities of signaling components and G-actin in transitioning from the isotropic phase to the later phases of cell spreading. We also assume that the membrane mechanical parameters are not varying in time. A recent study confirmed the validity of this assumption for the isotropic phase (N. C. Gauthier, M. A. Fardin, P. Roca-Cusachs, and M. P. Sheetz, unpublished), but suggested that this might not be the case at the transition to the contractile phase. Such changes in membrane mechanical parameters could be introduced in future computational models of the multiple phases of cell spreading.
We also have a simplification in our hybrid model. Information flows one way from the signaling network ODE model to the actin filament dynamics stochastic model. The forces calculated in the cytoskeleton dynamics model do not affect the integrin signaling network. However, within the stochastic cell-spreading model, the change in membrane forces in dynamically estimated, and these forces regulate the three actin filament remodeling reactions. The simplification of one-way coupling between the ODE and stochastic model appears valid because only ∼5% of the regulatory capability is required to drive isotropic cell spreading. The parameter variation simulations show that even if the membrane forces were to double or triple the activity of the signaling network, this would have a minimal effect on the observed whole-cell behavior.
Perspective
The phenomena described in this study on the influence of the signaling network dynamics on cell spreading are limited to the isotropic phase alone. These results should not be construed as an implication that the actin cytoskeleton machinery acts independently of the cell signaling components. The role of the integrin signaling network in the initiation of the isotropic spreading process, a spatially stochastic event (5), and the later contractile phase (Rho-kinase and MLCK regulation of myosin motors) is well established (43–45). It is very likely that the signaling network, including the adhesome (20), is responsible for transitions during the multiple phases of spreading and serves as a bookend to the isotropic phase.
Despite its limitations, our integrated computational model highlights the role of the plasma membrane as a feedback controller of actin filament biochemistry. Signaling from integrin's interaction with fibronectin is critical for the initiation of spreading. Because Arp2/3 and actin are present in large micromolar concentrations in cells (46), there is a large spare capacity for regulation. In some ways, this finding is akin to the spare receptor theory for G-protein-coupled receptors, which holds that 10% occupancy of the receptor will yield a full biochemical or physiological response. In both cases, the effectors turn out to be efficient filters or dampers of the cellular responses.
In the case of cell spreading, the physical properties of the plasma membrane control the rate of polymerization and are important for generating robust isotropic spreading behavior. Before it can deform the membrane and push it forward, the actin filament network has to overcome the energy barrier imposed by the plasma membrane. This energy barrier reduces the effective rate of reactions and polymerization for actin filaments, resulting in a slower growth of the filament network and a smaller deformation of the local membrane. Conventional analyses of feedback loops have focused on the signaling network architecture. In this work, however, we identify the role of biophysical properties as negative feedback regulators of biochemical events. It appears that during isotropic spreading, the negative feedback biophysical properties predominate over the positive stimulus from the integrin signaling network. Such a balance at the systems level provides an initial insight into how cohesive macroscopic behaviors can arise from multiple microscopic biochemical events.
Acknowledgments
We thank Dr. Ravi Ramamoorthi (University of California, Berkeley) for extensive help with programming, and Dr. Giovanni Meacci (Columbia University) for comments and feedback.
This research was supported in part by the National Institutes of Health (grants GM072853 and GM54508) and the Systems Biology Center (grant GM071558). P.R. was supported by a fellowship from training grant DK007645 (National Institute of Diabetes and Digestive and Kidney Diseases). The Virtual Cell is supported by the National Center For Research Resources, National Institutes of Health (grant P41RR013186).
Supporting Material
References
- 1.Bray D. Garland Science; New York: 2000. Cell Movements: From Molecules to Motility. [Google Scholar]
- 2.Mitchison T.J., Cramer L.P. Actin-based cell motility and cell locomotion. Cell. 1996;84:371–379. doi: 10.1016/s0092-8674(00)81281-7. [DOI] [PubMed] [Google Scholar]
- 3.Döbereiner H.G., Dubin-Thaler B., Sheetz M.P. Dynamic phase transitions in cell spreading. Phys. Rev. Lett. 2004;93:108105. doi: 10.1103/PhysRevLett.93.108105. [DOI] [PubMed] [Google Scholar]
- 4.Döbereiner H.G., Dubin-Thaler B.J., Sheetz M.P. Force sensing and generation in cell phases: analyses of complex functions. J. Appl. Physiol. 2005;98:1542–1546. doi: 10.1152/japplphysiol.01181.2004. [DOI] [PubMed] [Google Scholar]
- 5.Dubin-Thaler B.J., Giannone G., Sheetz M.P. Nanometer analysis of cell spreading on matrix-coated surfaces reveals two distinct cell states and STEPs. Biophys. J. 2004;86:1794–1806. doi: 10.1016/S0006-3495(04)74246-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dubin-Thaler B.J., Hofman J.M., Sheetz M.P. Quantification of cell edge velocities and traction forces reveals distinct motility modules during cell spreading. PLoS ONE. 2008;3:e3735. doi: 10.1371/journal.pone.0003735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cai Y., Rossier O., Sheetz M.P. Cytoskeletal coherence requires myosin-IIA contractility. J. Cell Sci. 2010;123:413–423. doi: 10.1242/jcs.058297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zhang X., Jiang G., Sheetz M.P. Talin depletion reveals independence of initial cell spreading from integrin activation and traction. Nat. Cell. Biol. 2008;10:1062–1068. doi: 10.1038/ncb1765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Peskin C.S., Odell G.M., Oster G.F. Cellular motions and thermal fluctuations: the Brownian ratchet. Biophys. J. 1993;65:316–324. doi: 10.1016/S0006-3495(93)81035-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mogilner A., Oster G. Cell motility driven by actin polymerization. Biophys. J. 1996;71:3030–3045. doi: 10.1016/S0006-3495(96)79496-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Schaus T.E., Borisy G.G. Performance of a population of independent filaments in lamellipodial protrusion. Biophys. J. 2008;95:1393–1411. doi: 10.1529/biophysj.107.125005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Schaus T.E., Taylor E.W., Borisy G.G. Self-organization of actin filament orientation in the dendritic-nucleation/array-treadmilling model. Proc. Natl. Acad. Sci. USA. 2007;104:7086–7091. doi: 10.1073/pnas.0701943104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Xiong Y., Rangamani P., Iyengar R. Mechanisms controlling cell size and shape during isotropic cell spreading. Biophys. J. 2010;98:2136–2146. doi: 10.1016/j.bpj.2010.01.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Mogilner A., Edelstein-Keshet L. Regulation of actin dynamics in rapidly moving cells: a quantitative analysis. Biophys. J. 2002;83:1237–1258. doi: 10.1016/S0006-3495(02)73897-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Carlsson A.E. Growth of branched actin networks against obstacles. Biophys. J. 2001;81:1907–1923. doi: 10.1016/S0006-3495(01)75842-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Carlsson A.E. Growth velocities of branched actin networks. Biophys. J. 2003;84:2907–2918. doi: 10.1016/S0006-3495(03)70018-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.DeMali K.A., Wennerberg K., Burridge K. Integrin signaling to the actin cytoskeleton. Curr. Opin. Cell Biol. 2003;15:572–582. doi: 10.1016/s0955-0674(03)00109-1. [DOI] [PubMed] [Google Scholar]
- 18.Martin K.H., Slack J.K., Parsons J.T. Integrin connection map: to infinity and beyond. Science. 2002;296:1652–1653. doi: 10.1126/science.296.5573.1652. [DOI] [PubMed] [Google Scholar]
- 19.Ballestrem C., Erez N., Geiger B. Molecular mapping of tyrosine-phosphorylated proteins in focal adhesions using fluorescence resonance energy transfer. J. Cell Sci. 2006;119:866–875. doi: 10.1242/jcs.02794. [DOI] [PubMed] [Google Scholar]
- 20.Zaidel-Bar R., Itzkovitz S., Geiger B. Functional atlas of the integrin adhesome. Nat. Cell Biol. 2007;9:858–867. doi: 10.1038/ncb0807-858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zamir E., Geiger B. Molecular complexity and dynamics of cell-matrix adhesions. J. Cell Sci. 2001;114:3583–3590. doi: 10.1242/jcs.114.20.3583. [DOI] [PubMed] [Google Scholar]
- 22.Virtual Cell. http://vcell.org
- 23.Mogilner A., Oster G. Force generation by actin polymerization II: the elastic ratchet and tethered filaments. Biophys. J. 2003;84:1591–1605. doi: 10.1016/S0006-3495(03)74969-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Meyer M., Desbrun M., Schroeder P., Barr A.H. Discrete differential-geometry operators for triangulated 2-manifolds. Proc. VisMath. 2002 June;35–57. [Google Scholar]
- 25.Giannone G., Dubin-Thaler B.J., Sheetz M.P. Periodic lamellipodial contractions correlate with rearward actin waves. Cell. 2004;116:431–443. doi: 10.1016/s0092-8674(04)00058-3. [DOI] [PubMed] [Google Scholar]
- 26.Peterson J.R., Mitchison T.J. Small molecules, big impact: a history of chemical inhibitors and the cytoskeleton. Chem. Biol. 2002;9:1275–1285. doi: 10.1016/s1074-5521(02)00284-3. [DOI] [PubMed] [Google Scholar]
- 27.Fardin M.A., Rossier O., Sheetz M.P. Cell spreading as a hydrodynamic process. Soft Matter. 2010;6:4788–4799. doi: 10.1039/c0sm00252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Varma A., Morbidelli M., Wu H. Cambridge University Press; Cambridge, UK: 1999. Parametric Sensitivity in Chemical Systems. [Google Scholar]
- 29.Nolen B.J., Tomasevic N., Pollard T.D. Characterization of two classes of small molecule inhibitors of Arp2/3 complex. Nature. 2009;460:1031–1034. doi: 10.1038/nature08231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Loisel T.P., Boujemaa R., Carlier M.F. Reconstitution of actin-based motility of Listeria and Shigella using pure proteins. Nature. 1999;401:613–616. doi: 10.1038/44183. [DOI] [PubMed] [Google Scholar]
- 31.Urban E., Jacob S., Small J.V. Electron tomography reveals unbranched networks of actin filaments in lamellipodia. Nat. Cell Biol. 2010;12:429–435. doi: 10.1038/ncb2044. [DOI] [PubMed] [Google Scholar]
- 32.Amann K.J., Pollard T.D. The Arp2/3 complex nucleates actin filament branches from the sides of pre-existing filaments. Nat. Cell Biol. 2001;3:306–310. doi: 10.1038/35060104. [DOI] [PubMed] [Google Scholar]
- 33.Amann K.J., Pollard T.D. Direct real-time observation of actin filament branching mediated by Arp2/3 complex using total internal reflection fluorescence microscopy. Proc. Natl. Acad. Sci. USA. 2001;98:15009–15013. doi: 10.1073/pnas.211556398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Eden S., Rohatgi R., Kirschner M.W. Mechanism of regulation of WAVE1-induced actin nucleation by Rac1 and Nck. Nature. 2002;418:790–793. doi: 10.1038/nature00859. [DOI] [PubMed] [Google Scholar]
- 35.Rohatgi R., Ho H.Y., Kirschner M.W. Mechanism of N-WASP activation by CDC42 and phosphatidylinositol 4, 5-bisphosphate. J. Cell Biol. 2000;150:1299–1310. doi: 10.1083/jcb.150.6.1299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Jones N.P., Peak J., Katan M. PLCγ1 is essential for early events in integrin signalling required for cell motility. J. Cell Sci. 2005;118:2695–2706. doi: 10.1242/jcs.02374. [DOI] [PubMed] [Google Scholar]
- 37.von Wichert G., Jiang G., Sheetz M.P. RPTP-α acts as a transducer of mechanical force on αv/β3-integrin-cytoskeleton linkages. J. Cell Biol. 2003;161:143–153. doi: 10.1083/jcb.200211061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.von Wichert G., Jiang G., Sheetz M.P. RPTP-α acts as a transducer of mechanical force on αv/β3-integrin-cytoskeleton linkages. J. Cell Biol. 2003;161:143–153. doi: 10.1083/jcb.200211061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Cuvelier D., Théry M., Mahadevan L. The universal dynamics of cell spreading. Curr. Biol. 2007;17:694–699. doi: 10.1016/j.cub.2007.02.058. [DOI] [PubMed] [Google Scholar]
- 40.Raucher D., Sheetz M.P. Characteristics of a membrane reservoir buffering membrane tension. Biophys. J. 1999;77:1992–2002. doi: 10.1016/S0006-3495(99)77040-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Raucher D., Sheetz M.P. Cell spreading and lamellipodial extension rate is regulated by membrane tension. J. Cell Biol. 2000;148:127–136. doi: 10.1083/jcb.148.1.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Reference deleted in proof.
- 43.Cohen M., Joester D., Addadi L. Spatial and temporal sequence of events in cell adhesion: from molecular recognition to focal adhesion assembly. ChemBioChem. 2004;5:1393–1399. doi: 10.1002/cbic.200400162. [DOI] [PubMed] [Google Scholar]
- 44.Lichtenstein N., Geiger B., Kam Z. Quantitative analysis of cytoskeletal organization by digital fluorescent microscopy. Cytometry A. 2003;54:8–18. doi: 10.1002/cyto.a.10053. [DOI] [PubMed] [Google Scholar]
- 45.Zaidel-Bar R., Cohen M., Geiger B. Hierarchical assembly of cell-matrix adhesion complexes. Biochem. Soc. Trans. 2004;32:416–420. doi: 10.1042/BST0320416. [DOI] [PubMed] [Google Scholar]
- 46.Pollard T.D., Blanchoin L., Mullins R.D. Molecular mechanisms controlling actin filament dynamics in nonmuscle cells. Annu. Rev. Biophys. Biomol. Struct. 2000;29:545–576. doi: 10.1146/annurev.biophys.29.1.545. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


