Cy3-DNA Stacking Interactions Strongly Depend on the Identity of the Terminal Basepair

Abstract

We characterized the effect of the first basepair on the conformational dynamics of the fluorescent dye Cy3 attached to the 5′ end of double-stranded DNA using Gaussian-mixture adaptive umbrella sampling simulations. In the simulations, the sampling of all five dihedral angles along the linker was enhanced, so that both stacked and unstacked states were sampled. The affinity of Cy3 for a T·A basepair (with the dye attached to T) was found to be significantly less than for the other basepairs. This was verified experimentally by measuring the activation energies for cis-trans isomerization of the dye. The simulation and experimental results indicate the existence of partially unstacked conformations amenable to photoisomerization. The simulations also showed that stacking of Cy3 straightens the DNA while stabilizing the first basepair. Our findings indicate that fluorescence is modulated by Cy3-DNA interactions in a sequence-dependent manner.

Introduction

Atomistic molecular dynamics (MD) simulation has emerged as an important tool for investigating the conformational dynamics of biomolecules, and for explaining and interpreting the results of experiments designed to elucidate those dynamics. Many biomolecules have multiple functionally relevant states with low free energies, and undergo conformational changes between different configurational states on the microsecond-to-second timescale. Although a few simulations on comparable timescales have recently been reported (1,2), such studies require extremely large computational resources; therefore, most research groups are limited to simulations of up to ∼100 ns in length. Consequently, techniques have been developed to enhance the sampling, so that biologically relevant dynamics can be simulated within the timescales amenable to simulation (3–26).

In many of these methods, the physical potential is augmented by a biasing potential to escape free energy basins. This biasing potential is often expressed in terms of a small number of collective coordinates that are expected to reflect the most important motions of the system; the simulation determines the free energy in terms of these collective coordinates. Examples of such methods include metadynamics (11) and the local elevation method (10), in which the biasing potential is expressed in terms of a history-dependent sum of spherical Gaussians, and adaptive umbrella sampling (21,22) in which histograms of the reaction coordinates are used for the biasing potential. Such methods are inherently limited to a small number of collective coordinates. For example, in metadynamics, the use of too many reaction coordinates would result in a very large space that would take a long time to fill with Gaussians, whereas adaptive umbrella sampling has the additional complication that its memory requirements for storing the histograms grow with the power of the number of collective coordinates.

These limitations have partially been overcome by the recently developed Gaussian-mixture adaptive umbrella sampling (GAMUS) method (26). Like adaptive umbrella sampling, GAMUS uses the negative of the estimated free energy surface as a biasing potential. However, GAMUS avoids the memory demands of adaptive umbrella sampling by estimating the free energy from a fitted probability distribution instead of from multidimensional histograms. The Gaussian-mixture fit is performed efficiently with the expectation-maximization algorithm (27). This makes it possible to use four or more reaction coordinates; for example, GAMUS was able to identify minima in the free energy surface of the alanine tripeptide as a function of its four backbone dihedral angles (26). The fit also optimizes the shape of the Gaussians, allowing for a more efficient filling of basins than with the metadynamics method.

In this work, we apply GAMUS to the dynamics of the Cy3 fluorescent dye attached to the 5′ end of a DNA duplex. Experiments have shown that the conformational dynamics of fluorescent dyes attached to biomolecules is highly complex and has a significant effect on the photophysics of the dyes. NMR structural studies show that Cy3 stacks on top of the first basepair when attached to the 5′ end of DNA (28), and photophysical studies suggest that similar stacking interactions occur between Cy3 and free nucleosides in solution (29).

Other fluorescence studies, however, indicate that the position of Cy3 relative to the DNA is not static. For example, in double-stranded DNA with Cy3 and Cy5 dye at each end, the FRET efficiency was found to oscillate as a function of helix length due to the changes in relative orientation of the stacked dyes. The amplitude of this oscillation, however, was less than that expected for dyes rigidly stacked on the ends of DNA (30).

The fluorescence anisotropy of Cy3 relaxes with biexponential kinetics, indicating the presence of a timescale for rotation of Cy3 about its linker in addition to the timescale for rotational tumbling of the Cy3-DNA adduct. In addition, the fluorescence quantum yield of Cy3 is significantly higher when it is bound to DNA than when it is free. This is due to Cy3-DNA interactions that inhibit the ability of the dye to photoisomerize to a nonfluorescent cis isomer. In the ground state, Cy3 exists in an all-trans conformation. Upon absorption, the singlet-excited state deactivates by competing processes, including fluorescence emission, nonradiative processes such as internal conversion, and rotation around a C-C bond of the polymethine chain which results in the ground-state cis isomer.

Because photoisomerization is an activated nonradiative process that competes with fluorescence emission, the fluorescence lifetime and quantum yield of Cy3 depend strongly on temperature and steric interactions that may hinder isomerization. The activation energy for photoisomerization was found to be less for double-stranded DNA than for single-stranded DNA, and strongly dependent on DNA sequence (31,32).

Taken together, these observations indicate that Cy3-DNA interactions are dynamic in nature. Experimental data is consistent with a model in which the dye exhibits restricted rotational mobility and longer excited state lifetimes when stacked on the terminal bases, and increased rotational freedom and shorter excited state lifetimes when unstacked. Both the changes in quantum yield and orientation affect the quantitative interpretation of fluorescence resonance energy transfer (FRET) data when Cy3 is used as a probe. Because the spectroscopic and photophysical properties of Cy3 depend strongly on dye-DNA interactions, the determination of molecular distances from FRET data is subject to uncertainties unless the effects of such interactions are well understood.

Dye-DNA interactions can, in principle, be studied by MD simulations, and a few DNA-dye simulations have been reported (33–36). These simulations, however, have been hampered by insufficient sampling of the possible conformations of the dye. A simulation of DNA with Cy5 and tetramethylrhodamine attached to the two ends showed Cy5 binding in only two different conformations and no more than a small number of transitions between those conformations were observed (33). In short (200-ps) simulations of double-stranded DNA with the Texas Red dye, unstacking never occurred (34).

Other simulations modeled solvent through generalized Born approaches (35) as, for example, a simulation of single-stranded DNA with fluorescein (36) and the aforementioned simulation of double-stranded DNA with Cy5 and tetramethylrhodamine (33). Use of these implicit solvent models for highly charged systems like DNA might be problematic though, because such models neglect correlations between the positions of the ions and discrete ion effects (37,38).

To overcome the limitations of insufficient sampling, while maintaining a fully atomistic representation for the dye, DNA, solvent, and ions, we used GAMUS to simulate the conformational dynamics of Cy3 attached to the 5′ end of DNA. In the simulations, the sampling of all five dihedral angles of the linker between Cy3 and DNA was enhanced. We studied Cy3 attached to all four different initial basepairs to assess the dependence of the dynamics and DNA-dye interactions upon sequence.

The simulations predicted a substantial sequence-dependent effect. In particular, Cy3 was found to have a much greater affinity for stacking to the A·T basepair (with the dye attached to A) than for the structurally related T·A basepair (with the dye attached to T). These predictions were verified experimentally by comparing the activation energy for cis-trans isomerization of the Cy3 dye in its excited state when attached to the different sequences. In addition, partially unstacked Cy3 conformations amenable to isomerization were identified, and the effect of Cy3 attachment on DNA structure was characterized.

Materials and Methods

GAMUS simulations

All simulations were conducted using the CHARMM nucleic acid force field (39,40) as implemented in the CHARMM program (41). Parameters for the Cy3 dye were adapted from the CHARMM general force field (42) and modified to fit the lowest vibrational modes of Cy3 as determined from normal mode calculations at the B3LYP/6-31g+(d,p) level (43,44). The optimized parameters are given in Table S2, Table S3, Table S4, and Table S5 of the Supporting Material. A total of four systems were simulated. Each consisted of Cy3 attached to a double-stranded DNA with sequence 5′-Cy3-XTCTTCAGTTCG-3′, where the initial base X equals C, A, G, or T. Construction of the initial coordinates is described in the Supporting Material. All simulations were performed in explicit water (45) in the NPT ensemble with the Nosé-Hoover method (46), using periodic boundary conditions and the particle-mesh Ewald method (47), a time step of 2 fs, and SHAKE constraints (48) for all bonds containing hydrogen atoms.

To sufficiently cover the relevant conformational space, we used GAMUS (26) to enhance the sampling of all five dihedral angles of the Cy3 linker in the production runs (Fig. 1). The systems with initial base A and T were simulated for a total of 70 ns; because convergence took longer for the other systems, systems with initial base G or C were simulated for a total of 80 ns. GAMUS is a novel adaptive umbrella sampling method, which uses a biasing potential to favor the exploration of unvisited areas in configuration space.

Figure 1.

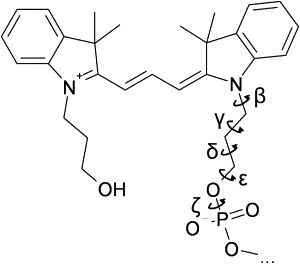
Reaction coordinates used for GAMUS.

The biasing potential operates on a preselected reaction coordinate q; here q is a five-dimensional vector consisting of the linker dihedral angles. The simulations are run for short amounts of time (here 1 or 2 ns, see below). After each run, a new and improved biasing potential is constructed using information harvested from all previous runs, and a new simulation is performed with the updated biasing potential. This iterative process is repeated until the calculated free energy surface converges. After each run i, the sampled configurations q_n,i (here stored at 0.2-ps time intervals) are used to construct the probability density P(q) from a Gaussian-mixture model fit,

$$P_{\left(i\right)}\left(q\right)={\pi }_{0,i}\gamma +\sum _{m=1}^M\frac{{\pi }_{m,i}}{{\left(2\pi \right)}^{D/2}|{\Sigma }_{m,i}{|}^{1/2}}\times \exp \left(-\frac{1}{2}{\left(q-{\mu }_{m,i}\right)}^T{\left({\Sigma }_{m,i}\right)}^{-1}\left(q-{\mu }_{m,i}\right)\right),$$ (1)

where π_m, μ_m, and Σ_m are the weight, mean, and variance-covariance matrix of the Gaussians, γ is the prior, D is the dimension of q, i is the index of the run, and T indicates the transpose operation. The weighted fit is performed with the expectation-maximization algorithm (27), using all sampled configurations from all runs. Because a biasing potential was used during the sampling, the sampled coordinates q_n,i have different weights w_n,i for the fit. These weights are given by

$$w_{n,i}=\frac{Z_i}{Z_0}{e}^{V_{b,i}\left(q_{n,i}\right)/kT},$$ (2)

where Z_i/Z₀ is the ratio of partition functions of the biased (Z_i) and unbiased system (Z₀) determined from the multistate acceptance ratio method (49), V_b,i is the biasing potential of simulation i, T is the temperature, and k the Boltzmann constant. The new biasing potential follows from the fitted probability density:

$$V_{b,i+1}\left(q\right)=kT\ln P_i\left(q\right)\text{.}$$ (3)

Upon convergence, −V_b,i equals the free energy.

During the first 50 ns of simulation, the biasing potential was adjusted every 1 ns. After this period, the free energy surfaces changed more slowly, and the interval between readjustments was increased to 2 ns to assure more accurate free energy surfaces. Configurations q_n,i were collected every 0.2 ps after an initial 200-ps equilibration period for each run. The number of Gaussians for the density fit was given by

$$N=\{\begin{array}{l}4+2i(i\le 15)\\ 34(15<i\le 50)\\ 34+2(i-50)(50<i<60)\\ 54(i\ge 60)\end{array}\text{.}$$ (4)

Initially, the trajectories explored many new free energy basins; therefore, the number of Gaussians was allowed to grow with time. Once the number of newly found basins slowed down, the cap of 34 Gaussians was used to prevent overfitting of the data (which can lead to excessively small Gaussians). After the cap, the number of Gaussians was allowed to increase again to allow for the fitting of newly discovered basins, followed by a cap of 54 basins to prevent overfitting of data.

Each fit consisted of 200 iterations of the expectation-maximization algorithm, repeated 32 times with different random number seeds; the fit with the highest likelihood was used for the construction of the new biasing potential. To avoid excessively narrow Gaussians, which can lead to numerical difficulties, constraints were placed on the variance-covariance matrices, such that a Gaussian could not be <5° wide in any direction. The prior γ, which is used to avoid excessive extrapolation of the biasing potential, was set to the lowest sampled probability, but capped to 10⁻⁵⁰ to avoid the deep artificial minima described earlier (26).

The free energy basins were identified using a previously described algorithm (50). The sampled configurations were sorted by basin, and maps of the transitions between basins were constructed for each simulation. Using the sampled configurations and their weights, the potential of mean force as a function of other coordinates could be calculated as well. We did this for the distance between the center of mass of Cy3 and the center of mass of the first base on the strand to which Cy3 was attached, and also for the rotation of Cy3 around the linker. This rotation angle was defined as the pseudodihedral between the two nitrogen atoms of the dye, the phosphorus atom to which the linker was attached, and the C6 (for T and C) or C8 (for A and G) atom of the complementary base.

To assess the effect of Cy3 on the stability of the first basepair, sampled configurations were divided into two groups, depending on the distance between Cy3 and the first base. Configurations for this distance >8.0 Å were considered unstacked; the other configurations were considered stacked. The 8.0 Å cutoff was chosen based on the calculated Cy3-first basepair distance free-energy surfaces; 8.0 Å is beyond the major basin. We then calculated separate free energy surfaces for the unstacked and stacked configurations as a function of the distance between the centers of mass of the two bases in the first basepair.

The basepair local and step parameters were analyzed with 3DNA (51), and overall DNA bending angles were calculated with MadBend (52) using the roll, twist, and tilt angles from 3DNA. In the latter calculation, the first and last basepair steps were excluded. All reported values of the local, step, and bending angles have been properly reweighted to account for the artificial biasing potential. Block analyses were performed (53) to determine the statistical uncertainties of structural parameters in the unbiased simulations; no attempt was made to determine these uncertainties in the biased simulations because of the complexity of doing so in conjunction with the reweighting. In addition to the GAMUS simulations, we also performed 50-ns unbiased MD simulations of the fully solvated unlabeled DNA sequences using the NAMD program (54).

The calculated internal, van der Waals, and electrostatic components of the interaction energy between the dye and the first basepair were properly reweighted to account for the artificial biasing potential. No solvation or dielectric components were included in these interaction energies, because no water molecules can enter between the dye and the first basepair when the dye is stacked on top of the first basepair.

Photophysics of Cy3-DNA conjugates

The following HPLC-purified DNA oligonucleotides and their complementary strands were obtained from Integrated DNA Technologies (Coralville, IA). Their purity was checked by 20% native polyacrylamide gel electrophoresis (PAGE):

$$5^{\prime }-\text{Cy}3\text{XTC}\text{TTC}\text{AGT}\text{TCA}\text{GCC}{3}^{\prime }\text{X}=\text{A}\mathrm{,}\text{C}\mathrm{,}\text{G}\mathrm{,}\text{T}\text{.}$$

Here, 5′-Cy3 represents a Cy3 molecule attached covalently to the terminal 5′ phosphate of the DNA strand. The strands are slightly longer than the ones used in the simulation studies to ensure duplex stability. Double-stranded DNA samples were prepared in 10 mM Tris buffer by mixing the Cy3-labeled strand with a 10% excess of the complementary strand to ensure absence of single-stranded, fluorescently labeled DNA. Native PAGE was used to verify proper annealing.

Fluorescence spectra and fluorescence quantum yields (ϕ) of the samples were measured on a QM-4/2005SE spectrofluorometer (Photon Technology International, Birmingham, NJ). Temperature was controlled using a water circulation system and was measured inside the cuvette with a calibrated thermocouple. Fluorescence spectra were measured using polarizers in both the excitation and emission paths. The excitation wavelength was set at 500 nm. The excitation and emission polarizers were kept at the vertical and the magic-angle positions, respectively, to minimize polarization effects (55). Fluorescence quantum yields were calculated as a function of temperature in the 5–45°C range. The quantum yields of each sample at 22°C (ϕ^X_22°C) were calculated using the published value for the sample with a terminal T (ϕ^T_22°C = 0.16) (55) as a reference according to

$$\begin{array}{l}{\varphi }_{22°\text{C}}^X={\varphi }_{22°\text{C}}^T\frac{I_{22\text{°C}}^X}{I_{22\text{°C}}^T}\frac{A^T}{A^X},\\ X=A,C,G,\end{array}$$ (5)

where I^X is the integrated fluorescence intensity and A^X is the absorbance of each sample measured at the excitation wavelength. Then, the remaining quantum yields were calculated relative to the value at 22°C as

$$\varphi ={\varphi }_{22\text{°C}}\left(I/I_{22\text{°C}}\right),$$

where I is the integrated fluorescence intensity at the other temperatures.

Fluorescence lifetimes were measured using the time-correlated single photon counting technique at room temperature. The setup has been described elsewhere (31). The sample was excited by vertically polarized light, and the fluorescence decay was collected with the emission polarizer kept at the magic-angle with respect to the excitation polarizer. The instrument response function was measured using a 2% scattering solution (Ludox colloidal silica; Sigma, St. Louis, MO). The measured full width at half-maximum was typically ∼50 ps.

The activation energy of photoisomerization (E_iso) was calculated experimentally by determining the fluorescence quantum yield of Cy3 as a function of temperature as described in previous work (31,56). The fluorescence quantum yield can be written as

$$\varphi \left(T\right)=\frac{k_f}{k_f+k_{nr}+k_{iso}\left(T\right)},$$ (6)

where k_f refers to the radiative fluorescence rate, k_nr represents nonradiative pathways, and k_iso is the rate of the bond twisting process that initiates isomerization from the singlet excited state. Writing k_iso in terms of the Arrhenius equation

$$k_{iso}=A\exp \left(-E_{iso}/RT\right),$$

and assuming that k_iso ≈ 0 in glycerol at 0°C, we obtain

$$\ln [{\varphi }^{-1}\left(T\right)-{\varphi }^{-1}\left(\text{glycerol},0°\text{C}\right)]=\ln \left(A/k_f\right)-E_{iso}/RT\text{.}$$ (7)

Equation 7 provides a means from which E_iso can be calculated from temperature-dependent fluorescence quantum yield data. The value of ϕ(glycerol, 0°C) was determined in previous work as 0.85 (31).

Results and Discussion

We performed MD simulations of four different Cy3-labeled double-stranded DNA sequences in explicit water. The dye was attached to the first base of the 5′ strand; the sequences differed in the identity of this first base, and will be referred to as the A·T (when attached to A), T·A, G·C, and C·G simulations. All simulations were started from a stacked configuration, similar to the configuration that was observed in NMR studies (57), in which the dye stacked onto the first basepair, extending the DNA strand by one artificial base.

In unbiased MD simulations of 10 ns, the dye remained in the stacked configuration and no unstacking was observed. In GAMUS simulations of the same length, the dye unstacked and multiple free energy basins were visited. The GAMUS production runs were 70 ns for the A·T and T·A simulations, and to 80 ns for the G·C and C·G simulations. Convergence of the GAMUS simulations was assessed by monitoring the growth in the number of free energy basins and the calculated free energies of the basins as time progressed. Although convergence could not be reached for all basins at very high free energies (≥9 kcal/mol above the minimum free energy basin; converging these will take substantially longer simulations), and not necessarily all high free energy basins were visited in the simulations, by our measures the simulations converged for the low and intermediate basins, resulting in an overall convergence that suited our purposes. Multiple stacking and unstacking events were recorded in the GAMUS simulations (four times for A·T, five times for T·A, four times for G·C, and two times for C·G). A time trace of the center-of-mass distance between the dye and the first base is shown in Fig. S4.

The free energy surface as a function of the distance between the center of mass of Cy3 and the center of mass of the first base on the strand to which Cy3 is attached is shown in Fig. 2 a. Surprisingly, the free energy of unstacking depends strongly on the identity of the base to which the dye is attached (Table 1). The free energy of unstacking contributes to the activation energy for Cy3 cis-trans isomerization in its excited state, because the Cy3 must unstack at least partially from the first basepair to isomerize (29,31,32).

Figure 2.

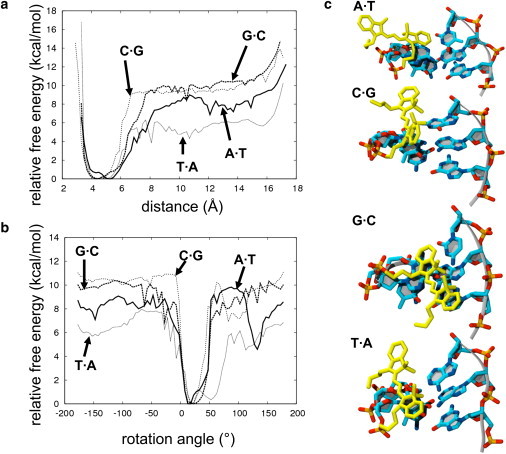
(a) Free energy as a function of the distance between the center of mass of the first base and the center of mass of the Cy3 ring system. (b) Free energy as a function of the rotation around the linker. (c) Examples of partially unstacked conformations from the four simulations.

Table 1.

Free energies for unstacking and activation energy for the cis-trans isomerization of Cy3

System	Unstacking free energy from simulation (kcal/mol)	Experimental activation energy for cis-trans isomerization (kcal/mol)
A·T	6.5	10.7
G·C	8.7	9.9
C·G	8.4	8.4
T·A	4.2	4.9

The activation energy for isomerization can be measured experimentally by determining the fluorescence quantum yield of the dye as a function of temperature. Therefore, our simulations produced an experimentally verifiable prediction: the activation energies for isomerization in Cy3-DNA complexes should depend on the identity of the first base, and should vary in the same order as the unstacking free energies. In particular, based on the results of Fig. 2, T·A was predicted to have a much lower activation energy than the other three bases, which were predicted to have similar activation energies. This prediction was verified experimentally by measuring the fluorescence lifetime, temperature-dependent quantum yield, and activation energy of photoisomerization for the four samples (Table 1 and Fig. 3).

Figure 3.

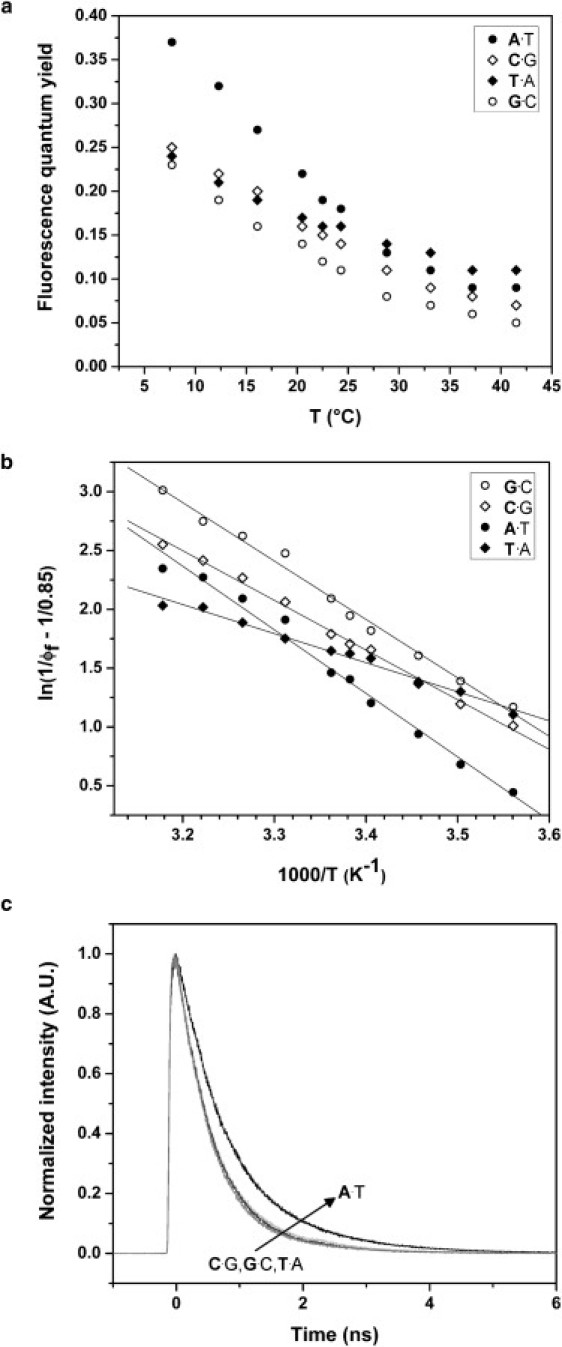
(a) Fluorescence quantum yield of Cy3-DNA conjugates. (b) Arrhenius plot of fluorescence quantum yield of Cy3-DNA conjugates according to Eq. 7. (c) Time-resolved fluorescence decays of Cy3-DNA conjugates.

Fig. 3 b shows the Arrhenius plot (Eq. 7), calculated from the temperature-dependent quantum yields shown in Fig. 3 a. The activation energies calculated from these plots are listed in Table 1. The difference in E_iso between T·A and the other samples is evident from the different slopes of the plots of Fig. 3 b. This lower activation energy is responsible for the less pronounced temperature-dependence of the quantum yield of T·A (Fig. 3 a), and is consistent with the prediction of the simulations described above. At room temperature, the fluorescence quantum yield of A·T is significantly higher than the corresponding values for the other samples. The same behavior was observed in time-resolved measurements (Fig. 3 c) that show that the excited state lifetime of A·T is notably longer than the lifetimes of C·G, T·A, and G·C, which overlap within the resolution of the experiment. The striking differences in the fluorescence properties of Cy3 when attached to A or T are consistent with the higher unstacking free energy calculated for A in the simulations.

The free energy barrier for isomerization of free Cy3 (unligated to DNA) in the excited state is 4.5 kcal/mol (31). When this 4.5 kcal/mol is added to the calculated unstacking free energies, the resulting energies are much larger than the observed activation energies for Cy3 isomerization (Table 1). This implies that it is not necessary for Cy3 to fully unstack from the DNA to isomerize. Several low free energy basins corresponding to partially unstacked conformations were identified in the simulations; representative structures are shown in Fig. 2, c–e. In the partially unstacked conformations, one ring of the Cy3 system is stacked on top of the first base on the strand to which the dye is attached, and the other ring is extended over the minor groove or sugar-phosphate backbone of the DNA. It has been hypothesized that lateral motion of the dye may explain the dependence of FRET efficiency on distance in a series of Cy3- and Cy5-labeled DNA molecules (30); such laterally displaced dyes might, in fact, correspond to the partially stacked conformations identified in the simulations.

The partially unstacked conformations were observed for A·T, C·G, and T·A as free energy wells in the free energy surface as a function of the rotation angle (Fig. 2 b). A similar well in the rotation angle profile was not observed for G·C, but a partially unstacked conformation was observed as a free energy basin in the five-dimensional free energy surface of the linker dihedral angles (see below). In the rotation angle free energy profiles, the free energy well at positive roll angles corresponds to the partially stacked conformation; the deeper free energy well near 0° corresponds to the fully stacked conformation. Barriers for negative rotation angles were significantly higher for G and C (10 kcal/mol) than for A (8 kcal/mol) and T (7 kcal/mol), and similar differences were observed for positive rotations. Out of the stacked or partially stacked basins, and into solution the dye rotated freely about the linker, as observed from the free energy surface (Fig. 2 b) and the simulation snapshots. Moreover, the dye did not enter the minor or major groove of DNA, but remained in the bulk solution.

The partially unstacked conformations were also observed as basins in the five-dimensional free energy surface in terms of the linker dihedrals. Analyses of these free energy surfaces revealed the mechanism by which Cy3 unstacks from the DNA (Fig. 4, shown for C·G). Starting from a fully stacked conformation (Fig. 4 a), in which the dye strongly interacts with the first basepair, the dye rotates laterally, weakening the interactions (Fig. 4 b). Subsequently, the dye loses interactions with the first base, and slides forward over the major groove (Fig. 4 c). The dye then adopts the partially stacked conformation (Fig. 4 d, see also Fig. 2 d), before it finally loses all interactions with the first basepair and rotates freely in the bulk (Fig. 4 e).

Figure 4.

Mechanism of Cy3 unstacking determined from basin analysis of five-dimensional free energy surface, shown for initial base C. Free energies are indicated underneath the structures (in kcal/mol); these are relative to the free energy of the fully stacked conformation.

It is not clear exactly why Cy3 has such a different unstacking free energy for the T·A basepair. Analysis of interaction energies between the dye and the first basepair showed that the van der Waals components reproduced the trend obtained for the unstacking free energies, with the T·A basepair having a weaker interaction with the Cy3 dye than the other three basepairs (Table 2). The electrostatic interaction energy component did not correlate with the unstacking free energies; trends in the electrostatic energy were less clear, however, inasmuch as the fluctuations in the electrostatic interaction energy were highly dependent on the identity of the base.

Table 2.

Interaction energy components between Cy3 and the first basepair in stacked conformations

System	van der Waals (kcal/mol)	Electrostatics (kcal/mol)
A·T	−16.5 ± 1.8	−35.9 ± 3.1
G·C	−17.4 ± 1.9	−37.3 ± 3.4
C·G	−18.2 ± 1.8	−33.3 ± 5.3
T·A	−15.6 ± 2.3	−41.6 ± 9.3

This suggests that a combination of stacking, steric, and entropic effects, rather than charge distributions, are responsible for the difference in relative affinities. Although most of the atoms of the first basepair are in the same plane and sp² hybridized, the methyl group of thymine is sp³ hybridized and the C-H bonds in this methyl group extend out of the plane of the base. Therefore, this group might block the dye from interacting with the first basepair via stacking interactions when the methyl group of thymine is on the same strand as the dye.

Our simulations revealed a remarkable impact of Cy3 on the structure and dynamics of the DNA strand. Fig. 5 shows the free energy surfaces in terms of the distance between the centers of mass of the bases of the first basepair for both stacked and unstacked states of the A and T simulations. In absence of the dye, the free energy cost of opening the first basepair is much lower (∼4 kcal/mol) than in the presence of the dye (≥10 kcal/mol). These results indicate that Cy3 can stabilize T·A and A·T basepairs by stacking interactions; in effect, Cy3 acts as an additional basepair. In the G and C simulations, fewer frames were observed in which the first basepair had opened up. This is probably due to the increased stability of C·G and G·C basepairs, having one more Watson-Crick hydrogen bond than A·T and T·A. Consequently, the effect of Cy3 on the opening of C·G and G·C basepairs has a greater statistical uncertainty, and is therefore not included in Fig. 5.

Figure 5.

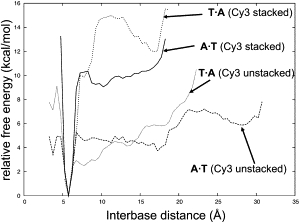
Potential of mean force as a function of distance for stacked and unstacked configurations. The distance is between the centers of mass of the two bases of the first basepair.

The stacking of Cy3 was also found to have an impact on the overall bending of Cy3. For T·A, C·G, and G·C the stacking of Cy3 caused the DNA to straighten slightly (Table 3). For A·T no significant change in DNA bending was detected. In addition, small but statistically significant decreases in roll angle of 1–5° were observed for many of the basepair steps in each strand when the dye was attached. This is consistent with the observation that changes in roll angle are responsible for most of DNA's bending flexibility (58). Small changes in other basepair step parameters were also detected, but these varied randomly in direction.

Table 3.

Overall bending angle of DNA as a function of initial base

System	Bending angle with dye	Bending angle without dye
A·T	19.3	18.6 ± 0.4
G·C	14.7	18.2 ± 0.4
C·G	13.7	18.8 ± 0.5
T·A	16.8	19.0 ± 0.5

Conclusions

We used the efficient GAMUS biasing method to enhance the sampling of all five dihedral angles of the linker of the fluorescent dye Cy3 attached to the 5′ end of four double-stranded DNA sequences. Starting from a stacked conformation of the dye, both stacked and unstacked conformations were sampled. The free energies of unstacking as a function of the first basepair were calculated, and the relative affinity of Cy3 for the four different basepairs was determined. Cy3 was found to have significantly less affinity for the T·A basepair than for the other three basepairs. These computational predictions were verified by photophysics experiments.

The experimentally measured energies of activation for isomerization followed the same trends as the free energies of unstacking from the simulation, with Cy3 attached to a T·A basepair showing a significantly lower activation energy than when attached to the other three basepairs.

The simulations and experiments also indicated the existence of partially unstacked states amenable to cis-trans isomerization. These findings indicate that it is not necessary for the dye to be completely unstacked and in solution for photoisomerization to a nonfluorescent isomer to occur. In addition, Cy3 was shown to have a small but significant effect on the structure of the DNA. The dye was shown to stabilize A·T or T·A basepairs through stacking interactions, acting as an additional basepair and preventing the fraying of the DNA. When stacked, the dye also straightens the DNA, reducing the roll angles between bases. When unstacked, the dye was found to rotate freely in solution.

Our studies show that the interactions between Cy3 and the DNA are highly dependent on the identity of the base to which the dye is attached. The findings indicate that a quantitative interpretation of FRET experiments on terminally labeled DNA requires the construction of sequence-dependent three-state models. To properly account for the fluorescence and competing photoisomerization reaction, the populations of the stacked, partially unstacked, and fully unstacked configurations must be taken into account. Our studies can aid the construction of such sequence-dependent models.