Evidence of Protein Collective Motions on the Picosecond Timescale

Abstract

We investigate the presence of structural collective motions on a picosecond timescale for the heme protein, cytochrome c, as a function of oxidation and hydration, using terahertz (THz) time domain spectroscopy and molecular dynamics simulations. The THz response dramatically increases with oxidation, with the largest increase for lowest hydrations, and highest frequencies. For both oxidation states the THz response rapidly increases with hydration saturating above ∼25% (g H₂O/g protein). Quasiharmonic vibrational modes and dipole-dipole correlation functions were calculated from molecular dynamics trajectories. The collective mode density of states alone reproduces the measured hydration dependence, providing strong evidence of the existence of these motions. The large oxidation dependence is reproduced only by the dipole-dipole correlation function, indicating the contrast arises from diffusive motions consistent with structural changes occurring in the vicinity of buried internal water molecules. This source for the observed oxidation dependence is consistent with the lack of an oxidation dependence in nuclear resonant vibrational spectroscopy measurements.

Introduction

Protein function relies on structural dynamics, with timescales ranging from picoseconds to beyond seconds. The transitions to the different configurations involved in function are routinely reproduced by trajectories involving only the first few structural collective vibrational modes, suggesting the importance of these modes in understanding and tailoring of protein interactions. However, there is some debate as to whether large-scale structural collective motions exist and if, instead, dynamics are entirely directed Brownian motion. Such uncorrelated diffusive motion would need to serendipitously access the proper configuration for protein-protein or protein-ligand binding.

Concerted motions could explain the observed high physiological on-rates and affinities (1–4). Recent neutron spin echo and x-ray inelastic scattering have verified that correlated motions do occur (5,6); however, these challenging measurements did not address the influence of these modes on function. The nature of these measurements limits their broad application for protein engineering. The question of coupling of large-scale motion is critical in the quest for tailoring allosteric interactions.

Computational studies of collective motions include normal modes (7), quasiharmonic modes (8), and coarse-grain modes (9). An example of a large-scale collective motion is the hinging motion of lysozyme. The hinge motion is immediately apparent as the upper and lower portions of the protein clamp-down upon the substrate, resulting in cleavage that is more effective. However, in the absence of substrate, the hinge is continuously oscillating. This motion was first calculated over 20 years ago by Brooks and Karplus (7) using normal mode analysis for lysozyme, with a hinge-bending resonant frequency of 3.6 cm⁻¹ = 0.108 THz. Although there is some skepticism whether these harmonic motions occur in vivo, it is agreed that at best they are overdamped. However, the calculated modes lead to root mean-squared displacements in good agreement with experimental results (8,10). The calculated timescales for these correlated motions can be from picosecond to nanosecond.

To fully characterize these motions requires an experimental tool which can resolve both energy and momentum transfer in the picosecond range. Inelastic neutron scattering is such a technique. However, its application is limited, since it is not a tabletop instrument and requires large samples (∼100 mg) and deuteration. Another relevant spectral technique is terahertz time domain spectroscopy (THz TDS). Previously, we and others have used THz TDS to measure the dielectric function of protein samples. The dielectric response has contributions from vibrational and diffusive motions in the protein and adjacent solvent,

$$\varepsilon \left(\omega \right)={\varepsilon }_o+\int \frac{f\left({\omega }^{\prime }\right)g\left({\omega }^{\prime }\right)}{\left({\omega }^{\prime 2}-{\omega }^2\right)+i\gamma \left({\omega }^{\prime }\right)\omega }d{\omega }^{\prime }+{\varepsilon }_r\underset{0}{\overset{\infty }{\int }}\frac{h\left(\tau \right)d\tau }{1+i\omega \tau },$$ (1)

where ɛ_o is the direct current dielectric constant. The second term on the right-hand side contains the vibrational density of states (VDOS) g(ω), oscillator strength f(ω), and damping coefficient γ(ω). The third term is the relaxational response, assuming Debye relaxation for a distribution of relaxation times h(τ). Typically, what is measured is the absorption coefficient α(ω) and the refractive index n(ω). Relating these measured quantities to the vibrational and relaxational response, one obtains

$$\begin{array}{l}{\alpha }_{vib}\left(\omega \right)=\int \frac{g\left({\omega }^{\prime }\right)f\left({\omega }^{\prime }\right)\omega \gamma \left({\omega }^{\prime }\right)}{{\left({\omega }^{\prime 2}-{\omega }^2\right)}^2+\gamma {\left({\omega }^{\prime }\right)}^2{\omega }^2}d{\omega }^{\prime }\\ \text{and}\\ {\alpha }_{relax}\left(\omega \right)n_{relax}\left(\omega \right)=\int \frac{1}{c}\frac{h\left(\tau \right)\tau {\omega }^2}{1-{\tau }^2{\omega }^2}d\tau ,\end{array}$$ (2)

where α_vib(ω) is the absorption coefficient which arises from the vibrational motions and α_relax(ω)n_relax(ω) is the product of the absorption coefficient and refractive index arising from the relaxational response. The relaxational response is always a broad absorbance. For small systems (5–20 atoms), the frequency dependence of the vibrational and relaxational responses are distinct, with the vibrational resonances widely spaced and relatively narrow. For large macromolecules, the collective vibrational modes become dense and individual modes begin to overlap. The spectrum becomes sufficiently dense that it is difficult to distinguish the structural vibrational response from localized side-chain relaxational rotations (11). Such a distinction is important for applications such as allosteric inhibitor design, where the binding of the inhibitor is constructed to interfere with the structural motions necessary for function (12).

Our ability to characterize global structural motions distinct from local diffusive ones is challenged by the similarity in the relaxational and vibrational response for large macromolecules. However, the manner in which these different types of motions change with environment or functional state can be distinct. To test for the presence and contribution of picosecond collective vibrational modes, we compare systematic measurements of cytochrome c (CytC) as a function of hydration and oxidation with the calculated response from the collective vibrational motions and the dipole-dipole correlation function which includes relaxational response. We find collective vibrational motions account for the hydration dependence observed in the THz dielectric response. However, the frequency dependence appears to be dominated by the relaxational motions of water and side chains. Furthermore, the large oxidation-dependent dielectric response observed experimentally is only reproduced when relaxational motions are included.

CytC is a protein of increasing interest as its multiple functions become revealed. The primary role of CytC is to participate in oxidative metabolism through the transfer of an electron from cytochrome c reductase to cytochrome c oxidase, both embedded in the inner mitochondrial membrane. Recently, it has become clear that CytC plays an important role in apoptosis, both within the mitochondria and during its release into the cytosol (13). Furthermore, CytC is an excellent model heme protein to consider fundamental questions of protein dynamics, as it is sufficiently small for systematic comparisons to theoretical modeling.

The physiochemical properties of CytC can be explained in terms of the differences in the dynamic behavior of the two redox states. Eden et al. (14) proposed that the oxidized form of CytC is more flexible than the reduced form, based on an estimated 40% increase in the apparent compressibility of CytC upon oxidation. X-ray diffraction measurements appear to give some support to higher flexibility in the ferric state, because the atomic mean-squared displacement (msd) as measured by the Debye-Waller factor increases for Ferri- over Ferro-CytC (15). The motions contributing to msd can be both collective, as in structural vibrational modes and local, as in side-chain librations.

A quantitative relationship can be drawn between the collective modes and the structural flexibility using the frequency dependence of the vibrational density of states (VDOS). Low frequency modes below k_BT are thermally occupied and these motions will contribute to the msd, whereas high frequency modes with energies of ∼k_BT or higher have lower occupancy and hence have a smaller contribution to the msd. THz-TDS was previously used to investigate whether the implied changes in the VDOS reflect increased flexibility change upon CytC oxidation (16).

A large increase in the THz dielectric response was observed with oxidation consistent with an increase in the low frequency VDOS and a higher flexibility. A number of observations since those studies have suggested caution when directly relating the dielectric response to the VDOS. These include the exploration of the role of local relaxational motions in the THz dielectric response in hydration measurements on lysozyme (17); nuclear vibrational resonance spectroscopy (NRVS) measurements showing a very slight increase in the VDOS for the modes coupled to the heme Fe with oxidation of CytC (18); and the report of a large enhancement in the dielectric response for water immediately adjacent to the protein over that of bulk water (19). This last point is critical in that, if the equilibrium water content is dependent on oxidation state, the THz contrast observed may arise from the different water contributions and not from a density-of-states change. It is therefore important that the comparison between oxidation states be made at equivalent water content.

More importantly, the systematic hydration and oxidation dependence data allows us to test the degree to which structural vibrational modes contribute to the terahertz response of CytC and to determine the origin of the oxidation dependence by comparison with molecular dynamics (MD) simulations. We present two analysis approaches, both using calculated molecular trajectories: harmonic vibrational response based on quasiharmonic analysis; and the full response as determined by the power spectrum of the dipole-dipole correlation function. Quasiharmonic analysis is also referred to as principle component analysis (PCA). Using PCA for the harmonic analysis accounts for changes in the effective force constant at nonzero temperature. In this method, the MD simulation is utilized to obtain effective modes of vibration from the atomic fluctuations about an average structure. These modes include the anharmonic effects neglected in a normal mode calculation (20).

This method introduces temperature-dependent anharmonicity, but still calculates the harmonic vibrational modes of the system as well as the dipole derivative for each mode, which is used to calculate the absorption coefficient. However, quasiharmonic analysis does not capture diffusive motion such as librational motion of side chains and individual rotational motion of solvent molecules. To capture the full dielectric response involving all motions, one must use the complete trajectory calculated from the full potential. The dipole-dipole correlation function is calculated from the MD trajectories and then the Fourier transform of the correlation function reveals the frequency-dependent absorption coefficient. We perform both types of calculations as a function of hydration and oxidation state and compare with the measured results.

We find the measured hydration dependence of the picosecond dynamics for both oxidation states of CytC deviates from the typical rapid increase at 30% wt, and that the VDOS calculated using PCA reproduces the observed hydration dependence. This ability to reproduce the measured hydration dependence with the quasiharmonic modes indicates the presence of collective modes at THz frequencies. However, PCA does not reproduce the observed oxidation or frequency dependence. We find that the calculated dielectric response from the full dipole-dipole correlation function, which includes diffusive motions, does reproduce the oxidation and frequency dependence. We propose that the THz dielectric response is dominated by the anharmonic motions such as surface side-chain rotational motions or possibly motion of an internally bound water molecule.

Materials and Methods

Sample preparation and characterization

Preparation of oxidized and reduced bovine heart CytC films measured in THz time domain spectroscopy is described in a previous study (16). Solutions were pipetted onto clean infrasil quartz substrates with half the substrate left bare for referencing. The films were characterized by ultraviolet visible spectroscopy absorption to verify the oxidation state (see the Supporting Material). The thickness of the dried films is measured to both verify uniformity and to determine absolute absorption coefficients and refractive indices. Film thicknesses were typically of ∼100 μm with thickness variation <5% for a given film. See Whitmire et al. (21) for method of film thickness determination.

Isotherm determination

To compare the picosecond dielectric response of Ferro and Ferri samples at equivalent water content, we measured the isotherms for both oxidation states. The water content for a given relative humidity often follows the B.E.T. thermal equation (22),

$$h\left(x\right)=\frac{a{h}_{m}x}{\left(1+x\right)\left[1+\left(a-1\right)x\right]},$$ (3)

where h(x) is the water content as % wt, that is, g water/100 g protein; a is a parameter representing the potential water absorption capacity of the protein; h_m is a parameter representing the humidity for monolayer of water; and x is the relative pressure of the gas, namely, the relative humidity. See the Supporting Material for method and results.

THz TDS

An N₂ purged terahertz time domain spectroscopy system (THz TDS) with bandwidth 5 cm⁻¹–86 cm⁻¹ is used to monitor the change in absorbance and index with oxidation states of CytC films at different hydration. The THz radiation is generated by a Hertzian dipole antenna and detected electrooptically (23,24). All measurements were performed at room temperature and under hydration control. Substrates are mounted on a brass holder with two apertures for the reference bare substrate and the CytC film. The plate is mounted in a closed hydration cell with the relative humidity controlled by flushing the cell with a hydrated gas from a dewpoint generator (Li-Cor Biosciences, Lincoln, NE). Nitrogen (air) was used as the flushing gas for the Ferro (Ferri) films. The closed hydration cell is placed at the focus of the THz TDS system.

We measure the terahertz dielectric response of both oxidized and reduced CytC films as a function of hydration. The time required for CytC films to reach hydration equilibrium is determined by thermogravimetric analysis and terahertz transmission and both found the time for dehydration was ∼1/2 h and for hydration ∼1 h was the time taken to achieve the final equilibrium value within 1%. To ensure equilibrium hydration, the samples were exposed to a given relative humidity in the hydration cell for at least 1 h for film dehydration and 2 h for film hydration. The vertically mounted substrates limited the highest hydration to below the film's threshold for flowing. For Ferri (Ferro)-CytC films, the highest water content achieved was 75% h (57% h). A transmission measurement consists of toggling between the sample and reference apertures. Absorption due to the gas phase water of the humidity cell is removed by the reference which is in the same humidity cell as the sample. The real part of the refractive index and the absorption coefficient are extracted from the terahertz transmission data in the standard way (25).

Molecular dynamics calculations

We used Version 32 of CHARMM (26) with all-atom parameter set 22 (27). The x-ray structure file 1hrc.pdb was used as the starting structure. Heme group partial charges for Ferro and Ferri states are taken from Autenrieth et al. (28). The heme group is patched to CytC though axial ligated bonds, Met⁸⁰ and His¹⁸ and covalent bonds, Cys¹⁴ and Cys¹⁷. Different hydrations are simulated by solvating the protein with a layer of water molecules with thicknesses between 1.5 Å and 7 Å by using the SOAK command in the program Insight II (Accelrys, San Diego, CA). This procedure initially places the water on the exterior of the protein. The structures of the solvated proteins are built in CHARMM using the TIP3 (TIP3p) force field. The energy-minimized structure was then used for MD simulations.

MD simulations were carried out with an integration time step of 0.001 ps. The system was heated to 300 K with a temperature increment of 100 K after each 1000 steps. Temperature equilibration was followed by a constant temperature MD run. Several different trajectories were calculated using random seeds for the initial velocities. Single 1-ns trajectories were run for both oxidation states for each hydration. In addition, for 4% hydration a total of eight 2-ns trajectories were run for each oxidation state, and a total of two 8-ns trajectories were run for each oxidation state. In all cases the first 399.9 ps is treated as the equilibrium run, being followed by subsequent production runs. For all trajectories, we find that very rapidly, within 50 ps, the waters migrate into the protein and over the surface, attaining a distribution resembling structural measurements.

From the production run of the MD simulation, the average structure of each protein was determined separately using the corresponding production run frames and, by superimposing each structure onto the average structure, a quasiharmonic vibrational analysis was performed. This is done by diagonalizing the whole covariance matrix for a given protein. The calculation output includes the eigenvalues (mode frequency), the eigenvectors, and the dipole derivatives for each mode (29).

For mode frequency ν_k , the integrated intensity Γ_k has units of molar absorptivity and is proportional to the absorption coefficient (30). We draw a distinction of Γ_k with the often calculated absorption intensity, A_k. A_k differs from Γ_k by a factor of ν_k and is not directly related to the derivation of the absorption coefficient from Fermi's Golden rule. The double harmonic approximation consists of modes calculated from a harmonic expansion of the potential and an approximation of the dipole moment inner product using the quadratic term in the Taylor expansion of the dipole. The value Γ can be obtained from the dipole derivatives calculated from the quasiharmonic analysis using (31)

$${\Gamma }_k=\frac{N_0{\pi }^2}{3c^2{\varepsilon }_0{\omega }_k}{\left(\frac{\partial p}{\partial Q_k}\right)}^2,$$ (4)

where ɛ₀ is the permittivity of vacuum, and N₀ is the Avogadro number and the magnitude of the dipole derivative.

The net calculated absorption coefficient is proportional to the sum of Lorentzian oscillators with relaxation rates γ such that we define our quasiharmonic calculated absorption coefficient as

$${\alpha }_{QH}\left(\omega \right)=\sum _k\frac{1}{\pi }\frac{{\Gamma }_k{\gamma }^2}{{\left(\omega -{\omega }_k\right)}^2+{\gamma }^2},$$ (5)

where γ is set to 4 cm⁻¹ in agreement with the full width at half-maximum observed for THz vibrational resonances for molecular crystals (32).

The absorption coefficient per unit length α(ω) and the refractive index n(ω) are related to the imaginary part of the dielectric constant ɛ″(ω) by α(ω)n(ω) = (ω/c) ɛ″(ω). Within linear-response theory, α(ω) n(ω) is given by the power spectrum of the time-correlation function of the total dipole operator (33),

$$\alpha \left(\omega \right)n\left(\omega \right)=\frac{2\pi {\omega }^2\beta }{3cV}\underset{-\infty }{\overset{\infty }{\int }}dt{e}^{-i\omega t}\langle M\left(0\right)M\left(t\right)\rangle ,$$ (6)

where M is the total dipole moment of the system, V is the volume of the system, and β = (k_BT)⁻¹ is the inverse temperature. We calculate the time dependence of the total dipole moment M(t) for the trajectory assuming constant partial charges for all atoms during the entire trajectory.

Results

In Fig. 1, we show the measured frequency dependence of the THz absorption coefficient α. The THz absorption of the Ferri-CytC and Ferro-CytC films increases monotonically with frequency. There are no distinct resonances observed in α; however, there is an obvious increase with oxidation. The refractive index of CytC films is nearly frequency-independent up to 85 cm⁻¹ and also has a large increase with oxidation (n_ferro = 1.65 to n_ferri = 1.80 for 3% hydration).

Figure 1.

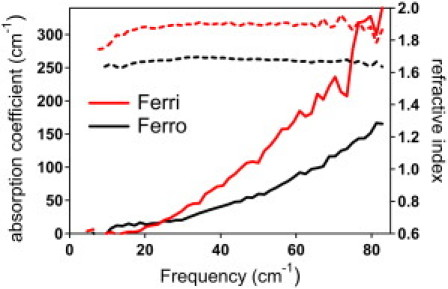
Frequency dependence of THz absorption coefficient (solid lines, left axis) and refractive index (dashed lines, right axis). The THz absorption coefficient and index are shown for a Ferri-CytC film (red) and a Ferro-CytC (black) film at 4% hydration.

We compare the absorption coefficients of Ferri-CytC and Ferro-CytC films as a function of water content in Fig. 2. At low frequencies the absorption coefficient appears to increase linearly with hydration. However, at higher frequencies, the absorption coefficient rapidly increases with hydration with the rate of increase abruptly decreasing at a crossover point ∼20–25% hydration. This crossover behavior from a rapid increase with hydration to a saturation behavior for both oxidation states is readily apparent in the refractive index data in Fig. 3.

Figure 2.

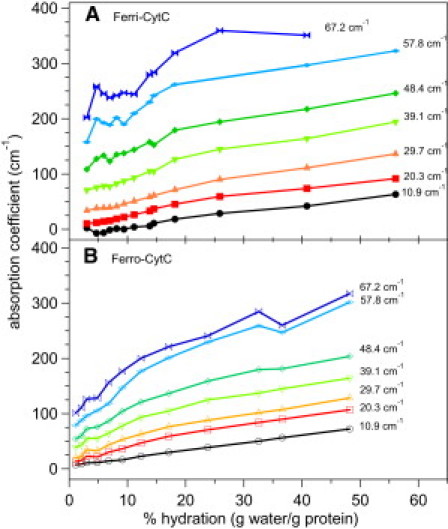
Hydration dependence of THz absorption coefficients. THz absorption coefficients of Ferri (A) and Ferro (B) CytC are shown for several representative frequencies as a function of % hydration. The data shows a rapid increase and then saturation of the response with increasing hydration.

Figure 3.

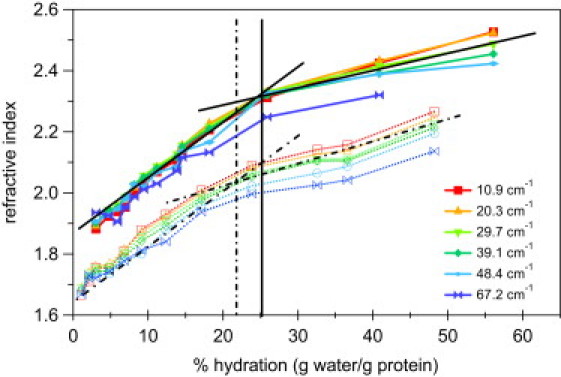
Hydration dependence of THz refractive indices. Refractive indices of Ferri (solid lines and symbols) and Ferro (dashed lines and open symbols) CytC are shown for several representative frequencies as a function of % hydration. Lines are drawn as guide to the eye showing an apparent saturation point at 20–25 wt % hydration. The rapid turnover of the hydration dependence is nearly frequency-independent in contrast to the absorption coefficients shown in Fig. 2.

Comparing the response at equivalent water content in Figs. 2 and 3, an obvious oxidation dependence of the picosecond response, as was reported earlier, is observed (16). The dependence is most dramatic for the refractive index measurements, where the Ferri state values are consistently larger for all hydrations and frequencies. Although the absorption coefficient does increase in the Ferri state at higher frequencies and lower hydrations, this contrast decreases with increasing hydration and at lower frequencies.

We compare the measured response to the calculated response for only collective modes and for the full response including local relaxational motions. In addition to the PCA calculations presented here, we performed the simpler normal mode analysis where the force constants are extracted from the curvature of the potential at the minimized energy. We found little agreement between the calculated normal modes and the measured frequency-, hydration-, or oxidation-dependence, indicating that normal mode analysis is inadequate for accurately describing the dynamics at room temperature.

We first examine the frequency and oxidation dependence calculated using PCA. The VDOS and absorptivity for oxidized and reduced CytC are shown in Fig. 4. At 4% hydration, the VDOS increases with frequency, reaching a peak at ∼30 cm⁻¹, and then decreases. As the hydration increases, the number of quasiharmonic modes for oxidized and reduced CytC also increases and the peak in the VDOS red-shifts. This frequency dependence does not resemble the measured dielectric response seen in Fig. 1. Similarly there is no apparent oxidation dependence in the VDOS. The absorptivity is calculated from the dipole derivative of the mode. It is assumed that the partial charges of the individual atoms remain constant as the atoms move along the eigenvector, which is a problematic but common assumption. Again, neither the frequency nor oxidation dependence of the calculated absorptivity from the collective modes resembles the measured response.

Figure 4.

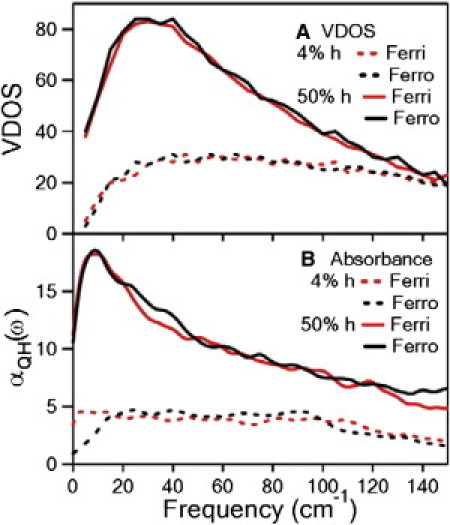
Frequency dependence of the calculated collective modes for Ferri (red) and Ferro (black) CytC for two different hydrations 4 wt % h (dashed lines) and 50 wt % h (solid lines). (A) The quasiharmonic VDOS and (B) the quasiharmonic absorbance α_QH(ω). Neither the oxidation dependence nor the frequency dependence agree with the data shown in Fig. 1.

Figs. 5 (Ferri) and 6 (Ferro) show a comparison of the hydration dependence of the measured absorption coefficient, the calculated VDOS, and the calculated absorption coefficient for several representative frequencies for the two oxidation states of CytC. The observed hydration dependence for CytC departs from the expected hydration dependence of protein dielectric response, as characterized over a broad frequency range up to 10 GHz 40 years ago (34). There, for lysozyme, the dielectric response increases slightly with hydration up to 30% hydration, then increases rapidly above this hydration. The rapid increase at 30% hydration is associated with anharmonic motions accessible with the increased plasticity with hydration (35–38). This departure from the expected hydration dependence of CytC response provides a test for the MD simulations. We see in Figs. 5 and 6 the collective mode VDOS reproduces the hydration dependence well for both oxidation states and over the entire frequency range.

Figure 5.

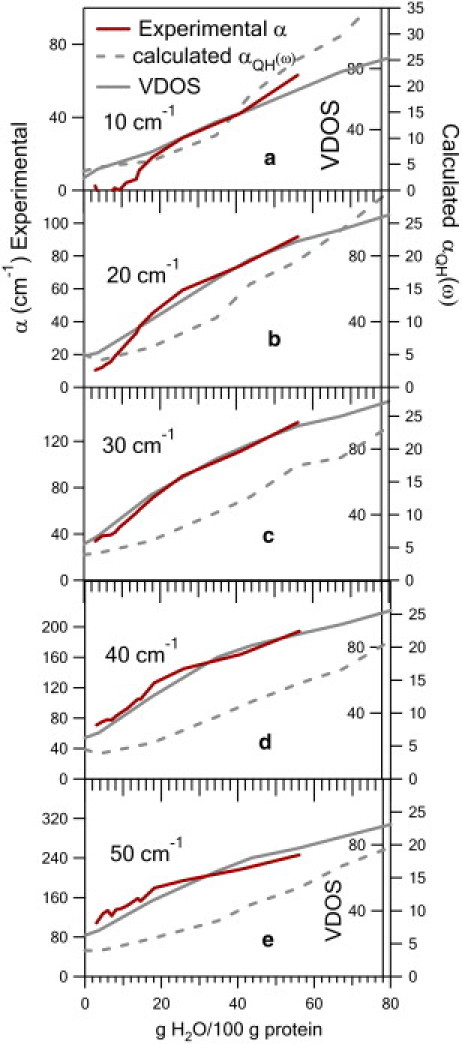
Comparison of the calculated collective modes to the measured hydration dependence for Ferri-CytC. The measured absorption coefficient, calculated quasiharmonic VDOS, and calculated absorbance α_QH(ω) are shown as a function of hydration for several representative frequencies. The calculated VDOS has good agreement with the measured hydration dependence, suggesting the hydration dependence arises from these motions.

Figure 6.

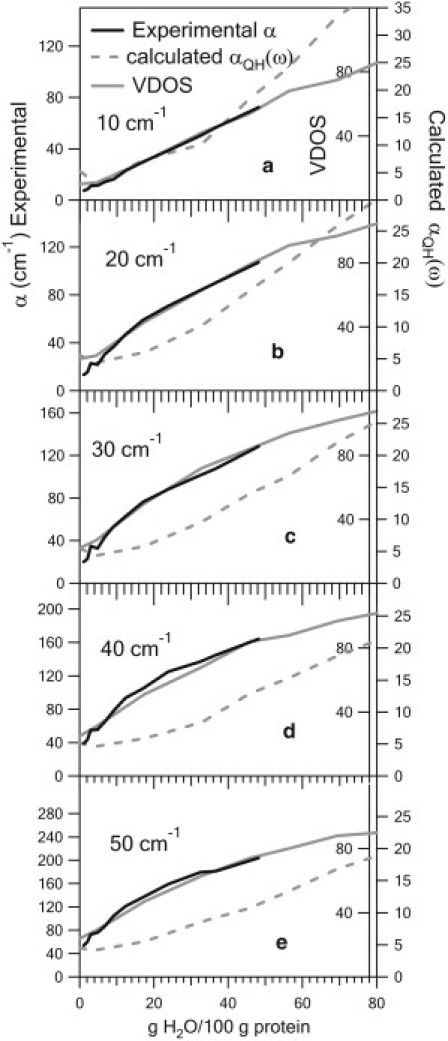
Comparison of the calculated collective mode to the measured hydration dependence for Ferro-CytC. The measured absorption coefficient, calculated quasiharmonic VDOS, and calculated absorbance α_QH(ω) are shown as a function of hydration for several representative frequencies. The calculated VDOS agrees well with the experimental results similar to the Ferri results in Fig. 4. The agreement suggests the hydration dependence arises from these motions.

This agreement suggests 1), the presence of structural vibrational modes contributing to the dielectric signal, and that 2), these modes are responsible for the observed hydration dependence. The hydration dependence of the calculated absorption coefficient does not reproduce the measurements as well. It is possible that this is in part due to the assumption of constant partial charges in the dipole derivative calculations.

It is clear that the collective modes do not give rise to the oxidation sensitivity of the THz response. The PCA calculations for this frequency range account for only extended oscillatory motions. The Fourier transform of the dipole-dipole correlation gives the product of the frequency-dependent absorption coefficient and the refractive index, α(ω)n(ω), which includes all motions contributing to the response, including local relaxational motions of water and surface side chains. As shown earlier, the measured refractive index has little frequency dependence, so we directly compare the calculated α(ω)n(ω) with the measured α(ω).

In Fig. 7 we show the frequency dependence for α(ω)n(ω) at several hydrations. The frequency dependence now resembles the measured absorption coefficient and we see that at low hydration there is a strong contrast between oxidized and reduced cytochrome c. As the hydration increases, this difference decreases. At the highest hydration levels one cannot distinguish between the two oxidation states. To examine the hydration dependence, only short 1-ns runs were performed; however, there was variation in the dipole-dipole correlation for the 1-ns runs and the hydration dependence was inconsistent. To determine whether the oxidation dependence shown is robust, we ran eight 2-ns and two 8-ns trajectories for each oxidation state, both hydrated to 4% h. Each run randomized initial velocities. These results reproduce the larger α(ω)n(ω) for Ferri-CytC, consistent with the results shown in Fig. 7 (see the Supporting Material). A more extensive multiple trajectory study as a function of hydration is, as of this writing, underway.

Figure 7.

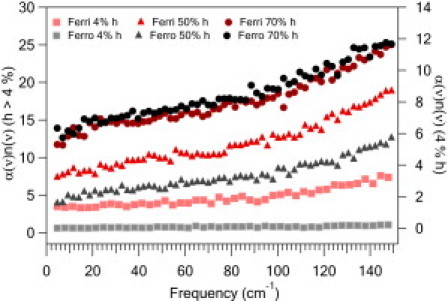
Frequency-dependent α(ω)n(ω) calculated from dipole-dipole correlation for oxidized and reduced CytC for several hydration levels. (Right axis) h < 4%. (Left axis) Hydration >4%. The 70% hydration data are offset by the same five units to avoid overlap with the lower hydration data. At low hydration the Ferro-CytC response is less than the Ferri-CytC. As the hydration increases, the difference with oxidation decreases. The calculated response includes both local diffusive motions and long-range collective motions.

Discussion

The hydration-dependent collective mode calculations indicate their contribution to the dielectric response. As seen in Fig. 4, the collective modes do not reproduce the frequency and oxidation dependencies. Although the modes at increasingly higher frequencies are progressively more localized, the motions even up to 300 cm⁻¹ are extended beyond individual residues (see the Supporting Material). The quasiharmonic VDOS never captures the low frequency diffusive motions of surface side chains. The residence times for these librational motions were calculated with typical times ∼2–10 ps (39). These motions have been discussed by Roh et al. (40) when analyzing the anharmonicity in the neutron temperature dependence and will be present in the calculated full trajectory. That the observed oxidation state dependence is not reproduced by any of the harmonic analysis, but is reproduced by the dipole-dipole correlation, indicates that the oxidation dependence arises from relaxational motions.

We suggest that the internal bound water dynamics are influenced by the local electrostatics and it is these motions that give rise to the oxidation dependence seen in the THz response. We find that the msd of waters within 7 Å of the heme are consistently higher for Ferri-CytC than Ferro-CytC for the hydrations studied. At low hydrations these few internally bound waters provide a large contribution to the overall signal, and therefore an oxidation dependence is observed. At higher hydrations the surface water, mobile surface side chains, and the correlated motions begin to dominate the signal, and the internal water has little net contribution, so the oxidation dependence is no longer significant at the higher hydrations.

We note the contrast seen in the THz measurements is not seen by another important protein dynamics characterization technique—nuclear resonant vibrational spectroscopy (NRVS) (41). An extensive NRVS study found only a very slight increase with oxidation for CytC (18,42). Accompanying this, msd simulations for the heme group and backbone had no discernible oxidation dependence. These calculations did not include the diffusive water or side-chain motion. The oxidation dependence arising from internal water diffusive motion could explain why little oxidation dependence is seen by NRVS, as there the samples were fully hydrated and the motions observed are vibrational modes coupled to the heme Fe.

Conclusions

Terahertz spectroscopy is sensitive to protein environment and functional state. Structural collective modes as calculated by PCA reproduce the measured hydration dependence of absorption coefficient, demonstrating their contribution to the picosecond response. The oxidation dependence of the picosecond response is only reproduced by analysis of the complete trajectory, demonstrating that it is manifest only in the diffusive motions of either the side chains or the internal water. The evidence of structural collective modes in these smaller molecular weight proteins is consistent with recent results using neutron spin echo measurements on somewhat more massive proteins (6,43). The terahertz spectroscopy approach may provide a critical complementary technique to neutron spin echo for collective modes on shorter timescales.