Abstract
The coordination of cellular behavior is a prerequisite of functionality of tissues and organs. Generally, this coordination occurs by signal transduction, neuronal control, or exchange of messenger molecules. The extent to which metabolic processes are involved in intercellular communication is less understood. Here, we address this question in layers of resting yeast cells and report for the first time the observation of intercellular glycolytic waves. We use a combined experimental and theoretical approach and explain the radial velocity of the waves to arise from the substrate gradient due to local substrate addition. Our results show that metabolic processes introduce an additional level of local intercellular coordination.
Introduction
Unraveling the mechanisms of cell-cell communication is important for the analysis of tissue and organ function, and related biomedical questions. In general, coordination of cellular behavior occurs either top down by signal transduction and neuronal control, or among tissue cells by exchange of messenger molecules. Well-known examples for the latter case are the ubiquitous second messengers Ca2+ and cAMP. Ca2+ coordinates tissue behavior via intercellular waves, e.g., in astrocyte networks and liver (1). cAMP waves synchronize the individual cells of the slime mold Dictyostelium discoideum (2,3), and give an example of how populations of unicellular organisms can be used to study aspects of the intercellular coordination.
Communication between cells via the exchange of metabolites, introduced as dynamic quorum sensing, was shown in stirred yeast cell suspensions (4). In this system, glycolytic oscillations have been observed. Glycolysis converts glucose to pyruvate and is occurring in nearly all organisms and cells. The oscillatory dynamics is known to result from feedback regulation of the phosphofructokinase reaction (5). It has been shown that, in stirred cell suspensions, glycolytic oscillations synchronize due to exchange of molecules between the individual cells with acetaldehyde being an important mediator of this process (6,7). Stirring of cell suspensions increases the global coupling of cells. It is an open question whether the coupling of cells without stirring would be sufficient for synchronization. This is intriguing because glycolytic oscillations have not only been observed in yeast, but also in cell types that are naturally arranged in tissues and organs, e.g., heart cells and pancreatic β-cells (8,9). We here address this question using a layer of resting yeast cells.
Materials and Methods
Experiments were performed with aerobically grown yeast cells from Saccharomyces carlsbergensis (ATCC 9080; American Type Culture Collection, Manassas, VA) cultivated aerobically in a rotary shaker (180 rpm) in liquid semisynthetic minimal medium (10) at 28°C. The cells were grown until the glucose in the medium was just exhausted at the transition from the logarithmic to the stationary growth phase. After harvesting the cells by centrifugation at 5000 × g at 21°C and washing them with distilled water, the cells were suspended in 0.1 M KH2PO4 buffer, pH 6.5, as a 20% suspension (weight/volume) and stirred at 23°C until the cells started to oscillate in NADH. This generally occurred after 3–5 h of starvation.
The dynamics of the cells is monitored by the changes in fluorescence of NADH, which serves as an indicator for the concentration changes in the extracellular acetaldehyde, because the oscillations of these two compounds exhibit a fixed phase relation (6). For the detection of waves, the yeast cells were diluted with phosphate buffer to a 10% suspension. A quantity of 1.9 ml of this suspension was transferred into a small glass petri dish of 40-mm diameter, yielding an ∼1.5-mm-thick liquid layer. The cells in suspension were monodisperse. The reactor was placed in the light beam of a two-dimensional spectrophotometer. The waves were initiated by local injection of 15 μl 1 M glucose solution into the suspension at two opposite sites in the yeast cell layer. The wave initiation occurred at latest 5 min after the transfer of the cell suspension into the petri dish. Subsequently, the petri dish was covered with a 0.17-mm-thick cover glass to avoid evaporation-induced convection. During the short duration of the experiments (∼20 min), no significant sedimentation of the cells was observed.
To test whether the cell suspensions are indeed active and show glycolytic oscillations, control experiments were performed and the temporal glycolytic dynamics were measured. This was done by monitoring the NADH-fluorescence of a stirred 10% yeast cell suspension in a fluorimeter.
The spatiotemporal dynamics of the glycolysis in yeast cells was monitored by a two-dimensional spectrophotometer. White light from a xenon lamp (Laser 2000, Munich, Germany) was shone through a UG-11 broadband filter (centered at ∼340 nm) and reflected by a dichroic mirror (LINOS Photonics, Munich, Germany) onto a petri dish containing the yeast cell suspension. Fluorescence light from NADH (at 460 nm) in the cell suspension passed through the dichroic mirror to an image-intensified, charge-coupled device camera (Corail; Optronis, Kehl, Germany). Any contribution from the reflecting excitation light was blocked by a 440-nm long-pass filter mounted directly in front of the camera objective. The recorded images thus show the spatial distribution of the fluorescence collected over the entire thickness of the cell suspension. The images were collected at a resolution of 38.5 μm pix–1 and a sampling rate of 2 Hz, digitized and stored on a computer for subsequent analysis. Details of the setup are summarized in Bagyan et al. (11).
The contrast of the acquired images was further enhanced by background subtraction, where the background was calculated as the temporal average of all images. Subsequently, the images were subjected to a histogram stretching, thus enhancing the contrast by making use of the full scope of the gray value scale. The image processing protocol aims at yielding a substantial enhancement of the contrasts of the image, thus enabling the detection of the dynamic structures, i.e., the NADH waves in the cell suspension.
Experimental Results
In the control experiments with stirred cell suspensions, the addition of glucose induces glycolytic oscillations in the cell population (Fig. 1 D). Here the synchronization is facilitated by mixing of the external medium, which enables a fast exchange of intermediates between the cells. In the absence of mixing, cells synchronize by local diffusion. Due to this interaction, the state of the oscillation travels across the cell layer. In fact, the local injection of glucose into the yeast cell suspension at two opposite sites leads to the formation of traveling circular waves which annihilate upon head-on collision (Fig. 1, A–C), a typical behavior of reaction-diffusion waves (12).
Figure 1.
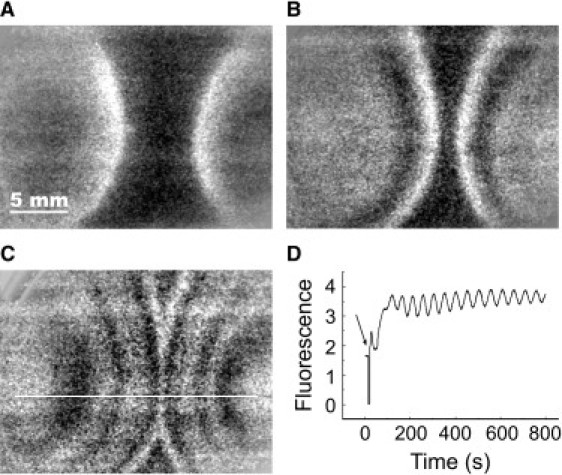
Repetitive traveling waves in an oscillating yeast cell suspension. (A–C) Snapshots of two traveling waves which are induced outside the field of view. The time interval is 152 s between panels A and B, and 200 s between panels B and C. (D) Oscillatory dynamics of yeast cells in a stirred solution. (Arrow) Addition of glucose.
Waves appear repetitively with a constant period (Fig. 2 A). The velocity at the origin of waves is ∼96 μm/s for the first and 87 μm/s for subsequent waves, respectively (see dotted and dashed white lines in Fig. 2 A). Thus, the initial wave velocity remains nearly constant for all waves. However, it is markedly reduced down to 12 μm/s for the first and 16 μm/s for subsequent waves when the waves approach each other (see dotted and dashed black lines in Fig. 2 A). The repetitiveness of wave formation is only observed when the yeast cells are oscillatory. In contrast, nonoscillating cells exhibit only an initial transient in NADH with no subsequent wave generation (Fig. 2 C). This initial NADH transient propagates as a single wave with a velocity of 78 μm/s through the cell layer (white dashed line). Again, in this case we find mutual annihilation of the NADH-transients together with a reduction of the wave velocity down to 25 μm/s (black dashed line).
Figure 2.
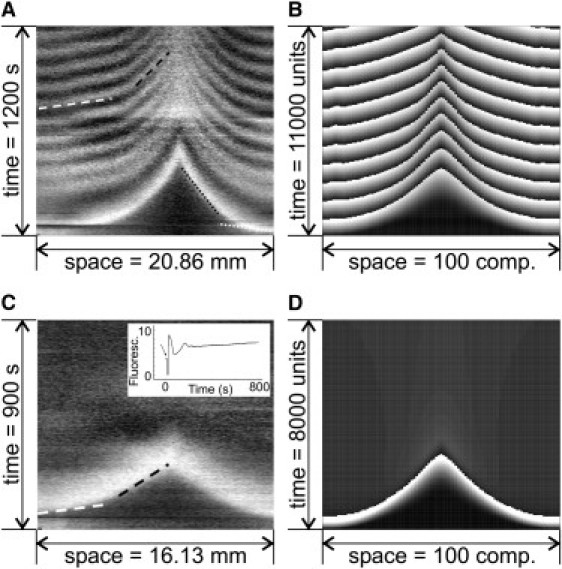
Dynamics of the cell layer in experiment (A and C) and simulation (B and D). (A) The time-space plot is constructed along the horizontal line in Fig. 1C. (C) Time-space plot of the measured NADH-fluorescence in nonoscillating yeast cell layers. (Inset) NADH-fluorescence in a stirred cell solution. (B and D) Simulated time-space plots corresponding to panels A and C. Shown are variables Xi in a part of the two-dimensional array. Parameters: Jmax = 8 × 10−3, KM = 3, αmain = 3 × 10−4, n = 2, κ = 0.13, ϕ = 0.1, dX = 0.05, dY = 0.002; (B) k2 = 0.15, and (D) k2 = 0.05. Substrate is applied to the system via an initial extracellular substrate concentration at two compartments each with Xex(t0) = 187,210.
Mathematical Model
Our mathematical analysis is based on a model that was recently suggested for the study of glycolysis in cell layers (13). It considers a two-dimensional array divided into N compartments. Each compartment contains one cell embedded in extracellular medium. The dynamics of each cell is described by a two-variable model, which is derived from core models of glycolysis. Such core models have also been used as a starting point for the analysis of synchronization phenomena in populations of stirred cells (14,15). The two variables lump intermediates of the upper and the lower part of glycolysis, respectively. The substrate glucose is actively transported into the cell and subsequently transformed so that it does not diffuse out of the cell. Several products of glycolysis, in particular acetaldehyde, can cross the membrane and, therefore, can be exchanged between cells.
In our model, the variable X represents the substrate, which is supplied to the extracellular medium and transported into the cell. The variable Y is the product in the system, which can cross the membrane. Therefore, the dynamics of an array of N compartments is given by the system of equations
| (1a) |
| (1b) |
| (1c) |
| (1d) |
where i = 1, …, N. Here, we use a rescaled version of the model given in Schütze and Wolf (13) that was derived by scaling all concentrations by a factor 1/K and the time by the factor k1
By rescaling the kinetic parameters
the kinetic parameters K and k1 are eliminated and all variables, kinetic parameters, and the time of equation system (1a–1d) are dimensionless.
Xi and Yi denote the concentrations of the cellular compounds X and Y, and Xiex and Yiex denote the corresponding concentrations in the extracellular medium of the compartment i, respectively. Central to the cellular system is an autocatalytic reaction transforming the substrate X into the product Y (last term in Eq. 1b and first term in Eq. 1c). The product Y can be converted into downstream metabolites (second term in Eq. 1c) or exchanged across the cell membrane (last term in Eq. 1c and first term in Eq. 1d). The compound X enters the cell via an active transport across the cell membrane (second term in Eq. 1a and first term in Eq. 1b). Extracellular substrate and product can diffuse between adjacent compartments (last terms in Eqs. 1a and 1d). Each compartment may receive an influx of the substrate X from the surroundings (first term in Eq. 1a). In the case of an initial substrate pulse, we set Jiin = 0 and apply the substrate via the initial extracellular substrate concentration. All processes are assumed to be unidirectional except for the transmembrane exchange of Y and the diffusion between compartments.
Yeast cells can be assumed to be largely similar but show a limited cell variability. To represent this in the model, the compartments are assumed to be identical in their kinetic parameters except for α. For this parameter, we use randomly distributed values in an interval ±10% around a main value. Consequently, the cells of the array slightly differ in their oscillation characteristics, e.g., frequency. For the exchange of metabolites between the cells and their compartments as well as between neighbored extracellular compartments, the kinetic parameters dX, dY, ϕ, and κ play important roles. The parameters dX and dY for diffusion between two neighbored extracellular compartments i and j are related to the diffusion coefficients DX and DY as
where L gives the size of the compartments. The parameter ϕ denotes the ratio of cellular and extracellular volume; κ is related to the membrane permeability, cell surface, and cell volume. For more details of the model and an analysis of its dynamics behavior, see Schütze and Wolf (13).
Modeling Results and Discussion
The model of the one-compartment system (i.e., the expressions in Eq. 1 for N = 1) may show stationary or oscillatory dynamic behavior depending on the kinetic parameters. Fig. 3 shows a bifurcation diagram in the (Jin, k2) parameter plane for that case. The region for the occurrence of limit cycles is marked in shading, indicating the existence of critical levels of the substrate injection flux and the degradation parameter for oscillations to arise.
Figure 3.
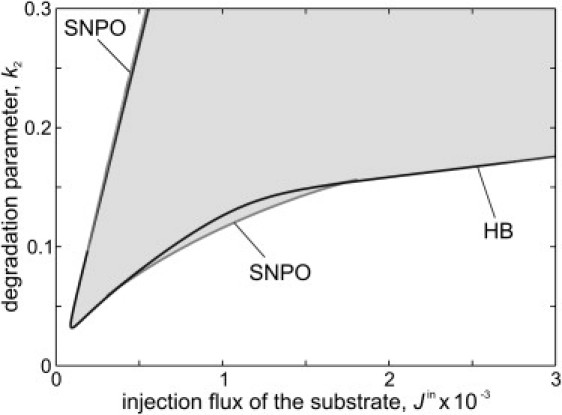
Bifurcation analysis of a one-compartment model (N = 1) in dependence on the substrate injection Jin and the degradation parameter k2. (Shaded) Region of the occurrence of oscillations. (Solid lines) Hopf bifurcations (HB). (Shaded lines) Saddle-node bifurcations of periodic orbits (SNPO). Parameters: Jmax = 8 × 10−3, KM = 3, αmain = 3 × 10−4, n = 2, κ = 0.13, and ϕ = 0.1.
For the simulation of the cell layer, we consider an array of 193 × 97 compartments. We first analyze the model for parameters that allow cellular oscillations for appropriate levels of external glucose, in particular k2 = 0.15 (see Fig. 3). The initial concentrations within all compartments are set to values close to zero. At time t = 0, the substrate X is added to the extracellular medium at the centers of the two halves of the array. Under these conditions, the propagation of circular wave fronts can be observed (see Fig. 2 B). The waves originate from the compartments with substrate addition. This can be explained by the fact that a local injection of substrate results in a transient substrate gradient and that cells supplied with high substrate concentration act as pacemaker of the wave fronts. Corresponding to the experimental observation, the model shows an annihilation of waves when they collide (see center of array).
To set the cells of the model mostly in a nonoscillatory state, we decrease the reaction parameter k2. For k2 = 0.05, most values for the substrate injection flux Jin do not allow oscillations, but instead a stable steady state in the corresponding cells (see Fig. 3). In that case, a stimulus initiates a single wave front only (see Fig. 2 D). No repetitive wave fronts are formed corresponding to the experimental observation in Fig. 2 C. We conclude that the formation of repetitive glycolytic waves requires yeast cells in an oscillatory state.
For both oscillating and nonoscillating cells, the propagation velocity of waves decreases with increasing distance from the wave sources in simulations as well as in experiments. The underlying reason for that observation is analyzed in the mathematical model. To determine the dependence of the wave propagation velocity as a function of the extracellular substrate concentration, we use a simulation in a one-dimensional chain of cells under constant substrate supply (see Fig. 4 A). Waves are initiated by an additional glucose feeding at one side of the chain. Fig. 4 A shows the dependence of the wave velocity on the extracellular substrate concentration obtained that way. Fig. 4, B and C, analyzes the relation for those compartments of the two-dimensional cell layer, which are represented in the time-space plot in Fig. 2 B. When the first waves collide, the substrate gradient is steep, resulting in a velocity ratio of 3 between the locations of wave source and wave annihilation (see dashed lines in Fig. 4, B and C). At a later time-point, the substrate gradient is reduced (depicted by the solid line in Fig. 4 B). Accordingly, the difference of the propagation velocity is less pronounced (see solid line in Fig. 4 C). This is in qualitative agreement with the experimental observation. However, a quantitative comparison shows the velocity ratio between the locations of wave source and wave annihilation to be lower than in the experiments. This discrepancy is mainly a size effect. While in experiments the diameter of interest is ∼20 mm, our simulations cover 2 mm only. Because the wave velocity decreases with the distance, smaller systems have lower velocity ratios than larger ones. Discrepancies may also arise from the fact that we use a simplified core model of glycolysis. Taken together, Fig. 4 demonstrates that the decreasing propagation velocity of the waves in the array results from substrate depletion.
Figure 4.
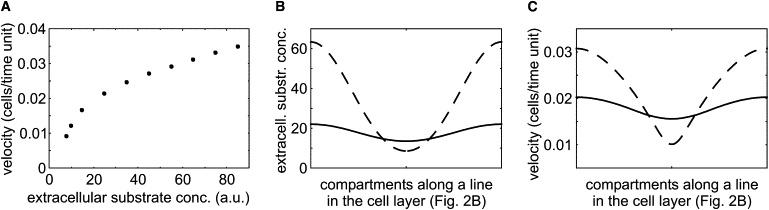
Dependence of the wave propagation velocity on the extracellular substrate concentration. (A) Wave velocity in a one-dimensional chain of cells. Parameters as in Fig. 2B, except α = 3 × 10−4 and dX = 0. (B) Extracellular substrate concentration in the line of compartments within the cell layer that are analyzed in Fig. 2B. Results are given for the first collision of wave fronts, t = 3500 units (dashed line) and the end time in Fig. 2B, t = 11,000 (solid line). (C) Wave velocity in the case of a chain corresponding to the extracellular substrate concentration in Fig. 4B.
Conclusions
In summary, we here report, to the best of our knowledge for the first time, metabolic waves in yeast cell layers. By using a combined experimental and theoretical approach, we can explain the radial velocity profile of the waves to arise from the substrate gradient due to local substrate addition. So far, glycolytic waves have been observed only in cell-free yeast extracts (e.g., (11,16)) and in a quasi-one-dimensional arrangement (17). The metabolic waves shown here demonstrate that the information about the intracellular metabolic state is not restricted to a cell, but can be fast and efficiently transmitted to neighboring cells.
Our findings imply that metabolic processes play an important role in the local intercellular communication and introduce an additional level of coordination supplementing known signaling processes. As shown in Fig. 2, C and D, this interaction does not require oscillatory dynamics. Our results prove that metabolic coupling of cells can act on the timescale of minutes. Therefore, it might be also important for slower cellular processes and rhythms, e.g., respiratory oscillations in continuous yeast culture (18,19). It remains an open question to which extent metabolic coupling contributes to the cellular communication in tissues. In that respect, it is interesting to note that glycolytic processes are discussed to be involved in regulation of insulin secretion in pancreatic β-cells and the synchronization of these cells (20).
In addition to the potential of information transfer, metabolic waves also offer new tools for experimental interventions on information processing in living cells—inasmuch as their dynamics can be controlled by external parameters, e.g., temperature (21).
Acknowledgments
J.S. is funded by the International Research Training Group “Genomics and Systems Biology of Molecular Networks” supported by the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG). T.M. and M.J.B.H. acknowledge financial support of the experimental work by the DFG. J.W. is supported by the FORSYS-program of the German Ministry of Education and Research. (Bundesministerium für Bildung und Forschung, BMBF)
Footnotes
We dedicate this article to Dr. Thomas Mair, who sadly passed away during the submission of the manuscript.
References
- 1.Falcke M. Reading the patterns in living cells—the physics of Ca2+ signaling. Adv. Phys. 2004;53:255–440. [Google Scholar]
- 2.Gerisch G. Periodic signals control pattern forming in cell associations. Naturwissenschaften. 1971;58:430–438. doi: 10.1007/BF00624616. [DOI] [PubMed] [Google Scholar]
- 3.Hilgardt C., Cejková J., Sevcíková H. Streamless aggregation of Dictyostelium in the presence of isopropylidenadenosin. Biophys. Chem. 2008;132:9–17. doi: 10.1016/j.bpc.2007.09.013. [DOI] [PubMed] [Google Scholar]
- 4.De Monte S., d'Ovidio F., Sørensen P.G. Dynamical quorum sensing: population density encoded in cellular dynamics. Proc. Natl. Acad. Sci. USA. 2007;104:18377–18381. doi: 10.1073/pnas.0706089104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Goldbeter A. University Press; Cambridge, UK: 1996. Biochemical Oscillations and Cellular Rhythms. [Google Scholar]
- 6.Richard P., Bakker B.M., Westerhoff H.V. Acetaldehyde mediates the synchronization of sustained glycolytic oscillations in populations of yeast cells. Eur. J. Biochem. 1996;235:238–241. doi: 10.1111/j.1432-1033.1996.00238.x. [DOI] [PubMed] [Google Scholar]
- 7.Poulsen A.K., Lauritsen F.R., Olsen L.F. Sustained glycolytic oscillations—no need for cyanide. FEMS Microbiol. Lett. 2004;236:261–266. doi: 10.1016/j.femsle.2004.05.044. [DOI] [PubMed] [Google Scholar]
- 8.Yang J.-H., Yang L., Weiss J.N. Glycolytic oscillations in isolated rabbit ventricular myocytes. J. Biol. Chem. 2008;283:36321–36327. doi: 10.1074/jbc.M804794200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chou H.-F., Berman N., Ipp E. Oscillations of lactate released from islets of Langerhans: evidence for oscillatory glycolysis in β-cells. Am. J. Physiol. 1992;262:E800–E805. doi: 10.1152/ajpendo.1992.262.6.E800. [DOI] [PubMed] [Google Scholar]
- 10.Hess B., Boiteux A. Mechanism of glycolytic oscillation in yeast. I. Aerobic and anaerobic growth conditions for obtaining glycolytic oscillation. Hoppe Seylers Z. Physiol. Chem. 1968;349:1567–1574. doi: 10.1515/bchm2.1968.349.2.1567. [DOI] [PubMed] [Google Scholar]
- 11.Bagyan S., Mair T., Müller S.C. Glycolytic oscillations and waves in an open spatial reactor: impact of feedback regulation of phosphofructokinase. Biophys. Chem. 2005;116:67–76. doi: 10.1016/j.bpc.2005.02.002. [DOI] [PubMed] [Google Scholar]
- 12.Mikhailov A.S., Showalter K. Control of waves, patterns and turbulence in chemical systems. Phys. Rep. 2006;425:79–194. [Google Scholar]
- 13.Schütze J., Wolf J. Spatio-temporal dynamics of glycolysis in cell layers. A mathematical model. Biosystems. 2010;99:104–108. doi: 10.1016/j.biosystems.2009.10.002. [DOI] [PubMed] [Google Scholar]
- 14.Wolf J., Heinrich R. Dynamics of two-component biochemical systems in interacting cells; synchronization and desynchronization of oscillations and multiple steady states. Biosystems. 1997;43:1–24. doi: 10.1016/s0303-2647(97)01688-2. [DOI] [PubMed] [Google Scholar]
- 15.Bier M., Bakker B.M., Westerhoff H.V. How yeast cells synchronize their glycolytic oscillations: a perturbation analytic treatment. Biophys. J. 2000;78:1087–1093. doi: 10.1016/S0006-3495(00)76667-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Mair T., Müller S.C. Traveling NADH and proton waves during oscillatory glycolysis in vitro. J. Biol. Chem. 1996;271:627–630. doi: 10.1074/jbc.271.2.627. [DOI] [PubMed] [Google Scholar]
- 17.Jacobsen H., Busse H.G., Havsteen B. Spontaneous spatio-temporal organization in yeast cell suspension. J. Cell Sci. 1980;43:367–377. doi: 10.1242/jcs.43.1.367. [DOI] [PubMed] [Google Scholar]
- 18.Murray D.B., Beckmann M., Kitano H. Regulation of yeast oscillatory dynamics. Proc. Natl. Acad. Sci. USA. 2007;104:2241–2246. doi: 10.1073/pnas.0606677104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tu B.P., Kudlicki A., McKnight S.L. Logic of the yeast metabolic cycle: temporal compartmentalization of cellular processes. Science. 2005;310:1152–1158. doi: 10.1126/science.1120499. [DOI] [PubMed] [Google Scholar]
- 20.Bertram R., Sherman A., Satin L.S. Electrical bursting, calcium oscillations, and synchronization of pancreatic islets. Adv. Exp. Med. Biol. 2010;654:261–279. doi: 10.1007/978-90-481-3271-3_12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mair T., Warnke C., Müller S.C. Control of glycolytic oscillations by temperature. Biophys. J. 2005;88:639–646. doi: 10.1529/biophysj.104.043398. [DOI] [PMC free article] [PubMed] [Google Scholar]


