Theoretical Modeling of Aging Effects in Microtubule Dynamics

Abstract

The microtubule (MT) network, an important part of the cytoskeleton, is constantly remodeled by alternating phases of growth and shrinkage of individual filaments. Plus-end tracking proteins (+TIPs) interact with the MT and in many cases alter its dynamics. Although it is established that some +TIPs modify MT dynamics by increasing rescues, the plus-end tracking mechanism is still under debate. We present a model for MT dynamics in which a rescue factor is dynamically added to the filament during growth. As a consequence, the filament shows aging behavior that should be experimentally accessible and thus allow one to exclude some hypothesized models regarding the inclusion of rescue factors at the MT plus end. This result is not limited to +TIPs and can be extended to any kind of mechanism shifting the parameters of dynamic instability. Additionally, we show that the cell geometry has a strong influence on the quantitative results.

Introduction

Microtubules (MTs) are semiflexible polymers that rapidly switch between a polymerizing and a depolymerizing state, a behavior known as dynamic instability (1). This feature of the MT dynamics allows cells to quickly reorganize their MT network to adapt to changes in their environment. The class of MT-associated proteins (MAPs) plays an important role in MT dynamics, and among these the plus-end tracking proteins (+TIPs) have received much attention in recent years (2–6). Typically, two different types of plus-end tracking mechanisms are presented (6): 1), a mechanism that relies on recognition of a structure at the end of the MT; and 2), a mechanism whereby the +TIP is dynamically included in the filament through the addition of new tubulin dimers.

The first experiment to show a correlation between MT dynamics and a +TIP involved the protein CLIP-170 (7). It is known that CLIP-170 must be in a complex with EB1, another +TIP, before it can bind to MTs (8–11). EB1 has been found to bind at high frequency to a binding site that is incorporated into a growing MT and then vanishes a few seconds after addition to the filament (9–12). The fluorescence signatures of +TIPs at MT plus ends are therefore controlled by the existence of the corresponding binding sites. It has been shown for both CLIP-170 and EB1 that their binding to MTs enhances rescues of MTs (13,14). In the absence of these +TIPs, the MTs are much more labile and have shorter lifetimes.

In this work, our goal was to develop a model that allows one to distinguish between a scenario in which the modification of dynamic instability is caused by a rescue factor that effectively copolymerizes with tubulin, or a rescue factor that binds preferentially at the plus end of the MTs. In this context, the term “dynamical inclusion” refers to the rescue factor being introduced because of the dynamics of the filament (i.e., by being built into the MT at growth), and the term “structural recognition” means that the rescue factor is added to or is present at the tip because of its property of being the end of the MT.

The distinction between the two scenarios can be made by the presence or absence of aging effects in the survival probabilities of MTs. This kind of aging has to be distinguished from the observed correlation between age and MT stability under the action of a destabilizing agent such as nocodazole (15). Instead, we refer to aging as a modification of the dynamic instability leading to different behavior of the MT over time. Technically, aging manifests itself by an autocorrelation function that depends on absolute times and not only on time differences. In this case, this can be translated to the time dependence of the filament's properties. For this, we present a stochastic model for MT dynamics whose key ingredients are a consideration of the cell boundary and a dynamical modification of the dynamic instability by means of a binding site to which a rescue-enhancing +TIP can bind at high frequency. We show that dynamical inclusion of such a binding site inevitably leads to aging, whereas structural recognition of the plus-end would not entail any aging effects. In a dynamical inclusion scenario, an MT ages at the cell membrane because no further rescue factors can be added to the tip if the MT is constrained by the finite cell geometry. The probability of being rescued upon depolymerization decreases drastically and the risk of complete depolymerization increases, an effect that we will henceforth refer to as “aging”. Our results thus demonstrate that the molecular mechanism of MT formation is intimately connected with aging.

It is known from a previously presented model by Govindan and Spillman (16) that boundary effects lead to a stationary distribution of MT lengths at a constant and finite value. There are also other scenarios that lead to finite length scales under free conditions (17–19). The influence of a rescue-enhancing mechanism was modeled by Antal et al. (20) for an in vitro scenario in which an unbounded growth of the MTs is considered. In contrast to previous work, we investigate the dynamics of MTs in a finite volume, which is relevant for the in vivo situation and may provide new insights by predicting aging of MTs under dynamic modifications of the dynamic instability.

Model

The basis of our model relies on the phenomenological description of dynamic instability, whose motion in the bulk is usually characterized by four parameters: growth velocity, shortening velocity, rescue (= transition from depolymerization to polymerization) frequency, and catastrophe (= transition from polymerization to depolymerization) frequency (21). Accordingly, the model consists of a linear filament (MT) of individual subunits (tubulin dimers) that is either in the growing or the shrinking state. Depending on its state, a tubulin dimer of length δ is added to or removed from the tip of the filament such that the growth and shortening rates (ν_g and ν_s, respectively) are obtained. Switching of states is stochastic with rescue frequency ν_r and catastrophe frequency ν_c (Fig. 1 A).

Figure 1.

Schematic representation of the model. (A) The filament is built from individual subunits of length δ and can be in either the growing or the shortening state. In the growing state, a subunit is added at a rate ν_g to the plus end of the filament. Depending on the scenario, the added subunit carries a binding site for a rescue-enhancing +TIP or not. Transitions to the shortening state happen with rate ν_c. In this state, the filament loses subunits from its plus end at rate ν_s regardless of the possible existence of a binding site. However, the switching back to the growing state depends on the presence of a binding site for the +TIP on the last subunit at the plus end and may happen with rate ${\tilde{\nu }}_r$ or ν_r depending on the state of the last subunit. At any time, a +TIP binding site disappears from the filament at rate ν_d. Boundary effects enter because reaching the cell boundary stops any growth and thus prevents the addition of binding sites for +TIPs. The distance between the MTOC and the cell boundary determines the length ratios between the +TIP-decorated and -undecorated parts of the MT. (B) The cell is an ellipse with half-axes a and b. From the MTOC, an MT grows in a random direction toward the cell boundary. The distance between the MTOC and the cell boundary in the current growth direction determines the maximum length l^∗ of that MT.

The model cell has a predefined geometry (an ellipse in our case) within which the origin of nucleating MTs (i.e., the MT organizing center (MTOC)) is chosen (Fig. 1 B). An MT grows in a random direction from the MTOC, which determines the maximum distance to the boundary l^∗. The filament follows the bulk dynamics until it reaches the boundary, where switching to the shrinking state is induced with a probability p_ind. This probability describes experimental observations (13) indicating that an MT filament pauses at the boundary, but that these pauses are too short to be caused by the stochastic switching that is characteristic of dynamic instability. An ensemble of such filaments is used to determine the stationary distribution of filament states.

The influence of a rescue factor such as the binding site for a +TIP is included in the model in the following way: A tubulin dimer that is added to the tip of a growing filament leads to the appearance of the binding site as the tubulin ring is complete and closes along the seam (6). +TIPs are then assumed to bind at such high frequency to these binding sites that the filament is considered to possess modified dynamic instability parameters for as long as the binding sites exist. The binding site disappears with rate ν_d as the corresponding part of the MT grows older. After the binding site vanishes, the +TIP can no longer bind. As for the filament dynamics, the presence of the +TIP only affects the rescue frequency, as has been shown in the case of CLIP-170 (13). Thus, if the MT tip is decorated with a binding site, a rescue occurs with frequency ${\tilde{\nu }}_r$ (>ν_r). A formal definition can be found in the Supporting Material.

We compare the results of this model with those from a model in which the binding sites are not dynamically included in the filament, i.e., filament rescues cannot be enhanced by +TIPs. The model does not explicitly take into account a realistic value for the stoichiometry of +TIP association to polymerized tubulin (14), because here we make a qualitative prediction about the aging effects that occur whenever the MT dynamics is altered by a dynamically introduced (i.e., only in the growing phases) rescue factor.

Materials and Methods

Simulation method

For the simulation of this model, a standard Monte Carlo algorithm was implemented. The sum of the rates of all possible moves in the current state was calculated before one of these moves was chosen via tower sampling (22). When the filament depolymerized completely to length zero, the new growth direction was drawn from a uniform distribution, and the resulting maximum filament length was determined and kept constant until the new filament depolymerized again. The cell geometry, including the position of the MTOC, was kept constant throughout the whole simulation.

Distribution of active plus-ends

Active plus-ends were defined as MT ends that were either growing or shrinking, in similarity to the approach of Komarova et al. (13). In our model, pausing filaments can only exist at the cell boundary where MTs have their maximum length if p_ind≠ 1 was chosen. In this case, the filament paused before depolymerizing and, consequently, the boundary site at l^∗ was excluded from the measurements of MT length distributions, because filaments at maximum length would not be identified as being active. All other MT lengths were classed into a histogram with five bins that represented 20% of the maximum length l^∗ each.

Shortening lengths and aging behavior

Shortening lengths were determined as the distance between the site on which catastrophe occurred and the site on which the filament was rescued. If the filament depolymerized completely, the rescue site was taken to be at the origin. The threshold of experimental measurements was 0.18 μm (13), which corresponds to ∼300δ, with a subunit length of δ ≈ 8/13 nm as in Govindan and Spillman (16). Because experimental measurements below this value were not possible, we excluded shortening events of <300 subunits from our statistics. The same applied to the excursions used to determine the aging behavior: If the excursions away from the cell boundary were below the experimentally detectable threshold, the counter for boundary hits was not increased.

Catastrophe and rescue frequency

Whenever an MT switched from growing to shrinking (shrinking to growing), a catastrophe (rescue) event was scored if the event did not take place at one of the boundary sites. The sum was then divided by the total simulated time.

Results

Choice of parameters

The MT dynamics is determined by seven parameters. Approximate values for the four fundamental parameters of dynamic instability (i.e., the growth and shortening rate, catastrophe, and rescue rate in the absence of CLIP-170) can be derived from Komarova et al. (13). Growth and shortening rates are with respect to the addition and removal of a single subunit of length δ, respectively.

The rate at which the +TIP binding site vanishes can be inferred from the observation that fluorescing CLIP-170 or EB1 comet tails usually have lengths of 1–3 μm. Assuming a first-order stochastic process, the average time spent on the MT is thus ∼6 s, which is consistent with previous estimations (9) and the observation that comet tails disappear ∼5 s after MT growth has stopped (23).

The probability of boundary-induced catastrophe p_ind is difficult to determine because few experimental data are available. Nevertheless, experimental trajectories of MTs without CLIP-170 (13) show that MT tips pause at the boundary before undergoing catastrophe. In combination with the growth rate, one obtains the value of p_ind shown in Table 1.

Table 1.

Standard set of parameters derived from experimental data

Parameter	Simulation value
Growth rate νg	600 s−1
Shortening rate νs	1000 s−1
Catastrophe rate νc	0.003 s−1
Rescue rate without CLIP-170 νr	0.024 s−1
CLIP-170 dissociation rate νd	0.15 s−1
Prob. of boundary-induced cat. pind	5 × 10−4

The remaining parameter—rescue frequency in the presence of the binding site ${\tilde{\nu }}_r$—determines the experimentally observed rescue frequency in the presence of CLIP-170. As mentioned above, the true stoichiometry of +TIP association with polymerized tubulin is not considered, such that ${\tilde{\nu }}_r$ is chosen to obtain the correct observed overall rescue frequency under the influence of CLIP-170 of 0.17 s^–1 (13). This leads to values of ${\tilde{\nu }}_r$ that are ∼100 times > ν_r but are still a lower bound for the real value, because it can be assumed that very rapid sequences of catastrophe and rescue were not observable in the experiments even though they were counted in our simulations. Such nanodepolymerization events were previously observed in another MT model (24).

Steady-state solution without +TIPs

Since we are particularly interested in the effects the existence of the binding site has on MTs, we also examine the case in which no binding sites occur if a new tubulin subunit is added to the filament. In this case, the model can easily be solved exactly in a manner similar to the model of Govindan and Spillman (16). The master equations for the steady-state probabilities in the bulk for the filament being in the growing or shortening state with length l that have to be solved are:

$$\begin{array}{c}\frac{\partial p_{+}\left(l,t\right)}{\partial t}={\nu }_g{p}_{+}\left(l-1,t\right)-{\nu }_g{p}_{+}\left(l,t\right)-{\nu }_c{p}_{+}\left(l,t\right)+{\nu }_r{p}_{-}\left(l,t\right)\\ \frac{\partial p_{-}\left(l,t\right)}{\partial t}={\nu }_s{p}_{-}\left(l+1,t\right)-{\nu }_s{p}_{-}\left(l,t\right)+{\nu }_c{p}_{+}\left(l,t\right)-{\nu }_r{p}_{-}\left(l,t\right)\end{array}$$

where p₊(l, t) and p₋(l, t) are the probabilities for the filament to be in the growing or shortening state, respectively, at time t with tip position 1 ≤ l < l^∗ − 1. The complete master equations, including the boundaries, can be found in the Supporting Material.

These equations are only slightly modified compared to those treated in Govindan and Spillman (16). Consequently, solving for the steady-state solution, i.e., setting the derivatives to zero, can be done straightforwardly in the same way. The solution reads:

$$\begin{array}{c}{p}_{+}\left(l\right)=\{\begin{array}{ll}A\times a^l\hfill & \text{for}0\le l<l^{\ast }-1\hfill \\ A\times a^{l^{\ast }-1}\left(\frac{1+\frac{{\nu }_c}{{\nu }_g}}{p_{ind}+\frac{{\nu }_c}{{\nu }_g}}\right)\hfill & \text{for}l=l^{\ast }-1\hfill \\ 0\hfill & \text{for}l=l^{\ast }\hfill \end{array}\\ p_{-}\left(l\right)=\{\begin{array}{ll}0\hfill & \text{for}l=0\hfill \\ A\times \frac{{\nu }_g}{{\nu }_s}{a}^{l-1}\hfill & \text{for}1\le l<l^{\ast }\hfill \\ A\times \frac{{\nu }_g}{{\nu }_s}{a}^{l^{\ast }-1}{p}_{ind}\left(\frac{1+\frac{{\nu }_c}{{\nu }_g}}{p_{ind}+\frac{{\nu }_c}{{\nu }_g}}\right)\hfill & \text{for}l=l^{\ast }\hfill \end{array}\end{array}$$

with

$$a=\frac{1+\frac{{\nu }_r}{{\nu }_s}}{1+\frac{{\nu }_c}{{\nu }_g}}$$

and A being a normalization constant such that${\sum }_{l=0}^{l^{\ast }}\left[p_{+}\left(l\right)+p_{-}\left(l\right)\right]=1$. We used these results to check the numerical simulations that served to produce the results in the spatial disorder case in the presence of CLIP.

Therefore, the stationary probability for the tip position is exponentially increasing in the bulk toward the cell boundary. For biologically relevant parameters (see Table 1), the value of a is close to one, such that the increase is not very dramatic. In any case, most of the probability mass is accumulated in the growing state at site l^∗ − 1 if the cell boundary induces catastrophe with a probability p_ind < 1.

In the dynamical inclusion scenario, the system exhibits spatial disorder, which renders an analytical treatment very challenging. Therefore, we instead performed extensive Monte Carlo simulations to obtain statistics for a large number of MTs over their entire lifetime.

Increased lifetime and geometry dependence

The addition of binding sites for the +TIP at polymerization of tubulin leads to persistent growth up to the cell boundary, where frequent switching between growth and shortening is observed (Fig. 2 A) before a filament eventually depolymerizes completely. Typical lifetimes are on the order of several minutes, as observed in experiments (25). If there are no binding sites for the +TIPs and the filament therefore cannot be rescued rapidly, the MTs will be very unstable and depolymerize entirely after a short sojourn time at the boundary (Fig. 2 B). This behavior is anticipated because switches from the growing to the shrinking state, and vice versa, are rare with respect to the growing and shrinking times resulting from the typical distance between MTOC and cell boundary. The cell geometry thus has a big impact on the results obtained in the absence of binding sites for the +TIP. Hence, the length distribution of shortening episodes is mainly an indicator of the cell shape rather than the MT dynamics. Indeed, simulations with different geometries reveal very different distributions of shortening lengths (see Fig. 3). Nevertheless, the qualitative behavior is conserved over a wide range of geometric parameters, and rescaled quantities, such as those presented in Fig. 2, C and D, correlate well with experiments.

Figure 2.

Simulation results of the model. (A and B) Life history plots of simulated MTs. (A) If binding sites for a rescue-enhancing +TIP are added under growth, the MTs show dynamic instability at the cell boundary with frequent rescues. (B) Without this effect, the MTs depolymerize completely after a short contact with the cell boundary. MT lifetimes are mostly determined by the time needed for polymerization to the cell boundary and depolymerization back to the MTOC. As cell geometry, an ellipse with half-axes a = 19.2 μm, b = 6.6 μm was chosen. The MTOC was placed 1.2 μm away from the center of the ellipse in the x- and in y-direction. (C and D) Histograms of the distribution of active plus ends along the cell radius (comparison with experiment). (C) After correction for paused MTs (see definition in Materials and Methods), the simulation results still show an increased number of active MT ends near the boundary if the rescue-enhancing +TIP is included. (D) In the absence of binding sites, the distribution of active MT ends increases only very slowly toward the boundary. As in the experiment, MT lengths are rescaled with the cell radius in the corresponding direction of the filament. These dimensionless lengths are robust to variations in cell shape, whereas the absolute ones are not (not shown). Experiments were performed on CHO-K1 and COS-7 cells injected with Cy-3-labeled tubulin (13). The experimental data were provided to us by Y. Komarova, and details on the experimental methods can be found in Komarova et al. (13). (E and F) Survival probability of an MT of maximum length l^∗ = 18 μm after boundary contact is made. (E) A dynamically introduced binding site for a rescue-enhancing +TIP induces aging of the MT. The survival probability of an MT after it hits the cell boundary for the N-th time at the time t_N is lower for higher values of N. (F) Without the positive effect on the rescue frequency, all MTs show the same behavior regardless of their past, i.e., the number of collisions with the cell boundary. Consequently, all curves collapse.

Figure 3.

Examples for distributions of shortening lengths in the absence of binding sites for different geometries. With the same set of parameters, very different distributions are obtained depending on the geometry. Reproducing the distribution experimentally determined in Komarova et al. (13) is thus a question of finding the correct geometry. The chosen geometries are an ellipse with half-axes a = 19.2 μm, b = 6.6 μm (MTOC at 1.2 μm, 1.2 μm off the center (A) or MTOC at the center (B)), an ellipse with half-axes a = 18 μm, b = 12 μm (MTOC at 0 μm, 3 μm (C)), and a circle of radius r = 18 μm (MTOC at the center (D)).

Distribution of MT lengths

Fig. 2, C and D, show the distribution of active plus ends, i.e., MTs that are not pausing (see definition in Materials and Methods), with respect to the fraction of the cell radius at which they are located. In contrast to alternative interpretations of the MT length distribution (13,16,23), our simulations indicate a very slow increase in the bulk with an accumulation of MT ends at the cell boundary (Fig. 4). In an experimental setup, the number of short filaments is systematically underestimated because the tips are located near the MTOC in a dense environment where they can scarcely be resolved (23). These difficulties obviously do not exist in a theoretical model, which explains the higher values of short MT lengths in our model compared with the experimental data (Fig. 2 C). The qualitative behavior is not affected by this shortcoming of the experimental method. In the absence of +TIP binding sites, the distribution of active MT ends is almost flat (Fig. 2 D) and thus corresponds well with the experimental data.

Figure 4.

Distribution of active plus ends along the cell radius with (solid line) and without (dashed line) enhancement of rescues through vanishing binding sites for a +TIP. The data are the same as those used to plot the histogram in Fig. 2, C and D. The plot is semilogarithmic, thus indicating that the increase of active MT plus ends toward the cell boundary is not part of an exponential distribution.

Aging of MTs

The presence of a binding site for a +TIP, which increases the rescue frequency, leads to a qualitatively different behavior of the MT dynamics. The association of a rescue factor with the growing plus end leads to observable aging at the cell boundary. This is because no further binding site can be added to the MT tip once it has stopped at the boundary, whereas the older ones continuously vanish from the filament (see Fig. 5). This reduces the probability of rescue occurring after a boundary-induced catastrophe. Consequently, the MT ages while resting at the boundary, resulting in a shorter remaining lifetime. To visualize this, the plot in Fig. 2 E shows the probability that an MT filament has not yet completely depolymerized at t − t_N seconds after hitting the boundary for the N-th time at the time t_N (where “hitting the boundary” refers to the contact between the filament and the cell boundary after an excursion away from the cell boundary that is larger than the experimental threshold; see Materials and Methods). Younger MTs (i.e., those with smaller N) have at all times higher survival probabilities. We chose to use the number of boundary hits instead of the time after the first contact with the boundary because longer excursions away from the boundary and back to it occur. During these excursions, the filament does not age, because new binding sites are added to the tip. In contrast to these results, the absence of binding sites eliminates the aging behavior, which means that all MTs show the very same behavior regardless of the time spent at the boundary. This is portrayed in Fig. 2 F, which shows identical curves for different values of N. Depending on the parameters of the rescue factor dynamics, the aging effect can be much stronger (Fig. S1).

Figure 5.

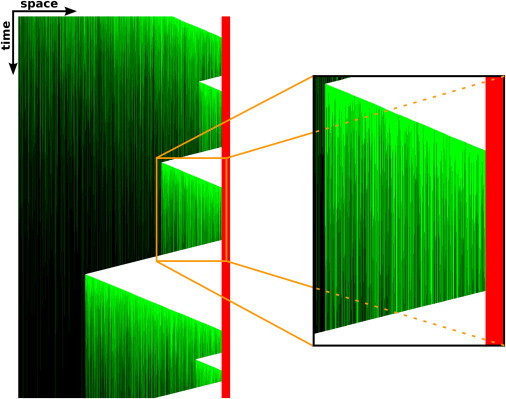
Evolution of a filament during the simulation. In similarity to a kymograph, every line corresponds to the tip of an MT that nucleated on the left and polymerized toward the cell boundary on the right (shown in red). +TIPs are shown in green (online) or gray (in print) and can be seen to slowly dissociate over time, thus causing the filament to be rescued less frequently. The right part of the figure shows an enlargement of the orange box.

Discussion

Cytoskeletal dynamics constitute one of the fundamental processes in which cells show generic nonequilibrium behavior. Here, we focus on the changes of the dynamic instability of MTs under the action of a rescue-enhancing +TIP, in which case boundary-induced catastrophes are frequently observed. Our results indicate that the actual quantitative results are strongly influenced by the cell geometry. First, the boundary effects induce a stationary distribution of MT lengths that is not exponentially decaying (26). In particular, the number of MTs in contact with the cell membrane is drastically increased such that the ability for interaction between the cytoskeleton and the cell membrane is enhanced. Second, quantitative parameters such as the distribution of shortening lengths or MT lengths depend strongly on the exact shape of the cell boundary. Nevertheless, the qualitative behavior is conserved over a wide range of geometric parameters and correlates with experimental results, yielding astonishingly good results even though several details of the cellular processes have been neglected.

We have shown that dynamical inclusion of the MT filament will lead to aging phenomena, meaning that quantities such as the remaining lifetime of the filament or the average extent of a shortening episode depend on its past. In contrast to this model of dynamic addition of binding sites to the MT, models in which plus-end tracking is ensured by the recognition of a structural feature at the plus end would not lead to observable aging, as recruitment of new +TIPs will occur as long as a plus end exists, and does not depend on the addition of tubulin subunits during growth phases. The existence of aging thus allows one to discriminate between these scenarios.

In a general way, aging of MTs will indicate the presence of a mechanism similar to the one presented here, in that the rescue-enhancing factor is dynamically introduced into a growing MT and then slowly disappears from the filament, thus leaving a destabilized filament behind if the MT stops its growth. For example, the frequently addressed GTP cap may fall into the same class of mechanism, as GTP remnants in the filaments have been proposed to be caused by slow hydrolysis and to be responsible for rescues (27). Thus, we expect aging of filaments to be observable in vivo whether it is due to the GTP cap or interaction with a rescue-enhancing +TIP. Furthermore, our results show that a dynamical inclusion leads to destabilization of static filaments over time. In this way, the cell is provided with the ability to adapt its shape to the environment.

To summarize, the model presented here offers the possibility of experimentally confirming whether the inclusion of a rescue factor is mediated by a dynamical interaction with the filament or a structural recognition of the MT plus end. The macroscopic effect of microscopic aging should manifest itself in a reduced remaining lifetime of the filament. This quantity is experimentally accessible, provided that sufficient statistics are obtained. Another quantity that can serve to identify the mechanism might be the length of excursions away from the cell boundary, which should become larger as the filament ages.