EEG Control of a Virtual Helicopter in 3-Dimensional Space Using Intelligent Control Strategies

Abstract

Films like Firefox, Surrogates, and Avatar have explored the possibilities of using brain-computer interfaces (BCIs) to control machines and replacement bodies with only thought. Real world BCIs have made great progress toward that end. Invasive BCIs have enabled monkeys to fully explore 3-dimensional (3D) space using neuroprosthetics. However, non-invasive BCIs have not been able to demonstrate such mastery of 3D space. Here, we report our work, which demonstrates that human subjects can use a non-invasive BCI to fly a virtual helicopter to any point in a 3D world. Through use of intelligent control strategies, we have facilitated the realization of controlled flight in 3D space. We accomplished this through a reductionist approach that assigns subject-specific control signals to the crucial components of 3D flight. Subject control of the helicopter was comparable when using either the BCI or a keyboard. By using intelligent control strategies, the strengths of both the user and the BCI system were leveraged and accentuated. Intelligent control strategies in BCI systems such as those presented here may prove to be the foundation for complex BCIs capable of doing more than we ever imagined.

I. INTRODUCTION

In the 1982 movie Firefox, a fighter jet’s weapons were controlled by thought. Although the movie was science fiction, brain-computer interfaces (BCIs) are approaching such capabilities. Current invasive systems allow paralyzed humans to operate a computer [1]–[3] and monkeys to select keys, move a computer cursor, and control a prosthetic arm to feed themselves [4]–[7]. Non-invasive systems, such as those based on scalp-recorded electroencephalography (EEG) [8],[9], have been able to emulate the performance of invasive systems up to establishing control in two dimensions. This includes controlling a computer cursor [10], a humanoid robot [11], or a wheelchair in a real environment [12],[13]. Limited exploration of 3D space has been demonstrated by a non-invasive BCI [14]. However, in that study, the targets were confined to the corners of a virtual box, the cursor was confined to the inside of the box, and did not exhibit the capacity for continuous control.

Full and continuous exploration of 3D space is an unaccomplished goal for non-invasive systems. Here we report our investigation which demonstrates that human subjects can fly a virtual helicopter to any point in 3D space using an EEG-based BCI. We achieved this result through a conventional four class system typically used for 2-dimensional (2D) control [8],[10],[15], but used intelligent control strategies [11]–[13], [16]–[17] to navigate in 3D space quickly and fluently. Non-invasive BCI control of continuous movement to any point in 3D space represents a major advancement in the field. The potential of this methodology extends beyond the scope of this study. It represents a new way of thinking about 3D control that expands the user population, reduces training barriers, and optimizes control signal economy.

II. METHODS

A. Participants

Four young, healthy, human subjects participated in the study. This study was conducted according to a human protocol approved by the Institutional Review Board of the University of Minnesota. None of the four subjects were particularly skilled in video games, or in virtual reality navigation. None identified themselves as gamers. All four had been trained in BCI usage in previous studies. Subjects began by using a 1D left/right cursor control BCI similar to that used in [16] for 8 to 11 sessions. Sessions lasted approximately two hours including capping and hair washing time. Time of actual BCI usage during a session was typically around 45 minutes. After mastering left/right, the subjects attempted 1D control of up/down. Once subjects were comfortable with up/down control, the subjects performed 2D cursor control before attempting to control the helicopter. Eye movements were monitored during training on the cursor task to ensure that subjects were not using eye movements to control the cursor. In total, subjects 1–4 completed 33, 31, 24, and 21 sessions, respectively, before the data presented here.

B. Data Acquisition and System Design

Subjects wore an EEG cap that recorded sensorimotor rhythms from motor imagination [18],[19]. EEG recording methods and processing in BCI2000 were the same as in previous studies [15],[16]. In brief, a 64 channel EEG cap was plugged into a Neuroscan amplifier. The signal was then fed to a computer running BCI2000. We used BCI2000’s standard 2-dimensional cursor task [20] to generate two control signals: left/right and up/down. Each subject’s control signal was individualized during their training to those seen in Table I. Electrodes were limited to those recording sensorimotor cortex. The autoregressive spectral amplitude was calculated for each of the electrodes and frequency bins indicated. The left/right control signal was the subtraction of the electrodes and frequencies of the left hemisphere from the electrodes and frequencies of the right hemisphere. The up/down control signal was the inverted addition of left and right. Using this scheme, subjects imagined moving their right hand to go right, their left hand to go left, both hands for up, and rest for down to create a four class system. Each control signal was normalized to zero mean and unit variance. The control signals were continuously fed through a UDP port (every 20–50 ms) to a virtual world modeled in Blender. The subjects sat motionless in a comfortable chair in front of a flat screen computer monitor. They only saw the virtual world of Blender.

TABLE I.

Subject Specific Electrodes and Frequencies Used for Control

Subject	Right	left
1	C4: 12, 15, and 18 Hz CP2: 9 and 15 Hz	C3: 12 Hz
2	C6: 15 and 18 Hz	C3: 12 Hz
3	C4: 9, 12, and 15 Hz CP4: 9, 12, and 15 Hz	C3: 15 Hz C1: 15 Hz
4	C4: 9, 12, and 15 Hz CP4: 12 and 15 Hz	CP5: 18 Hz

Electrode names are given according to the 10–20 international system. For each cell above, each frequency bin designated by the center frequency listed was weighted equally with all the other frequency bins listed (bin width = 3 Hz). Left/right control in BCI2000 was the subtraction of the left column from the right column. Up/down control in BCI2000 was the addition of the left column to the right column.

C. Helicopter Control and Virtual World

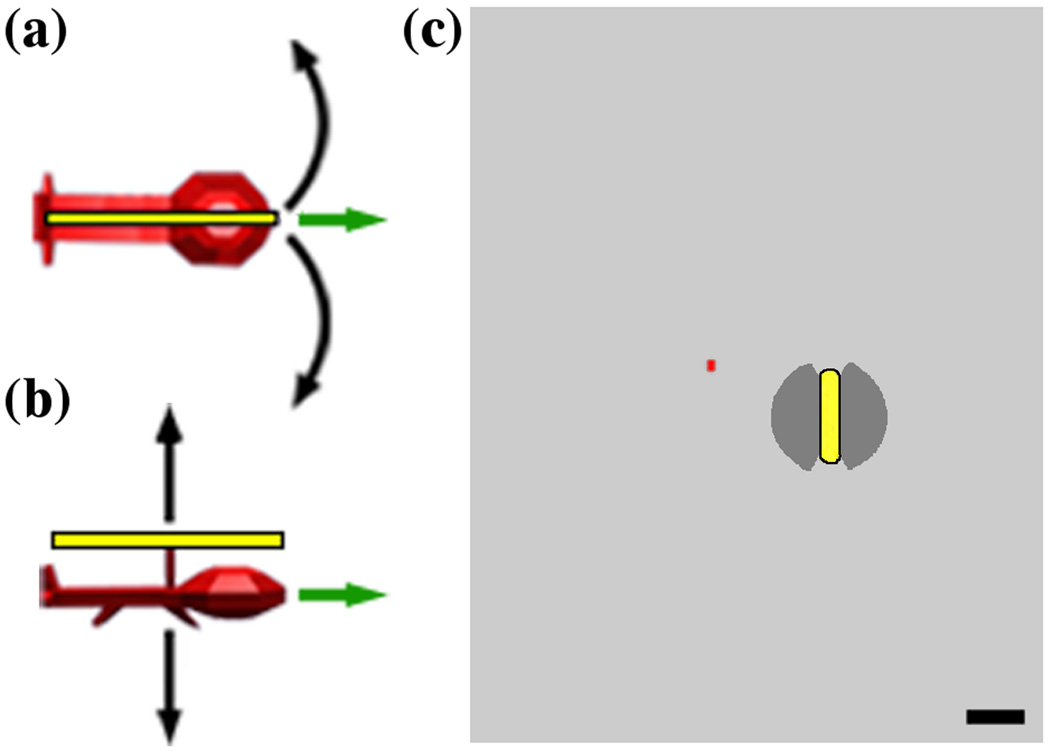
Although the subjects were using two control signals, they were able to control the helicopter in 3D space. The left/right control signal from BCI2000 was used to control the helicopter’s rotation (Fig. 1a). If the subject imagined left, the helicopter would turn to the left. If the subject imagined right, the helicopter would turn to the right. The up/down control signal from BCI2000 was used to control the helicopter’s vertical position in space (Fig. 1b). The helicopter had a constant forward speed of 0.5 Blender units per second (bu/s).

Fig. 1.

Control strategy and world size. (a) and (b) Two control signals adjust the helicopter’s position in 3D space. The helicopter has a constant forward speed (green arrows). (a) Top view. The left/right control signal adjusts rotation (black arrows). (b) Side view. The up/down control signal adjusts elevation (black arrows). (c) Size comparison of ring (yellow), helicopter (red), cone of guidance (dark grey), and allowable space for the helicopter (light grey). The black scale bar in the lower right hand corner has a length of 2 Blender units (bu).

The subjects' control signals were continuously controlling the helicopter, but in a different manner for left/right versus up/down. The left/right control signal was linearly tied to the rotation of the helicopter, with gains that could be independently adjusted for right and left for each subject. An additional restraint on the rotation was that a turn was limited to a maximum of 20 degrees per screen update, which occurred at approximately 5 Hz. The up/down control signal was cubically tied to a force that acted upon the helicopter. The magnitude of the force could be independently adjusted for up and down for each subject. Three of the four subjects preferred to dampen the effects of the force by reducing the helicopter's vertical linear velocity to 97% of its value each screen update. The up/down control signal was further limited by capping it to a range of −1.5 to 2, a reasonable range for a zero mean, unit variance signal. Subjects' left, right, up, and down gain coefficients were often the same from session to session, but were adjusted according to subject preference if the subject requested.

The virtual world was large and the helicopter was not confined to the ring space. The rings were confined to a space of 69 bu³. The helicopter was allowed within a space of 4,285 bu³, which is more than 600% of the volume occupied by the rings. However, if the helicopter did reach the edge of this large space (Fig. 1c), it was reset to the starting position. To give the subjects reference, the virtual world was based on the Northrop Mall area of the University of Minnesota (Fig. 2). The buildings were added to the virtual world mainly to give the subjects reference. They were not designed to be significant obstacles. Given that the helicopter could easily fly above all the buildings, they occupied minimal flying space. In fact, the buildings only occupied five percent of the total allowed volume.

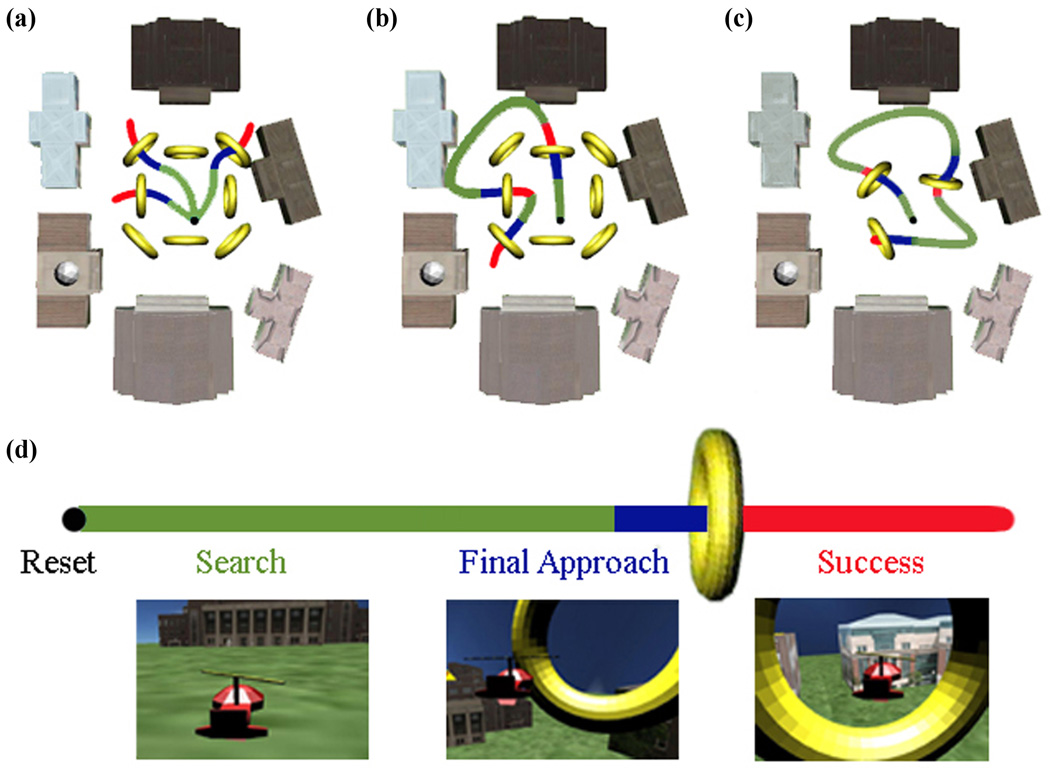
Fig. 2.

Experimental paradigms and virtual world. (a) – (d) The colors correspond to the different phases of a trial: black dot for reset, green for search, blue for final approach, and red for success. Reset is the time the helicopter was motionless. Success was the time after fly through, but before the ring changed position. (a) Trial-based discrete paradigm. After successful completion, the helicopter reset to the starting position. (b) Continuous discrete paradigm. The helicopter did not reset to the starting position after flying through a ring. (c) Continuous random paradigm. The rings could be anywhere within the original ring space at any vertical orientation. (d) Examples of what the subject saw during each phase of a trial.

D. Experimental Paradigm

Each session, subjects completed 7–13 five-minute runs. The exact number depended on the subject’s availability. At the start of a run, the helicopter hovered stationary slightly above ground at the starting position for 3 seconds and then began to move forward. At that time, the subject gained control of the helicopter’s motion. A run consisted of as many ring attempts as could be completed in a five-minute period. During each session, approximately half the runs ± 2 used the cone of guidance, a form of shared control. By sharing control between the subject and the BCI system [11]–[13], [16], we were able to leverage the expertise of both brain and computer to create a system more powerful than either individually. The cone of guidance directed the helicopter through the ring during the final approach. It was implemented as a training aid and to reduce frustration. The cone of guidance was not visible to the subject. The area of assistance resembled a cone originating from the center of the ring with a radius of 2 bu. The upper and lower boundaries were defined such that the helicopter had to approach no more than 60 degrees from horizontally even with the ring. The side boundaries required that the helicopter approach the ring with a clear path through it. Each session alternated whether the first half or the second half of the session used the cone of guidance.

The subjects had to find the ring in a large space and then fly through it (Fig 1c). This can be compared to finding a needle in a haystack, and then threading it. Both tasks are difficult on their own, and combining the two could be very frustrating. The cone of guidance can be thought of as a needle threader. Effectively, the cone of guidance changed the ring into a balloon-shaped target shown in Fig. 1c. This target size was consistent with many other invasive and non-invasive BCI studies [7]–[10],[14]–[16]. Each session, half the runs ± 2 used the cone of guidance. The exact number was chosen to minimize subject frustration. In some runs, the cone of guidance also prevented the user from hitting a building. Some users requested that they be allowed to hit the buildings since their strategy to maximize the number of rings flown through involved resetting upon colliding with a building when quite distant from the ring. As expected, the cone of guidance improved performance, but it was not necessary for successful performance. All subjects were able to fly through the ring without the assistance of the cone of guidance.

The subjects controlled the helicopter under three different paradigms: trial-based discrete, continuous discrete and continuous random (Fig. 2a–c). The subjects began with trial-based discrete (Fig. 2a). From the starting position, the subjects attempted to find and then fly through a ring that was located at one of eight discrete positions. Only one ring was present at a time. A map similar to Fig. 2a–c in the lower portion of the subject’s screen indicated the position of the ring. The subjects had 57 s to fly through the ring. Otherwise, the helicopter reset to the starting position. If a subject hit a building, the helicopter also reset to the starting position.

After completing 3 sessions of trial-based discrete (4 for subject 2), subjects then completed 3 sessions (4 for subject 2) of continuous discrete (Fig. 2b). The major difference between the two paradigms was that, in continuous discrete, the helicopter did not reset after passing through a ring. Instead, the helicopter kept flying as another of the 8 possible rings appeared. Subjects then completed 2 sessions (3 for subject 1) of continuous random (Fig. 2c). In this paradigm, the ring could appear anywhere within the box defined by the original 8 rings. The ring could be at any rotation about its vertical axis, but it had to be at least 3 bu from the previous ring. In both of the continuous paradigms, there was no time limit on how long a subject could attempt to pass through a given ring. In all three paradigms, subjects were instructed to pass through as many rings as possible in the five-minute run. Any discrepancy between subjects in number of sessions was due to subject availability.

Fig. 2d shows example images of what the subject saw during a trial. Additional features were on the subjects' monitor during a run. An "instrument panel" was located on the bottom of the screen which contained the map mentioned above, a joystick whose position corresponded to the position of the cursor on the 2D BCI2000 screen, the number of rings flown through during the run, and the time remaining in the trial. Small white numbers indicating programming variables such as BCI2000 source time and target code were located in the upper left hand corner of the screen for the experimenter's reference. These variables, 4 to 6 depending on paradigm, were designed to be as unobtrusive as possible to the subject. Personal monitoring of the EEG during the helicopter experiments showed that processing the complex environment was not affecting the control signal.

E. Experimental Controls

In order to gauge the subject’s performance, we implemented two experimental controls. Each session started with the subject playing the game using the keyboard for approximately 5 minutes. The keyboard controlled the helicopter in the same manner as the BCI, with rotation controlled by the left/right arrows, and vertical forces controlled by the up/down arrows. This allowed us to analyze the degree of control subjects were able to achieve using the BCI as compared to when they had standard control using the keyboard. The subjects completed 21, 13, and 9 runs of trial-based discrete, continuous discrete, and continuous random, respectively. That resulted in 451, 267, and 236 rings being flown through for the three paradigms, respectively. For the second experimental control, the helicopter flew for two sessions of ten runs of each paradigm with environmental noise as the input to BCI2000. This was achieved by running Neuroscan and BCI2000 without an EEG cap attached to the amplifier. This generated two random control signals with zero mean and unit variance. These sessions served as our chance performance. Chance performance was able to fly through a few rings during its 20 runs of each paradigm: 28, 18, and 28 for trial-based discrete, continuous discrete, and continuous random, respectively.

F. Data Analysis

Average path to a ring plots (Fig. 3) present averages of all paths to a ring that concluded with the helicopter passing through the ring (946 total trials of 1370). Trials that ended in a reset (297) or a time out (127) were excluded from Fig. 3. All paths were resampled to 1001 points for the purposes of averaging and other data analysis. The standard error of the mean was calculated for the x, y, and z coordinate for each of the 1001 plotted points based on the 946 trials averaged. The width of the shaded area in Fig. 3 at each of the 1001 plotted points is the standard error of the mean averaged over the 3 dimensions, x, y, and z, for that particular point. The following measures were not normal according to a 2-sided Lillilifors test: the percent of flight time spent at each normalized distance to the ring, information transfer rate, rings/min, time to ring, and path length. The statistical analysis performed on those measures was a 2-sided sign test. Alpha = 0.05 for all tests. The percent of flight time spent at each normalized distance to the ring is plotted as a cumulative percent. The metric was calculated for distance intervals representing 1% of normalized distance where the starting distance to the ring was defined as a distance of 1 for all trials. Statistics were calculated for each 1% distance bin.

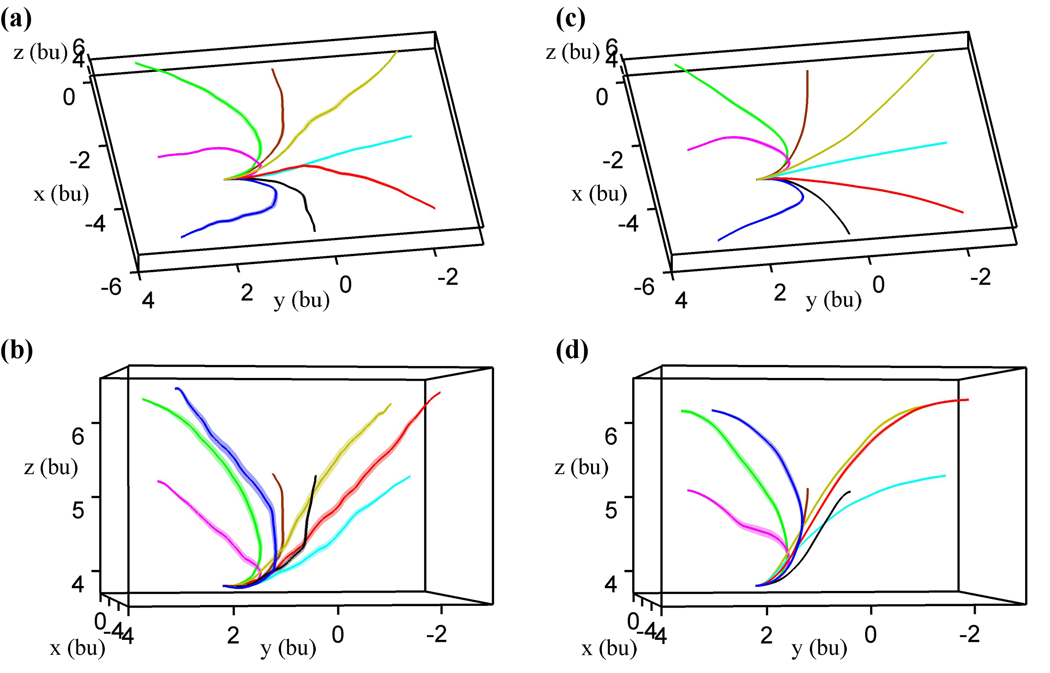
Fig. 3.

Average paths in trial-based discrete correlate strongly between BCI and keyboard control. (a) – (d) The path to an individual ring has the same color throughout. The shaded area represents the standard error of the mean around average trajectories (solid line) to each ring. bu indicates Blender units. (a) and (b) The group average BCI paths when viewed from above (a) and the side (b) with a slight rotation. Rotate Fig. 2a–c ~90 degrees clockwise to achieve the orientation of (a) and (c). n = 946 total trials, with 106–131 per ring. (c) and (d) The group average keyboard paths viewed from the same perspectives as in (a) and (b). n = 451 total trials, with 53–62 per ring.

Information transfer rate and rings/min were calculated for each run of each subject, for a total of 132, 112, and 87 values for trial-based discrete, continuous discrete, and continuous random, respectively. Time to ring and path length were calculated for each ring successfully flown through, for a total of 946, 566, and 608 for the three paradigms. Since chance successfully flew through so few rings in comparison to the keyboard and BCI data, a statistical comparison against chance is not meaningful. Thus, the measures calculated for each ring are not presented for chance. Each ring successfully flown through counted as 3 bits of information transferred for the discrete paradigms. Time to ring and path length were normalized to the keyboard path length for trial-based discrete. Otherwise, they were normalized to the starting distance to the ring.

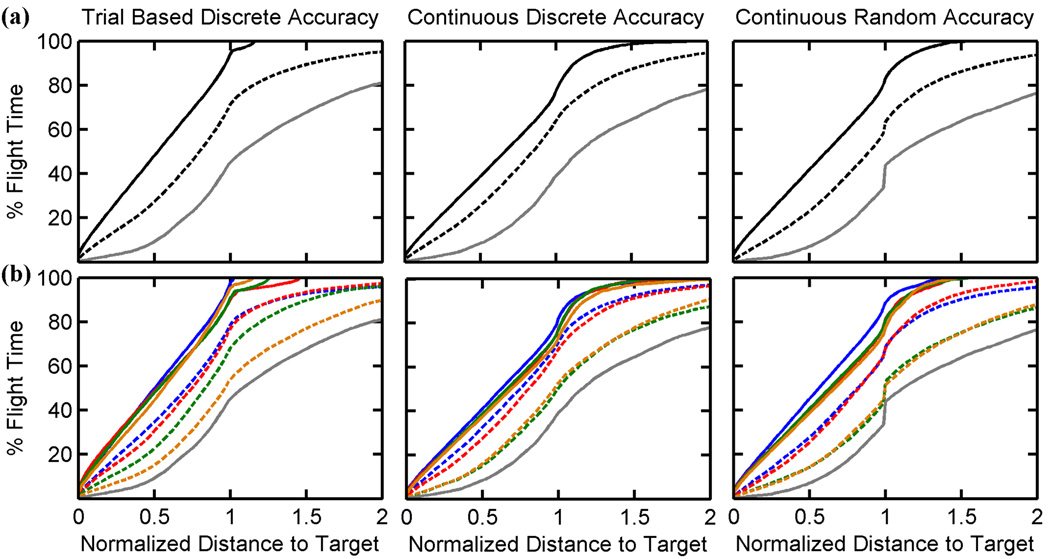
The subject’s goal was to fly through as many rings as possible. Some subjects used resets as part of this strategy. If these subjects wandered off and found themselves very far away from the ring, they would purposely hit a building or the bounding box to reset. This way, they would not need to spend the time flying back to the ring and could go through more rings in the same run. Because this strategy was not penalized, presenting the number of rings obtained as a fraction of total trials is unfair. A better metric, and the one presented in Fig. 6, is the number of rings flown through per minute. Another fair metric is the percent of total flight time spent at each normalized distance to the ring, as presented in Fig. 5.

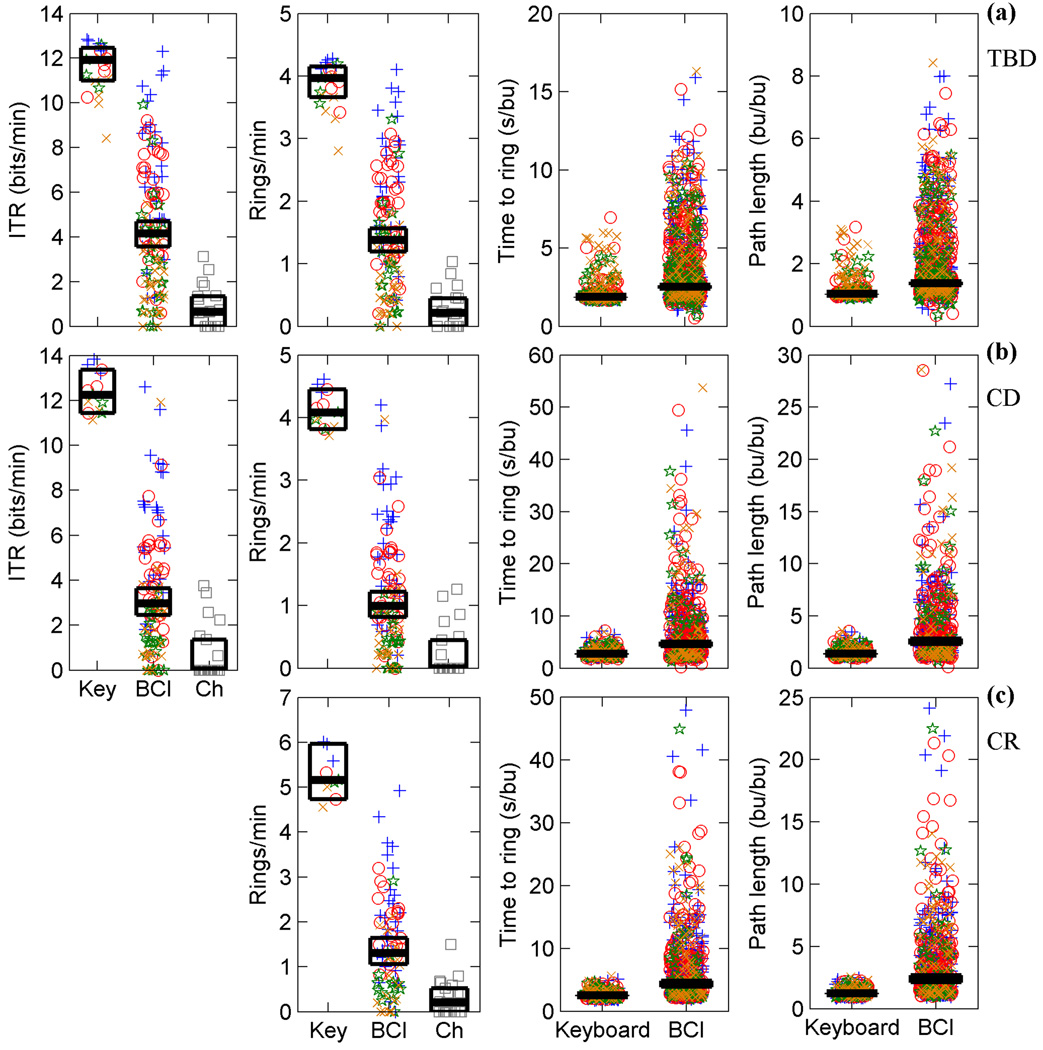
Fig. 6.

Movement quality measures. (a) – (c) Scatter plots of the data by subject and paradigm. Each row shows the paradigm labeled on the right. Subject 1 is represented by a blue +, subject 2 by a red O, subject 3 by a green star, and subject 4 by an orange x. Chance performance is represented by grey squares. Group medians are indicated by the thick black line. The black box indicates the 95% confidence interval of the median. Median and box are present on all plots but may not be distinguishable from each other due to proximity. ITR = Information transfer rate, Key = Keyboard, Ch = Chance, bu = Blender units. (a) Data for trial-based discrete, TBD. (b) Data for continuous discrete, CD. (c) Data for continuous random, CR.

Fig. 5.

Subjects effectively and accurately controlled the helicopter in all paradigms. (a) and (b) Percent of total flight time spent at or closer to each normalized distance to the target. 1 represents starting position. 0 represents ring position. Solid black or colored lines indicate keyboard performance. Dotted lines indicate BCI performance. Solid grey lines indicate chance. Each column presents the data for the labeled paradigm. (a) Grouped data. (b) Individual subject data. Subject 1's data are in blue, subject 2 in red, subject 3 in green, and subject 4 in orange.

III. RESULTS

All four subjects successfully navigated in 3D space. A supplementary video of each subject is available at http://ieeexplore.ieee.org. The videos feature all three paradigms. Fig. 3 shows the trial-based discrete group average path (Fig. 3a–b) to each of the 8 rings. The paths closely resemble the paths the subjects took when they were using the keyboard (Fig. 3c–d). The cross-correlation at 0 delay between the average BCI and keyboard paths was greater than 0.99 for all 8 rings. For individual subjects, the average cross-correlation for all 8 paths was 0.9946, 0.9940, 0.9915, and 0.9664 for subjects 1 through 4, respectively.

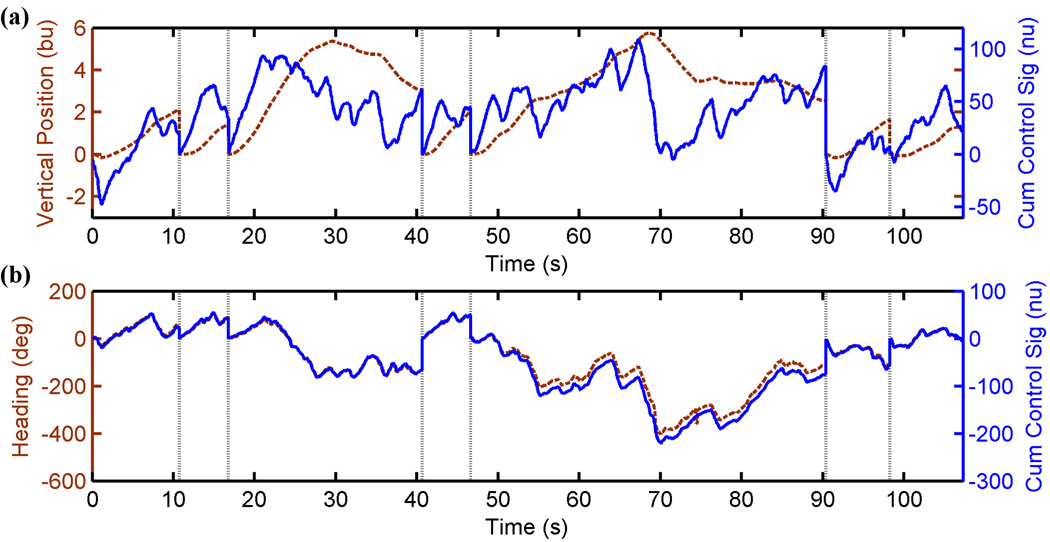
Subjects achieved movement control by successfully controlling their EEG signal in a goal-directed manner. Fig. 4 plots the position of the helicopter and the BCI control signals during subject 1's trial-based discrete, no cone of guidance trials shown in supplementary video 1. The combination of video 1 and Fig. 4 show that the subject appropriately modulated their EEG to create a control signal that flew the helicopter in a very goal directed manner through the ring. In five of the seven trials, the subject progressed swiftly through the ring. In the third trial, the subject started flying to the right, and then realized that the target was actually off to the left. When they had circled to the left, the subject realized the helicopter was too high, so the subject descended. In the fifth trial, the subject missed on their first approach to the ring, and so had to circle around for two more attempts before successfully flying through the ring. The other three videos show similar purposeful control from the other three subjects. Fig. 4 shows that the control of the helicopter as seen in video 1 is a direct result of modulation of the EEG creating the control signal since Blender translated the control signal to helicopter position with such high fidelity. In Fig. 4, the cross-correlation between the helicopter's heading and the subject's left/right control signal is 0.997 at a delay of 0. The cross-correlation between the vertical position and up/down control signal is 0.817 at a delay of 0 and reaches a max of 0.837 at a delay of approximately 2.1s. Between the videos and Fig. 4, we show that the subjects were purposely modulating their EEG to control the flight of the helicopter.

Fig. 4.

Control signal and helicopter position/heading correlate strongly. (a) and (b) Vertical lines indicate different trials shown in Supplemental Movie S1 of subject 1 performing trial-based discrete. (a) The cumulative up/down control signal (right axis, solid blue line) plotted with the vertical position (left axis, dotted brown line) as a function of time. (b) The cumulative left/right control signal (right axis, solid blue line) plotted with the helicopter’s heading (left axis, dotted brown line) as a function of time. Upward slope indicates rightward rotation. Downward slope indicates leftward rotation. bu = Blender units. deg = degrees. nu = normalized units.

We assessed the quality of the movement control through several measures. We first analyzed the percent of time the helicopter spent closer to the ring than it was upon ring presentation. Fig. 5a presents the grouped data. In trial-based discrete, the helicopter spent 93 % of flight time closer to the ring than it started when controlled by the keyboard. It spent 67% of flight time closer to the ring than it started when controlled by the BCI, and 44% when controlled by chance, or the random controller. The same data for continuous discrete are 76%, 63%, and 38% when controlled by keyboard, BCI, and chance, respectively. For continuous random the data are 81%, 59%, and 34%. Since the helicopter had a constant forward speed, subjects were forced to move away from rings behind them while turning around. This is reflected in the fact that the keyboard data do not achieve 100%. Individual subject data is shown in Fig. 5b. For all three paradigms, subjects performed significantly better than chance. For some distance intervals, subject performance was statistically the same whether using the BCI or keyboard. This was true of subject 1 for 34% of the distance intervals between 0 and 2 in continuous discrete (all intervals were greater than or equal to 1.24) and 14.5% of continuous random (all intervals were greater than or equal to 1.26). This was true of subject 2 for 26.5% of continuous discrete (all intervals were greater than or equal to 1.48) and 16% of continuous random (1.27–1.58). For the remaining distance intervals, subject performance was not statistically the same whether using the BCI or keyboard. Also of interest, in continuous discrete, subjects 1 and 2's BCI performance approached subjects 3 and 4's keyboard performance, as can be seen by the proximity of the blue and red dotted lines to the green and orange solid lines.

Additional quality measures assessed include information transfer rate (ITR), number of rings/min, time to ring, and path length. Fig. 6 shows all subjects' data for these measures. The ITR and rings/min using the BCI were over 5 and 6.5 times that of chance, respectively. All subjects' ITRs and rings/min were significantly better than chance. The range of ITRs and rings/min achieved with the BCI overlapped the range achieved with the keyboard. In fact, in trial-based discrete, Subjects 2 and 3 achieved an ITR using BCI which was not significantly different than that with keyboard control. In the grouped data, the time to ring was only 34% longer with the BCI than with the keyboard, with a path length 38% longer for trial-based discrete. The continuous paradigms’ time to ring were 70% longer using the BCI than using the keyboard, with a path length roughly 90% longer. For both time to ring and path length, subjects performed slightly better in continuous discrete than continuous random, when compared to keyboard performance.

The above results show that continuous control is harder than trial-based control, even when controlling for distance travelled. Continuous discrete had a median keyboard path length over 41% longer than trial-based discrete, whereas continuous random had a median keyboard path length only 4% longer. (Median keyboard path lengths were 4.95bu, 7.00bu, and 5.16bu for trial-based discrete, continuous discrete, and continuous random, respectively.) However, both paradigms had similar BCI-to-keyboard ratios that were higher than those for trial-based discrete.

IV. DISCUSSION

In this study, the challenge of navigating 3D space was surmounted through novel means. Subject expertise in 2D control was leveraged by identifying the crucial components of 3D flight and directing control capabilities to their accomplishment. In the field of BCI, this reductionist method is revolutionary in its efficient approach to 3D navigation. This implementation opens the doors of 3D BCI navigation by reframing it as a 2D control problem. Through these means we have developed a system that allows subjects to fluently navigate 3D space. The system requires minimal training beyond an established 2D BCI of any variety. Since the system does not require 3D expertise, subjects who can master 2D but struggle with 3D can now navigate in 3D space. It allows subjects to reach targets that require both positional and rotational control accuracy while providing control in both trial-based and continuous control scenarios. The potential of this methodology extends beyond the scope of this study. It represents a new way of thinking about 3D control that expands the user population, reduces training barriers, and optimizes control signal economy.

Some may find the control strategy in this study limited in its lack of a stop command. However, an airplane in flight is a common real world example of a system with similar limitations. If a plane arrives at its destination and needs to wait before it can land, it begins a holding pattern, effectively circling around the intended destination. Our subjects exhibited similar behavior and circled around if they missed the ring on their first attempt. In that way, the control exhibited by the subjects emulated the control available to an airplane pilot once in the air. The goal of this study was to navigate within 3D space and not address the takeoff or landing. Such improvements could be a goal for future work. The current study only utilized left and right hand motor imagery. Other types of motor imagery could be utilized to provide additional control [8].

Subjects in this study mastered 3D space in a manner that has not been previously accomplished by a non-invasive BCI. Not only did the subjects demonstrate positional and rotational control, but also they did not have the assistance of being confined to the same space as their targets. In this study, the 3D space through which subjects navigated was much larger than the space occupied by the targets. The subjects were not able to navigate to a wall and then follow the wall to their desired location. That added a great amount of complexity to the task when compared to previous studies [14]. Furthermore, subjects demonstrated continuous control, going directly from one ring to another. Finally, subjects successfully flew through rings that were randomly placed within the target space.

In a recent study, three dimensional hand movements were reconstructed from non-invasive EEG recordings [21]. Their work could serve as the foundation for yet another 3D BCI. However, this research is still in preliminary stages. In this study, actual hand motions were reconstructed after data collection in an offline system. The algorithm has not yet run in real time, which is necessary in order to provide feedback to a BCI user. It will also be interesting to see if motor imagery can be decoded with the same accuracy.

Subjects in the current study were able to master 3D space more easily because of the assistance of the intelligent control strategies used by the BCI. In this study, the subject and the BCI shared control when using the cone of guidance. As expected, the cone of guidance improved performance. However, it was not necessary for successful performance. For example, the cross-correlation in the grouped data between the average BCI and keyboard path went from 0.990 without using the cone of guidance to 0.996 when using the cone of guidance.

An interesting implication of the constant forward velocity of the helicopter is that timing became more important for successful task completion. In order to successfully fly through a ring, the subjects had to not only navigate to the ring, but also approach the ring from the correct angle. If the subject was approaching from the side, they had to wait for the right moment to turn through the ring. Similarly, subjects had to be at the right altitude before arriving at the ring. The subjects were well acquainted with this constraint. Many of the delays in flying through the ring were caused by either misjudging the time required to maneuver, or executing the wrong maneuver at the worst possible time. In those cases, the subjects circled around and tried again. The timing factor can be seen in Fig. 4a. In that figure, peak correlation between control signal and helicopter position occurred at a delay of approximately 2.1s. This was interesting since the subject had commented on how they felt as if they always had to be planning about 2s ahead. When the subjects were using the cone of guidance, the subjects still had to navigate to the ring. However, the timing constraints were not quite as challenging since the actions at pivotal moments were executed for the subjects. As seen in the improvement in cross-correlation between BCI and keyboard path given above, this was the primary cause of performance improvement using the cone of guidance.

Another interesting timing constraint was seen in the transition from trial-based control to continuous control. As seen in the BCI to keyboard ratios, the subjects found continuous control harder than trial-based, even when distances were similar. One possible reason for this, as mentioned in interactions with the subjects, was that continuous control did not provide any mental breaks. An additional advantage of the cone of guidance was that, while the helicopter was under the control of the BCI system, the user could mentally relax and not attempt to control their EEG. Our personal experience with the subjects made it clear that they took advantage of this opportunity to take a small mental break until the next ring was presented.

By using the cone of guidance, we were able to leverage the expertise of both brain and computer to create a system more powerful than either individually. Shared control is widely used in systems that we interact with daily. These systems are multidisciplinary solutions to complex goals. Anti-lock braking systems in vehicles perform a function the human driver performed in older car models. The car pumps the brakes faster and more efficiently than the driver, improving safety. Point and shoot cameras dominate the camera market, allowing any person to take quality pictures without detailed knowledge of f-stops and shutter speeds. Even real helicopters have a variety of shared control functions such as landing assistance and obstacle avoidance. Likewise, brain-computer interfaces are intrinsically multi-disciplinary. Neuroscience, engineering, and computer science combine to create a complex system. The future of BCIs lies in leveraging the potential of all disciplines involved.

Not only is shared control used in everyday systems, shared control has been previously used in BCI research [11]–[13], [15]. In one study, subjects drove a real wheelchair around obstacles [13]. The intelligent wheelchair used environmental sensors and shared control to ensure obstacle avoidance and safe driving. Although limited to 2D due to the constraints of a wheelchair, this study demonstrated that shared control can be used by a BCI in the real world to improve performance and safety.

In conclusion, we achieved movement to any point in 3D space using scalp-recorded EEG. Prior to this study, such navigation was only possible through invasive means. The building blocks of this system, rotational control [12],[13], [22],[23], virtual environments [2], [3], [8]–[10], [12]–[16], [22],[23], and continuous control [17] are well-established in the field of BCI. Through the synthesis of these elements, we were able to create a system capable of quickly and fluently navigating 3D space. The system’s efficient use of control signals allows a subject trained in 2D control to be directly translated to our 3D control system with little additional training. This work provides a platform for the development of 3D non-invasive BCIs that are open to a wide subject population. The three-dimensional world we live in demands such functionality from BCI systems. Here we demonstrate the potential of non-invasive systems to meet that demand.