Interaural fluctuations and the detection of interaural incoherence. IV. The effect of compression on stimulus statistics

Abstract

The purpose of this experiment was to determine whether the normalized interaural cross-correlation (CC) model or a model based on interaural phase and level differences can better describe incoherence detection data. The ability to detect interaural incoherence in three sets of reproducible dichotic noises was tested in six listeners. The first set contained noises with a constrained value of the CC and the CC including signal compression. The second set contained noises with a constrained value of the CC including signal compression. The third set contained noises with constrained values in the fluctuations in the interaural differences. Modeling showed that neither the CC model nor the model using the interaural differences could account for the data in any set. Examination of the statistical properties of the stimuli showed that including compression before the calculation of the interaural CC causes a substantial correlation of this metric to the fluctuations in the interaural phase difference. This finding implies that it may be more difficult to discriminate between the common types of binaural models than previously thought.

INTRODUCTION

Over the past 60 years, three types of models have been extensively used to describe binaural phenomena like incoherence detection, binaural masking level differences (BMLDs), and interaural time difference (ITD) sensitivity. They are the cross-correlation (CC) model (Osman, 1971, 1973), the equalization-cancellation (EC) model (Durlach, 1963), and interaural difference models (e.g., Webster, 1951; Hafter, 1971) that utilize ITDs and∕or interaural level differences (ILDs) in various ways. The models, which started as essentially “black-box” models, have become more physiologically motivated over the years. They presently often include auditory filtering, cochlear compression, rectification, loss of phase locking for high-frequency signals, and adaptation. For example, a CC model with physiological transformations has been used to describe ITD sensitivity of high-frequency modulated stimuli with varied rate, envelope sharpness, and modulation depth (Bernstein and Trahiotis, 2009). Breebaart et al. (2001a,b,c), 4, 5 developed an EC-like model with physiological transformations, which was used to describe many spectral and temporal facets of incoherence detection and BMLD data. Despite these models describing ever increasing amounts of binaural data, no type of model has yet been able to describe all of the data and become decidedly better than the others.

The idea of creating discriminating binaural data sets has been around for many years. Domnitz and Colburn (1976) concluded that the CC, EC, and interaural difference models predicted the psychophysical data for Gaussian noises equally well (in 1976), and that more discriminating data sets were needed to determine the appropriate type of binaural model to be used. One way to create such a data set is by using reproducible stimuli. In psychophysical measurements for randomly generated signals like random-phase noises, testing procedures often estimate thresholds by drawing trials from an effectively infinite set of stimuli. Therefore, the same signal is probably never presented twice. However, studies using reproducible stimuli present each token several times in an experiment. Such studies provide a more stringent test of models because the models need to predict both the average listener response and the individual stimulus responses. For example, the Breebaart EC model (Breebaart et al., 2001a,b,c, 4, 5) accounts for average thresholds for a number of BMLD data but cannot describe individual stimulus responses (Davidson et al., 2009). The purpose of the present study was to create model-discriminating data sets for reproducible stimuli where listeners detected interaural incoherence in narrowband noises.

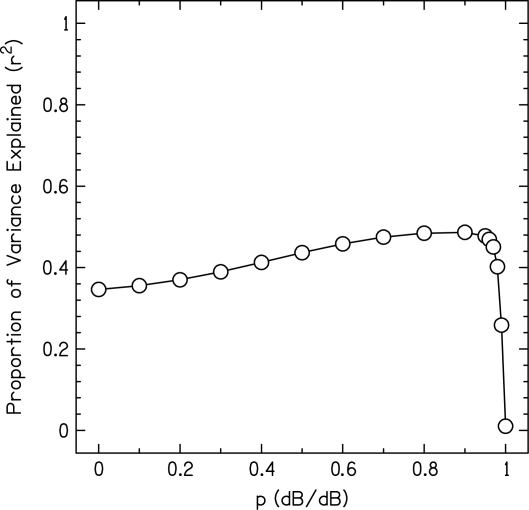
The experiment aimed to create data that would discriminate between an interaural difference model and the normalized CC model, which was also the focus of recent work by Goupell and Hartmann (2006, 2007a,b, 18).1Goupell and Hartmann (2007b) measured incoherence detection with sets of 100 reproducible dichotic stimuli where the value of the interaural correlation was constrained (i.e., constant to several significant digits) at 0.992. For stimuli with a 14-Hz bandwidth and a 500-Hz center frequency, the model that best described the data used the sum of the standard deviations over time in the interaural phase difference (IPD) and ILD (r² = 0.76). Since the value of the interaural correlation was nearly the same for all the stimuli, the CC model could not describe the variation in the data. However, after including physiologically relevant stages of processing in the CC model (auditory filtering, rectification, envelope compression, and temporal windowing), the model could describe the data fairly well (r² = 0.61). Following the same methodology as Goupell and Hartmann (2007b), a new analysis of that published data found that the envelope compression was the most important transformation for describing the data. Envelope compression raises the envelope to a fractional power, p, which is measured in dB∕dB (Bernstein et al., 1999). Examining the effect of compression further, Fig. 1 shows the amount of variance described by the normalized CC model with only compression over the entire signal duration for the data from Goupell and Hartmann (2007b). A priori, it might be expected that if the binaural system utilizes such a metric in detecting incoherence, the function in Fig. 1 should peak at the value of p corresponding to the value measured in other psychophysical tasks, namely about 0.4 (Oxenham and Moore, 1995; van de Par, 1998; van de Par and Kohlrausch, 1998; Bernstein et al., 1999). Figure 1 shows that any amount of signal compression less than p = 0.99 allowed the CC model with compression to describe the psychophysical data about equally well. On one hand, adding compression before the calculation of the CC allowed for differences in the value of the CC, which was constrained to a single value in that experiment. A non-constant metric is a prerequisite when trying to find a non-zero correlation between a stimulus metric and psychophysical data. On the other hand, it was the result that any amount of compression was needed in the model and the relatively flat function in Fig. 1 that motivated trying to understand the effect of compression and the current study. Admittedly, the r² values in Fig. 1 are between 0.3 and 0.5, which are fairly unimpressive; one must be careful in assuming that the binaural system utilizes a stimulus metric that explains such a small proportion of the variance in the data.

Figure 1.

The proportion of variance explained by the normalized CC over the entire stimulus duration for stimuli from Goupell and Hartmann (2007b) as a function of the amount of compression, p, applied to the envelope.

Given the results in Fig. 1, this study was designed to focus on the compression stage of the CC model. Logically, if a stimulus metric is constrained to a single value and if the performance for a task is closely related to this stimulus metric, detection performance should be also constrained to a single value or small range of values; but if instead the performance for a task is not closely related to this stimulus metric, detection performance should not change appreciably by constraining the stimulus metric. Therefore, by carefully choosing sets of reproducible stimuli, a larger difference between the CC and interaural difference models should be observed. Three sets of reproducible stimuli were generated such that the interaural correlation or fluctuations in the IPD and ILD were constrained. This was done by creating numerous randomly generated dichotic noises and using only those that fell within a small range around a listener’s threshold for that metric, essentially making that metric constant. For the stimuli in the first set, the value of the interaural correlation both without or with compression were constrained to a very small range. This set was predicted to produce detection data that would be difficult for a CC model without or with compression to predict, which should address any shortcomings of the stimuli in Goupell and Hartmann (2007b). For the stimuli in the second set, the interaural correlation without compression was unconstrained, but the interaural correlation with compression was constrained. For the stimuli in the third set, the interaural correlation without or with compression were unconstrained, and the fluctuations in the IPDs and ILDs were constrained. This set was predicted to produce detection data that would be difficult for an interaural difference model to predict. It was predicted that these sets of tightly controlled stimuli would elucidate the effectiveness of the models to describe incoherence detection data.

EXPERIMENT

Listeners and equipment

Six listeners participated in this study. They were 21–29 yrs old and all had audiometrically normal hearing. Listener S1 was the author of this study and was listener M from Goupell and Hartmann (2006, 2007a,b, 18). Because of limited availability, listener S6 only participated in a subset of the data collection.

A personal computer was used to control the experiment. The stimuli were output via a 24-bit stereo analog-to-digital (A∕D) to digital-to-analog (D∕A) converter (ADDA 2402, Digital Audio, Denmark) using a 32-kHz sampling rate per channel. The analog signals were sent through a headphone amplifier (HB6, Tucker-Davis Technologies, Florida), an attenuator (PA4, Tucker-Davis Technologies), and presented to the listeners via headphones (HDA200, Sennheiser, Germany). Calibration of the signals at the headphones was performed using a sound level meter (2260, Brüel & Kjær, Denmark) connected to an artificial ear (4153, Brüel & Kjær, Denmark).

Stimuli

The stimuli were dichotic noises chosen such that the value of interaural correlation (without or with compression) or values of the interaural differences were constrained, the generation of which is described in detail below. The stimuli had equal-amplitude components with random phases, 1-Hz frequency spacing, and a −3-dB bandwidth of 10 Hz after a raised-cosine spectral window was applied. The center frequency of the band had a 500-Hz arithmetic mean. The noises were reproducible; each was generated only once and saved to a hard drive. The stimuli were presented at a random A-weighted sound pressure level in the range of 70 ± 3 dB.

The duration of the stimuli was 250 ms, chosen because it nearly maximized the spread of the interaural differences for this bandwidth.2 A raised-cosine temporal window with a 30-ms rise-fall time was applied.

Precise values of the normalized interaural correlation (Bernstein and Trahiotis, 1996) and interaural differences were calculated for each stimulus. The normalized interaural correlation was calculated via

$$\rho =\frac{\int x_{\mathrm{R}}(t)\cdot x_{\mathrm{L}}(t)dt}{\sqrt{\int x_{\mathrm{R}}{}^2(t)dt}\sqrt{\int x_{\mathrm{L}}{}^2(t)dt}},$$ (1)

where x_R is the signal in the right channel and x_L is the signal in the left channel. The normalized interaural correlation including envelope compression (Bernstein et al., 1999) was calculated via

$${\rho }_{\text{comp}}=\frac{\int x_{\mathrm{R}}{}^{\prime }(t)\cdot x_{\mathrm{L}}{}^{\prime }(t)dt}{\sqrt{\int x_{\mathrm{R}}{}^{{\prime }^2}(t)dt}\sqrt{\int x_{\mathrm{L}}{}^{{\prime }^2}(t)dt}}=\frac{\int E_{\mathrm{R}}{(t)}^{p-1}{x}_{\mathrm{R}}(t)\cdot E_{\mathrm{L}}{(t)}^{p-1}{x}_{\mathrm{L}}(t)dt}{\sqrt{\int E_{\mathrm{R}}{(t)}^{2p-2}{x}_{\mathrm{R}}{}^2(t)dt}\sqrt{{\int E_{\mathrm{L}}(t)}^{2p-2}{x}_{\mathrm{L}}{}^2(t)dt}},$$ (2)

where x′_R is the compressed signal of the right channel, x′_L is the compressed signal of the left channel, E_R is the envelope of the right channel, E_L is the envelope of the left channel, and p is the compressive power applied to the envelope.3 An exponent of p = 0.4 was used for all the stimuli (Oxenham and Moore, 1995; van de Par, 1998; van de Par and Kohlrausch, 1998; Bernstein et al., 1999).

The interaural differences were calculated from the analytic signal of the waveforms as a function of time. They are defined as

$$\text{IPD}=\Delta \Phi (t)={\varphi }_{\mathrm{R}}(t)-{\varphi }_{\mathrm{L}}(t)$$ (3)

and

$$\text{ILD}=\Delta L(t)=20{\log }_{10}\left[\frac{E_{\mathrm{R}}(t)}{E_{\mathrm{L}}(t)}\right],$$ (4)

where ϕ_R(t) is the instantaneous phase of the right channel and ϕ_L(t) is the instantaneous phase of the left channel. The standard deviation of the IPD over time, s_t(ΔΦ), and standard deviation of the ILD over time, s_t(ΔL), were used to measure the size of the interaural fluctuations. Psychophysically transformed interaural differences, Ψ_ΔΦ(t) and Ψ_ΔL(t), were also calculated (Goupell and Hartmann, 2007b). These transformations included “laterality compression,” which compresses the physical interaural differences to a perceived lateral position scale, and “envelope weighting,” which discounts IPDs when the envelope of the signal was below 20% of the root-mean-square envelope value of either channel.4

The stimuli were generated for a target value of the interaural correlation (ρ_target). The Gram–Schmidt orthogonalization (GSO) procedure (Culling et al., 2001) ensured that the measured value of the stimulus interaural correlation (ρ_measured) was close to ρ_target, any small difference occurring because of the onset∕offset gating, which was applied after the GSO procedure. In the GSO procedure, after obtaining orthogonal noises, the interaural correlation or similarity between two waveforms (ρ) can be controlled by proportionally mixing the independent noises. It is also possible to define the mixing factor or dissimilarity (α), which covaries with ρ. For the stimuli in this experiment, which have equal power in each channel, these two factors are related by

$$\rho =\sqrt{1-{\alpha }^2}.$$ (5)

Although the interaural correlation ρ is thought of as the most important relationship for dichotic noises and this metric is pervasive throughout the binaural literature, the dissimilarity α may also be important because of the functional relationship between them and the fluctuations of the interaural differences (see Sec. 2D). Therefore, both ρ and α will be used in this report. The value α was used primarily to choose the scale of the threshold measurements and numerical calculations.

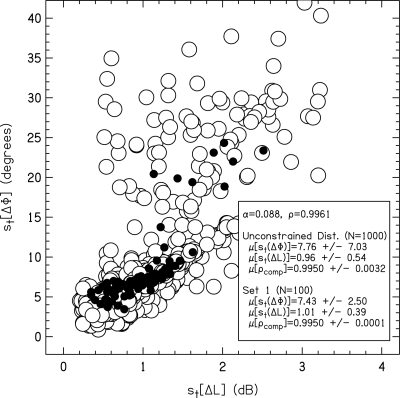
Three sets of stimuli were produced for each listener with the purpose of generating detection data that would discriminate between the CC and interaural difference models. These sets were (1) a set with constrained ρ, constrained ρ_comp, and unconstrained s_t(ΔΦ) and s_t(ΔL); (2) a set with unconstrained ρ, constrained ρ_comp, and unconstrained s_t(ΔΦ) and s_t(ΔL); and (3) a set with unconstrained ρ, unconstrained ρ_comp, and constrained s_t(ΔΦ) and s_t(ΔL). Note that Goupell and Hartmann (2007b) used stimulus sets with constrained ρ, unconstrained ρ_comp, and unconstrained s_t(ΔΦ) and s_t(ΔL). Stringent limits were placed for stimuli in the sets, which can be seen from the small standard deviations for the constrained (bold) values in Table TABLE I.. Each set contained either 25 or 100 stimuli. Set 1 was calculated to be at each listener’s individual ρ threshold (see Sec. 2C1). Using the listener’s individual ρ threshold, a distribution of 1000 noises was generated, and the average of each interaural metric was found. The average of each interaural metric was designated the target value. For set 1, the measured value of ρ and ρ_comp were selected to be within 0.0001 of the target value of ρ and ρ_comp (for S1, S2, S3, and S4) or 0.001 (for S5 and S6).5 Figure 2 shows an example set 1 with 100 noises (closed symbols) compared to an unconstrained distribution with 1000 noises (open symbols). Reported on the figure are the average and standard deviations for s_t(ΔΦ), s_t(ΔL), and ρ_comp. Sets 2 and 3 were designed to “bracket” threshold for values of ρ (i.e., the sets contained stimuli with values of ρ_target above and below a listener’s threshold, but yielded an average P_c for the set near threshold). Twenty-five reproducible stimuli were chosen in total for each set, such that there were five reproducible stimuli for five different ρ_target values. The five stimuli were chosen from an unconstrained distribution of 100 reproducible stimuli with a certain ρ_target. For example, for listener S1 and set 2, stimuli were chosen such that there were five stimuli for each value of ρ_target equal to 0.999, 0.998, 0.995, 0.992, and 0.989 (α_target = 0.05, 0.0625, 0.1, 0.125, and 0.15). For set 2, the stimuli were selected by visual inspection that would approximately maximize the spread of s_t(ΔΦ) and s_t(ΔL) values. For set 3, the stimuli were selected that would maximize the spread of ρ_comp, while the measured values of s_t(ΔΦ) and s_t(ΔL) needed to be within 1° and 0.1 dB of the distribution averages, respectively.

Table 1.

Average (Ave) and standard deviation (SD) of stimulus interaural correlation and interaural difference metrics for an unconstrained distribution at ρ threshold, and for experimental sets. The number of stimuli in each set (N) is reported. Correlations between different stimulus metrics (corr) are also reported. Metrics that are constrained in a set are marked in bold.

	Distribution		Set 1		Set 2		Set 3		Distribution		Set 1		Set 2		Set 3
	Ave	SD	Ave	SD	Ave	SD	Ave	SD	Ave	SD	Ave	SD	Ave	SD	Ave	SD
	Listener S1								Listener S2
ρ	0.9974	0.0002	0.9973	0.0001	0.9961	0.0023	0.9945	0.0037	0.9972	0.0002	0.9972	0.0001	0.9961	0.0023	0.9946	0.0038
ρcomp	0.9964	0.0024	0.9964	0.0001	0.9964	0.0001	0.9930	0.0045	0.9961	0.0028	0.9961	0.0001	0.9961	0.0001	0.9933	0.0043
st(ΔΦ)	6.94	6.44	6.15	1.69	7.92	4.46	6.45	0.50	7.39	7.47	6.16	1.62	8.01	5.41	7.16	0.60
st(ΔL)	0.88	0.50	0.89	0.29	1.27	0.63	0.96	0.16	0.90	0.55	0.85	0.31	11.36	0.80	1.00	0.20
st(ψΔΦ)	1.00	0.31	1.07	0.20	0.88	0.21	1.10	0.14	0.98	0.31	1.06	0.20	0.87	0.28	1.07	0.12
st(ψΔL)	0.89	0.36	0.93	0.25	1.16	0.44	0.98	0.08	0.91	0.38	0.90	0.25	1.17	0.51	0.99	0.08
corr[st(ΔΦ), st(ΔL)]	0.76		0.72		0.71		0.41		0.77		0.71		0.80		0.52
corr[st(ΔΦ), ρcomp]	−0.81		−0.07		0.19		0.26		−0.85		0.14		−0.04		0.20
corr[st(ΔL), ρcomp]	−0.67		−0.12		0.06		0.41		−0.70		0.08		0.19		0.47
N	1000		100		25		25		1000		25		25		25
	Listener S3								Listener S4
ρ	0.9961	0.0001	0.9961	0.0001	0.9961	0.0023	0.9946	0.0037	0.9952	0.0001	0.9953	0.0001	0.9941	0.0030	0.9941	0.0030
ρcomp	0.9950	0.0032	0.9950	0.0001	0.9950	0.0001	0.9926	0.0048	0.9938	0.0039	0.9938	0.0001	0.9938	0.0001	0.9918	0.0040
st(ΔΦ)	7.76	7.03	7.43	2.50	9.32	5.21	7.49	0.60	8.97	8.14	9.25	3.49	9.71	4.70	8.57	0.61
st(ΔL)	0.96	0.54	1.01	0.39	1.45	0.83	1.03	0.10	1.10	0.60	1.29	0.46	1.69	0.83	1.18	0.12
st(ψΔΦ)	1.10	0.35	1.19	0.27	1.03	0.27	1.19	0.14	1.19	0.37	1.32	0.23	1.16	0.30	1.30	0.14
st(ψΔL)	0.98	0.38	1.04	0.29	1.24	0.51	1.03	0.10	1.10	0.42	1.20	0.31	1.46	0.58	1.19	0.10
corr[st(ΔΦ), st(ΔL)]	0.73		0.81		0.89		0.19		0.80		0.70		0.56		0.79
corr[st(ΔΦ), ρcomp]	−0.82		−0.04		−0.01		−0.20		−0.83		0.23		0.36		0.06
corr[st(ΔL), ρcomp]	−0.65		−0.08		0.10		0.33		−0.71		0.16		−0.12		0.06
N	1000		100		25		25		1000		25		25		25
	Listener S5								Listener S6
ρ	0.9862	0.0005	0.9862	0.0005	0.9841	0.0064	0.9841	0.0066	0.9702	0.0017	0.9700	0.0006	—	—	—	—
ρcomp	0.9824	0.0093	0.9824	0.0001	0.9824	0.0001	0.9771	0.0090	0.9620	0.0193	0.9620	0.0006	—	—	—	—
st(ΔΦ)	15.56	11.84	12.86	3.99	14.32	5.85	13.84	0.61	23.46	16.47	19.00	4.54	—	—	—	—
st(ΔL)	1.79	0.82	1.76	0.55	2.31	0.99	1.80	0.08	2.46	1.01	2.60	0.75	—	—	—	—
st(ψΔΦ)	1.84	0.52	1.97	0.37	1.78	0.46	2.03	0.13	2.54	0.66	2.58	0.49	—	—	—	—
st(ψΔL)	1.66	0.50	1.69	0.35	1.94	0.56	1.77	0.09	2.17	0.57	2.23	0.48	—	—	—	—
corr[st(ΔΦ), st(ΔL)]	0.69		0.72		0.77		−0.32		0.59		0.52		—		—
corr[st(ΔΦ), ρcomp]	−0.82		−0.07		−0.15		−0.32		−0.84		−0.02		—		—
corr[st(ΔL), ρcomp]	−0.58		−0.01		−0.24		0.32		−0.43		0.02		—		—
N	1000		25		25		25		1000		100		—		—

Figure 2.

Fluctuations of IPD [s_t(ΔΦ)] vs fluctuations of ILD [s_t(ΔL)] for N=1000 randomly generated stimuli with α=0.088 (open circles). The mean of the distributions (μ) and the standard deviation is reported for s_t(ΔΦ), s_t(ΔL), and ρ_comp. An example experimental set of 100 stimuli, set 1 for listener S3, is also shown (closed circles). Note that some of the 1000 open circles are located outside the plotted area.

Procedure

The procedure mostly followed that used in Goupell and Hartmann (2007b), with some exceptions. The task was a three-interval-two-alternative forced-choice procedure, where the first interval always contained a coherent (ρ = 1) reference noise. One of the following intervals contained the incoherent (ρ < 1) target noise to be detected, while the other contained a coherent noise. Unlike Goupell and Hartmann (2007b) where three different reproducible stimuli were presented in the three intervals, the same reproducible stimulus was presented either coherently (diotic presentation of x_L) or incoherently (dichotic presentation of x_L and x_R) in all three intervals; i.e., x_L was the same in all three intervals and x_R was the same in two intervals. This was done to eliminate the possibility that the listener might confuse monaural envelope cues with interaural decorrelation, which was shown to occur in experiment 5 of Goupell and Hartmann (2006). Listeners indicated the incoherent interval via a response pad. Feedback was provided after each trial.

Threshold measurement

The procedure of Goupell and Hartmann (2007b) included a “confidence judgment” for each forced-choice decision. If a listener was very confident that they could correctly identify the target interval, they were allowed to respond so. This extended the performance range of the experiment because several listeners were near the performance ceiling without confidence judgments in that study. To avoid confidence judgments in the present study, individual sets of stimuli were made for each listener at or near threshold.

Individual thresholds were determined from psychometric functions. Twenty reproducible stimuli were generated for different values of $\alpha =\sqrt{1-{\rho }^2}$ that were constrained in s_t(ΔΦ), s_t(ΔL), s_t(Ψ_ΔΦ), and s_t(Ψ_L).6

The threshold measurements began with a training section that also approximated the range of the psychometric function. Ten stimuli with α = 0.25 (although with constrained interaural differences) were presented to listeners ten times. The percentage of correct responses (P_c) was recorded for each stimulus. The value of α was decreased in steps of 0.025 until listeners had an average P_c < 60% for two values of α in a row. The last value of α tested was repeated, followed by values of α that were increased in steps of 0.025 until listeners had an average P_c > 90% for two values of α in a row. This method determined the approximate endpoints of the psychometric function to be used for the threshold measurement and provided training to the listeners. Two listeners showed some training effects (S2 and S3).

Next, listeners were presented 20 stimuli ten times for various values of α, starting with the last value of α from the training and proceeding in the same fashion as before. Psychometric functions were then calculated by fitting cumulative Gaussian distributions to the average P_c (not including the training data) as a function of α. Threshold corresponded to 75% correct on the psychometric function. Four listeners (S1, S2, S3, and S4) were very sensitive to incoherence with thresholds of ρ = 0.9974 – 0.9952. Two listeners (S5 and S6) were not as sensitive to incoherence with thresholds of ρ = 0.986 and 0.970.

Main experiment

Each stimulus in a set was presented 40 times. The order of stimulus presentation was random in a given set. Listeners were presented with stimuli from set 1, then set 2, and finally set 3. The number of times the target was in the second interval was equal to the number of times it was presented in the third interval.

Stimulus statistics

The purpose of this section is to understand the relationships of different binaural metrics for large groups of noises with various amounts of interaural correlation. Understanding these relationships may provide insight to the psychophysical results.

Figure 3 shows the statistics for distributions of 1000 randomly generated dichotic noise stimuli with various amounts of incoherence. The waveform dissimilarity, α, was used as the independent variable in Fig. 3 because the interaural differences varied in a nearly linearly or logarithmically functional form of α for the interaural differences in Figs. 3B and 3E. Two bandwidths are shown (top row, 10 Hz; bottom row, 100 Hz). The 100-Hz bandwidth is included because several studies on incoherence detection and BMLDs utilize stimuli with bandwidths near 100 Hz at this center frequency (Gilkey et al., 1985; Gilkey and Robinson, 1986; Koehnke et al., 1986; Isabelle and Colburn, 1991; Culling et al., 2001; Evilsizer et al., 2002; Goupell and Hartmann, 2006). Larger bandwidths are not shown because the distributions of the interaural differences become increasingly narrow for large bandwidths, and the statistics of all incoherent stimuli become essentially the same (Goupell and Hartmann, 2006).

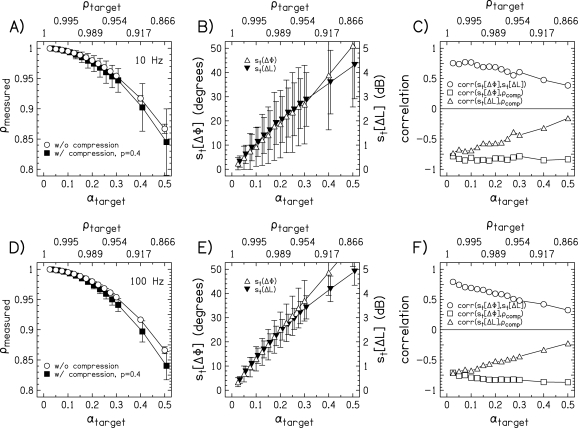
Figure 3.

Distribution statistics for sets of 1000 stimuli at different target values of α. The top axis shows the targeted value of interaural correlation, ρ, for the corresponding value of α. The top row shows data for 10-Hz bandwidth stimuli. The bottom row shows data for 100-Hz bandwidth stimuli. Panels (A) and (D) show the average measured value of ρ for different values of α, without and with envelope compression as open circles and closed squares, respectively. Panels (B) and (E) show the average measured interaural phase fluctuations, s_t(ΔΦ), as open triangles and interaural level fluctuations, s_t(ΔL), as closed triangles. Error bars in panels (A)–(D) represent ±1 standard deviation of the mean. Panels (C) and (F) show the correlation between the stimulus metrics s_t(ΔΦ), s_t(ΔL), and ρ_comp.

Figures 3A and 3D show ρ_measured after stimulus generation for different values of ρ_target. The values of ρ_measured without compression [ρ from Eq. 1] are shown as open circles. The values of ρ_measured with compression [ρ_comp from Eq. 2] are shown by the closed squares. As can be seen from the error bars, which represent the standard deviation of the measurements, the stimuli had a large spread of values of ρ_measured with compression for different values of ρ_target. This shows why it was possible for a variable related to ρ_comp to describe a large proportion of the variance in the data from Goupell and Hartmann (2007b). As expected, for the 100-Hz bandwidth, the spread of ρ_comp values was smaller compared to the 10-Hz bandwidth.

Figures 3B and 3E show how the average and standard deviations of the distributions of s_t(ΔΦ) (open triangles) and s_t(ΔL) (closed triangles) increase with decreasing ρ_target. These means and standard deviations can be compared to those reported for the example in Fig. 2. Again, the spread of s_t(ΔΦ) and s_t(ΔL) is smaller for the larger bandwidth.

Figures 3C and 3F show how s_t(ΔΦ), s_t(ΔL), and ρ_comp are interrelated for individual stimuli for various target correlations. Note that the vertical axis is the correlation between different interaural stimulus metrics, which is different from the target interaural correlation on the horizontal axis. As seen in Goupell and Hartmann (2006, 2007a,b), the values of s_t(ΔΦ) and s_t(ΔL) for an individual stimulus are highly and positively correlated. However, for decreasing ρ_target, s_t(ΔΦ) and s_t(ΔL) become less correlated. It can also be seen that s_t(ΔL) and ρ_comp are highly and negatively correlated, although they become almost uncorrelated for ρ_target = 0.866. The most interesting relationship in panels (C) and (F) is the correlation between s_t(ΔΦ) and ρ_comp, shown by squares. These two stimulus metrics are highly and negatively correlated at approximately −0.8, and this correlation is independent of ρ_target. Another way to think about this is that ρ_comp is a nearly isomorphic statistic to s_t(ΔΦ). This apparently occurs by adding the envelope terms to the interaural correlation, which can be seen in Eq. 2. Indeed, a short-term time-varying interaural correlation was approximated by using the cosine of the IPD, which was developed by Isabelle and Colburn (2004), and was used in Goupell and Hartmann (2007b). Envelope compression by definition reduces ILD variability and thus emphasizes the contribution of phase fluctuations to the interaural correlation. Thus, it may not be surprising that ρ_comp and s_t(ΔΦ) appear to be intrinsically intertwined. The implications of the correlation between ρ_comp and s_t(ΔΦ) are discussed in Sec. 4. For now, returning to the experimental design, it may seem impractical to attempt to choose stimulus sets with unconstrained ρ_comp and constrained s_t(ΔΦ), or vice versa, since they are so strongly correlated. However, by choosing the rarest of randomly generated stimuli [e.g., stimuli that would have the uncommon combination of a large s_t(ΔΦ) and a large ρ_comp], these stimuli may provide an opportunity to discriminate between the CC and interaural difference models.

Results and discussion

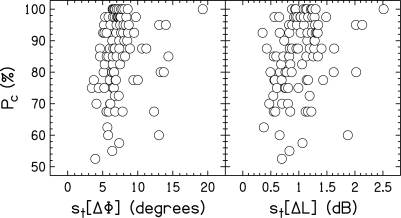
An example of set 1 results from a typical listener is shown in Fig. 4. This figure shows values of P_c placed in order of value of s_t(ΔΦ) (left panel) or increasing value of s_t(ΔL) (right panel). The most important aspect of this figure is that P_c for individual reproducible noises spanned the entire range from guessing to perfect performance. It also shows that attempting to order the stimuli with respect to s_t(ΔΦ) or s_t(ΔL) does not lead to an obvious relationship between those metrics and P_c.

Figure 4.

The detection data for the 100 stimuli in set 1 for listener S3. The stimuli are arranged in increasing order of s_t(ΔΦ) in the left panel. The stimuli are arranged in increasing order of s_t(ΔL) in the right panel.

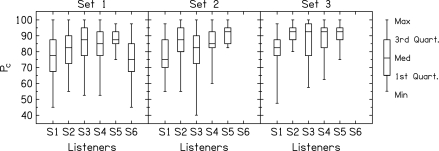
Figure 5 shows the P_c distribution information for each listener and for different sets of stimuli. Note that for this task chance performance should be 50%. Figure 5 shows that for set 1, which was made for the individual listener threshold (and so the median score should be approximately 75%), the median P_c was near 75% for listeners S1 and S6. For the other listeners, the median scores were around 85%, which means they were operating above threshold performance. The maximum scores were always near 100% for all six listeners; the minimum scores were around 50% except for S5, whose minimum score was 75%. A smaller range of scores could possibly be detrimental to model detection scores. Interestingly, since the P_c values for individual reproducible stimuli spanned the maximum range from guessing to perfect performance (with the exception of S5), the two constrained metrics in this set (ρ and ρ_comp), which have a very small range of possible values, are probably unable to describe the wide range in performance.

Figure 5.

P_c from the three different sets for each listener.

For set 2, a similar pattern of performance was found, where the P_c values for individual reproducible stimuli spanned the full range from guessing to perfect performance (again with the exception of S5). Thus, the constrained statistic in this experiment, ρ_comp, is probably unable to describe the variance in the data for these stimuli.

For set 3, a similar pattern of performance was again observed, but now two listeners operated above threshold (S2 and S5). It could have been the case that the average improvement of S2 was due to training. Again, it is interesting that the P_c values spanned the full range from guessing to perfect performance. Thus, the two constrained metrics in this experiment, s_t(ΔΦ) or s_t(ΔL), are probably unable to describe the variance in the data for these stimuli.

The stimulus sets were designed so that P_c values would be approximately constant for the set with the salient stimulus parameter constrained; salient meaning the parameter that is utilized by the binaural system to detect incoherence. Contrary to expectation, the data in Fig. 5 show that there is no set with absolutely constant P_c values. However, it may be the case that one set has relatively constant P_c values. This was checked by converting P_c values for each reproducible noise to rationalized arcsine units (RAUs) (Studebaker, 1985), which linearized the variance in the data so that the standard deviation of sets for different average P_c values could be compared. The standard deviation of the listener RAUs for the reproducible noises, averaged over listeners, was 24.4, 26.3, and 21.0 for sets 1, 2, and 3, respectively. Two-sample t-tests between the sets showed that no set had a significantly smaller spread of RAU scores than another (p > 0.1 for all comparisons). Hence, no set produced relatively more constant values of P_c than another set.

If only one type of metric is used by the binaural system to detect interaural incoherence, such as the interaural correlation or interaural differences, it was hypothesized that the values of P_c in one of the sets used in this experiment would be relatively constant. Since the results show that none of the three sets produce relatively constant performance for any listener, it seems unlikely that any single metric can describe the variance in the reproducible noise data for all three sets. A modeling analysis was therefore done utilizing different forms of the CC and interaural difference models to determine which, if any, model could describe the variance in the data in any set.

MODELING ANALYSIS

Method

The P_c values from each listener and stimulus set were correlated to the stimulus metrics. This was done by using the Pearson-product moment correlation (r²).

Models

Five models were used to describe the psychological data, two interaural difference models and three CC models. The first model was the weighted combination of the fluctuations of the interaural differences:

$$\text{ST}=a\cdot s_t(\Delta \Phi )+(1-a)\cdot s_t(\Delta L),$$ (6)

where a is a weighting parameter that varies between 0 (only ILD) and 1 (only IPD), and s_t is the standard deviation over time. The second model was like the first, only including psychological transformations (see Sec. 2B),

$$\text{ST}(\Psi )=a\cdot s_t({\Psi }_{\Delta \Phi })+(1-a)\cdot s_t({\Psi }_{\Delta L}).$$ (7)

These two models were the best models at describing incoherence detection data for reproducible stimuli (Goupell and Hartmann, 2007b). The ST model was also the best models at describing BMLD data for reproducible stimuli (Davidson et al., 2009). Many other interaural difference models were attempted in Goupell and Hartmann, and Davidson et al., but they resulted in smaller r² values and thus proved to be inferior to these.

The third model was the normalized CC model that utilized ρ from Eq. 1. The fourth model, called CC_comp, was the normalized CC model including compression that utilized ρ_comp from Eq. 2. The fifth model, called CC_PP, was the CC model with several stages of peripheral processing (van de Par, 1998; van de Par and Kohlrausch, 1998; Bernstein et al., 1999). This model utilized a metric, ρ_PP, that included filtering by a fourth-order Gammatone filter centered at 500 Hz, envelope compression with p = 0.46, half-wave rectification, fourth-order low-pass filtering with a 425-Hz cutoff, and an additional second-order low-pass filtering with a 150-Hz cutoff before the calculation of the normalized interaural correlation.

Results and discussion

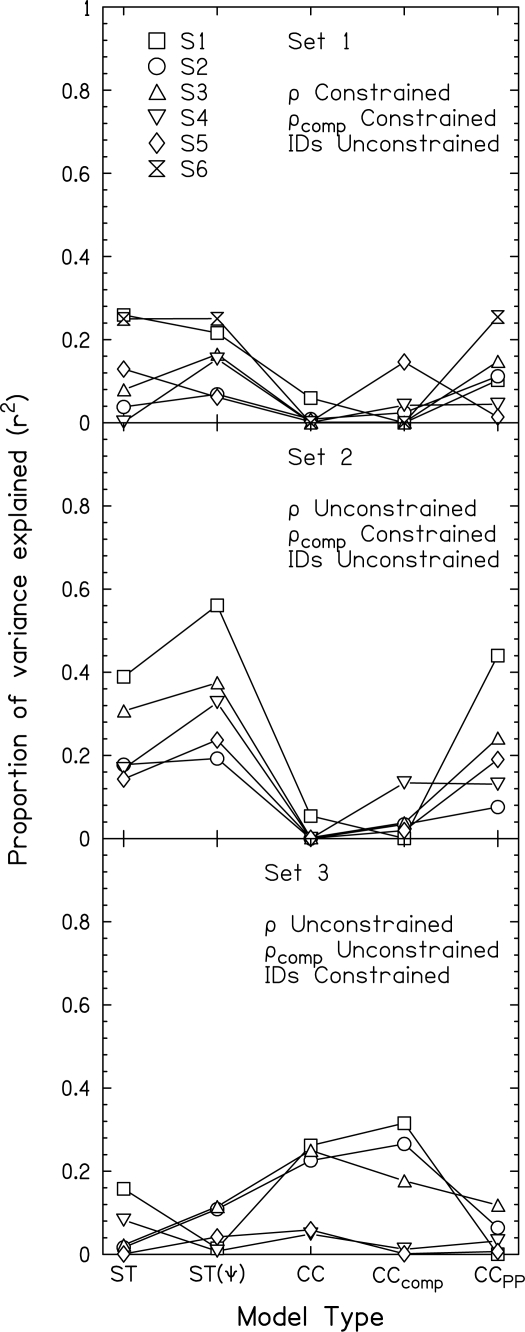
The modeling results for all three sets are shown in Fig. 6. The average proportion of variance described for each model and set is given in Table TABLE II.. For set 1, where s_t(ΔΦ) and s_t(ΔL) were unconstrained, but ρ and ρ_comp were constrained, the proportion of variance explained was worst for the CC and CC_comp models. This was expected due to the design of the stimuli in this set. The ST and ST(Ψ) models described at most 26% of the variance for one listener. For all of the listeners, these two models did not perform noticeably better than the CC and CC_comp models. The CC_PP model performed similarly to the ST and ST(Ψ) models. Note that the ST(Ψ) model performed much better for the data in Goupell and Hartmann (2007b), where it described 76% of the variance. This can be partially explained by the range of stimuli selected in set 1. If the standard deviation of s_t(ΔΦ) and s_t(ΔL) over the “unrestricted” distribution is compared to that in set 1 in Table TABLE I., there is a decrease of about 66%. An example of this reduction can also be seen visually in Fig. 2. This decrease is obviously due to the relationship between s_t(ΔΦ), s_t(ΔL), and ρ_comp shown in Fig. 3C. In other words, it could be that the modeling correlations were so small because the range of s_t(ΔΦ) and s_t(ΔL) was reduced to too small a range.

Figure 6.

The proportion of variance in the detection data explained by each model. The models are the sum of interaural differences (ST), the sum of interaural differences after psychological transformations [ST(Ψ)], the normalized CC, the normalized CC with envelope compression (CC_comp), and the normalized CC model including several other stages of peripheral processing (CC_PP).

Table 2.

Average r² values over listeners for the five different types of models and three sets.

	ST	ST(Ψ)	ρ	ρcomp	ρpp
Set 1	12.6	15.2	1.2	3.6	11.2
Set 2	23.7	33.9	1.1	4.5	21.6
Set 3	5.6	5.8	16.9	15.4	4.4

Similar trends can be seen in the modeling results for set 2. The CC and CC_comp models were the poorer performing while the ST, ST(Ψ), and CC_PP models were the better performing. The amount of variance described for the latter models was larger on average for set 2 compared to set 1, the best being 56% for the ST(Ψ) model for S1. This was probably due to the increase in the spread of s_t(ΔΦ) and s_t(ΔL) over stimuli in set 2 compared to set 1, shown in Table TABLE I.. This was achieved because only ρ_comp was constrained in set 2, not ρ. By having only one metric constrained, it allowed for a larger spread of s_t(ΔΦ) and s_t(ΔL) values for individual stimuli.

A nearly opposite trend can be seen in the modeling results for set 3. In this set, ρ and ρ_comp were unconstrained, and thus the ρ and ρ_comp models did relatively better for three listeners, when compared to the performance of the other models in sets 1 and 2. The other models did generally worse for set 3 compared to the other sets.

A form of the ST(Ψ) model was used in Goupell and Hartmann (2007b) to incorporate some perceptual phenomena; the addition of these transformations increased the amount of variance described by the models. Comparing the ST and ST(Ψ) models for the data in this study, the ST(Ψ) model described more of the variance than the ST model. Table TABLE II. shows that on average, compared to the ST model, the ST(Ψ) models improved r² by 2.6% for set 1, 10.2% for set 2, and 0.2% for set 3. This shows that the transformed interaural differences in the ST(Ψ) model were a better predictor of performance than the physical interaural differences in the ST model.

In all three sets, there appeared to be a correlation between the ST, ST(Ψ), and CC_PP models. The correlation between s_t(ΔΦ) and ρ_PP was −0.87 for all the stimuli from the three sets used in the experiment, and the correlation between s_t(ΔL) and ρ_PP was −0.76. Hence, the strong correlation between the CC and the interaural difference models also extends to the CC model commonly used in the binaural literature. The reason for this strong correlation is partially due to the ρ_PP metric including envelope compression, which was shown to be important for the correlation between ρ_comp and the fluctuations in the interaural differences.

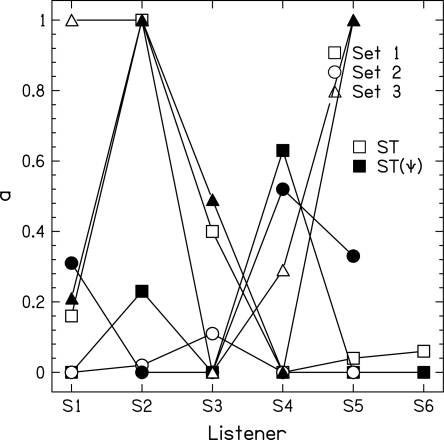
The weighting factor a of IPD vs ILD needed to yield the best results from the ST and ST(Ψ) models is shown in Fig. 7. Both interaural difference models seemed to describe the most variance when weighting ILD fluctuations more heavily than IPD fluctuations, although there are some listeners and sets that favor IPD fluctuations. There are also more relatively equal weightings for the ST(Ψ) model compared to the ST model. A weighting that favors ILDs is contrary to that found in Goupell and Hartmann (2007b), which showed that the most variance was described when IPDs and ILDs had equal weighting for the individual and average listener data. This may be a consequence of constraining ρ_comp or s_t(ΔΦ) in the experiment, which were shown to be highly correlated. This weighting is also contrary to that found in van der Heijden and Joris (2009), who used mixed modulation in binaural detection. They found a weighting that favored ITDs entirely.

Figure 7.

The weighting (a) used to achieve the maximum proportion of the variance explained (r²) by the two interaural difference models for individual listeners and for each set.

GENERAL DISCUSSION

The purpose of this experiment was to utilize sets of reproducible stimuli that could produce detection data that would discriminate between CC and interaural difference models, especially when perceptual and physiological transformations were included. It was hypothesized that detection scores for one of the sets would be nearly constant if the signal parameter constrained in that set was used by the binaural system to detect incoherence. Unfortunately, none of the sets produced constant detection data. Additionally, modeling could account for only a small amount of the variance in the detection data. This is in contrast to Goupell and Hartmann (2007b) who found that interaural difference models and a CC model with compression added were able to describe their reproducible psychophysical data reasonably well. Hence, the experiment failed to determine whether a CC or interaural difference model more accurately describes how the binaural system detects incoherence.

Incoherence detection and BMLD (specifically NoSπ detection) are closely related binaural detection tasks (Koehnke et al., 1986). More effort has been put into modeling NoSπ data with reproducible stimuli (Gilkey et al., 1985; Gilkey and Robinson, 1986; Isabelle and Colburn, 1991; Evilsizer et al., 2002; Isabelle and Colburn, 2004; Davidson et al., 2009) than incoherence detection data with reproducible stimuli (Goupell and Hartmann, 2007b). The recent work from Davidson et al. (2009) modeled many BMLD reproducible stimuli sets with bandwidths of 50, 100, and 2900 Hz with an extensive number of binaural models ranging in sophistication. In the end, they found that the ST model (their W_ST model) described the most variance over the different sets of data, but the amount of variance described was unimpressively small. Therefore, their modeling results of binaural detection are fairly consistent with the poor modeling results of this experiment.

There could be several reasons as to why the currently described experiment produced a lack of noteworthy results. First, some changes to the methods were made compared to Goupell and Hartmann (2007b). For example, confidence judgments were removed by providing stimulus sets near the individual listener threshold. Recent work by Culling (2007) described an experiment where the performance of an EC and CC model can be discriminated. If the NoSπ stimuli were above listener threshold, it was shown that the EC model could predict the data but the CC model could not. Perhaps by choosing stimuli in this study near threshold, as opposed to above threshold as in Goupell and Hartmann (2007b), the ability to distinguish between interaural difference and CC models was lost. Nonetheless, P_c scores spanned the full range of guessing to perfect performance in this study (see Figs. 4 and 5). Perhaps the saturation of the performance near the floor and ceiling caused factors like internal noise to dominate the experimental results, which would tend to reduce r² values. Another change to the procedure was that monaural envelope effects were removed in this study by presenting the same reproducible stimulus, either diotically or dichotically, in all three intervals. Goupell and Hartmann (2006) showed the potential for confusions in binaural tasks due to monaural effects. Therefore, the removal of this confounding effect would most likely improve the modeling results, not worsen them.

The poor modeling results are more likely due to the range of values of s_t(ΔΦ), s_t(ΔL), and ρ_comp, which were much smaller (a reduction of 66%) in this experiment compared to Goupell and Hartmann (2007b). This was a consequence of trying to constrain different signal metrics in this study. The data from Goupell and Hartmann (2007b) were reanalyzed with a reduced range of s_t(ΔΦ) and s_t(ΔL) values to evaluate this effect. The average confidence-adjusted data (not P_c) from three listeners were analyzed and only the ST model was used. For the 100 stimuli of that experiment, the original r² was equal to 0.48 (r = 0.69). If only stimuli from within ±0.5 standard deviations of the mean of the s_t(ΔΦ) − s_t(ΔL) distribution are used, there are 20 stimuli and r² becomes 0.005 (r = 0.07). If the range is reduced to that comparable to that used in set 1 of this study, there are eight stimuli and r² becomes 0.29 (r = −0.54). Therefore, the stimuli with very large and very small interaural fluctuations were most likely dominating the correlations found in that study. The surprisingly large negative correlation found for the very middle of the distribution of Goupell and Hartmann (2007b) for the smallest range in the data reanalysis may be due to the above mentioned differences between the studies, such as the monaural effects.

The basic approach of binaural detection modeling has been to attempt to separate models into categories like interaural correlation and interaural difference models. However, it may be that binaural detection involves some combination of these metrics. For example, Faller and Merimaa (2004) developed a sound localization model for complex listening environments, such as rooms. This model utilized the ITDs and ILDs only when the signal was reasonably coherent. Such a model is attractive from the standpoint that it processes localization information only at times when conflicting information (e.g., room reflections) is absent. Although it has been shown that interaural differences and the value of the interaural coherence are strongly correlated, a novel combination of the metrics may improve modeling attempts.

Another consideration is the role of the stimulus and internal neural variability. The bandwidth of the stimuli in this study was only 10 Hz, which results in very slow changes in the envelope and fine-structure of the stimuli. Despite the small bandwidth, it may be that the stimulus variability is too large for attempting to model 250-ms reproducible stimuli. Perhaps listeners are utilizing only short portions of the stimuli, as would occur in a multiple-looks model (Viemeister and Wakefield, 1991). Minimizing the number of “looks” possible for a stimulus (i.e., shorter stimuli) may improve modeling attempts. For the internal variability, Shackleton and Palmer (2006) showed that although there was a measurable proportion of stimulus variability between different reproducible stimuli, it was quite small compared to the intrinsic neural variability when measuring discharge rates in inferior colliculus neurons in the guinea pig. However, as admitted by Shackleton and Palmer (2006), the population response to reproducible incoherent stimuli may be different than the single-unit responses that they measured. If internal neural variability truly dominates detection of incoherence, the result from this study that P_c scores varied from guessing to perfect performance (see Figs. 4 and 5) when the interaural correlation and∕or interaural differences were constrained would be difficult to explain. If internal noise dominated the measurements, then there should be very few values near 100%. Thus, although neural variability surely plays some role in incoherence detection with reproducible stimuli, using reproducible stimuli still seems to be a useful tool in understanding binaural detection.

The most intriguing result from this study was the relationship between the interaural correlation with envelope compression (ρ_comp) and the fluctuations in the IPD [s_t(ΔΦ)], which was shown in Fig. 3C. Logically, the value of the interaural correlation is related to the time-varying IPD and ILDs for randomly generated noises. However, the studies by Goupell and Hartmann (2006, 2007a,b) attempted to show that the value of the interaural correlation could not adequately describe all sets of psychophysical data because the interaural correlation is only an approximation of the time-varying IPDs and ILDs. This approximation holds reasonably well for large bandwidth stimuli, but becomes a worse approximation as the bandwidth decreased. In the present experiment, Fig. 3 shows that the measured interaural correlation with envelope compression and the fluctuations in the IPD were negatively correlated at about 0.8, independent of the targeted interaural correlation. Said another way, adding envelope compression to a binaural stimulus produces an interaural correlation statistic that is nearly isomorphic to the standard deviation of the IPD over time. It may be the case that the success of CC or interaural difference models to describe binaural detection is due to this near isomorphism of binaural metrics. Therefore, it seems that the method of using reproducible stimuli and more sophisticated binaural models has come full circle to the work of Domnitz and Colburn (1976): Not only is it the case that “all binaural detection models in the literature are closely related to [interaural difference or interaural correlation models]” (Domnitz and Colburn, 1976, p. 598) but it is also the case that due to the modification of those models over the years, they are much more closely related to each other than was previously thought, at least for data near threshold.

Further insight on the understanding of ρ_comp might be gained from work by Buss et al. (2003) showing that the CC model including compression could not describe NoSπ thresholds for short duration signals placed at masker minima or maxima. It was argued that listeners could “listen in the dips” when signals were placed in a masker minimum, thus yielding lower NoSπ thresholds. Therefore, those data not only favor a model that uses time-varying ITDs and ILDs but also favor modeling attempts over shorter time scales around tens of milliseconds long.