The feasibility of patient size-corrected, scanner-independent organ dose estimates for abdominal CT exams

Abstract

Purpose: A recent work has demonstrated the feasibility of estimating the dose to individual organs from multidetector CT exams using patient-specific, scanner-independent CTDI_vol-to-organ-dose conversion coefficients. However, the previous study only investigated organ dose to a single patient model from a full-body helical CT scan. The purpose of this work was to extend the validity of this dose estimation technique to patients of any size undergoing a common clinical exam. This was done by determining the influence of patient size on organ dose conversion coefficients generated for typical abdominal CT exams.

Methods: Monte Carlo simulations of abdominal exams were performed using models of 64-slice MDCT scanners from each of the four major manufacturers to obtain dose to radiosensitive organs for eight patient models of varying size, age, and gender. The scanner-specific organ doses were normalized by corresponding CTDI_vol values and averaged across scanners to obtain scanner-independent CTDI_vol-to-organ-dose conversion coefficients for each patient model. In order to obtain a metric for patient size, the outer perimeter of each patient was measured at the central slice of the abdominal scan region. Then, the relationship between CTDI_vol-to-organ-dose conversion coefficients and patient perimeter was investigated for organs that were directly irradiated by the abdominal scan. These included organs that were either completely (“fully irradiated”) or partly (“partially irradiated”) contained within the abdominal exam region. Finally, dose to organs that were not at all contained within the scan region (“nonirradiated”) were compared to the doses delivered to fully irradiated organs.

Results: CTDI_vol-to-organ-dose conversion coefficients for fully irradiated abdominal organs had a strong exponential correlation with patient perimeter. Conversely, partially irradiated organs did not have a strong dependence on patient perimeter. In almost all cases, the doses delivered to nonirradiated organs were less than 5%, on average across patient models, of the mean dose of the fully irradiated organs.

Conclusions: This work demonstrates the feasibility of calculating patient-specific, scanner-independent CTDI_vol-to-organ-dose conversion coefficients for fully irradiated organs in patients undergoing typical abdominal CT exams. A method to calculate patient-specific, scanner-specific, and exam-specific organ dose estimates that requires only knowledge of the CTDI_vol for the scan protocol and the patient’s perimeter is thus possible. This method will have to be extended in future studies to include organs that are partially irradiated. Finally, it was shown that, in most cases, the doses to nonirradiated organs were small compared to the dose to fully irradiated organs.

INTRODUCTION

The radiation exposure associated with computed tomography (CT) imaging procedures has been identified as a significant component of the total medical radiation exposure to the population of the United States.¹ While the specific stochastic risks from low levels of ionizing radiation are difficult to precisely determine, it has been suggested that the most appropriate quantity for assessing the risk due to diagnostic imaging procedures is the radiation dose to individual organs.^{2, 3, 4, 5, 6}

Currently, the standard method to measure and monitor radiation dose from CT utilizes the CT dose index (CTDI) paradigm.^{7, 8} These metrics were designed to approximate the average dose to the central slice of a cylindrical polymethylmethacrylate phantom from a contiguous axial or helical exam with a scan length much greater than the width of the x-ray beam. Typically, CT manufacturers report the volume CTDI (CTDI_vol) value on the scanner control console for each exam based on the scan protocol. Recently, new dose metrics have been suggested that address the limitations of CTDI to characterize modern multidetector row CT (MDCT) scanners with wider nominal beam widths (e.g., 40–160 mm).⁹ It is important to note that each of these metrics quantify dose to a simple, homogenous phantom and are not meant to directly indicate a dose value that should be associated with any particular organ in any particular patient.

A recent work by Turner et al.¹⁰ demonstrated the feasibility of using CTDI_vol values to account for differences among 64-slice MDCT scanners from various manufacturers when estimating organ doses in patients. It was shown that CTDI_vol values vary across scanners in a similar fashion as organ doses obtained from scanner-specific Monte Carlo simulations. As a result, when organ doses from each scanner were normalized by the corresponding CTDI_vol, the variation across scanners reduced from 31.5% (without normalization) to 5.2% (after normalization with CTDI_vol) on average across all radiosensitive organs. The authors concluded that it was feasible to generate scanner-independent CTDI_vol-to-organ-dose conversion coefficients for each organ that could be used to estimate organ doses from a full-body scan for any scanner to within approximately 10% of the dose values obtained through detailed Monte Carlo simulations.

That study by Turner et al.¹⁰ was performed by simulating 120 kVp full-body (head to toe) helical exams using a single patient model, namely, an adult female (Irene) from the GSF family of voxelized phantoms.^{11, 12} As a result, the reported CTDI_vol-to-organ-dose conversion coefficients were valid only for that specific scan protocol and patient model. Several investigators^{13, 14, 15, 16} have demonstrated that patient size has a significant effect on the absorbed dose and, even more specifically, on organ dose for a specific scanner output (e.g., CTDI_vol). These reports have all shown that for the same exposure conditions (i.e., same technical parameter settings), organs in smaller patients (including pediatric patients) receive higher radiation doses than those in larger patients.

Therefore, the purpose of this study was to extend the work of Turner et al.¹⁰ by determining the effects of patient size on CTDI_vol-to-organ-dose conversion coefficients. Specifically, this study focused on abdominal scans using a cohort of eight voxelized patient models that represented a range of sizes from infant to large adult that included males and females. Since an abdominal exam does not cover the entire body, some organs will be fully included in the scan region (fully irradiated, such as kidney and liver), some will be only partly located within the scan region (partially irradiated, such as colon), and some will be fully outside the scan region (nonirradiated, such as thyroid). The primary focus of this investigation is on the radiation dose to those organs that are fully irradiated during the abdominal scan. The radiation dose to partially and nonirradiated organs is also considered, but is not the primary focus.

MATERIALS AND METHODS

Patient models

The patient models used to obtain organ dose values for this work were the GSF family of voxelized phantoms.^{11, 12} These voxel-based models were created from high resolution CT or magnetic resonance images using automated, semiautomated, and manual segmentation techniques. Each patient model is comprised of a three-dimensional matrix of numbers, each of which corresponds to a different organ or nonanatomic material (such as air or the patient bed).

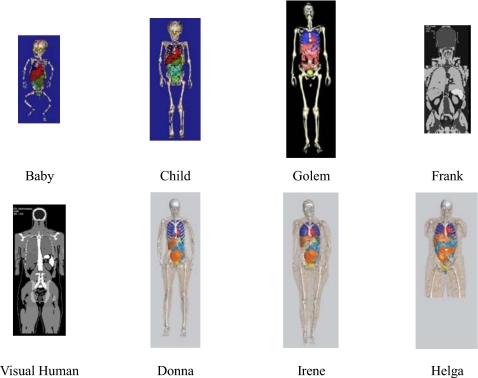
For this study, eight different models were used (shown in Fig. 1) that included two pediatric models (Baby and Child), three adult males (Golem, Frank, and Visible Human), and three adult females (Irene, Donna, and Helga). Additional information about these models is provided in Table 1. While some members of the GSF family are not whole-body models, each model included the full abdominal region along with a similar set of contoured abdominal organs and thus was appropriate for simulations of typical abdominal CT exams.

Figure 1.

Illustrations of the GSF family of voxelized phantoms as described in Petoussi-Henss et al. (Ref. ¹¹) and Fill (Ref. ¹²). Additional information provided in Table 1.

Table 1.

Information about the GSF family of voxelized models as described in Petoussi-Henss et al. (Ref. ¹¹) and Fill et al. (Ref. ¹²).

Name	Gender	Age	Phantom type	Weight (kg)	Height (cm)	Scan length (cm)a	Perimeter (cm)b
Baby	Female	8 weeks	Whole body	4.2	57	15.2	36.3
Child	Female	7 yr	Whole body	21.7	115	24.8	59.7
Golem	Male	38 yr	Whole body	68.9	176	31.2	87.4
Frank	Male	48 yr	Torso and head	(65.4)c	(96.5)c	26.0	124.5
Visible Human	Male	38 yr	From knees upward	103.2 (87.8)c	180 (125)c	33.0	102.9
Irene	Female	32 yr	Whole body	51	163	25.5	66.5
Donna	Female	40 yr	Whole body	79	170	29.0	95.0
Helga	Female	26 yr	From midthigh upward	81 (76.8)c	170 (114)c	33.0	106.2

^aRefers to abdominal scan length defined as ∼1 cm superior to the top of the diaphragm to ∼1 cm inferior to the illiosacral joint.

^bRefers to perimeter of the phantom taken from the central slice of the scan region.

^cData in parentheses refer to the weight or height of the voxelized phantom; data not in parentheses refer to the weight or height of the actual patient whose images were used to generate the model.

It has been suggested that organ dose values can be characterized using patient perimeter as a metric for patient size.¹⁴ Therefore, the perimeter of the central slice of the scan region for each patient was determined (in cm) and is included in Table 1. Perimeter values were obtained using a graphics software package that featured a semiautomated segmentation tool. A contour was placed around the outside of the patient and its length was recorded.

Each patient model provided by the GSF was converted into a standardized data format for use with the Monte Carlo simulation package described below. Twenty distinct materials, including various anatomical tissues whose composition and density were defined by the ICRU Report 44,¹⁷ air, and graphite (for the patient bed) were used in this work. As described by Turner et al.,¹⁰ for each material, the mass energy-absorption coefficient (μ_en∕ρ) was generated based on the values reported by Hubbell and Seltzer¹⁸ for energies ranging from 1 to 120 keV.

The GSF patient models were originally constructed with their arms down at their sides. In the majority of abdominal CT exams, the patient’s arms are positioned up and out of the scan region. Because this study focuses on abdominal scans, it is desirable to avoid extra beam attenuation due to arm tissue that typically would not be present in an actual exam. Since it was not possible to alter the placement of the GSF arm tissue, all voxels belonging to the arms were set to air, effectively removing the arms from the scan region. This was done for all patient models except for the Baby model, since it is common to allow an infant’s arms to remain down in actual exams.

The CT scanners and exam protocols

This study included a third generation, 64-slice MDCT scanner from each of the four major CT scanner manufacturers: The LightSpeed VCT (GE Healthcare, Waukesha, WI), Brilliance CT 64 (Philips Medical Systems, Cleveland, OH), SOMATOM Sensation 64 (Siemens Medical Solutions, Forcheim, Germany), and Aquilion 64 (Toshiba Medical Systems, Inc., Otawara-shi, Japan). All scanners are equipped with x-ray beam filtration that includes from one to three available bowtie filters.

In order to ensure that the dosimetry simulations performed for this study were as comparable as possible across scanner models, all simulations were carried out using a tube voltage of 120 kVp, the bowtie filter designed for the adult body, and the widest available collimation setting for each scanner. Consequently, the selected bowtie filter was kept constant for each scanner, even when smaller sized patient models (including pediatric) were being simulated. While it is recognized that this may not be how some scanners would be used in a clinical setting, keeping the bowtie filter selection constant across patient models allowed the effect of patient size to be isolated under constant source conditions. The selected nominal beam width and detector configuration settings were 40 mm (i.e., 64×0.625 mm) for the LightSpeed VCT, 40 mm (i.e., 64×0.625 mm) for the Brilliance CT 64, 28.8 mm (i.e., 24×1.2 mm) for the Sensation 64 scanners, and 32 mm (i.e., 64×0.5 mm) for the Aquilion 64. The simulation package described below models the actual longitudinal beam width of each scanner (defined as the FWHM of the longitudinal dose profile measured with Optically stimulated luminescence strips), which are 42.4 mm for the LightSpeed VCT, 43.7 mm for the Brilliance CT 64, 32.2 mm for the Sensation 64, and 36.9 mm for the Aquilion 64. All organ dose simulations were performed as helical scans with a pitch value of 1, even if the scanner cannot actually perform a scan of pitch 1. Each scanner was randomly assigned an index number, either 1, 2, 3, or 4, and will be referred to by its assigned index from this point on.

Physically measured CTDI values

Conventional techniques⁸ were performed to measure exposure and calculate CTDI_vol values for scanners 1–4. All exposure measurements were acquired with a standard 100 mm pencil ionization chamber and a calibrated electrometer using a 1 s rotation time and a sufficiently high mA s value (ranging from 200–300 mA s∕rotation) to ensure reproducible measurements. For this work, CTDI_vol values were obtained using a 32 cm diameter (body) CTDI phantom using the tube potential, beam collimation, and bowtie filter settings described in Sec. 2B. The resulting CTDI_vol values were recorded on a per mA s∕rotation basis (denoted mGy∕mA s).

Organ dose simulations

Overview of Monte Carlo simulation techniques

All organ doses were obtained using a previously described MDCT simulation package¹⁹ that was built on the MCNPX (Monte Carlo N-Particle eXtended v2.7.a)^{20, 21} radiation transport code. The MCNPX code allows users to specify the initial position, direction of flight, and energy of a large number of source photons which are each transported through a defined geometry where various quantities, such as photon energy fluence, can be tallied in regions of interest. In order to model specific MDCT scanners, the standard MCNPX source code was modified so that the initial position and direction of each source photon was randomly selected based on scanner-specific geometry specifications (i.e., source to isocenter distance, fan-angle, etc.) and the energy was determined by randomly sampling the energy spectrum of the scanner of interest. Attenuation due to filtration (including the bowtie filter) was modeled by altering the statistical weight of each source photon’s contribution to the final tally as a function of the filter material and the path length it traverses for its given trajectory based on the scanner-specific filtration description.

For each of the scanners used in this study, the scanner-specific energy spectra and filtration descriptions were generated based on the “equivalent source” method described by Turner et al.,²² with a correction applied to the equivalent bowtie profile generation method to account for the inverse-square intensity drop off of the bowtie profile measurements. Center and periphery CTDI₁₀₀ simulations using both the 32 cm diameter (body) and 16 cm diameter (head) CTDI phantoms were performed and compared to CTDI₁₀₀ values derived from analogous measurements in order to validate the accuracy of the corrected equivalent source models. CTDI₁₀₀ simulations agreed with measurements to within 1.3%, 0.9%, 2.1%, and 3.5% on average across all center and periphery CTDI₁₀₀ values for scanners 1–4, respectively.

Organ dose simulations were performed in photon mode with a low energy cutoff of 1 keV. This approach assumed that all transferred energy is deposited at the interaction site, creating a condition of charged particle equilibrium (CPE). The dose calculations utilized the assumption that under conditions of CPE, the absorbed dose is equal to the collision kerma. Therefore, the dose contributed by each source photon was calculated by first tracking the energy fluence in regions of interest within a patient model using the MCNPX^*F4 tally type.^{20, 21} Then, the energy fluence value was converted to collision kerma by multiplying by the material and energy dependent mass energy-absorption coefficients (μ_en∕ρ) using the MCNPX dose energy and dose function cards.^{20, 21} In this manner, the dose in regions of interest was tallied in mGy∕simulated source photon. For all simulations performed in this study, the number of photon histories was selected to ensure statistical simulation errors less than 1% for all tallies.

Since the MCNPX code reported dose values on a per simulated source photon basis (mGy∕source photon), the simulation results did not take into account the change in absolute photon fluence due to varying the beam collimation. So, in order to accurately model the fluence characteristics for each scanner’s selected beam width, the simulation results were each converted to absolute dose per total mA s (from mGy∕source photon to mGy∕total mA s) using the normalization technique described by DeMarco et al.¹⁹ Note that total mA s is the cumulative mA s value over the entire scan, not the mA s value typically quoted by the scan protocol which refers to mA s∕rotation (total mA s=mA s∕rotation×number of rotations). Specifically, scanner-specific Monte Carlo normalization factors were derived for each MDCT scanner as the ratio of 120 kVp CTDI₁₀₀ values (mGy∕total mA s) calculated from in-air exposure measurements and corresponding 120 kVp CTDI₁₀₀ in-air simulations (mGy∕source photon).

Abdominal exam simulations

For scanners 1–4, Monte Carlo simulations of helical exams that utilized the scanning protocol described in Sec. 2B were performed using each of the GSF patient models described in Sec. 2A. For each patient model, the abdominal scan region was defined as approximately 1 cm superior to the top of the diaphragm to approximately 1 cm inferior to the illiosacral joint. It should be noted that this is the region over which the x-ray source is turned on, not just the usual extent of image data and, therefore, is meant to include the effect of overscan that typically occurs for these MDCT scanners on organ doses. The resulting scan length for each patient model is reported in Table 1. Using the simulation process outlined in Sec. 2D1, doses (in mGy∕total mA s) were tallied for each of the ICRP Publication 103 (Ref. ⁵) radiosensitive organs included in each patient model. Finally, in order to account for the differences in total mA s across scanners due to the variation in the number of rotations necessary to traverse the scan length, organ dose values were converted into units of mGy∕mA s (where mA s refers to mA s∕rotation) by multiplying each mGy∕total mA s value by the total number of rotations used in the corresponding helical scan simulation (from mGy∕total mA s to mGy∕mA s).

Data analysis

CTDI_vol normalized organ doses

Each simulated abdominal helical scan resulted in a unique organ dose value for each patient and scanner combination. Adopting the convention introduced by Turner et al.,¹⁰ these organ dose values will be denoted as D_P,S,O, where P refers to the patient model, S to scanner, and O to organ. Each dose value (D_P,S,O) was normalized by the measured CTDI_vol value (also in mGy∕mA s) corresponding to the simulated scanner, resulting in a unitless value, denoted nD_P,S,O. It should be emphasized that organ doses for all patient models, including pediatric patients, were normalized by the CTDI_vol measured with the 32 cm diameter (body) phantom in order to hold all study parameters constant except for patient model. For each patient and organ combination, the average nD_P,S,O was calculated across scanners and denoted ${\overline{nD}}_{P,O}$ (where ${\overline{nD}}_{P,O}=1∕4{\sum }_{S}n{D}_{P,S,O}$).

Organ coverage analysis

In a scan of the abdomen, there are several ICRP Publication 103 (Ref. ⁵) radiosensitive organs that are expected to be completely contained within the anatomically defined scan region (e.g., stomach, liver, kidney), while others may only be partially encompassed by the scan (e.g., colon, lung, and breast) and still others that are entirely outside of the scan region’s boundaries (e.g., testis, brain, and thyroid). The majority of dose to anatomy located within the scan region is due to direct radiation from the CT source and, conversely, any dose to anatomy outside the scan region can be attributed to scattered radiation.

For each patient model, the fraction of each organ’s volume that was included in the scan region was calculated (denoted percent coverage). Based on the value of its percent coverage, each organ was classified as either “fully irradiated” (i.e., percent coverage of 100% for all patient models), “partially irradiated” (percent coverage greater than 0% in at least one patient model and less than 100% in at least one patient model), or “nonirradiated” (percent coverage of 0% for all patient models; these organs are expected to receive only scattered radiation as they are outside the scan region). Not all radiosensitive organs were found in each patient as some organs are gender-specific and others were not explicitly contoured in one or more models.

Seven organs were fully irradiated in all of the patients, including the liver, stomach, adrenals, kidney, pancreas, spleen, and gall bladder. Thirteen organs were identified as partially irradiated including the colon, small intestine, heart, ovaries, uterus, lung, esophagus, glandular breast tissue, skin, muscle tissue, red bone marrow, bone surface (endosteal tissue), and bladder. Finally, seven organs were identified as being completely absent from the scan region for all patient models, including the testis, thyroid, brain, salivary glands, extrathoracic region, prostate, and thymus.

Fully irradiated organ analysis

First, in order to demonstrate the validity of scanner-independent CTDI_vol-to-organ-dose conversion coefficients (as reported by Turner et al.¹⁰ for one patient model) for all the patient models used in this study, the coefficients of variation (CoVs) across scanners of the nD_P,S,O values were determined for fully irradiated organs in all eight patient models. The CoV across scanners was calculated as the standard deviation of nD_P,S,O values divided by the mean (i.e., ${\overline{nD}}_{P,O}$).

Then, for each fully irradiated organ, the relationship between ${\overline{nD}}_{P,O}$ values and patient size was investigated. For each fully irradiated organ, ${\overline{nD}}_{P,O}$ was plotted as a function of patient perimeter to determine if a correlation exists. Based on the plots, exponential regression equations were obtained in the form of

$${\overline{nD}}_{P,O}=A_O\text{\hspace{0.17em}exp}\left(B_O\times \text{perimeter}\right),$$ (1)

where unique A_O and B_O values (denoted size coefficients) exist for each organ. The correlation coefficient (R²) of the exponential fit was also obtained for each organ.

Partially irradiated organ analysis

The GSF models described above were generated from actual patient models and thus reflect realistic variations in the placement, shape, and size of organs. As a result, the fraction of each partially irradiated organ’s volume located within the abdominal scan region (denoted percent coverage) is expected to differ across all patient models. In order to quantify this variation, the average and standard deviation of percent coverage was determined for each partially irradiated organ across patients.

In order to determine if a size dependency exists between ${\overline{nD}}_{P,O}$ values and patient size for partially irradiated organs, a similar regression analysis as described in Sec. 2E3 was performed. Correlation coefficients (R²) were determined for each organ to assess the association between ${\overline{nD}}_{P,O}$ and patient perimeter.

Nonirradiated organ analysis

Organs that were not directly exposed to primary x-ray radiation received the majority of their dose from scattered x rays, and, therefore, were expected to have very low associated dose values relative to directly exposed organs. In order to perform a quantitative comparison, the ratio of each nonirradiated organ’s ${\overline{nD}}_{P,O}$ value to the mean ${\overline{nD}}_{P,O}$ across the fully irradiated organs was calculated and expressed as a percentage.

RESULTS

Fully irradiated organ results

The CoV across scanners of nD_P,S,O values, expressed as a percentage, were less than 10% for all fully irradiated organs in all patients. Specifically, the CoV values ranged from 3.2% to 9.8% across all patients and organ combinations. These results verify that for all fully irradiated organs, the mean CTDI_vol normalized dose across scanners is a sufficient approximation of the value specific to any particular scanner (i.e., ${\overline{nD}}_{P,O}\cong n{D}_{P,S,O}$ for any S). This analysis agrees with the results of Turner et al.,¹⁰ which was performed for a single patient model. This demonstrates that ${\overline{nD}}_{P,O}$ values can serve as scanner-independent CTDI_vol-to-organ-dose conversion coefficients for each fully irradiated organ for all the patient models used in this study.

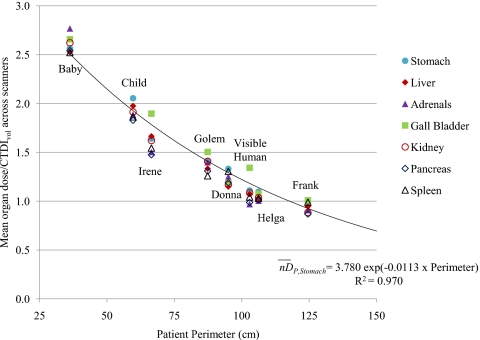
For each fully irradiated organ, a plot of ${\overline{nD}}_{P,O}$ values as a function of patient perimeter is shown in Fig. 2, which indicates a decreasing exponential relationship (the exponential regression line and equation for stomach is displayed as an example). Exponential regression equations, as described by Eq. 1, were obtained for each fully irradiated organ. The size coefficients (A_O and B_O), along with the correlation coefficient of the exponential regression analysis (R²), are displayed in Table 2. The correlation coefficients are all ≥0.95, indicating that perimeter is an excellent predictor of ${\overline{nD}}_{P,O}$ values for fully irradiated organs.

Figure 2.

nD_P,O (mean organ dose∕CTDI_vol across scanners) as a function of patient perimeter (in cm). The exponential regression curve, equation, and correlation coefficient for stomach are shown as an example.

Table 2.

Results of exponential regression analysis describing ${\overline{nD}}_{P,O}$ as a function of perimeter (cm) for fully irradiated organs.

Organs	Exponential regression coefficients		Correlation coefficient
	AO	BO	R2
Liver	3.824	−0.0120	0.98
Stomach	3.780	−0.0113	0.97
Adrenals	4.029	−0.0128	0.95
Kidney	3.969	−0.0124	0.99
Pancreas	3.715	−0.0122	0.97
Spleen	3.514	−0.0111	0.95
Gall bladder	3.994	−0.0115	0.95

Partially irradiated organs

The percent coverage of each partially irradiated organ is reported in Table 3 for each patient model. A large portion of organs such as colon and small intestine were included for almost all patient models. Other organs (i.e., lung, esophagus, skin, etc.) had 50% or less of their volume encompassed by the scan for all patient models. Finally, a number of organs, such as ovaries, uterus, glandular breast tissue, and bladder, were fully or partially scanned in some patient models, while not irradiated at all in others. It should be noted that for patients models that were not whole-body (Frank, Visible Human, and Helga), the percent coverage values are artificially high for truncated organs, such as skin, muscle, and bone, relative to their values if they were whole-body models.

Table 3.

Percent coverage of each partially irradiated organ (i.e., percentage of organ volume located within the abdominal scan region). The last two columns report the average and standard deviation across patient models. A dash indicates that the organ was not included for the given patient model.

	Baby	Child	Golem	Frank	Visible Human	Irene	Donna	Helga	Avg	SD
Colon	87	91	83	80	76	76	81	98	84	8
Small intestine	100	98	81	65	90	39	58	87	77	21
Heart	59	86	53	50	50	15	51	61	53	19
Ovaries	100	100	–	–	–	0	0	0	40	55
Uterus	100	95	–	–	–	0	0	0	39	53
Lung	45	50	32	30	30	16	29	43	34	11
Esophagus	40	–	33	42	37	8	29	39	32	12
Glandular breast tissue	0	–	–	0	–	6	88	61	31	41
Skin	38	23	20	31a	27a	16	19	38a	26	9
Muscle tissue	31	28	19	30a	22a	19	20	26a	24	5
Red bone marrow	26	21	18	19a	24a	16	18	28a	21	4
Bone surface	27	22	19	20a	25a	17	19	29a	22	4
Bladder	54	17	0	0	0	0	0	0	9	19

^aPercent coverage value is artificially high because a portion of the actual organ anatomy was truncated when the partial-body model was generated.

An exponential regression analysis to determine how ${\overline{nD}}_{P,O}$ varied as a function of patient perimeter was performed for the partially irradiated organs. Table 4 shows the correlation coefficient of the regression analysis relative to the average and standard deviation of the percent coverage of each organ (last two columns in Table 3). For almost all of the partially irradiated organs, a strong exponential correlation does not exist between ${\overline{nD}}_{P,O}$ and patient perimeter. The only exception is the colon, which had a relatively high percent coverage (average across patients of 84%) with a relatively low standard deviation across patient models (8%) compared to other organs. The correlation coefficients did not appear to be directly related to either the average percent coverage or the standard deviation of the percent coverage across patient models.

Table 4.

Average and standard deviation of the percent coverage of each partially irradiated organ and the correlation coefficient resulting from the exponential regression relating ${\overline{nD}}_{P,O}$ to perimeter.

Organ	Correlation coefficient	Average percent coverage	Standard deviation of percent coverage
Colon	0.94	84	8
Small intestine	0.62	77	21
Heart	0.51	53	19
Ovaries	0.52	40	55
Uterus	0.60	39	53
Lung	0.56	34	11
Esophagus	0.29	32	12
Glandular breast tissue	0.02	31	41
Skina	0.29	26	9
Muscle tissuea	0.63	24	5
Red bone marrowa	0.70	21	4
Bone surfacea	0.67	22	4
Bladder	0.56	9	19

^aAverage and standard deviation of the percent coverage is artificially high because a portion of Frank, Visible Human, and Donna’s actual organ anatomy was truncated when partial-body models were generated.

Nonirradiated organs

In order to evaluate the magnitudes of the doses received by nonirradiated organs, their ${\overline{nD}}_{P,O}$ values were compared to those of the fully irradiated organs. Table 5 reports the percent ratio of each nonirradiated organ’s ${\overline{nD}}_{P,O}$ value to that of the average ${\overline{nD}}_{P,O}$ value across all fully irradiated organs. It can be seen that, on average across patients, the dose to almost all nonirradiated organs is less than 5% of the mean dose to fully irradiated organs. Therefore, from a practical standpoint, it may be acceptable to consider the doses to most organs absent from the scan region as negligible.

Table 5.

Ratio of dose to each nonirradiated organ relative to average fully irradiated organ dose, expressed as a percentage. The last two columns report the average and standard deviation across patient models. A dash indicates that the nonirradiated organ was not included for the given patient model.

	Baby (%)	Child (%)	Golem (%)	Frank (%)	Visible Human (%)	Irene (%)	Donna (%)	Helga (%)	Avg (%)	SD (%)
Testis	8.1	2.2	0.3	–	0.8	–	–	–	2.9	3.1
Thyroid	5.7	6.7	3.4	2.8	4.3	1.6	3.8	7.1	4.4	1.8
Brain	0.6	0.4	0.1	0.1	0.1	0.1	0.2	0.4	0.2	0.2
Salivary glands	–	–	–	0.5	0.9	0.4	–	1.9	0.9	0.6
Extrathoracic region	–	–	–	0.2	0.6	0.3	0.6	1.2	0.6	0.3
Prostate	–	–	0.0	4.1	2.6	–	–	–	2.2	1.7
Thymus	17.1	16.4	7.8	22.3	6.0	9.2	16.9	23.4	14.9	6.1

The thymus, a relatively small organ located near the superior boundary of the abdominal scan region, was the only exception. On average, the thymus received a dose of 14.9% of that to the fully irradiated organs. The standard deviation across patients was also larger (6.1%) as the exact size and proximity to the abdominal scan region of this organ had appreciable variations across patient models.

DISCUSSION

This study demonstrated the dependence of CTDI_vol-normalized organ doses on patient size for typical abdominal CT exams using a wide range of patient models. Detailed, scanner-specific Monte Carlo simulations were performed using eight different voxelized patient models in order to obtain accurate organ dose values. For each patient, organ doses were normalized by the CTDI_vol corresponding to the simulated scanner at the operating conditions described (120 kVp, body bowtie, widest available beam width, and a pitch of 1.0) and the mean across scanners was obtained for each organ. The analysis of these data was separated into three categories: Organs fully encompassed in the scan region (fully irradiated), organs partially encompassed (partially irradiated), and organs that were not directly irradiated (nonirradiated).

The analysis of fully irradiated organ data was performed to extend the methodology to accurately estimate organ doses from CT introduced in Turner et al.¹⁰ In that previous work, it was shown that for a single patient model (Irene from the GSF family of voxelized models), normalizing organ doses by CTDI_vol resulted in values that varied by less than 10% across different 64-slice MDCT scanners for all fully irradiated organs. A similar analysis was performed for each of the patient models used in this study. These results verify that for every fully irradiated organ in any patient model, the CoV across scanners is less than 10%. Thus, extending the work of Turner et al.,¹⁰ it is feasible to estimate organ dose for fully irradiated organs simply by multiplying the patient-specific ${\overline{nD}}_{P,O}$ by the reported CTDI_vol, regardless of the scanner model.

This study demonstrates that the CTDI_vol obtained with a 32 cm (body) CTDI phantom can be utilized to account for organ dose disparities from different scanners, even for small adults and pediatric patients. Also, for this study, all abdominal scan simulations were performed with the bowtie filter that would be used for an adult abdomen. This was done in order to isolate the effects of the size of the patient model on the results under a specific set of operating conditions. Future studies should be performed to determine the regression coefficients for other parameter (such as bowtie filter, kVp, and collimation) settings, especially for predicting dose to smaller patients, since it is likely that a smaller bowtie filter would be used for scanners that feature multiple filtration options.

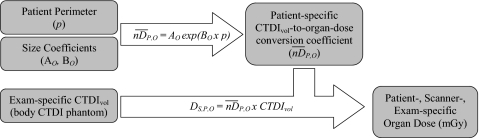
In order to devise a method to estimate patient-specific CTDI_vol-to-organ-dose conversion coefficients $\left({\overline{nD}}_{P,O}\right)$ for any fully irradiated organ in any patient, the dependence of ${\overline{nD}}_{P,O}$ values on patient size was investigated. It was demonstrated that ${\overline{nD}}_{P,O}$ values have a strong dependence on patient perimeter. As shown by the plot in Fig. 2, there was a declining exponential relationship between ${\overline{nD}}_{P,O}$ and patient perimeter (in cm) obtained from the central slice of the scan region. The exponential regression analysis resulted in correlation coefficients greater than 0.95 for all seven fully irradiated organs. The organ-specific regression coefficients, A_O and B_O from Eq. 1, are displayed in Table 2. The strong correlations indicate that the reported size coefficients can be used to calculate ${\overline{nD}}_{P,O}$ for most patients using Eq. 1 (these results have not been verified for patients with perimeters much greater than those examined in this work or for very large patients with tissue outside the scan’s field of view). Then, as described above, patient-specific, scanner-specific, and exam-specific organ dose estimates can be obtained by multiplying ${\overline{nD}}_{P,O}$ by the scanner’s reported CTDI_vol (which takes the technique of the exam into account). A schematic description of this proposed dose estimation process is presented in Fig. 3. It must be emphasized that in order to carry out this process with the size coefficients reported in Table 2, the CTDI_vol value should refer to the 32 cm (body) CTDI phantom, which is not always the case with the value reported by the scanner for pediatric abdominal exams protocols.

Figure 3.

The proposed method to estimate patient-specific, scanner-specific, and exam-specific organ dose using the size coefficients (A_O,B_O), patient perimeter (in cm), and the CTDI_vol reported by the scanner.

While the primary focus of this manuscript was on fully irradiated organs, results of radiation dose to partially irradiated organs were presented as well. This analysis indicates that the proposed method of size adjustment may be limited in its ability to estimate dose to organs not fully encompassed in the scan region. As indicated in Table 3, there was considerable variability in the percent coverage for most partially irradiated organs across different patient models. This variability was due to the fact that the relative position of organs, with respect to the anatomical landmarks used to define the scan region, differed between the patient models. As a result, ${\overline{nD}}_{P,O}$ values for most partially irradiated organs did not correlate well with patient size. The results in Table 4 show that the correlation coefficients from the exponential regression analysis ranged from 0.29 to 0.70 for all organs except the colon. The colon was almost fully covered in the majority of the patient scans and appeared to have a similar size dependency as the fully irradiated organs. Furthermore, there was not an obvious relationship between the average percent coverage or the standard deviation across patients and the exponential regression correlation of ${\overline{nD}}_{P,O}$ with patient size.

The analysis of the nonirradiated organs showed that they receive small doses compared to directly irradiated organs. This can be attributed to the fact that doses due only to scattered radiation are expected to be much lower than doses from primary radiation directly from the source, especially for organs located a considerable distance from the scan region. This study showed that for typical abdominal exams, the majority of nonirradiated organs were located a sufficient distance outside of the scan region so that they received very little scattered radiation. Doses to organs such as the thyroid, brain, salivary glands, extrathoracic region, testis, and prostate were effectively zero.

The thymus, a relatively small nonirradiated organ situated in the center of the upper chest, was close enough to the superior boundary of the exam region that its ${\overline{nD}}_{P,O}$ value was ∼20% of the average across fully irradiated organs for some patients. This is a good example of how small organs just outside of the scan may receive a nontrivial dose. The dose levels to adjacent nonirradiated organs, such as the thymus for abdominal exams, appear to be a function of both the organ’s size and its proximity to the scan region. For a given patient, the latter is a function of the exact start and stop location (i.e., where the x-ray beam is turned on and off) relative to the organ’s exact position. A conservative approach to estimating doses to small organs near the scan region might be to assign a dose value equal to some percentage of the average dose to fully irradiated organs (e.g., 20% of the fully irradiated organs to the thymus for abdominal exams). Of course, these organs and their assigned dose percentages will be different for exams of other body regions. In future studies that focus on estimating dose from other typical clinical exams (i.e., chest, pelvis, head, etc), those nonirradiated organs that receive a significant dose will be identified and recommendations for assigning dose values based on dose to fully irradiated organs will be established.

Patient perimeter was the metric used for patient size for this study. The correlation between perimeter and CTDI_vol-to-organ-dose conversion coefficients for fully irradiated organs proved to be very strong. However, this work focused on the abdomen in which perimeter does not typically fluctuate much over the scan region for a given patient. In other anatomical regions, it might be difficult to determine the best location at which to obtain a representative perimeter measurement. Furthermore, the software necessary to obtain perimeter measurements from patient images (as done in this study) may not be supported by the current scanners’ image analysis packages. Future studies will be performed to evaluate other metrics that may correlate with CTDI_vol-normalized organ doses. For example, a metric that utilizes patient attenuation data throughout the scan region would be advantageous since this information is directly measured by the CT scanner and reflects patient morphology and composition in addition to size.

It should be emphasized that the size coefficients (A_O and B_O) presented in this work are only appropriate for abdominal CT exams and only for those performed with a fixed tube current. Coefficients for other scan regions, such as chest, pelvis, and head scans, will need to be generated in future studies. For some of these regions, such as the chest and pelvis, it may be necessary to create gender-specific and age-specific patient cohorts since, unlike the abdomen, significant anatomical differences exist between these groups. The GSF family of voxelized models consists of two pediatric, three adult male, and three adult female models and, as displayed in Tables 3, 5, there are several organs that are not contoured in one or more models. In order to determine accurate size coefficients for other scan regions, additional patient models may therefore be necessary. Additionally, investigations into the effects of tube current modulation (TCM) are underway. TCM is used routinely in abdominal scans^{23, 24} and, depending on the type of TCM used, the scheme may adjust the tube current for patient size as well as modulate along the z-axis and within the x-y plane. Therefore, techniques to account for TCM similar to those described by Angel et al.^{14, 24} will be investigated.

This study was conducted to investigate the feasibility of accounting for patient size when determining scanner-independent CTDI_vol-to-organ-dose conversion coefficients. It was shown that for fully irradiated organs, there was a strong correlation with patient perimeter. The exponential size coefficients presented in Table 2 could thus be used to calculate CTDI_vol-to-organ-dose conversion coefficients for most patients based only on their measured perimeter. Then, with knowledge of the scanner’s CTDI_vol for the given exam protocol, an accurate estimate of organ dose can be obtained using the method outlined in Fig. 3. This approach makes it possible to prospectively or retrospectively estimate organ doses individual patients and introduces the potential to calculate patient-specific risk estimates based on the organ dose-dependent calculations outlined in the BEIR VII Report.²

Future work is needed to investigate several aspects not fully covered in this manuscript, including (a) the effects of tube current modulation and (b) the development of methods to estimate radiation dose to nonirradiated and partially irradiated organs; for the latter, developments will have to take into account not only the effects of patient size, but also other relevant factors including the beam on and beam off location and the percent of organ irradiated during the scan. This work is currently underway and will hopefully be reported soon.