Projecting human pharmacokinetics of therapeutic antibodies from nonclinical data

Abstract

The pharmacokinetics (PK) of therapeutic antibodies is determined by target and non-target mediated mechanisms. These antibody-specific factors need to be considered during prediction of human PK based upon preclinical information. Principles of allometric scaling established for small molecules using data from multiple animal species cannot be directly applied to antibodies. Here, different methods for projecting human clearance (CL) from animal PK data for 13 therapeutic monoclonal antibodies (mAbs) exhibiting linear PK over the tested dose ranges were examined: simple allometric scaling (CL versus body weight), allometric scaling with correction factors, allometric scaling based on rule of exponent and scaling from only cynomolgus monkey PK data. A better correlation was obtained between the observed human CL and the estimated human CL based on cynomolgus monkey PK data and an allometric scaling exponent of 0.85 for CL than other scaling approaches. Human concentration-time profiles were also reasonably predicted from the cynomolgus monkey data using species-invariant time method with a fixed exponent of 0.85 for CL and 1.0 for volume of distribution. In conclusion, we expanded our previous work and others and further confirmed that PK from cynomolgus monkey alone can be successfully scaled to project human PK profiles within linear range using simplify allometry and Dedrick plots with fixed exponent.

Introduction

The projection of human pharmacokinetic (PK) profiles to help estimate dose and dosing regimens is important during clinical development, especially prior to first-in-man studies, as drug efficacy and toxicity are usually linked to drug exposure. Often, it also supports an early assessment of efficacious doses and commercial viability. Our data suggest that, for monoclonal antibodies (mAbs), simple allometric scaling might not be the optimum method for projecting multi-exponential PK profiles. Equations to describe allometric scaling are based on the premise that physical or physiological parameters in species vary as a function of body weight. Interspecies PK parameters have been frequently scaled using a simple allometric equation, Y = aX^b, where Y is the PK parameter such as clearance (CL), X is the body weight, a is the scaling coefficient and b is the scaling exponent.¹ The constant a may be specific for a particular system, e.g., the drug or species used, whereas the scaling exponent b is expected to follow the theoretical predictions and is dependent on the type of physiological or kinetic variable being analyzed.²

The allometric scaling approach has been widely used to predict human PK parameters of small molecules. Generally, PK parameters from three or more non-clinical species such as mouse, rat, dog or monkey have been used. Based on a number of studies, it has been shown that allometric scaling of CL works best when elimination occurs primarily through physiological processes, such as hepatic metabolism and renal or biliary excretion and protein binding is inconsequential.³ However, PK scaling across species fails in some cases, including when the method is applied to compounds with low hepatic extraction ratio, non-linear PK, qualitative and quantitative differences in disposition pathways.³

Most therapeutic mAbs bind to the non-human primate antigen more often than to rodent antigen due to the greater sequence homology observed between monkey and human. Given the qualitative and quantitative differences in PK between rodents and non-human primate, we believe the non-human primate, usually the cynomolgus monkey, is the most relevant species for conducting preclinical PK studies.⁴ In addition to a similar binding epitope, binding to the neonatal Fc receptor (FcRn), which protects IgG from catabolism, binding affinity to antigen (Kd), tissue cross-reactivity profiles, as well as disposition and elimination pathways of the mAb are similar between monkey and human. In the current study, using a data set of 13 mAbs demonstrating linear PK, we expanded previous work done by ourselves⁵ and others^6,7 and further confirmed that human CL (CL_h) can be reasonably projected based on cynomolgus monkey CL (CL_c) alone with a fixed scaling exponent of 0.85 compared to allometric scaling based on three species. Human concentration-time profiles can also be well projected from available cynomolgus monkey PK profiles using the species-invariant time method with a fixed exponent of 0.85 for CL and 1.0 for volume of distribution.⁸

Results

The mAbs analyzed in this study are summarized in Table 1. For mAbs that are cleared significantly via antigen-mediated mechanisms (omalizumab, GNE mAb S, GNE mAb T and GNE mAb Y), CL at doses that saturated the antigen-mediated clearance pathway was used for the analysis. The CL of 13 mAbs ranged from ∼3–16 mL/day/kg in mouse, ∼4–15 mL/day/kg in rats, ∼5–12 mL/day/kg in cynomolgus monkeys and ∼3–6 mL/day/kg in humans within their linear range.

Table 1.

Predicted human clearance for different monoclonal antibodies using various scaling methods

Monoclonal Antibodya1,a2	CLobsf				Simple allometric scalingg			Maximum life potential (MLP) as correction factorg			Brain weight (BrW) as correction factorg			Rule of Exponents k		Scaling from cyno data using a fixed exponent of CL of 0.85
	mouse	rat	cyno	human	xh	CLpred	PBj	yh	CLpred	PHj	zh	CLpred	PEj	CLpred	PEj	wi	CLpred	PBj
Pertuzumab	7.02	8.93	5.15	3.31	0.939	4.87	47.1	13.5	3.79	14.5	1.94	3.42	11	4.87	47.1	0.832	3.29	−0.73
Bevacizumab	15.7	4.83	5.37	3.35	0.794	2.34	−43.1	1.21	1.82	−84.0	1.80	1.58	−112	2.34	−43.1	0.875	343	2.28
Trastuzumabc	7.80	ND	5.52	3.80	1.00	5.53	45.5	0.906	4.28	12.6	1.87	2.39	−60.0	NA	NA	0.783	3.52	−7.89
Onializuniab	3.12	6.67	4.32	2.40	1.06	6.31	163	1.47	4.91	105	2.06	4.25	77.1	4.25	77.1	0.733	2.76	14.9
ONE mAb S	5.50	8.00	8.72	5.57	1.09	11.9	114	1.50	9.29	66.8	2.09	8.04	44.3	8.04	44.3	0.850	5.56	−0.11
ONE mAb Td	ND	14.6	6.26	4.79	0.679	2.40	−99.6	1.31	4.34	−10.4	2.03	6.09	27.1	NA	NA	0.785	3.99	−19.9
ONE mAb Xb	10.3	11.6	8.62	4.40	0.966	8.37	90.2	1.38	6.44	46.4	1.97	5.54	25.9	8.37	90.2	0.776	5.50	25.00
ONE mAb Y	8.80	5.09	3.06	2.68	0.777	1.44	−86.1	1.20	1.24	−116	1.79	1.07	−150	1.44	−86.1	0.886	1.95	−37.3
ONE mAb Z	5.33	10.2	6.21	3.23	1.021	8.56	165	1.43	6.49	101	2.02	5.43	68	5.43	68	0.970	3.96	22.7
ONE mAb U e	ND	ND	2.36	2.16	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	0.956	1.51	−43.5
ONE mAb Vc	16.5	ND	4.34	3.08	0.741	2.00	−54	1.87	1.87	−64.7	1.74	1.8	−71	NA	NA	0.842	2.77	−11.2
GNE mAb We	ND	ND	11.5	6.00	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	NA	0.804	7.34	22.3
Anti-CD40b	10.4	12.8	10.8	4.85	1.01	11.94	146	1.42	9.15	88.7	2.01	7.86	62.1	7.86	62.1	0.923	6.89	42.1

ND, no data; NA, not applicable.

^a1All antibodies except for GNE mAb T, GNE mAb X and GNE mAb U are humanized IgG antibodies. GNE mAb T is chimeric, and GNE mAb X and U are human antibodies.

^a2Used reported body weight for mice (20 g), rat (250 g) and cynomolgus monkeys (3.5 kg) except when indicated.

^bUsed the observed body weight in the study.

^cOnly mouse and monkey PK data were available. Regression was done based on two species.

^dOnly rat and monkey PK data were available. Regression was done based on two species.

^eOnly monkey PK data was available. No regression was done.

^fCL values were obtained by two-compartmental analysis. CLs were reported as mean values for mouse, rat and monkeys. If anti-therapeutics antibody (ATA) has significant impacts on CL, only ATA negative animals were included for CL calculations, otherwise, all animals were included for CL calculations. CLs in humans were reported as typical values in population pharmacokinetics analysis, which include ATA positive and ATA negative subjects.

^gregression R² > 0.96 for all molecules.

^hsimple allometric scaling: CL = a•BW^x; allometric scaling with MLP as correction factor: MLP•CL = b•BW^y; allometric scaling with BrW as correction factor: BrW•CL = c•BW^z; where a, b and c are the coefficient and x, y and z is the exponent of the allometric equation.

ⁱthe exponent w for the antibodies were back calculated based on the observed mean CL in cynomolgus monkeys and in humans. The mean ± SD of w was 0.847 ± 0.07.

^jPercentage errors (PEs) are [(CL_h, predicted − CL_h, observed)/CL_h, observed] × 100% for over-prediction and [(CL_h, predicted − CL_h, observed)/CL_h, predicted] × 100% for under-prediction.

^kRule of exponents (ROE) proposed by Mahmood for mAbs was only applied to eight mAbs with preclinical PK data from three species available for the simple allometric scaling method: MLP as a correction factor is not needed when exponents of simple allometry are greater than 0.71 but less than 1; brain weight is required to improve the prediction of human CL when exponents of simple allometry are greater than 1.

Simple allometric scaling and allometric scaling method with correction factors.

Out of eight mAbs that had observed human data for comparison, simple allometric scaling using mouse, rat and cynomolgus monkey PK data overestimated human CL for six antibodies with percent prediction error (%PE) values ranging from 47.1–165% (Table 1). Four of these six mAb had %PE >100%, which is out of the 2-fold range of observed CL_h. Incorporation of correction factors [maximum life potential (MLP) or brain weight (BrW)] improved the prediction and decreased the %PE values for overprediction in comparison to simple allometric scaling. For the mAbs with CL estimates underestimated by simple allometric scaling, incorporation of MLP or BrW as correction factors made the prediction worse. For example, the %PE for bevacizumab CL_h was −43.1, −84 and −112% using simple allometric scaling, MLP and BrW as correction factor, respectively (Table 1). The %PE is 45.5, −99.6 and −54% for trastuzumab, rituximab and GNE mAb V, respectively, with preclinical PK data from only two species available for the simple allometric scaling method.

Allometric scaling based on rule of exponents.

Rule of exponents (ROE) proposed by Mahmood for mAbs⁹ was applied to eight mAbs with preclinical PK data available from three species. MLP correction was not necessary for four mAbs with exponents of simple allometry between 0.71 and 0.99 (pertuzumab, bevacizumab, GNE mAb X and GNE mAb Y) as suggested by the ROE. The %PE for CL_h prediction based on ROE is 47.1, −43.1, 90.2% and −86.1% for pertuzumab, bevacizumab, GNE mAb X and GNE mAb Y, respectively. However, MLP correction can improve CL_h prediction for pertuzumab and GNE mAb X. The %PE is 14.5 and 46.4% for pertuzumab and GNE mAb X, respectively, after MLP correction. Brain weight correction was applied for four mAbs (omalizumab, GNE mAb S, GNE mAb Z and anti-CD40) with exponents of simple allometry greater than 1 to reduce the CL_h prediction; nevertheless, three of them still had % |PE| greater than 50% (Table 1).

Determination of scaling exponent for CL and volume of distribution (V) based on cynomolgus monkey data only.

The scaling exponent, w, which is derived from Equation 4 and the observed CL_c and CL_h values, ranged from 0.776–0.875 for the four mAbs in the training data set (Table 1), with a mean ± SD value of 0.831 ± 0.042. In addition, the population mean of w for pertuzumab, bevacizumab, trastuzumab and GNE mAb X estimated by nonlinear mixed effects modeling was 0.826 with 95% confidence interval of [0.805, 0.845]. A scaling exponent of 0.85 was therefore used for projecting CL_h using monkey data alone. The %|PE| for CL_h prediction from CL_c is less than 50% for the nine mAbs in the validation data set with fixed exponent as 0.85. After combining the training and validation data set, the scaling exponent, w, ranged from 0.733–0.970 for the 13 mAbs (Table 1), with a mean ± SD value of 0.847 ± 0.07. This result further confirmed the fixed exponent of 0.85 for prediction of CL_h from CL_c.

The volume distribution at steady state (V_ss) and volume of distribution for central compartment (V_c) of the mAbs used in the study was observed to be ∼75 mL/kg and ∼40 mL/kg, respectively, in both monkeys and humans and appeared to be proportional to the body weight (data not shown). Therefore, an exponent of 1 was assumed for scaling the V of antibodies using monkey data alone.

Scaling of CL and V in humans based on cynomolgus monkey data only.

The projected CL_h of each antibody using a fixed exponent of 0.85 and the observed CL_c in Equation 4 was within 50% of the observed values, with 11 of the 13 antibodies showing a %|PE| of <25% (Table 1). The projected V_ss and V_c in humans was close to the observed values, with the %|PEs| ranging from 4.26%–74.7% (data not shown).

Projection of PK profiles in humans based on cynomolgus monkey data only.

The CL, V_ss and V_c estimated from the projected human serum concentration-time profiles were in agreement with the observed data (data not shown). Additionally, using pertuzumab as an example, the predicted human concentration time profiles obtained by Monte-Carlo simulation based on the projected human PK parameters, were consistent with observed Phase 1 data (Fig. 1).¹⁰

Figure 1.

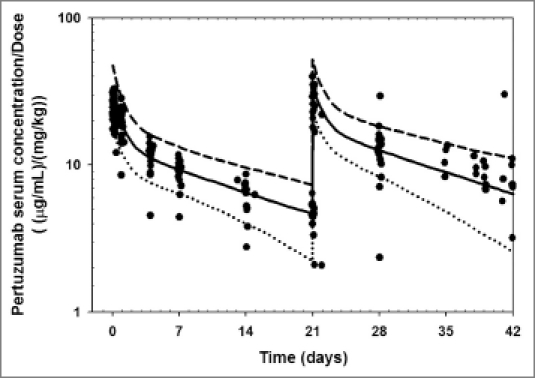
Observed (•) and predicted pertuzumab serum concentration-time profiles [median (−), 2.5%, 97.5% quantile (−−)] in humans normalized by dose. Pertuzumab concentration-time profiles were scaled from cynomolgus monkey using Dedrick approach with exponent of 0.85 and 1 for CL and V, respectively. The predicted CL, V_ss and V_c for pertuzumab obtained by fitting compartmental modeling were 3.39 mL/kg/day, 69.8 mL/kg and 34.36 mL/kg, respectively, which is consistent with the observed values (CL = 3.31 mL/day/kg, V_ss = 70.0 mL/kg and V_c = 40.9 mL/kg).

Discussion

This is a detailed analysis of projected versus actual CL_h using current available methods. Allometric scaling using three species for eight mAbs and two species for three mAbs (Table 1) showed that projected CL values of most mAbs were generally inconsistent with observed values. The use of correction factors such as BrW and MLP, as well as the application of ROE, helped to improve the estimations, but the overall %|PE| was still relatively high (Fig. 2). Notably, allometric scaling from a single species (cynomolgus monkey) for 13 mAbs, a fixed scaling exponent of 0.85 and the Dedrick plot,⁸ clearly demonstrated that this method can be reliably used to project CL_h and concentration-time profiles prior to initiating first-in-human trials. In fact, as outlined in Figure 2, this method resulted in the lowest %PE compared to other commonly used scaling methods.

Figure 2.

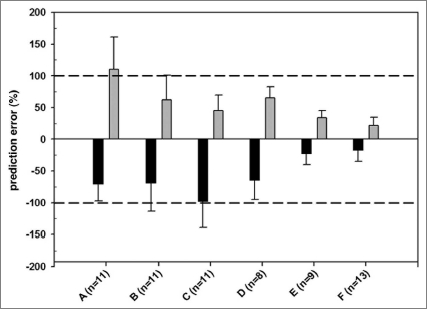
Accuracy of allometric scaling of human clearance of 13 therapeutic mAbs from observed clearance using various scaling methods [(A) simple allometric scaling, (B) simple allometric scaling with maximum life potential as correction factor; (C) simple allometric scaling with brain weight as correction factor; (D) allometric scaling based on ROE (rule of exponent) for therapeutic Abs; (E) scaling from cynomolgus monkey using a fixed exponent of clearance of 0.85 (validation data set n = 9); (F) scaling from cynomolgus monkey using a fixed exponent of clearance of 0.85 (full data set n = 13)]. No rodent PK studies were conducted for GNE mAb U and GNE mAb W, therefore, only allometric scaling from cynomolgus monkey were performed for these two mAbs. The percent prediction error (%PE) is the difference between the estimated clearance and observed clearance divided by observed or predicted clearance ×100 for over-prediction () and under-prediction (■), respectively. The solid line represents %PE = 0. The dashed lines represent %PE = 100% or −100%.

Based on data from only two mAbs, Ling concluded that simple allometric scaling using three species is useful for mAbs PK scaling.⁶ However, our more comprehensive data suggested that projection of CL_h using multiple animal species can not be directly applied to mAbs. The reasons for inaccuracies observed when CL_h is projected using both rodents and monkeys could be multi-factorial. The PK impact from interaction of mAbs with FcRn is species-specific.¹¹ Notably, the binding affinity of human IgG1 for murine FcRn is ∼2.5-fold higher than that for human FcRn.¹¹ This may result in altered distribution and PK of the therapeutic mAbs in mouse, i.e., slower relative CL in mouse, therefore projecting an artificially fast CL_h. In addition, antibodies can be immunogenic in animal species, which may result in a fast CL, therefore predicting an artificially faster CL_h. Over-prediction may also result from the regression algorithm used for allometric scaling; data points at the ends of the regression have a higher leverage than the ones at the center. A high correlation constant in the allometric scaling based on three species does not necessarily imply a good prediction.¹²

In 1996, Mahmood proposed a rule of exponents (ROE) for predicting human CL of small molecules based on data from 46 drugs: if the exponent from simple allometry is between 0.55 and 0.7, simple allometry is applied; if the exponent is between 0.71 and 0.99, the product of CL and MLP is used; if the exponent is greater than 1.0, the product of CL and BrW is used.¹³ He later proposed another ROE for predicting human CL of proteins based on data from 11 protein drugs: MLP as a correction factor is not needed when exponents of simple allometry are greater than 0.71 but less than 1; BrW is required to improve the prediction of human CL when exponents of simple allometry are greater than 1.¹⁴ Of note, there were no mAbs in the protein data set and only one antibody Fab fragment was included. Mahmood also acknowledged that it was not known if interspecies scaling would predict PK parameters of mAbs with reasonable accuracy.⁹ In a recent publication,⁹ he reexamined ROE for antibody constructs using nine therapeutic antibodies and concluded that the same ROE used for therapeutic proteins could be applied to mAbs. However, only three full-length mAbs and one fusion protein with available human data were included in the dataset. Therefore, whether this ROE can be generally applied to full-length mAbs is still unknown.

Our results suggest that MLP correction may be needed for a better prediction when the CL_h prediction using the simple allometry is over-predicted and the exponents of simple allometry are greater than 0.71 but less than 1. The ROE proposed by Mahmood for therapeutic antibodies can be applied to a majority of mAbs in our data set (six out of eight) and gives a better prediction compared to simple allometric scaling; however the %PE is still greater compared with using cynomolgus monkey data alone with fixed exponent as 0.85 (Fig. 2).

The prediction of drug clearance in humans using one pre-clinical species with fixed coefficients and exponents has been suggested to be an inappropriate method based on ∼50 small molecules¹⁵ and limited number of mAbs.⁹ Due to the significant differences observed in the PK properties of mAbs and small molecules, we investigated the possibility of accurately estimating human PK of mAbs from monkey data using a fixed exponent. A number of therapeutic mAbs will bind both human and primate antigen, but not the equivalent murine or rodent antigen. Therefore, primate PK could provide the most relevant information for the prediction of human PK of humanized antibodies. Primate PK data for 13 mAbs with linear PK were used for prediction of human PK and then the predicted PK parameters were compared with the observed clinical PK data. We found that using CL scaling exponents of 0.85 gave a good estimation of CL_h for mAbs. The use of a single species and a fixed exponent for human CL prediction has been suggested recently.^6,7 Based on our previous work,⁵ Ling et al.⁶ suggested that mAb CL_h can be reasonably predicted using exponent 0.85 or 0.9 from cynomolgus monkey data. Additionally, Wang et al. have made similar recommendations.⁷ Our current work expanded our previous work⁵ and that of others^6,7 (only bevacizumab and trastuzumab overlapped with the Ling et al. and Wang et al. datasets) and further confirmed that CL_h can be reasonably predicted using monkey data alone with fixed exponent.

Several examples can be found in the literature that outline projected CL_h using various methods.^6,9,16–20 The overall accuracy in projecting CL_h has been limited. The CL_h for a humanized anti-hepatocyte growth factor mAb (AMG 102), for example, was accurately projected to be 13.4 mL/hr based on cynomolgus monkey data.¹⁷ However, the projected CL_h of another humanized mAb, anti-CD40, was ∼3-fold higher than the observed CL_h based on three species allometric scaling.¹⁸ The projected CL_h for the anti-epidermal growth factor receptor mAb, which was murine antibody, was 4-fold slower than the observed CL_h.¹⁶ Murine mAbs have relatively low binding affinity to the human FcRn compared to mouse FcRn,²¹ which may have further contributed to a lower projected and a higher observed CL in humans. The most likely reason for this disparity might be the significant impact of antigen binding on CL that is not accurately projected from animal species to humans. Additionally, species specific differences in antigen-mAb binding affinity (Kd), antigen density and turn-over rate and size of the antigen-mAb complex are important determinants for antigen-mediated mAb CL.²¹

The scaling of antigen-mediated CL of mAbs is difficult due to the uncertainty and inherent biological variability associated with this mode of CL. The antigen load in humans, especially in patients, is generally variable and potentially higher than in monkeys (binding species). Given these differences between animals and patients and the uncertainty of the actual antigen expression in patients, allometric scaling of non-linear PK has not yet been successful. Scaling of non-linear PK profiles using the species-invariant time method may be possible if the Michaelis-Menten variables (Km and Vmax) in monkeys and humans are assumed scalable.

Subcutaneous administration is an important route of administration for antibodies. It is reasonable to assume that the systemic CL following subcutaneous and intravenous administration for mAbs is similar. However, the scaling of bioavailability and absorption rate following subcutaneous administration of mAbs from animals to humans is not relevant for various reasons, e.g., differences in the physiological structure of the skin between pre-clinical species and humans, unknown mechanisms of the pre-systemic CL after subcutaneous administration for mAbs (such as FcRn roles).

In summary, this report, based on a data set of 13 mAbs, supports our thesis that scaling using a binding species such as cynomolgus monkey is pharmacologically appropriate for therapeutic mAbs that demonstrate linear CL. Simple allometric scaling of CL_c with an exponent of 0.85 provided a good estimate of CL_h. Concentration-time profiles of mAbs in humans were also projected reasonably well based on PK data in cynomolgus monkeys using the Dedrick approach. Although a scaling exponent of 0.75 has been used to provide a conservative estimate of safety margins and 0.9 to project human efficacious doses,⁵ a single exponent of 0.85 allows for accurate projection of CL_h. Scaling of antigen-mediated CL in humans continues to remain a major challenge and will likely be accomplished when we better understand the biological differences in the antigen properties between cynomolgus monkeys and humans and factors contributing to the antigen-mediated clearance in patients.

Methods

Simple allometric scaling.

Clearance (CL) of the mAb in each animal species was plotted against the animal body weight (BW) on a log-log scale according to the following allometric equation:

$$\text{CL = a}•{\text{BW}}^{\text{x}}$$ (1)

where a is the coefficient and x is the exponent of the allometric equation. The coefficient a and exponent x were calculated from the intercept and slope of the linear regression line, respectively. If no specific body weight information was found in the actual study, body weights of 20 g (mouse), 250 g (rat), 3.5 kg (cynomolgus monkey) and 70 kg (human) were used.

Allometric scaling with correction factors.

Clearance (CL) of the mAb in each animal species was multiplied by the maximum life-span potential (MLP, Equation 2) or brain weight (BrW, Equation 3) of the animal species and then the product was plotted as a function of body weight on a log-log scale.

$${\text{MLP • CL = b • BW}}^{\text{y}}$$ (2)

$${\text{BrW • CL = c • BW}}^{\text{z}}$$ (3)

where b and c are the coefficient and y and z are the exponent of the allometric equation. MLP (in years) was calculated as previously reported.²² Standard brain weight²³ were used.

Allometric scaling based on rule of exponents.

Rule of Exponents (ROE) proposed by Mahmood⁹ for therapeutic proteins including mAbs was applied to eight mAbs with PK information from mouse, rat and monkey. MLP as a correction factor is not needed when exponents of simple allometry are greater than 0.71 but less than 1; brain weight is required to improve the prediction of human CL when exponents of simple allometry are greater than 1.

Estimation of scaling exponent and projection of CL_h based on cynomolgus monkey data only.

The CL_h of mAbs were predicted based on the cynomolgus monkey data using the simple allometric equation:

$$C{L}_h=C{L}_c•{\left[\frac{B{W}_h}{B{W}_c}\right]}^w$$ (4)

where BW_h and BW_c stand for the body weights of human and cynomolgus monkey, respectively, and w is the scaling exponent for CL. Based on the observed CL_h and CL_c and the typical body weights of cynomolgus monkey and humans, w for each antibody was calculated using Equation 4. A group of four mAbs (pertuzumab, bevacizumab, trastuzumab, omalizumab and GNE mAb X) was selected as a training data set to estimate w. To estimate w by nonlinear mixed-effects modeling, the observed CL of pertuzumab, bevacizumab, trastuzumab and the GNE mAb X was expressed as a function of the observed body weight of each individual monkey and a typical body weight for the human subject (70 kg), and the data was analyzed using NONMEM (double precision, version VI, level 1.0; UCSF, San Francisco, CA) with an NM TRAN preprocessor (version III, level 1.0) and PREDPP routines (version IV, level 1.0). The remaining nine mAbs were used as a validation data set for the estimation of w. Finally, all 13 mAbs in the whole data set were used to confirm the w.

Projection of human PK profiles based on cynomolgus monkey data only.

The mAb serum concentration-time profiles in monkeys following 5, 15 and 50 mg/kg IV administration of pertuzumab were transformed to human concentration-time profiles using the species-invariant time method described by the following equations:⁸

$$Tim{e}_{human}=Tim{e}_{cyno}•\left(\frac{{\text{Body weight}}_{human}}{{\text{Body weight}}_{cyno}}\right)Exponen{t}_{volume}-Exponen{t}_{clearance}$$ (5)

$$Concentratio{n}_{human}=Concentratio{n}_{cyno}•\left(\frac{Dos{e}_{human}}{Dos{e}_{cyno}}\right)•\left(\frac{{\text{Body weight}}_{cyno}}{{\text{Body weigh}}_{human}}\right)Exponen{t}_{volume}$$ (6)

The allometric equations used scaling exponents estimated as above for CL and 1 for V, respectively. The bi-exponential PK profiles were fit to a two compartmental model IV bolus input, first order elimination and micro rate constants (Model 7, WinNonlin Pro, version 5.1; Pharsight Corporation, Mountain View, CA) to estimate the PK parameters, which served as input for Monte Carlo simulations of serum mAb concentrations in humans. The simulations were performed in NONMEM (double precision, version VI, level 1.0; UCSF, San Francisco, CA) with an NM TRAN preprocessor (version III, level 1.0) and PREDPP routines (version IV, level 1.0) for 1000 subjects. Covariates effects on PK parameters and covariance between CL and V_c was not included in the model structure. The inter-individual variability on CL and V_c was assumed to be 30%, which was based on the observed inter-individual variability of these parameters for mAbs in humans.²⁴

Statistical analysis.

Percentage errors (PEs), which are [(CL_h, predicted − CL_h, observed)/CL_h, observed] × 100% for over-prediction and [(CL_h, predicted − CL_h, observed)/CL_h, predicted] × 100% for under-prediction, were used to assess the prediction performance.²⁵ Two-fold differences on CL will be translated into PE = 100% and −100% for over- and under-prediction respectively.

Abbreviations

PK

pharmacokinetics

mAb

monoclonal antibody

IgG

immunoglobulin G

CL

clearance

CL_h

human CL

Cl_c

cynomolgus monkey CL

FcRn

neonatal Fc receptor

BW

body weight

BW_h

body weights of human

BW_c

body weight of cynomolgus monkey

BrW

brain weight

PE

prediction error

MLP

maximum life potential

V

volume of distribution

V_c

volume of distribution for central compartment

V_ss

volume of distribution at steady state

ROE

rule of exponents

Conflict of Interest

R.D., S.I., F.P.T., D.L.M., P.J.F. and S.P. are employees of Genentech Inc., which supported the study financially.