Abstract
A Bayesian network expansion algorithm called BN+1 was developed to identify undocumented gene interactions in a known pathway using microarray gene expression data. In our recent paper, the BN+1 algorithm has been successfully used to identify key regulators including uspE in the E. coli ROS pathway and biofilm formation.18 In this report, a synthetic network was designed to further evaluate this algorithm. The BN+1 method was found to identify both linear and nonlinear relationships and correctly identify variables near the starting network. Using experimentally derived data, the BN+1 method identifies the gene fdhE as a potentially new ROS regulator. Finally, a range of possible score cutoff methods are explored to identify a set of criteria for selecting BN+1 calls.
Key words: bayesian network, network expansion, BN+1, gene interaction, microarray data analysis, E. coli, reactive oxygen species, ROS, biofilm, synthetic network
Biological interaction networks and pathways have been simulated and analyzed by various computational methods, for example, Bayesian networks,1,2 mutual information,3,4 neural network,5,6 and centrality network analysis.7 These methods can be used to reconstruct biological pathways and potentially identify new genes and hypotheses for guiding further experimental tests.
A Bayesian network (BN) is a representation of a joint probability distribution over a set of random variables.1 A BN includes two components: a directed acyclic graph (DAG) with vertices representing variables and edges indicating conditional dependence relations, and a set of conditional distributions for each variable given its parents in the graph. Bayesian networks that most accurately describe a given dataset can be learned automatically by searching through large numbers of network topologies and retaining the most significant top-scoring networks. BNs are able to identify causal or apparently causal relationships.8 In biology, BNs have been used in biology to identify relationships amongst sets of variables (e.g., genes) in various biological pathways. Due to their ability to model linear and nonlinear relationships, robustness to error and noise and human interpretability, Bayesian networks are ideal for modeling pathways using high throughput data.
Most biological pathways have only been partially defined for most organisms. Given the increasing number of microarray measurements, it is possible to reconstruct such pathways and uncover missing components and connections based on high throughput gene expression data. Several machine learning approaches for identifying hidden or unknown factors have appeared in the literature recently.9–17 In our recent study, we developed a novel algorithm termed “BN+1” which implements Bayesian network expansion to predict new factors that participate in a specific pathway.18 Broadly, the BN+1 algorithm iteratively tests to see if any single variable added to a given pathway will significantly improve the likelihood of the overall network. The hypothesis here is that those variables which are hidden and regulate or are regulated by a network will be more likely ranked with high posterior probability scores. The BN+1 algorithm was used to predict novel factors that influence the E. coli reactive oxygen species (ROS) pathway using a compendium of microarray gene expression data obtained from E. coli.18 Our study identified many new ROS and biofilm regulators and some of them (e.g., uspE and its interaction with gadX) were further experimentally verified.
This addendum aims to provide more insights into the BN+1 algorithm. To further establish the validity and evaluate potential pitfalls of the algorithm, a synthetic regulatory network was developed for testing the BN+1 algorithm. In the previous ROS pathway analysis and PLoS One paper, the second most highly-ranked BN+1 gene was formate dehydrogenase fdhE. This gene is further elucidated in this article. Finally, cutoff criteria for selecting significant BN+1 genes and methods to improve the algorithm are discussed.
BN+1 Simulation Using Synthetic Data
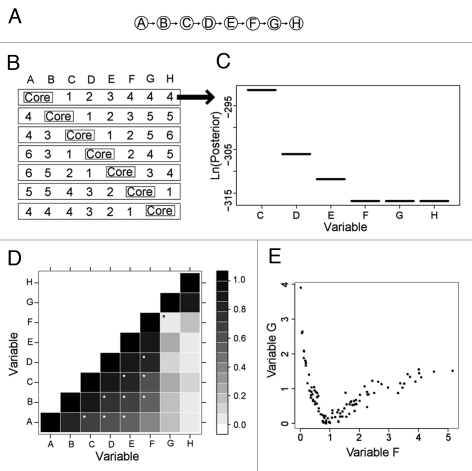
A synthetic network was constructed by generating a set of mathematical functions which define the relationships amongst a set of variables (Fig. 1). In this model, eight variables are linked together in tandem (Fig. 1A) by the following functions:
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
where N(n,s) represents normally-distributed noise with n as the mean and s as the standard deviation. Biological data frequently include noise which can reduce the predictive capability of BNs and other modeling approaches. To reflect this reality, various levels of noise are added to the functional relationships. The function abs( ) is the absolute value of the enclosed quantity. Synthetic data were generated from these functions by sampling from the Gaussian-distributed variable A and then sampling corresponding data values for subsequent variables in the pathway based on the above functions.4 This particular synthetic network contains different types of relationships amongst variables, e.g., nonlinear polynomial and biphasic relationships.
Figure 1.
Synthetic network and corresponding BN+1 results for two-variable core expansion. (A) A synthetic eight-variable network. (B) Seven distinct core networks composed of two adjacent variables were used for BN+1 expansion analysis. In each row, integers represent the ranks of the BN+1 variables (where 1 = top scoring gene, etc.,). (C) The posterior score distribution of BN+1 variables identified in the first row of (A). (D) Plot of absolute values of pair-wise Pearson correlations for all variables. The black star denotes a relationship (between F and G) that has a poor Pearson correlation (coefficient = 0.056). White stars denote good relations between variables with correlation coefficient ≥0.5 and separated by at least one variable in the synthetic network (A). (E) A nonlinear relationship between variables F and G.
To further evaluate the BN+1 algorithm, a series of BN+1 simulations were designed and analyzed (Fig. 1B). In each simulation, two adjacent variables from the synthetic network are selected as a ‘core’ network (i.e., a known seed subnetwork) and used to identify the other six variables in terms of their roles in the overall network. The predicted variables, which are coined the BN+1 variables, are ranked according to their best log posterior scores obtained for the network containing a BN+1 variable and core network variables. This experiment was repeated for each pair of core variables in the model (Fig. 1B).
When the core sub-network is located at the end of the synthetic network (i.e., A→B or G→H), the BN+1 successfully identified those variables that are closely associated to a core network in sequential order (Fig. 1B). For example, when the core network is A→B, BN+1 identifies the top four variables that are associated with this core network as C, D, E, F, in correct order. It is interesting that the last two variables G and H have the same score as F when they are individually added to the core network (Fig. 1C). A further examination indicates that none of the three variables F, G and H is connected to A or B in the final BN network containing A, B and one of the three variables. The disconnection of these three variables from the core A→B makes it possible for the posterior probabilities to be the same.
When the core subnetwork is located in the middle of the synthetic network (e.g., B→C or C→D), the variables identified by BN+1 are ranked in sequential order in either side of the core network. For example, for the core network C→D, the BN+1 variables on the right side are ranked 1 (E), 2 (F), 5 (G) and 6 (H), and the BN+1 variables on the left side are ranked 3 (B) and 4 (A) (Fig. 1B). It is interesting that the second best-ranked gene (F) is located on the same side as the best scoring gene (E) instead of direct association with C in the C→D network. Despite the direct link between B and the core network, F has stronger association (with higher posterior probability) with the core network than B. This asymmetric pattern suggests that top ranked BN+1 variables are ranked based on their extent of associations with the core network instead of physical closeness to the core network.
One advantage of BN+1 over many linear correlation-based methods is that our Bayesian network-based approach is able to identify those interactions that show nonlinear correlations with core variables. Pearson correlation is a typical method for defining the extent of a linear relationship between the variables.19 The correlation coefficients between all possible pairs in the original dataset were calculated using Pearson correlation method. Although all of the functions are nonlinear, over the range of parameters tested, some may be approximately linear, while others may be more strongly nonlinear. Figure 1D shows a matrix representation of the Pearson correlations observed for each pair of variables and their synthetically-generated data. In general, Pearson correlation coefficients decrease as the distance between variables (or the distance of one variable from the diagonal of the matrix) increases. Overall, Pearson correlations can not only detect those variables directly associated with one specific variable, but also identify those that are remotely associated with sequential order (white stars in Fig. 1D). However, Pearson correlation failed to identify the association between F and G (black star in Fig. 1D). A further examination indicates that F and G share a clear nonlinear relationship (Fig. 1E). Such a nonlinear relationship is correctly detected by BN+1. For example, when G and H are used as a core network, F is identified as the best ranked BN+1 variable (Fig. 1B).
Identifying a New Regulator fdhE in the E. coli ROS Pathway Using BN+1
The BN+1 algorithm was applied to predict new genes critical to existing reactive oxygen species (ROS) pathway.18 Many new participants in the ROS pathway were identified. The top three BN+1 genes are dusB, fdhE, and uspE. The dusB gene (encoding RNA-dihydrouridine synthase B) and the ROS gene fis exist within the same operon. A clear linear correlation was observed between the expressions of dusB and fis (Fig. 3A reviewed in ref. 18). The uspE gene was also further analyzed by computational and experimental methods and found to play a critical role in ROS and biofilm pathways.18 However, the fdhE was barely studied in the original paper. The gene fdhE encodes an E. coli formate dehydrogenase accessory protein that regulates the activity of catalytic sites of aerobic formate dehydrogenases and their redox activities.20 The role of fdhE in the ROS pathway is unclear. To provide more insights in the role of fdhE in its potential participation and regulation of the ROS pathway, we provide more analysis results here.
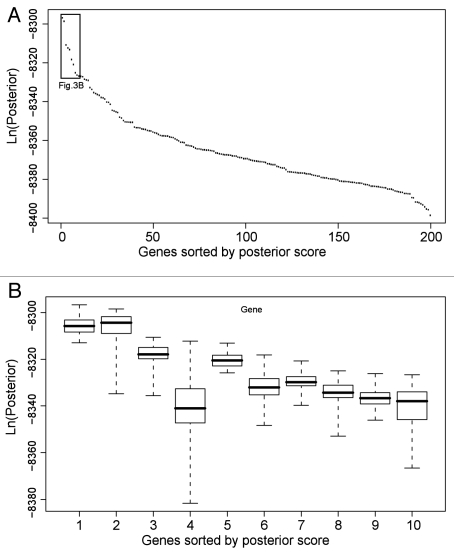
Figure 3.
Analysis of top BN+1 genes in the RO S use case. (A) Generic plot of best score for top 200 BN+1 genes. (B) Variation in scores for top 10 genes. The BN+1 genes are ranked by maximum scores of all networks containing the core genes plus one additional gene. Genes sorted by posterior scores are shown in horizontal axis. Box plots for the set of scores pertaining to each gene are displayed. The variations are calculated based on various simulations in different computers. To perform each simulation, a simulated annealing approach was used with an unfixed structural prior (i.e., the core network edges) with multiple replicates and moderate simulation time to allow a comprehensive though non-exhaustive search.
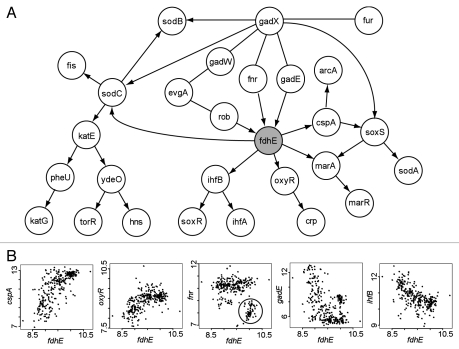
Our BN+1 simulation indicated that fdhE was influenced by three E. coli ROS genes (parent nodes) rob, fnr and gadE (Fig. 2A). For example, a plot of the data for the genes fdhE and fnr demonstrated a special nonlinear pattern with two distinct regions (Fig. 2B). According to the plot, when the expression of fnr is low with a value of 7–8.5, the expression of fdhE is usually high. However, a E. coli strain carrying the fnr gene mutation was reported to have two-fold reduced fdhE expression.21 Therefore, while both BN simulation and experimental data indicated a significant fnr→fdhE regulation, there appears to be a contradiction in terms of how fnr regulates fdhE expression. Our further analysis of the microarray data found that low fnr and high fdhE expressions occurred mostly in the microarray studies with overexpression of certain E. coli genes, particularly those associated with responses to DNA damage (e.g., dinI, recA, ruvA, umuD, uvrA and dnaA) and stress (e.g., lexA, mazF, sulA, cpxR, cspA, dnaT, era and uspA). How fnr and fdhE interact may deserve further experimental investigation. Furthermore, how fdhE interacts with the other parent nodes rob and gadE is also unclear.
Figure 2.
Analysis of the potential RO S gene fdhE predicted by BN+1. (A) Consensus Bayesian network generated from 13 networks sharing the same top log posterior score. (B) Selected relationships between fdhE and its associated genes. Nonlinear relationships were often observed. The ellipse in the fnr-fdhE plot highlights a group of fnr-fdhE associations that are discussed in the text.
Based on our BN+1 simulation, fdhE influences five other genes (child variables), including ihfB, oxyR, marA, cspA and sodC (Fig. 2A). These predicted interactions have not been reported in the literature. Many of the interactions are nonlinear relationships (Fig. 2B). In summary, the BN+1 analysis suggests that fdhE plays an important role in the ROS pathway by regulating many E. coli genes and being regulated by other genes.
The Challenge of Identifying Meaningful BN+1 Cutoffs
After all genes are ranked by the BN+1 simulation, what cutoff should be used to select the top ranked BN+1 genes for further analysis? While the top few BN+1 genes prove important in the ROS pathway, many more genes shown in the list of top BN+1 genes are also related to the ROS pathway (Fig. 3A). Our Gene Ontology (GO) enrichment analysis of the top 100 genes in the sorted BN+1 gene results (∼2.4% of the total genes on the microarray) showed that they were enriched for ROS-related activities or functions (Data not shown). This means that a certain number of top-scoring BN+1 genes are all related to the core gene pathway.
One feasible criterion is based on the possible loss of connection between a BN+1 variable and the core network. In our synthetic data simulation, we found that the disconnected variables share the same score (Fig. 1). This cutoff shows that all subsequent BN+1 genes will be disconnected from the core gene network. Similar results were also observed in the ROS pathway simulation. The last 1,457 genes in the sorted BN+1 gene list were all disconnected from the core gene network. This suggests that these 1,457 genes have no relationship with the ROS pathway based on the selected microarray data and selected core network. However, the cutoff based on the loss of connection between a BN+1 gene and a core network is loose and may result in too many genes being included for further testing. For example, in our ROS example, 2,760 genes remain after the last 1,457 genes are excluded. While the loose cutoff removes roughly a third of the genes, there are still many genes which may or may not closely relate to the ROS pathway network.
To make a tighter and possibly more useful cutoff, we analyzed the distribution of sorted posterior scores. In the ROS analysis, the sorted posterior scores of BN+1 genes quickly drop across the first ten variables, followed by a slowdown of score dropping (Fig. 3A). Therefore, it is possible to suggest a cutoff in the beginning of the slowdown. However, these cutoffs are still artificial because we do not know which one(s) would be optimal for maintaining the real biological predictions. Furthermore, the “best” posterior probabilities of BN+1 variables' networks often have variations across large amounts of simulations in different computers (Fig. 3B). Current variable rankings are based on the highest log posterior scores among all simulated networks for the selected BN+1 variable and core variables. Multiple scores may be obtained and saved for a selected BN+1 variable and core variable set. If the median scores for each set of BN+1 results were used instead, the rankings of BN+1 genes could change (e.g., the 4th and 5th genes in Fig. 3B). It is unlikely the median scores would ever be used since the BN optimization approach always seeks the best (or most optimal) result. The resulting variation is probably due to the failed achievement of convergence. To achieve a final convergence, more execution time will be needed. More computation time will reduce the variation in scores for each individual BN+1 variable and improve the overall confidence in the rankings of the BN+1 variables. Because our synthetic data use case only includes eight variables, it is relatively easy to achieve convergence. For example, Fig. 1C shows no score variation in replicates for each of the BN+1 variables in our synthetic network (hence the box plots appear as lines denoting the median scores), suggesting sufficient convergence was achieved by the algorithm.
To make the experimental testing more meaningful, an empirical cutoff such as the top 10% of the score distribution or top 100 genes may be helpful. Although this type of cutoffs is heuristic and does not establish the statistical significance of those results, subsequent exploration of the top BN+1 results based on this cutoff may still lead to novel discoveries.18
Perspectives and Future Directions
Many variations of the BN+1 algorithm are available. For example, BN+1 can be continuously implemented like BN+1+ 1+… After each BN+1 run, the top BN+1 variable (i.e., gene) can be added to the core network, followed by another BN+1 run with the aim to identify another BN+1 variable.9 This approach will lead to identification of a list of genes closely associated and interacting with the original core network. Another variation is the addition of two or more genes at one time to the core network, forming a strategy of BN+2 or BN+n. This approach may be very time consuming since there are more options of every two (or more) genes to be included to the core. However, it is possible to filter out the list of genes to be included based on initial gene expression or functional analysis. Alternatively, it is possible to remove one or more genes at one time from the core network to form a strategy of BN-1 or BN-n. This strategy can discover which variable has the least influence on the core network. It may be a valuable approach when the initial core network is large and hard to dissect the roles of individual genes.
Since many BN+1 genes are predicted, additional criteria and analysis may be needed to justify which BN+1 gene(s) to be selected for further experimental studies. For example, researchers may need to run functional analyses of the top BN+1 genes using GO enrichment and gene functionality. It would also be ideal to incorporate experimental descriptions and curated information when identifying the biological bases for the underlying interactions inferred by the BN+1 algorithm. In this case, natural language processing (NLP) and literature mining will help further define which experimental conditions are specific for different gene interactions. For example, using an internally developed literature term enrichment method based on Fisher's exact test, we were able to infer the roles of uspE and gadX and their interactions in biofilm from experimental descriptions.18
In order to make the BN+1 algorithm more widely accessible, we have developed a web-based system called MARIMBA (marimba.hegroup.org/). MARIMBA provides a user-friendly graphic user interface environment that simplifies the dataset selection, variable inclusion, observational file processing and settings selection for BN and BN+1 analysis. The user interface and project/analysis management approach permit large-scale analyses such as BN+1 through parallel-execution on internal servers at the University of Michigan.2 MARIMBA and the BN+1 algorithm can be applied to the analysis of many other types of high-throughput data and biological networks.
Acknowledgements
This research was supported in part by NIH Grant U54-DA-021519, NIH Training Grant (5 T32 GM070449-04), 2008 Rackham Spring/Summer Research Grant at the University of Michigan, and the University of Michigan Bioinformatics Program.
Footnotes
Previously published online: www.landesbioscience.com/journals/cib/article/12845
References
- 1.Friedman N. Inferring cellular networks using probabilistic graphical models. Science. 2004;303:799–805. doi: 10.1126/science.1094068. [DOI] [PubMed] [Google Scholar]
- 2.Xiang Z, Minter RM, Bi X, Woolf P, He Y. miniTU-BA: medical inference by network integration of temporal data using Bayesian analysis. Bioinformatics. 2007;23:2423–2432. doi: 10.1093/bioinformatics/btm372. [DOI] [PubMed] [Google Scholar]
- 3.Margolin AA, Nemenman I, Basso K, Wiggins C, Stolovitzky G, Dalla Favera R, et al. ARACNE: an algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC Bioinformatics. 2006;7:7. doi: 10.1186/1471-2105-7-S1-S7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Luo W, Hankenson KD, Woolf PJ. Learning transcriptional regulatory networks from high throughput gene expression data using continuous three-way mutual information. BMC Bioinformatics. 2008;9:467. doi: 10.1186/1471-2105-9-467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhang Y, Xuan J, de los Reyes BG, Clarke R, Ressom HW. Reconstruction of gene regulatory modules in cancer cell cycle by multi-source data integration. PLoS ONE. 2010;5:10268. doi: 10.1371/journal.pone.0010268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chen Y, Xu D. Understanding protein dispensability through machine-learning analysis of high-throughput data. Bioinformatics. 2005;21:575–581. doi: 10.1093/bioinformatics/bti058. [DOI] [PubMed] [Google Scholar]
- 7.Ozgur A, Xiang Z, Radev D, He Y. Literature-based discovery of IFNγ and vaccine-mediated gene interaction networks. J Biomed Biotechnol. 2010;426479:13. doi: 10.1155/2010/426479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Friedman N, Linial M, Nachman I, Pe'er D. Using Bayesian networks to analyze expression data. J Comput Biol. 2000;7:601–620. doi: 10.1089/106652700750050961. [DOI] [PubMed] [Google Scholar]
- 9.Needham CJ, Manfield IW, Bulpitt AJ, Gilmartin PM, Westhead DR. From gene expression to gene regulatory networks in Arabidopsis thaliana. BMC Syst Biol. 2009;3:85. doi: 10.1186/1752-0509-3-85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Parikh A, Huang E, Dinh C, Zupan B, Kuspa A, Subramanian D, et al. New components of the Dictyostelium PKA pathway revealed by Bayesian analysis of expression data. BMC Bioinformatics. 2010;11:163. doi: 10.1186/1471-2105-11-163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yu T, Li KC. Inference of transcriptional regulatory network by two-stage constrained space factor analysis. Bioinformatics. 2005;21:4033–4038. doi: 10.1093/bioinformatics/bti656. [DOI] [PubMed] [Google Scholar]
- 12.Tanay A, Shamir R. Computational expansion of genetic networks. Bioinformatics. 2001;17:270–278. doi: 10.1093/bioinformatics/17.suppl_1.s270. [DOI] [PubMed] [Google Scholar]
- 13.Herrgard MJ, Covert MW, Palsson BO. Reconciling gene expression data with known genome-scale regulatory network structures. Genome Res. 2003;13:2423–2434. doi: 10.1101/gr.1330003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ihmels J, Friedlander G, Bergmann S, Sarig O, Ziv Y, Barkai N. Revealing modular organization in the yeast transcriptional network. Nat Genet. 2002;31:370–377. doi: 10.1038/ng941. [DOI] [PubMed] [Google Scholar]
- 15.Hashimoto RF, Kim S, Shmulevich I, Zhang W, Bittner ML, Dougherty ER. Growing genetic regulatory networks from seed genes. Bioinformatics. 2004;20:1241–1247. doi: 10.1093/bioinformatics/bth074. [DOI] [PubMed] [Google Scholar]
- 16.Pena JM, Bjorkegren J, Tegner J. Growing Bayesian network models of gene networks from seed genes. Bioinformatics. 2005;21:224–229. doi: 10.1093/bioinformatics/bti1137. [DOI] [PubMed] [Google Scholar]
- 17.Gat-Viks I, Shamir R. Refinement and expansion of signaling pathways: the osmotic response network in yeast. Genome Res. 2007;17:358–367. doi: 10.1101/gr.5750507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hodges AP, Dai D, Xiang Z, Woolf P, Xi C, He Y. Bayesian network expansion identifies new ROS and biofilm regulators. PLoS ONE. 2010;5:9513. doi: 10.1371/journal.pone.0009513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zou KH, Tuncali K, Silverman SG. Correlation and simple linear regression. Radiology. 2003;227:617–622. doi: 10.1148/radiol.2273011499. [DOI] [PubMed] [Google Scholar]
- 20.Luke I, Butland G, Moore K, Buchanan G, Lyall V, Fairhurst SA, et al. Biosynthesis of the respiratory formate dehydrogenases from Escherichia coli: characterization of the FdhE protein. Arch Microbiol. 2008;190:685–696. doi: 10.1007/s00203-008-0420-4. [DOI] [PubMed] [Google Scholar]
- 21.Schlindwein C, Giordano G, Santini CL, Mandrand MA. Identification and expression of the Escherichia coli fdhD and fdhE genes, which are involved in the formation of respiratory formate dehydrogenase. J Bacteriol. 1990;172:6112–6121. doi: 10.1128/jb.172.10.6112-6121.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]