Robust EPI Nyquist Ghost Elimination via Spatial and Temporal Encoding (EPI-GESTE)

Abstract

Nyquist ghosts are an inherent artifact in EPI acquisitions. An approach to robustly eliminate Nyquist ghosts is presented that integrates two previous Nyquist ghost correction techniques: temporal domain encoding (Phase Labeling for Additional Coordinate Encoding: PLACE) and spatial domain encoding (Phased Array Ghost Elimination: PAGE). Temporal encoding modulates the EPI acquisition trajectory from frame to frame, enabling one to interleave data to remove inconsistencies that occur between sampling on positive and negative gradient readouts. With PLACE, one can coherently combine the interleaved data to cancel residual Nyquist ghosts. If the level of ghosting varies significantly from image to image, however, the signal cancellation that occurs with PLACE can adversely affect SNR-sensitive applications such as perfusion imaging with Arterial Spin Labeling (ASL). This work proposes integrating PLACE into a PAGE-based reconstruction process to yield significantly better Nyquist ghost correction that is more robust than PLACE or PAGE alone. The robustness of this method is demonstrated in the presence of magnetic field drift with an in-vivo ASL perfusion experiment.

Introduction

Modern neuroimaging methods that require fast data acquisition often rely on echo planar imaging (EPI). EPI acquisitions achieve high temporal resolution by sampling multiple lines of k-space data after each RF excitation pulse. Sampling on a Cartesian grid requires multiple readout gradient pulses of alternating polarity combined with smallphase-encode “blips” (1). When data acquired during positive readout gradients, +G_x, is not properly aligned with data sampled during negative readout gradients, −G_x, Nyquist ghosts can occur (2). These ghosts are characterised as faint copies of the imaged material, shifted from the true image by one-half the field-of-view (FOV).

There have been many methods to correct for Nyquist ghosts. Early on, Ahn and Cho (3), proposed a 1D phase-correction method to align the +G_x and −G_x echoes. This method employs a reference scan with the EPI “blip” amplitudes set to zero. The reference data is then used to estimate the constant and linear phase errors between data sampled on +G_x versus data sampled using −G_x. However, the dependence on reference data acquired before image acquisition leaves the image reconstruction susceptible to variations that may occur during the experiment. In our experience, when reference data is used to correct Nyquist ghosts, even small phase variations can leave significant residual Nyquist ghosts. Dynamic correction methods, such as proposed by Jesmanowicz et. al. (4), can partially compensate for temporal variations in a series acquisition. These methods typically acquire additional k-space lines at each temporal image point, to determine the constant and linear phase terms for each image. This can remove the dependence of the reference scan, but at the cost of a slightly longer ETL.

It was later noted that double-sampled EPI (5), which measures each k-space line twice in quick succession—once each for +G_x and −G_x—completely eliminates Nyquist ghosts. Each positive/negative readout data set satisfies the Nyquist criterion, and separating the sets removes the effects from data incoherence between them. This approach has the unfortunate effect of doubling the echo train length (ETL), however, which exaggerates EPI geometric distortion artifacts caused by magnetic field inhomogeneity.

Other methods have been proposed that do not increase the ETL. For example, Buonocore and Zhu (6) demonstrated that phase error correction maps could be generated directly from image domain analysis of the acquired data. Chen and Wyrwicz (7) expanded this approach using fully-encoded reference scans. However, these methods have been shown to be less effective in oblique scan planes (8). A dependence on reference data, and complications from phase wrapping effects and in estimating the map in regions of low signal, also limit its applicability (8).

More recent methods employ spatial and/or temporal domain encoding to correct for Nyquist ghosts. The phase labeling for additional coordinate encoding (PLACE) method (9) provides exceptional ghost suppression. In PLACE, the temporal encoding is performed by shifting the acquired k-space grid on alternating acquisitions. For ghost elimination, a shift of 1Δk_y is performed, and data from +G_x and −G_x readout lines is interleaved to form two images, each associated with one readout gradient polarity. Any phase difference between these images, which arises due to a shift in the underlying k-space sampling grid, is then corrected before the images are added coherently. Residual ghosts in each image should have opposite phase. Thus, a coherent combination effectively cancels any ghosts that may appear in the interleaved data. As with all interleaved data methods, however, the cost is lower temporal resolution in the image series.

Methods that employ spatial domain encoding for phased array ghost elimination, e.g. (PAGE) (10), leverage parallel imaging methods such as SENSE (11) to correct Nyquist ghosting. The authors of PAGE recognized that when data acquired after a single excitation are separated into separate +G_x and −G_x sets, sampling incoherence is removed and a 2x acceleration is introduced in each data set. These sets can each be reconstructed using SENSE, via coil sensitivity estimates derived from low temporal resolution data (as in TSENSE (12)). In PAGE, images so formed are combined in a coherent fashion using a weighted summation derived from the point spread function (PSF). In cases where the PSF needs to be estimated, the weighting coefficients can be derived from a time-averaged covariance matrix for each pixel. The latency in this method is significant, however, as both the coil sensitivity and PSF estimation requires data from multiple imaging time points.

This method was extended to a low-latency real-time PAGE scenario by Kim, et. al., in (8). Here, the authors alter the acquisition to alternate the readout gradient polarity order on each frame. That is, data for odd-numbered time points would be acquired with the readout polarity ordered {+, −, +, ···}, while even-numbered time points would be acquired with {−, +, −, ···} readout gradient ordering. In the real-time PAGE method, data from two adjacent frames are interleaved to estimate coil-sensitivities—one each for +G_x and −G_x data, significantly reducing the PAGE latency costs. These coil sensitivities are then used with SENSE to reconstruct images from the separated +G_x and −G_x data for each time point, with the final image formed using a non-coherent combination (root-sum-of-squares) of the two images.

While PAGE and PLACE are better at suppressing Nyquist ghosts than more traditional methods, unresolved issues remain in both methods. PAGE suffers from long latency, from both the estimation of the coil sensitivity maps and from the solution of an inverse problem to identify the coherent image summation weights. Real-time PAGE corrects the latency issue, but rejects the coherent summation approach in place of the faster root-sum-of-squares operation. While this method is simple and effective, it is unsuitable in applications where phase information is needed. Finally, in PLACE, the effect of ghost cancellation can adversely affect SNR sensitive applications such as Arterial Spin Labeling (ASL) perfusion imaging. Nyquist ghosts arise from displaced signal information. Rather than correcting the location of this shifted information, PLACE effectively cancels the displaced signal, including areas where ghosts overlap tissue of interest. Thus, temporal neighbors in an image series can exhibit significant intensity variations if the ghosting level varies from image to image before the PLACE correction. For ASL imaging, where the perfusion signal is found by calculating image differences, PLACE can introduce subtraction errors.

Our goal was to develop a self-referenced Nyquist ghost elimination method that addresses each of these problems. A self-referenced method was sought to remove the dependence on reference data in either a prescan step or a longer EPI echo train. A low latency method was sought to be insensitive to variations from both unintentional changes—such as those caused by gradient coil heating or patient breathing—and intentional changes in the acquisition, including real-time FOV modifications and/or PROPELLER acquisitions (13). The method also needs to be robust and repeatable to prevent visible errors in the temporal difference domain. We have found this to be extremely important in low SNR applications such as ASL, where ghost correction errors can obscure the information of interest.

The method we present here achieves these goals by integrating the spatial (real-time PAGE) and temporal (PLACE) encoding methods presented previously. While the PAGE method includes the option of coherent phase image combinations, the stated benefit of such a method is to maintain the signal phase—the goal of residual ghost suppression was not considered. In contrast, we specifically employ PLACE to eliminate ghosts in the data used for self-referenced parallel imaging coefficient calibration. As we show in the results, this enables our EPI Ghost Elimination via Spatial and Temporal Encoding (EPI-GESTE) method to be more robust to acquisition variability with significantly improved ghost suppression.

Methods

EPI Acquisition Design

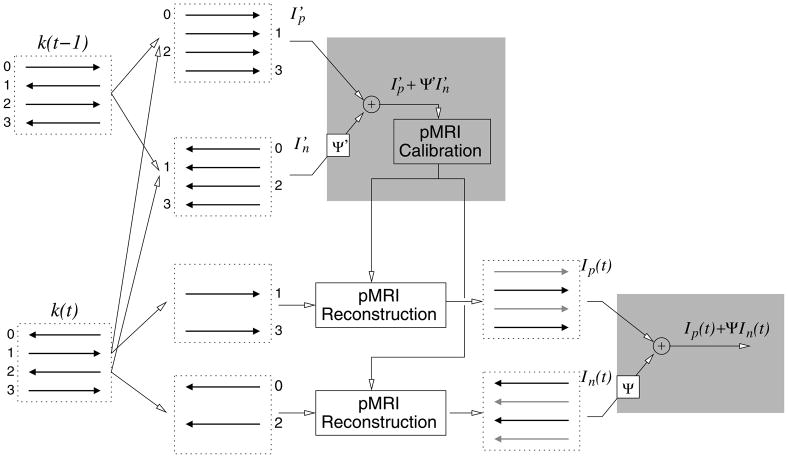
The foundation of our method is to employ both spatial and temporal domain encoding in EPI acquisitions. Spatial encoding is achieved using a multiple channel receiver coil array. Temporal encoding can be achieved by either shifting the EPI acquisition in k-space by 1Δk_y along the phase encoding dimension (9), or by alternating the readout gradient polarity on successive frames (8). The goal with either method is to ensure that data at a particular phase encode line that is sampled in one frame with a positive readout gradient, +G_x, is sampled by a negative readout gradient, −G_x, in neighboring frames. This enables one to interleave data from temporal neighbors, as shown in the alternating readout polarity method illustrated in the far-left column of Fig. 1.

Figure 1.

A diagram showing our proposed data acquisition and image reconstruction steps for unaccelerated multi-coil EPI acquisitions. The method is similar to the method in (8), with the exception of PLACE employed in the regions shown by the gray boxes. Each dashed box represents data from one coil of a multi-coil array.

Reconstruction Methods

EPI-GESTE

Our strategy to reconstruct multi-coil EPI acquisitions is shown in the remainder of Fig. 1. Starting with k-space data from two temporally encoded image frames, k(t − 1) and k(t), we interleave the positive readout data to form one set of k-space data, $k_p^{\prime }$, and then interleave the negative readout data to form a second set of k-space data, $k_n^{\prime }$. Notably, the images associated with each of these data sets, $I_p^{\prime }$ and $I_n^{\prime }$, should have minimal Nyquist ghosts, as most sampling inconsistencies between +G_x and −G_x should be removed by interleaving.

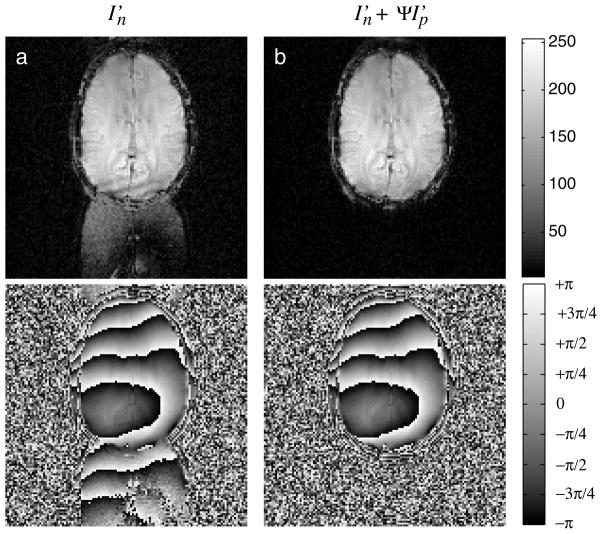
Variations may in fact occur between the sampling of k(t − 1) and k(t), which lead to residual Nyquist ghosts in images from interleaved data. An example is shown in Fig. 2 in the Results. As noted by Xiang and Ye (9), however, ghost artifacts that appear in images from interleaved temporally encoded EPI data, e.g. $I_p^{\prime }$ and $I_n^{\prime }$, will have opposite phase polarity. Thus, if one corrects for the phase difference between the images and combines the images coherently, the visible artifacts will be noticeably reduced through signal cancellation.

Figure 2.

An image-domain comparison of the pMRI calibration data available in the method, with both magnitude (top) and phase (bottom) images shown. Image (a) shows significant ghosting in the image formed from interleaved data, caused by unintentional sampling inconsistencies between each of the two interleaved frames. Image (b) shows the ghosts are removed after applying a phase-alignment and addition operation. Note that in (a) and (b), pixels in the signal-void region are shown amplified by a factor of 5 to enhance ghost visibility.

Here, we employ a subspace identification method (14) to identify an operator Ψ′ to correct for the phase difference between $I_n^{\prime }$ and $I_p^{\prime }$. Specifically, we first compute the normalized cross-correlation matrix, $Q=(\text{conj}\{I_n^{\prime }\}\circ I_p^{\prime })/\left|\right|I_n^{\prime }\circ I_n^{\prime }\left|\right|$, where “◦” is an element-by-element matrix multiplication operator (Schur product), to calculate the phase difference between $I_n^{\prime }$ and $I_p^{\prime }$. Then, the singular vectors, {u⃗, v⃗}, associated with the largest singular value of the matrix, Q, are identified through a singular value decomposition (SVD). A linear fit to the unwrapped phase of these individual vectors is then calculated. The slopes of these linear fits correlate to the k-space coordinate shift between $k_n^{\prime }$ and $k_p^{\prime }$. The measured slopes of ∠u⃗ and ∠v⃗ are then used to form linear phase terms for Ψ′. The zero-order phase-difference term is then identified and included in Ψ′. Both corrections are then applied to one of the two images, aligning the phase between them. A distinct advantage of this SVD registration method is that phase unwrapping is performed on one-dimensional signals rather than a 2-D image, as both ∠u⃗ and ∠v⃗ are vectors. A second advantage is that the projection of the phase difference data along rows and columns improves the algorithms’ effectiveness in low SNR applications.

Applying Ψ′ to the $I_n^{\prime }$ image and then adding to $I_p^{\prime }$ produces an image free of Nyquist ghosts, due to the ghost cancellation effect described by the authors of PLACE (9). However, a disadvantage of the PLACE method is reduced temporal resolution. To overcome this limitation, we instead only employ this composite image data to calibrate parallel MR imaging reconstruction parameters. As we showed in (15), eliminating ghosts in the calibration data has a dramatic effect on the quality of the parallel imaging reconstructions. The calculation of parallel imaging reconstruction coefficients is very sensitive to errors in calibration data, particularly in regards to phase information. Eliminating errors associated with Nyquist ghosts in self-referenced pMRI calibration data greatly enhances the applicability of these methods to EPI imaging.

Thus, we use the Nyquist ghost free data, ( $I_p^{\prime }+{\mathrm{\Psi }}^{\prime }{I}_n^{\prime }$), to determine parallel imaging reconstruction coefficients for each frame. These coefficients are then used to reconstruct an image from the data acquired at time t, k(t). As in the real-time PAGE method (8), here we also separate the positive and negative readout data for each frame. In unaccelerated data sets, this separation creates two data sets, each effectively sub-sampled by a factor of 2 and acquired using the same readout gradient polarity. We then reconstruct the missing lines in each set using parallel imaging. One can use either GRAPPA-based (16) or SENSE-based (11) methods. To form the final image, we again estimate and employ an operator Ψ to correct for the zero- and first-order phase difference between the reconstructed images. This has the effect of noticeably reducing residual pMRI reconstruction artifacts, as again the images associated with each readout polarity, I_n(t) and I_p(t), will have similar artifacts of opposite phase. In the Results below, we employ GRAPPA to perform the pMRI reconstruction steps. Thus, a root-sum-of-squares combination across the coil dimension of I_p(t)+ ΨI_n(t) is employed to form the final images. The exception to this is the example shown in Fig. 2, where a virtual body coil (17) calculation is employed to preserve phase. If SENSE is used in place of GRAPPA, the coil data combination step is unnecessary.

The notable differences between our method and the real-time PAGE method described in (8) are shown in gray in Fig. 1, where we use PLACE to form composite images. Thus, instead of calibrating the pMRI reconstruction coefficients on $I_n^{\prime }$ and $I_p^{\prime }$ separately, we compute our pMRI reconstruction coefficients on an image that is truly free of Nyquist ghosts. Similarly, rather than employing a root-sum-of-squares across the combined multi-coil data for both the positive and negative gradient readout images at time t, we construct the image for each frame through coherent addition to both maintain image phase and suppress residual artifacts.

Implementation Details for Previous Methods

In the results below, the same measured data was reconstructed using multiple methods. These methods can be described relative to Fig. 1. For images reconstructed using the Ahn & Cho static method, the linear and constant phase correction parameters were estimated from a reference scan at the beginning of the acquisition with the phase encoding gradients set to zero (i.e. k_y = 0). To simulate a dynamic Ahn & Cho correction from the same raw data, the linear and constant phase parameters were estimated from the EPI-GESTE images, rather than an extended EPI echo train. This change does not affect the comparison, as the estimated values should be the same, and generating them from EPI-GESTE images is more reliable than from a limited number of k_y=0 phase-encode data lines. Real-time PAGE images were reconstructed in two stages. First, $I_p^{\prime }$ and $I_n^{\prime }$ were each used to estimate pMRI reconstruction coefficients for the +G_x and −G_x data at k(t), respectively. The reconstructed images were then combined using a root-sum-of-squares calculation across all 16 images—8 coils each of +G_x and −G_x data. The PLACE images are equivalent to ( $I_p^{\prime }+{\mathrm{\Psi }}^{\prime }{I}_n^{\prime }$) in Fig. 1. To emphasize the loss in temporal resolution, PLACE images are referenced at time (t − 1/2).

Data Acquisition

The goal of the experiments presented in the Results is to highlight the advantages of our ghost elimination method compared to current standard methods of Nyquist ghost correction. In particular, in our experience with SNR-sensitive imaging methods such as ASL perfusion imaging, we have noticed subtle but significant shading and subtraction-error artifacts in ASL experiments when previous ghost correction methods were employed. [See Fig. 6, for example.] These experiments highlight these errors and demonstrate that EPI-GESTE corrects them.

Figure 6.

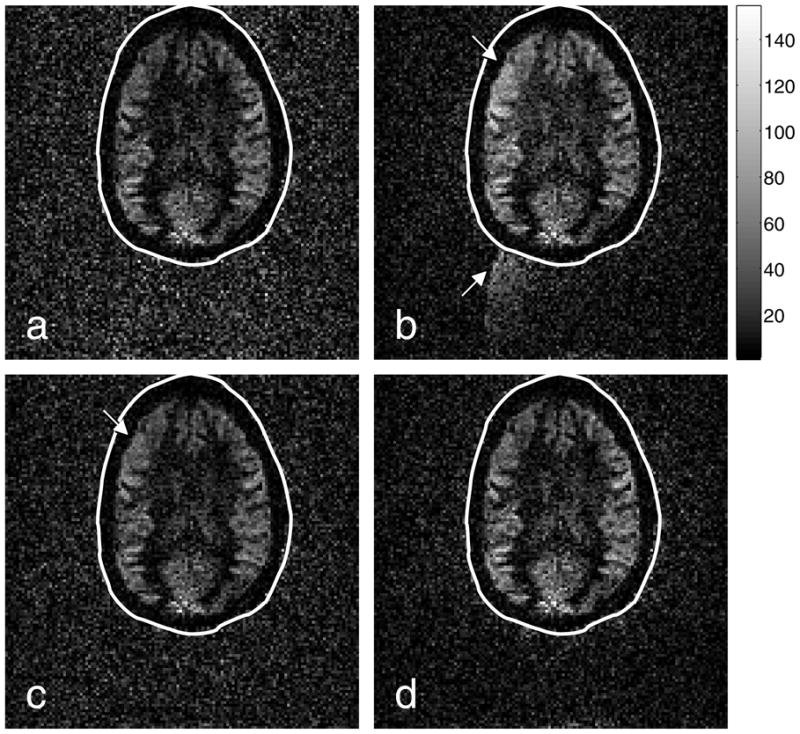
Perfusion images generated from the (a) Ahn-and-Cho dynamic, (b) real-time PAGE, (c) PLACE, and (d) EPI-GESTE methods. The perfusion data is shown with a normal gray scale inside the ellipse. Outside the ellipse, the signal-void region has been amplified by a factor of four, to enhance ghost visibility. The arrows point to regions affected by Nyquist ghosts, which appear as image brightening in the upper left brain quadrant and ghost artifacts in the signal-void region.

ASL Perfusion Imaging Experiment

Data for 124 image frames were acquired using an EPI sequence modified to acquire perfusion weighted images with a Q2TIPS-FAIR pulse sequence (18), (19), (20), using an 8-channel head coil on a GE EXCITE 1.5T scanner (v14M3) with a TwinSpeed gradient coil (GE Healthcare Inc., Milwaukee, WI). The imaging parameters were: image size = 128×128, TR/TE=2.5s/55.1ms, slice thickness = 8mm, FOV = 28mm × 28mm. Perfusion imaging is achieved by taking the difference between two images: a label image where the magnetization of the inflowing blood is inverted or saturated, and a control image where the inflowing blood is fully relaxed. The different magnetic states are achieved by a pair of global and slice selective inversion pulses. When the control image is subtracted from the label image, the static tissue signal is removed. The remaining signal is proportional to the blood that has perfused into the imaged region. Control and label images are acquired alternating in time through the sequence. For this experiment, temporal encoding was introduced by shifting the k-space sampling grid by (1Δk) on every other control/label pair. 62 control and label pair differences (124 frames) were averaged together to produce the final perfusion weighted image.

Signal-to-Noise Measurement Experiment

To quantify the effect of our method on SNR, images of a structured water phantom were acquired using the alternating readout polarity trajectory. Twelve axial images were acquired using the acquisition parameters: TR/TE = 1sec/53msec; FOV=20cm; Slice thickness=5mm; image matrix size=128×128. Twelve double-oblique images were acquired using the acquisition parameters: TR/TE = 2sec/53msec; FOV=24cm; Slice thickness=5mm; image matrix size=128×128. SNR was measured globally by generating a mask representing the image region with signal at least 10% of the maximum pixel value for all images. The temporal mean and variance of the pixels both inside and outside this region were calculated across the 12 images in the series.

Ghosting Level Quantification

Nyquist ghost levels were compared between methods by calculating the L₂-norm of the pixel magnitude values in two 13-pixel-square boxes, one in a nearly constant region of the image, S_s, and a second in a signal-void region with Nyquist ghosts, S_g. The ghost to signal ratio (GSR) is then reported as a percentage of the ratio ||S_g||₂/||S_s||₂.

Results

The results below illustrate the effectiveness of EPI-GESTE, which combines the Nyquist ghost suppression of PLACE within a real-time PAGE framework.

Improvement in self-referenced parallel imaging calibration

When temporal encoding is employed, Nyquist ghost reduction can often be achieved by interleaving two frames using data associated with one readout gradient polarity. When intentional (e.g. real-time FOV updates) or unintentional (e.g. scanner heating) changes in the acquisition occur between scans, however, interleaving alone may prove to be insufficient. An example of such an occurrence can be seen from the ASL perfusion experiment, where a significant unintentional change occurred between the acquisition of two frames. Fig. 2(a) shows the result of simple interleaving between two images frames using data acquired on the negative readout gradients. Sampling errors produced an inconsistency between the two frames, which produces significant visible ghosting in the interleaved image. In contrast, if one employs PLACE instead of simple interleaving, the residual ghosts will cancel to yield the image shown in Fig. 2(b). While excellent ghost elimination is achieved with PLACE, it comes at a cost of lowered temporal resolution due to data interleaving. To maintain the original temporal resolution in our method, this ghost-corrected interleaved data is used instead to calibrate the pMRI reconstruction parameters. Removal of ghosts in this calibration data improves the quality of the subsequent image reconstructions that rely on these parameters.

Robustness to Scanner Instability

The ASL perfusion imaging data was acquired on a system known to show increasing Nyquist ghost levels over the course of long image acquisition sessions. A possible reason for this is scanner field drift due to scanner heating (21).

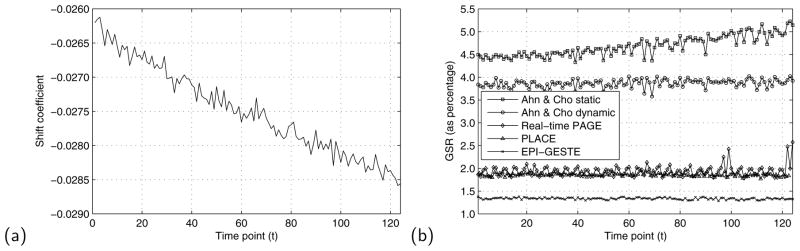
Fig. 3(a) shows the effect of this field drift over the course of the 124 acquired ASL perfusion measurement images. Here, the value of the linear phase shift correction term, as calculated by the EPI-GESTE method, is plotted against image acquisition time. The plot shows a clear linear trend in this coefficient, indicating a slow drift in the relative position between the positive and negative EPI readout data of each temporal frame as the experiment progresses. Fig. 3(b) shows the measured ghost-to-signal ratio for each frame, measured at the locations shown in the boxes of Fig. 4. As expected, a static Ahn & Cho correction (Ahn & Cho static) shows a gradual increase in GSR levels over time, as the shift measurement was calculated only once at the beginning of the acquisition. Switching to a variable shift parameter (Ahn & Cho dynamic) removes this general trend. The real-time PAGE method (8) can reduce ghosts further, although the correction tends to have wide variability indicated by the jump in GSR at frames 97, 99, 122, and 124. These spurious jumps are caused by significant ghosts in the interleaved data that corrupt the GRAPPA coefficient calibration at those time frames. This wide variability is absent in the PLACE method, because the ghosts appear equal in magnitude but with opposite phase, and are thus cancelled at each frame. This robustness in PLACE comes at a cost of decreased temporal resolution, however.

Figure 3.

(a) A plot of drift in the estimated positive/negative readout gradient line shift correction coefficient as measured with EPI-GESTE over the image series. (b) A plot of the ghost-to-signal ratio as a function of data acquisition time, comparing five reconstruction methods. EPI-GESTE exhibits much lower GSR than Real-time PAGE or PLACE, some of which is attributed to the background noise suppression effect discussed in the text.

Figure 4.

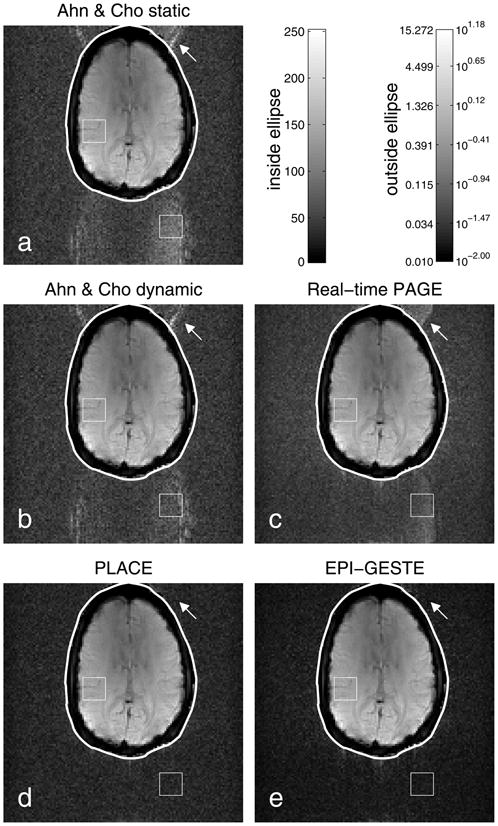
Image reconstructions to compare EPI Nyquist Ghost Correction methods: (a) Ahn & Cho static; (b) Ahn & Cho dynamic; (c) Real-time PAGE; (d) PLACE; and (e) EPI-GESTE. The squares in each image show the regions used to calculate the ghost-to-signal ratio shown in Fig. 3. The arrows highlight a ghost visible in previous methods that is not visible in PLACE or EPI-GESTE. Pixels within each drawn ellipse are shown on a standard gray scale, shown above. To enhance ghost visibility relative to the brain tissue signal, pixels outside of each ellipse are shown using a logarithmic gray scale shown on the upper right. The EPI-GESTE image (e) has notably reduced signal energy in the signal-void region outside the ellipse compared to other single frame methods (a–c). The cause of this effect is explained in the text and illustrated in Fig 8.

In contrast, our method (EPI-GESTE) shows a further reduction in GSR in Fig. 3(b). In addition to good ghost suppression, EPI-GESTE benefits from a background noise suppression effect that notably lowers the measured GSR. The source of this effect is described later in the SNR section of the text. Comparing for now the GSR time course variance for each of the spatial/temporal encoding methods, we measured: Real-time PAGE = 0.015546; PLACE = 0.001380; and EPI-GESTE = 0.000893. This demonstrates that EPI-GESTE has significantly lower ghost variability than the previous methods.

Images from a particularly problematic point in time, t = 99, are shown in Fig. 4 for each reconstruction method. Note that to improve ghost visibility, pixels in the signal-void region are shown on a logarithmic scale that is common across all images and spans the full gray-level scale. Specifically, a mask was determined from the EPI-GESTE image to cover all pixels greater than 1.6% of the maximum value. This mask was then filtered to remove any holes, using a 3×3 two-dimensional median filter. The base-10 logarithm of signal values outside of the mask was then computed. These signal-void values were then scaled such that the minimum value was zero and the maximum value in this region across all images was equal to the maximum gray level value within the ellipse. The signal-value to gray-level map for each region is shown in the upper left of Fig. 4.

Here again, the ghost visibility in each image is consistent with the measured GSR levels shown in the previous plot, with the Ahn & Cho images showing much greater visible ghosting than the images reconstructed using spatial and/or temporal encoding. By combining the strengths of PLACE and real-time PAGE, EPI-GESTE is able to capture and correct errors that confound the real-time PAGE method at a higher temporal resolution than PLACE alone. There is also a notable reduction in the background signal level of the signal-void region compared to the other images generated from a single frame of data (Fig. 4a–c). The signal level in the background region of the GESTE image is, however, comparable to the two-frame PLACE image in Fig. 4d. This effect is discussed further in the SNR results below.

Nyquist ghosts are visibly absent in both the PLACE and GESTE images of Fig. 4. However, Fig. 5 demonstrates that the GESTE image has higher fidelity to the measured data than PLACE. The figure shows two images of the signal that is lost during the coherent summation step in both PLACE, Fig. 5(a), and GESTE, Fig. 5(b). Specifically, Fig. 5(a) shows the coherent difference, $I_n^{\prime }-\mathrm{\Psi }{I}_p^{\prime }$, between the interleaved positive and negative gradient images that form the PLACE image. This illustrates the ghost artifact that is cancelled by PLACE, which for this frame is significant. In comparison, the coherent difference between the intermediate images that form the GESTE image, I_n − ΨI_p, shows significantly less signal. The signal that is cancelled in the GESTE method is limited to parallel imaging artifacts and field inhomogeneity effects. This improves the robustness of the method for each time-point in an image series, by limiting the level of variability in the cancelled signal from time-point to time-point.

Figure 5.

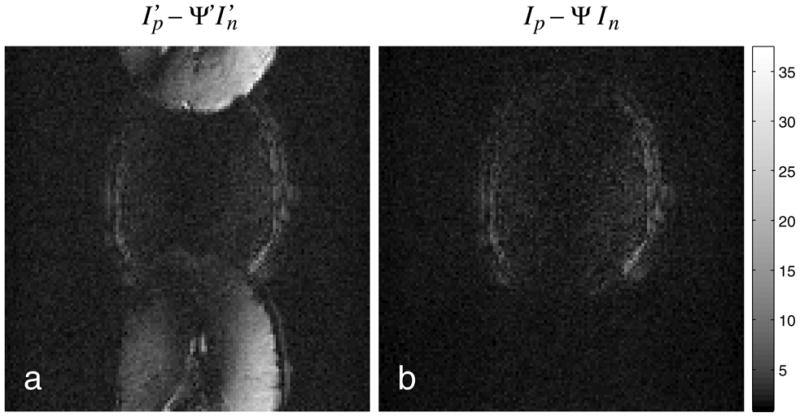
Images of discarded signal in (a) PLACE and (b) GESTE for a single time point. In each method, a coherent addition is performed to cancel residual artifact. In PLACE, this signal is dominated by the residual ghost signal present after interleaving. In GESTE, this signal is limited to artifacts from parallel imaging and field inhomogeneity effects. Significantly more signal is lost with PLACE, which can lead to unwanted variability in an image series.

Fig. 6 shows the ASL perfusion images associated with the structural images shown previously, in Fig. 4. The perfusion image derived from the Ahn & Cho dynamic images, Fig. 6(a), shows reasonably good discrimination between the gray and white matter perfusion, consistent with the current standard in EPI ASL imaging. In contrast, the perfusion image associated with the real-time PAGE method, Fig. 6(b), shows the influence of the Nyquist ghost variations, with both ghost-related signal visible in the signal-void region, and an increase in overall signal intensity on the upper-left quadrant of the brain. Fig. 6(c) shows that with PLACE the ghosts are removed, but the brightening remains. With EPI-GESTE, both the ghosts and the brightening are absent.

The presence or absence of this brightening is clearly seen in the images shown in Fig. 7, which show the arithmetic difference between the Ahn & Cho dynamic image (current standard practice) and the more modern methods. This difference image shows that the subtle brightening effect in the Real-time PAGE and PLACE perfusion images is due primarily to improperly corrected ghost signals. In contrast, Fig. 7(c) illustrates that the EPI-GESTE perfusion image in Fig. 6(d) shows no false perfusion brightening compared to the standard image in Fig. 6(a).

Figure 7.

Difference images between the Ahn & Cho ASL perfusion image and the (a) Real-time PAGE, (b) PLACE, and (c) EPI-GESTE ASL perfusion images. The unusual perfusion brightening visible in the Real-time PAGE and PLACE images of Fig. 6 appear here as dark regions in the upper left quadrant of the brain region. The shading of these regions is consistent with incorrect ghost suppression.

Effect on Noise / SNR

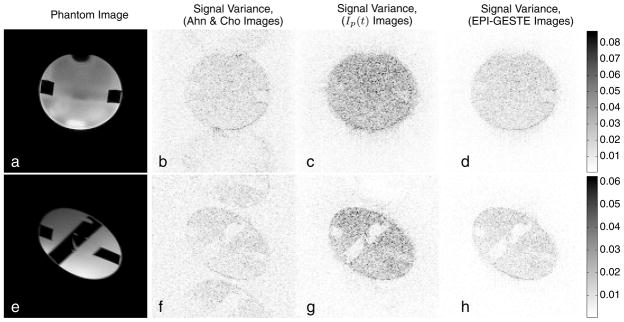
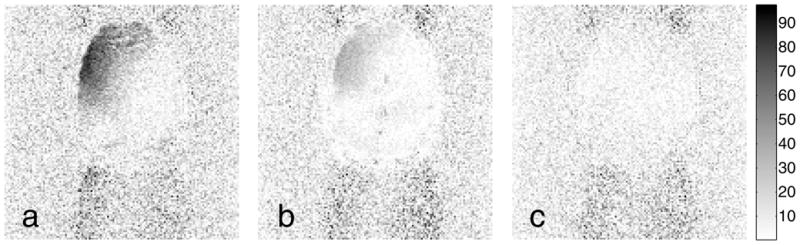
Close inspection of the in-vivo EPI-GESTE images shown previously reveals that the noise level in the signal-void region appears to be comparable to the temporally averaged PLACE image and lower than the other ghost elimination methods. An evaluation of the water phantom image reconstructions was performed to better understand the source of this noise suppression. Fig. 8(a) shows an axial image of the water phantom used for the SNR experiments. Fig. 8(e) shows a double-oblique view of the same phantom. The remaining images in the figure show the signal variance across the temporal image series for each pixel, for the Ahn & Cho dynamic images (center left), the output of one pMRI reconstruction channel, I(p) from Fig. 1 (center right), and the EPI-GESTE images (far right).

Figure 8.

Phantom (a,e) and signal variance images associated with (b,f) Ahn & Cho ghost correction, (c,g) the output of a single pMRI reconstruction channel, I_p(t), and (d,h) the final EPI-GESTE reconstruction, I_p(t) + ΨI_n(t). The top row shows an axial view of the phantom. The bottom row shows a double-oblique view.

The Ahn & Cho images in Fig. 8(b,f) show moderate signal variance in the phantom region. In areas where ghosts appear, the signal variance is slightly higher than in the background. It is well known that SNR will decrease in accelerated parallel imaging applications, and this is consistent with the increase in signal variance shown in images (c) and (g). Notably, the noise in the signal-void region does not increase significantly, as this area is unaffected by the coil sensitivities and thus fall outside the region of increased noise described by the g-factor (22), (23). When the final EPI-GESTE image is formed (d,h), however, two accelerated images contribute, I(p) and I(n). This combination decreases the signal variance across the entire image, unguided by the coil sensitivity. This yields a return of the signal variance to unaccelerated levels in the signal region, while the noise in the signal-void region is also reduced to yield a reduction in signal variance in regions unaffected by the g-factor.

This effect of noise suppression in the signal-void region is confirmed quantitatively, where the average signal variance level within the signal region and in the signal-void region was measured to be: axial images (b): 0.0121, 0.0062; (c): 0.0243, 0.0051; and (d): 0.0120, 0.0026; and for double-oblique images (f): 0.0081, 0.0050; (g): 0.0155, 0.0034; and (h): 0.0079, 0.0018, respectively. That is, the signal variance in the image region affected by coil sensitivity roughly doubles for each intermediate GRAPPA image, but then drops back to the original level when the two GRAPPA images, I_p(t) and I_n(t), are combined. In contrast, at the GRAPPA image stage the mean variance in the signal-void region drops slightly, from 0.0062 to 0.0051 for the axial images, due to the improved ghost suppression. When the two GRAPPA images are combined, the variance level in the signal-void region also drops in half as expected. We note that in comparable PLACE images, the noise variance is roughly one-half of the Ahn & Cho images due to averaging: measured at (0.0056, 0.0027) for the axial images; and (0.0036, 0.0023) for the double-oblique images.

This implies that single image estimates of SNR, using a ratio between signal measured over regions of the phantom and a region in the signal-void, need to account for this effect. Pair-wise subtraction or multiple image measurements, e.g. (24), to estimate SNR with EPI-GESTE are preferable. Similarly, if one compares the GSR measurements of PLACE and EPI-GESTE in Fig. 2, one finds that the mean ratio over the time course is 1.40—or roughly a factor of $\sqrt{2}$. This large difference is a direct result of the background noise suppression effect in EPI-GESTE.

Discussion and Conclussions

We have demonstrated that our EPI-GESTE method, a fusion of previous temporal and spatial encoding methods to suppress Nyquist ghosts, achieves the goals we set at the outset. Specifically, through the use of temporal encoding, EPI-GESTE is self-referenced. EPI-GESTE has low latency in that it requires data from only one previous image volume to calibrate the pMRI reconstruction coefficients. We have also shown that the method is more robust than previous methods to temporal or dynamic changes. In addition, we have shown the method is extremely consistent, and in perfusion imaging does not produce the subtraction errors that both the PLACE and the real-time PAGE methods may introduce. The method appears to be robust to gradient imperfections and can be used successfully in oblique-plane EPI where such errors can be more pronounced (25). Most significantly, however, the achieved ghost suppression level is well below current standard expectations, with less than 1.5% GSR in the perfusion imaging example shown here. The large difference in GSR between EPI-GESTE and competing methods is attributable to the additional background signal suppression provided by the method. In some applications, such as ASL perfusion imaging, we have found this additional background suppression to be beneficial.

We have demonstrated that either blip-shifting or readout gradient toggling can be used for temporal encoding. One advantage of using the alternating readout gradient method is that it maintains the same echo time for each acquisition. One potential concern is that the toggling of the readout gradients may produce slightly different eddy currents in the two acquired frames, which may lead to an inherent mismatch in the interleaved data. We briefly investigated this potential problem by measuring GSR levels after EPI-GESTE reconstruction with and without eddy current compensation provided by the manufacturer. We found no discernible difference in image quality or GSR levels. However, even if the difference in eddy currents was appreciable for certain imaging protocols, our method would still be robust to these differences. Each image in the final output series is reconstructed independently and the interleaved data is used only for parallel imaging calibration. This calibration typically employs only low spatial frequency information. Thus, any eddy current effects would likely be inconsequential.

One challenge of our method in real-time EPI applications is the repeated computation of the pMRI reconstruction coefficients. This can be mitigated as described by Kim, et. al. (8), by performing the pMRI calibration in a process separate from the image reconstruction pipeline and updating the pMRI reconstruction parameters on an as-needed basis.