Skip to main content
PMC home page
Systematic Biology logoLink to Systematic Biology
. 2011 Jan 20;60(2):225–232. doi: 10.1093/sysbio/syq089

Biologically Inspired Phylogenetic Models Strongly Outperform the No Common Mechanism Model

John P Huelsenbeck 1,*, Michael E Alfaro 2, Marc A Suchard 3,1
PMCID: PMC3038349  PMID: 21252385

Abstract

But Tuffley and Steel (1997) introduced a model called No Common Mechanism (NCM), in which characters may—but are not required to—vary their relative rates independently, both within and between branches. Because the independent variation is taken only as a possibility, not as a requirement, NCM would apply to almost any situation, and so may be accepted as realistic. This is useful because Tuffley and Steel also showed that maximum likelihood under NCM selects the same trees as does parsimony. With the realistic NCM in the background, then, most parsimonious trees have greatest power to explain available observations.

—Farris (2008)

The maximum parsimony method is widely used to infer the genealogical history, or phylogeny, of species by selecting the tree that minimizes the number of character state changes as the best estimate (Edwards and Cavalli-Sforza 1963, Camin and Sokal 1965). Interestingly, the development of the method as a way to infer phylogeny preceded attempts to justify its use as a coherent method of inference. Attempts to justify the use of the parsimony method have taken two courses. One approach justifies the use of the parsimony method based on philosophical considerations. At various times, the parsimony method was thought to adhere to the hypothetico-deductive framework of scientific inference (Wiley 1975, Gaffney 1979) or conform to Popper's theory of corroboration (Siddall and Kluge 1997). The other approach to justify the parsimony method starts with the idea that good methods of inference are statistical; the approach then attempts to find probabilistic models of evolution that—when implemented using a standard statistical method of estimation, such as maximum likelihood—order the possible phylogenetic trees in the same way as the parsimony method. Several evolutionary models yield a correspondence between maximum parsimony and maximum likelihood, with most sharing the feature that the number of parameters increases as fast as the data are added (Farris 1973, Goldman 1990), with the most interesting being the no common mechanism model (Tuffley and Steel 1997). (Steel and Penny [2004] show that maximum likelihood and parsimony also order the trees in the same manner when the number of possible states is sufficiently large.)

The no common mechanism model posits an independently estimated branch-length parameter for every alignment site in the data and every branch in the phylogeny. An alignment of N sequences each of length L has (2N − 3)×L branch-length parameters to estimate in an unrooted phylogeny. Note that extending the alignment by one site introduces an additional set of 2N − 3 branch parameters to estimate. The no common mechanism model has captured the attention of systematic biologists for two reasons. First, the model has been used to strongly justify the use of the parsimony method (Farris 2008). The idea is that the parameterization under the no common mechanism model is so general that some realized combination of the many parameters must surely capture reality. By contrast, the standard biologically inspired evolutionary models used in phylogenetic inference usually have one length parameter for every branch, with all sites sharing the 2N − 3 branch parameters and, thus may be too simple to adequately capture the evolutionary process, or allow reliable estimation of phylogeny. Second, the no common mechanism model provides a bridge between the parsimony method and standard implementations of stochastic models in phylogenetics that typically have few parameters (Kim and Sanderson 2008).

The models typically used in phylogenetic analysis and molecular evolution have been carefully crafted to account for new biological phenomena as they were discovered. For example, the discovery that transitions (A↔G and C↔T substitutions) occur at a higher rate than transversions (A↔C, A↔T, C↔G, and G↔T substitutions) in DNA sequences led directly to the development of models that allowed transitions to occur at a different rate than transversions (Kimura 1980, Hasegawa et al. 1985). Similarly, the idea that natural selection acts to remove mutations that cause proteins to change secondary structure, and hence their function, led to the development of models that allow rates of substitution to vary across a sequence (Yang 1993) and to models that allow the nonsynonymous rate of substitution to vary across a protein (Nielsen and Yang 1998). Even the parameterization of the branch lengths on a phylogenetic tree has a biological motivation. There should be more opportunity for change to occur along the longest branches of an evolutionary tree. Hence, one should assign different branch-length parameters to different branches of the evolutionary tree to accommodate the differing opportunities for change along short and long branches. The careful crafting of phylogenetic models to reflect biology stands in contrast to the approach used in the no common mechanism model, which holds a profusion of parameters that have little to do with the underlying biology. That said, it remains an open question whether the biologically inspired approach of incrementally improving models or an alternative approach in which the number and identity of the parameters is not determined in advance is better.

METHODS

Our goal is to compare several traditionally parameterized phylogenetic models, such as the models first described by Jukes and Cantor (1969), Felsenstein (1981), Hasegawa et al. (1984), Hasegawa et al. (1985), or Tavaré (1986) with or without rate variation across sites as modeled by a gamma probability distribution (Yang 1993, Yang 1994), to two variants of the no common mechanism model and also to submodels of the no common mechanism model. In this section, we describe the necessary background for understanding the different possible branch-length parameterizations used in phylogenetics as partitions, how we choose among competing models using Bayes's factors, and the details of three analyses performed in this study.

Submodels of the No Common Mechanism Model

The idea of a partition of the branch/site elements among branch-length parameters provides the bridge between the no common mechanism model and the simplest conceivable phylogenetic model. A partition of a set of objects divides the objects into nonoverlapping subsets. The degree of the partition is the number of subsets. In this case, the objects to be partitioned are the branch/site elements and the subsets represent branch/site elements that share the same branch-length parameter. The simplest model has a single branch parameter shared by all sites in the alignment and all branches of the phylogeny. For example, the simplest partition for an alignment of N = 4 sequences each of length L = 5 is

graphic file with name sysbiosyq089fx1_ht.jpg

using the restricted growth function notation for a partition (Stanton and White 1986). The most complicated model, on the other hand, is the no common mechanism model with an independently estimated length parameter for every branch and every site, which is represented as

graphic file with name sysbiosyq089fx2_ht.jpg

Between these two extremes lives a large number of models with an intermediate number of branch-length parameters. The total number of such partitions is described by the Bell (1934) numbers. Examples of partitions of degree 5 (for the case where N = 4 and L = 5) include

graphic file with name sysbiosyq089fx3_ht.jpg

The last partition shown represents the “traditional” grouping of branch/site elements according to the branch on the evolutionary tree; each branch has a single length parameter that all the sites share.

Comparing Models in a Bayesian Context

We formally evaluate the fit to data of the no common mechanism model and its numerous submodels by comparing marginal likelihoods, an approach commonly advocated to choose among competing models in a Bayesian context (Jeffreys 1961). The ratio of the marginal likelihoods of two models, M1 and M2, is called the Bayes's factor

graphic file with name sysbiosyq089fx4_ht.jpg

where A is the sequence data alignment. A Bayes's factor greater than 1 indicates that the data are more probable under M1 than M2, and values much greater than 1, say 1000 or more (Kass and Raftery 1995), proffer decisive statistical support in favor of M1 over M2. The opposite is true for Bayes's factors less than 1. Note that the models may also contain unique sets of unknown parameters, denoted θ1 and θ2 for models M1 and M2, respectively. The marginal likelihood takes into account all possible values of the parameters unique to the model via integration, Pr(A|Mi) = ∫θif(A|θi,Mi)p(θi|Mi)dθi for i = 1,2, where f(A|·,·) is the data likelihood and p(·|·) is the parameter prior density. In this way, the marginal likelihood automatically and naturally penalizes an overly parameter-rich model; a parameter-rich model spreads the prior probability over a wider area, placing less prior density on combinations of parameters. Models that are sensibly parameterized show improvement in the marginal likelihood that outweighs the cost of the more diffuse prior, whereas those models with poorly chosen parameterizations cannot adequately explain the observations despite the increased complexity of the model.

Data Analysis Using Markov Chain Monte Carlo

We assume that the N sequences are related to one another through an unknown evolutionary tree. Here, we consider the tree to be a fixed part of the analysis; we use the maximum parsimony tree in all analyses. The tree of N sequences has 2N − 3 branches. Under the no common mechanism model, every site and every branch has an independently estimated branch-length parameter. The length of the ith branch and jth site is denoted νij. The branch-length parameters are arranged in the order ν(1,1),…,ν(1,L),ν(2,1),…,ν(2,L),…,ν(2N − 3,1),…,ν(2N − 3,L). As described, above, the (2N − 3)×L branch-length parameters can be constrained to be equal to one another in many different ways, with the combinatorics described by the Bell (1934) numbers. In this study, we either constrain the degree of the partition (but explore various partitions of that degree) or fix the partition.

In our first set of analyses, we compare the marginal likelihoods of phylogenetic models with the traditional branch-length parameterization to two different variants of the no common mechanism model. The traditional models we examine include the models first proposed by Jukes and Cantor (JC69; 1969), Felsenstein (F81; 1981), Hasegawa et al. (HKY85; 1984, 1985), and Tavaré (GTR; 1986). These models—all variants of continuous-time Markov models—describe how substitutions occur along the branches of the phylogeny. The rate matrix characterizing how substitutions occur under the GTR model

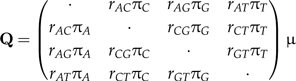graphic file with name sysbiosyq089fx5_ht.jpg

has six exchangeability parameters (rAC,rAG,rAT,rCG,rCT,andrGT) and four stationary frequency parameters (πA,πC,πG,andπT). The diagonal elements of the rate matrix are specified such that each row sums to zero. The scaling factor, μ, is chosen such that the average rate of substitution is one. The other models we examined—the JC69, F81, and HKY85 models—are all special cases of the GTR model. The HKY85 model constrains the exchangeability parameters such that rAC = rAT = rCG = rGT and rAG = rCT. The JC69 and F81 models further restrict the exchangeability parameters such that rAC = rAG = rAT = rCG = rCT = rGT. Three of the models examined (the F81, HKY85, and GTR models) make no restrictions on the stationary frequency parameters. However, the JC69 model restricts the stationary frequencies of the nucleotides to be equal.

We allowed the rate of substitution to vary across a sequence; specifically, we treated the rate at a site as a random variable drawn from a mean-one gamma distribution (Yang 1993, Yang 1994). We denote models with gamma-distributed rate variation with the suffix “ + Γ.”

Under the no common mechanism model, substitutions are assumed to occur under some continuous-time Markov model; the no common mechanism model described by Tuffley and Steel (1997), for example, assumes the simple continuous-time Markov model first described by Jukes and Cantor (1969). We implemented two versions of the no common mechanism model: One assumed that substitutions occur according to the JC69 model, whereas the other assumed the GTR model. In both cases, the length parameter for each site and branch are allowed to vary independently. We place a gamma prior probability distribution on the lengths of the branches. The transition probabilities are

graphic file with name sysbiosyq089fx6_ht.jpg

where Q is the rate matrix, I is the identity matrix, and the branch-lengths are integrated over the gamma prior probability distribution with shape and scale parameters α and λ, respectively (Suchard et al. 2002, Suchard et al. 2003, Sinsheimer et al. 2003, Huelsenbeck et al. 2008). We chose the shape and scale parameters in such a way that the branch lengths had exponential prior distributions (the gamma distribution is equivalent to the exponential distribution when α = 1). The parameter of the exponential prior is fixed such that the marginal likelihood is maximized under the no common mechanism model (implemented with the Jukes and Cantor [1969] model).

The GTR model has 8 additional parameters compared with the Jukes and Cantor (1969) model. We implemented two variants of the GTR model when allowing branch-length parameters to vary independently of one another. Our first attempt allowed the exchangeability parameters (rAC,rAG,rAT,rCG,rCT,rGT) and base frequencies (πA,πC,πG,πT) to vary independently for each branch and site. This implementation is in the spirit of the no common mechanism model. The total number of parameters in this model is (2N − 3)×L×8. Our second implementation of the GTR model assumed a common parameterization for the GTR parameters. This model is more in the spirit of the traditional parameterization of the GTR model, which has a common set of parameters for all the observations. The total number of parameters for our second implementation of the GTR model is (2N − 3)×L + 8.

In our second set of analyses, we calculated the marginal likelihoods for models intermediate between the traditional branch-length parameterization and the no common mechanism model. We allowed the branch-length partition to be considered a random variable but fixed the degree of the partitions considered. The degrees of the simplest, traditional, and no common mechanism branch-length parameterizations are D = 1, D = 2N − 3, and D = (2N − 3)×L, respectively. The degree of the partitions explored in the second set of analyses were intermediate, with 2N − 3 < D < (2N − 3)×L.

In our third set of analyses, we compared the marginal likelihoods for the traditional branch-length parameterization to random permutations of the traditional parameterization. Returning to the example of branch-length partitions discussed above, the traditional branch-length parameterization for an alignment of N = 4 sequences each of length L = 5 is

graphic file with name sysbiosyq089fx7_ht.jpg

Note that each branch has a common length parameter that is shared by all the sites. Random permutations of the tradition branch-length parameterization include

graphic file with name sysbiosyq089fx8_ht.jpg

The number of branch elements in each subset (i.e., the number of 1s, 2s, etc.) is maintained, but their assignment to branch/sites is random.

We estimate the branch-length partitions and branch-length parameters using Bayesian inference. Specifically, we calculate the joint posterior probability distribution of the branch-length parameters, conditioned on the alignment (A), a phylogenetic tree (τ), and the degree of the partition (D). Assuming independence of the substitutions at different sites and branches, the likelihood can be calculated as the product of the site likelihoods. We use the usual method for calculating site likelihoods described by Felsenstein (1981).

The joint posterior probability distribution of the branch-length parameters cannot be calculated analytically, except in the maximally parameterized case of the no commonmechanism model (Huelsenbeck et al. 2008). We use Markov chain Monte Carlo (MCMC) to approximate the posterior probability distribution (Metropolis et al. 1953, Hastings 1970). Our MCMC procedure works as follows. First, a branch/site element is removed from its current subset. The likelihood is then recalculated when the branch/site element is placed in each of the D subsets (including the subset from which it was removed); the branch/site element is assigned to a new subset with a probability proportional to the likelihoods. This MCMC procedure is similar to the one proposed by Pritchard et al. (2000) for analysis of population structure. We did not constrain the MCMC in such a way that every subset had at least one branch/site element. Another MCMC proposal mechanism we implemented proposes a new branch length for each of the D subsets, accepting or rejecting the proposed branch length according to the Metropolis–Hastings acceptance probability. Each MCMC iteration included a scan of all (2N − 3)×L branch/site elements and an update attempt for each of the D branch-length parameters. Markov chains were run for a total of 1,000,000 iterations. Each analysis was repeated.

We examined 6 alignments on fixed (maximum parsimony) phylogenetic trees: 1) gophers (N = 5, L = 379; Hafner et al. 1994), 2) fish of the family Labridae (N = 17, L = 443; Westneat and Alfaro 2005), 3) seed plants of the family Ericales (N = 4, L = 170; Geuten et al. 2007), 4) primates (N = 6, L = 768; Drummond et al. 2006), 5) vertebrate ATPase8 gene (N = 10, L = 162; Cummings et al. 1995), and 6) vertebrate ND4L gene (N = 6, L = 294; Cummings et al. 1995). We compared the different models using the marginal likelihoods. Marginal likelihoods were computed from the output of the MCMC analysis (Newton and Raftery 1994). We also evaluated the marginal likelihoods of several biologically inspired models often used in maximum likelihood and Bayesian analyses. These models—the JC69 (Jukes and Cantor 1969), F81 (Felsenstein 1981), GTR (Tavaré 1986), and GTR+Γ (Tavaré 1986, Yang 1993)—have far fewer parameters compared with the no common mechanism model.

RESULTS AND DISCUSSION

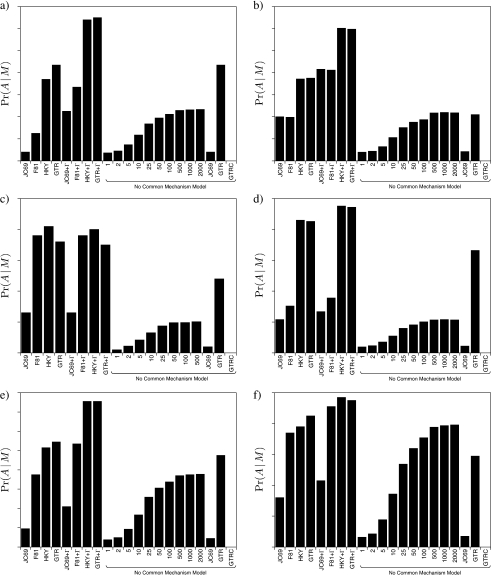
Figure 1 plots the marginal likelihoods for the models examined in this study. (Table 1 also summarizes the main results of the first analysis.) We do not expect the no common mechanism model, itself, to perform well when compared with the biologically inspired models we examine, as the no common mechanism model is also equivalent to a model with equal branch lengths, where the branch-length parameters are not estimated from the data (Huelsenbeck et al. 2008, Holder et al. 2010). However, the submodels of the no common mechanism model are not as severely overparameterized and merit considerable interest. As expected, the marginal likelihood is largest for a degree intermediate between the two extremes of the parameter-rich no commonmechanism model and the oversimplified model where all branch/site elements share a single branch-length parameter (Kim and Sanderson 2008). Unexpectedly, however, the biologically inspired parameterizations used in parametric inference of phylogeny, such as the GTR + Γ (Tavaré 1986, Yang 1993) and GTR (Tavaré 1986) models, fit the data much better than even the submodels of the no common mechanism model (implemented with the JC69 model) that we examined.

FIGURE 1.

FIGURE 1.

Open in a new tab

The marginal likelihoods for various submodels of the no common mechanism model and several common parametric models used in phylogenetic analysis. The graphs depict the results for the sequence alignments of a) gophers, b) fish of the family Labridae, c) seed plants of the family Ericales, d) primates, e) vertebrate TPase8 gene, and f) vertebrate ND4L gene.

TABLE 1.

The marginal likelihoods for some of the models examined in this studya

Model A B C D E F
JC69 – 1345 – 2319 – 460 – 1981 – 1553 – 1779
F81 – 1328 – 2320 – 435 – 1959 – 1497 – 1737
HKY85 – 1279 – 2233 – 432 – 1820 – 1469 – 1733
GTR – 1266 – 2231 – 437 – 1822 – 1463 – 1726
JC69 + Γ – 1308 – 2211 – 460 – 1968 – 1530 – 1768
F81 + Γ – 1286 – 2213 – 435 – 1946 – 1465 – 1720
HKY85 + Γ – 1225 – 2118 – 433 – 1797 – 1421 – 1714
GTR + Γ – 1223 – 2120 – 438 – 1799 – 1421 – 1716
NCM-JC69 – 1345 – 2398 – 471 – 2024 – 1563 – 1804
NCM-GTR – 1266 – 2314 – 449 – 1869 – 1477 – 1752
NCM-GTRC – 1353 – 2419 – 473 – 2035 – 1572 – 1811
Open in a new tab
a

The columns give the results for the sequence alignments of (A) gophers, (B) fish of the family Labridae, (C) seed plants of the family Ericales, (D) primates, (E) vertebrate ATPase8 gene, and (F) vertebrate ND4L gene. The three variants of the no common mechanism model are: NCM-JC69, the parameterization discussed by Tuffley and Steel (1997); NCM-GTR, the no common mechanism model implemented with the GTR model with the parameters of the GTR model shared across sites and branches; and NCM-GTRC, the no common mechanism model with independently estimated GTR parameters for each site and branch.

The marginal likelihoods under the no common mechanism model implemented with a common set of GTR parameters was larger than the no common mechanism model implemented using the JC69 model (and described by Tuffley and Steel 1997). In fact, the GTR version of the no common mechanism model was better than many of the traditional models that we examined. However, the details of the implementation of the GTR model were quite important. The marginal likelihoods were high only when the GTR parameters were shared across sites/branches; the marginal likelihood was low when each site/branch had independently estimated GTR parameters. Clearly models that allow parameters to be shared across sites/branches are favored. Many other ways of allowing the GTR parameters to be shared—that are intermediate between the two versions of the GTR no common mechanism model we examined—can be imagined but were not implemented in this study.

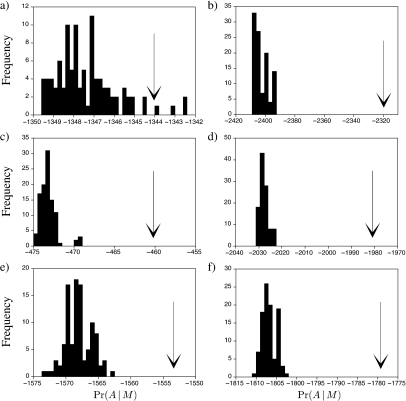
We also compare the traditional branch parameterization—in which each branch of the phylogenetic tree has a single length parameter (i.e., the Jukes and Cantor 1969 model)—against random permutations of the traditional model. Figure 2 shows the frequency histogram of the marginal likelihoods for random permutations of the branch parameters and also plots the marginal likelihood of the traditional branch parameterization. The traditional branch parameterization does a much better job of explaining the sequence alignment than randomly permuted partitions of the same size.

FIGURE 2.

FIGURE 2.

Open in a new tab

Comparison of the marginal likelihood for the traditional method for assigning branch-length parameters to a tree (arrow) versus random permutations of the traditional method, each of which does not take into account the varying opportunities for substitution along long and short branches of the tree. The graphs depict the results for the sequence alignments of a) gophers, b) fish of the family Labridae, c) seed plants of the family Ericales, d) primates, e) vertebrate ATPase8 gene, and f) vertebrate ND4L gene.

The no common mechanism model would seem a good one to use in a phylogenetic analysis because of the model's many parameters and their many opportunities to explain an alignment of DNA sequences. By contrast, the biologically inspired models used in parametric inference of phylogeny have few parameters and, to a first approximation, appear to be too simplistic. However, model choice is not simply a matter of choosing the model with a greater number of parameters. There is a tradeoff between the bias and variance in parameter estimates caused by subtracting and adding parameters from a model. Here, we show, through a direct comparison of the no common mechanism model and the more carefully crafted (and, ironically, more parsimonious) models typically used in phylogenetic analysis of molecular data, that the biologically inspired models strongly outperform the no common mechanism model (and its submodels) in a classical model-choice framework. First, the marginal likelihoods for the biologically inspired phylogenetic parameterizations, such as the GTR + Γ model, are many orders of magnitude higher than under the no common mechanism model, or under its submodels. Second, the widely used idea of assigning one branch-length parameter to every branch of the tree, with all the sites in the alignment sharing that parameterization, is substantially better than random assignments of branch-length parameters to sites.

No statistical model can perfectly reflect reality. The models used by evolutionary biologists to estimate phylogeny and to examine questions in molecular evolution are no exception and, at best, only approximate the underlying processes of interest. That said, this study suggests that evolutionary biologists have been on the right track all along by devising models that are biologically inspired.

FUNDING

This research was supported by grants from the National Science Foundation (DEB-0445453) and National Institutes of Health (GM-069801 awarded to J.P.H. and GM-086887 to M.A.S.).

Acknowledgments

We thank Brian and Mary Moore for helpful comments and discussion.

References

  1. Bell ET. Exponential numbers. Am. Math. Mon. 1934;41:411–419. [Google Scholar]
  2. Camin JH, Sokal RR. A method for deducing branching sequences in a phylogeny. Evolution. 1965;19:311–326. [Google Scholar]
  3. Cummings MP, Otto SP, Wakeley J. Sampling properties of DNA sequence data in phylogenetic analysis. Mol. Biol. Evol. 1995;12:814–822. doi: 10.1093/oxfordjournals.molbev.a040258. [DOI] [PubMed] [Google Scholar]
  4. Drummond AJ, Ho SY, Phillips MJ, Rambaut A. Relaxed phylogenetics and dating with confidence. PLoS Biol. 4:e88. 2006 doi: 10.1371/journal.pbio.0040088. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Edwards AWF, Cavalli-Sforza LL. The reconstruction of evolution (abstract) Ann. Hum. Genet. 1963;27:104–105. [Google Scholar]
  6. Farris JS. A probability model for inferring evolutionary trees. Syst. Zool. 1973;22:250–256. [Google Scholar]
  7. Farris JS. Parsimony and explanatory power. Cladistics. 2008;24:825–847. [Google Scholar]
  8. Felsenstein J. Evolutionary trees from DNA sequences: a maximum likelihood approach. J. Mol. Evol. 1981;17:368–376. doi: 10.1007/BF01734359. [DOI] [PubMed] [Google Scholar]
  9. Gaffney ES. An introduction to the logic of phylogeny reconstruction. Phylogenetic analysis and paleontology. In: Cracraft J, Eldredge N, editors. Columbia University Press; 1979. pp. 79–111. [Google Scholar]
  10. Geuten W, Massingham T, Darius P, Smets E, Goldman N. Experimental design criteria in phylogenetics: where to add taxa. Syst. Biol. 2007;56:609–622. doi: 10.1080/10635150701499563. [DOI] [PubMed] [Google Scholar]
  11. Goldman N. Maximum likelihood inference of phylogenetic trees with special reference to a Poisson process model of DNA substitution and to parsimony analyses. Syst. Zool. 1990;39:345–361. [Google Scholar]
  12. Hafner MS, Sudman PD, Villablanca FX, Spradling TA, Demastes JW, Nadler SA. Disparate rates of molecular evolution in cospeciating hosts and parasites. Science. 1994;265:1087–1090. doi: 10.1126/science.8066445. [DOI] [PubMed] [Google Scholar]
  13. Hasegawa M, Kishino H, Yano T. Dating the human-ape splitting by a molecular clock of mitochondrial. DNA.J. Mol. Evol. 1985;22:160–174. doi: 10.1007/BF02101694. [DOI] [PubMed] [Google Scholar]
  14. Hasegawa M, Yano T, Kishino H. A new molecular clock of mitochondrial DNA and the evolution of hominoids. Proc. Jpn. Acad. Ser. B. 1984;60:95–98. [Google Scholar]
  15. Hastings WK. Monte Carlo sampling methods using Markov chains and their applications. Biometrika. 1970;57:97–109. [Google Scholar]
  16. Holder MT, Lewis PO, Swofford DL. The Akaike information criterion will not choose the no common mechanism model. Syst. Biol. 2010;59:477–485. doi: 10.1093/sysbio/syq028. [DOI] [PubMed] [Google Scholar]
  17. Huelsenbeck JP, Ané C, Larget B, Ronquist F. A Bayesian perspective on a non-parsimonious parsimony model. Syst. Biol. 2008;57:406–419. doi: 10.1080/10635150802166046. [DOI] [PubMed] [Google Scholar]
  18. Jeffreys H. Theory of probability. Oxford: Oxford University Press; 1961. [Google Scholar]
  19. Jukes TH, Cantor CR. Evolution of protein molecules Mammalian protein metabolism. In: Munro HN, editor. Academic Press; 1969. pp. 21–123. [Google Scholar]
  20. Kass RE, Raftery AE. Bayes factors. J. Am. Stat. Assoc. 1995;90:773–795. [Google Scholar]
  21. Kim J, Sanderson MJ. Penalized likelihood phylogenetic inference: bridging the parsimony-likelihood gap. Syst. Biol. 2008;57:665–674. doi: 10.1080/10635150802422274. [DOI] [PubMed] [Google Scholar]
  22. Kimura M. A simple method for estimating evolutionary rates of base substitutions through comparative studies of nucleotide sequences. J. Mol. Evol. 1980;16:111–120. doi: 10.1007/BF01731581. [DOI] [PubMed] [Google Scholar]
  23. Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953;21:1087–1092. [Google Scholar]
  24. Newton MA, Raftery AE. Approximate Bayesian inference by the weighted likelihood bootstrap. J.R. Stat. Soc. B. 1994;56:3–48. [Google Scholar]
  25. Nielsen R, Yang Z. Likelihood models for detecting positively selected amino acid sites and applications to the HIV-1 envelope gene. Genetics. 1998;148:929–993. doi: 10.1093/genetics/148.3.929. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Pritchard JK, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000;155:945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Siddall ME, Kluge AG. Probabilism and phylogenetic inference. Cladistics. 1997;13:313–336. doi: 10.1111/j.1096-0031.1997.tb00322.x. [DOI] [PubMed] [Google Scholar]
  28. Sinsheimer JS, Suchard MA, Dorman KS, Fang F, Weiss RE. Are you my mother? Bayesian phylogenetic inference of recombination among putative parental strains. Appl. Bioinformatics. 2003;2:131–144. [PubMed] [Google Scholar]
  29. Stanton D, White D. Constructive combinatorics. New York: Springer-Verlag; 1986. [Google Scholar]
  30. Steel MA, Penny D. Two further links between MP ad ML under the Poisson model. Appl. Math. Lett. 2004;17:785–790. [Google Scholar]
  31. Suchard MA, Weiss RE, Dorman KS, Sinsheimer JS. Oh brother, where art thou? A Bayes factor test for recombination with uncertain heritage. Syst. Biol. 2002;51:715–728. doi: 10.1080/10635150290102384. [DOI] [PubMed] [Google Scholar]
  32. Suchard MA, Weiss RE, Dorman KS, Sinsheimer JS. Inferring spatial phylogenetic variation along nucleotide sequences: a multiple changepoint model. J. Am. Stat. Assoc. 2003;98:427–437. [Google Scholar]
  33. Tavaré S. Some probabilistic and statistical problems on the analysis of DNA sequences. Lect. Math. Life Sci. 1986;17:57–86. [Google Scholar]
  34. Tuffley C, Steel M. Links between maximum likelihood and maximum parsimony under a simple model of site substitution. Bull. Math. Biol. 1997;59:581–607. doi: 10.1007/BF02459467. [DOI] [PubMed] [Google Scholar]
  35. Westneat MW, Alfaro ME. Phylogenetic relationships and evolutionary history of the reef fish family. Labridae. Mol. Phylogenet. Evol. 2005;36:370–390. doi: 10.1016/j.ympev.2005.02.001. [DOI] [PubMed] [Google Scholar]
  36. Wiley EO. Karl R. Popper, systematics, and classification: areply to Walter Bock and other evolutionary taxonomists. Syst. Biol. 1975;24:233–243. [Google Scholar]
  37. Yang Z. Maximum likelihood estimation of phylogeny from DNA sequences when substitution rates differ over sites. Mol. Biol. Evol. 1993;10:1396–1401. doi: 10.1093/oxfordjournals.molbev.a040082. [DOI] [PubMed] [Google Scholar]
  38. Yang Z. Maximum likelihood phylogenetic estimation from DNA sequences with variable rates over sites: approximate methods. J. Mol. Evol. 1994;39:306–314. doi: 10.1007/BF00160154. [DOI] [PubMed] [Google Scholar]

Articles from Systematic Biology are provided here courtesy of Oxford University Press

RESOURCES