Second Harmonic Generation for time-resolved monitoring of membrane pore dynamics subserving electroporation of neurons

Abstract

Electroporation of neurons, i.e. electric-field induced generation of membrane nanopores to facilitate internalization of molecules, is a classic technique used in basic neuroscience research and recently has been proposed as a promising therapeutic strategy in the area of neuro-oncology. To optimize electroporation parameters, optical techniques capable of delivering time and spatially-resolved information on electroporation pore formation at the nanometer scale would be advantageous. For this purpose we describe here a novel optical method based on second harmonic generation (SHG) microscopy. Due to the nonlinear and coherent nature of SHG, the 3D radiation lobes from stained neuronal membranes are sensitive to the spatial distribution of scatterers in the illuminated patch, and in particular to nanopore formation.We used phase-array analysis to computationally study the SHG signal as a function of nanopore size and nanopore population density and confirmed experimentally, in accordance with previous work, the dependence of nanopore properties on membrane location with respect to the electroporation electric field; higher nanopore densities, lasting < 5 milliseconds, are observed at membrane patches perpendicular to the field whereas lower density is observed at partly tangent locations. Differences between near-anode and near-cathode cell poles are also measured, showing higher pore densities at the anodic pole compared to cathodic pole. This technique is promising for the study of nanopore dynamics in neurons and for the optimization of novel electroporation-based therapeutic approaches.

1. Introduction

Second Harmonic Generation (SHG) microscopy is a nonlinear optical technique suitable for structural and functional imaging of biological structures such as collagen, muscle and cell membranes [1–5]. Since SHG is a coherent process, it requires repetitive anatomical features, either intrinsically scattering or endowed with exogenous dyes, to produce a constructive optical signal [6]. The resulting optical signature is modulated by the orientation [7], electrical properties [8] and, most relevant here, the spatial distribution of the scatterers [9]. Substantial theoretical data on these unique characteristics of SHG are available, granting interest in further development of their experimental applications.

Electropermeabilization or electroporation is a method widely employed for delivery of biomolecules into cells [10–12]. A pulsed electric field (duration usually ≈ 1ms) is created by a pair of electrodes, opening transient pores in proximal cell membranes and facilitating passive entry of molecules. Recently electroporation has received renewed attention because of the development of electrochemotherapy, a new therapeutic approach for highly localized delivery of drugs to a wide range of cancer types [13, 14] including hard to treat neuro-oncology tumors [15].

Theoretical work has delivered predictions regarding the number, spatial distribution, and size of pores produced by the electric field, as well as on the transient transmembrane potentials ocurring concomitantly with electroporation [16–18]. Experimental studies with voltage-sensitive dyes have confirmed the anticipated membrane potentials [19] whereas electron microscopy (EM) was used for direct visualization of pore size and spatial distribution at specific points in time [20]. Conventional fluorescence imaging of dye diffusion provides a dynamic view of fluorophore entry but it remains challenging to resolve sub-wavelength features of nanopore populations [21–25]. A novel time and space resolved optical technique suitable to directly gather information on sub-wavelength pore populations would be advantageous.

We reasoned that, since nanopore formation results in spatial redistribution of scatterers in stained membranes, a coherent process such as SHG could be used to report on nanopore formation.

Indeed, two models, the phase-array model [9, 26] and Green’s function formulation [27, 28], are often used to describe SHG generation by scatterers. Both predict that changes in the spatial distribution of the scatterers at the nanometer scale result in the rearrangement of the 3D radiation pattern. Here we describe a novel method based on SHG to characterize transient redistribution of the scatterers and pore formation by electropermeabilization. Modeling and experiments were conducted providing a “proof of principle” of the technique.

2. Materials and methods

2.1. Experimental approach

Figure 1 illustrates the experiment. A conventional multiphoton microscope, Leica TCS SP5 MP, was adapted for SHG imaging. The 905 nm laser line was used to illuminate a membrane patch of SynaptoredTM C2-stained membrane of an in-vitro hippocampal neuron (see below for detailed culture and staining protocols). Since the maximum two photon absorption wavelength for SynaptoredTM C2 is close to 1064 nm, the incoming beam wavelength was chosen at 905 nm to reduce photobleaching. A 63× objective (1.4 NA) was used to focus on the sample in addition to 450/10 nm (Semrock) filters for forward and backward collection of SHG (Fig. 1), respectively. The detection system in the forward direction made use of a photon multiplier tube (PMT, Hamamatsu R6350) and a condenser with NA = 0.5 or alternatively NA = 0.11 (as indicated in the text and figures). Occasionally the central region of the collection area was blocked with an opaque disk (diameter 13 mm) corresponding to a blocked angle of acceptance of 6.3 degrees.

Fig. 1.

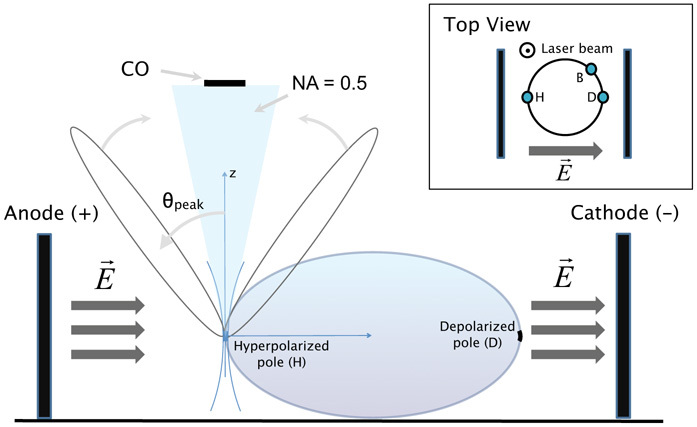
Lateral view sketch of the set-up for SHG imaging with simultaneous electroporation (CO = central obscuration, NA = numerical aperture, H = hyperpolarized pole, D = depolarized pole, B = border region). Inset: top view.

For each neuron the plane of maximum cell diameter was first identified by obtaining a stack of images along the z axis. Subsequently various regions of the membrane (at both poles and lateral areas) were illuminated to obtain an SHG signal while simultaneously performing electroporation. A 2-lobed SHG radiation pattern is expected, as previously described for such configurations.

The point spread function of the system was measured as Dong et al. [29], obtaining a focal volume of 0.4 × 0.4 × 1.9 µm³. SHG and TPF imaging were performed by laser raster scanning with dwell time per pixel of 2.44 µs, image resolution of 512 × 32 pixels² and image dimension of 3.84 × 0.23 µm². The input power at the sample plane in all the experiments was kept below 20 mW, to avoid side effects like photoporation or photogeneration of membrane potential in the cells [30, 31].

For simultaneous imaging and electroporation, two (anode and cathode) Ag/AgCl wire electrodes were submerged at a separation of 1 cm and with a length of 1 cm per electrode. One or multiple pulses of 1–4 ms in the range of 100V–500V were applied using the GENEPULSER II with Capacitor Extender (BioRad). The ensuing electric field E⃗ is perpendicular to the membrane at the poles and partly tangent to other areas of the membrane, and creates short-lived nanopores and transmembrane potential transients, of hyperpolarizing nature (potential decrease) at the anodic pole and depolarizing nature (potential increase) at the cathodic pole.

2.2. Cell culture and staining

Dissociated cultures of mouse hippocampus neurons were prepared as previously described [32]. Briefly, hippocampi were dissected from E18 embryonic mice, dissociated with papain (13 units ml⁻¹) at 37°C and gently triturated. Fresh cells were seeded at densities ranging from 104 neurons dish⁻¹ (3×10² neurons mm⁻²) in Neurobasal and supplemented with 2% B27, 2 mM L-glutamine, 5% horse serum (all from Invitrogen) and 20 µg ml⁻¹ gentamycin (Sigma). After 2 days, the dish volume was replaced by medium without horse serum to slow down glial proliferation. Prior to plating, glass bottom dishes (MatTek) had been coated overnight with 0.1% poly-D-lysine.

Cells were stained for imaging with 100 µg/ml of SynaptoredTM C2 dye (Biotium, Hayward, CA) and incubated for 1 min. Successful electroporation was tested by observation of the internalization of PI (Propidium Iodide, Invitrogen). As PI binds DNA its quantic efficiency increases by a factor of 20- to 30-fold [33]. Electroporation medium was prepared with 20 µl of PI diluted in 2 ml of Neurobasal supplemented with 2% B27, 2 mM L-glutamine and 20 µg ml⁻¹ gentamycin.

2.3. Mathematical methods

We calculated the far-field SHG radiation pattern generated by a collection of molecules under the influence of a tightly focused field E_ω, i.e. high NA configuration, using a phased array approach [9, 26]. The active volume in which essentially all SHG is generated was defined by the focal volume. The SHG radiation pattern, due to its coherent nature, depends acutely on the spatial distribution of the scatterers inside this volume. We present only the final equation for calculating the SHG power per solid angle:

$$P_{2\omega }(\theta ,\phi )\propto {\mid \left[\left(\begin{array}{c}\hat{\theta }\\ \hat{\phi }\end{array}\right)\right]{\vec{\mu }}_{2\omega }\left(0\right)(\theta ,\phi )\int N\left(\vec{q}\right)A_{\left(d\right)}(\theta ,\phi ;\vec{q})d\vec{q}\mid }^2$$ (1)

where μ⃗_2ω(0) is the second-harmonic dipole moment, N(q⃗) comprises the components of the expansion in its Fourier series of the distribution of scatterers N(x⃗), and A_(d) is an “antenna” factor arising from the phased-array summation of the radiated fields from the distributed sources, also dependent on the dimensionality of scatterer distribution d.

The dipole moment μ⃗_2ω(0) depends on the tilt angle of the chromophore axis with respect to the membrane normal and, for an ensemble of molecules, the angular dispersion considers the possible different orientation of the molecules embedded in the cell membrane. We calculated the dependence of the SHG radiation pattern for the poles D and H (inset in Fig. 1) over the angular dispersion of the molecules, and found that it does not modify the SHG pattern distribution. Further, the effect of the tilt angle over the voltage-dependence of the SHG power for SynaptoredTM C2, was studied by J. Jiang et al. [8] with similar NAs for focusing and collection. It was observed that, for this particular chromophore, there was little change of the SHG transient as a a function of laser polarization.

3. Results and discussion

3.1. Numerical model of SHG generated by nanopore-free and nanopore-populated membranes

At rest, prior to electroporation, the nanopore-free membrane can be modeled for the purpose of SHG radiation as a collection of SynaptoredTM C2 scattering molecules, uniformly distributed in space. The following parameter values were used: N(x⃗) = N_l, Gouy shift ξ = 0.5, and the corresponding focal volume measured for our set up, in Eq. (1).

An off-axis (angle θ_peak = cos⁻¹(ξ)) two-lobed radiation diagram (blue trace in Fig. 2(a)) results from this model, in accordance with previous theoretical and experimental work [9, 27, 28].

Fig. 2.

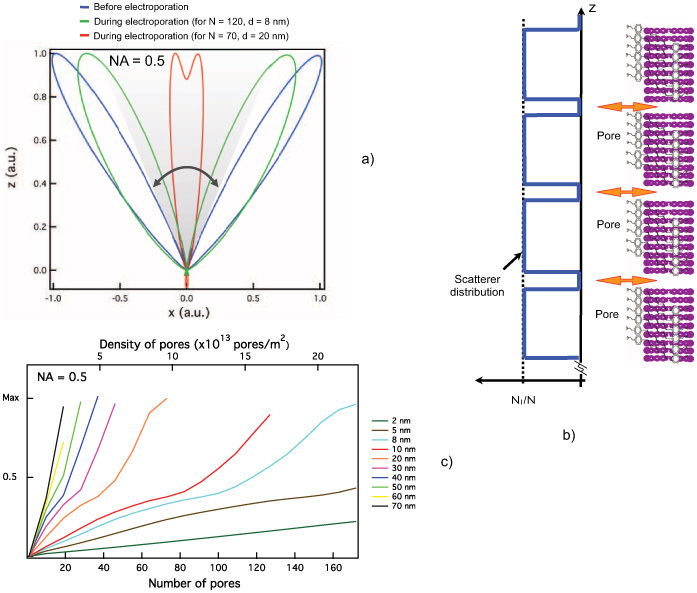
(a) Simulated SHG radiation pattern prior to and during an electroporation pulse peak. (b) Fluorophore and nanopore distribution at cell poles during electroporation as used for the grid version of the SHG model (based on Mertz et al. [9]). (c) Magnitude of the electroporation-induced SHG transient predicted by the model as a function of pore density and nanopore diameter in an illuminated patch at the cell poles, condenser NA = 0.5.

The creation of pores in the membrane by electroporation alters the spatial distribution of scatterers, and consequently the SHG radiation pattern. A periodic square function (Fig. 2(b)) is used to model the nanopore population,

$$N\left(z\right)=\frac{N_1}{\left(\mathit{Na}\right)}\underset{\mathrm{m=}\mathrm{1}}{\overset{N}{\mathrm{\Sigma }}}\mathit{rect}\left(\frac{x-\mathit{md}}{a}\right)$$ (2)

where N_l is the fluorophore density, N is the number of pores, d is the periodicity of the pores, and a is the pore size.

To choose realistic pore densities and diameters for the model we used theoretical results from Krassowska et. al.’s [18] model of electroporation. According to this model, an electric field pulse of 40 kV/m and 1 ms in duration succeeds in sufficiently deflecting membrane potential, V_m, at the polar regions of the cell (membrane regions closest to the electrodes), to surpass the electroporation threshold and transiently create a large number of nanopores (density in the range 10¹³ pores/m²). The same model predicts an increase of V_m (depolarization) and large nanopores (average diameter ≥ 20 nm) at the pole nearest to the cathode, compared to the anodic pole where a decrease of V_m (hyperpolarization) and smaller nanopores (diameter ≈ 1–2 nm) are predicted. Further, zero or a single pore is predicted away from the poles.

Figure 2(a) shows the radiation diagram for realistic nanopore densities of 10×10¹³ and 16×10¹³ pores/m² and pores with a diameter of ∼ 20 nm and ∼ 8 nm respectively, i.e., within value ranges expected at the poles. Note that our numerical results suggest that nanopore formation leads to lobe rearrangement increasing the predicted SHG signal within the collection cone corresponding to NA = 0.5 (gray area in Fig. 2(a)).

A systematic parameter space exploration is illustrated in Fig. 2(c). An increase in the SHG signal is predicted as the number and diameter of the pores within the illuminated patch increase.

3.2. SHG transients caused by electroporation

Figure 3(a) shows TPF and (b) SHG images of SynaptoredTM C2-labeled hippocampal neurons before electroporation. The SHG and TPF signals were stable prior to electroporation, suggesting limited spontaneous internalization of SynaptoredTM C2 or PI.

Fig. 3.

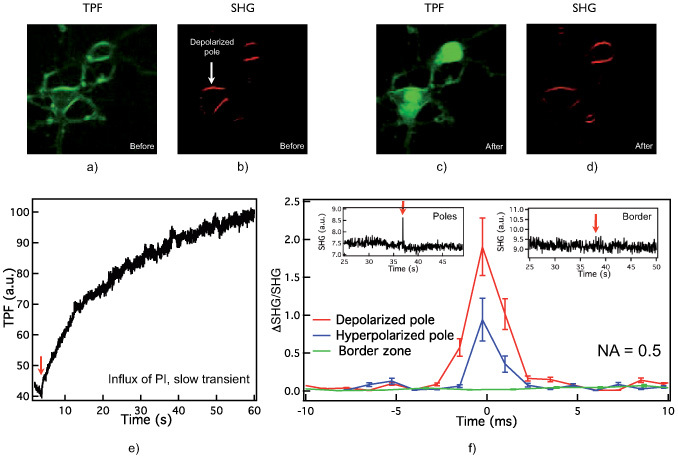
Images of hippocampal neurons labeled with SynaptoredTM C2, (a) backward TPF before electroporation, (b) forward SHG before electroporation showing localization of the depolarized (cathodic) pole; (c) backward TPF after electroporation of the same cells, (d) forward SHG after electroporation (same cells). (e) TPF signal after electroporation at the hyperpolarized pole. (f) Averaged SHG normalized to SHG when no pores are present, at depolarized (red trace), hyperpolarized (blue) poles, and border region (green), collected with NA = 0.5 condenser.

An exponentially-decaying voltage pulse (τ ≈ 2–3 ms and 400 V) was applied to the electrodes resulting in electroporation of PI dye. Figure 3(c) shows in TPF mode an increase of intracellular fluorescence upon internalization of PI. An SHG image post-electroporation is shown in Fig. 3(d) indicating stable membrane staining by SynaptoredTM C2.

Figure 3(e) shows the time profile with slow build up of fluorescence as PI binds to DNA post electroporation over aproximately 30 seconds ((ΔTPF/TPF_uniform)avg ∼ 80%, for 7 cells).

The averaged time profile (n = 8) of the fast SHG signal during electroporation is shown in Fig. 3(f), including data from a membrane patch at the depolarized (red trace) and hyperpolarized (blue) poles as well as at side/border locations (green). The insets further illustrate the absence of SHG transient in the raw data (unaveraged) from a lateral (border) location but an SHG peak clearly above noise at the poles, suggesting presence of pore populations.

These results are consistent with theoretical predictions from Krassowska et. al.’s [18] model predicting differences in nanopore densities amongst cell poles and scant presence of pores at lateral locations.

3.3. Lobe rearrangement and voltage-sensitivity

SynaptoredTM C2 displays voltage-sensitivity, i.e. modulation of its SHG signal by changes in the membrane potential, such as those occurring during electroporation, even in the absence of pores [5, 8].

To confirm that lobe rearrangement is the main contributor to SHG transients produced by electroporation, as opposed to voltage-transient sensing, we blocked the central region of the collection cone (see sketch included in Fig. 1).

Should voltage-sensitivity play a substantial role in SHG transients, their relative magnitude should be independent from the collection angle. Lobe rearrangement (Fig. 2(a)) would not be present or would contribute little. Under these assumptions, blocking of the central area would then result in fewer photons detected by the PMT but unchanged ratio between electroporation peak and resting signal.

Yet Fig. 4(a) shows a dramatic effect of the central obscuration (middle bar), reducing the relative change of SHG during electroporation by ∼ 80%, confirming that electroporation rotates the radiation lobes to partially cover the central (blocked) region of the collection angle. Further, a condenser with NA = 0.11 was used as a complementary experiment, excluding photons at large angles (right bar in Fig. 4(a)). A reduction of the total photon number but a moderate change of the relative SHG change during electroporation with respect unblocked collection were observed.

Fig. 4.

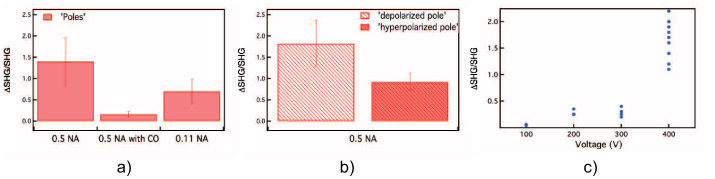
Experimental results: (a) electroporation-related SHG transient, normalized to SHG when no pores are present, at polar locations collected with different configurations of the set-up (without obscuration, with central obscuration CO, and limited NA), (b) same at the depolarized and hyperpolarized poles, and (c) electroporation-related SHG, normalized to SHG when no pores are present, as a function of the voltage of the electroporation pulse.

Moreover, based on previous work on SHG voltage-sensitivity (see [5, 8]) and on electroporation (see [18]) the effect of membrane potential on SHG variation could account for 20 to 60% whereas redistribution of the scatterers, and the resulting lobe rearrangement, can potentially generate larger SHG transients according to our model. All in all, lobe rearrangement appears to be key in the SHG transient effect, providing a source for information on nanopore population.

Should be notice that, using this configuration for focusing (1.4 NA) and collecting (0.5 NA), the combination of a decrease in the SHG related to pure electro-optic effect (expected at the hyperpolarized pole) is competing with the rearrangement of the lobes, that leads to an increase of the SHG. The final result showed the predominant effect of the pattern redistribution.

Finally, the backward-directed SHG was collected in an epi-fluorescence configuration, using the same objective for focusing and for collection. No SHG signal was observed in the backward direction, confirming the lobe arrangement proposed in Fig. 2(a).

3.4. SHG-based estimation of inter-pole nanopore differences

The duration of the SHG transient (average 2±1 ms) suggests the presence of short-lived pores at both cell poles upon electroporation. Yet differences were observed between opposite poles.

At 40 kV/m the SHG collected at the hyperpolarized and depolarized poles of the cell showed an average transient increase of ∼ 90±20% and 180±20%, respectively (Fig. 4(b) and 3(f)). Previous modeling work by Krassowska et al. [18] estimated the diameter of electroporation induced nanopores at 20 nm and 2 nm for depolarized and hyperpolarized poles respectively. Using these results and the theoretical data from Fig. 2(c) relating pore diameter, densities of pores and SHG signal magnitude, we estimate that the observed SHG transients correspond to densities of 10×10¹³ pores/m² at depolarized and 50×10¹³ pores/m² at the hyperpolarized pole.

We observed a slow buildup of TPF fluorescence at the hyper-polarized pole, over 30 s post-electroporation (Fig. 2(e)), indicating efficient electroporation at the pole with SHG-predicted highest pore density. Such inter-pole SHG and TPF differences are consistent with work by Gabriel et al. and Pucihar et al. [23, 34] experimentally confirming that PI molecules enter the cell mainly through the hyperpolarized pole.

3.5. Electroporation threshold determined from SHG transient

In Fig. 4(c) the magnitude of the SHG transient correlated with electroporation is plotted as a function of voltage pulse value in the range 100–400V, corresponding to 10KV/m–40KV/m. A 3 to 4 fold increase of the SHG signal is observed from 300V to 400V suggesting a threshold for large-scale nanopore formation between 30 KV/m and 40KV/m. Consistent with usual electroporation threshold empirically determined for cultured cells [35].

4. Conclusion

The therapeutic applications of electroporation techniques would greatly benefit from improvements in efficiency and reproducibility of the transfection process as well as from the reduction of irreversible cell damage. Further, cell subtype selectivity in the transfection process based on cell geometry would be advantageous. This is the case of neuronal tissue in which selective transfection of specific neuronal populations, e.g. granular cells versus Purkinje cells in cerebellum, is therapeutically relevant and appears conceivably possible due to well-established differences in cell body and axonal and dendritic tree geometries across cell type.

Transfection success rates can be monitored optically and cell viability assays post-transfection are available. Yet informed optimization of electroporation protocols would be facilitated by access to the phenomena, pore population formation, subserving electroporation, as offered by the SHG described here; examples are the optimization of electrode position in relation to target neuron subpopulation and refinement of voltage amplitude and pulse duration for efficient but low-toxicity transfection.

The SHG technique presented here shows potential for space and time resolved monitoring of membrane dynamics during electroporation. Radiation lobe rearrangement, resulting from redistribution of scatterers in the membrane, can be related to pore population characteristics, shedding light on electroporation, a biophysically complex but promising technique from a therapeutic perspective.