The Dam1 ring binds to the E-hook of tubulin and diffuses along the microtubule

Several models of Dam1 complex function at the kinetochore have been proposed. Here we show that removal of the E-hooks of tubulin reduces Dam1 binding 40-fold. We also report the first structure of the Dam1 ring around microtubules and evidence that this ring freely diffuses on microtubules based on imaging individual rings.

Abstract

There has been much effort in recent years aimed at understanding the molecular mechanism by which the Dam1 kinetochore complex is able to couple microtubule depolymerization to poleward movement. Both a biased diffusion and a forced walk model have been proposed, and several key functional aspects of Dam1-microtubule binding are disputed. Here, we investigate the elements involved in tubulin-Dam1 complex interactions and directly visualize Dam1 rings on microtubules in order to infer their dynamic behavior on the microtubule lattice and its likely relevance at the kinetochore. We find that the Dam1 complex has a preference for native tubulin over tubulin that is lacking its acidic C-terminal tail. Statistical mechanical analysis of images of Dam1 rings on microtubules, applied to both the distance between rings and the tilt angle of the rings with respect to the microtubule axis, supports a diffusive ring model. We also present a cryo-EM reconstruction of the Dam1 ring, likely the relevant assembly form of the complex for energy coupling during microtubule depolymerization in budding yeast. The present studies constitute a significant step forward by linking structural and biochemical observations toward a comprehensive understanding of the Dam1 complex.

INTRODUCTION

The budding yeast Dam1 kinetochore complex, a 210-kDa heterodecamer, has been shown to be essential for chromosome segregation and to be regulated by the Aurora B kinase, Ipl1 (Cheeseman et al., 2002; Westermann et al., 2005). In vitro, the Dam1 complex is capable of forming rings around microtubules and coupling microtubule (MT) depolymerization to minus-end–directed movement under load (Miranda et al., 2005; Westermann et al., 2005; Asbury et al., 2006). Two recent studies demonstrated that recruiting the Dam1 complex to DNA lacking a centromere, and therefore lacking a site for kinetochore formation, significantly rescued proper chromosome segregation by attaching the centromere to spindle microtubules and recruiting other kinetochore proteins. (Kiermaier et al., 2009; Lacefield et al., 2009). These results clearly identify the Dam1 complex as part of the minimal machinery needed for chromosome segregation in budding yeast.

There have been a flurry of studies of the Dam1 complex in the last few years. Of greatest interest has been the question of how the complex can harness the energy of dynamic microtubules during mitosis to move chromosomes (Miranda et al., 2005, 2007; Westermann et al., 2005, 2006; Asbury et al., 2006; Efremov et al., 2007; Franck et al., 2007; Gestaut et al., 2008; Grishchuk et al., 2008a, 2008b; Wang et al., 2007). A number of aspects related to the interaction of the complex with microtubules, and with itself to form oligomeric structures, remain controversial. One controversy is over the contribution of tubulin’s E-hooks, the highly acidic C-terminal tails rich in glutamic acid residues in the interaction of the Dam1 complex with the microtubule. Conclusions have differed widely, with one study proposing an absolute requirement for the E-hook of tubulin for binding and another indicating that the region could be deleted without any effect on binding (Westermann et al., 2005; Miranda et al., 2007).

The second controversy centers around the mobility of the Dam1 ring when bound to the microtubule. Two models of Dam1 ring movement on depolymerizing plus-ends have been proposed: a biased diffusion model and a forced walk model (Efremov et al., 2007; Gestaut et al., 2008; Grishchuk et al., 2008b). A key difference in the assumptions of these models is whether or not the ring can diffuse on the microtubule lattice. In the biased diffusion model, the Dam1 ring is able to freely diffuse along the microtubule lattice and follows a microtubule’s depolymerizing end because the microtubule end represents a barrier to diffusion. Such a barrier then biases the movement of the complex, and any attached cargo (the chromosome in the in vivo case), toward the minus end of the microtubule. The forced walk model views Dam1 rings as nondiffusive on the microtubule lattice. The model proposes that Dam1 rings stay stationary until they contact a wave of outwardly peeling protofilaments from the depolymerizing plus end. These peels push against the Dam1 complex and provide the power stroke required to move it to a new position along the lattice.

Small oligomers of the Dam1 complex have been observed diffusing on microtubules in fluorescence experiments. These follow the depolymerizing microtubule end likely through biased diffusion (Gestaut et al., 2008; Grishchuk et al., 2008b). Larger structures have been reported to be nondiffusive, but whether they were rings and the possiblity of complicating experimental issues, such as aggregation or protein adhering to the coverslip, remain unresolved (Grishchuk et al., 2008b). A number of arguments support the ring as the most probable form of Dam1 at the kinetochore. From a mechanistic point of view, a ring structure would provide processivity as an intrinsic property of its closed structure. Processivity is a key feature in budding yeast, which has only one microtubule attachment per chromosome. Experimentally, in vitro assembly of the Dam1 complex into a ring around microtubules is readily achieved using the wild-type complex but is negatively affected by phosphomimetic mutants of the Aurora B phosphorylations sites (Wang et al., 2007). Quantitative in vivo fluorescence data indicate that the copy number of the Dam1 complex at the budding yeast kinetochore is sufficient to form a ring structure (Joglekar et al., 2006). Furthermore, recent studies of yeast mitotic spindle by electron tomography have identified ring-like structures near the plus ends of kinetochore microtubules (Richard McIntosh, personal communication).

RESULTS

The flexible C-terminus of tubulin is a major contributor to Dam1-microtubule binding

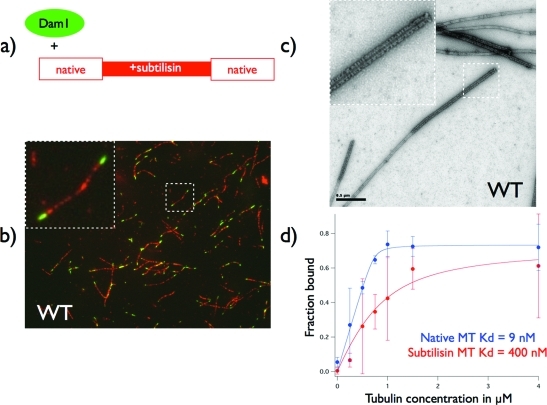
To investigate the effect of the tubulin E-hooks on the binding and assembly of the Dam1 complex around microtubules, we designed an internally controlled binding reaction. We generated hybrid microtubules having regions of native tubulin and of E-hook–depleted tubulin (Figure 1). At a low ratio of the Dam1 complex to tubulin (1:32 molar ratio), the Dam1 complex decorates the native microtubule lattice but does not bind the microtubule lattice lacking the E-hook (Figure 1B). Examination of the sample by negative stain electron microscopy revealed tightly packed decoration by Dam1 rings or spirals at the ends of microtubules, where the native lattice is expected to be. Only a few discrete rings of Dam1 could be seen in the central, subtilisin-treated region of the microtubule (Figure 1C). These results show unambiguously that the Dam1 complex prefers regions of intact tubulin that contain its C-termini and are consistent with the results of Westermann et al. (2005), who also observed a role for the E-hook in Dam1 binding. At high ratio of Dam1 complex to microtubules (1:2 molar ratio), the Dam1 complex binds and fully saturates microtubules, irrespective of whether the microtubules have been proteolytically treated or not (Supplemental Figure S1b). It is important to notice that, at a 1:2 molar ratio of Dam1 complex to tubulin, there is a high background of unassembled complexes. This result explains the observation of Miranda et al. (2007), who found that saturating amounts of Dam1 complex can bind and fully decorate microtubules lacking C-termini.

FIGURE 1:

Binding of Dam1 complex to hybrid native/subtilisin-treated microtubules. (A) Cartoon of experimental setup used in (B–D) The subtilisin-treated microtubule seeds (lacking the tubulin E-hooks) are rhodamine-label. (B) Fluorescence image of Alexa–Dam1 complex bound to hybrid microtubules showing Dam1 complexes preferentially binding to the native tubulin lattice present at microtubule ends. (C) Negative stain electron micrograph of the same conditions shown in (B). Dam1 rings and spirals tightly decorate the microtubule ends, where the native lattice is expected, while very sparsely decorating the central E-hook lacking region. (D) Binding curves derived from pelleting assays using WT Dam1 and either native or subtilisin-treated microtubules. E-hook removal results in a 40-fold decrease in binding affinity.

To quantify the effect of the E-hook on the binding of the Dam1 complex, we also performed pelleting assays (Figure 1D). Dam1 binding saturates at a similar level with both types of microtubules, supporting the observation that, at high concentrations of Dam1, microtubules can be fully decorated with or without the E-hook of tubulin. However, at lower concentrations, there is an obvious decrease in binding of Dam1 to subtilisin-treated microtubules. Fitting binding curves to the fraction of Dam1 bound over a range of tubulin concentrations allowed us to estimate the K_d of their interaction. Because the amount of free Dam1 is comparable to the amount bound to the microtubule, we cannot use the approximation of the K_d being the concentration where half the ligand is bound. We must instead solve a quadratic equation correcting for the changing amount of free ligand, as was also done in the analysis of Ndc80 binding to microtubules (Ciferri et al., 2008). Dam1 binding to native microtubules showed a strong binding of 9 nM. Removal of the E-hook of tubulin decreased binding 40-fold to a K_d of 0.4 μM. These values disagree with previous pelleting assays, which measured a much lower affinity (Westermann et al., 2005). However, this previous measurement used the half-binding approximation, that the K_d equals the concentration of ligand when half saturation occurs, which we feel is inappropriate for this experimental condition. These previous curves are very similar to our current results, suggesting that the differences in the reported K_d come soley from this difference in analysis. Our current measurement does agree with another reported K_d of 6 nM using single-molecule fluorescence microscopy (Gestaut et al., 2008).

Altogether, the present results reconcile previous, apparently contradictory results and reveal that, although the E-hook is not absolutely essential for Dam1 complex binding to microtubules, it contributes significantly to the affinity of this kinetochore complex for microtubules. We believe that this may be most relevant in vivo, where the amount of complex is limited.

Contribution of Dam1p’s C-terminal domain to binding and assembly around microtubules

Our previous experiments have shown that the C-terminal domain of Dam1p plays a role in regulation of the Dam1 complex’s self-assembly, as well as in its interaction with microtubules (Westermann et al., 2005; Wang et al., 2007). Electron microscopy (EM) analysis of unassembled Dam1 complex showed it to have an elongated shape. It is a rod with a central domain, which is the main site of interaction in the oligomerization of Dam1 complexes, from which a protrusion extends (Wang et al., 2007). Based on both the shape of the complex in images of Dam1 rings that had fallen off the microtubule, and the cryo-EM structure of Dam1 spirals around microtubules, the protrusion was proposed to extend toward the microtubule surface in the assembled state of the complex (Wang et al., 2007). Interestingly, the EM structure of a mutant Dam1 complex with a C-terminal truncation of Dam1p (ΔC-Dam1) in an unassembled state showed a loss of density in the center of the protrusion region: the density bridging the tip of the protrusion and the central domain was missing (Wang et al., 2007). This result suggested that the bridge corresponds to the protrusion region of the unassembled complex (Wang et al., 2007).

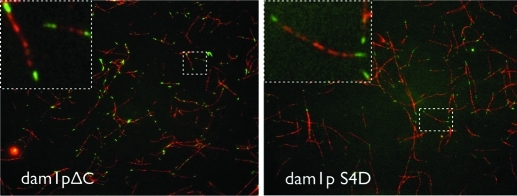
If the C-terminus of Dam1p pointed toward the microtubule, it would be well placed to interact with the E-hook of tubulin. To test whether it does interact with the E-hook, we performed fluorescence microscopy binding assays of mutant Dam1 complexes on chimeric microtubules, as described above for the WT Dam1 complex. Both the ΔC- and SD4-Dam1 (containing phosphomimetic mutations of Ipl1 sites on Dam1p) complexes behave similarly to the WT Dam1, binding with higher affinity to the native tubulin microtubule lattice than to that lacking the E-hooks (Figure 2). However, images of both mutant complexes with MTs suffer from increased background fluorescence (or background protein density in the EM images) as compared with the WT complex, indicative of fewer bound complexes and weaker interactions with MTs. The fact that mutants with deleted or phosphomimetic C-terminal domains can still distinguish the native and subtilisin-cleaved tubulin lattices suggests that additional regions outside of Dam1p’s C-terminal domain are involved in Dam1’s interaction with the E-hook of tubulin. One candidate is the Duo1 protein, which has been previously implicated in microtubule binding (Cheeseman et al., 2001; Miranda et al., 2007).

FIGURE 2:

Contribution of Dam1p C-terminus to microtubule binding. Dam1 complex binding experiments with hybrid native/subtilisin-treated microtubules (as in Figure 1C) using ΔC Dam1 complex and the phosphomimetic dam1pS4D mutant complex. Although having lower affinity for the microtubule, both complexes still show the same preference for the native microtubule lattice as the WT complex.

Diffusive character, structure, and interations of the Dam1 ring bound to the microtubule

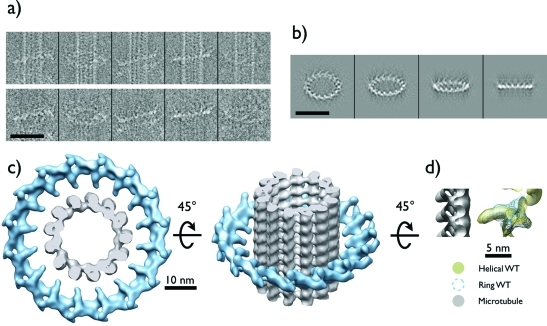
We approached the question of Dam1 ring motility and its interaction with the microtubule by visualizing Dam1 rings on microtubules using cryo-EM. We incubated taxol-stabilized microtubules with WT Dam1 complex at concentrations that produced sparse ring decoration. After incubation at room temperature for approximately 1 h to ensure that the rings had reached equilibrium with the microtubule and the environment, the sample was frozen and imaged under cryo-EM conditions (Figure 3A, top). A total of 286 rings from 84 microtubules in 50 micrographs were picked, giving on average 3.4 rings/microtubule and ∼300 nm between rings. The large distance separating the rings allowed us to treat them as independent objects for our measurements.

FIGURE 3:

Reconstruction of the Dam1 ring assembled around microtubules. (A) Top, gallery of representative “sparse” rings assembled on microtubules used for data analysis. Bottom, same ring images shown with microtubule component removed computationally (Ramey et al., 2009). (B) Reprojections of the final reconstruction showing four successive out-of-plane tilts. (C) Top and tilted views of the structure. There is a mismatch between the 16-fold symmetry of the ring and the 13- and 14-protofilament microtubules seen in this study. (D) Side view of the structure of a single Dam1 complex extracted from the helical structure of Dam1 double spirals (Wang et al., 2007) (golden) and from the current single particle reconstruction of the ring (blue mesh) (tubulin shown in gray). The superposition shows good agreement between both structures, which only differ in their packing (helical vs. circular), but not in their interface of oligomerization or their apparent mode of binding to the microtubule. Scale bars in (A) and (B) are 50 nm.

These imaging data allow us to take a statistical mechanics approach to the ring’s dynamics when bound to the microtubule. By observing static snapshots of the state of many rings bound to the microtubule, we can infer the dynamic state of a single ring. Specifically, we are interested in whether the assembled ring can diffuse along the microtubule. We expect distinct ring distributions along microtubules depending on whether the ring is diffusive or not. Specifically, the distribution of angles between the plane of the rings and the microtubule axis depends on the binding interface between them and the ability of the ring to move between binding sites (Efremov et al., 2007). Additionally, the way rings distribute themselves along a microtubule at different concentrations provides clues to their ability to diffuse (discussed in more detail below).

We determined the orientation of Dam1 rings relative to the underlying microtubule axis through the process of calculating the single-particle, three-dimensional (3-D) reconstruction of individual rings (Figure 3). Ring images were first processed to remove the microtubule from the image (Figure 3A, bottom) (Ramey et al., 2009). The microtubule must be removed to align and average Dam1 rings because the two structures sit in many different orientations with respect to one another. This result in itself reflects the flexible nature of the structural elements involved in ring–microtubule interactions (Miranda et al., 2007; Wang et al., 2007) and the fact that they contain distinct symmetries (Westermann et al., 2006). During computational removal of the microtubule from the images, the angle of the microtubule axis was calculated and saved. The images of individual rings were aligned by projection matching to initial models of either a featureless toroid or a ring of spheres, then used to generate a 3-D structure of the ring by backprojection of individual ring images in an iterative projection-matching process. A range of rotational symmetries was examined during the refinement of the structure. Sixteenfold symmetry was the only symmetry that produced a convergent refinement, judging by the consistency of the final structure starting from different initial models and its stability when the parameters of the refinement were changed. This rotational symmetry agrees with previous observations of Dam1 assembled into rings and spirals (Wang et al., 2007; Westermann et al., 2006). Refinement against both reference models yielded the same reconstruction (data not shown). The ring structure is in good agreement with the structure of the Dam1 complex assembled into spirals, which we reported previously, using both classical Fourier Bessel helical reconstruction (Wang et al., 2007) and single-particle methods (Ramey et al., 2009) (Figure 3D).

The Dam1 ring is insensitive to microtubule polarity

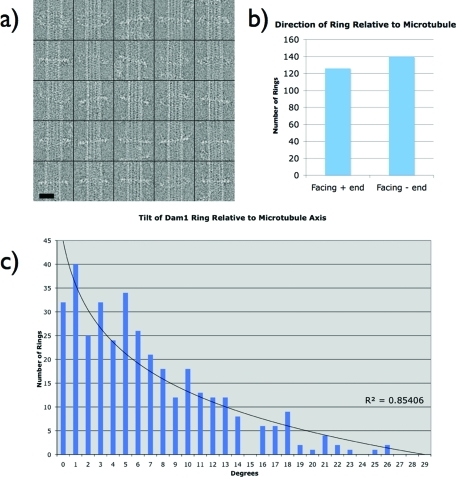
We have previously proposed, based on the antiparallel nature of double Dam1 spirals (Wang et al., 2007), that the Dam1 ring should be insensitive to the polarity of the underlying microtubule, as the two spiral strands face the microtubule in opposite directions. In our analysis of ring-decorated microtubules, unedited segments, such as those shown in the top of Figure 4A, were also refined against a microtubule model to determine whether the Dam1 ring had any preference for microtubule polarity. After sorting segments based on the microtubule protofilament number, they were aligned to a previously calculated 3-D reconstruction of a microtubule using a projection-matching scheme. The microtubule signal dominated the alignment of these segments due to its much larger mass and repeating pattern. The resulting structures were microtubules with a diffuse cloud of noisy density around them corresponding to the Dam1 ring, reflecting the different symmetries of the microtubule and the ring. By docking in the tubulin atomic structure (PDB: 1JFF), the polarity of the microtubule in the reconstruction, and therefore the polarity in each image, was determined. Combining this information with the orientation parameters of the ring in each segment showed that the Dam1 ring has no preference for facing either the plus or minus end of the microtubule (Figure 4B). This confirms our previous predictions and strongly argues for an interaction between the Dam1 complex and the microtubule that is mediated by flexible regions originating from one or both sides of the interaction interface. A Dam1 ring at the kinetochore would presumably have a preferred orientation determined by its interaction with other kinetochore components, such as Ndc80 (Wong et al., 2007; Lampert et al., 2010; Tien et al., 2010).

FIGURE 4:

Quantitative analysis of the Dam1 ring microtubule decoration. (A) Gallery of Dam1 rings assembled around microtubules. The average density of rings was one to two rings per micron of microtubule, and thus rings were treated as isolated structures that are not affecting one another. Scale bar is 20 nm. (B) Ring orientation is independent of microtubule polarity. The plot shows occurrence of rings facing either the plus or minus end of the microtubule. The “face” of the ring was arbitrarily chosen to be the one shown in Figure 4C (right). This result argues that the ring either does not have a footprint on the microtubule lattice or its binding motif is so flexible that it can easily rotate 180 degrees to accommodate either orientation. (C) Histogram showing the distribution of angles between the microtubule axis and the plane of the ring obtained from microtubule images with “sparse” ring occupancy, as in A. Angles were derived from projection matching of each ring image to a 3-D reference structure during the process of reconstruction and refinement for the ring structure shown in Figure 3. The experimentally derived angles fit to an exponential function with good agreement. This exponential distribution centered at zero degrees argues for either many binding sites on the lattice or a highly flexible attachment, such as the E-hook. In either case, the energy barrier to transition between sites would be low and therefore allow for diffusion of the ring.

Statistical mechanics analysis of Dam1 ring angles support a diffusive ring model

In the process of generating the Dam1 ring reconstruction using microtubule-edited segments, each image of a single ring was assigned a tilt angle to bring it into register with its corresponding model projection. By combining this information with the previously measured microtubule angle, we obtained the angle of each ring relative to the microtubule axis (Figure 4C). These correspond to the angle Θ in the work of Efremov et al. (2007); however, we expect our current measurements to be more faithful representations of the position of the ring, since the previous study used images of rings that were dried and stained, a proceedure that frequently distorts the sample. Applying the maximum tilt angle seen in the distribution (26 degrees) to the model shown in Figure 3 brings the protrusion of the Dam1 ring to within <1 nm of the microtubule wall (Supplemental Figure S2). Further tilt is thus prevented by steric clash between the protrusion and microtubule wall. The histogram of these angles follows an exponential distribution. This result shows that the ring does not have a preference for any angles that maximize the number of contacts between the planar ring and the helical pattern of the microtubule. This distribution is most easily explained by a simple spring-like restoring force acting on the ring that increases with larger tilt, perhaps through the increasing steric clash of flexible elements from both sides.

Assuming that the rings we observed are at equilibrium with their surroundings, the distribution of angles tells us about the dynamics of a single ring through time. This conceptual extrapolation is due to the fact that we can treat the frequency of an observed angle, α, also as the relative amount of time any single ring spends in that state. For instance, if we observe 10% of rings tilted by an angle α, we can say that any given ring spends 10% of its time tilted at an angle α. Being able to “watch” a ring tilt by making this logical leap common to statistical mechanics gives us insight into the mobility of the ring on the surface of the microtubule and tells us whether it is capable of diffusion. If the ring can tilt with a low energy barrier, that is, if tilting is relatively easy, this implies that moving along the microtubule lattice is also easy, since both processes involve making and breaking bonds with tubulin.

The measured histogram of Dam1 ring tilt angle along a MT shows that the Dam1 ring tilts quite evenly with respect to the normal direction of MT surface (from approximately −30 to +30 degrees). There is no obvious preferred angle for which the ring aligns itself to maximize contacts with the helical microtubule lattice. This observation suggests that the Dam1 ring does not “see” the helical arrangement of the tubulin subunits along the MT. Orientations that maximize direct contacts between cannonical motor-binding sites on tubulin (like that of kinesin (Kikkawa et al., 1995; Mizuno et al., 2004; Sindelar and Downing, 2010) and the Dam1 protrusion, such as pointing the Dam1 binding element into the interface between alpha and beta tubulin, are not favored over others. This argues against a previous model of Dam1 binding to the microtubule with a distinct footprint on the lattice (Efremov et al., 2007). In this previous “footprint” model, the ring would jump between specific angles that optimize the number of binding events between Dam1 and the microtubule. This behavior is incompatible with our present observations.

From the distribution of ring tilt angles, it also follows that the energy barrier for the MT-bound ring to move between different positions on the helical lattice of tubulin subunits should be equal or less than the thermal noise energy of ∼1 k_BT. This is essentially stating, in energetic terms, what we observed qualitatively above. The preference for following the helical pattern of the microtubule, if there is such a preference, is so small that it is on the same scale as the thermal energy of the bath in which the reaction sits. This result is significant because it implies that the energy barrier for jumping between adjacent tubulin dimers is also low, since the helical pattern is made of repeating dimers. This parameter, the energy barrier for moving from one dimer to the next, is at the heart of the question of whether the ring can diffuse, with a low energy barrier allowing diffusion and a high barrier requiring large forces for movement. Because of the importance of this interaction, we are going to focus on the energy required to move from one tubulin dimer to the next, 8 nm longitudinally along the microtubule. This is not to suggest that the Dam1 complex takes discrete 8-nm steps along the microtubule, but rather that the binding energy landscape for the complex along the microtubule is not uniform and has a repeating period according to either the tubulin dimer or monomer (8 or 4 nm). Understanding this landscape will further our understanding of Dam1 ring motility.

To focus in on this transition between one repeating tubulin subunit and the next, we can consider the Dam1 ring–MT interaction as a one-dimensional problem: a particle interacting with a straight line consisting of repeating units. When the ring tilts, it effectively changes the position of the particle along the straight line and, hence, changes the binding energy between them. At equilibrium, this resulting energy change upon ring tilting dictates the probability distribution of the tilt angle, which obeys a Boltzmann distribution. Given the large sample size of the Dam1 rings, the tilt angle histogram should represent the equilibrium weight of the population of each tilt angle. We therefore can calculate the binding energy potential for the Dam1 ring along MTs from the measured ring tilt angle histogram.

Based on the local geometry, the inner radius of the ring, R (R = 35 nm), and the tilted angle of the ring, α, the effective deviation distance of the Dam1 ring from the center of its underlying subunit is l = R sin α. This is the distance along the microtubule that one edge of the ring moves when the ring is tilted. We assume that the ring binds to the tubulin subunit via a harmonic binding potential, which is a function of the deviation length 1/2kl². A harmonic binding potential would be expected for electrostatic interactions between flexible elements like those at the Dam1-MT interface. For each tilt angle, the corresponding value of the Boltzmann distribution is then ∝ exp (-1/2kl²/2K_BT). Consequently, we can extract from the histogram the spring constant k. The average value is 0.40 pN/nm, with the smallest being 0.13 pN/nm and the largest being 1.08 pN/nm.

Now we are in a position to be able to calculate the energy barrier for the Dam1 ring crossing between neighboring tubulin subunits along the MT. If we take the periodicity of the MT as 8 nm (suggesting that the repeating binding site is a tubulin dimer), then the complex must move at most half of the repeat length, which is 4 nm, to move in the energy landscape from one potential well to the next. In our model, this means that we must find the energy associated with moving the complex 4 nm from the center of the energy well, specifically that l = 4 nm. The binding energy potential 1/2k. (4nm)² stands for the energy barrier for the Dam1 ring crossing between neighboring tubulin dimers. Our calculations show that this energy barrier is ∼1.5 k_BT on average, with the range of 0.5–4.0 k_BT. If we instead take the periodicity of the MT as 4 nm (meaning that the complex cannot distinguish between alpha- and beta-tubulin and the monomer is the important repeating feature), then the corresponding energy barrier is on average ∼0.38 k_BT, with the range of 0.13–1.0 k_BT. Whether the Dam1 complex sees the dimer or the monomer as its repeating binding site, our tilt angle histogram suggests that the energy barrier for Dam1 ring crossing to the neighboring tubulin subunit should be comparable to the thermal energy ∼1 k_BT. In other words, the local “texture” of the energetic interaction between the Dam1 ring and the tubulin subunit is “smeared” by the thermal noise, which confers rapid Dam1 ring diffusion along MT.

It is important to point out that the calculated energy barrier of ∼1.5 kT is distinct from that derived from the binding affinity curve (obtained in the pelleting assay of Dam1 ring on MTs), which is about 18.5 kT (Kd = 9 nM). The latter is a measure of how much energy would be needed to dissociate the bound Dam1 ring from the MT, whereas the energy barrier here refers to the energy required in order for the Dam1 ring to change its position along MT, while still bound to it. Thus, according to our calculation, even though it is tightly bound to the MT (i.e., rarely falling off from it), the Dam1 ring is capable of moving along the MT lattice, instead of being fixed at its arrival/assembly position.

Steric exclusion of neighboring Dam1 rings further supports ring diffusion

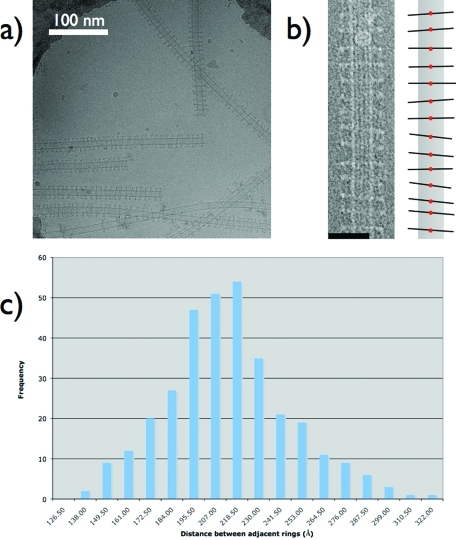
Further evidence for a diffusive Dam1 ring comes from micrographs of Dam1 assembled on microtubules at concentrations ∼10-fold higher than those used for the ring tilt data. When imaged under cryo-EM conditions, these microtubules show dense but subsaturating decoration by Dam1 rings (Figure 5). What is immediately striking about these micrographs is that rings exhibit a narrow range of distances between them and have a smaller range of tilts, with most being near zero degrees. Distances between neighboring rings were measured based on the location of the center of each ring, as shown in the schematic in Figure 5B.

FIGURE 5:

Analysis of Dam1 rings assembled at high density on microtubules. (A) Cryo-EM image of Dam1 rings around microtubules at a higher density that those used in Figures 3 and 4. (B) Left, image of a densely Dam1 ring-decorated microtubule. Right, schematic of the image. The red dots are the points selected for measuring the distance between rings. The schematic also illustrates the limited range of angles the Dam1 rings adopt when they are close together. We attribute this to steric clash during ring “wobbling.” (C) Histogram of distances between adjacent rings for “dense” ring decoration. The most common distance is ∼210 ν, far outside the range of apparent direct interaction between Dam1 rings. Scale bars are 50 nm unless marked otherwise.

If we assume that the ring is not able to diffuse along the microtubule, then it should become anchored wherever it assembles. That is, the MT would provide a periodic energy barrier, and the tubulin subunit length would define its period. In order to hold the ring and keep it from getting across to the neighboring tubulin subunit under the influence of thermal fluctuations, such an energy barrier would have to be higher than 10 kT. Under this assumption, calculation of the equilibrium distribution of the neighboring ring distance can be translated into a well-defined statistics problem: N particles are put on a straight line with M equally spaced binding sites, in which the spacing is defined by the microtubule periodicity (8 nm). Each binding site can accommodate no more than one particle. One can then calculate the statistical distribution of particles along with the resulting neighboring distance between particles if they are placed randomly. A combinatorial calculation shows that P(j), the probability for a neighboring ring distance of j is:

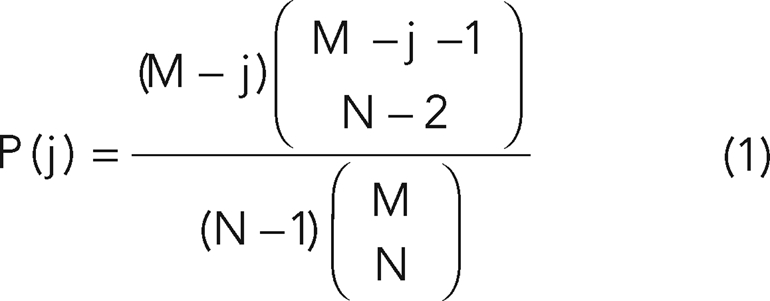Our numerical calculation shows that the equilibrium distribution is a strict decreasing function of the neighboring distance, starting at the distance of 8 nm (see Supplemental Figure S3, where M = 100 and N = 10). We must emphasize that this qualitative feature remains the same while varying M and N. However, this result is very different from the measured histogram, in which there is a well-defined peak at ∼20 nm (Figure 5C).

If Dam1 rings do not diffuse, what would be the repulsive forces that could cause this distribution? Under the present experimental conditions, the system is in a solution with a salt concentration equivalent to 75 mM of NaCl. At this salt concentration, the electrostatic screening length (Debye length) is 1–2 nm. Although Dam1 rings are positively charged, their electrostatic interaction is thus largely truncated into a short-range repulsion. Therefore, the effective range of electrostatic repulsion between neighboring rings is much shorter than the MT periodicity (8 nm), and hence, such repulsion will not change the calculated distribution of neighboring ring distance.

Alternatively, the ongoing tilting of the ring while sitting in place could preclude close binding. The tilt angle histogram demonstrates that most of the rings do not tilt very far, with few rings tilting more than 20 degrees. In fact, under the conditions of our measurements of neighboring ring distance, Dam1 rings tilt significantly less than in the conditions under which we obtained the tilt angle histogram. The half height of the histogram, corresponding to a tilt angle of ∼10 degrees, would exclude neighboring rings only by 8 nm, given that the outer diameter of the ring is ∼50 nm. Although this exclusion effect could be at play, it still cannot explain why the observed peak value of the neighboring ring distance is 20 nm.

In conclusion, one could explain our experimental results by invoking a repulsive force that acts to keep the nondiffusing rings from assembling within ∼20 nm of each other in a nondiffusive model. However, we cannot envision any such repulsive forces under our experimental conditions that act over such a long range. Our data, on the other hand, can be explained by a model in which Dam1 rings can diffuse rapidly and freely along the microtubule, bouncing off one another and excluding each other from close proximity by steric clash.

DISCUSSION

There has been a long-standing interest in understanding how kinetochore complexes couple microtubule dynamics to chromosome motion during mitosis (Koshland et al., 1988). Recently, with the advent of structural (Wang et al., 2007) and biophysical experimental data (Asbury et al., 2006; Efremov et al., 2007; Franck et al., 2007; Gestaut et al., 2008; Grishchuk et al., 2008a, 2008b) on the yeast Dam1 kinetochore complex, several models have been proposed to explain the complex’s ability to bind and track the plus end of depolymerizing microtubules. We sought to clarify two major aspects of Dam1’s molecular properties: its binding to microtubules and its ability to diffuse on the microtubule lattice.

First, we addressed the conflicting reports of the importance of tubulin E-hooks in Dam1 complex binding (Westermann et al., 2005; Miranda et al., 2007). One problem with comparing these previous results is that the experiments where carried out under very different conditions. Our approach to detemine whether the tubulin E-hooks make a contribution to the binding affinity of microtubules for the Dam1 complex was to visualize the presence of rings on hybrid microtubules containing both native and cleaved tubulin lacking the E-hook. By testing a range of relative concentrations, we were able to reconcile previous results. We find that, at subsaturating concentration of Dam1 complex relative to microtubules, the complex exibits a clear preference for native tubulin. On the other hand, at suprastoichiometric amounts, rings can be seen decorating both types of lattices. These results demonstrate that the E-hooks contribute to the interaction of microtubules with this kinetochore complex but that additional elements on tubulin can contribute to the interaction. We believe that the contribution of the E-hook to the binding affinity is of biological significance, as the amount of the complex relative to tubulin in vivo is obviously substoichiometric (Ghaemmaghami et al., 2003; Miranda et al., 2005; Joglekar et al., 2006).

Second, we investigated whether the ring form of Dam1 was capable of diffusion, a property that has major implications for funtional models. We investigated this through quantitative observation of the angles, spacing, and orientation of Dam1 rings bound to microtubules using cryo-EM. A previously published analysis of images of Dam1 rings on microtubules showed a peak angle of approximately 0.3 radians (17-degree tilt) in their distribution, rather than the maximum at near zero tilt that we observe, and was used to argue for a model where Dam1 has one specific binding site per tubulin dimer (Efremov et al., 2007). These angles were measured from images of samples that were attached to a carbon support, then stained and dried. That procedure is known to cause flattening and therefore is likely to have caused the collapse of the rings onto the microtubule, compromising quantitative analysis of tilt angles. By studying frozen hydrated samples, we preserved the shape and position of the rings with respect to the microtubule. We were, therefore, able to produce an accurate snapshot of Dam1 ring–microtubule orientations. The distribution of angles we see here would come, according to the modeling of Ataullakhanov and colleagues (Efremov et al., 2007), from two binding sites on the microtubule wall. However, we would also expect to see a similar distribution from Dam1–microtubule binding involving flexible elements, for example, interactions between the E-hook of tubulin and extended elements from the Dam1 complex. Based on the wide range and distribution of tilt angles and the Gaussian distribution of distances observed at high but nonsaturating ring densities, our data are consistent with a model where rings are capable of diffusion. However, this is an inference based on static images. Therefore, we do not know the kinetics of this diffusion and whether it is fast enough to be relevent physiologically. Further experiments are required to show conclusively that diffusive spots seen on the microtubule can be rings.

A possible alternative explaination of our data is that the ring is capable of tilting without breaking its bond with the E-hook of tubulin and therefore may not in fact be diffusive. This seems unlikely given the geometry of the Dam1–microtubule interaction. The E-hooks of tubulin range between 10 and 18 amino acids, and therefore, when fully extended, could cover a distance of up to ∼3.5 nm (Redeker et al., 1992). When fully tilted, to 26 degrees, the microtubule binding protrusion of the Dam1 complex moves ∼16 nm along the microtubule lattice, a full two tubulin dimers longitudinally. This would leave a ∼12.5-nm gap to be bridged by a flexible element of the Dam1 complex. Secondary structure prediction of the two proteins known to bind the microtubule, Duo1 and Dam1, did not reveal any unstructured regions nearly long enough for such a long range interaction (Miranda et al., 2007; Cole et al., 2008). Thus it seems likely that tilting requires the making and breaking of bonds with adjacent E-hooks, implying that a ring that can tilt can also diffuse.

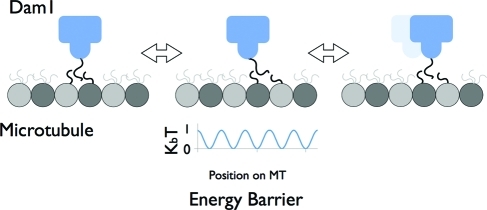
Overall, our studies support a ring-based, biased-diffusion model for the tracking of depolymerizing microtubule ends by the Dam1 complex (Liu and Onuchic, 2006; Westermann et al., 2006). Together with previous studies, our data support a model of Dam1 motility by which the ring, using 16 inward-facing protrusions, contacts, in a number of possible alternative arrangements, the E-hook of tubulin and one or more aditional sites on the microtubule lattice (Westermann et al., 2005; Miranda et al., 2007). These connections must involve flexible elements on both tubulin and the Dam1 complex that, coupled to the mismatch in oligomeric arrangements, facilitate diffusion along the lattice (Figure 6). This diffusion could then become biased when the ring meets the depolymerizing end of the microtubule. However, it is important to point out that our data do not rule out a forced walk model, which could become the operating mode in situtions where load pulls the ring opposite to the direction of depolymerization while the ring is at the tip. Under these conditions, the ring geometry would be ideal to remain attached to the flared microtubule ends and harness their energy for poleward movement.

FIGURE 6:

Model of Dam1 interaction with tubulin and diffusion on a microtubule. Schematic of Dam1 diffusing along the microtubule surface. Flexible extensions from the Dam1 complex interact with the E-hook of tubulin to mediate binding. E-hooks are shown in constant motion, extending a cloud of charge around the microtubule. The easy “handing-off” from one extension to another (shown in the middle panel) allows Dam1 to diffuse along the microtubule since all positions above the microtubule have similar energy. To underscore this point, a schematic of the energy barriers along the microtubule is shown under the middle panel. This energy landscape assumes a repeating barrier of 4 nm, that is, the Dam1 complex binds to the mononer as the repeating unit. The maximum barrier of 1 k_BT would be easily surmounted by random thermal fluctuations in the system. The previous position of the Dam1 complex is shown dimly to highlight movement between panels.

Interestingly, a phosphomimetic mutant, in which the three serine residues in the C-terminus of Dam1p that are phosphorylated by the Ipl1 kinase have been mutated to aspartates (in addition to a fourth one at the N terminus of the protein) (S4D-Dam1), shows a decreased ability to oligomerize in the presence of microtubules (Wang et al., 2007), in agreement with an important role of this region of Dam1p in the coupling of microtubule interaction and self-assembly of the Dam1 complex. Recent studies investigating the interaction between the Dam1 complex and the outer kinetochore complex Ndc80 have shown that, although their interaction in solution is not strong, they colocalize and act cooperatively when bound to microtubules (Lampert et al., 2010; Tien et al., 2010). We speculate that the Ndc80 complex is recognizing the assembled form of Dam1 by binding to the oligomerization interface between Dam1 complexes, perhaps involving this regulatory region of Dam1p. Phosphorylation of the C-terminus of Dam1p could then disrupt Dam1 complex oligomerization, but also interrupt Dam1 complex–Ndc80 complex binding, allowing the kinetochore–microtubule attachment to reset. Additionally, it has also been shown that the Ndc80 complex requires the E-hooks of tubulin to bind microtubules. This raises the question of whether the Dam1 complex and Ndc80 would compete for binding sites on the microtubule. It is possible that, at high, nonphysiological concentrations, that would be the case. However, at very low, physiological concentrations, there would be an excess of available E-hooks, and the electrostatic and very likely diffusive interaction of the complexes with the tubulin substrate may be critical for the Ndc80 and Dam1 complexes to encouter and bind each other on the microtubule surface.

At the kinetochore, the orientation of the Ndc80 complex is likely to be defined by its interaction with the rest of the KMN network and ultimately with the inner kinetochore components, as well as its well-defined orientation with respect to kinetochore microtubules (Alushin et al., 2010). For the Dam1 complex, which is blind to microtubule polarity, it is likely that its interaction with other kinetochore complexes, such as the Ndc80 complex (Wong et al., 2007), would be the only factor determining its orientation. Our current 3-D reconstruction of single Dam1 rings in vitro may serve as a good template to detect the Dam1 ring’s orientation at the yeast kinetochore in 3-D reconstructions by electron tomography.

MATERIALS AND METHODS

Generation of hybrid microtubules

We formed stabilized, subtilisin-treated microtubule seeds (subtilisin selectively cleaves the tubulin E-hook) as described previously (Westermann et al., 2005). Native tubulin was then added to extend microtubules. Both types of lattice were taxol stabilized. Only one lattice, subtilisin treated or native, was labeled with rhodamine for identification by fluorescence imaging (Figure 1A and Supplemental Figure S1a). These hybrid microtubules were then incubated with Alexa488-labeled–Dam1 complex at different ratios. Using fluorescence microscopy, decoration of microtubules by the Dam1 complex was clearly observed.

Pelleting assays

WT Dam1 complex was bound to either subtilisin-treated (E-hook cleaved) or native microtubules, pelleted, and analyzed as described previously (Westermann et al., 2005). Representative gels that contributed to the binding curve in Figure 1D are shown in Supplemental Figure S4.

Cryo-EM

Samples were applied to a C-Flat carbon support grid (Protochips, Raleigh, NC), blotted, and plunged into a liquid ethane slush using a Vitrobot (FEI Company, Hillsboro, OR). The grid was transferred into a Gatan 626 cryo holder (Gatan, Pleasanton, CA) under liquid nitrogen temperature and imaged in a Tecnai F20 TEM (FEI Company). Images were collected on a Gatan 4k Ultrascan CCD camera using a low electron dose of 20 e⁻/Ų.

Structure determination

The WT Dam1 ring data were first processed to remove the microtubule signal as described (Ramey et al., 2009). The rings were then input into a projection-matching program using the SPIDER software package (Frank et al., 1996). The Fourier Shell Correlation plot can be found in Supplemental Figure S5. The density map has been deposited in the EMDB with accession number 5254 (http://www.ebi.ac.uk/pdbe/emdb/).

Note added in proof. The present version of the article differs from the manuscript version published in MBoC In Press in that Figure 2 was simplified. While we believe the data in the manuscript version were valid, a clear interpretation was not possible. Given that the data concerned were peripheral to the main points of the paper, they were removed in the final version.

Abbreviations used:

3-D

three dimensional

MT

microtubule