Pathway Analysis of Liver Metabolism under Stressed Condition

Abstract

Pathway analysis is a useful tool which reveals important metabolic network properties. However, the big challenge is to propose an objective function for estimating active pathways which represent the actual state of network. In order to provide weight values for all possible pathways within the metabolic network, this study presents different approaches, considering the structural and physiological properties of metabolic network, aiming at a unique decomposition of the flux vector into pathways. These methods were used to analyze the hepatic metabolism considering available data sets obtained from perfused livers of fasted rats receiving burn injury. Utilizing unique decomposition techniques and different fluxes revealed that higher weights were always attributed to short pathways. Specific pathways including pyruvate, glutamate and oxaloacetate pools, and urea production from arginine were found to be important or essential in all methods and experimental conditions. Moreover, the pathways including serine production from glycine and conversion between acetoacetate and B-OH-butyrate were assigned higher weights. Pathway analysis was also used to identify the main sources for the production of certain products in the hepatic metabolic network to gain a better understanding of the effects of burn injury on liver metabolism.

1. Introduction

Liver has many complex physiological functions including lipid, protein and carbohydrate metabolism, synthesis of bile and urea production. It is well known that the hepatic response to severe injury and other stressors is characterized by a significant up-regulation of glucose, fatty acid, and amino acid turnover (Banta et al., 2007; Lee et al., 2003; Lee et al., 2000; Vemula et al., 2004). Yarmush and his co-workers (Yarmush et al., 1999) found that burn injury results in an increase in gluconeogenesis from lactate and the contribution of pyruvate to the oxaloacetate pool. Furthermore, up-regulation in the expression levels of genes involved in the urea cycle, gluconeogenesis, and the metabolism of several amino acids were also reported (Banta et al., 2007; Vemula et al., 2004).

Metabolic pathway analysis based on extreme pathways and elementary modes has proven to be a useful tool and has been extensively applied in the literature (Cakir et al., 2004; Diniz et al., 2006; Klamt and Gilles, 2004; Kromer et al., 2006; Papin et al., 2002; Stelling et al., 2002; Wiback et al., 2003). Elementary modes consist of the minimum number of reactions that exist as a functional unit whereas extreme pathways are the independent subset of elementary modes (Klamt and Stelling, 2003). Every flux distribution can be written as a linear combination of the elementary modes, or extreme pathways, thus a weight can be assigned to each corresponding pathway and can be interpreted as an indication of the importance of that pathway in the network. Pathway analysis identifies pathways which are important for desired products (yield analysis), evaluates how much of a flux is carried out by each pathway and to what extent an external metabolite taken by the cell affects the output of the pathway. This analysis can also elucidate important information about metabolic regulatory mechanisms and how dominant pathways are controlled. However, one of the main problems in pathway analysis is that the decomposition of a steady state flux vector into pathways is not always unique because for large networks the number of pathways is not usually equal to the dimension of the null space of the stoichiometric matrix (Schilling et al., 2000).

To provide a unique decomposition of the steady state flux distributions into elementary modes or pathways, different optimization methods have been proposed in the literature. Nookaew and his co-workers (Nookaew et al., 2007) proposed the maximization of the number of elementary modes as the optimization objective function. This was based on the assumption that the cells try to use as many pathways as possible to increase their robustness to environmental changes. Schwartz and Kanehisa (Schwartz and Kanehisa, 2005; Schwartz and Kanehisa, 2006) proposed the minimization of the elementary mode activity and they further investigated the effect of change in enzymatic kinetics on the weights of elementary modes by incorporating kinetic modelling. Zhao and Kurata (Zhao and Kurata, 2009) proposed a new algorithm based on the entropy maximization principle for estimating the active elementary modes. This is derived from Shannon’s entropy theory where the entropy of a random variable is defined by its probability distribution. In their work, it was assumed that each elementary mode could be regarded as a random event and the probability of elementary mode was calculated as the ratio of the substrate uptake rate in the mode to the overall uptake flux of that substrate.

Although metabolic objectives of some living systems are well defined such as biomass formation in microorganisms (Ibarra et al., 2002), we do not know the appropriate metabolic objectives in mammalian cells which are important in driving the organ function. This obstacle prevents utilization of various metabolic tools and system biology methods for mammalian cells (Uygun et al., 2007). Therefore we search topological and physiological properties of hepatic metabolic network such as lengths of the pathways which might provide clues regarding the liver objectives. Schwarz and his co-workers (Schwarz et al., 2005) underlined the importance of short pathways in elementary mode analysis and assumed that short pathways are the modes which contribute most to gene expression (Stelling et al., 2002; Wagner and Fell, 2001). Rutter and Zufall (Rutter and Zufall, 2004) investigated whether the evolutionary properties of a metabolic network could be determined by the network characteristics such as the pathway length. In their analysis, examining amino acid biosynthetic pathways across 48 sequenced organisms, it was demonstrated that longer pathways exhibit lower rates of change in pathway structure than shorter pathways, which suggest that long pathways may show slower rates of evolutionary adaptation, thus they are more conserved. They claimed that it may be very difficult for alternative pathways to develop rapidly enough to compete with the original long pathways, and change in upstream genes, and moreover, they may require simultaneous compensatory change in many downstream genes. Short pathways with high variability in structure across the organisms can also be regarded as important properties since they are specific to the organism, which has been developed as a result of adaptive responses to environmental changes. Therefore, in this work we formulated a quadratic optimization problem where activities of short pathways are maximized.

An objective function based on the physiological properties of the metabolic network can also be formulated. For example, urea production in liver metabolism has been used as one of the important hepatic functions (Sharma et al., 2005; Uygun et al., 2007). Since the data used in this work was obtained from perfused livers of fasted rats (Lee et al., 2000), gluconeogenic pathway should be up-regulated. Therefore we assume that pathways including gluconeogenesis should be important. Identifying the relation between physiologically relevant objective function, pathway length and weight of pathway can lead to important knowledge regarding metabolic properties.

In this context, the aim of this work is to utilize alternative methods based on different underlying assumptions to provide information regarding the metabolic objectives and investigate the metabolic properties of liver under stress. In order to estimate the active pathways and pathway importance for the production of a desired product, these methods are applied to elementary modes and fluxes that are calculated using data sets obtained from perfused livers isolated from rats that underwent experimental burn injury.

2. Materials and Methods

2.1. Metabolic Network and Experimental Data

The network model of liver metabolism (Table S1 in “Supplementary Materials”) was originally developed for perfused livers (Arai et al., 2001; Banta et al., 2005; Banta et al., 2007; Lee et al., 2003; Lee et al., 2000) and slightly modified in this paper in the following way. The pentose phosphate pathway (reaction number 8 in Table S1) was considered as one reaction in order to reduce the complexity of the network. All external reactions (reaction numbers from 46 to 74 in Table S1) were explicitly included in the model to demonstrate the network uptakes and outputs in pathway analysis. Since all data used in this work have been obtained from perfused livers of fasted rats, it was assumed that gluconeogenesis is active while glycolysis is inactive. It was also assumed that glycogen has been depleted (Lee et al., 2003). Given these properties, the network involves all major pathways active in liver, including gluconeogenesis, urea cycle, fatty acid metabolism, pentose phosphate, TCA cycle, and amino acid metabolism.

In order to determine flux values for the reactions involved in the metabolic network, experimentally measured fluxes provided by (Lee et al., 2000) were used. This data set was obtained from perfused livers of fasted rats which received sham and burn treatments (Lee et al., 2000). They studied the effects of burn injury on liver intermediary metabolism by applying metabolic flux analysis to perfused livers explanted from rats on the 4^th day after experimental burn injury or sham treatment (uninjured control).

2.2. Flux Balance Analysis

The flux distribution was calculated by using stoichiometric matrix S of the metabolic network, where the rows correspond to the metabolites and the columns correspond to reactions. The mass balances can be written as follows (Varma and Palsson, 1994):

$$\frac{\mathit{\text{dX}}}{\mathit{\text{dt}}}=S.v$$ (1)

where X is the vector of metabolite concentrations and v is the flux distribution. It is generally assumed that the internal metabolites are at pseudo steady state, since metabolic transients are rapid compared to environmental changes (Varma and Palsson, 1994). Therefore, the mass balance constraints can be considered as follows:

$$\begin{array}{c}S.v=0\hfill \\ v_i\ge 0,\forall i\in \{\text{irreversible fluxes}\}\hfill \end{array}$$ (2)

The metabolic network model used herein is largely based on a previously published model and it has been shown that there is a good consistency between the measurements and assumed biochemistry of this model (Lee et al., 2000). In order to obtain a unique flux distribution satisfying mass balance constraints which is required for decomposition of flux vector into pathways, a prediction objective has to be used. Although a number of objectives have been proposed for optimization based models such as maximization of growth, an appropriate metabolic objective in flux balance analysis for mammalian cells has proven difficult (Uygun et al., 2007). Since experimental measurements (or external fluxes) are related to internal reactions, this information can be used directly to identify the unknown fluxes which has been proven to be quite useful (Burgard and Maranas, 2003; Nolan et al., 2006; Uygun et al., 2007):

$$\begin{array}{cc}\text{Minimize}\hfill & {\displaystyle \sum _j}{\left(\frac{v_j-v_j^{\mathit{\text{obs}}}}{v_j^{\mathit{\text{obs}}}}\right)}^2,\forall j\in \{\text{external fluxes}\}\hfill \\ \text{Subject to}\hfill & S.v=0,\hfill \\ \hfill & v_i\ge 0,\forall i\in \{\text{irreversible fluxes}\}\hfill \end{array}$$ (3)

where v_j and $v_j^{\mathit{\text{obs}}}$ are the predicted and observed external flux values, respectively. In problem (3) all flux vectors were calculated by solving the optimization problem of minimizing the normalized error between the observed and calculated external reactions. The prediction errors were normalized in order to prevent flux estimation biased towards the measured fluxes with large values. Sensitivity analysis was also performed to evaluate the model dependence on flux measurements, which is explained in details in “Supplementary Materials”.

2.3. Pathway Analysis

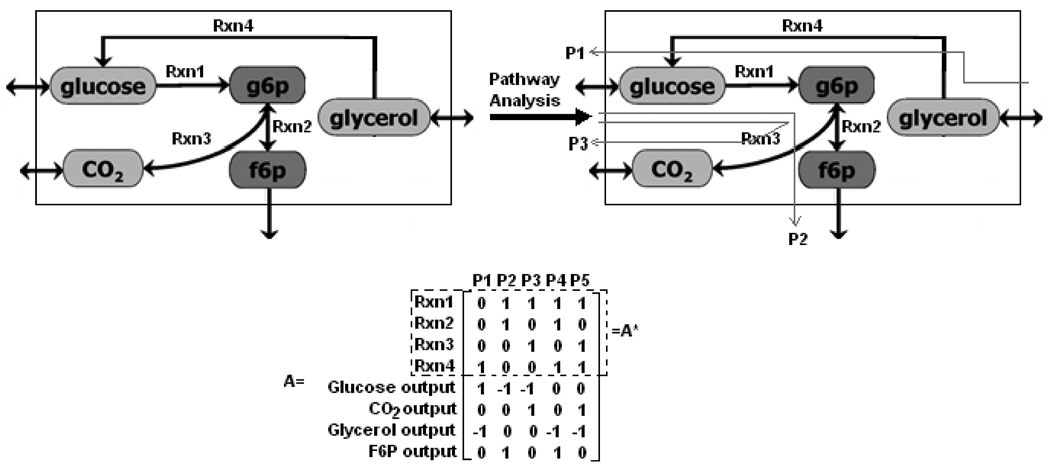
Elementary modes and extreme pathways are represented by vectors generated from the network stoichiometry and can be used to define the steady state solution space for the reaction network. In this work, elementary modes were only used to identify the structure of the metabolic network. A small example (Figure 1) is used to illustrate the basic ideas of the elementary mode analysis. Representative pathways connecting uptakes to outputs are illustrated in Figure 1. A represents the pathways in matrix form, where rows correspond to the reactions and columns indicate the modes. For example Mode 1, corresponding to column 1 (P1), expresses the transformation of glycerol to glucose and involves glycerol uptake, Rxn 4 and glucose secretion. Elementary modes were calculated using a MATLAB package, CellNetAnalyzer (Klamt et al., 2007) which is the successor and further development of FluxAnalyzer (Klamt et al., 2003).

Figure 1. Metabolic pathway analysis of a simple network.

Five different elementary modes are identified for the simple network in matrix form A where rows represent the reactions and columns indicate the modes. A* is matrix of elementary modes including only internal reactions.

Any steady state flux vector v can be expressed as a linear combination of elementary modes or extreme pathways (Llaneras and Picó, 2007; Wiback et al., 2003):

$$v=w·A,w_k\ge 0,\forall k\in \{\text{irreversible pathways}\}$$ (4)

where w denotes a vector involving the weight for each elementary mode; and A is the matrix of elementary modes. In this study, reversible pathways were split into two irreversible pathways so that the system could be defined as a non-negative linear combination of elementary modes. The decomposition of a steady state flux vector into pathways is not always unique, because the number of pathways is not usually equal to the dimension of the null space of the stoichiometric matrix of larger networks (Schilling et al., 2000). The dimension of null space of the hepatic network used in this study was found to be 26. Given that the number of pathways (more than 36,000 pathways were calculated in the metabolic network studied in this work) exceeds the dimension of null space of this system, the pathways do not uniquely describe every point in the solution space. To overcome this limitation, different optimization methods were used as outlined below:

1. The first method considers the minimization of the length of the weight vector as an objective function (Schwartz and Kanehisa, 2005) as follows:

   $$\begin{array}{cc}\text{minimize}\hfill & {\displaystyle \sum _{j=1}^{n_p}{w}_j^2}\hfill \\ \text{subject to}\hfill & {\displaystyle \sum _{j=1}^{n_p}{A}_{\mathit{\text{ij}}}{w}_j=v_i,i=1\dots n_r,}\hfill \\ \hfill & w_j\ge 0,j=1\dots n_p.\hfill \end{array}$$ (5)

   where n_r is the total number of reactions, and n_p is the total number of pathways.
2. In the second method the entropy of the system is maximized. The evaluation of the entropy term is based on Shannon’s entropy as proposed by Zhao and Kurata (Zhao and Kurata, 2009). According to their formulation the Shannon’s entropy is defined as follows:

   $$I=-{\displaystyle \sum _{j=1}^m{s}_j}\text{ log }{s}_j$$ (6)

   where s_j is the probability of any random event and ${\displaystyle \sum _{j=1}^m{s}_j=1}$; where j represents the random event, and m is the total number of random events.
   Zhao and Kurata (Zhao and Kurata, 2009) assumed that elementary modes include all possible pathways and each elementary mode could be regarded as a random event. Any elementary mode except internal loops has at least one uptake reaction, thus the flux of a substrate uptake reaction can be calculated from the expression, $\frac{{\displaystyle \sum _{j=1}^{n_p}{A}_{\mathit{\text{susbtrate uptake}},j}·w_j}}{v_{\mathit{\text{susbtrate uptake}}}}=1$. The probability of the j-th elementary mode in Shannon’s entropy can be provided as:

   $$s_j=\frac{A_{\mathit{\text{susbtrate uptake}},j}·w_j}{v_{\mathit{\text{susbtrate uptake}}}}$$ (7)
   Thus, the nonlinear optimization problem to maximize entropy is formulated as follows:

   $$\begin{array}{cc}\text{maximize}\hfill & -{\displaystyle \sum _{j=1}^{n_p}{s}_j}\text{ ln }{s}_j\hfill \\ \text{subject to}\hfill & {\displaystyle \sum _{j=1}^{n_p}{A}_{\mathit{ij}}{w}_j=v_i,}i=1\dots n_r,\hfill \\ \hfill & w_j>0,j=1\dots n_p,\hfill \\ \hfill & s_j=\frac{A_{\mathit{\text{susbtrate uptake}},j}·w_j}{v_{\mathit{\text{susbtrate uptake}}}},j=1\dots n_p.\hfill \end{array}$$ (8)
3. In this method, the number of pathways is maximized (Nookaew et al., 2007). The basic assumption behind this formulation is that the cells increase their robustness with respect to environmental changes by introducing redundancy. The formulation which leads to mixed integer programming problem is as follows:

   $$\begin{array}{cc}\text{maximize}\hfill & {\displaystyle \sum _{j=1}^{n_p}{\beta }_j}\hfill \\ \text{subject to}\hfill & {\displaystyle \sum _{j=1}^{n_p}{A}_{\mathit{\text{ij}}}{w}_j=v_i,}i=1\dots n_r,\hfill \\ \hfill & w_j\ge 0,j=1\dots n_p,\hfill \\ \hfill & {\delta }_1{\beta }_j\le w_j\le {\delta }_2{\beta }_j,{\beta }_j\in \{0,1\},j=1\dots n_p.\hfill \end{array}$$ (9)

   where β_j is a Boolean variable that assigns a value of 1 when the corresponding pathway is used in reconstructing a flux distribution, and zero when that mode is not used. δ₁ and δ₂ are positive scalars, which correspond to very small and very large number, respectively, and forces the Boolean variable to be 1 if the corresponding pathway is active, otherwise it takes the value of zero.
4. In this method, the activity of short pathways is maximized. The length (l) of any pathway is equal to the number of reactions involved in that pathway (Papin et al., 2002) and is calculated using the binary matrix of elementary modes, P, where P_ij is equal to 1 if A_ij is different than zero, otherwise P_ij is zero:

   $$l_j={\displaystyle \sum _{i-1}^{n_r}{P}_{\mathit{\text{ij}}},j=1\dots n_p.}$$ (10)
   Thus the following quadratic problem was proposed in this study:

   $$\begin{array}{cc}\text{minimize}\hfill & {\displaystyle \sum _{j=1}^{n_p}{(l_j{w}_j)}^2}\hfill \\ \text{subject to}\hfill & {\displaystyle \sum _{j=1}^{n_p}{A}_{\mathit{\text{ij}}}{w}_j=v_i,}i=1\dots n_r,\hfill \\ \hfill & w_j\ge 0,j=1\dots n_p.\hfill \end{array}$$ (11)

   where l_j denotes the length for elementary mode j. This method is based on the idea that short pathways can be more important since short pathways are the modes which contribute most to gene expression (Schwarz et al., 2005). They are also less conserved (Rutter and Zufall, 2004); therefore they might have been developed as a result of adaptive responses to environmental changes.
5. Finally, the activity of pathways including glucose and/or urea production is maximized.

   $$\begin{array}{cc}\text{maximize}\hfill & {\displaystyle \sum _f^{}{w}_f}\hfill \\ \text{subject to}\hfill & {\displaystyle \sum _{j=1}^{n_p}{A}_{\mathit{\text{ij}}}{w}_j=v_i,}i=1\dots n_r,\hfill \\ \hfill & w_j\ge 0,j=1\dots n_p.\hfill \end{array}$$ (12)

   where f indicates pathways responsible for urea and/or glucose production. This method is directly related to liver metabolism and the investigated experimental conditions. It is based on previous studies revealing that urea production is intrinsic to liver metabolism (Uygun et al., 2007). Also, all data used in this work were obtained from perfused livers of fasted rats where the pathways related to glucose production are important.

2.4. Determining Weights of Limited Number of Pathways Selected Randomly

Given the following method (Wang et al., 2007), possible weight values of a number of pathways which are used to reconstruct flux vector can be calculated. In this formulation, weights of a subset of pathways (randomly selected) are evaluated by minimizing the error between the real flux vector and the reconstructed one. This procedure is repeated many times to make certain that all pathways are selected. The formulation of the problem is as follows:

$$\begin{array}{cc}\text{Minimize}\hfill & {\displaystyle \sum _k^{n_k}{(A_{\mathit{\text{ik}}}{w}_k-v_i)}^2,i=1\dots n_r,}\hfill \\ \hfill & w_k\ge 0,k=1\dots n_k.\hfill \end{array}$$ (13)

where w_k is the weight of pathway k. A_ik is the matrix whose columns are composed of k pathways. A total of k pathways (ranging between 50–1,000) were randomly selected among all elementary modes and for each k, problem (13) was solved n times (ranging from 1,000 to 20,000).

All linear optimization problems, mixed integer linear programming and quadratic programming problems were solved using MATLAB (Mathworks Inc, Massachusetts) and GAMS with the interface program MAT-GAMS and a Pentium(R) processor at 2.80 GHz with 1.00 GB of memory.

3. Results and Discussion

3.1. Elementary Modes and Flux Balance Analysis

Extreme pathways and elementary modes are quite similar, that is, extreme pathways are a subset of elementary modes. The only difference is that extreme pathways are systematically independent, implying that none of the extreme pathways can be expressed as a non-negative combination of other extreme pathways. Analyzing a biological system through a set of extreme pathways can result in the exclusion of possibly important modes (Klamt and Stelling, 2003; Trinh et al., 2009). Therefore, in this work elementary modes were used to analyse the topology of the metabolic network. The number of all possible elementary modes of the hepatic metabolic network was found to be 36463. Among them, only 6 pathways are reversible (note that in this article we also use the term “pathways” for the “elementary modes”).

In this study, we used a metabolic network that was previously used to characterize the flux distribution in perfused rat livers (Arai et al., 2001; Banta et al., 2005; Banta et al., 2007; Lee et al., 2003; Lee et al., 2000). Although since then large scale hepatic networks have been constructed (Gille et al., 2010; Jerby et al., 2010), we chose the smaller network, which focuses on central carbon and nitrogen metabolism and for which a set of measurements was already available. The larger network would be considerably more difficult to separate into elementary modes, and a much more comprehensive set of measured metabolites would be needed to obtain meaningful information.

Flux vectors were calculated using available experimental data (Lee et al., 2000) and flux balance analysis as described in section “Materials and Methods”. The flux values are given in the Table S1 in “Supplementary Materials”. The data set corresponds to perfused livers of fasted animals which received sham and burn treatment. In the objective function of flux balance model, the prediction error was normalized with respect to the observed values to prevent bias towards fluxes with large values. Sensitivity analysis showed that only glucose, lactate, urea, O₂ and CO₂ outputs out of 28 measured external fluxes (see “Supplementary Materials”) had significant impact on unknown fluxes. Investigating the impact of the external fluxes on the values of the unknown fluxes (see Figure S2 in “Supplementary Materials”) elucidated that the most sensitive unknown flux is pentose phosphate pathway (PPP). PPP is one of the important branches in central metabolism where glucose-6-P is degraded to CO₂. It is also known that O₂ consumption affects the TCA cycle and electron chain system, which in turn influence PPP. Flux balance analysis gives more information when two different conditions are compared. Our model found that flux value of PPP following the burn injury was much higher. Lee and co-workers (Lee et al., 2000) had already identified that the activity of glucose-6-P dehydrogenase catalyzing the rate controlling step in the PPP increased in response to burn injury, and they also found that the PPP was significantly up-regulated after burn injury by measuring the conversion rate of exogenously added [1-¹⁴C]glucose into ¹⁴CO₂.

3.2. Decomposition of Flux Vectors into Pathways

3.2.1. Dominant pathways

To identify possible important pathways that characterize hepatic metabolism, the methods presented in the previous section were first applied to determine the unique decomposition of the flux vector into pathways (note that all methods correspond to convex optimization problem and thus there is no need to utilize global optimization approaches). It was observed that each method determined different number of active pathways at different conditions, whose weight values are greater than zero (see “Supplementary Materials” and Table S2 for details). The method of maximizing the number of active pathways selected 14357 active pathways after sham treatment. This was increased to 21858 after burn treatment. In general an increase was observed in the number of active pathways in all methods following the burn treatment. More than 80% of active pathways estimated by the methods of minimizing the length of weight vector and maximizing the activity of shortest pathways were identical in both conditions (Table S2 in “Supplementary Materials”).

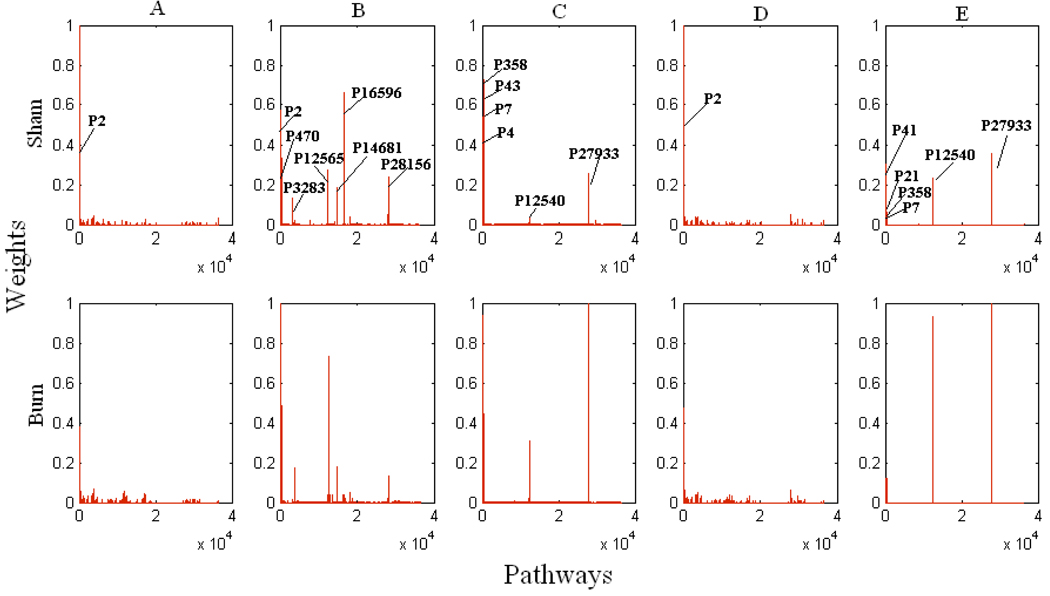
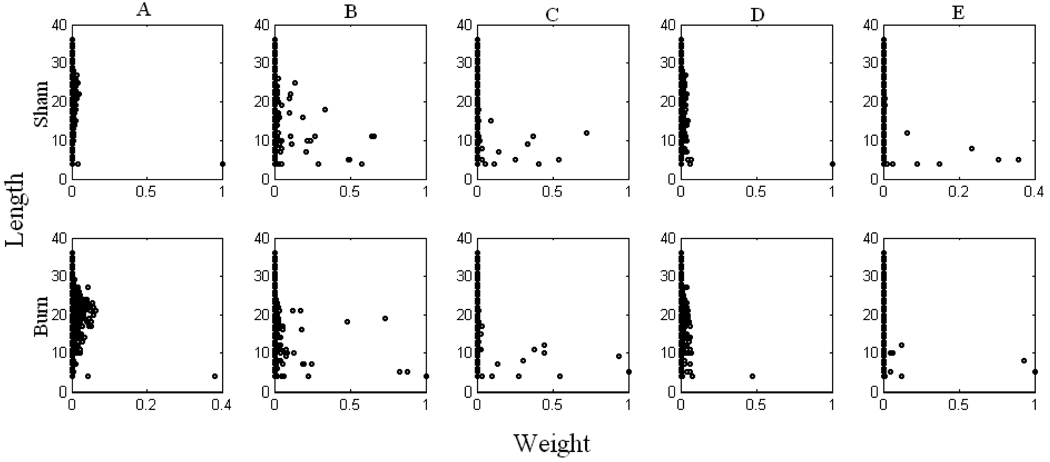
In order to gain a systematic understanding for the response of hepatic metabolism to burn trauma, dominant pathways (having larger weight values) at all methods and conditions were further analyzed. Figure 2 compares the weight vectors of two states that correspond to burn and sham treatment. Panels in the first row in Figure 2 represent the sham data, and the second row represents the burn data. Each column indicates a different method. Some pathways found to be important are given in Figure 3. Pyruvate, glutamate and oxaloacetate correspond to important transition pools in those pathways. Pathway 2 (P2) was always found to be active, independent of method or experimental data used. It includes arginine uptake, formation and secretion of ornithine and urea (reaction of arginase), which is a very short pathway (Figure 3). The presence of P2 for both sham and burn using all methods indicates a strong relationship between arginine uptake and urea secretion. Nolan and his co-workers (Nolan et al., 2006) found urea and ornithine exchange reactions are important in their analysis where they investigated the metabolic response of rat liver to burn injury by combining metabolic flux analysis and free energy balances.

Figure 2. Weight values of pathways.

Panels in the first row represent the sham data, and the second row the burn data. Panels in each column indicates different method: A) Minimizing the length of weight vector, B) Maximizing the entropy, C) Maximizing the number of pathways, D) Maximizing the activity of shortest pathways, E) Maximizing the activity of pathways including glucose and /or urea production. Weights of some pathways, P 358, P43, P7, and P4, which are not clear on the panels of column C, are respectively 0.72, 0.34, 0.02, and 0.01 after sham treatment, and 0.44, 0.93, 0.45, and 0.02 after the burn treatment. Weights of P41, P21, P358, and P7 on the panels of column E are respectively 0.30, 0.08, 0.12, and 0.001 after sham treatment, and 0.05, 0.12, 0.06, and 0.06 after burn treatment. Note that in each method all weights values are normalized according to largest one observed among the sham and burn results.

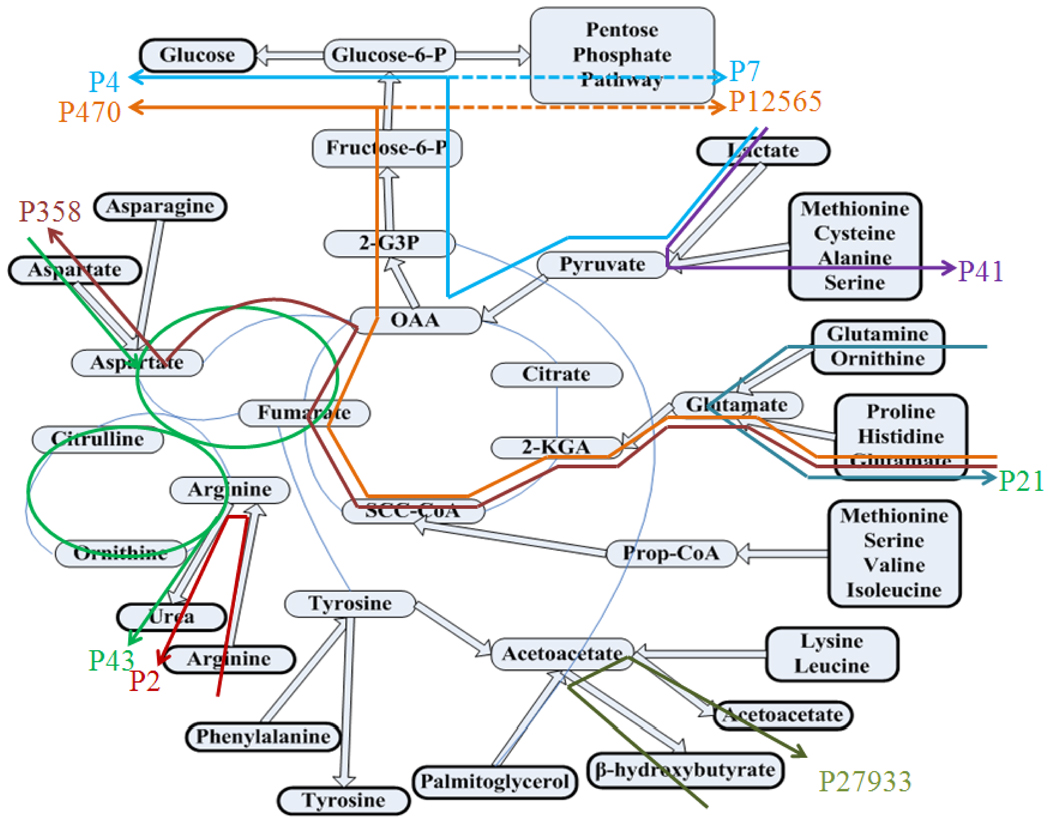
Figure 3. Some important pathways (frequently observed at all methods and experimental conditions) on a simplified hepatic metabolic network.

Lactate enters P4 and P7 to produce glucose or to go into PPP. Similarly, glutamine is also used for glucose production (P470), aspartate (P358) or PPP (P12565). P43 shows the conversion of aspartate to urea. There are also pathways where conversion of lactate to cysteine and alanine (P41); and glutamine to glutamate (P21) take place. P2 includes arginine uptake, formation and secretion of ornithine and urea. P27933 are related to ketone bodies where conversion between acetoacetate and B-OH-butyrate by B-OH-butyrate dehydrogenise is seen. Note that external metabolites are given in bold boxes.

There are also pathways where conversion of lactate to alanine and cysteine (P41, including lactate dehydrogenase, alanine amino transferase and cysteine transaminase); glutamine to glutamate (P21 including glutaminase); and glutamate to aspartate (P358 which in turn affects the urea cycle and thus production of urea) takes place (Figure 3). In P43, aspartate feeds the loop formed by oxaloacatete and fumarate, which affects the urea cycle. P27933 is also a typical characteristic of liver cells, where ketogenesis takes place (B-OH butyrate formation from acetoacetate by B-OH butyrate dehydrogenase). P470 and P12565 are similar pathways since both of them include glutamate uptake (or glutamine since glutamine is first converted to glutamate), formation of oxaloacetate by an anaplerotic route via the TCA cycle and gluconeogenesis. The only difference is that P470 involves glucose formation, and P12565 enters the PPP, which can provide important information regarding the branch point where the flux is divided into PPP and glucose production. Similarly P4 and P7 include glucose production or PPP, respectively, from lactate through oxaloacetate and gluconeogenesis.

Some other dominant pathways which appear in Figure 2 are not shown on the network in Figure 3. In some methods P12540 gained higher weights. This pathway is a very short pathway where conversion of glycine to serine (including glycine dehyrogenase and aminomethyltransferase) occurs. P16596 is also a short pathway where both formation of cysteine from lactate through pyruvate and formation of serine from glycine take place. Serine likely plays a critical role in liver physiology. Sharma and his co-workers (Sharma et al., 2005) in their optimization study also interprets that serine concentrations should be doubled for optimal hepatic function. It is known that liver regulates serine levels in the body (De Koning et al., 2003) since it is a precursor for neurotransmitters glycine, D-serine and taurine (Uygun et al., 2007), and it might also behave as a sink for excess pyruvate (Uygun et al., 2007). P3823 is formed as a linear combination of P470 and P4. In other words, it includes glucose production and both lactate and glutamine uptakes. P28156 is also resulted from a linear combination of P12540 and P27933, which demonstrates the importance of ketogenesis and serine production in the liver. P14681 is very similar to P43, but this pathway has asparagine uptake which is converted to aspartate first and feeds the oxaloacatete-fumarate- aspartate loop and urea cycle. Chan and her co-workers (Chan et al., 2003a; Chan et al., 2003b), according to their experimental observations from cultured hepatocytes, interpreted that urea synthesis may be limited by aspartate availability.

Methods of maximizing the metabolic redundancy (Figure 2 column C) and maximizing the weights of pathways including glucose and/or urea production (Figure 2 column E) determined that burn injury up-regulated ketogenesis (P27933) and serine production from glycine (P12540). In the method of maximizing the metabolic redundancy, it was also observed that burn injury up-regulated P43 (where urea production from aspartate takes place), and gluconeogenesis through lactate input (P4 and P7) with increasing importance of P7 which indicates that lactate was mostly directed to PPP. Similar results were obtained with the method of maximizing the weights of pathways related to glucose and urea production, where the increase in P7 and P21 (glutamate formation from glutamine, which might be used for TCA cycle and gluconeogenesis or urea cycle) were observed after burn injury. In the same method, down-regulation in P41 (alanine and cysteine production from lactate) represents that lactate might be directed to glucose production and PPP after burn injury. Burn injury also down-regulated P358 (aspartate production from glutamine) implying that glutamine was directed to other pathways, especially those including PPP or glucose production (Figure 2 column C). It should be noted that the method of maximizing the number of active pathways resulted in more than 14,000 active pathways with very small weight values (less than 10⁻⁵) which are not shown in Figure 2 column C.

The method of maximizing the entropy of the system (Figure 2 column B) found a different set of active pathways. After burn injury, this method determined that P470 and P12565 were up-regulated (but more increased upregulation in P12565 implies that glutamate was mostly directed to PPP). On the other hand, down-regulation in P16596 where lactate and glycine are used for cysteine and serine production, respectively, was observed. The methods of minimizing the length of weight vector (Figure 2 column A) and maximizing the activity of shortest pathways (Figure 2 column D) determined similar weight values for the pathways. In general, results from all methods revealed that burn injury facilitated the usage of lactate and glutamine for glucose production and PPP, on the other hand down regulated the production of other aminoacids such as alanine, cysteine, and aspartate from lactate and glutamine.

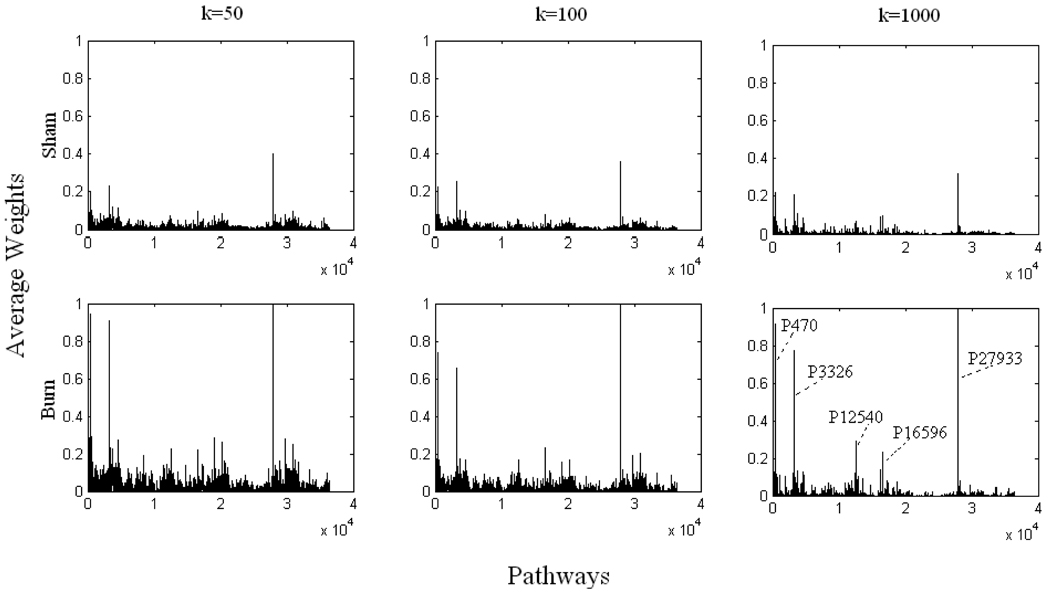
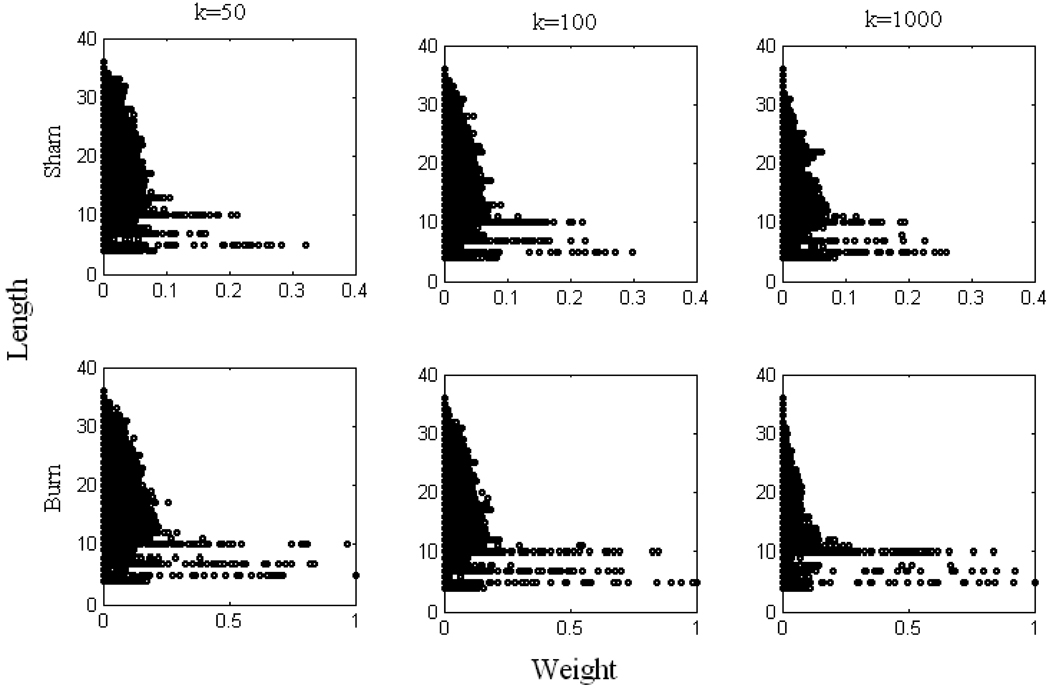
We also used problem (13) to attribute weight values to a limited number of pathways randomly selected, to understand the pathway importance. A total of k pathways were forced to have weights by solving problem (13) to define the flux distribution. Using this method, weights were assigned to pathways that were not selected by the decomposition methods discussed above. Since all pathways have equal chance to be selected, for each k, the reconstruction procedure was repeated n times to guarantee that all the pathways could be selected (Wang et al., 2007). In this study, k was chosen to be 50; 100; 1,000, respectively, and n ranged from 1,000 to 20,000 so that each pathway could be equally selected for each k (see “Supplementary Materials” and Figures S3 and S4 for details). For each k, we plotted the average value of weights that each pathway could get (Figure 4), and it is clear that an increase was observed in the average weight values after burn injury, which indicates that burn injury up-regulated fluxes being carried. Similar to previous findings, P27933, P16596, P12540, P3326 and P470 always got higher weights.

Figure 4. Average weights obtained from problem (13).

Panels in each column represent different k. Panels in the first row correspond to sham data, and the second row burn data. Some important pathways which are always observed with higher weights are shown on the figure (see text for details). Note that at different k, all weights values are normalized according to largest one observed among the sham and burn results.

3.2.2. Network inputs and outputs

An interesting result of pathway reconstruction is to identify how much of a flux is carried out by each pathway. This can be then used to compare the efficiency of different pathways converting any substrate to the desired product. This further enables the identification of alternative substrates required for the formation of desired product. Determining efficient pathways for a desired product allows the development of metabolic engineering strategies to design an optimal system for its production.

Glucose production via gluconeogenesis and the disposal of excess nitrogen via urea synthesis are among the most critical metabolic functions of the liver. It has been observed that glucose and urea production in liver metabolism play a critical role under a stress such as burn injury (Banta et al., 2007; Lee et al., 2003; Lee et al., 2000; Yarmush et al., 1999). Pathway analysis showed that asparagine, arginine, lactate, glutamine and serine contribute most to the production of urea and glucose. In Table 1 we quantified the proportion of a metabolite that entered a particular pathway (for glucose and urea production) after sham and burn treatments. Since each method identified different number of active pathways, maximum and minimum quantities among the results obtained from the methods are given in Table 1. For example, after sham treatment, the method of minimizing the length of weight vector identified that 10.59 µmol/g liver /h of lactate (corresponding to 87% of the total lactate uptake) entered the pathways related to glucose production, whereas no lactate (or no glutamine) went into any pathways producing glucose in the method of maximizing the activity of pathways related to glucose and urea. This might be explained from the fact that lactate and glutamine were first converted to other metabolites such as serine or asparagine, which could then be used as a source of glucose production. On the other hand, all methods found that after sham treatment arginine was never used as a source for glucose production while all arginine was utilized for urea. Similarly, lactate was never used for urea production after sham treatment. It should be noted that, although this is not explicitly shown in Figure 3, NH4⁺ fixation always takes place in the pathways where nitrogen is needed. Therefore, TG can also be an input for the pathways producing urea, where the glycerol moiety can lead to oxaloacetate, which in turn can provide the carbon backbone, via fumarate and aspartate, for urea. Another interesting result is related to asparagine and serine. In all methods, these two external metabolites were always used in the pathways producing glucose and urea, but this is not always the case for other metabolites given in Table 1. In some instances the ratio of a flux to uptake is greater than 1 if there is also internal production of the metabolite. For example, the total serine uptake was 3.3 µmole/g liver /h, while up to 18.25 µmole/g liver /h of serine (7.56 fold higher) could enter the pathways producing glucose. This indicates that there might be other active internal pathways producing serine (mainly from glycine, threonine and pyruvate pool), which then entered pathways for glucose production. This might be also related to adaptation mechanisms of liver to environmental changes, i.e., excess lactate or other metabolites contributing to pyruvate pool might be excreted through serine metabolism. We also provided the participation number of an external metabolite, which is the ratio of active pathways involving that specific metabolite and leading to a particular product (glucose or urea) to all active pathways leading to that same product. It can be observed in Table 1 that serine participated most in the pathways producing glucose and urea. After the burn injury serine involvement in the pathways producing glucose and urea seemed to be increasing. Similarly, lactate and arginine participation in urea and glucose production, respectively, increased after burn injury.

Table 1. Main sources for glucose and urea production after burn injury^a.

Since each method finds different set of active pathways, and thus fluxes carried out by pathways, minimum and maximum quantities of participation numbers, amounts and ratios observed in all methods are only given.

GLUCOSE	Sham			Burn
	Participation	Amount	Ratio	Participation	Amount	Ratio
Lactate	0–0.20	0–10.59	0–0.87	0–0.21	0–6.0	0–0.37
Glutamine	0–0.18	0–7.04	0–0.82	0–0.22	0–3.14	0–0.27
Serine	0.44–0.77	0.01–14.09	0.04–4.30	0.23–0.80	2.54–18.25	1.05–7.56
Asparagine	0.08–0.14	2.10–3.85	0.54–1.00	0.03–0.8	0.01–6.87	0.002–1.00
Arginine	0	0	0	0–0.07	0–0.44	0–0.21
TG	0.08–0.80	0.11–0.90	0.12–0.58	0.05–0.44	0.23–1.06	0.07–0.44
UREA	Sham			Burn
	Participation	Amount	Ratio	Participation	Amount	Ratio
Lactate	0	0	0	0–0.05	0–1.27	0–0.07
Glutamine	0–0.28	0–3.43	0–0.40	0–0.27	0–5.75	0–0.49
Serine	0.23–0.65	0.01–3.04	0.003–0.92	0.14–0.52	0.01–2.90	0.006–1.20
Asparagine	0–0.14	0–3.85	0–0.99	0–0.12	0–1.70	0–0.24
Arginine	0.0002–0.25	2.40–3.20	1–1.32	0.11–0.40	2.11–6.15	1.00–2.91
TG	0–0.75	0–0.19	0–23	0–0.80	0–0.39	0–0.16

Participation number is the ratio of active pathways including both uptake and product (for example, lactate and glucose) to all active pathways including the product.

Amount indicates how much an uptake-metabolite enters the pathways producing the specific product (in µmole/g liver/h).

Ratio is the ratio of amount of uptake metabolite taken by the pathways producing the specific product to its overall uptake.

It has been previously observed that the hepatic response to severe injury is described by a significant up-regulation of glucose, and amino acid turnover (Lee et al., 2003; Lee et al., 2000; Yarmush et al., 1999) and up-regulation in the expression levels of genes involved in the urea cycle, gluconeogenesis, and the metabolism of several amino acids, with specific transporters for glutamine and arginine (Banta et al., 2007; Vemula et al., 2004). It is also known that burn injury leads to negative nitrogen balance with accelerated hepatic amino acid metabolism in patients. It is estimated that 80–90% of urinary nitrogen loss in burn patients occurs as urea (Tredget and Yu, 1992). Therefore, glutamine and arginine serving as substrates in urea production might play a critical role (Pan et al., 2004; Pawlik et al., 2000). Arginine and glutamine have already been proposed as a dietary supplement to enhance hepatic functions during catabolic state (Espat et al., 1996). Besides these amino acids, our analysis showed that serine and asparagine are also important amino acids which were found to contribute significantly to urea production. Moreover, these amino acids as well as lactate were also used for the production of glucose which is needed to maintain a fuel supply required for other organs during the catabolic state. Therefore, these metabolites could be potential nutrients which might be utilized to manipulate biochemical environment in order to reduce the stress caused by burn injury.

3.2.3. Relation between Pathway Lengths and Weights

Pathway analysis is a very useful tool, but unique decomposition of flux vector into pathways in a redundant system is a major obstacle. We searched topological properties of hepatic metabolic network (such as lengths of the pathways) which might provide clues regarding the liver objectives (or important reaction sets) that could be utilized to describe the redundant system.

Figure 5 compares the lengths of pathways and their corresponding weight vectors. It was observed that short pathways always gained higher weights in all methods and in any condition. Figure 6 illustrates the results of the solution of problem (13). Similarly, higher weights were assigned to short pathways.

Figure 5. The relation between weight value and pathway length.

Panels in the first row represent the sham data, and the second row the burn data. Panels in each column indicates different method: A) Minimizing the length of weight vector, B) Maximizing the entropy, C) Maximizing the number of pathways, D) Maximizing the activity of shortest pathways, E) Maximizing the activity of pathways including glucose and /or urea production. Note that in each method all weights values are normalized according to largest one observed among the sham and burn results.

Figure 6. The relation between weight value and pathway length obtained from problem (13).

Panels in each column represent different k. Panels in the first row correspond to sham data, and the second row burn data. Note that at different k, all weights values are normalized according to largest one observed among the sham and burn results.

The short pathways with large weights are related to four major metabolite sinks (ketone body, pyruvate, glutamate and oxaloacetate pools). Excluding the pathway input and output, P27933 has only one main reaction which is catalysed by B-hydroxybutyrate dehydrogenase, where conversion between acetoacetate and B-OH-butyrate takes place. This pathway exhibits a very high weight. One of the important properties of liver is lipid metabolism where triglycerides are oxidized to produce energy and ketone bodies which can be re-used by liver or other part of body as an energy source by being converted to acetyl-CoA that enters the TCA cycle. Ketone bodies play key role in sparing glucose utilization and reducing proteolysis during periods of glucose deficiency, and also it stimulates insulin release and provides alternative source of energy for the brain (Laffel, 1999). Pathways related to pyruvate pool (P12540, P41, P16596, P3326) where serine, alanine or cysteine are produced from glycine or lactate, represent the second group that have higher weights (these are also very short pathways). Among these pathways, P12540 where serine is produced by the enzymes glycine dehydrogenase and aminomethyltranferase is also consistently observed with a higher weight. Inter-conversion between serine and glycine play crucial roles in liver metabolism which maintains the serine level in a certain range (Xue et al., 1999). Glutamate is another transition metabolite observed in the pathways (P4, P21, and P470) including glutamine and glutamate inputs that are some main amino acid-exchange reactions feeding the liver metabolism. Liver specific glutaminase which is not inhibited by the product of glutamate is the major enzyme of glutamine catabolism which is required for simultaneous glutamine degradation to remove glutamine from the circulation (Watford, 2000).

The oxaloacetate pool is also found to be important. Pathways where PPP, glucose, or aspartate are produced from glutamine, glutamate or lactate (P4, P470, P7, P12565, P358) pass through the oxaloacetate pool. However, these pathways are relatively longer. Oxaloacetate is an intermediate species in the gluconeogenesis pathway, as well as a precursor for fumarate and (together with NH₄⁺) aspartate. The three internal metabolites, oxaloacatete, fumarate, and aspartate, form a loop which feeds the urea cycle. Oxaloacetate is also produced by several other metabolites, primarily pyruvate and glutamate, but also propinoyl-CoA, tyrosine, aspartate, and the glycerol part of TG. Pyruvate can be produced by a vast number of metabolites, such as lactate, methionine, cysteine, alanine and serine. Glutamate also has many sources, such as glutamine, ornithine, proline, and histidine.

The structure of a metabolic network is the result of diverse and numerous biochemical and genetic factors, and it links the cellular phenotype to the corresponding genotype (Trinh et al., 2009). Assignment of higher weights to short pathways is a result of the network structure and the experimental observations since in all methods the constraint “A.w=v” should be satisfied (A is the matrix of pathway, w is weight vector and v is flux vector). The matrix A is only related to metabolic network structure, and v is based on experimental observations. This is better explained by investigating some specific examples regarding the liver metabolism. For example, the reaction where glutamate is produced from glutamine by the enzyme of glutaminase is very active in liver metabolism. Previous perfusion experiments (Arai et al., 2001; Banta et al., 2005; Banta et al., 2007; Lee et al., 2003; Lee et al., 2000) also showed that high glutamine uptake was always associated with high glutamate production. Therefore higher weight can be attributed to the pathway including glutamine uptake and production of glutamate. On the other hand, pathway analysis also reveals that glycerol moiety from TG can contribute to urea synthesis through oxaloacetate, which requires a number of internal reactions as well as exchange reactions including NH₄, urea, TG and some other amino acids. But assignment of higher weight for this pathway is not observed in this study. In longer pathways, more metabolic regulations at different levels, and more branch points where fluxes are divided are involved. Therefore, longer pathways might be less robust to environmental changes compared to shorter pathways.

4. Conclusions

This paper presents different approaches considering the structural and physiologic properties of a metabolic network for the pathway reconstruction of flux vectors. The methods were applied to the hepatic network and data set obtained from perfused livers of fasted rats treated with burn injury. As a result of this comprehensive analysis, several important observations were made. First, although different methods for unique decomposition of flux vectors were used, it was always found that short pathways have higher weights, which is related to topological properties of hepatic metabolic network and flux distribution. When all possible weight vectors were analyzed, some pathways, including pyruvate, oxaloacetate, and ketone bodies, and urea production from arginine, and serine production from glycine, were found to be important. Finally, pathway analysis enabled the identification of pathways between certain substrates and products, which provided a systematic comparison between sham and burn states.