Bacterial flagellum as a propeller and as a rudder for efficient chemotaxis

Abstract

We investigate swimming and chemotactic behaviors of the polarly flagellated marine bacteria Vibrio alginolyticus in an aqueous medium. Our observations show that V. alginolyticus execute a cyclic, three-step (forward, reverse, and flick) swimming pattern that is distinctively different from the run–tumble pattern adopted by Escherichia coli. Specifically, the bacterium backtracks its forward swimming path when the motor reverses. However, upon resuming forward swimming, the flagellum flicks and a new swimming direction is selected at random. In a chemically homogeneous medium (no attractant or repellent), the consecutive forward t_f and backward t_b swimming times are uncorrelated. Interestingly, although t_f and t_b are not distributed in a Poissonian fashion, their difference Δt = |t_f - t_b| is. Near a point source of attractant, on the other hand, t_f and t_b are found to be strongly correlated, and Δt obeys a bimodal distribution. These observations indicate that V. alginolyticus exploit the time-reversal symmetry of forward and backward swimming by using the time difference to regulate their chemotactic behavior. By adopting the three-step cycle, cells of V. alginolyticus are able to quickly respond to a chemical gradient as well as to localize near a point source of attractant.

Enteric bacteria, such as Escherichia coli, swim by rotating a set of flagella that forms a bundle when the flagellar motors turn in the counterclockwise (CCW) direction (1–3). The bundle falls apart when one or more motors turns in the clockwise (CW) direction, and the bacterium tumbles (4). A new swimming direction is selected upon resuming the CCW rotation of the flagellar motors. By modulating the CCW and CW intervals according to external chemical cues, the cells are able to migrate toward attractants or away from repellents (5, 6).

Certain bacterial species possess a single polar flagellum with a bidirectional motor similar to E. coli. Being single polarly flagellated, low Reynolds number (Re) hydrodynamics dictates that, aside from random thermal motions, the bacterium can only backtrack its trajectory when the motor reverses. This raises an interesting question concerning how this type of cells performs chemotaxis. Studies of motility patterns of single polarly flagellated bacteria Pseudomonas citronellolis showed that the bacteria change the swimming direction by a brief reversal between two long runs. From the published trajectories (7), each reversal typically results in a small change in cell orientation, and thus several reversals appear to be necessary for a significant change in the swimming direction. Backtracking was also observed in a number of single flagellated marine bacteria such as Shewanella putrefaciens, Pseudoalteromonas haloplanktis, and Vibrio alginolyticus, which execute the so-called run–reverse steps when following attractants released from porous beads and from algae (8–10). A pioneering experiment in V. alginolyticus revealed that the time-reversal symmetry in the run and the reverse intervals is broken when the cell swims near a surface. In such a case, although the forward swimming remains more or less straight, the backward trajectory is remarkably curved and often forms a tight circle a few bacterial lengths in diameter (9). This asymmetry in swimming can be explained by a hydrodynamic interaction with the surface that produces a turning (yawing) moment on the cell body (11). A recent experiment also demonstrated that hydrodynamic interactions between a swimming cell (Caulobacter crescentus) and a surface can amplify thermal fluctuations, causing more efficient randomization of swimming trajectories (12). These observations together suggest that single polarly flagellated bacteria may perform chemotaxis effectively only near surfaces.

Herein we report observations of motility patterns of marine bacteria V. alginolyticus in a chemotaxis buffer away from surfaces. We found that the bacteria employ a unique cyclic three-step (forward–reverse–flick) swimming pattern for chemotaxis; they regulate both forward and backward swimming times according to a given chemical profile. The time-reversal symmetric trajectories in the forward and the backward swimming are randomized by the last step, where the flick “steers” the cell to a new direction. Our experiment shows that the flagellum at the base is flexible and is actively involved in the directional change. We also found that although the flicking angle θ appears to be random, it has the highest probability at θ ≈ 90°, which maximally randomizes the swimming trajectory. To our knowledge, this function of the bacterial flagellum has not been previously discussed or appreciated, and it raises interesting questions about its molecular components and role in chemotaxis. It should be emphasized that although backtracking in polarly flagellated bacteria has been previously reported (7), the cyclic three-step sequence is, in our opinion, not previously recognized or characterized. By employing the three-step chemotactic strategy, cells of V. alginolyticus are able to focus on a point source of attractant rapidly and form a compact swarm around it. This apparently is a significant niche of V. alginolyticus, which live in ocean where nutrients are scarce and rapidly dispersed by currents.

Results and Discussion

The Steady-State Motility Pattern of V. alginolyticus Is a Cyclic Three-Step Process.

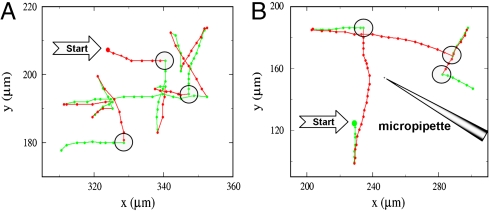
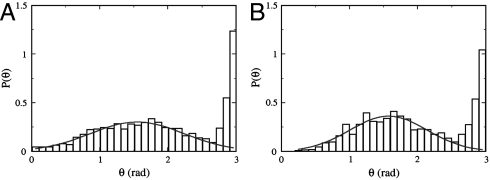
We conducted our measurements (see Materials and Methods) using a mutant strain V. alginolyticus YM4 (Pof⁺ Laf^-) that possesses a single left-handed polar flagellum and a flagellar motor powered by Na⁺ ions (13). The handedness of the flagellum dictates that when the flagellar motor rotates in the CCW direction, it pushes the cell body forward, but when the motor reverses, it pulls the cell body backward. We found that the bacterial swimming trajectories, even far from surfaces (> 500 μm), are not smooth but interrupted by sharp kinks and bends. Fig. 1A displays such a quasi-two-dimensional bacterial swimming trajectory in a motility medium TMN [50 mM Tris-HCl (pH 7.5), 5 mM MgCl₂, 5 mM glucose, 30 mM NaCl, 270 mM KCl]. Because the surface is sufficiently far, the observation suggests that the bacteria are actively involved in changing swimming directions. A study of a large number of trajectories (∼800) shows that the abrupt change in the swimming direction θ is always associated with motor reversal and belongs to one of the two categories, those that change with a large angle θ ∼ 180° and those that change with an intermediate angle 0 < θ < 180°. Fig. 2A is a plot of the probability density function (PDF) P(θ), which displays a bimodal distribution with a sharp peak centered at θ ≈ 180° and a broader peak around θ = 90°. This bimodal distribution indicates the existence of two distinct processes responsible for changes in the swimming direction.

Fig. 1.

Bacterial trajectories in a motility medium TMN (A) and in a steep chemical gradient created by a micropipette filled with 1 mM serine (B). The big solid circles are the starting points of the bacterial tracks, and the small solid circles represent the positions at an equal time interval of 0.067 s. The green and the red segments correspond to the forward and the backward trajectories, respectively. The large open circles marked the flicking events; for clarity, not all flicking events are marked in A.

Fig. 2.

Flicking angle θ distribution in a homogeneous medium (A) and in a sharp chemical gradient created by a point source of attractant (1 mM serine) (B). The distribution in both cases contains two peaks, a broad one at θ ≈ π/2 and a narrow one at π. The solid lines in the figure are fittings using a Gaussian function.

In an effort to clarify in details the motion of the bacteria, particularly the orientation of the flagellum with respect to the cell body during the transient period of the directional change, we used fast video imaging and fluorescence microscopy to record bacterial swimming in TMN (movies in SI Materials and Methods). The fluorescence labeling renders the flagellum visible under the microscope so that the swimming directions can be determined. We found that the large directional change (θ ∼ 180°) is always associated with the transition from forward to backward swimming, which gives rise to the distinctive, cusp-like segments in bacterial trajectories as displayed in Fig. 1A. The transitions from backward to forward swimming, on the other hand, always result in more varied turning angles θ and are responsible for the broad peak in Fig. 2A. Because a forward run must be preceded by a backward run and vice versa, it follows that the steady-state motility pattern of the bacterium is a three-step process, which we call the run–reverse–flick process. The last step allows the cell to veer to a new direction, and the three-step process ensues. This is in contrast with the motion of E. coli, which cycles through a two-step (run–tumble) process, and the directional randomization occurs during the CW period (6).

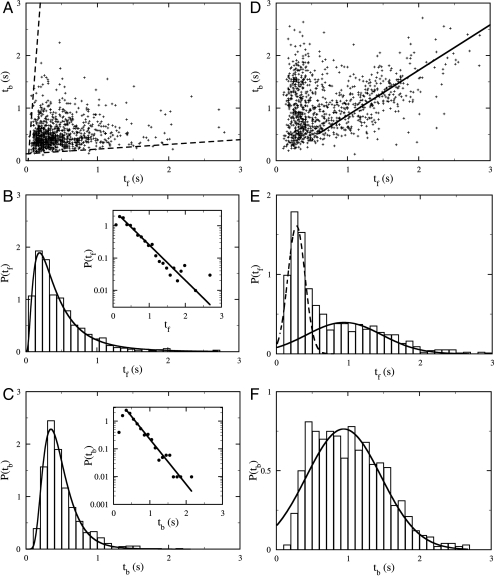
Although the three-step cycle is deterministic and has been observed in nearly all bacteria in the population as long as they swim with a normal speed (i.e., v_sw≥45 μm/s), the bacterial swimming pattern is stochastic in that the forward and the backward intervals, t_f and t_b, as well as the flicking angle θ, fluctuate from moment to moment. Fig. 3A displays a scattered plot of the measured pairs of forward and backward swimming times (t_f, t_b) between two flicks for an ensemble of ∼800 bacteria. The uniform distribution of the data points on the graph indicates that there is little or no correlation between t_f and t_b. We also calculated PDFs of t_f and t_b, which are displayed in Fig. 3 B and C. A prominent feature of P(t_f) and P(t_b) is that they are both peaked at short times, ∼0.2 and ∼0.3 s, respectively. It is only for long time intervals that the data display an exponential behavior (see Insets of Fig. 3 B and C) with the characteristic times of 0.40 and 0.27 s for P(t_f) and P(t_b), respectively. Thus, the forward and the backward swimming times of V. alginolyticus do not obey the Poisson statistics, which is at variance with E. coli cells (14). Moreover, according to Fig. 3 B and C, there is no significant difference between the distributions of t_f and t_b, or equivalently between the forward and the backward swimming distances; the latter is evident in the trajectory displayed in Fig. 1A. Hence, we conclude that the swimming trajectories of V. alginolyticus are also different from those of P. citronellolis; P. citronellolis make a brief reversal to generate a small change θ in the swimming directions (7), but in V. alginolyticus a single flick can generate a large θ, as shown in Fig. 1A.

Fig. 3.

Statistical distribution of t_f and t_b in a homogeneous motility buffer (A–C) and near a sharp serine gradient (D–F). In A and D, pairs of consecutive forward t_f and backward t_b swimming intervals between two flicks are plotted with random shifts of less than 0.03 s to avoid data points overlapping. In the homogenous medium, there is no correlation between t_f and t_b, whereas in the attractant gradient there is a strong correlation between t_f and t_b. The biological cause of such a correlation is discussed in SI Results and Discussion. The solid line in D is a linear fit to the data points with large t_f and has a slope of 0.86. The PDFs of t_f and t_b in the two cases are plotted in B and E and in C and F, respectively. The Insets in B and C are semilog plots of the same datasets as in the main figures. The solid lines are exponential fits to the tail parts of the data. The good agreement between the data and the fits shows that for large t_f and t_b the PDFs are exponential. The solid line in F is a Gaussian fit. The same fitting curve was rescaled and replotted in E as the solid line. The broken line in E is a Gaussian fit to the short-time peak of P(t_f).

The Bacterial Flagellum Is Actively Involved in Randomizing Swimming Directions.

The change in the swimming direction can be achieved either by spontaneous rotational diffusion of the cell body or by a thrust force generated by the flagellum. It is evident from a mathematical analysis of swimming in low Re (∼10^-5) that a sharp change in the swimming direction (θ ∼ 90°) cannot be accomplished if the flagellum and the cell body remain coaxial. Nor can it be achieved via a simple cyclic movement of the flagellum with respect to the cell body by the so-called scallop motion, because such one-degree-of-freedom motion at low Re always recovers the bacterium’s starting configuration (15). Inspections of fast video images [100 frames per second (fps)] showed that the transitions from forward to backward swimming are rapid, within ∼1/30 s, but the transitions from backward to forward swimming take a longer time, up to ∼1/10 s. Approximating the bacterial cell body as an ellipsoid with a semiminor axis a = 0.4 ± 0.1 μm and a semimajor axis b = 2.3 ± 0.4 μm, the rotational diffusion coefficient about its minor axis is D_r ≈ k_BT × (ln(2b/a) - 0.5)/(8πηb³/3) ≈ 0.084 rad²/s (16). Thus, the typical angular variation is δθ ≡ (4D_rΔt)^1/2 ≈ 0.10 rad for Δt = 0.03 s and δθ ≈ 0.18 rad for Δt = 0.1 s. We noticed that the former agrees rather well with the width of the sharp peak in Fig. 2A, but the latter is about a factor of ten smaller than the center position (∼90°) of the broad peak in Fig. 2A. In other words, the flicking angle distribution cannot be accounted for by the passive rotational diffusion of the cell body. The broadness of P(θ) in Fig. 2A suggests that the distribution of the flicking angle may be spatially uniform given by (1/2) sin θ. However, experimentally we found that a Gaussian distribution fits our data better as illustrated by the solid line in the figure. The fitting procedure yields a mean of 89° and a standard deviation of 30°.

We also conducted measurements using fluorescence microscopy, where V. alginolyticus were labeled with dye Nano Orange (see Materials and Methods). Fig. 4 displays a labeled cell whose flagellum is discernible. However, because of its rapid rotation, the fine helical structure is blurred. Careful analyses of fluorescence video images such as these ones showed that upon switching to forward swimming, the flagellum and the cell body are not coaxial, and a small kink forms between them (see Fig. 4A). This small kink is rapidly amplified by the CCW rotation of the flagellar motor that pushes the cell body at an angle. As shown in Fig. 4 B and C, the angular amplification is rapid and efficient; i.e., the cell rotates by ∼90° in less than 0.1 s while its center of mass translates only approximately one-half of its body length. After the new direction is selected, the flagellum aligns with the cell body axis via a large swing with its tip tracing out a hyperbolic spiral. This last step in the flicking process is depicted schematically in Fig. 4F. The entire flicking process, which includes initiation, amplification, and flagellum alignment, was captured in movies in SI Materials and Methods. As one can see, the flicking employs both bending and rotation of the flagellum, bypassing the limitation of the scallop theorem (15). Using a resistive-force theory (17), we show in SI Results and Discussion that for an initial bending angle θ₀ > 10°, it is possible to account for the fast kinetics of this angular amplification based on the thrust force generated by the flagellar motor. This suggests that no other active element may be required to produce the rapid turning movement of the cell body seen in our experiment. However, large initial angles θ₀, which could sometimes exceed 40°, suggest that the initiation of the directional change may not be totally passive and may be assisted by an active element or by the release of the elastic energy stored in the motor-flagellum complex during the backward swimming interval.

Fig. 4.

Fluorescent images of a swimming cell of V. alginolyticus (A–E). The bacterium is labeled with Nano Orange dye. The flagellum is visible when it is in the focal plane. A bend at the base of the flagellum is discernible and becomes amplified over time, as indicated by the red arrows. However, when the flagellum flicks, it moves out of the focal plane and becomes blurred, such as the one indicated by double arrows in B. The time interval between the images is 1/30 s, and the cell body length is ∼3 μm. The 3D drawing in F depicts the relative positions of the flagellum to the cell body at the last stage of flicking. Specifically, to align with the cell-body axis, the tip of the flagellum starts from position 1, traces out a hyperbolic spiral, and ends at position 3. The forward swimming ensues.

We also observed that the flicking of the flagellum is correlated with the bacterial swimming speed. In de-energized cells, either by reducing Na⁺ ions from the motility medium or by oxygen depletion, the bacteria abolish the last flicking step altogether. Likewise, increasing the viscosity of the motility medium has the effect of slowing down motor rotation as well as inhibiting flagellar flicking. These observations together suggest that these two processes, active swimming and flicking, are linked, supporting the idea that the same propulsion apparatus is used for both types of movements.

In order to verify that the three-step process is an intrinsic swimming pattern adopted by V. alginolyticus, we also studied two additional strains, VIO5 (Pof⁺ Laf^-) and 138-2 (wild type) (18). The bacterium 138-2 is capable of expressing both polar and lateral flagella. However, when grown in a liquid medium, only the polar flagellum is expressed. VIO5 is a mutant strain of V. alginolyticus that expresses a single polar flagellum. Our observations showed that both bacterial strains execute the three-step cycles identical to YM4. By curiosity we also examined the swimming pattern of P. haloplanktis, which was reported to be an efficient chemotaxer (19). Our observation showed that P. haloplanktis also incorporate flicks in their motility. However, because of its fast speed and long swimming intervals, our limited observation would not allow us to conclude that the motility pattern is a cyclic three-step process (SI Results and Discussion). It remains an intriguing possibility that in this marine bacterium the flick movement is on-demand, which enables the cell more flexibility in performing chemotaxis.

A Comparison Between Three-Step and Two-Step Motility Patterns for Bacterial Chemotaxis.

Approximating bacterial trajectories as a random walk, we found that there is a considerable difference between the canonical two-step process of E. coli and the three-step process found in this study. The most significant difference is that by using the forward–reverse–flick cycle, the bacterium is capable of backtracking its previous path, which is not possible for the cell executing the run–tumble swimming pattern. Taking this into account, the diffusion approximation yields an effective “diffusivity” of the bacterium given by

[1]

where v_sw is the bacterial swimming speed, l is the net displacement in a cycle, and α = 〈 cos(θ)〉 is the average of the directional cosine of the trajectories (20). We noted that for the two-step process l = v_swt_CCW and is always positive (l > 0). However, for the three-step process l = v_sw|t_f - t_b|; it can be positive or even be zero depending on the time difference Δt = |t_f - t_b|. Thus, the bacteria executing the three-step cycle have the potential to regulate the CW and CCW intervals to significantly increase or decrease l; the former is preferred for migration in a chemical gradient and the latter is required for localization.

Finally, we noticed that even though the distributions of t_f and t_b are not Poissonian, their difference |t_f - t_b| and hence l are Poissonian, to a good approximation. The distribution P(|t_f - t_b|) is displayed in SI Results and Discussion, where a linear fit to the semilog plot of P(|t_f - t_b|) vs. |t_f - t_b| yields a characteristic time of 0.31 s (see Inset). The Poisson distribution of l along with the broad distribution of the flicking angle, which peaks at θ ≈ 90° or α ≈ 0, makes the swimming trajectories of V. alginolyticus close to an unbiased random walk, allowing the bacterium to efficiently explore its immediate neighborhood uniformly. In comparison, the swimming trajectories of E. coli cells are biased in the forward direction with α ≈ 0.33 (16). It thus takes a few tumbles to completely randomize their swimming trajectories, which requires a longer time.

V. alginolyticus Use the Same Three-Step Motility Pattern to Navigate in a Chemical Gradient.

To learn whether and how V. alginolyticus use the three-step strategy to migrate in a chemical gradient, we performed a tracking experiment near the mouth of a micropipette tip filled with different concentrations of serine, which is an attractant to the cells (21). We found that for 1 mM of serine, cells of V. alginolyticus can rapidly swarm around the tip, forming a compact cluster in a few tens of seconds. We followed the trajectories of ∼700 cells, and found that the bacteria still exhibit the three-step swimming pattern near the point source, which is shown in Fig. 1B. Fig. 3D is a scattered plot of t_b vs. t_f between two flicks. The data fall into two groups; those with very short t_f but relatively long t_b, and those with t_b being proportional to t_f (i.e., t_b ∼ t_f). The PDFs of the forward t_f and the backward t_b swimming intervals are displayed in Fig. 3 E and F, respectively. We found that P(t_f) can be decomposed into two distributions with one sharply peaked at t_f ∼ 0.3 s and the other broadly distributed. The broad peak in P(t_f) is nearly identical to P(t_b) as delineated by the solid lines in Figs. 3 E and F. Interestingly, even when the cells swarm around the point source, the flicking angle θ is still broadly distributed with a mean of 92° and a standard deviation of 32°. The similarity between the measured P(θ) in the presence (Fig. 2B) and absence (Fig. 2A) of the chemical gradient suggests that the angle θ is not regulated by the chemotaxis network.

The above observation shows that near a point source, the swimming intervals t_b and t_f of V. alginolyticus are strongly correlated, which is very different from that seen in a homogeneous medium (see Fig. 3A). One of the branches in the swimming interval distribution, where t_b is close to t_f(t_b ∼ t_f), corresponds to localization of cells with a small “diffusivity” D (see the solid line in Fig. 3D). The other branch with a short t_f but a longer t_b corresponds to a correction response of the bacterium when moving in an unfavorable direction. A detailed explanation of these peculiar correlations is further discussed in SI Results and Discussion.

Different Motility Patterns Matter for Cell Localization.

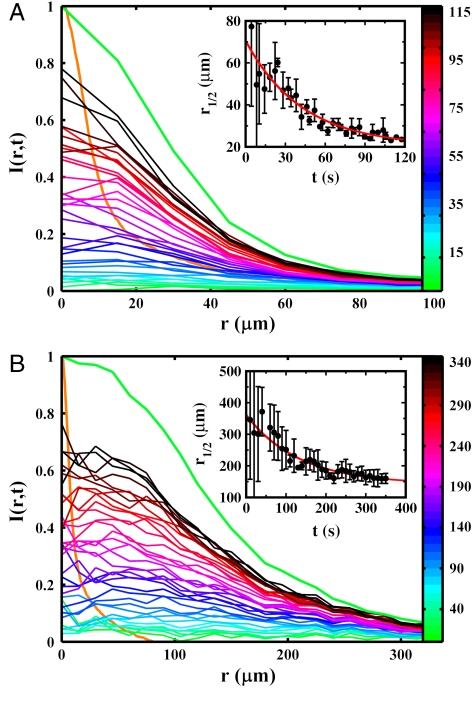
To investigate the effect of bacterial motility patterns on chemotaxis, we assessed the ability of bacteria to swarm around a point source of attractant. We carried out systematic measurements using cells of V. alginolyticus and E. coli. To aid visualization, the bacteria were transformed with plasmids encoding yellow fluorescent protein (YFP) (see SI Materials and Methods). In the measurement, a micropipette filled with different concentrations of serine (5 × 10^-4 < c₀ < 50 mM) was used, and fluorescent images were acquired at equal time intervals. Fig. 5 A and B display the time-dependent bacterial profiles B(r,t) acquired with c₀ = 500 μM, which causes nearly a maximum response for both bacteria. In the figure, the normalized YFP fluorescent intensity I(r,t), which is proportional to the cell density B(r,t), is plotted as a function of r measured from the center of the swarm. One observes that I(r,t) evolves from a uniform distribution at t = 0 and gradually becomes peaked at r = 0 over time; for convenience, each profile is color coded. Also displayed in Fig. 5 A and B are the quasi-steady-state bacterial profiles B(r) ∼ I(r) and the serine profile c(r), which are represented by the thick green and orange curves, respectively. It is evident from these measurements that B(r) is much narrower for V. alginolyticus than for E. coli, and both are significantly broader than c(r). Moreover, compared to V. alginolyticus, E. coli take a much longer time to reach the final state.

Fig. 5.

Normalized fluorescence intensity profiles I(r,t) for V. alginolyticus (A) and E. coli (B). The intensity profiles are proportional to the bacterial concentration profiles B(r,t). The individual runs are color coded according to the color bar (in seconds). Note the significantly different spatial and temporal scales used in these plots, indicating that the swarm size and the aggregation time are quite different between the two bacteria. As a comparison, the normalized steady-state bacterial and the serine profiles are displayed by the thick green and orange curves, respectively. The Insets represent the time-dependent half-height radii r_1/2(t) of the corresponding bacterial profiles B(r,t). The red lines are exponential fits, which are described in the main text.

To quantify the swarming dynamics, we measured the evolution of the half-height radius r_1/2(t) of I(r,t) as a function of time t for both bacteria, which is displayed in Figs. 5 A and B. As shown by the red lines in the Insets, our measurements can be adequately mimicked by the exponential function, r_1/2(t) = r₀ exp(-t/τ) + r_∞, with τ = 31 ± 4 s and r_∞ = 23 ± 4 μm for V. alginolyticus, and τ = 107 ± 21 s and r_∞ = 151 ± 10 μm for E. coli. The above measurements leave us with little doubt that for the moderate serine concentration (c₀ = 500 μM), cells of V. alginolyticus cannot only swarm faster (three times) but also form a much tighter cluster (seven times) than their E. coli counterparts. The swarming behaviors were also investigated for different serine concentrations, and the results are presented in SI Results and Discussion. In a nutshell, we found that there exists a threshold in the serine concentration (∼50 μM) for both strains of bacteria. Below the threshold, no swarm can be observed. However, above the threshold, V. alginolyticus form a much more compact and denser swarm near the source than E. coli, indicating a significantly higher nutrient exposure.

Mathematically, chemotactic aggregation in a bacterial population can be described by the Keller–Segel (KS) model (22), which relates bacterial density fluctuations B(r,t) to chemoeffector concentration fluctuations c(r,t) through a set of coupled partial differential equations. In the limit of high diffusivity of the chemical, c(r) can be considered time independent, and KS model assumes the following simple form:

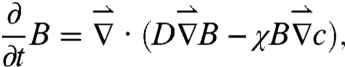where D is the diffusivity of the bacterium, which in general depends on c(r), and χ is the chemotactic coefficient, which gives the drift velocity 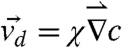. It is evident that a competent chemotaxer should have a large χ but a small D in order to migrate rapidly in a chemical gradient and to localize if needed. For both of these requirements, chemotactic strategy is clearly important, and there are distinctive differences between two-step and three-step swimmers in achieving these requirements. We note firstly that because of backtracking, the three-step swimmer can reexploit the patch it found during the previous forward swimming interval. This significantly improves a cell’s ability to localize, but this is not feasible for a two-step swimmer who immediately randomizes its swimming direction even though the search in its previous run is favorable. Secondly, because both the forward and backward swimming intervals produce motility (i.e., with a 100% duty cycle), with a proper regulation (or a response function) the three-step swimmer can generate a positive net displacement along a chemical gradient in both intervals (23). In comparison, for a two-step swimmer, the tumbling interval is nonmotile, and a displacement can only be generated during the run interval, which is typically 50–80% of the cycle (14, 24). A larger mean displacement along a chemical gradient in one swimming cycle means a greater drifting velocity. It follows that with everything being equal, the three-step swimmer cannot only localize better but also migrate faster than its two-step counterpart. Both of these attributes are evidently significant in competitive foraging or in a rapidly fluctuating environment, and the large differences between V. alginolyticus and E. coli are demonstrated in our experiment.

Conclusions

Through the prism of bacterial chemotactic behaviors of V. alginolyticus, we have observed a remarkable innovation in a biological system. Despite the simple propulsive apparatus, consisting of only a two-state (CCW and CW) motor and a helical propeller, cells of V. alginolyticus are able to overcome the diffusion barrier of low-Re swimming (i.e., inefficient rotational diffusion) by incorporating a unique flicking movement to efficiently randomize their swimming directions. Our experimental data showed that by employing the three-step motility pattern, the cells display a significant ability to move toward a point source of nutrient and to localize near it.

Much remains to be studied in future experiments. First of all, little is known about the molecular mechanism by which cells of V. alginolyticus perform the flicking movement. Is this driven by some active elements in the flagellar motor, or is it simply an elastic instability due to overcoiling during backward swimming? Secondly, it would be very interesting to know how the three-step motility pattern is regulated by the chemotaxis network elicited by external chemical stimuli. By sequence alignments, V. alginolyticus appear to possess all the chemotaxis genes of (E. coli cheA, cheB, cheR, cheW, cheY, and cheZ) with the addition of cheV, which is present in Bacillus subtilis but not in E. coli (21). This naturally leads to the question of whether the bacterium’s response to a brief chemical stimulus is still biphasic as in E. coli. Thirdly, it is reasonable to assume that different swimming patterns arise as a result of the bacteria’s habitats. One may then ask why the three-step swimming pattern is particularly well suited for an ocean environment. We believe that the flicking and the backtracking are the key. Whereas a flick allows a bacterium to randomize its swimming direction swiftly, the backtracking allows it to explore environments that are structured rather than spatially homogeneous. One lesson learned from fluid dynamics studies is that small-scale distributions of a passive scalar, such as a dye or a chemoattractant, consist of fine structures that are either filament-like or sheet-like (25, 26). Cells crisscrossing such a distribution can develop anticipatory responses in that going down the gradient does not necessarily indicate that the situation will continuously get worse. If necessary, a motor reversal can readily bring the cell back to the high concentration region. We posit that the three-step motility pattern may be selected for this type of spatially anisotropic distribution of nutrients, and it improves the fitness of the bacterium. Finally, in light of what we have observed in V. alginolyticus and to a less extent in P. haloplanktis, it would be rather surprising if flicking or cyclic three-step motility patterns are not widespread in other marine bacterial species. Thus, a careful survey would be very useful.

Materials and Methods

Video Imaging Microscopy.

To obtain the bacterial swimming trajectories of V. alginolyticus, a sample chamber was made by sandwiching a 1.2-mm-thick silicon gasket between two coverslips. The chamber was filled with bacteria culture and observed under an inverted microscope (Nikon, TE-300) with a 20× objective, which has a depth of field ∼6 μm. The position of the objective was adjusted so that the focus was ∼600 μm from both surfaces. Videos were taken at 30 fps by a CCD camera (Hamamatsu, EM-CCD C9100). We used ImageJ (National Institutes of Health) and Matlab (The Mathworks, Inc.) to analyze the video images.

The following procedure was used to track the bacteria: A bacterium in the field of view was picked at random and was followed until it disappeared from the x–y boundary or became defocused in the z direction. Only those tracks that contain at least two flicking events were kept, because these were sufficient for a pair of forward and backward swimming times (t_f, t_b) to be identified. For the measurement in TMN, we tracked ∼800 cells, a majority of which consisted of only 1 pair of (t_f, t_b) and a few more than 10 pairs. From these tracks, a total of 1,022 pairs of (t_f, t_b) were obtained. To test if there was a sampling bias in our procedure, we studied (t_f, t_b) of cells that were confined in a semen counting chamber (Hawksley, Z3BC1B) with a depth of 10 μm. In this case all the cells at different depth were visible albeit some of the trajectories were not straight because of their closeness to a surface. However, this did not affect the (t_f, t_b) measurements. The measured PDF in this shallow sample showed no statistical difference from the PDF acquired using the thick sample.

Because V. alginolyticus swim at a high speed, with an average v_sw ∼ 45 μm/s, their positions can be accurately determined by video microscopy operating at 30 fps. For instance, with a 20× objective, the bacterium moves ∼1.5 μm between two frames, corresponding to a displacement of two pixels on the CCD camera, and can be readily resolved. However, because of fluctuations in the bacterial swimming speed, particularly during the transitions from forward to backward or vice versa, the spatial and temporal resolutions are somewhat compromised, resulting in the uncertainty of t_f and t_b to be ∼0.07 s or two frames.

Video microscopy was also performed on P. haloplanktis using a 40× objective, and the swimming trajectories were constructed. We found that P. haloplanktis’ forward and backward swimming intervals are longer and their swimming speed higher, making the trajectory measurements more difficult.

For fluorescence microscopy, cells were labeled with Nano Orange dye (Invitrogen) and observed using a 100× oil-immersion objective (27). The fluorescence images were taken close to the surface for a better image quality. The fast video images were acquired in a phase contrast mode using the 100× oil-immersion objective and a Phantom V digital camera. The focal plane was set at 100 μm above the cover slip.

Chemotaxis near a Point Source of Attractant.

For the tracking and the swarming measurements in a chemical gradient, we used an open chamber, which has a diameter of ∼2 cm and allows a micropipette to be inserted from top. The chamber was mounted on the inverted microscope for observation. The micropipette tip was prepared by a glass pipette puller (Narishige, PP-830) and had an inner diameter smaller than 1 μm so that bacteria could not accumulate inside. The serine-filled tip was placed ∼200–300 μm above the bottom surface of the chamber and its content was ejected at a constant rate, 6 × 10^-12 L/s, by a 22-mm water column. Using fluorescein dye, we calibrated the serine concentration profile, which is displayed by the orange lines in Fig. 5. Our experiment showed that the dye concentration profile could be established very quickly, in less than 1 s after the medium was homogenized by stirring. This time scale can be considered instantaneous compared to the time required for E. coli or V. alginolyticus to establish a stable swarm.

To observe YM4’s swimming patterns near the tip, we first stirred up the fluid in the chamber to produce a uniform cell distribution. We then video recorded the chemotactic activities of the bacteria using the Hamamatsu camera. For a relatively low cell density, bacteria could be followed for the first 30 s near the tip, which allowed pairs of (t_f, t_b) to be measured. Altogether, we tracked ∼700 cells and obtained ∼1,001 pairs of (t_f, t_b).

For the swarming experiment, we used YM4 or RP437 harboring the plasmid pZA3R-YFP. The cell density was adjusted to ∼10⁷ mL^-1 for both with the help of the counting chamber. We video recorded the spatial and temporal evolution of the fluorescence intensity profile using a 10× microscope objective. For each measurement, we first stirred up the medium in the chamber so that the bacteria were uniformly distributed. This defined the time t = 0. The fluorescence video was taken for minutes until the swarm around the tip reached a quasi steady state. Using the images at the end of the video, the swarm center (x₀, y₀) was determined: 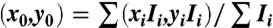, where x_i and y_i are the coordinates of each pixel, and I_i(x_i,y_i) is the background subtracted intensity. To minimize noises in the intensity, the time-dependent I_i(x_i,y_i,t) was circularly averaged from r to r + Δr, where Δr = 15 μm. This was denoted as I(r,t) and plotted in Fig. 5 A and B.