Abstract
Using a modular amino acid based chiral ligand motif, a library of ligands was synthesized systematically varying the substituents at two positions. The effects of these changes on ligand structure were probed in the enantioselective allylation of benzaldehyde, acetophenone, and methylethyl ketone under Nozaki-Hiyama-Kishi conditions. The resulting three-dimensional datasets allowed for the construction of mathematical surface models which describe the interplay of substituent effects on enantioselectivity for a given reaction. The surface models were both extrapolated and manipulated to predict the enantioselective outcomes of several previously untested ligands. Analyses were also used to predict optimal ligand structure of a minimal dataset. Within the dataset, a linear free energy relationship was also discovered and a direct comparison of both the linear prediction as well as the three-dimensional prediction illustrates the potential predictive power of using a three-dimensional model approach to asymmetric catalyst development.
Keywords: catalysis, enantioselective, modeling, carbonyl allylation
A centerpiece of modern organic chemistry is the development of new catalytic enantioselective methods to obtain valuable enantiomerically enriched synthetic building blocks (1, 2). Asymmetric catalysis, in practice, initiates from the discovery of a new catalytic reaction or identification of a reaction of interest. Subsequently, a number of chiral ligand classes are experimentally explored in hope of finding a “lead” which generates a promising enantiomeric ratio (er). Further optimization of the reaction conditions and ligand structure can ultimately yield a mature catalytic asymmetric method. This process is highly empirical and the results can be unsatisfactory for a given reaction. The empiricism inherent in reaction development has been addressed by computational chemistry via stereocartography and various other methods (3–10). Even with the impressive impact computational chemistry has had on the field, the small energy differences in the diastereomeric transition states (∼2–3 kcal/mol or 8.2–12.3 kJ/mol) leading to enantiomerically enriched products are not easily rationalized. Additionally, these methods generally depend on a detailed understanding of the parent chiral catalyst structure. Furthermore, kinetic analyses of asymmetric catalytic reactions often reveal the general complexities of catalysis and highlight the importance of the Curtin-Hammett principle (11, 12), but do not often expose the key catalyst structural features responsible for enantioselection. These issues highlight an underlying challenge in the field of asymmetric catalysis: how does one design a ligand for a given reaction type without engaging in a long-term, empirical investigation of multiple ligand classes?
A goal of our program has been to utilize classic linear free energy relationships (LFER) to predict the enantioselective outcomes of new catalytic systems (13). We have recently disclosed the use of steric parameters originally developed by Taft and modified by Charton (14–17) to quantitatively evaluate ligand effects on enantioselectivity in several Nozaki-Hiyama-Kishi (NHK) carbonyl allylations (18, 19). Because the product distribution of enantiomers (R vs. S) is directly related to the differences in free energy arising in the diastereomeric transition states, we were able to correlate er with the corresponding Charton steric parameter. We had hoped that the resulting LFERs would be a useful tool in optimizing ligands as well as de novo catalyst design. However, at the conclusion of these studies, we were puzzled at the observed breaks in the linear correlations mitigating the ability to predict the outcome of entirely new catalyst structures by extrapolation (20, 21). Herein, we report a more sophisticated approach to the problem in which a library of catalysts is used to generate a three-dimensional relationship of free energy to substituent size leading to successful predictions of catalyst performance.
Results and Discussion
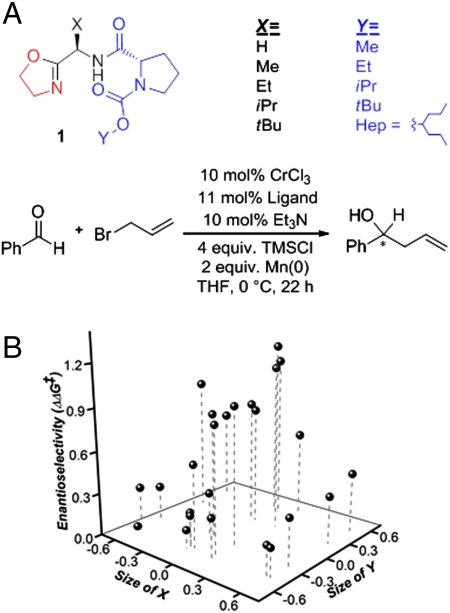
The modular ligand scaffold developed for the NHK allylation presented us with the unique ability to vary the substituents at both the X and Y positions of ligand 1 (Fig. 1A). It was hypothesized that both the X and Y positions may contribute synergistically to the selectivity of the system. Taking advantage of the ligand’s modularity and the commercial availability of amino acids, we initially synthesized a 25 member library (22–24).
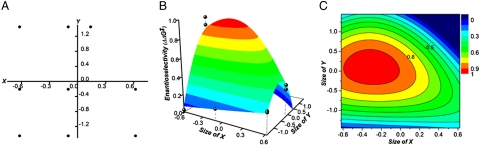
Fig. 1.
(A) Library of modular chiral oxazoline ligands for the enantioselective allylation of benzaldehyde under Nozaki-Hiyama-Kishi conditions. (B) Three-dimensional scatterplot for the allylation of benzaldehyde where the X and Y axes are the adjusted Charton steric parameter for positions X and Y in ligand 1 and the enantioselectivity described in terms of free energy (ΔΔG‡) (kcal/mol) is the Z axis.
The library was tested initially in the NHK allylation of benzaldehyde. Benzaldehyde was selected as a model substrate because we had not extensively examined this reaction with ligand scaffold 1 (21). The library of ligands was evaluated at random under the conditions shown in Fig. 1 and each data point presented was reproduced. The raw data shown in Fig. 1B was initially analyzed as data slices in two dimensions by holding one variable constant and evaluating the variation in the other variable. Two-dimensional analysis was simpler but ultimately failed to substantiate any relationships between X and Y. The dimensionality of the dataset led to the abandonment of this type of linear regression analysis.
To approach this issue in a more rigorous manner, the three-dimensional dataset required a three-dimensional function (a surface) to accurately model the data. Inspection of the dataset indicated that adequate surface models could be achieved through simple polynomial functions. Polynomial models were attractive due to their simplicity wherein the functions would contain steric parameters for X and Y as the independent variables and enantioselectivity (expressed in terms of the free energy, ΔΔG‡) as the dependent variable. It quickly became evident that the development of three-dimensional surface models would be a highly iterative and subjective process, particularly when using different algorithms to create models. In order to limit the subjectivity involved, principles in experimental design were employed (25–28).
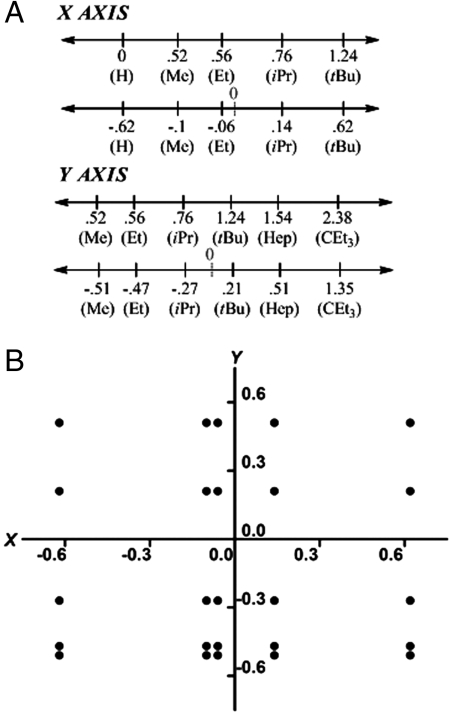
The first key principle in fitting a polynomial model to the data was modifying the Charton parameters. A problem with higher order polynomials is that the greater the distance from the origin the more difficult it becomes to distinguish second order from third order character. To better determine the true polynomial character of the dataset, the steric parameters were translated from their reported values to new values which centered about zero (Fig. 2A). This translation was accomplished by determining the center point for the range of parameters used in the library and setting it equal to zero. No information is lost in the translation as these parameters were originally based on relative rates (14–17). New values for each substituent were calculated based on the new center point with no change in the relative values. Simply, the parameter values coincide with the center point in our ligand libraries’ range along both the X and the Y axes.
Fig. 2.
(A) Graphical representation of the translation of the original Charton values to those used in this study. (B) Array of all 25 ligand substituent values in the XY plane.
The next key principle in developing a model to fit the data was assembling a surface function. Polynomials were initially selected through inspection of the raw two-dimensional data slices, observing linear and quadratic character. Full third order polynomials of the form
were the initiation point of each process. The coefficient values (z0,a,b,c,d,f,g,h,i,j) were solved using multivariable linear least squares regression analysis.* In order to perform the regression, two matrices were mapped: (i) the design matrix consisting of the independent variable values and (ii) the corresponding response matrix of measured enantioselectivity described in terms of free energy. The coefficient values could then be calculated according to least squares regression
where C is the matrix of calculated coefficients, X is the design matrix, XT is the transpose of the design matrix, and Y is the response matrix. The preliminary model was then simplified by eliminating terms with significant covariance and simultaneously maximizing the goodness of fit. The goodness of fit was determined primarily through the errors associated with the coefficient values but other relevant statistics including R2 and ANOVA analysis were taken into account.
Some considerations in our method of analysis warrant discussion. The first consideration is that Charton steric parameters are not continuous. As an example, there is no value between H and Methyl (Me). Additionally, purely carbon frameworks at the X and Y position were solely evaluated because the inclusion of heteroatoms might perturb the system in ways not related to their steric influence. These issues limit the ability to use the principles of experimental design in their purest form. The second major consideration is the synthetic availability of ligands. It was observed in the synthesis of the X = tBu series of ligands, that reactions proceed prohibitively slow for groups larger than Y = tBu. The final consideration is that the complexity of the polynomial models might not arise purely from steric interactions in the transition state. Some of the complexity contained in the models might arise from deficiencies is the parameters used (29) †.
Initially, a model was developed based on all 25 ligands evaluated. The alignment of data points collected in the XY plane is shown in Fig. 2B. Experimental design dictates that to maximize statistical significance the data array should be symmetrical about the center point of the graph (25–28). This example shows the data slightly weighted toward the third quadrant. Nonetheless, a surface model given by the following equation was constructed:
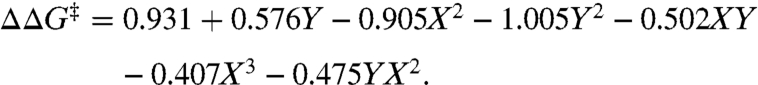 |
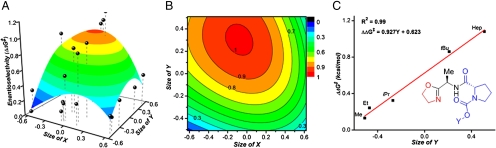
Fig. 3A is a graphical representation of this equation and Fig. 3B is a contour plot of the same model. Close inspection of the data revealed a LFER for the ligand series in which X = Me (Fig. 3C). The LFER predicts that installing a very large group at the Y position would result in a highly enantioselective catalytic system (Fig. 4). The three-dimensional surface prediction differs from the linear estimate considerably, predicting a more modest enantiomeric ratio (er). Synthesis and evaluation of the ligands bearing a much larger group on Y results in a breakdown of the linear model but to our delight the three-dimensional analysis accurately predicts the performance of three new catalysts.
Fig. 3.
(A) The raw data overlaid with the surface model given by ΔΔG‡ = 0.931 + 0.576 Y - 0.905X2 - 1.005Y2 - 0.502XY - 0.407X3 - 0.475YX2. R2 = 0.78. (B) Contour plot of the surface model. (C) Linear free-energy correlation for ligands with X = Me.
Fig. 4.
Comparison of predictions made by the LFER and three-dimensional model to the experimentally determined values (er = enantiomeric ratio).
By using the entire dataset, the outcomes of new catalysts can be predicted accurately through extrapolation. The magnitude of the extrapolation along the Y axis is almost double the data range indicating the robustness of this model. However, as one removes data from this model, the number of degrees of freedom in the analysis is reduced and the error of the prediction becomes greater. Additionally, the model relies on crossterms of X and Y providing evidence of the hypothesized synergistic effect.
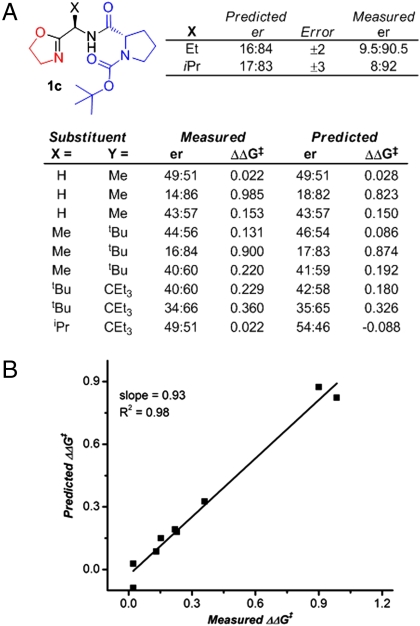
While extrapolation can yield important results, the power of using experimental design lies in the ability to simply define maxima and minima within a given domain with statistical significance. In the realm of asymmetric catalysis, the most powerful application would be to quickly identify the optimal ligand structure from a set of systematically varied ligands. However, synthesis of 25 or even 16 ligands to determine optimal structure may be impractical. Therefore, analysis of a much simpler 3 × 3 design matrix was performed including the newly synthesized ligands where Y = CEt3. The design of this matrix encompasses all of the synthetically practical values for X and Y and the full domain of available Charton parameters. It should be noted that the adjusted Charton values have changed to include this expanded domain as compared to the analysis of the 5 × 5 matrix (Fig. 5A). The entry for X = tBu and Y = CEt3 is missing because that ligand proved impractical to synthesize and has been substituted with the X = i Pr and Y = CEt3. A ramification of this substitution is that areas of the model beyond this value would carry less significance. A surface model given by the equation was determined:
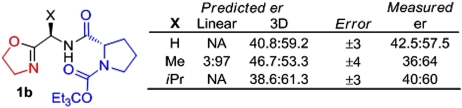
The local maximum of the graph and contour plot in Fig. 5 shows that the optimal ligand for the reaction would be either of the ligands in Fig. 6A (X = Et or i Pr). Neither of these ligands was used in the experimental data processed to create the surface model. The predictions are lower than their experimentally determined values; however, of all 29 ligands evaluated for this reaction, these two ligands gave the highest er. Close comparison of this new model with a smaller dataset as compared to the model in Fig. 3 shows a modest change in the maximum of the plot but a similar general shape. Both do predict that the ligand with Y = tBu and X = i Pr as the optimal ligand structure.
Fig. 5.
(A) Pseudo 3 × 3 data array used in analyzing the optimal ligand structure for the allylation of benzaldehyde. The X = tBu and Y = CEt3 ligand has been replaced with the X = i Pr and Y = CEt3 ligand. (B) The raw data for the allylation of benzaldehyde overlaid with the three-dimensional surface described by the equation ΔΔG‡ = 0.857 - 0.489X + 0.813X2 - 0.361Y2 - 0.422XY - 0.571YX2. R2 = 0.97. (C) Contour plot of the surface model.
Fig. 6.
(A) Prediction vs. measured enantioselectivity for the evaluated catalysts in benzaldehyde allylation. (B) Plot of measured vs. predicted ΔΔG‡.
To further validate the simpler 3 × 3 dataset model, the measured ΔΔG‡ was compared to the predicted ΔΔG‡ for the ligands evaluated (Fig. 6 A and B). The resultant linear correlation gives a slope of 0.93 where 1.00 would be a perfect fit. This excellent correlation confirms the reliability of the model. For similar analysis of all of the models, see the SI Appendix.
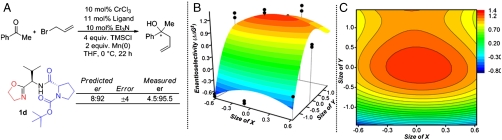
Next, we moved to the allylation of acetophenone under conditions shown in Fig. 7A. Development of a model for the 3 × 3 dataset described above led to the following equation:
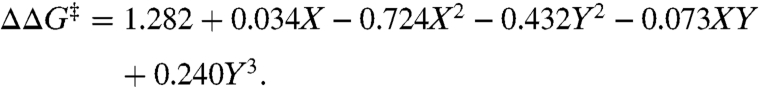 |
The surface and contour graphs in Fig. 7 present a maximum which is nearest the modified Charton values for ligand 1d. The model correctly predicts the catalyst which we had previously optimized and published for the allylation of a variety of aromatic ketones including acetophenone (21). Again, this ligand was not utilized in the analysis. An interesting feature of this surface is that it crosses zero on the Z axis representing a change in product facial selectivity. In the initial studies, this ligand was found primarily through empirical ligand evaluation. Even though this ligand performed well, it was never known to be the optimal ligand structure. A power of this three-dimensional modeling method is the level of confidence in identifying the optimal catalyst is considerably higher.
Fig. 7.
(A) Predicted optimal catalyst for acetophenone allylation. (B) Surface described by the equation ΔΔG‡ = 1.282 + 0.034X - 0.724X2 - 0.432Y2 - 0.073XY + 0.240Y3R2 = 0.87 (C) Contour plot of the surface model.
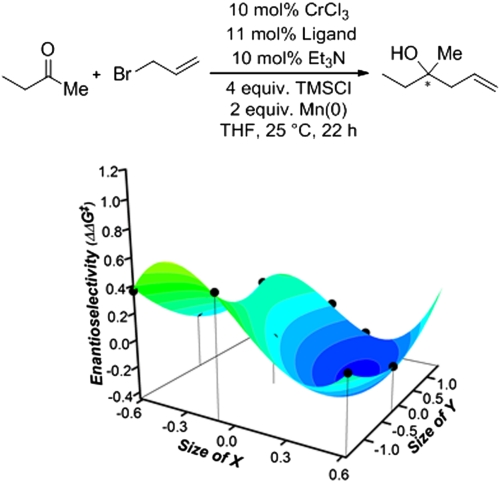
Finally, we applied this system to probe an interesting and synthetically promising reaction class. The NHK allylation of aliphatic ketones in Fig. 8 does not result in high selectivity using our previously published ligands (and many analogs). Our efforts to develop a useful, enantioselective variant have thus far been unsuccessful. Therefore, we sought to evaluate the simplest aliphatic ketone, methylethyl ketone, with the ligand library and use the results to guide the development of a highly enantioselective catalyst. Using the approach described for the determination of the optimal catalyst for both benzaldehyde and acetophenone, the reaction using the simple 3 × 3 ligand set was evaluated. The resulting data was modeled by the following equation:
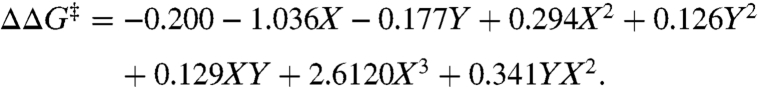 |
The model confirmed our empirical observation that the best selectivity we could hope for using this ligand scaffold was a mere 40% enantiomeric excess. Interestingly, the best result obtained in the screen was using the ligand where X = Me and Y = Me, indicating that smaller features were potentially desirable. The ultimate conclusion from this analysis is that the current ligand scaffold will most likely not result in the desired outcome for this difficult reaction. Therefore, we have since diverted our attention to developing new scaffolds that may hold more promise. This example illustrates that the three-dimensional model analysis can be useful in determining the optimal ligand structure, but also can show the limitations of ligand structure on the enantioselectivity of a system.
Fig. 8.
Surface describing the allylation of methylethyl ketone ΔΔG‡ = -0.200 - 1.036X - 0.177Y + 0.294X2 + 0.126Y2 + 0.129XY + 2.6120X3 + 0.341YX2. R2 = 0.97.
In conclusion, we have developed a unique means to analyze ligand steric effects on enantioselective reactions. A ligand library with two independently tunable substituents was evaluated for the NHK allylation of benzaldehyde, acetophenone, and methylethyl ketone. The resultant ΔΔG‡ derived from the measured enantiomeric ratios were plotted vs. Charton steric parameters for the two groups. Using the principles of experimental design to manipulate and fit the data to a modified third order polynomial provided a surface model that could successfully predict the performance of previously unknown catalysts. Of potential practical importance, a 3 × 3 matrix of ligands was evaluated using this approach to successfully predict the best catalyst for a given reaction even though this catalyst was not used in the analysis. Additionally, evaluation of methylethyl ketone using the three-dimensional modeling approach revealed the use of the current ligand template would most likely not result in an effective asymmetric catalyst (29)‡.
This approach does not rely on precise knowledge of a catalyst’s solution structure which is elusive in many reactions. To employ a three-dimensional free energy relationship analysis requires the ability to readily synthesize catalysts wherein at least two structural variables can be independently and systematically varied. One can envision using any thermodyanamic or kinetic parameter of specific substituents [e.g., Hammett parameters (30), cone angle, or pKa values] to construct three-dimensional free energy relationships to facilitate catalyst design in broad areas of catalysis. Additionally, one is not limited to three dimensions as other reaction parameters (solvent, temperature, and concentration) often used in experimental design could be evaluated simultaneously with ligand substituents and modeled to find both the optimal ligand and conditions. These approaches are currently under investigation in our laboratory in the context of developing new and improved catalytic processes.
Supplementary Material
Acknowledgments.
We would like to thank Professor Joel Harris for critical discussions on data analysis. This work was supported by the National Science Foundation (CHE-0749506).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1013331108/-/DCSupplemental.
*For more details regarding how equations were solved and for step-by-step walkthrough of how models were developed, the reader is referred to the SI Appendix.
†In the following paragraphs, we will describe the methods used for different subsets of data to make meaningful predictions. All of the models described below were derived using the process described above and in the SI Appendix. Statistical analyses were also made on each individual model and we refer the reader to the SI Appendix for a step by step example of how the analyses were performed.
‡It should be noted the cases presented here have utilized the manipulation of Charton steric parameters. In these studies, meaningful data and results have been observed; however, situations have been and may be encountered where these steric parameters do not appear adequate (29). Charton’s correlation to Van Der Waals radii might be insufficient in cases where conformational constraints limit free rotation about bonds. One must take care in choosing steric parameters and substituents to incorporate into the experimental design based on the problem at hand.
References
- 1.Jacobsen EN, Pfaltz A, Yamamoto H. Comprehensive asymmetric catalysis I-III. Berlin: Springer; 1999. [Google Scholar]
- 2.Walsh PJ, Kozlowski MC. Fundamentals of asymmetric catalysis. Sausalito: University Science Books; 2008. [Google Scholar]
- 3.Oslob JD, Akermark B, Helquist P, Norrby P-O. Steric influences on the selectivity of paladium catalyzed allylation. Organometallics. 1997;16:3015–3021. [Google Scholar]
- 4.Lipkowitz KB, D’Hue CA, Sakamoto T, Stack JN. Stereocartography: a computational mapping technique that can locate regions of maximum stereoinduction around chiral catalysts. J Am Chem Soc. 2002;124:14255–14267. doi: 10.1021/ja0207192. [DOI] [PubMed] [Google Scholar]
- 5.Kozlowski MC, Panda M. Computer-aided design of chiral ligands. Part 2. Functionality mapping as a method to identify stereocontrol elements for asymmetric reactions. J Org Chem. 2003;68:2061–2076. doi: 10.1021/jo020401s. [DOI] [PubMed] [Google Scholar]
- 6.Alvarez S, Schefzick S, Lipkowitz K, Avnir D. Quantitative chirality analysis of molecular subunits of bis(oxazoline)copper(II) complexes in relation to their enantioselective catalytic activity. Chemistry—Eur J. 2003;9:5832–5837. doi: 10.1002/chem.200305035. [DOI] [PubMed] [Google Scholar]
- 7.Kozlowski MC, Dixon SL, Panda M, Lauri G. Quantum mechanical models correlating structure with selectivity: predicting the enantioselectivity of β-amino alcohol catalysts in aldehyde alkylation. J Am Chem Soc. 2003;125:6614–6615. doi: 10.1021/ja0293195. [DOI] [PubMed] [Google Scholar]
- 8.Lipkowitz KB, Kozlowski MC. Understanding stereoinduction in catalysis via computer: new tools for asymmetric synthesis. Synlett. 2003;10:1547–1565. [Google Scholar]
- 9.Chen J, Jiwu W, Mingzong L, You T. Calculation on enantiomeric excess of catalytic asymmetric reactions of diethylzinc addition to aldehydes with topological indices and artificial neural network. J Mol Catal A: Chem. 2006;258:191–197. [Google Scholar]
- 10.Urbano-Cuadrado M, Carbo JJ, Maldonado AG, Bo C. New quantum mechanics-based three-dimensional molecular descriptors for use in QSSR approaches: application to asymmetric catalysis. J Chem Inf Model. 2007;47:2228–2234. doi: 10.1021/ci700181v. [DOI] [PubMed] [Google Scholar]
- 11.Mueller JA, Cowell A, Chandler BD, Sigman MS. Origin of enantioselection in chiral alcohol oxidation catalyzed by Pd[(—)-sparteine]Cl2. J Am Chem Soc. 2005;127:14817–14824. doi: 10.1021/ja053195p. [DOI] [PubMed] [Google Scholar]
- 12.Halpern J. Mechanism and stereoselectivity of asymmetric hydrogenation. Science. 1982;217:401–407. doi: 10.1126/science.217.4558.401. [DOI] [PubMed] [Google Scholar]
- 13.Jensen KH, Sigman MS. Systematically probing the effect of catalyst acidity in a hydrogen-bond-catalyzed enantioselective reaction. Angewandte Chemie International Edition. 2007;46:4748–4750. doi: 10.1002/anie.200700298. [DOI] [PubMed] [Google Scholar]
- 14.Charton M. Steric effects. I. Esterification and acid-catalyzed hydrolysis of esters. J Am Chem Soc. 1975;97:1552–1556. [Google Scholar]
- 15.Charton M. Steric effects. II. Base-catalyzed ester hydrolysis. J Am Chem Soc. 1975;97:3691–3693. [Google Scholar]
- 16.Charton M. Steric effects. III. Bimolecular nucleophilic substition. J Am Chem Soc. 1975;97:3694–3697. [Google Scholar]
- 17.Charton M. Steric effects. 7. Additional v Constants. J Org Chem. 1976;41:2217–2220. [Google Scholar]
- 18.Miller JJ, Sigman MS. Quantitatively correlating the effect of ligand-substituent size in asymmetric catalysis using linear free energy relationships. Angewandte Chemie International Edition. 2008;47:771–774. doi: 10.1002/anie.200704257. [DOI] [PubMed] [Google Scholar]
- 19.Sigman MS, Miller JJ. Examination of the role of Taft-type steric parameters in asymmetric catalysis. J Org Chem. 2009;74:7633–7643. doi: 10.1021/jo901698t. [DOI] [PubMed] [Google Scholar]
- 20.Lee J-Y, Miller JJ, Hamilton SS, Sigman MS. Stereochemical diversity in chiral ligand design: discovery and optimization of catalysts for the enantioselective addition of allylic halides to aldehydes. Org Lett. 2005;7:1837–1839. doi: 10.1021/ol050528e. [DOI] [PubMed] [Google Scholar]
- 21.Miller JJ, Sigman MS. Design and synthesis of modular oxazoline ligands for the enantioselective chromium-catalyzed addition of allyl bromide to ketones. J Am Chem Soc. 2007;129:2752–2753. doi: 10.1021/ja068915m. [DOI] [PubMed] [Google Scholar]
- 22.Rajaram S, Sigman MS. Modular synthesis of amine-functionalized oxazolines. Org Lett. 2002;4:3399–3401. doi: 10.1021/ol0264758. [DOI] [PubMed] [Google Scholar]
- 23.Rajaram S, Sigman MS. Design of hydrogen bond catalysts based on a modular oxazoline template: application to an enantioselective hetero diels—Alder reaction. Org Lett. 2005;7:5473–5475. doi: 10.1021/ol052300x. [DOI] [PubMed] [Google Scholar]
- 24.Miller JJ, Rajaram S, Pfaffenroth C, Sigman MS. Synthesis of amine functionalized oxazolines with applications in asymmetric catalysis. Tetrahedron. 2009;65:3110–3119. [Google Scholar]
- 25.Deming SN, Morgan SL. Experimental design: a chemometric approach; data handling in science and technology. Vol. 11. Amsterdam-London-New York-Tokyo: Elsevier; 1993. [Google Scholar]
- 26.Deming SN. In: Chemometrics Mathematics and Statistics in Chemistry. Kowalski BR, editor. Dordrecht: D. Riedel Publishing Company; 1983. pp. 267–304. [Google Scholar]
- 27.Argawal AK, Brisk ML. Sequential experimental design for precise parameter estimation. Ind Eng Chem Process Des Dev. 1985;24:203–210. [Google Scholar]
- 28.Issanchou S, Cognet P, Cabassud M. Sequential experimental design strategy for rapid kinetic modeling of chemical synthesis. AIChE J. 2005;51:1773–1781. [Google Scholar]
- 29.Gustafson JL, Sigman MS, Miller SJ. Linear free-energy relationship analysis of a catalytic desymmetrization reaction of a Diarylmethane-bis(phenol) Org. Lett. 2010;12:2794–2797. doi: 10.1021/ol100927m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Leventis N, Meador MAB, Zhang G, Dass A, Sotiriou-Leventis C. Multiple substitution effects and three-dimensional nonlinear free-energy relationships in the electrochemical reduction of the N,N‘-Dibenzyl viologen and the 4-Benzoyl-N-benzylpyridinium cation. J. Phys. Chem. B. 2004;108:11228–11235. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.