Abstract
In this study, we developed numerical methods for investigating the sources of epileptic activity from intracranial EEG recordings acquired from intracranial subdural electrodes (iEEG) in patients undergoing pre-surgical evaluation at the epilepsy center of the Mayo Clinic (Rochester, MN). The data were analyzed using independent component analysis (ICA), which identifies and isolates maximally independent signal components in multi-channel recordings. A realistic individual head model was constructed for a patient undergoing pre-surgical evaluation. Structural models of gray matter, white matter, CSF, skull, and scalp were extracted from pre-surgical MR and post-surgical CT images. The electromagnetic source localization forward problem was solved using the Boundary Element Method (BEM). Source localization was performed using the Sparse Bayesian Learning (SBL) algorithm. The multiscale patch-basis source space constructed for this purpose includes a large number of dipole elements on the cortical layer oriented perpendicular to the local cortical surface. These source dipoles are combined into overlapping multi-scalepatches. Using this approach, we were able to detect seizure activity on sulcal walls and on gyrus of the cortex.
I. INTRODUCTION
Epilepsy is one of the most common neurological disorders, affecting 50 million people worldwide. In approximately 30% of these patients, seizures cannot be controlled by any available medical therapy. About 4.5% of all patients with epilepsy are thus potential candidates for surgical treatment. Epilepsy surgery has a good chance of success in this patient group, but only if the brain region generating seizures can be accurately localized and then safely removed. For this purpose, in selected cases, recordings are acquired using subdural and/or depth electrode (intracranial) pre-surgical evaluation. The aim of this study was to model and analyze the dynamics of epilepsy using intracranial EEG recordings recorded by Dr. Worrell at the Mayo Clinic. We combined independent component analysis (ICA) with source localization of the identified signal components. For this purpose, a realistic boundary element method (BEM) head model of a patient was created. The inverse problem was solved using a sparse bayesian learning (SBL) algorithm using a multi-scale cortical patch-basis. Selected ICA components of recorded seizure activity were localized. Sulcal and gyral cortical patch sources were identified for these signal components, respectively.
A. Forward Problem
In electromagnetic source imaging, head models are built to represent the geometry and conductivity of the head tissues (e.g., the brain, skull, CSF, and scalp). Then, potentials arising on the sensor locations are determined from each given model source distribution (constituting a solution of the forward problem). Inverse source localization is then performed by finding a source distribution whose forward solution best matches a set of measurements at the electrodes. Successful source imaging from EEG measurements of epileptic activity involves three main challenges: (1) A realistic, subject specific head model must be constructed, (2) epileptiform discharges must be identified and isolated in the EEG background signal, and (3) their sources must be localized taking physiological constraints into account.
The accuracy of the head model used in electrical source imaging affects the accuracy of the source localization significantly. A spherical head model may estimate the location of the seizure onset with up to 2–3 cm error [1]. Also, the influence of post-surgical defects in the skull and the influence on forward field computation of the plastic sheet in which the subdural electrodes are embedded cannot be neglected [2]. When realistic head models are feasible, the forward problem should be solved numerically. Here, we used an accurate Boundary Element Method (BEM) implementation by Akalin Acar and Gencer [3] that allows the use of intersecting tissue boundaries (eyes, holes in the skull etc.) and can handle models with multiple compartments inside the skull [4].
Another factor that affects the epilepsy source localization is the identification and isolation of epilepsy related sources from the EEG background signal. Ebersole and Hawes-Ebersole have shown that much of the epileptic spike activity recorded by subdural electrodes is not visible on the scalp [5]. Several researchers investigated the size of the cortical source area that must be synchronously active for the spikes to be visible on the scalp EEG recordings. While smaller cortical areas create signals that can be measured from the scalp, the amplitude may not be high enough to be recognizable as producing spikes in the scalp EEG activity, which includes the activities of other cortical sources as well as non-brain potentials arising from muscle activity, cardiac activity, eye movements, etc.. In this study, we use Infomax Independent Component Analysis (ICA) as developed by Makeig et al [6] to remove eye and muscle activity artifacts and also to identify and separate functionally independent components. So far only a few studies have applied ICA to EEG data recorded from epilepsy patients. These papers have demonstrated that ICA may aid detection of epileptic seizure activity [7], [8]. For example, in an analysis of 24 EEG seizures from medial temporal lobe epilepsy patients, successful lateralization of spike activity rose from 75% to 96% after applying ICA [9].
B. Inverse Problem
The EEG source localization problem is inherently under-determined. The solution of the inverse problem must take into account physiological constraints and, if possible, prior information about the measurements. Inverse problem algorithms can be considered to fall into two general categories. ‘Equivalent current dipole’ (parametric) methods assume the potentials can be approximated by one or more sources with dipolar far-field projections. ‘Distributed source’ (linear inverse) methods assume that potentials are generated by a large number of small dipolar sources distributed within the brain or on the cortical surface [10]. While the parametric methods search for a fixed number of dipolar sources, the linear inverse methods use a very large number of dipoles placed within the brain volume, and try to determine the activity of these sources. Since there are a very large number of possible solutions, additional constraints must be included in the solver to find a uniquely acceptable solution. Various approaches have been suggested for this purpose. Baillet et al formulated a Bayesian approach using cortical patches corresponding to groups of contiguous source voxels that are simultaneously active [11]. Other source models have been suggested to be more physiologically accurate, such as multi-scale cortical patches with fixed source intensities [12]. Wipf et al present an overview of different methods and a unified bayesian framework for this problem [13].
In this work, ICA is applied to 78-channel intracranial EEG data. The forward problem is solved using a realistic BEM head model, and the inverse problem using the sparse bayesian learning (SBL) algorithm [14]. The dictionary (lead field matrix) for the SBL solver is constructed from overlapping Gaussian patches [15]. Below, methods for generating realistic head models are explained and the results of using the model generated for this study are given. In the third section, the use of ICA for source localization is discussed.
II. Head modeling of an open skull
Some patients who will undergo epilepsy surgery first undergo a pre-surgical procedure in which a part of their skull is removed and areas around the suspected epileptogenic zone are recorded and stimulated to determine whether the seizure generating region is localized and suitable for recision, e.g. not within or too close to eloquent cortex. Before this pre-surgical procedure, magnetic resonance (MR) images are acquired. After the surgery, to locate the intracranial electrodes CT images of the head are acquired. Our earlier study investigated forward and inverse problem solutions on an epilepsy patient undergoing this pre-surgical procedure [16]. For this purpose an accurate numerical head model of the patient had to be generated. The head model generated by co-registering and segmenting pre-surgical MR and post-surgical CT images is shown in Figure 1. In the previous study, this model was used in forward and inverse problem calculations to localize independent sources of simultaneously recorded intracranial iEEG and scalp sEEG. We also presented simulation results and showed that it is crucial to use an accurate head model for correct source localization.
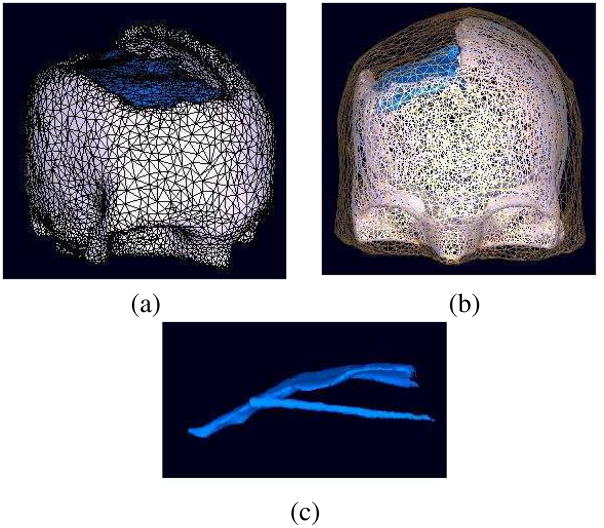
Fig. 1.
BEM model of the scalp, skull and the plastic sheet, represented by 10,000, 30,000, and 7,000 faces, respectively. (a) Skull and electrode sheet faces, (b) scalp, skull and sheet faces, (c) plastic sheet model of the plastic grid and strip electrode matrices.
In this study we used the same head model and focused on solving the inverse problem, using ICA to separate the EEG data into independent components and SBL for source localization with multi-scale cortical patches as the source model.
III. ICA and Source Localization
This section describes Independent Component Analysis of the iEEG recordings. Source localization is performed for selected components using the realistic BEM head model and SBL with a patch-based dictionary.
A. Independent Component Analysis
Infomax Independent Component Analysis (ICA) has proven to be an effective method for removing eye and muscle activity artifacts from scalp EEG data, thus increasing the potential signal-to-noise ratio of sources in subsequent analyses [6]. ICA can also identify and separate functionally independent brain-based components, which for normal scalp EEG prove to be most often associated with scalp maps matching the projection of a single equivalent current dipole [17].
In this work, fifteen minutes of 78-channel subdural iEEG data (Figure 2) from an epilepsy patient including two seizure periods were decomposed by extended infomax ICA ([6]) into 78 maximally independent component (IC) processes. ICA decomposition returned a vector of weights giving the relative strength and polarity of the projection of each IC source process to each of the electrodes, and an ‘activation’ time series giving the time course of activity of each IC process during the data time period. Figure 3 shows maps of the projection patterns of two IC processes to the patient’s cortical surface in (a) and (b), and to the subdural electrode grids in (c) and (d). The patient’s cortical model was derived from the patient MR head image by using Freesurfer (http://surfer.nmr.mgh.harvard.edu/).
Fig. 2.
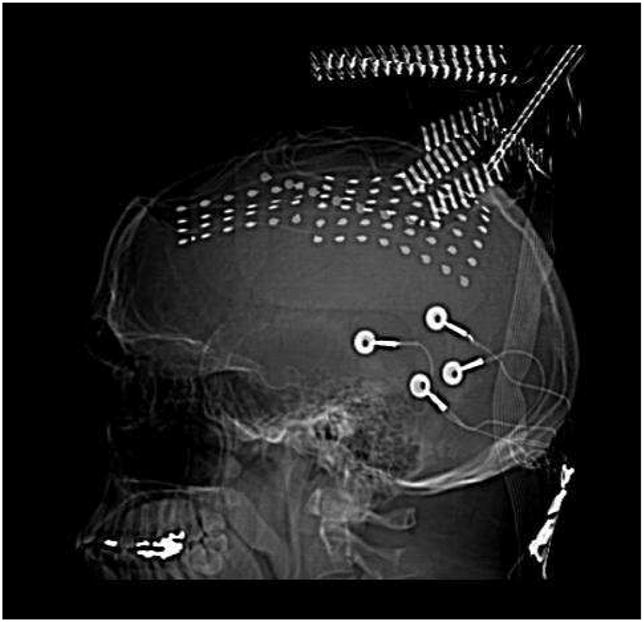
CT image of the implanted grid electrodes. The two grids (6 × 8, 4 ×6) and one medial strip (1 ×8) implanted in the patient for clinical monitoring purposes.
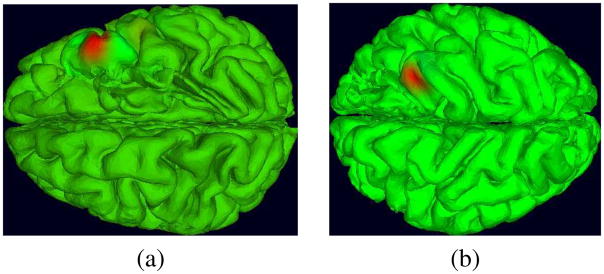
Fig. 3.
Potential maps of two IC processes projected on the brain (a) and (b), and on the intracranial electrodes (c) and (d). Warm-color potentials represent positive values and cool colors, negative values (green represents 0). Multiplying these maps by the (two-sided) IC time courses gives the activity at each channel associated with the IC source.
These two components were chosen because they exhibit spatially orthogonal activity patterns. The IC shown in Figure 3(a) and (c) projects to a small number of adjacent electrodes with the same polarity, thus most likely representing a gyral source. The IC on Figure 3(b) and (d), on the other hand, appears to be a sulcal source projecting to two separate pools of adjacent electrodes with opposite polarities. The results of ICA decomposition applied to these and similar data force a reinterpretation of the nature of iEEG signals. In both clinical and research practice, it is nearly universally assumed that proximal signal sources must dominate signals received by electrodes placed on or in the brain surface, despite the potential influences of volume-conducted potentials from all parts of the brain on each electrode. That is, it is currently most often assumed that each iEEG channel signal may be considered to be a wholly locally generated signal independent of other more distal source activities. ICA decomposition, by removing or minimizing the presence of volume conducted signal summation at the electrodes, demonstrates that each recorded iEEG signal is in fact the sum of a number of more proximal and more distal source processes. For cortical grid electrodes, the percent variance accounted for by the most strongly contributing single (and typically proximal) IC source ranges in our data between about 20% and 80%. In particular, the two IC sources in Figure 3 account for at most 47% (left) and 22% (right) of channel variance at the respective channels to which each projects most strongly.
We generated a realistic cortical source space including a large number of dipole elements oriented perpendicular to the local cortical surface from subject MR head images using tessellated FreeSurfer gray and white matter surfaces. To create a multi-scale cortical patch dictionary on this surface, we selected seed points (single voxel dipoles), then extended each patch conformally to a set of gaussian-tapered patches in three scales with areas in the range 50–200 mm2 [15]. Figure 4 shows same gaussian patches at three different size scales. For our inverse problem analysis, we calculated the forward problem for 80,130 dipoles and generated a lead field matrix for a dictionary of 240,390 patches.
Fig. 4.
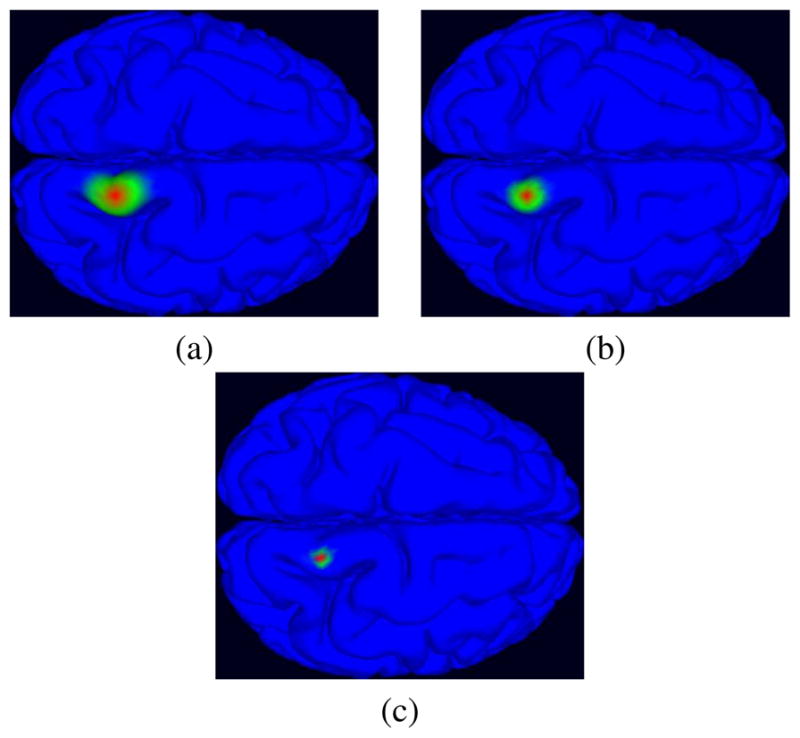
Three Gaussian patches in different scales with radius (a) 10 mm, (b) 6 mm, and (c) 3 mm.
B. Sparse patch-based inverse problem solution
We solved the EEG inverse problem by identifying cortical regions responsible for generating independent EEG components defined by a maximally sparse collection patch basis elements. For this purpose, we applied a sparse Bayesian learning (SBL) based method [14], a Bayesian inverse problem algorithm that finds sparse solutions within the provided lead field matrix (or dictionary). If the columns of the lead field matrix are generated from cortical patches, then these patches will form the overcomplete basis used by the SBL algorithm, and the resulting source image will consist of a weighted mixture of sparse cortical patches.
To generate the patches, we first generated a realistic cortical source space. The source space consists of a large number of dipole elements oriented perpendicular to the local cortical surface acquired from subject MR head images. Here, the tessellated gray and white matter surfaces from Freesurfer were used to compute the locations and orientations of these dipoles.
To create a multi-scale cortical patch basis on this surface, we selected a spatially uniform set of seed points (single voxel dipoles), then extended each patch conformally to a set of gaussian-tapered patches of three size scales with areas in the range 50–200 mm2 [15]. Figure 4 shows same gaussian patch at three different size scales. For our inverse problem analysis, we calculated the forward problem for 80,130 dipoles and generated a lead field matrix for a dictionary of 240,390 patches.
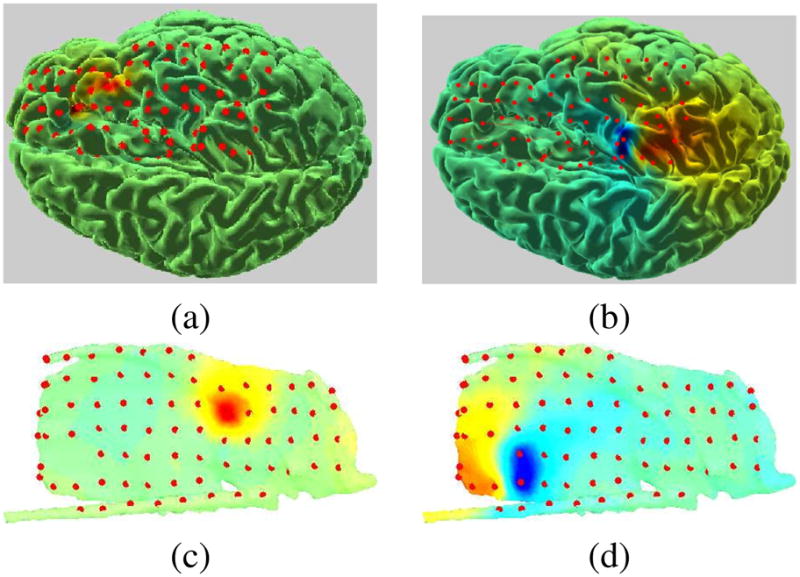
Figure 5 shows the cortical activity of IC maps shown in Figure 3. The SBL algorithm managed to identify sparse mixtures of overlapping patches that accurately describe both these components. It can be seen that the source in Figure 5(a) is a gyral source, whereas (b) is a sulcal source, consistent with the ICA component projections shown in Figure 3.
Fig. 5.
Inverse problem results for the two ICs shown in Figure 3. Red and blue (not seen here) indicate activity with opposite signs, green indicates no activity
IV. CONCLUSIONS AND FUTURE WORK
Here, we analyzed intracranial EEG recordings using ICA and numerical forward and inverse methods, and presented preliminary results of patch-based source localization of seizure data sources in an epilepsy patient.
This may be the first time that volume-conducted distal and near-field proximal portions of data recorded from the human cortex have been separated and used to localize and visualize iEEG sources projecting to the cortical electrode grid. We believe these results constitute good preliminary evidence to support our hypothesis that we can use intracranial EEG recordings to image cortical sources, including those located within sulcal folds.
As a next step, the generation and propagation of seizures will be investigated using this model including non-stationary extensions. We will also investigate state transitions between ictal and interictal EEG data by applying multiple- mixture ICA decomposition [18]. This will provide information about the ability of ICA to isolate seizure components. Simultaneously acquired resting scalp and intracranial EEG data is also available for this patient. Source localization will be performed using scalp and intracranial EEG data and the relationship between noninvasive and invasive recordings of their electrical brain activity will be explored. This research could provide valuable insights into the dynamics of epilepsy and the electrophysiology of the human brain.
Acknowledgments
This work is supported by The Swartz Foundation (Old Field, NY).
Contributor Information
Zeynep Akalin Acar, Email: zeynep@sccn.ucsd.edu, Swartz Center for Computational Neuroscience, Institute for Neural Computation, University of California San Diego, La Jolla, CA, USA.
Gregory Worrell, Email: Worrell.Gregory@mayo.edu, Department of Neurology, Mayo clinic, Rochester, MN, USA.
Scott Makeig, Email: scott@sccn.ucsd.edu, Swartz Center for Computational Neuroscience, Institute for Neural Computation, University of California San Diego, La Jolla, CA, USA.
References
- 1.Assaf BA, Ebersole JS. Continu ous Source Imaging of Scalp Ictal Rhythms in Temporal lobe epilepsy. Epilepsia. 1997;38(10):1114–1123. doi: 10.1111/j.1528-1157.1997.tb01201.x. [DOI] [PubMed] [Google Scholar]
- 2.Zhang Y, Ding L, van Drongelen W, Hecox K, Frim DM, He B. A cortical potential imaging study from simultaneous extra-and intracranial electrical recordings by means of the finite element method. NeuroImage. 2006;31:1513–1524. doi: 10.1016/j.neuroimage.2006.02.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Akalin Acar Z, Gencer NG. An advanced BEM implementation for the forward problem of Electro-magnetic source imaging. Physics in Med and Biol. 2004;49(5):5011–28. doi: 10.1088/0031-9155/49/21/012. [DOI] [PubMed] [Google Scholar]
- 4.Gencer NG, Akalin Acar Z. Use of the isolated problem approach for multi- compartment BEM models of electro-magnetic source imaging. Physics in Med and Biol. 2005;50:3007–22. doi: 10.1088/0031-9155/50/13/003. [DOI] [PubMed] [Google Scholar]
- 5.Ebersole JS, Hawes-Ebersole S. Clinical application of dipole models in the localization of epileptiform activity. J Clinical Neurophysiology. 2007;24(2):120–129. doi: 10.1097/WNP.0b013e31803ece13. [DOI] [PubMed] [Google Scholar]
- 6.Makeig S, Bell AJ, Jung TP, Sejnowski TJ. Independent component analysis of electroencephalographic data. In: Touretzky D, Mozer M, Hasselmo M, editors. Advances in Neural Information Processing Systems. Vol. 8. MIT Press; Cambridge, MA: 1996. pp. 145–151. [Google Scholar]
- 7.Jing M, Sanei S. A novel constrained topographic independent component analysis for seperation of epileptic seizures. Comp Intelligence and Neuroscience. 2007;2007 doi: 10.1155/2007/21315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kobayashi K, James CJ, Nakahori T, Akiyama T, Gotman J. Isolation of epileptiform discharges from unaveraged EEG by independent component analysis. Clinical Neurophysiology. 1999;110:1755–1763. doi: 10.1016/s1388-2457(99)00134-0. [DOI] [PubMed] [Google Scholar]
- 9.Nam H, Yim TG, Han SK, Oh JB, Lee SK. Independent Component Analysis of ictal EEG in medial temporal lobe epilepsy. Epilepsia. 2002;43:160–164. doi: 10.1046/j.1528-1157.2002.23501.x. [DOI] [PubMed] [Google Scholar]
- 10.Michel CM, Murray MM, Lantz GL, Gonzalez S, Spinelli L, de Peralta RG. EEG source imaging. Clinical Neurophysiology. 2004;115:2195–2222. doi: 10.1016/j.clinph.2004.06.001. [DOI] [PubMed] [Google Scholar]
- 11.Baillet S, Garnero G. A Bayesian approach to introducing anatomo-functional priors in the EEG/MEG inverse problem. IEEE Trans on Biomed Eng. 1997;44(7):374–385. doi: 10.1109/10.568913. [DOI] [PubMed] [Google Scholar]
- 12.Im C-H, Lee C, Jung H-K, Lee SY. A New Neuronal Electrical Source Model Considering Electrophysiology to Simulate Realistic Electroencephalography (EEG) Forward Signals. IEEE Trans on Magnetics. 2008;44(6) [Google Scholar]
- 13.Wipf D, Nagarajan S. A unified Bayesian framework for MEG/EEG source imaging. NueroImage. 2009;44:947966. doi: 10.1016/j.neuroimage.2008.02.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wipf D, Ramirez RR, Palmer JA, Makeig S, Rao BD. Analysis of empirical Bayesian methods for neuroelectromagnetic source localization. NIPS. 2007:1505–1512. [Google Scholar]
- 15.Ramirez RR, Makeig S. Neuroelectromagnetic source imaging using multiscale geodesic neural bases and sparse Bayesian learning. 12th Annual Meeting of the Organization for Human Brain Mapping; Florence, Italy. 2006. [Google Scholar]
- 16.Akalin Acar Z, Makeig S, Worrell G. Head modeling and cortical localization in epilepsy. Proc. of IEEE EMBC; 2008; Vancouver, Canada. [DOI] [PubMed] [Google Scholar]
- 17.Makeig S, Westerfield M, Jung TP, Enghoff S, Townsend J, Courchesne E, Sejnowski TJ. Dynamic Brain Sources of Visual Evoked Responses. Science. 2002;25:690–694. doi: 10.1126/science.1066168. [DOI] [PubMed] [Google Scholar]
- 18.Palmer JA, Kreutz-Delgado K, Rao BD, Makeig S. Modeling and Estimation of Dependent Subspaces. Proceedings of the 7th International Conference on Independent Component Analysis and Signal Separation; 2007; 2003. p. 25612573. [Google Scholar]