Material and Energy Productivity

Abstract

Resource productivity, measured as GDP output per resource input, is a widespread sustainability indicator combining economic and environmental information. Resource productivity is ubiquitous, from the IPAT identity to the analysis of dematerialization trends and policy goals. High resource productivity is interpreted as the sign of a resource-efficient, and hence more sustainable, economy. Its inverse, resource intensity (resource per GDP) has the reverse behavior, with higher values indicating environmentally inefficient economies. In this study, we investigate the global systematic relationship between material, energy and carbon productivities, and economic activity. We demonstrate that different types of materials and energy exhibit fundamentally different behaviors, depending on their international income elasticities of consumption. Biomass is completely inelastic, whereas fossil fuels tend to scale proportionally with income. Total materials or energy, as aggregates, have intermediate behavior, depending on the share of fossil fuels and other elastic resources. We show that a small inelastic share is sufficient for the total resource productivity to be significantly correlated with income. Our analysis calls into question the interpretation of resource productivity as a sustainability indicator. We conclude with suggestions for potential alternatives.

Short abstract

Richer countries have better resource productivities, thanks to their high levels of nonsubsistence resource use: Are higher productivities really more sustainable?

Introduction

The simplicity of the GDP output per resource input ratio makes resource productivity an appealing and widespread environmental sustainability indicator. An abundant literature discusses both resource productivity and its inverse, resource intensity, for a variety of resources (see the Supporting Information for a partial list). The goal of this article is to analyze and explain the links between economic activity and resource productivity. The basic assumption underlying the use of resource productivity as an indicator is that, under business-as-usual circumstances, resource use scales proportionally with economic growth, and that deviations from this proportionality are to be commended or discouraged on environmental grounds. In fact, as we show, in current industrialized societies, the scaling rule between economic growth and resource use depends on the type of resource, with significant implications for the interpretation of this popular indicator. We start by reviewing the different interpretations of resource productivity: as a measure of technology, efficiency, or savings and dematerialization.

Technology: The IPAT identity by Commoner, Ehrlich, and Holdren^1,2 describes environmental impact, I, as the product of Population (P), Affluence (A), and Technology (T), defining as Impact/GDP. In many cases (though not for specific pollutants), resource use can be a proxy for environmental impact, so quite often Technology = Resource/GDP. This term is also known as “intensity of use”(3) and “resource intensity.” Technology is a measure of the technological performance of an economy: the more advanced, the lower this ratio. In this interpretation, T is the only lever against the twin growing drivers Population and Affluence, since T can presumably be reduced.^4,5 Following the Factor Four call for a quadrupling in productivity (6), resource productivity became a cornerstone of the EU sustainable resource use policy (7) and of the Japanese 3R material flow policy.(8) In ongoing climate negotiations, China and India are proposing carbon intensity targets rather than emissions targets.

Efficiency: Resource productivity/intensity is often used to measure the overall efficiency of the economic process.(9) The meaning of the efficiency increase goes beyond technology, and encompasses economic structural shifts.(10) This interpretation is further explored through Index Decomposition Analysis^10,11 and Structural Decomposition Analysis(12) which quantify the contributions of both economic and technical drivers to changes in resource use. These methods often use sector-specific productivities, which we expect to be more informative environmental indicators than the national averages.

Savings or Dematerialization: In this viewpoint, any increase in productivity is seen as a sign of a real reduction in resource use. Even if total resource use grows, it is argued that without the improvement in resource productivity, the growth in resource use “would be even larger”. Two quotes help illustrate this point of view. “Weighted by 1990 activity levels, intensities were roughly 15−20% lower in 1994/5 than in 1973, which in turn meant real savings of energy; energy demand in IEA countries is roughly this much below what it would have been for the same GDP had these savings not occurred.”(13) “We define dematerialization, or resource sparing by consumer behavior, as a declining [energy intensity]...”.(5)

Resource productivity, and its change over time, are often used in conjunction with projections of economic and population growth to create scenarios of future resource use or emissions. Differences in development patterns are used to hypothesize future trends.^14,15 Past trends are studied for carbon emissions(16) through the Kaya identity,(17) a variant of IPAT, and for global material use,(18) with applications in scenarios.^19,20

Several authors have expressed skepticism toward resource productivity as a robust or informative indicator. Buttel expressed concerns with the accuracy of measurement,(9) and Auty argued for a detailed causal analysis of changes in material intensity.(21) Ang points out that both the resource and economic measures are rather arbitrarily weighted composites, with contributions from many sectors at varying prices for GDP, and diverse fuel types of varying quality for energy.(10) Sun(15) argues that changes in resource productivity should be assessed differently if they come from changes in renewable or nonrenewable resource use. The dependency of productivity on both resource and economic composition has been noted by many authors,^3,22,23 even some who argue it measures resource efficiency and savings.^10,13

In this work, we conduct an international study of resource productivity for a variety of resources at one point in time: the year 2000. Innovatively, we systematically relate our results to the measured income elasticities of these resources. This relation provides an analytic framework connecting international and time series research on resource productivity. The data are described in Materials and Methods, the mathematical relations are explained in simple terms in the Analysis, and these are followed by the Results and Discussion.

Materials and Methods

Our data set is compiled for the year 2000. For resource use, we choose energy (two alternative data sets in energy units), material flows, and carbon emissions (in mass units). The first energy accounting system is that of the International Energy Agency, at the Total Primary Energy Supply (TPES) level.^24,25 The IEA includes biomass sources only when they are used for heating or cooking purposes, not when used as food or fodder. In fact, TPES has no “biomass” category: the closest equivalent is “Combustible renewables and waste”, which includes both wood fuel and municipal waste incinerators with energy recovery. Thus we also analyze Domestic Energy Consumption (DEC), which encompasses an energy estimate of all biomass inputs to the society: as energy, food, fodder, and materials, as well as fossil, nuclear, and high-tech renewables.^26,27 For materials, Domestic Material Consumption (DMC) comprises four principal categories: fossil fuels, biomass, construction minerals, and ores/industrial minerals.(28) As for DEC, biomass DMC includes food, fodder, energy, and materials uses. Finally, we also include territorial carbon emissions from fossil fuels and the manufacture of cement.(29) The energy and materials data are apparent consumption: extraction + physical imports − physical exports. An indicator often used in material flow analysis is DMI, extraction + imports: a parallel analysis yielded results nearly identical to those for DMC.

GDP is in Market Exchange Rate USD currency.(30) Our results are also presented in terms of Purchasing Power Parity in the Supporting Information. The data on population come from the FAO.(31) Because none of these databases cover the same group of countries, the largest possible reliable data sample for each resource category is used in our analysis, resulting in varying sample sizes and some inconsistencies in the results. We prefer this choice than to limit ourselves to the small number of countries with all types of data. For measuring correlations, we conduct linear least-squares regressions on logged variables.

Analysis

This study is based on three total quantities, measured at the national level: (i) resource use (materials energy, and emissions, such as CO₂), (ii) GDP, and (iii) population. To compare countries of vastly different sizes, the preferred indicators are scale-invariant ratios of these total quantities−intensive rather than extensive variables. (Note that we use the term “consumption” to mean “national resource use per capita”, not final or household consumption.)

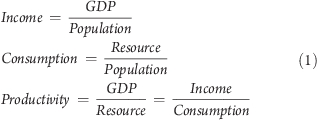It is obvious that income, consumption, and productivity are not independent quantities, but are closely connected to each other. The goal of this work is to understand these connections, and their implications for the interpretation of resource productivity as an indicator.

In order for our analysis to be sensitive to nonlinear relationships, we use the usual log−linear expression to relate consumption/capita and income:

The exponent b is the quantity of interest (as a is just a scaling constant): b is known in economics as the “income elasticity” of resource use.

The income elasticity quantifies the nonlinearity of the relation between income and consumption: b is the percentage change in per capita resource use corresponding to a 1% increase in income:

• •b = 1: consumption is proportional to income; a 1% increase in income will result in a 1% increase in resource use per capita.
• •b > 1: consumption is elastic with income; a 1% increase in income will result in a larger increase in resource use per capita.
• •0 < b < 1: consumption is inelastic with income; a 1% increase in income will result in a smaller increase in resource use per capita.
• •b = 0: consumption is independent of income.
• •if b < 0, consumption decreases with growth in income.

The mathematical relation among productivity, income, and income elasticity can be expressed as follows (combining eqs 1 and 2):

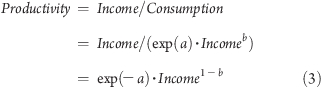It is clear that the link between consumption and income, quantified by the income elasticity, in fact determines the relation between productivity and income (as previously noted in refs (5 and 28)). We can expect international resource productivity to vary between rich and poor countries when b ≠ 1: when the relation is between income and consumption is not proportional. This can be tested by conducting linear least-squares regressions on the following equation, and verifying that d = 1 − b:

In the IPAT framework, the link between income and technology (the inverse of productivity) would lead to a simplifying of the equation:

so that the entire IPAT relation becomes equivalent to eq 2.

These simple mathematical relations among consumption, income, and productivity lead to very different conclusions. Waggoner and Ausubel,(5) who interpret resource productivity as dematerialization, rejoice at the dependence of resource productivity on income and elasticity: “Because declining intensity of use [...] is dematerialization, raising income inescapably dematerializes whenever income elasticity of consumption per person is less than 1. Conversely, lowering income materializes whenever elasticity of consumption per person is less than 1 and so does not lessen impact in proportion to the declining income.” In other words, the value of the productivity indicator is of more importance than the actual level of consumption. In our previous work, where we independently derived the same functional interdependency, we came to the opposite conclusion:(28) “These results call into question the use of material productivity or material intensity as an international indicator of environmental performance, since it would seem to favor high income countries (which also have higher material use) over low income countries, simply because materials have an inelastic relation with income.”

In the rest of this analysis, we explore the implications of the links between income and productivity through elasticity.

Results

First, we measure the income elasticities for energy, materials, and CO₂ emissions (column 1 of Table 1). We consider the subcomponents of the total energy and materials, dividing these into biomass, fossil, and other components. The components have markedly different behavior, with biomass (necessary for the most basic subsistence) and fossil fuels (used by highly industrialized economies) at either extreme. The consumption of fossil fuels, whether measured as energy, material, or CO₂ emissions, is almost proportional to income, with income elasticities above 0.8. (Any difference between the fossil fuels results from the TPES and DEC data sets comes from slight differences in conversion factors and the country sample). In contrast, biomass consumption (energy or materials) has a very poor correlation with income, with elasticities at or below 0.1: consumption is totally inelastic. Along with the low goodness-of-fit, this signifies that variations in biomass consumption cannot be explained by differences in income, but by other factors, such as resource endowment.(26) The “other” energy category resembles fossil fuels, whereas construction materials and ores/industrial minerals emerge as intermediate between biomass and fossil fuels, with income elasticities of 0.49 and 0.7, respectively. In general, the resource components with higher income elasticities have strong correlations between consumption and income (and poor correlations between productivity and income), and the reverse is true for low-elasticity biomass. Interestingly, total material and energy have strong correlations with income for both consumption and productivity.

Table 1. Regression Results for Income−Consumption (eq 2) in Column 1 and Productivity−Income (eq 4) in Column 2^a.

		(1) Income−Consumption		(2) Income−Productivity		number of countries
		R2	income elasticity b	R2	d
Total Primary Energy Supply—TPES
	total	0.736	0.582 (0.031)	0.590	0.418 (0.031)	131
	fossil	0.691	0.810 (0.048)	0.110	0.190 (0.048)	131
	biomassb	0.000	−0.009 (0.114)	0.387	1.010 (0.114)	125
	otherc	0.466	0.910 (0.092)	0.008	0.090 (0.092)	115
Domestic Energy Consumption—DEC
	total	0.663	0.435 (0.024)	0.768	0.565 (0.024)	164
	fossil	0.731	0.918 (0.044)	0.021	0.082 (0.044)	164
	biomass	0.047	0.082 (0.029)	0.860	0.918 (0.029)	167
	otherc	0.491	0.943 (0.082)	0.003	0.057 (0.082)	140
Domestic Material Consumption—DMC
	total	0.636	0.366 (0.022)	0.840	0.634 (0.022)	155
	fossil	0.690	0.924 (0.049)	0.015	0.076 (0.049)	161
	biomass	0.075	0.104 (0.029)	0.857	0.896 (0.029)	165
	const. min.	0.755	0.491 (0.022)	0.767	0.509 (0.022)	159
	ores/ind. min.	0.417	0.696 (0.073)	0.120	0.304 (0.073)	131
GHG emissions
	fossil CO2	0.729	0.891 (0.043)	0.039	0.109 (0.043)	162

^aR² is the goodness-of-fit, ranging from 0 (no correlation) to 1 (perfect correlation), and can be interpreted as the percentage of variation in log(y) explained by log(x). Values of R² above 0.4 are shown in bold. The values in parentheses are the standard errors of the coefficients.

^bThe TPES biomass category is known as “combustible renewables and waste”, and is a mixture of traditional biomass for heating and high-tech energy recovery from waste incineration.

^cThe “other” energy category includes all nonfossil nonbiomass energy sources: principally hydraulic and nuclear electricity.

The results in Table 1 verify the relation between the coefficients b and d: d = 1 − b (eqs 3 and 4). The consumption−income and productivity−income relations are thus not independent. The elasticity b is the slope of the consumption−income fit lines in Figure 1, where the flatness of the biomass line contrasts with the steepness of the fossil fuels line. In contrast, in Figure 2, the coefficient d is the slope of the productivity−income fit lines, and fossil fuels have the flattest lines, while biomass is the steepest (and total resource use is somewhere in between).

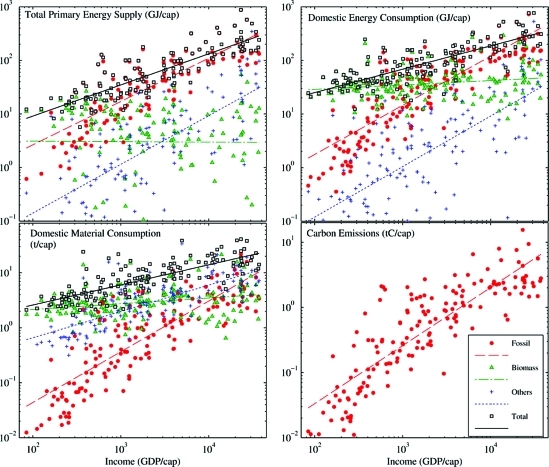
Figure 1.

Consumption vs income for four resource aggregates, divided into fossil fuels, biomass, and other (Other consists of mostly hydraulic and nuclear electricity for energy, whereas for materials it includes ores, industrial, and construction minerals. Energy consumption below 0.1 GJ/cap for this category is not shown.). The income elasticity b is the slope of the fit lines.

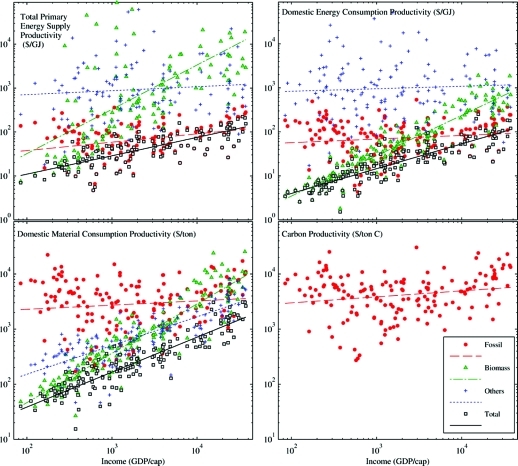
Figure 2.

Productivity vs income for four resource aggregates, divided into fossil fuels, biomass, and other (Other consists of mostly hydraulic and nuclear electricity for energy, whereas for materials it includes ores, industrial, and construction minerals. Energy productivity above 9 × 10⁴ GJ/cap is not shown.). The coefficient d is the slope of the fit lines.

Resource productivity is usually measured for total materials or total energy. It is thus interesting to understand how total resource consumption changes with income. Total TPES, DEC, and DMC behave as composites, with intermediate income elasticities of 0.58, 0.43, and 0.37, respectively (Table 1). These elasticities reflect the decreasing share of fossil fuels in these indicators. Fossil fuels constitute 81% of the TPES of the countries under consideration, but only 57% of DEC, and 20% of DMC (Table S1). Simply put, the larger the share of high-elasticity components (such as fossil fuels), the larger the elasticity of the total resource.

This point is crucial in order to comprehend what resource productivity really measures. If the resource consumption is proportional to income (income elasticity close to 1), the resource productivity will not vary with income. However, if the resource is inelastic, its productivity will increase with income, i.e., the more inelastic the resource, the steeper the increase of productivity with income. Indeed, in Table 1, the categories with lower elasticity have productivities that are highly correlated with income (such as the biomass components and totals). The correlation of energy and material consumption with income is driven by the fossil component, whereas it is the more stable biomass component that causes higher income countries to have better productivities than their poorer counterparts. This phenomenon was previously detected for global changes in material intensity.(18)

There is one interesting exception to this rule: biomass TPES is totally inelastic (income elasticity of 0), and its productivity is only weakly correlated with income; whereas total TPES has a much higher elasticity (0.58), and its productivity is highly correlated with income. The biomass category of TPES is a mixture of traditional biomass use for energy (such as wood fuel and charcoal) and high-tech energy recovery from biomass waste incineration in industrialized countries. The consumption level of biomass TPES thus depends on a combination of resource availability and technical infrastructures, and thus has a different behavior than biomass DEC and DMC, which measure the totality of biomass inputs to society for food, material, or energy purposes.

For greenhouse gas emissions, we are limited by only using fossil CO₂ emissions, which behave exactly like fossil inputs. CH₄ and NO_x, other potent greenhouse gases, are closely tied to agriculture and land use, and have been shown to be quite inelastic.(32) The inelasticity of non-CO₂ GHG emissions is relevant to the discussion of the regressivity of CO₂ or GHG taxes.(33) Total GHG emissions would thus be expected to also behave as an aggregate, with both GHG per capita and GHG productivity highly correlated with income.

Total resource productivity thus tends to systematically increase with income, and increases faster if the indicator used for measuring resource use has a larger share of nonfossil, or inelastic, components, such as biomass. Intuitively, a composite resource indicator will tend to behave like its dominant component. This can be easily demonstrated. Imagine an aggregate measure of resource use, with consumption per capita C_total, composed of two parts C₁ and C₂, with elasticities b1 and b2:

The elasticity of the total resource consumption is

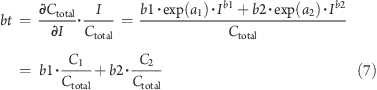It is clear from eq 7 that the total elasticity bt will lie between b1 and b2, and will be closest to the elasticity of the component with the largest share of consumption. Simply put, a fossil-dominated aggregate, such as TPES, will behave most like fossil fuels, and a biomass-dominated aggregate like DMC will behave more like biomass.

An elasticity-based understanding of composite resource consumption (eq 6) shows that it is extremely unlikely that economies will reduce fossil fuels in favor of biomass consumption, as suggested by Sun(15) for “environmentally friendly” improvements in energy intensity, for example by shifting to biofuels. From an elasticity perspective, the use of biomass in high-tech applications will not reduce resource use overall, but instead increase the elasticity of biomass consumption by coupling it ever more tightly to the economy. Because biomass is a renewable but limited resource, the implications for subsistence consumption in low-income countries are quite alarming.

There is more to be learned from the analysis of aggregate resource elasticity in eq 7. The shares of resource consumption are also dependent on income: as income rises, so does the share of elastic resources. At low incomes the lower elasticity component will dominate, at higher incomes the higher elasticity component will dominate. The total elasticity is thus a logistic curve going from the lower elasticity value at low incomes to the higher elasticity value at high incomes:

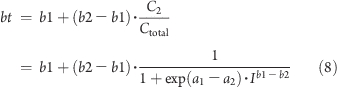Discussion

What are the implications of our findings for the interpretation of productivity/intensity as an indicator of the technological achievement of an economy, with energy and materials as input, and GDP as output? We have learned that international differences in productivity are correlated with income, and that this correlation can be explained by the inelasticity of resource use as an aggregate, itself caused by an inelastic component, usually biomass.

The rationale for using resource productivity as an indicator of environmental sustainability assumes that resource use scales with the economy and that a higher economic output per resource use indicates more sustainable economic activity. The resource productivities of all of the total energy and material indicators considered are strongly correlated with income. If resource productivity were naively interpreted as an indicator of more sustainable economic performance, the conclusion would be that richer countries are more sustainable, despite their higher levels of resource use.

In technological terms, higher productivity economies are benefiting from an apparent effect: they produce GDP in (more or less) exact proportion to their consumption of fossil fuels, but more than proportionally to their consumption of biomass. Biomass consumption varies from country to country, but almost entirely independently of income: poor countries, which consume similar levels of biomass, but far less fossil fuels, than rich countries, thus have a lower aggregate productivity. In economic efficiency terms, economic output can be seen as mainly fossil-driven, with rather steady fossil productivity across countries of different incomes (Table S1). The inclusion of inelastic biomass in the energy/material input to economies makes those who are consuming less fossil fuels seem inefficient in comparison with their richer counterparts.

In terms of the “resource efficiency of an economy” interpretation of resource productivity, it would be desirable to remove the systematic dependence on income. To correct international productivity comparisons for systematic income dependence, several options are possible. The first would be to compare national productivities not to each other, but to their position along the international income trend, i.e., compare the residuals rather than absolute values, as first suggested by Van der Voet et al.(34) Other options would limit either the income range or the resources under consideration: compare countries within narrow income ranges, where the income effect is expected to be small compared to the cross-country variability; or limit resource productivity comparisons to economically bound resources, those with income elasticities above 0.75, for example.

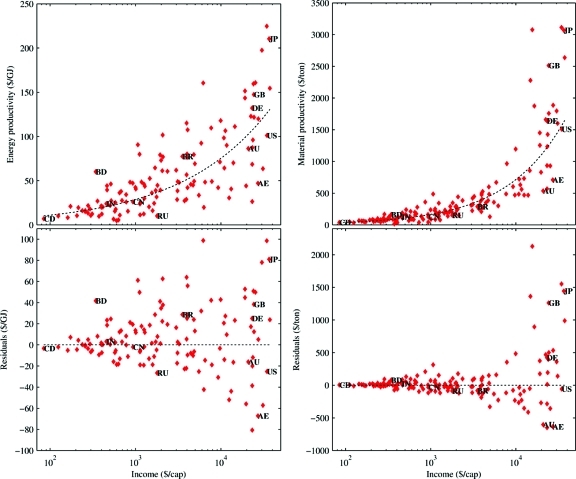
An example of the income-corrected (or elasticity-corrected) residual approach is shown for energy (TPES) and materials (DMC) in Figure 3. Energy productivity of Bangladesh is half that of the United Kingdom; in the income-corrected perspective, they are very similar. The U.S., United Arab Emirates, and Australia have material productivities far above the global average, but when these are corrected for income, they are either exactly average (U.S.) or far below (Australia and United Arab Emirates). In general, extractive and fossil-exporting economies have lower income-corrected productivities, while poorer, smaller, or importing countries have higher income-corrected productivities. Recent studies have performed trade-corrected estimations of national consumption for CO₂ and GHG emissions.^32,35,36 Trade-corrected emissions would reduce the gap between exporting and importing nations, thus leading to even stronger income dependence for productivity.

Figure 3.

Productivity and income-corrected residuals for energy (TPES, left) and materials (DMC, right). From left to right: CD − Dem. Rep. Congo, BD − Bangladesh, IN − India, CN − China, RU − Russia, BR − Brazil, AU − Australia, DE − Germany, GB − United Kingdom, AE − United Arab Emirates, US − United States, JP − Japan.

As an indicator used in analysis of trends and as a basis for scenarios, with the goal of explaining past and future resource use, income elasticity of consumption is a more meaningful and robust quantity than resource productivity. In contrast to resource productivity, income elasticity is likely to evolve slowly over time, mostly in response to price and technology. Efficiency improvements in the delivery of energy services have been shown to model long-term economic growth impressively well.(37) The understanding of past changes in income elasticities,(38) along with considerations of trade shifts and macro-economic rebound effects,(39) should thus be emphasized as a research priority in order to improve resource and climate scenarios. Other research priorities could be the study of this phenomenon over time, as our results hold only for the year 2000 and should change depending on the development trajectories of different countries. Further disaggregation by resource composition is also promising: for instance ores/industrial materials and construction minerals have distinct profiles from each other and fossil fuels.

In terms of resource savings or dematerialization, our conclusion is that resource productivity indicates no such thing, since it is mostly determined by national income and international elasticity. If economic growth and development result in ever growing incomes, dematerialization in fact requires null or negative income elasticity: the economic growth must be accompanied by decreases in resource use. It is likely that such a decrease in resource use is only possible at low economic growth rates: at or below the rates of physical technical improvement.

As a policy target,^7,8 resource productivity mostly rewards business-as-usual developments of simultaneous economic, productivity, and resource consumption growth. If the objective is an absolute reduction in resource use and emissions, productivity targets are insufficient, unless they are coupled with limits to economic growth—politically a difficult proposal. Direct emphasis on resource inputs and emissions is ultimately the only way to ensure effective policy.

Supporting Information Available

Additional discussion, results, acronyms, and literature cited. This material is available free of charge via the Internet at http://pubs.acs.org.