Curvature-Driven Lipid Sorting in Biomembranes

Abstract

It has often been suggested that the high curvature of transport intermediates in cells may be a sufficient means to segregate different lipid populations based on the relative energy costs of forming bent membranes. In this review, we present in vitro experiments that highlight the essential physics of lipid sorting at thermal equilibrium: It is driven by a trade-off between bending energy, mixing entropy, and interactions between species. We collect evidence that lipid sorting depends strongly on lipid–lipid and protein–lipid interactions, and hence on the underlying composition of the membrane and on the presence of bound proteins.

Lipid trafficking depends on lipid–lipid and lipid–protein interactions within membranes. Trade-offs between bending energy, mixing entropy, and interactions between species may drive the sorting of lipids into transport vesicles.

Lipid and protein sorting are key processes that allow eukaryotic cells to maintain membrane homeostasis among organelles during intracellular transport (van Meer et al. 2008). It is known that lipids are not evenly distributed throughout the organelles of the cell. As an example, the percentage of sphingolipids increases along the secretory pathway, going from the endoplasmic reticulum (almost 0%) to the plasma membrane (about 30%) (van Meer and Lisman 2002). In the face of continuous lipid trafficking of vesicular intermediates back and forth along this pathway, the cell must be endowed with ways to preferentially sort these lipids to establish and maintain compositional specificity of each organelle.

There is now compelling evidence that sorting occurs during the formation of highly curved transport intermediates (vesicles and tubules). For instance, it has been observed that tubules emanating from endosomes (Mukherjee and Maxfield 2000; Gruenberg 2003; Maxfield and McGraw 2004), as well as vesicles budding from the Golgi apparatus (Brugger et al. 2000; van Meer and Sprong 2004; Klemm et al. 2009), have a lipid composition significantly different from the compartment from which they originate. Mukherjee et al. found that an unsaturated lipid dye was enriched in live cell endosomal tubes, in contrast with a longer chain saturated lipid dye that was excluded (Mukherjee et al. 1999). Furthermore, quantitative analysis of the lipid composition of the vesicles formed from the trans-Golgi network showed these vesicles to be enriched in sphingolipids (Klemm et al. 2009), whereas COPI-coated vesicles trafficking from the cis-Golgi network to the endoplasmic reticulum were found to be depleted in sphingolipids (Brugger et al. 2000). These observations, that sphingolipids are depleted from retrograde carriers and are enriched in anterograde ones, are perfectly consistent with the maintenance in the cell of an increasing gradient of this type of lipid along the secretory pathway.

How composition differences between cell organelles are maintained despite intense intracellular lipid exchanges is still poorly understood. Clearly, there is a need for protein and lipid sorting. The case of protein is relatively well explained. For instance, coat proteins are known to specifically bind to transmembrane proteins containing certain peptide sequences, which in turn bind to specific soluble cargoes (Cosson and Letourneur 1994; Stamnes et al. 1995; Barlowe 2000; Ehrlich et al. 2004). The specificity of this type of sorting is largely absent for lipids. Lipids, then, must use other physico-chemical means for their sorting:

One way to sort is by the lateral segregation at the nanoscale into domains known as rafts. This very popular hypothesis asserts that proteins that recognize and bind to a given type of raft may form vesicles with the lipid composition of that raft (Simons and Van Meer 1988; Simons and Ikonen 1997; van Meer and Sprong 2004; for a recent review, see Lingwood and Simons 2010). In this mechanism, the lipid composition of the raft is fixed before membrane budding (Fig. 1A).

Figure 1.

Possible physico-chemical mechanisms for lipid sorting. (A) Lipid sorting based on the raft hypothesis. The composition and destination of newly formed vesicles are determined by the type of raft from which the vesicle originates. (B) Different lipid species and their shape. Lipids are characterized by a shape based on the size of the head group, the number of chains, and the degree of chain saturation. From left to right the shapes are inverted-conical for Lyso-Phosphatidic acid (LPA), cylindrical for unsaturated 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), and conical for 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine (DOPE). Bottom: saturated cylindrical Sphingomyelin (SM) and cholesterol. (C) Two physical states relevant for cellular membranes. Top: drawing of a liquid-disordered (L_d) membrane, which is rich in unsaturated lipids (with little chain order); bottom: drawing of a liquid-ordered (L_o) membrane, which is rich in saturated lipids (with high degree of chain ordering) and cholesterol. (D) Lipid sorting based on spontaneous curvature. The membrane consists of cylindrical, inverted-conical. and conical lipids. The outer leaflet of the budding region is enriched in cylindrical and inverted conical lipids, whereas the inner leaflet is enriched in conical ones. (E) Lipid sorting based on composition dependence of the bending stiffness. The highly curved budding region is enriched in unsaturated lipids, so that the bending stiffness of this region is lower than the surrounding membrane.

A second way to sort is by the coupling between lipid composition and the curvature energy of the membrane. Following this mechanism, an inhomogeneously curved membrane could produce an inhomogeneous lipid distribution to minimize the energy cost of bending the membrane (Mukherjee and Maxfield 2000; van Meer and Lisman 2002; Maxfield and McGraw 2004; van Meer and Sprong 2004). Cells can generate inhomogeneous membrane curvature in several ways. For example, COPI or clathrin coats can self-assemble on a membrane surface to form a membrane bud with significantly higher curvature than its surroundings (Antonny 2006). Also, molecular motors walking on microtubules can attach to an intracellular membrane surface and extract a nanoscale-radius tube, which then becomes a transport intermediate (Leduc et al. 2004). The energy cost of bending the membrane into these highly curved shapes depends on the deformability of the bilayer containing different lipids and on the molecular shapes of these lipids. Based on these two membrane properties, lipid sorting between regions of different curvature can reduce the cost of membrane bending. Mathematically, a simple continuum model can be used to describe the coupling between curvature and composition (see Box 1).

The energy needed to bend a patch of membrane of area A is $E=(1/2)\kappa (C-C_0){\hspace{0.17em}}^{2}A$, where κ is the bending stiffness, C is the mean curvature, and C₀ is the spontaneous (relaxed) curvature (see Box 1 for a short introduction to membrane physics). The spontaneous curvature is a local quantity of the membrane, depending on asymmetry between the two leaflets making up the bilayer. Both C₀ and κ depend on the composition of the curved patch. If this patch is more curved than its surroundings, the bending energy can be lowered by adjusting the composition to reduce κ and/or to have C₀ match C. This idea has been explored theoretically, with special emphasis on the interplay between lipid inhomogeneity and the mechanical properties of vesicles (Markin 1981; Seifert 1993; Derganc 2007; Jiang and Powers 2008; Sorre et al. 2009).

The connection between the membrane bending energy and the lipid composition has its origin at the microscopic scale. First, to understand why the notion of spontaneous curvature is related to lipid sorting, consider, for example, a spherical vesicle containing two types of lipids of different shape, one whose head group is wider than its tail, known as inverted-conical (such as lyso-phosphatidic acid (LPA) (Fig. 1B), and another whose head group is roughly as wide as its tail, having a cylindrical shape (such as DOPC) (Fig. 1B). If the outer leaflet is richer in the inverted-cone lipids and the inner leaflet is richer in the cylindrical lipids, then the vesicle will have a positive spontaneous curvature. Conversely, one would expect that the two leaflets of a spherical vesicle would readjust their composition so that C₀ can match the curvature of the vesicle (Leibler 1986; Gruner 1989; Kozlov and Helfrich 1992; Seifert 1993). In this case, a transverse asymmetry (i.e., across the leaflets) occurs in the lipid composition, with the outer leaflet being relatively enriched in inverted-conical lipids (Fig. 1D).

In addition, sorting of lipids within a vesicle containing compartments of varying degrees of curvature can occur because of the composition dependence of the bending stiffness (Szleifer et al. 1988; Rawicz et al. 2000; Marsh 2006; Pan et al. 2008; Reeves et al. 2008; Fig. 1E). As the bending stiffness is an elastic property of a patch of membrane, this effect cannot be understood based on individual lipid geometry. Generally speaking, bending a thicker membrane causes greater differential strains between the head and tail groups of a single leaflet than it does in a thinner leaflet, and therefore a thicker membrane has a higher bending stiffness. Modeling and experiments confirm that the bending stiffness depends in particular on the square of the bilayer thickness (Evans 1974). Ternary mixtures containing cholesterol, saturated and unsaturated lipids are known to display coexistence of a saturated lipid-rich liquid-ordered (L_o) phase and an unsaturated lipid-rich liquid-disordered (L_d) phase (Dietrich et al. 2001; Veatch and Keller 2002; Baumgart et al. 2003; Goni et al. 2008) (Fig. 1C). From AFM measurements (Yuan et al. 2002; Lawrence et al. 2003; Connell and Smith 2006), it has been shown that L_o membranes are thicker than L_d membranes, and therefore stiffer, as has been measured by tube pulling experiments (Cuvelier et al. 2005; Roux et al. 2005) and pipette aspiration (Rawicz et al. 2008). Typical values of κ of ternary vesicles in the L_o phase are 50–60 kT, whereas in the L_d phase, typically 20–30 kT. Here, k is Boltzmann's constant and T is room temperature, such that kT = 4.2 ×10⁻²¹. It was suggested that when a uniformly mixed membrane is subject to inhomogeneous curvature, the bending energy can be reduced by enriching the highly curved regions in the lipids that predominate in the L_d phase of phase separated membranes (Mukherjee and Maxfield 2000; van Meer and Lisman 2002; Maxfield and McGraw 2004; van Meer and Sprong 2004) (Fig. 1E).

Although the simple picture of curvature-induced sorting of lipids based on molecular geometry (steric effects) is visually quite appealing, experiments and theory have shown that this is not an effective driving mechanism against the homogenizing effect of entropy (Safran et al. 1990, 1991; Derganc 2007; Mukhopadhyay et al. 2008; Sorre et al. 2009). This result is quite surprising given the widespread view in the past that curvature was a likely candidate to sort lipids based on their shape (Lodish et al. 2003) (Fig. 1D). A simple order of magnitude calculation highlights the importance of entropy. The gain in bending energy in transferring a sphingolipid from a tube of radius R = 20 nm to a flat reservoir, given a liberal estimate of the difference in bending stiffness between the tube and reservoir of 40 kT, is $\mathrm{\Delta }E=(1/2)(\mathrm{\Delta }\kappa /R^2)a=(1/40)\mathit{kT}$, for an area per lipid equal to a = 0.5 nm². We see that this energy is much smaller than kT, the scale of thermal energy, meaning that entropy will win out over any gain made in making the transfer. The small value of ΔE is because of the small size of the lipid dimension compared with the radius of the tube. The above calculation is valid, however, only if we consider the membrane to be an ideal solution of lipids. Membranes consisting of a mixture of lipids are characterized not only by elastic bending but also by the short-range interactions among the different lipid species (see Box 1). Below the miscibility temperature, these interactions give rise to large-scale domains, as seen, for example, by the coexistence of L_o and L_d phases (Bagatolli and Gratton 2000; Dietrich et al. 2001; Veatch and Keller 2002; Baumgart et al. 2003; de Almeida et al. 2003; McConnell and Vrljic 2003).

Similar to the bulk behavior of a binary solution, the thermodynamic behavior of mixture membranes results from a competition between entropy and enthalpy (interactions). At high temperatures, thermal fluctuations tend to smooth out compositional heterogeneities, whereas at lower temperatures, depending on the overall composition of the membrane, favorable interactions between like species give rise to domain formation and phase coexistence (see Box 1). Conversely, phase separation can be induced at fixed temperature by adjusting the fractions of cholesterol and saturated and unsaturated lipids (Bagatolli and Gratton 2000; Dietrich et al. 2001; Veatch and Keller 2002; Baumgart et al. 2003; de Almeida et al. 2003; McConnell and Vrljic 2003). This is the more biologically relevant case. As domains have been observed in model membranes mimicking the cell membrane, it is therefore also expected that entropy and interactions play important roles in curvature-induced lipid sorting.

Motivated by an increasing amount of experimental evidence that lipid sorting occurs in cells, there has been a renewed interest recently to develop model membrane systems that can be used to quantify the effectiveness of curvature-based sorting and to compare with theoretical predictions. In this review, we focus on recent works that have been possible because of the convergence of biological interest in lipid sorting and technological advances that have allowed its measurement in vitro. We examine below a number of works that have quantitatively measured the importance that cooperative behavior has on curvature-induced lipid redistribution. Some have considered lipid sorting caused by differences in spontaneous curvature between lipids, whereas others have considered sorting caused by the dependence of bending stiffness on sorting. The overriding conclusion of these works was that curvature is generally ineffective in sorting lipids because of prohibitive entropy costs, yet will be significantly amplified if the membrane composition is tuned to maximize the importance of lipid–lipid interactions.

LIPID SORTING REQUIRES LIPID–LIPID INTERACTIONS

The dependence of the bending stiffness on composition causes lipid sorting between membrane regions of different curvature. Furthermore, lipid–lipid interactions favor like lipids to aggregate. Both effects tend to segregate lipid species and thus act cooperatively to produce significant sorting. In fact, a simple calculation based on a two-component model of the membrane (see Box 1) shows that the degree of sorting is 20 times greater if lipid–lipid interactions are such that the system is only 5% away from the critical point than if there are no interactions at all. This highlights the importance of lipid–lipid interactions and proximity to phase separation for lipid sorting.

Roux et al reported the first results on the effect of curvature on lateral lipid organization in vesicle-tubule model systems (Roux et al. 2005). Their work led to two important findings. In the first part of their study, they showed that tubes pulled from L_o-L_d phase-separated vesicles by molecular motors were found to be almost exclusively in the L_d phase. This finding agreed with theory stating that a smaller force is needed to pull a tube with lower bending stiffness. This demonstration showed that collective behavior, here indicated by the existence of domains, was a sufficient condition for curvature-induced lateral organization. In a second part to their work, Roux et al. (2005) also found evidence of curvature-induced lipid sorting in homogenous L_d-phase vesicles. By using two different fluorescent dyes that partition differently in L_o and L_d domains, they observed that the relative fluorescence of the two dyes was not the same in the tube and in the vesicle. This indicated that a curved membrane could have a different composition than the homogeneous membrane from which it originated. In another study, Parthasarathy et al. studied lateral segregation of lipid domains in inhomogeneous membranes using supported bilayers (Parthasarathy et al. 2006). Here, a substrate was etched to have a periodically modulated (“bumpy”) curvature, onto which a membrane was laid. On deposition, the membrane was observed to undergo phase separation in L_o and L_d domains, with the L_o domains preferentially nucleating and localizing in the regions of low curvature. They found, however, that alignment of domains along the weakly curved parallel ridges only occurred below a threshold minimum curvature, indicating the balance between gain in bending energy in aligning versus the entropic tendency to randomize the domains. The results of this paper were in agreement with those of Roux et al. (2005), indicating that a strong spatial gradient of membrane curvature is able to sort L_o and L_d domains.

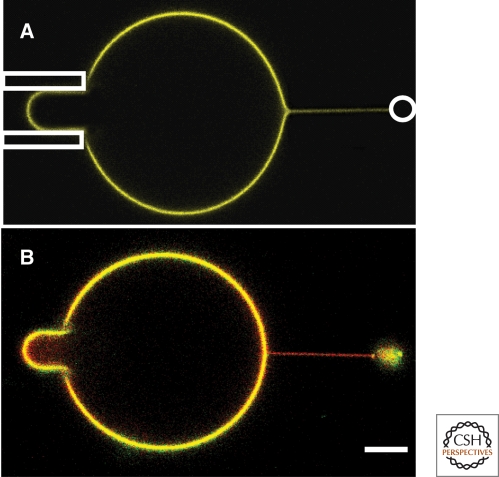
More recently, the works of Sorre et al. (2009) and Tian et al. (2009) quantitatively measured the importance of lipid interactions on sorting using a set-up consisting of a micropipette used to hold a ternary mixture GUV, from which a tube was pulled and held in place either by an attached bead in an optical trap (Sorre et al. 2009) or by a second micropipette (Tian et al. 2009) (Fig. 2). As originally developed by E. Evans (Waugh and Evans 1979), the aspiration pressure, controlled hydrostatically, fixes the tension in the membrane, a key quantity in determining the radius of the tube and the force needed to pull on it; the greater the tension, the narrower the tube. Optical trap or micropipette tube pulling experiments provide numerous advantage over experiments on small vesicles (Fig. 2), or even those on tubes pulled by motor proteins. In these experiments, the curvature of the tube can be controlled continuously by adjusting the membrane tension, and the mechanical properties of the membrane can be quantified using the force needed to pull the tube. Moreover, although tubes are rather narrow, their long length ensures that sufficient fluorescence signal can be detected in sorting experiments. Tubes pulled from large vesicles mimic the in vivo situation in which a narrow tether is often extracted from a relatively flat organelle. Furthermore, although small spherical vesicles can only be used to measure differential composition across the bilayer, as might result because of spontaneous curvature differences of lipids, tubes can be used to probe curvature sorting because of both spontaneous curvature and the compositional dependence of the bending stiffness. In this way, the high curvature contrast with the GUV provides an excellent means to test the hypothesis that curvature gradients can sort lipids.

Figure 2.

Tube pulling and fluorescence images. (A) A nanoscale-radius tube is extracted from a micron-scale GUV that is in turn held by aspiration in a micropipette (left side of image). The tube is held by a Polystyrene bead in an optical trap (indicated by white circle). Here, the membrane composition is far from phase separation. Confocal fluorescence shows that the dye compositions in the tube and GUV are the same. (B) The membrane composition is close to phase separation (BSM:Chol:DOPC 30:35:35 mole%). Quantitative fluorescence measurement shows a 2.9-fold relative enrichment of the red (Texas red DHPE) over green (BodipyFL-C5-GM1) in the tube relative to the GUV. Scale bar, 5 µm.

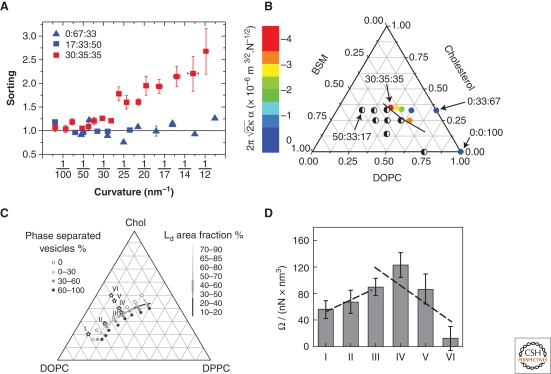
Sorre et al. measured the importance of collective effects on sorting using an integrated tube pulling and confocal imaging setup (Sorre et al. 2009) (Fig. 2A). This setup allowed two ways to detect sorting: by fluorescence microscopy and by pulling force measurement. The GUVs used contained the saturated lipid sphingomyelin (SM), cholesterol, and the unsaturated lipid DOPC, as representative of the plasma membrane. The compositional difference between the tube and vesicle was measured using the partitioning behavior of two types of fluorescent probes. One probe used, Texas Red, is known to preferentially partition into the L_d-phase of a phase-separated vesicle, whereas the other used, a fluorescent GM1 (GM1*), partitions roughly equally between L_d and L_o phases. An enrichment of Texas Red relative to GM1* in the tube over that in the vesicle would then be interpreted as a measure of the relative enrichment of unsaturated over saturated lipids in the tube, consistent with earlier observations that stiffer saturated lipid-rich L_o-phase domains are expelled from tubes in phase separated vesicles (Roux et al. 2005). This is exactly what was observed, but not for arbitrary mixtures of the three lipid types: proximity to phase separation was critical for observing sorting. In fact, the amount of lipid sorting was found to increase dramatically near phase separation: as shown in Figure 3A, the sorting value was equal to one, independent of curvature, for a SM fraction up to 15% (a value of one corresponds to identical compositions in the tube and in the vesicle), whereas it increased strongly with curvature when the SM fraction was equal to 30%, beyond which phase separation occurs. A simple theoretical model, treating the membrane as a binary mixture (the fraction of cholesterol was held roughly constant in the experiments), found that the amount of sorting should increase quadratically with tube curvature, in agreement with experiment (Sorre et al. 2009). It is important to note that sorting measured here could only be because of a dependence of bending stiffness on composition, and not to spontaneous curvature. This follows because the measured fluorescence was the signal integrated over the bilayer, and could not distinguish the difference in signal between the two leaflets.

Figure 3.

Lipid sorting increases near phase separation. (A) Lipid sorting versus tube curvature, as measured by the partitioning of fluorescent lipid dyes. No sorting is observed for two compositions far from phase separation (the ratio BSM:Chol:DOPC equal to 0:67:33 and 17:33:50). Sorting increases with curvature for a composition near phase separation (30:35:35). Panel adapted from and replotted with express permission from Sorre et al. (2009). (B) The mechanical sorting parameter $2\pi \sqrt{2\kappa }\alpha$ increases when the membrane composition approaches the demixing region of the phase diagram of the BSM:Chol:DOPC mixture. Panel adapted from Sorre et al. (2009) and reprinted with express permission from the author. (C,D) The curvature dependence of κ_eff, indicated by the parameter Ω, also increases for compositions close to phase separation. The lipid mixture used was DPPC:Chol:DOPC. Compositions indicated by numerals I through VI on the phase diagram in C correspond to the histogram bins in D. Panels C and D adapted from Tian et al. (2009) and reprinted with permission from Elsevier © 2009.

The measurement of the pulling force on the tube provided a second way to assess the coupling between lipid sorting and the energy cost of membrane bending. The force on a tube that has the same composition as the mother vesicle is given by the classical expression $f=2\pi \sqrt{2\kappa \sigma }$ (Hochmuth and Evans 1982; Waugh et al. 1992; Evans and Yeung 1994; Derényi et al. 2002; Powers et al. 2002), where σ is the membrane tension. Thus, a plot of f as a function of $\sqrt{\sigma }$ should be linear with a slope proportional to $\sqrt{\kappa }$; this relationship has been confirmed experimentally, and used as a means to measure bending stiffness. Things are not quite as simple if the compositions on the tube and on the vesicle are different. In fact, for those membrane compositions for which sorting was detected by fluorescence, a clear departure of the dependence of force on tension from the classical law was observed. Intuitively, one expects that at very low tension, for which sorting is small, the force would be given by the usual law; this is what was indeed measured, allowing a measure of κ, the bending stiffness of the vesicle. As the tension increases, however, the tube becomes richer in lipids forming a more flexible membrane, and hence a reduction relative to $2\pi \sqrt{2\kappa \sigma }$ of the force should be observed. This was found experimentally and confirmed by a model (Sorre et al. 2009); theoretically, the effect of sorting on the force was found to follow $2\pi \sqrt{2\kappa \sigma }(1-\alpha \sigma )$, and experimentally the sorting parameter α was found to increase monotonically as the region of demixing was approached on the ternary phase diagram (Fig. 3B).

Tian et al. (2009) used various mixtures of unsaturated DOPC, Chol, and saturated DPPC in their tube-pulling experiments, before which they had mapped out the phase diagram to study the effect of proximity of a given GUV composition to phase separation on lipid sorting. For a single component vesicle, or one in which the lipid composition is everywhere homogeneous, the radius of the tube is given by $R=\sqrt{(\kappa /2\sigma )}$. Instead of measuring the force, Tian et al. measured the tube radius, independently of the tension, by measuring the change in vesicle projection in the pipette when the length of the tube is varied. They found that R follows the well-known square root law with tension for all compositions, and consequently the bending stiffness is independent of curvature, except when the composition is very close to phase separation. Near phase separation they found that the effective bending stiffness, as defined as κ_eff = 2σR², decreased because of sorting, following the law κ_eff = κ₀−Ω/R², where κ₀ is the bending stiffness of the vesicle and Ω is a parameter than increases as phase separation is approached (Fig. 3C,D). Although the techniques and measurements were quite different, the results of Tian et al. (2009) are equivalent to those obtained by Sorre et al. (2009).

A second class of experiment aimed to measure curvature-induced transverse asymmetry based on the spontaneous curvature of different lipid species. Kamal et al. recently measured the transverse distribution of cylindrical, conical, and inverted-conical fluorescent marker lipids in spherical egg-PC vesicles of radii ranging from 10–100 nm (Kamal et al. 2009). Based on steric effects, they expected to see that the outer leaflet of small vesicles would be enriched in inverted-conical lipids, whereas the inner leaflet would be enriched in conical lipids (Fig. 1D). They did observe some asymmetry in the transverse distribution of their lipid markers, from which they were able to measure the spontaneous curvature of the marker, but found that the asymmetry in the distribution on the two leaflets only reached a maximum of about 20% for very small vesicles, of 20 nm in radius. Furthermore, they observed that the asymmetry in the distribution was negligible for vesicle radii greater than 50 nm. Importantly, they considered a dilute amount of labeled lipids to study. As in any dilute system, the effects of lipid–lipid interactions are very weak relative to the entropy of mixing, and hence will not be able to boost the curvature-induced lipid composition asymmetry. Their work was consistent with the negligible asymmetry in lipid marker composition that Tian and Baumgart measured on highly curved tubes pulled from vesicles far away from phase separation (Tian and Baumgart 2009). The key conclusion from these works was that lipid shape alone is not enough to drive measurable lipid sorting; lipid-lipid interactions or lipid-protein interactions are necessary to amplify the curvature-based sorting. This is consistent with calculations on surfactant systems, showing that sufficiently strong lipid interactions are required to maintain the leaflet asymmetry needed to stabilize unilamellar vesicles over flat membranes (Safran et al. 1990). Molecular dynamics simulations have furthermore confirmed very weak leaflet asymmetry in two-component spherical vesicles (Cooke and Deserno 2006); they concluded that transverse sorting in vesicles on the scale of 50 nm is negligible unless some other physico-chemical agent is involved, such as lipid–lipid interactions.

PROTEIN BINDING ENHANCES LIPID SORTING

Membrane-bound proteins interact differently with the various lipid species in the membrane and thus can strongly influence lipid distributions. First, when a protein binds to multiple lipid receptors, it clusters these lipids; the resulting cluster generally has a preferred curvature and thus can be sorted into or out of highly curved membrane regions. Second, proteins can interact indirectly with different lipid species based on weaker, nonspecific interactions between protein receptors and other lipids. This can also lead to changes in lipid distribution, depending on the membrane curvature.

As mentioned earlier, curvature-induced lipid sorting is generally quite weak because of the small size of the lipids. The area of a protein is typically an order of magnitude or more greater than that of a lipid. As a result, even at low concentrations, because of their shape membrane-bound and transmembrane proteins are quite easily sorted by curvature. This effect was first studied theoretically by Leibler (1986) and subsequently by Netz and Pincus (1995), Kralj-Iglic et al. (1996), and Ramaswamy et al. (2000). Analogous to lipids sorted based on spontaneous curvature, a protein has a preferred curvature and when bound or inserted, it will locally deform the membrane (see, for instance, Tsafrir et al. 2001; Campelo et al. 2008; Auth and Gompper 2009); this energy will be minimized if the membrane curvature matches that of the protein. As a result, because of this curvature-concentration coupling, the bending energy of a tube pulled from a vesicle is reduced by either excluding or enriching the tube in proteins, depending on their intrinsic shape. This leads to a reduction of the bending stiffness of the membrane. In fact, this has been measured for conical-shaped transmembrane proteins such as calcium ATP-ase (Girard et al. 2005), whereas no reduction of the bending stiffness was measured for the cylindrical shaped protein pump bacteriorhodopsin (Manneville et al. 1999). Confocal microscopy of membrane nanotubes has also revealed the sorting of the curvature-sensitive GTP-ase ArfGap1 (Ambroggio et al. 2010). In addition, cholera (Sorre et al. 2009; Tian and Baumgart 2009) and Shiga toxins (Safouane et al. 2010) bound to DOPC membranes with small amounts of the toxin lipid receptor have been observed to be strongly excluded from tubes. Both types of toxin prefer negative curvature, whereas tubes have positive curvature, and hence on energetic grounds should be excluded from tubes when bound to the outer leaflet. Although sorting of cholera toxin was observed (Sorre et al. 2009; Tian and Baumgart 2009), because of the low concentration no concomitant effect was detected on the bending stiffness (Sorre et al. 2009). Thus, on the one hand, the specific binding of curvature-sensitive proteins to certain lipids can be seen as a means to selectively sort these lipids. On the other, proteins can indirectly aid in sorting of lipids that are not bound to the protein, if the membrane composition is near phase separation, as discussed below.

The clustering of some lipids, such as the binding of cholera toxin to GM1 (Ribi et al. 1988) or of Shiga toxin to Gb3 (Ling et al. 1998), may have an entropic effect on the sorting of other lipids in the membrane, such as that of sphingolipids discussed earlier. Generally, clustering a certain type of lipid by a protein or even actin filaments can induce phase separation in a homogeneous membrane even if this component is present in a very small quantity (Hammond et al. 2005; Liu and Fletcher 2006; Römer et al. 2010) and (Safouane et al. 2010). The effects of protein on the phase behavior of lipid membrane are an interesting phenomenon and can be understood as follows. Consider a homogeneous ternary mixture of SM, DOPC, and cholesterol in the L_d-phase, with a very small percentage of GM1. Because of lipid–lipid interactions, SM prefers to aggregate with itself or with cholesterol, and repels DOPC. For compositions outside the coexistence region, entropy prevents this segregation. GM1 interacts favorably with sphingomyelin. For a fixed ratio of SM, cholesterol, and DOPC, adding a small amount of GM1 can slightly tip the balance of entropy versus phase separation-causing interactions in favor of interactions. Furthermore, if GM1 is clustered together, the cost of entropy in segregating lipid species is lower. Thus, clustered GM1 can bring the membrane closer to phase separation. This has the effect of making the membrane more susceptible to curvature-induced lipid sorting.

These effects were actually observed by Sorre et al. (2009), wherein a small percentage of GM1 lipids were clustered together by the pentameric B-subunit of cholera toxin bound to the outer leaflet of the membrane. In this case, for membrane compositions near phase separation, the mechanical quantity α, measuring the effect of sphingolipid sorting on the force, was found to increase substantially in magnitude on cholera toxin binding, consistent with the protein bringing the membrane composition even closer to phase separation. It should be noted that the curvature dependence of cholera toxin might also affect the lipid sorting and the pulling force. Yet, the results of Sorre et al. showed that the dominant effect of cholera toxin binding was to enhance the susceptibility for sorting, consistent with studies showing that a small amount of cholera toxin bound to homogeneous vesicles can trigger phase separation (see above).

This indirect effect of proteins on lipid organization may be relevant to plasma membranes, where it has been observed that the formation of macroscopic domains on plasma membrane spheres is triggered by specific protein binding (Lingwood et al. 2008). Additionally, in vitro experiments on reconstituted COPI-coated vesicles indicated that the membrane compositions underneath coated regions were enriched in unsaturated lipids compared with the bare regions (Manneville et al. 2008) in agreement with (Brugger et al. 2000). Very generally, one might expect that in vivo clustering of lipids or of proteins can shift the membrane composition close to phase separation, thus aiding in lipid sorting and raft formation.

Up to now, we have discussed sorting mechanisms that may explain the decrease of sphingolipid concentration in transport intermediates along the retrograde pathway. It fails, however, to account for the observed enrichment of these lipids between the TGN and the plasma membrane. We discuss briefly how protein may play a key role in concentrating sphingolipids into highly curved transport intermediates. In Safouane et al. (2010), tubular invaginations were induced on GUVs by the binding of the B-subunit of Shiga toxin to its lipid receptor Gb3. Using different fluorophores, it was found that the concentration of sphingolipids in the tubes increased as the membrane composition approached that of phase separation. This finding was rather striking, given that earlier, sphingolipids were found to be depleted in tubes (see above). This observation was explained by noting that sphingolipids have favorable interactions with Gb3 relative to those between DOPC and Gb3. These interactions were found to be strong enough so that sphingolipids were essentially “dragged” along with the curvature-sorted Gb3-Shiga complexes, outweighing the increase in bending stiffness of the tube caused by the sphingolipid enrichment, in line with (Klemm et al. 2009).

CONCLUDING REMARKS

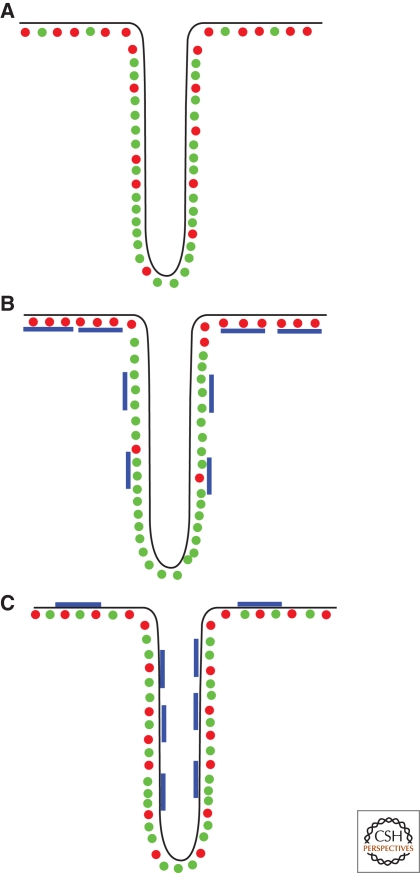
In cell membranes, it is very unlikely that individual lipids, unassisted by interactions with themselves or with proteins, can be enriched in curved regions simply based on their shape alone. Rather, larger-scale effects, resulting from lipid–lipid interactions or from lipid–protein interactions, appear to be essential in making the membrane susceptible to curvature-driven sorting (see Fig. 4 for a cartoon summarizing the different sorting cases). An interesting corollary is that the direction of lipid sorting, into or out of highly curved vesicles, may be dependent on the type of protein that interacts with it either directly or indirectly. This is very different from protein cargoes that are known to be selected and transported by specific ligand-receptor interactions with membrane-bound proteins. In the case of lipids, protein-aided transport is mediated by weaker nonspecific interactions of longer range. It seems crucial, although, that the membrane composition be close to phase separation in order for protein-induced redistribution to be effective. Many open questions remain, however. For instance, how the cell membrane keeps it composition close to phase separation despite the continuous exchanges of matter between the various compartments is a mystery. Therefore, it will be necessary, yet difficult, to measure the compositions and magnitudes of lipid fluxes that occur during the formation and fusion of vesicles from and with membranous organelles (Patterson et al. 2008). We conclude by noting that energy minimization is not the only factor in determining lipid distribution. In a cell, in which lipid sorting and vesicle formation are dynamic processes, there will always be competition between different physical effects occurring at different time scales, such as lipid diffusion, budding, fusion, and fission.

Figure 4.

Summary diagram of lipid sorting with: (A) No protein. Unsaturated lipids (in green) are enriched in the tube to minimize bending energy if close to demixing. (B) Protein having a preference for negative curvature (blue) interacting with saturated lipids (red) on the outside. The protein is depleted from the tube and assists in further excluding saturated lipids. (C) When the protein is on the other side, saturated lipids are enriched in the tube.

BOX 1. ENERGY OF A TWO-COMPONENT MEMBRANE.

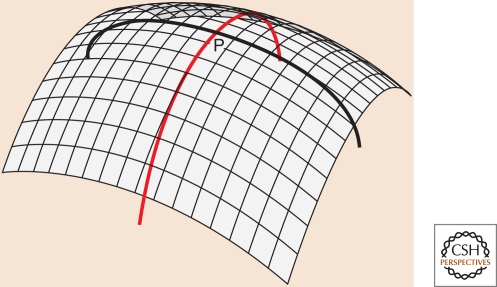
The Helfrich model describes the energy cost of bending a membrane in terms of its curvature (Canham 1970; Helfrich 1973). The Helfrich energy is expressed in terms of two local quantities, the principal curvatures C₁ and C₂, as shown in the figure (Fig. B1). They may be positive or negative, and the sign convention is arbitrary. For a closed vesicle or organelle, the principal curvatures are chosen to be positive if the corresponding curves bend toward the inside, and negative if they bend toward the outside.

Figure B1.

The principal curvatures at point P are the inverses of the radii of the two circular arcs drawn above. Arbitrarily close to point P the two arcs lie on the surface, but deviate from it moving away from P. Of all possible circular arcs passing through P, the arcs of principal curvature are the ones with maximal and minimal curvature.

The bending energy is expressed in terms of the total curvature C = C₁ + C₂. For example, the total curvature of a tube is just C = 1/R, where R is the tube radius, and of a sphere C = 2/R, where R is the sphere radius. The energy per unit area of a bilayer membrane is

$$f_b=\frac{1}{2}\kappa (C-C_0){\hspace{0.17em}}^2(1)$$ 1

where κ is the bilayer bending stiffness and C₀ is the spontaneous curvature.

The composition dependence of κ can give rise to different lipid distributions in the differently curved regions of a vesicle or organelle. Lipid segregation is opposed, however, by loss of mixing energy.

Consider a closed vesicle consisting of two lipid types, 1 and 2, containing a highly curved tube of small area, connected to a large, nearly flat spherical reservoir. The mixing energy penalty per unit area is

$$\mathrm{\Delta }{f}_m=\frac{1}{2}\lambda \mathrm{\Delta }{\varphi }^2(2)$$ 2

where λ is known as the de-mixing susceptibility; Δϕ = ϕ_t − ϕ_ν and ϕ_t and ϕ_ν are the fractions of lipid 1 in the tube and reservoir, respectively (the fractions of lipid 2 are given by 1−ϕ_t and 1−ϕ_ν). The susceptibility is given by

$$\lambda =\frac{\mathit{kT}}{a}(\frac{1}{{\varphi }_v(1-{\varphi }_v)}-2\chi )(3)$$ 3

where a is the area per lipid and χ measures the strength of short-range lipid–lipid interactions. The first term in parentheses in Eq. (3) represents the entropic “stiffness” for de-mixing; it is largest when ϕ_ν is close to zero or one, because then it is highly improbable that very few lipids of type 1 or of type 2 will spontaneously corral together in a small region. Note, however, that this corralling is considerably easier if one of the lipid species is found in the form of clusters. A positive value of χ means that type 1 lipids prefer to be among each other, as do type 2 lipids, which has the effect of reducing λ. In fact, as χ increases, λ vanishes for ϕ_v = 0.5 and χ = 2; this is the critical de-mixing point. For larger values of χ, a uniformly mixed vesicle with ϕ = 0.5 can lower its mixing energy by spontaneously phase separating into lipid-1-rich and lipid-2-rich domains of sizes much greater than that of an individual lipid.