Inconsistency with Prior Knowledge Triggers Children’s Causal Explanatory Reasoning

Abstract

What events trigger causal explanatory reasoning in young children? Children’s explanations could be triggered by either consistent events (suggesting that explanations serve a confirmatory function) or inconsistent events (suggesting that they promote discovery of new information). In two studies with preschool children (N = 80), events that were consistent with children’s prior knowledge were simultaneously contrasted with events that were inconsistent with prior knowledge, and children were invited to explain either outcome (or both). Results demonstrate that inconsistent outcomes are an especially powerful trigger for children’s explanations, and that the explanations children provide for inconsistent outcomes refer to internal causal properties, overriding perceptual appearances. In sum, the data provide empirical evidence that inconsistent events motivate children to construct explanations, thereby suggesting that children’s explanations function in the service of discovery.

“Observation is always selection. It needs a chosen object, a definite task, an interest, a point of view, a problem.”

-Popper, 1963

A fundamental task for all humans is explaining why things happen. By 3 years of age, children can use causal knowledge to make predictions (Shultz, 1982), engage in effective interventions (Kushnir & Gopnik, 2005; Schulz & Gopnik, 2004), and provide explanations for things that happen (Wellman, Hickling, & Schult, 1997). Not only do young children frequently seek explanations by asking questions, they also construct their own explanations (Callanan & Oakes, 1992; Hickling & Wellman, 2001).

At the same time, young children are surprisingly poor at assessing their own explanatory understanding. This ability develops dramatically across development, but adults and especially children overestimate the detail and depth of their explanatory knowledge (Mills & Keil, 2004; Wilson & Keil, 1998). Thus, on the one hand, children are active explanation-seekers and readily request and provide causal explanations. Yet on the other hand, they seem to be poor at assessing their own causal knowledge and often think they understand things when they do not. What then motivates children to ask questions and generate explanations? More specifically, what kinds of events provoke causal explanatory reasoning in children? Children could make use of causal-explanatory understanding when reasoning about either consistent events (when events unfold as anticipated based on prior knowledge) or inconsistent events (when something unusual or contrary to prior knowledge happens).

Accordingly, children’s explanations may serve at least two distinct functions. First, explanation might be systematically confirmatory. Research on the development of scientific reasoning provides evidence for a confirmation bias in both children and adults (Nickerson, 1998) whereby reasoners tend to seek information that supports a favored hypothesis and to interpret events in ways that are partial to that hypothesis. Both children and adults also tend to avoid, ignore, or distort information that is inconsistent with their beliefs (Kuhn, 1989). Confirmatory information can be favored and privileged even when people have no vested interest in a hypothesis (Bruner, Goodnow, & Austin, 1956; Nickerson, 1998).

There is much evidence for a confirmation bias in older children and adults. But young children may be especially prone to such a bias, because they are early in the process of developing explanatory knowledge, and so can benefit from consolidating, confirming, and deepening their current explanations. Thus, not only do young children anticipate that future outcomes will proceed in accord with prior expectations (Gopnik, Sobel, Schulz, & Glymour, 2001; Schulz & Gopnik, 2004; Kushnir & Gopnik, 2007), they may also find such outcomes easy to explain and worthy of explanation.

Alternatively, however, young children’s explanation might be especially triggered by inconsistent information, that is information inconsistent with expectations. If so, providing explanations might be as much a childhood process of discovery as a process of confirmation. Children may systematically attend to and attempt to explain information that is inconsistent with expectations. Notably, the motivation to construct causal explanation may be driven by the puzzle of inconsistent outcomes, and not merely by unpredicted, low probability, or novel outcomes. Forming explanations for inconsistent outcomes may provide children with the opportunity to generate new hypotheses, and to accommodate inconsistent information in the context of prior beliefs.

Several arguments and findings make this alternative possibility plausible as well. The idea that inconsistent, problematic, or surprising outcomes play an important role in causal reasoning for adults and school-age children appears across multiple literatures—including philosophy of science (Hempel, 1965), social psychology (Hilton, 1995; Weiner, 1985), and educational research (Chi, Bassok, Lewis, Reimann, Glaser, 1989; Wong & Weiner, 1981). Moreover, it is well documented that infants often attend to inconsistent or unexpected outcomes (Baillargeon, 2002).

Against these theoretical possibilities, there is a dearth of empirical research on what actually motivates young children to construct explanations. Thus it is unclear which model better predicts children’s causal explanations. We take an empirical approach by assessing what motivates young children to provide the explanations that they do.

The present studies focus on children’s explanations for confirmatory versus disconfirmatory events. We provided children with the following basic scenario. Children viewed two equivalent events simultaneously: one in accord with prior knowledge and the other not. If for young children explanation is largely confirmatory then they should simply explain what they already have an explanation for. If explanation is instead especially employed for discordant or anomalous information, children should explain the event that falls outside their prior expectations. We measured not only what children explain but also how they do so, by examining whether they appealed to surface features or instead to less-obvious causal properties and category membership. We assume that explanations reflect the nature of children’s conceptual understanding (Keil, 2006; Legare, Wellman, & Gelman, 2009; Lombrozo, 2006; Medin, Coley, & Storms, 2003; Sloman, 1994). For example, consider category membership. Even children as young as 3 years of age can categorize objects in terms of novel, non-obvious properties (Gelman & Coley, 1990; Gelman & Markman, 1986, 1987; Graham, Kilbreath, & Welder, 2004; Jaswal & Markman, 2007), apply names to objects with the same functional properties (Kemler-Nelson, 1995), and categorize and name objects based on novel causal properties (Gopnik & Sobel, 2000), overriding perceptual appearances. Whether and how preschool children might make use of such information in their causal explanations (as opposed to their predictions or judgments) is, however, an open question.

STUDY 1

To address these issues, we designed a set of novel “light boxes” – devices that glowed brightly when activated. The activation of the boxes was experimenter-controlled, but appeared to be caused by placing an object on top (modeled after Gopnik & Sobel, 2000; Gopnik et al., 2001). These materials were used first to teach children briefly about different categories of objects that turned a box on, turned it off, or did nothing. In Study 1, these training objects were labeled according to their causal properties: “starters” (which lit the light box when placed on top), “stoppers” (which turned off a lit box), and “do-nothings” (which neither lit nor unlit the light box). Items within each object category (e.g., “do-nothings”) were perceptually identical. After training, children were presented with scenarios in which a new object that looked like one type (e.g., it looked like a “starter”) actually behaved like another type (e.g., it behaved like a “do-nothing”). This was simultaneously paired within test trials where a contrasting object looked and behaved like those previously seen (e.g., it looked like a “do-nothing” and behaved like a “do-nothing”). Upon viewing such paired outcomes, children were asked a non-specific explanatory question ambiguously referring to either (visible) outcome: “Why did that happen?”

Comparing outcomes consistent or inconsistent with prior knowledge was our primary interest, but state-changes and negative outcomes may also function as explanatory triggers. Therefore two focal conditions were designed that controlled for these factors by holding them constant. In the generative condition, both light boxes began off, both turned on in one of the test trials, and both remained off in the other test trial. So, in the test trial in which both boxes turned on, both outcomes involved state-change and neither outcome involved a negative outcome (defined here as failing to turn the boxes on). In the parallel test trial in which both boxes stayed off, neither outcome involved a state-change, and both outcomes involved a negative outcome (failing to turn the boxes on). In the contrasting inhibitory condition, both light boxes began on and this pattern of outcomes was reversed.

Prior to these test trials but after initial training, children participated in a confirmation trial. The confirmation trial served to remind children of how various objects functioned, but also had the advantage of isolating change-of-state outcomes from outcomes inconsistent with prior knowledge. For example, in the confirmation trials, because both outcomes work as expected based on prior experience, “starters” and “stoppers” changed the state of the box, and “do-nothings” did not change the state of the box.

Our interest was in which events yielded not just greater attention, but most importantly, increased explanation. If state-change plays a role, on the confirmation trials children should differentially explain outcomes when a box turned off (after being on) or turned on (after being off). If negative outcomes provoke explanation, on the confirmation trials children should differentially explain outcomes when a box failed to turn on, or when a box turned off. Most importantly, if the role of explanations for children is confirmatory, children should be interested in and provide explanations for the consistent event in each test trial pair, whereas if the role of explanations is discovery, children should be specifically interested in and provide hypotheses and explanations for the inconsistent event in each test trial pair.

Method

Participants

Sixteen 3-year-olds (M age 3,6; range 3,2 to 3,11), 16 4-year-olds (M = 4,6; range 4,0 –4,11), and 16 5-year-olds (M = 5,3; range 5,0 – 5,6) were recruited from a Midwestern U.S. university town. Participants were primarily White and from middle-class families. Approximately equal numbers of boys and girls participated in the study.

Materials

Four “light boxes” (5 in × 5 in × 5 in) were made of wood with thin translucent laminate tops. The boxes were identical except one pair was red and the other pair was yellow. Each pair of boxes (red or yellow) was attached to a switch box operated surreptitiously by a confederate. If the switch was turned on, the box would light up and stay on until it was switched off. Alternately, if the switch was turned off, the box would turn off and stay off until it was switched on. For objects with a causal effect, each box was turned off or on as soon as an object made contact with it, and would stay off or on until the object was removed. This yielded the strong impression that some objects turned the boxes on, some turned them off, and some had no effect on the boxes. The switchbox was hidden from the children’s view, and none of the participants mentioned the confederate or indicated any suspicion that the confederate influenced the functioning of the boxes.

There were four perceptually distinct sets of objects, shown in Figure 1, each consisting of five identical wooden blocks (20 blocks total). Objects were always presented in paired sets. The perceptual features of different kinds of objects were not indicative of the observed causal properties of the objects (lighting or not lighting the boxes). Additionally, the placement of the objects on the boxes was counterbalanced across trials.

Figure 1.

Studies 1 and 2: Pictures of object stimuli

Design

Trials were designed both to isolate state-change and negative outcomes as potential explanatory triggers (confirmation trial) and to control for these factors by holding them constant (test trials). To help assess these factors there were two different conditions. In the generative condition, the boxes (either yellow or red, counterbalanced across children) started with the light off, and in the training trial, the two distinctive sorts of objects were labeled as either “starters” or “do-nothings”. In the inhibitory condition this pattern was reversed; the boxes started with the light on, and, in the training trial, the objects were labeled as either “stoppers” or “do-nothings”. One test trial displayed both light boxes turned on and the other test trial displayed both light boxes turned off. Therefore in each test trial, inconsistency with prior knowledge was isolated; one outcome was inconsistent with prior knowledge, and one outcome was consistent with prior knowledge, but both changed (or didn’t change) state, and both boxes were on (positive) or off (negative).

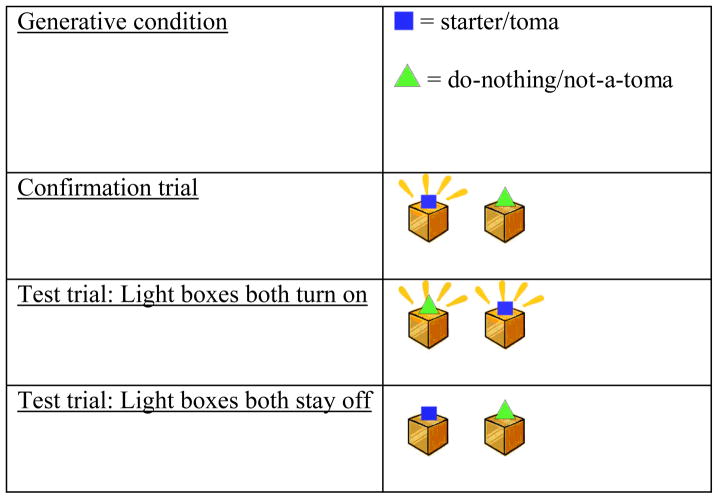
Generative condition

Table 1 provides an outline of the factors and design for the entire study. In each condition, after training, there was one confirmation trial followed by two test trials. For the generative condition, in the confirmation trial, both outcomes were consistent; there was no inconsistent outcome. As listed in Table 1, the object that looked like a starter turned the box on and therefore produced a state-change and a positive outcome (light box was on). The object that looked like a do-nothing did not change the state of the box and produced a negative outcome (light box was off) (Figure 2). So if the child was motivated to explain a state-change, he/she would have explained the outcome involving the object that looked like a starter first, and if the child was motivated to explain the negative outcome he/she would have explained the object that looked like a do-nothing first.

Table 1.

Studies 1 and 2: Study design:

Condition	Generative (Off→X)						Inhibitory (On→X)
Trial	Confirmation Trial		Test Trial		Test Trial		Confirmation Trial		Test Trial		Test Trial
Initial State of Light Box	Off	Off	Off	Off	Off	Off	On	On	On	On	On	On
Type of Object	Starter	Do- nothing	Starter	Do- nothing	Starter	Do- nothing	Stopper	Do- nothing	Stopper	Do- nothing	Stopper	Do- nothing
Final State of Light Box	On	Off	Off	Off	On	On	Off	On	Off	Off	On	On
Inconsistent Outcome=1	0	0	1	0	0	1	0	0	0	1	1	0
State- change=1	1	0	0	0	1	1	1	0	1	1	0	0
Negative Outcome =1 (off)	0	1	1	1	0	0	1	0	1	1	0	0
Isolates	State-change/Negative Outcome		Inconsistent Outcome		Inconsistent Outcome		State-change/Negative Outcome		Inconsistent Outcome		Inconsistent Outcome

Figure 2.

Studies 1 and 2: Generative Condition

In the generative test trial in which both boxes turned on, both outcomes involved state-change and neither involved a negative outcome (defined here as failing to turn the boxes on). However, the object that looked like a starter produced an outcome consistent with prior knowledge and the object that looked like a do-nothing produced an outcome inconsistent with prior knowledge (see Table 1). Therefore, if the child was motivated to explain inconsistency with prior knowledge, he/she should explain the object that looked like a do-nothing first. In the parallel generative test trial in which both boxes stayed off, neither outcome involved a state-change, and both outcomes involved a negative outcome (both failed to turn the boxes on). In this trial, instead of the object that looked like a do-nothing producing an inconsistent outcome, it was the object that looked like a starter that produced an inconsistent outcome.

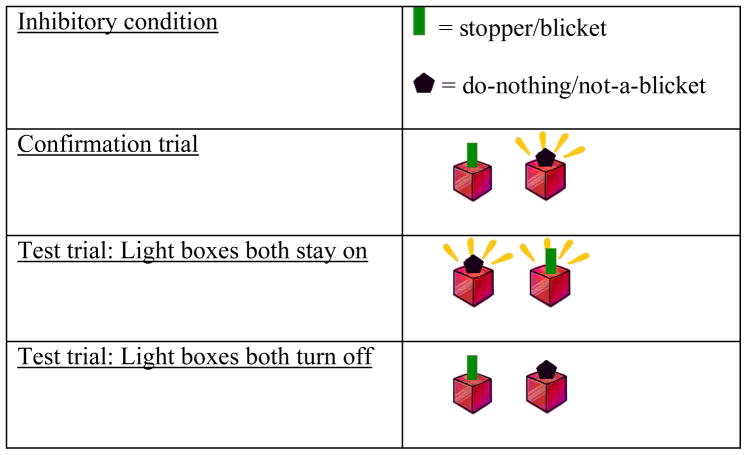
Inhibitory condition

In the inhibitory confirmation trial, again both outcomes were consistent; there was no inconsistent outcome. As seen in Table 1, the object that looked like a stopper turned the box off and therefore produced a state-change and a negative outcome (the light box was off). This correspondence of a state-change and negative outcome was unlike the generative condition, in which state-change and negative outcome competed in the confirmation trial. The object that looked like a do-nothing did not change the state of the box and produced a positive outcome (the light box was on) (Figure 3). So if the child was motivated to explain a state-change or a negative outcome, he/she would have explained the outcome involving the object that looked like a stopper first. If neither state-change nor negative outcomes were explanatory triggers, the child would have explained the object that looked like a do-nothing first.

Figure 3.

Studies 1 and 2: Inhibitory Condition

In the inhibitory test trial in which both boxes turned on, neither outcome involved state-change or a negative outcome. However, the object that looked like a do-nothing produced an outcome consistent with prior knowledge, and the object that looked like a stopper produced an outcome inconsistent with prior knowledge (see Table 1). Therefore if the child was motivated to explain inconsistency with prior knowledge, he/she should explain the object that looked like a stopper first (the opposite pattern of the generative condition in the test trial, in which both boxes lit up). In the parallel inhibitory test trial in which both boxes turned off, both outcomes involved a state-change, and both outcomes involved a negative outcome (both turned the boxes off). In this trial, instead of the object that looked like a stopper producing an inconsistent outcome, it was the object that looked like a do-nothing that produced an inconsistent outcome.

Procedure

Children were tested individually in a 15-minute session seated across from the experimenter and confederate at a table on which a pair of the wooden boxes was placed. Each child participated in both conditions: generative and inhibitory. After the objects’ functions and labels were presented individually in the training trials, both objects were presented simultaneously on three trials: one confirmation trial followed by two test trials. Although the objects in the confirmation and test trials were perceptually identical to the objects in the training trial, they were never labeled for the child. For example, in the generative condition, after demonstrating how a starter and a do-nothing work for one set of objects in the training trial, the experimenter placed another object perceptually identical to a starter and another object perceptually identical to a do-nothing simultaneously on two unlit boxes. In this confirmation trial, both objects worked in a manner consistent with prior knowledge (upon contact with one box, the object that looked like a starter turned the light on, and the object that looked like a do-nothing had no effect). Children were asked to explain this initial paired event, to provide a baseline comparison for their subsequent test-trial explanations. Specifically, with both objects on their boxes, one box on and one off, children were asked, “Why did that happen?”

For each test trial, two objects were again simultaneously placed on the boxes. One object worked in a manner consistent with prior knowledge and the other object worked in a manner that was inconsistent. Unlike the confirmation trial, in the test trials, the outcomes in both cases were causally identical (both boxes lit up in one test trial and neither box lit up in the other test trial). After viewing the paired outcomes of each trial, children were again asked, “Why did that happen?” Children were prompted several times in a non-directed manner after that initial causal question to provide additional explanatory information (e.g., “Can you tell me more?” or “Do you have any other ideas?”). For each trial, the child was encouraged to provide as many explanations as possible, and the trial was terminated after the child indicated that he or she had no other information to share.

Each child had one generative block of trials with one pair of light boxes (one confirmation trial and two test trials) and one inhibitory block of trials with the other pair of light boxes (one confirmation trial and two test trials). Which condition came first (generative or inhibitory) was counterbalanced.

Transcription and Coding

Interviews were videotaped and transcribed verbatim yielding the following measures for each trial: what the child looked at first, what he or she explained first, his or her overall explanatory response, and the kind of explanations he or she provided. During the confirmation trial, the outcome the child looked at first was coded (starter/stopper =1, do-nothing=0), followed by the outcome the child mentioned first (starter/stopper=1, do-nothing=0, both=0.5, if a child referred to both outcomes in their first explanation).

For each test trial per condition, as in the confirmation trial, the outcome the child looked at first was coded (inconsistent=1, consistent=0). The outcome the child explained first was coded (inconsistent =1, consistent=0, both=0.5), followed by a similar coding (inconsistent, consistent) for any additional explanations the child provided. Children’s explanations for inconsistent and consistent outcomes were coded separately. For example, if the child provided an explanation for the inconsistent outcome, “’Cause this starter is broken, the parts inside don’t work,” and then provided an explanation for the consistent outcome, “’Cause this do-nothing is working, it doesn’t make anything happen to the box,” the child was coded as explaining the inconsistent outcome first, and then their overall explanations were coded individually as providing at least one explanation for the inconsistent outcome and providing at least one explanation for the consistent outcome.

Explanatory Categories

Children’s explanations were also coded for content, separately for consistent and inconsistent outcomes. Causal explanations for inconsistent outcomes were coded into 3 primary categories: category switch, causal function, and causal action. In category switch explanations, children referred to a switch in category membership based on function (e.g., “It is a do-nothing now” or “It’s really a starter; it only looks like a do-nothing”); see Table 2 for more examples. Notably, such explanations go beyond the past history of perceptually identical objects.

Table 2.

Sample causal explanations for inconsistent outcomes

Category Switch (Study 1): “It looks like there was one do-nothing, and it seems like it wasn’t going to start but it did start. It’s really a starter.” ““It looks like that one was a do-nothing, but it wasn’t a do-nothing it was a stopper. It makes the box stop.” “Because that is a starter, too. Because some are starters, too. Some of these are starters too.”

Causal Function (Study 1): “The stopper isn’t working anymore; it’s broken inside.” “Because this went out of power. Because it doesn’t have stoppers in it.” “Because it’s broken. I think because it doesn’t have batteries in it.”

Causal Action (Study 1): “You set the starter on the wrong side.” “The stopper should be on the other box, that’s why it isn’t working right.” “They are on the wrong boxes.”

Causal Category (Study 2): “It’s a toma, it just looks like it isn’t one.” “It turned on because it is a blick.” “Because that one can make it turn off. It is the same kind of thing as the toma.”

Causal Function (Study 2): “The toma isn’t working anymore; it’s broken inside.” “Maybe because this one has more air and energy.” “The toma didn’t stop. It didn’t stop because it doesn’t have any magnets in it.”

Causal Action (Study 2): “You set the blicket on the wrong side.” “The toma should be on the other box; maybe try putting it on there.” “Because that one (blicket) is supposed to be on the other side and the one that isn’t a blicket is supposed to be on the other box.”

Explanations that discussed a problem with the functioning of the object were coded as causal function explanations. These explanations included reference to the object being broken (“The stopper is not working anymore. It is broken”), the box being broken (“The box does not light anymore. It is broken”), or differences among the objects (“This one is heavier than the others”). Explanations that referred to insides were also included (“There aren’t stoppers inside” or “All out of batteries”). Explanations that referred to problems using the objects or problems with the placement of the objects were coded as causal action explanations (“You set the stopper/do nothing on the wrong sides” or “It’s on the wrong box”); see Table 2.

Non-causal explanations were coded into 4 other categories: expectation violation, descriptive statements, psychological references, and don’t know. Explanations that described what could be expected to happen on the basis of appearance or past events without providing a cause were coded as expectation violation (e.g., “it wasn’t supposed to turn on”). Explanations that referred to the criteria children used as a basis for their conclusion without further explanation were coded as descriptive statements (e.g., “It’s not on because it’s not glowing up”). Explanations that referred to psychological constructs such as preference or desire (e.g., “maybe it wanted to”) were also recorded, although these were quite rare. If children were unable to provide an explanation, their responses were coded as don’t know.

Causal explanations for consistent outcomes were coded into three primary parallel categories: category label, causal function, and causal action. Explanations that referred to category membership using a label were coded as category label explanations (e.g., “Because this one is a stopper” or “this one is a do-nothing”). Unlike the category switch explanations for inconsistent outcomes, category label explanations involved providing a label that was consistent with the past history of perceptually identical objects. Causal function, causal action, and non-causal explanations for consistent outcomes were coded using the same criteria as explanations for inconsistent outcomes.

Inter-rater reliability was established using a randomly selected sample of 25% of the data. Two persons independently coded the reliability sample with 95% agreement. Reliability was also calculated for explanatory coding categories for both consistent and inconsistent outcomes, with Kappas ranging from .86 to .94 (near-perfect levels; Landis & Koch, 1977).

Results

We examined separately the events that resulted in greater attention and the events that resulted in increased explanation.

Which outcomes do children look at and explain first?

Confirmation trials

In the confirmation trials, children were asked to explain a paired event in which both objects functioned in a manner consistent with prior knowledge. Out of two possible trials, children were more likely both to look first at the object (starter or stopper) that changed the state of the box (63% of the time), t(47) = 2.84, p < .01, and to first explain the object that changed the state of the box (71% of the time), t(47) = 4.57, p < .001, as compared to the object that had no effect on the box (do-nothing). Beyond initial attention, children were significantly more likely to first explain the object that changed the state of the box in both the generative (M = 69%) and the inhibitory (M = 74%) conditions, with both of these greater than chance, ps < .001. Thus, in the absence of an inconsistent event or outcome, state-change systematically trigged children’s explanations. Negative outcomes, however, did not; even in the generative condition, where the confirmation trial pitted a state-change event against a negative outcome event, children were significantly more likely to first explain the state-change outcome than the negative outcome.

Test trials

In the test trials, events inconsistent with children’s prior knowledge first attracted children’s attention and provoked their explanations. Thus, across age groups and test trials (out of 4 possible trials), children were much more likely to look first at the inconsistent outcomes than the consistent outcomes (M = 3.73, or 93% of the test trials), t(47) = 18.61, p < .001. More importantly, children were much more likely to explain the inconsistent outcome first (M=3.18 out of 4, or 80%), t(47) = 11.72, p < .001.

In order to investigate potential age and condition-related effects, we conducted two separate repeated-measures ANOVAs involving age group (3-, 4-, 5-year-olds) X condition (inhibitory versus generative) X final-outcome (both boxes on versus both boxes off). Condition and final-outcome were within-subjects factors, and age group was a between-subjects factor. One ANOVA involved first-look responses; the other involved first-explanation responses. In all age groups and conditions, children were very likely to look first at (3-year-olds on 90% of their test trials, 4-year-olds 95%, 5-year-olds 95%) and explain first (3-year-olds 85%, 4-year-olds 78%, 5-year-olds 78%) the inconsistent outcome. There was no main effect of age (for either the first look or first explanation analysis). Similarly, there were no significant main effects of condition (inhibitory versus generative) or final-outcome (both on versus both off).

However, for the first-explanation analysis, the condition X final-outcome interaction was significant, F(1,45) = 4.62, p < .05. Posthoc tests indicated that for the inhibitory condition, children were more likely to explain the inconsistent outcome when both boxes remained on (no state change) (84% of the time) than when both boxes turned off (state change) (M = 70%), p < .05. Importantly however, in both cases children were significantly more likely to look first at the inconsistent outcome than chance alone would predict, ps < .001.

As noted earlier, children participated in a confirmation trial prior to the test trials. One possibility is that participating in a confirmation trial may have influenced the pragmatics of the explanation task. For example, because children provided an explanation for an outcome in the confirmation trial, they may have been motivated to explain a different outcome in the trial that came next (i.e., the first test trial). Thus, if children provided an explanation for a state-change outcome in the confirmation trial (object that looks like a starter turned the box from off to on), and if their first test trial included a perceptually identical outcome (object that looks like a starter turned the box from off to on) compared to a different outcome (object that looks like a do-nothing turned the box from off to on), they may have been motivated to explain the latter because they had just explained the former on the prior (confirmation) trial. To investigate whether this sequencing influenced the results, we compared what the children explained first in their first test trial (following the confirmation trial) to what they explained first in their second test trial. There were no significant differences for test trial order, t(47) = .97, ns.

We also analyzed children’s spontaneous explanations (provided prior to an explicit explanatory question) in order to address pragmatic concerns with the procedure. Namely, this analysis allows us to rule out the possibility that children were simply generating the explanation they believed the experimenter was requesting. For first explanations, spontaneous explanations revealed the same pattern of responses as elicited explanations. Sixteen of 48 children (33%) provided a spontaneous explanation at least once in the test trials. For 81% of the spontaneous explanations, children explained the inconsistent outcome first, F(1,47) = 132.89, p < .001. Children’s spontaneous explanation of inconsistent outcomes provides clear evidence that they were not merely explaining what they thought the experimenter was interested in.

Which outcomes do children provide an explanation for overall?

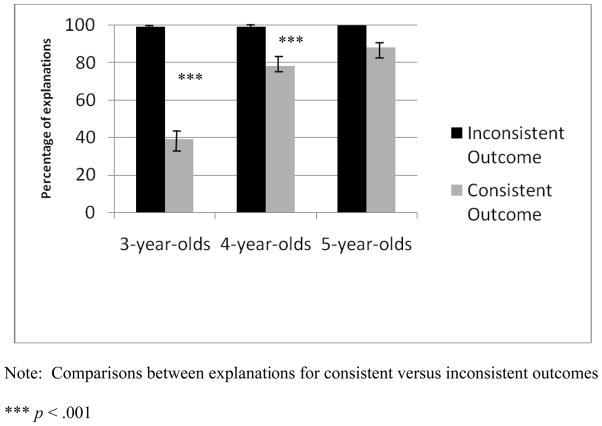
Children often provided multiple explanations for any test trial: 19%, 25%, and 50% of trials at ages 3, 4, and 5 years, respectively. For this analysis, the total number of explanations provided was the dependent variable. We conducted a 3 age group (3-, 4-, 5-year-olds) X 2 condition (inhibitory versus generative) X 2 final-outcome (both boxes on versus both boxes off) X 2 consistent-vs.- inconsistent outcome repeated measures ANOVA on the entirety of children’s explanations. Condition, final-outcome, and consistent-vs.-inconsistent outcome were within-subjects factors. As can be seen in Figure 4 there were significant main effects for age group, F(2,45) = 14.18, p < .001, condition, F(1,45) = 12.71, p < .001, and, most importantly, consistent-vs.-inconsistent outcome, F(1,45) = 63.12, p < .001. Posthoc tests indicated that 5-and 4-year-olds gave explanations more consistently than 3-year-olds (Ms = 94%, 89%, and 69% of total responses, respectively), which is not surprising, given developmental changes in children’s language skills over this age period. Most importantly, however, the significant main effect for consistent-vs.-inconsistent outcome demonstrates that inconsistent outcomes were more likely to be explained than consistent outcomes (Ms=3.98 and 2.73 out of 4, or 99% and 68%, respectively). Not shown in Figure 4 is that overall explanations were more prevalent in the inhibitory (M = 88%) than the generative condition (M = 80%), as shown by the effect of condition. We can offer no firm account for this effect, but perhaps children found the initial-state of the light boxes being on (inhibitory condition) more novel or unexpected than the initial-state of the light boxes being off (generative condition).

Figure 4.

Study 1: Percentage of explanations children provided for inconsistent versus consistent outcomes by age group

The ANOVA also yielded a significant consistent-vs.-inconsistent outcome X age group interaction, F(2,45) = 13.90, p < .001, indicating developmental differences in the outcome children were most likely to explain overall. Posthoc tests reveal that although 3- and 4-year-olds were more likely to explain inconsistent than consistent outcomes, ps < .001, 5-year-olds were equally likely to explain both. The lack of effect for 5-year-olds reflects a ceiling effect (see Figure 4). There were as well a significant condition X consistent-vs.-inconsistent outcome interaction, F(1,45) = 12.62, p < .001, a condition X final-outcome interaction, F(1,45) = 6.88, p < .05, and a three-way interaction with condition X final-outcome X consistent-vs.-inconsistent outcome, F(1,45) = 8.25, p < .001. Nonetheless, for all four test trials (in each condition and each final-outcome) children were more likely to provide an explanation for an inconsistent than a consistent outcome.

The kinds of causal explanations children provided

Recall that children’s explanations were coded into three primary causal categories: category switch (or category label in the case of consistent events), causal function, and causal action explanations. The majority of children’s explanations at all age groups were causal (rather than the non-causal categories of expectation violation, descriptive statements, psychological references, and don’t know). This was true for both inconsistent outcomes (55%, 81%, and 95% of the explanations provided at ages 3, 4, and 5, respectively) and consistent outcomes (76%, 74%, and 88% of the explanations provided at ages 3, 4, and 5). Explanations that made use of psychological explanations were very rare; only one 3-year-old and two 4-year-olds used psychological language in their explanations (“This one thinks it’s a starter”).

An age group (3-, 4-, 5-year-olds) X condition (inhibitory, generative) X consistent-vs.-inconsistent outcome X causal explanation type (causal function, causal action, category label/category switch) repeated measures ANOVA was conducted in order to investigate age and condition-related changes in the kinds of causal explanations children provided. Condition, consistent-vs.-inconsistent outcome, and causal explanation type were within-subject factors. The number of total explanations provided (of each type) was the dependent variable. This analysis yielded the same main effects for age group F(2,45) = 10.83, p < .001 and consistent-vs.-inconsistent outcome F(1,45) = 24.19, p < .001 described earlier, therefore only results involving the different types of causal explanations given will be discussed here. Here there was a significant main effect for causal explanation type, F(2,90) = 11.64, p < .001. Causal function and category switch explanations (or category label explanations for consistent outcomes) were most common (and not significantly different from one another), and each was more frequent than causal action explanations, ps < .01.

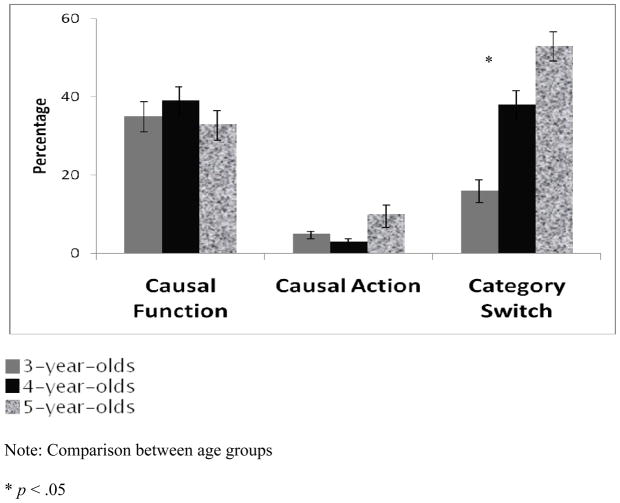
Additionally, the age group X consistent-vs.-inconsistent outcome X causal explanation type interaction was significant, F(4,84) = 2.74, p < .05. In post-hoc simple effects analyses of children’s explanations for inconsistent outcomes only, as shown in Figure 5, causal function (M = 1.44 out of 4 trials or 36%) and causal action (M = 0.23 out of 4 trials or 6%) explanations remained constant across age groups. Category switch explanations, however, increased significantly with age (16%, 38%, and 53% of total explanations at ages 3, 4, and 5), F(2,47) = 3.95, p < .05. The percentage of participants that gave category switch, causal function, and causal action explanations at least once was calculated. These data are displayed in Table 3a. This analysis is a useful supplement to the data on proportion of total explanations of each explanatory type, because it demonstrates that a substantial portion of 3- and 4-year-olds make use of this kind of explanation. This finding is especially noteworthy, given that category switch explanations require overriding perceptual appearances and prior knowledge about an object and spontaneously redefining category boundaries around function.

Figure 5.

Study 1: Percentage of explanation types for inconsistent outcomes by age group

Table 3a.

Study 1: Percentage of children giving each kind of causal explanation for inconsistent outcomes at least once by age group

	Category switch	Causal function	Causal action
3-year-olds	31%	56%	19%
4-year-olds	56%	69%	6%
5-year-olds	69%	56%	19%

For consistent outcomes (not shown in Fig 5), whereas causal function explanations (M = 1.19 out of 4 trials or 30%) and causal action explanations (M = 0.21 or 5%) remained constant across age groups, F(2,47) = 1.47, ns; F(2,47) = 1.78, ns, category label explanations increased with age (6%, 24%, and 31% of total explanations at ages 3, 4, and 5), F(2,47) = 3.56, p < .05. The increase in category label explanations with age for consistent outcomes parallels the increase in category switch explanations with age for inconsistent outcomes.

Discussion

The test trial data from Study 1 demonstrate that inconsistent outcomes are an especially powerful trigger for children’s explanations. Given that children had readily available explanations for the consistent outcome, they could have easily ignored the inconsistent outcome and just explained the consistent outcome. Instead, children found outcomes inconsistent with prior knowledge especially noteworthy, and were much more likely to explain an inconsistent outcome first, as well as more likely to provide multiple explanations for an inconsistent outcome overall. This pattern held across the generative and inhibitory conditions. Further, if children had just been paying attention to the perceptual outcome (such as state-change or negative outcome), the event they explained should have been at chance, given that in the test trials the outcomes were identical (both boxes were on or off). Indeed, data from the confirmation trials showed that in the absence of an inconsistent event or outcome, state-change did serve as a trigger for children’s explanations. But on test trials children explained inconsistent outcomes whether they involved state-change or not. Finally, one could argue that children were primed to provide an explanation for the consistent outcomes prior to the test trials, because the confirmation trial (which appeared first) asked children to explain outcomes that were consistent with their prior knowledge about how the objects function. Nonetheless on test trials children systematically explained inconsistent events.

At the same time, it was not the case that children never explained consistent outcomes and therefore that children’s explanations were never confirmatory. In their overall explanations children did competently and easily provide explanations for consistent events as well. Constructing explanations for events that are consistent with children’s prior knowledge and experience must at times also be important, providing children with opportunities to deepen their understanding of expected phenomena. (Indeed, in our data children often did generate “deeper” explanations of consistent events by generating causal function explanations that cited possible mechanisms, such as underlying causal properties and internal components.) In short, we propose that outcomes inconsistent with prior knowledge are especially powerful triggers for causal explanatory cognition, not that children do not or cannot generate explanations for outcomes consistent with their prior knowledge.

Exactly how children explain events provides further insight into their understanding of the causal basis for the outcome. Children provided three distinct kinds of causal explanations: causal function, category switch (or category label in the case of consistent outcomes), and causal action explanations. Across age groups, causal function explanations were given quite frequently overall, with more than half of the children at each age providing at least one such explanation. Causal function explanations referred to alternative or problematic functioning for inconsistent outcomes, and referred to the object functioning correctly for consistent outcomes. Causal function explanations often included information about unobserved inside parts (power, batteries) or underlying causal properties (energy, electricity). For example, a 3-year-old explained, “Because this ran out of lights. Because it doesn’t have light stoppers in it”, and according to a four-year-old, “The starter isn’t working right, its inside parts must be all broken”.

Category switch explanations for inconsistent outcomes were also frequent (e.g., “It’s really a starter; it only looks like a do-nothing” or, “Hey! This one is a starter too! I thought it wasn’t but it is!”). These explanations are noteworthy because they entail spontaneously redefining category boundaries and privileging functional information over appearance. When explaining consistent outcomes, children also evoked the category label (e.g., “Because it’s a starter. Starters make the light in the boxes turn on.”), but without these additional features. Category switch explanations increased with age, and by 5 years of age, over two-thirds of participants provided at least one such explanation for inconsistent outcomes.

Prior research shows that even 3-year-olds can categorize objects in terms of novel, non-obvious properties (Gelman & Coley, 1990; Gelman & Markman, 1986, 1987), can apply names to objects with the same functional properties (Kemler-Nelson, 1995), and can categorize and name objects based on novel causal properties (Gopnik & Sobel, 2000). What is unique about the present task is that children spontaneously generated nonobvious, invisible properties for items and recruited this sort of reasoning to explain why items functioned in both expected and unexpected ways.

Several open questions remain, in particular about our use of functional labels in Study 1. Children’s responses might have been scaffolded by the object labels (starters, stoppers, and do-nothings), which were straightforward descriptions of their functions. For example, during inconsistent events, rather than truly noting the inconsistent outcomes, children instead may have noted the inconsistency of the observed function compared to the (inferred) label. Additionally, among the most interesting kinds of explanations provided by children in Study 1 were category switch explanations. However, given the nature of the functional label, it is unclear whether children were actually relabeling on the basis of causal effects or whether instead they were simply giving a more literal description of function (i.e., “it’s not really a starter” may be equivalent to “it didn’t start it”). Study 2 was designed specifically to address these possibilities.

STUDY 2

Study 2 addressed whether explanations for events not in accord with prior knowledge were scaffolded by the use of functional labels (“starters,” “stoppers,” and “do-nothings”) in Study 1, because the objects violated labeled functions. To investigate this, in Study 2 we used novel, non-functional labels for the objects (“toma,” “blicket”). Given that even 2-year-olds can extend novel labels based on function (Kemler-Nelson, 1995), we expected that children in Study 2 would also make use of information about function and underlying causal properties, much as in Study 1, even when the labels are novel and do not, in themselves, provide additional causal information. Additionally, based on Study 1 we predicted that children would again focus more on explaining events inconsistent with prior knowledge, even when the labels themselves do not carry any functional information.

Method

Participants

Given the near ceiling performance by 5-year-olds on several measures in Study 1, here we focused on younger children. Sixteen 3-year-olds (M age 3,5; range 3,0 to 3,10) and 16 4-year-olds (M age 4,4; range 4,0 to 4,11) who had not participated in Study 1 were recruited from a Midwestern U.S. university town. Participants were primarily White and from middle-class families. Approximately equal numbers of boys and girls participated in the study.

Materials

The materials used in Study 2 were identical to those from Study 1.

Procedure

The procedure for Study 2 was modeled on Study 1, with a single critical modification: the objects were given non-functional, novel labels (“a toma”/“not a toma” and “a blicket”/“not a blicket”), and were never referred to as “a starter,” “a stopper,” or “a do-nothing.” The confirmation and test trials were identical to those of Study 1.

Transcribing and Coding

The same procedure for coding Study 1 was amended slightly for Study 2 (to encompass reference to tomas and blickets instead of starters and stoppers). Table 2 provides examples of category switch, causal function, and causal action explanations from Study 2. Inter-rater reliability was established using a randomly selected sample of 25% of the data. Two persons independently coded the reliability sample with 98% agreement. Reliability was calculated for explanatory coding categories for both consistent and inconsistent outcomes, with Kappas ranging from .92 to .94, all within near-perfect levels (Landis & Koch, 1977).

Results

As in Study 1, we assessed whether events inconsistent with prior knowledge led to greater interest and attention, and most importantly, were first and most often explained.

Which outcomes do children look at and explain first?

Confirmation trials

In the confirmation trials children were more likely to look first at the object that changed the state of the box (started or stopped it) (64% of the time), t(31) = 2.06, p < .05, and to first explain the object that changed the state of the box (62% of the time), t(31) = 1.97, p < .05, as compared to the object that had no effect on the box. Although children were more likely to first explain the object that changed the state of the box in both conditions, in the generative condition (M = 70%) they did so above chance, t(31) = 2.63, p < .01, but in the inhibitory condition (M = 53%) they were at chance, t(31) = 0.32, ns. One possible explanation is that children are more compelled by an object that fails to turn the light box off than an object that fails to turn the light box on. More importantly, and as in Study 1, in the generative condition, where the confirmation trial pitted a state-change event against a negative outcome, children were significantly more likely to first explain the state-change outcome than the negative outcome.

Test trials

Again, inconsistent outcomes both attracted children’s attention first and provoked children’s explanations. Across age groups, children were much more likely to look first at the inconsistent outcomes than the consistent outcomes (M = 3.25 out of 4 or 81%), t(31) = 7.44, p < .001. Likewise, children were much more likely to explain the inconsistent outcome first (M = 3.05 or 76%), t(31) = 9.86, p < .001.

In order to investigate potential age- and condition-related effects, an age group (3-, 4-year-olds) X condition (inhibitory, generative) X final-outcome (both boxes on, both boxes off) repeated measures ANOVA was conducted. Condition and final-outcome were within-subjects factors and age group was a between-subjects factor. As in Study 1, at all age groups and conditions children were very likely to look at (3-year-olds 83%, 4-year-olds 80%) and explain (3-year-olds 75%, 4-year-olds 78%) the inconsistent outcome first. Thus, there was no significant main effect of age (for either the first look or first explanation analysis). There were also no significant main effects of condition (inhibitory versus generative) or final-outcome (both on versus both off). Moreover, unlike Study 1, none of the interactions were significant.

As in Study 1, to investigate the possibility that the sequential structure of the task may have influenced the outcome children were motivated to explain first, across conditions, the outcome children explained in the test trials they were presented with first (following the confirmation trial) were compared to the outcome they explained in the test trials they were presented with second. There were no significant differences for test trial order, t(31) = .71, ns.

Spontaneous explanations children provided prior to an explicit explanatory question were also analyzed as a supplementary analysis. As in Study 1, spontaneous explanations revealed the same pattern of responses as elicited explanations for first explanation. Ten of the 32 children participating provided a spontaneous explanation at least once in the test trials (31%). For 90% of the spontaneous explanations children explained the inconsistent outcome first, F(1,31) = 185.61, p < .001. Children’s interest in explaining inconsistent outcomes even without an explicit explanatory question provides clear evidence that children were not merely explaining what they thought the experimenter was interested in.

Which outcomes do children provide an explanation for overall?

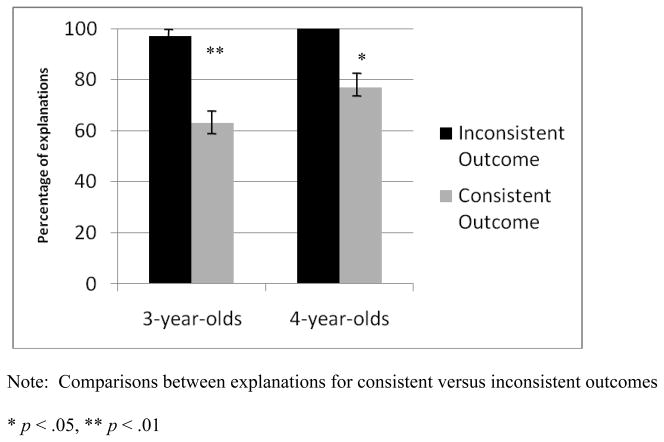
As in Study 1, children often provided multiple explanations. When focused on the total number of explanations provided, children were again much more likely to explain events inconsistent with their prior knowledge than events consistent with their prior knowledge. In order to investigate potential age and condition-related effects, we conducted a 2 age group (3-, 4-year-olds) X 2 condition (inhibitory, generative) X 2 final-outcome (both boxes on, both boxes off) X 2 consistent-vs.-inconsistent outcome repeated measures ANOVA on the entirety of children’s explanations. Condition, final-outcome, and consistent-vs.-inconsistent outcome were within-subjects factors. The only significant effect was for consistent-vs.-inconsistent outcome, F(1,30) = 22.64, p < .001, reflecting that inconsistent outcomes were more likely to be explained than consistent outcomes (M = 3.94 or 99% for inconsistent outcomes and M = 2.78 or 70% for consistent outcomes). As shown in Figure 6, both 3-year-olds (t(15) = 3.47, p < .01) and 4-year-olds (t(15) = 2.7, p < .05) showed this effect. The lack of any significant effects for age group and condition may reflect the more narrow age range in Study 2 (only 3- and 4-year-olds) in comparison to Study 1 (3-, 4-, and 5-year-olds).

Figure 6.

Study 2: Percentage of explanations children provided for inconsistent versus consistent outcomes by age group

The kinds of causal explanations children provided

As in Study 1, the majority of children’s explanations at all age groups were causal, for both inconsistent outcomes (81% and 84% at ages 3 and 4) and consistent outcomes (63% and 74% at ages 3 and 4). An age group (3-, 4-year-olds) X condition (inhibitory, generative) X consistent-vs.-inconsistent outcome X causal explanation type (causal function, causal action, category label/category switch) repeated measures ANOVA was conducted in order to investigate age-related changes in the kinds of causal explanations children provided. Condition, consistent-vs.-inconsistent outcome, and causal explanation type were within-subject factors. The number of total explanations provided (of each type) was the dependent variable.

As predicted, and as noted earlier, there was a significant main effect for consistent-vs.- inconsistent outcome, F(1,30) = 25.94, p < .001. The main effect for causal explanation type was also significant, F(2, 60) = 9.77, p < .001. Posthoc tests indicate that children were more likely to provide causal function explanations than causal action explanations, ps < .01. This can be seen in Figure 7.

Figure 7.

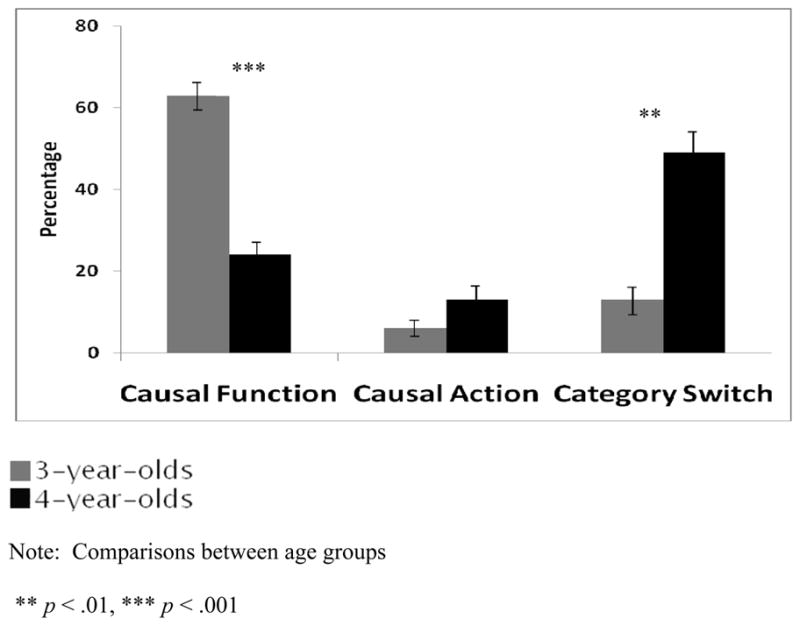
Study 2: Percentage of explanations types for inconsistent outcome by age group

The three-way age group X consistent-vs.-inconsistent outcome X causal explanation type interaction was also significant, F(2, 60) = 5.64, p < .01. This interaction indicates, as in Study 1, that there were changes with age in the kinds of causal explanations that children provided for inconsistent outcomes. Whereas causal action explanations remained constant (and infrequent) across age groups, causal function explanations decreased with age, p < .001, and category switch explanations increased with age, p < .01 (see Figure 7). We also examined the number of participants that gave category switch, causal function, and causal action explanations for inconsistent outcomes at least once. These results are informative because, as in Study 1, they indicate that a substantial portion of 3-year-olds and most 4-year-olds provided at least one category switch explanation, but also that 3-year-olds were very likely to provide explanations based on the causal functioning of the objects, even though the objects were given novel, nonfunctional labels (Table 3b).

Table 3b.

Study 2: Percentage of children giving each kind of causal explanation for inconsistent outcomes at least once by age group

	Category switch	Causal function	Causal action
3-year-olds	25%	94%	13%
4-year-olds	69%	50%	19%

For consistent outcomes (not shown in Figure 5), whereas causal function explanations and causal action explanations remained constant across age groups, category label explanations increased with age, p < .05. As in Study 1, this parallels the increase in category switch explanations with age for inconsistent outcomes.

Additional posthoc tests revealed that 3-year-olds were more likely to give causal function explanations for inconsistent (M = 2.5 out of 4 or 63%) than consistent outcomes (M = 1.4 or 35%), p < .01. Four-year-olds were more likely to give causal action explanations for inconsistent (13%) than consistent outcomes (3%), p < .05, and more likely to give category switch explanations for inconsistent outcomes (48%) than category label explanations for the consistent outcomes (24%), p < .01. Explanations that made use of psychological causes/descriptions were very rare; only two 3-year-olds and one 4-year-old used psychological language in their explanations (“This one doesn’t know how to act; it isn’t working right”).

Comparing Studies 1 and 2

Overall, the results from Studies 1 and 2 were highly similar. Across both studies, children’s explanations on the confirmation trials focused on state changes. For test trials for both studies, inconsistent outcomes were especially likely to provoke children’s explanations. Moreover in both studies, the content of children’s explanations, specifically category and causal function explanations, consistently referred to underlying, internal causal mechanisms, overriding perceptual appearances. This is especially noteworthy for Study 2, where the labels were novel and provided no explicit functional information. Thus, the results of Study 1 cannot be attributed merely to the use of functional labels. One difference did occur: children were more likely to look at the inconsistent outcome first in Study 1 (93%) than in Study 2 (81%), F(1,79) = 7.24, p < .01, indicating that the functional labels seem to have increased children’s attention to the inconsistent outcome. However, in both studies, children were equally likely to explain the inconsistent outcome first (80% in Study 1 and 76% in Study 2). Thus, children’s explanations of inconsistent outcomes depend on noticing those outcomes, but language can influence children’s attention and explanation.

Discussion

Study 2 further demonstrates that children focus more on explaining events inconsistent with prior knowledge than events consistent with prior knowledge, even when the labels themselves do not provide functional information. Moreover, children’s causal explanations make reference to function and underlying causal properties. As in Study 1, children privileged function information over perceptual features, evoked causal mechanisms and unobservable, internal causal properties, and spontaneously used (novel) labels to redefine category boundaries around shared function. Thus, several key results of Study 1 were not merely redescription based on the functional labels provided there. Finally, Study 2 provides evidence that use of functional labels was not what drew children to explain inconsistent events (because of the inconsistency of the outcome with a functional label), but instead children are more generally motivated to provide explanations for outcomes that were inconsistent with their prior knowledge.

General Discussion

Causal explanation is a goal-directed cognitive activity that depends on what is relevant or important to the explainer. Given the potentially unlimited number of outcomes one could explain, especially for young children early in the process of developing causal knowledge, identifying the specific kinds of events, outcomes, and goals that trigger explanation provides insight into what motivates and guides causal cognition. Although a substantial amount of developmental literature has demonstrated that young children frequently seek (Callanan & Oakes, 1992) and provide explanations (Wellman, Hickling, & Schult, 1997), little is known about what triggers this childhood explanatory activity.

If children have a cognitive model of the world based on a framework of anticipatory regularities, they would be well-equipped to rapidly form expectations contingent upon prior beliefs or knowledge. Indeed, even infants differentially attend to and explore events or objects inconsistent with such anticipatory regularities (Baldwin, Markman, & Melartin, 1993). In our data so do preschoolers; they first attend to inconsistent over consistent outcomes. Attention is not explanation, however. Research on confirmation bias in scientific reasoning provides evidence that patterns of attention do not guarantee sufficient motivation to generate explanations or promote causal learning (Dunbar & Klahr, 1988; Kuhn, 1989). Children could easily note inconsistent outcomes but be motivated primarily to explain consistent outcomes. Because such events conform to known expectations, they provide a foundation for constructing more generalizable causal explanations—particularly for young learners. In contrast, our data demonstrate that inconsistent outcomes were an especially powerful trigger for young children’s explanations. Across both generative and inhibitory conditions, with meaningful functional labels and with arbitrary novel labels, children were much more likely not only to attend to but also to explain the inconsistent outcome.

In the course of this research we considered additional factors possibly relevant to children’s explanations (such as state-change or negative outcomes). An important feature of the test trials in Studies 1 and 2 was that they controlled for these additional potential explanatory triggers by holding them constant. Confirmation trials, however, allowed examination of state-change or negative outcome as a potential explanatory trigger in the absence of an inconsistent outcome. Although inconsistency with prior knowledge is a compelling trigger for children’s causal explanations, in the absence of this information, state-change was an additional explanatory trigger. We suggest that attention to state-change may hold generally, beyond the particulars of this experiment. For example, children may expect individuals to stay healthy or objects to remain in motion—in which case state-changes, such as contracting illness, may trigger children’s explanations.

Another interesting possibility is that there may be differences in what one attends to, depending on where one is in the theory construction process. It is quite striking that children attend to and explain inconsistent outcomes after only minimal exposure to the contingencies. It may be the case that earlier in the theory construction process children are more receptive to inconsistent information and less so later on. Schema research supports this possibility. The memory advantage of schema-inconsistent items became weaker as the proportion of anomalous or schema-inconsistent items becomes larger (Rojahn & Pettigrew, 1989). Attending to frequency information would also help reconcile the motivation to seek causal regularities while responding to inconsistent information. Research on clustering accounts of causal learning predicts that inconsistent items are better remembered because they are differentiated from clusters that capture regularities (Sakamoto & Love, 2004). Frequency information may then drive the decision to integrate inconsistent information into an existing cluster or schema or create an additional schema to accommodate the new information. Further exploration of the conditions in which children focus on consistent information versus inconsistent information would be an interesting direction for future research.

More generally, an important open question is the role that explanatory processes play in children’s development. There is mounting evidence that children’s causal explanations may in fact constitute a mechanism for causal learning (Chi et al., 1989). When children are asked to explain events, they learn better than when given simple feedback about whether their predictions are correct (e.g., Amsterlaw & Wellman, 2006; Chi, DeLeeuw, Chiu, & LaVancher, 1994; Siegler, 1995). But how does this work? If explanation is a mechanism for learning, children should provide explanations for events that have the potential to teach them something new. Events that are inconsistent with prior knowledge provide just such an opportunity. Such an explanatory tendency could aid in learning by focusing children on events that challenge current causal knowledge and provoke additional, amended causal reasoning. Given that mere attention to inconsistent information is insufficient to ensure causal learning or theory revision (Kuhn, 1989), explanation may serve as a critical mechanism for integrating and reconciling inconsistent information with existing theories or knowledge structures.

The nature of children’s explanations, in appealing to unobserved explanatory processes and functional properties, could similarly aid learning. Explanations that appeal to underlying causes and mechanisms engage children in the important interplay between data and theory that leads to theory change (Wellman & Gelman, 1998). Children’s explanations for inconsistent outcomes, in particular, systematically referred to such features. For example, as shown in Table 2, children explained inconsistent outcomes by stating that “All the energy is gone” or “Maybe that toma doesn’t have batteries in it.” Additionally, category switch explanations (e.g., “It looks like a toma, but it’s not. It’s not really a toma at all”) indicate that even 3-year-olds privilege functional information over appearances.

Our data offer insight into the function of children’s explanations by providing empirical evidence for the kinds of events that guide causal cognition by motivating children to construct explanations. Although the present experiments do not directly test the hypothesis that children’s explanations play an active role in the learning process, they are consistent with this proposal and provide a promising empirical basis for investigating the interplay of explanation and learning in ongoing and future research.