Strain in the ostrich mandible during simulated pecking and validation of specimen-specific finite element models

Abstract

Finite element (FE) analysis is becoming a frequently used tool for exploring the craniofacial biomechanics of extant and extinct vertebrates. Crucial to the application of the FE analysis is the knowledge of how well FE results replicate reality. Here I present a study investigating how accurately FE models can predict experimentally derived strain in the mandible of the ostrich Struthio camelus, when both the model and the jaw are subject to identical conditions in an in-vitro loading environment. Three isolated ostrich mandibles were loaded hydraulically at the beak tip with forces similar to those measured during force transducer pecking experiments. Strains were recorded at four gauge sites at the dorsal and ventral dentary, and medial and lateral surangular. Specimen-specific FE models were created from computed tomography scans of each ostrich and loaded in an identical fashion as in the in-vitro test. The results show that the strain magnitudes, orientation, patterns and maximum : minimum principal strain ratios are predicted very closely at the dentary gauge sites, even though the FE models have isotropic and homogeneous material properties and solid internal geometry. Although the strain magnitudes are predicted at the postdentary sites, the strain orientations and ratios are inaccurate. This mismatch between the dentary and postdentary predictions may be due to the presence of intramandibular sutures or the greater amount of cancellous bone present in the postdentary region of the mandible and requires further study. This study highlights the predictive potential of even simple FE models for studies in extant and extinct vertebrates, but also emphasizes the importance of geometry and sutures. It raises the question of whether different parameters are of lesser or greater importance to FE validation for different taxonomic groups.

Introduction

Finite element analysis (FEA) is a tool that is becoming popular with morphologists and biomechanists for the study of the mechanical behaviour of biological structures (Rayfield, 2007). It permits the assessment of stress, strain and deformation within a structure with material properties and boundary conditions (applied loads and fixed constraints) that mimic a particular functional or behavioural scenario (feeding, locomotion, etc.). The structure in question is divided into a finite number of prescribed geometric entities, called elements, which are joined at apices and, in some cases, side edges by nodal points. Displacements in response to the applied loading conditions and constraints are calculated, taking into account the user-defined elasticity of the structure. These displacements are then used to calculate element strain, from which element stresses may be subsequently determined, producing a composite characterization of the mechanical behaviour of the structure [for more detailed descriptions of the finite element (FE) method and stress analysis, see Richmond et al. 2005; Zienkiewicz et al. 2005].

The nature of FEA means that the mechanical behaviour of complex shapes can be studied and, as such, the technique lends itself well to the analysis of biological structures. The past 10 years or so have witnessed a number of FEA studies of living and extinct vertebrates, focussing primarily on craniofacial mechanical function during feeding (for examples from only the last few years, see Barrett & Rayfield, 2006; Rayfield et al. 2007; Curtis et al. 2008; Moazen et al. 2008; Moreno et al. 2008; Snively & Cox, 2008; Wroe, 2008; Falkingham et al. 2009; Jasinoski et al. 2009; Moazen et al. 2009a,b; Stayton, 2009; Strait et al. 2009; Tseng, 2009).

A key question when using FEA is: how well do our results reflect reality? Before making functional and behavioural predictions based on FE results, models should ideally be validated against similar real-world loading conditions. There are, however, many reasons why FE models may not accurately represent real biological behavior. (i) Bone is a composite, heterogeneous structure, with anisotropic material properties (Reilly & Burstein, 1975; Currey, 2002). This level of material complexity is hardly ever achieved in existing craniofacial FE models, which typically employ isotropic material properties [although some do characterize heterogeneity (see McHenry et al. 2007; Wroe et al. 2007a,b; Wroe, 2008) and some have integrated orthotropic property data (see Strait et al. 2005, 2009)]. For extinct taxa, the problem is compounded further as the exact material properties of the bone will never be known, and the user must rely on identifying histological similarities with extant bone (e.g. Rayfield et al. 2001) or employing a phylogenetic bracketing approach (similar to Erickson et al. 2002) to estimate the elasticity of fossil bone. (ii) There is a question as to how complex a FE model should be, in terms of the FE resolution. A convergence test may be performed, sequentially reducing the element size until subsequent results do not differ, but the overwhelming question is whether this level of resolution (and, by default, computing power) is necessary to address the question at hand (see Gröning et al. 2009). (iii) Dumont et al. (2009) have outlined how models for which boundary conditions are poorly known may be scaled to the same surface area (or have scaled loads applied), in order to viably compare structural strength parameters (i.e. stress and strain patterns). Similarly, a volume scaling may be applied to compare strain energy. (iv) A further geometric issue is whether detailed structural features, e.g. trabecular plates, can or should be included, given the added complexity that they confer to the FE model [as performed in a macaque mandible and cranial model, respectively (Panagiotopoulou et al. 2010; Kupczik et al. 2009)]. (v) A further important issue is whether to include sutures (Moazen et al. 2009a). (vi) Muscle loading is frequently complex, with muscles firing at different stages of the feeding cycle and to varying activation levels (Ross et al. 2005). Muscle activation patterns may be recorded using electromyography in living taxa but, of course, this option is not available in fossil taxa, where muscle origination, insertion, dimensional and force output data must be estimated using osteological correlates (e.g. muscle scars sensu Witmer, 1995) and variants of the ‘dry skull method’ of Thomason (1991) that use adductor chamber dimensions to calculate the muscle cross-sectional area, which can subsequently be used to estimate muscle force [for an example, see methods in Rayfield et al. (2001)]. (vii) The FE model must be constrained from movement, yet where to place these constraining points and how many degrees of freedom of movement models can be assigned without generating erroneous stress and strain concentrations are further modelling problems that must be overcome (e.g. McHenry et al. 2006).

Despite these potential problems, studies that have validated experimentally gathered bone strain data against FE models have shown surprisingly good correlation between experimental and FE strain (Ross et al. 2005; Strait et al. 2005; Kupczik et al. 2007; Farke, 2008; Gröning et al. 2009). Not surprisingly, as the models incorporate better biological parameters, such as material properties that are anisotropic (Strait et al. 2005) and muscle activation data (Ross et al. 2005), this correlation improves. What is perhaps remarkable, however, is that even models with homogeneous, isotropic properties [e.g. Gröning et al. 2009; Kupczik et al. 2007; some models in Strait et al. (2005)] or those that treat the cranium as fused and do not consider the effect of sutures (Ross et al. 2005; Strait et al. 2005) show good correlation between experimental and FE strain type and patterns, and reasonable correlation with strain orientation. The approximation of strain magnitude tends to depend on the complexity of the model. Exceptions are the studies of Marinescu et al. (2005) on the macaque mandible and Metzger et al. (2005) on alligator crania, both of which found discrepancies between experimentally recorded and FE-derived strain orientations and magnitudes. For the latter example, the authors concede that a lack of correlation may have been due to the simplicity of the FE model (approximately 2400 uniform thickness shell elements with fairly generic material properties, rather than higher resolution solid elements that better represent such a complex 3D structure).

The majority of FE validation studies in the biomedical literature focus upon human material, mainly postcrania (e.g. Keyak & Falkinstein, 2003; Yosibash et al. 2007; Trabelsi et al. 2009; but see Wilcox, 2007). With the exception of Metzger et al. (2005), all other craniofacial validation studies have been performed exclusively on macaque skulls. As well as a need to perform more detailed validation studies on these existing taxa, there is also a need to validate other vertebrate taxa. One reason is that mammals have classically ‘akinetic’ skulls with a single bone comprising the lower jaw. Many other vertebrates have looser, patent and, in some cases, kinetic sutures, different bony material properties (e.g. Zapata et al., 2010), many more bones forming the mandible and skull, differences in tooth insertion, or indeed absence of teeth altogether in beaked animals. In general, we do not know if the parameters that influence model results in mammalian validation studies are the same in non-mammalian taxa. If the FE method is to be appropriately applied to organisms across the vertebrate lineage, including fossil forms, it is important to clarify this situation further.

Main body

In order to increase the breadth of taxa that have been subjected to FE validation, the aim of this study was to record strain within the mandible of an ostrich under controlled in-vitro conditions that partly simulate functional pecking loads and then to compare the experimental strain with strains recorded in a subject-specific FE model. This study will expand our understanding of FE validation in non-mammalian taxa, and also provide the first experimental data on strain within the avian skull, although postcranial functional strain has been recorded in a number of studies (e.g. Biewener & Dial, 1995; Main & Biewener, 2007).

It is important to note that the strains recorded here are from in-vitro rather than in-vivo loading. Although not a direct replication of behavioural loads, the advantage of in-vitro loading is that experimental parameters such as force application and constraints can be easily characterized and controlled, removing any in-vivo biological uncertainty or variability. Specimen-specific FE models can be created, and the position of strain gauges, loads and constraints can be precisely recorded and replicated in silico. In-vitro loadings have been employed frequently in biomedical studies, and a few zoological studies, where a like-for-like comparison is required to test how well the FE model replicates a controlled system (Marinescu et al. 2005; Kupczik et al. 2007; Yosibash et al. 2007; Trabelsi et al. 2009).

Ostriches were chosen for this study as a representative bird taxon. Ostriches are a useful model for practical reasons as the skull is large, thereby increasing the choice and success of strain gauge placement. Preliminary experiments (EJ Rayfield, unpublished data, described below and in Fig. S1) have also measured pecking forces in ostriches of similar age to those studied here, and so the magnitude of functional loads experienced during pecking is approximately known. Modern birds are also a useful model system to refer to when studying the craniofacial biomechanics and evolution of extinct avians and their non-avian theropod dinosaur ancestors. As paleognath birds, ostriches possess a palate that is more similar to the palate of theropods (and basal birds such as Archaeopteryx) than is the neognath palate (Zusi, 1993). Furthermore, ostriches appear to be the only species amongst paleognathous birds in which the cranial sutures tend to remain unfused in all but the oldest individuals (personal observation). The presence of sutures enables the testing of their importance to FE results, especially as sutures are present and frequently patent in most extinct archosaur taxa.

Materials and methods

Ostrich ‘pecking’ data

The preliminary pecking force was measured in two approximately 6-month-old ostriches reared at the Royal Veterinary College, UK. A force plate transducer was used to record seven trials of multiple pecks, each trial lasting between 6 and 8 s (see Supporting Information). The peak peck force recorded across all trials was 42 N. Food bait was not used to entice the ostriches to peck, and so the peck force can be considered to be exploratory, rather than explicitly feeding related. Although these data are rudimentary, they do provide a preliminary estimate of the forces experienced by the anterior tip of the cranium and mandible during pecking behaviour. This value was used as a guide to inform the value of 50 N that was selected to be applied to the isolated mandibles via the hydraulic loading machine.

Computed tomography scanning

Three 10-month-old free-range farmed ostrich heads were obtained postculling for meat (courtesy of Stan Stewart of MNS Ostriches, Devon, UK). Heads were frozen fresh, and were not stored in alcohol or formalin. Each head was thawed and scanned intact in a Picker PQ5000 medical/veterinary computed tomography (CT) scanner (Royal Veterinary College, London) (120 kV, 1 mm slice thickness). The slight variability in size resulted in the first ostrich being scanned with a slightly smaller field of view (FoV), resulting in an initial pixel size of 0.234 mm for ostrich 1 (FoV: 120 × 120 mm), and a pixel size of 0.273 mm for ostriches 2 and 3 (FoV: 140 × 140 mm).

Experimental strain recording

Post CT scanning, mandibles were dissected from the skull, taking care to limit dehydration by applying a 50 : 50 glycerine : water solution to the bone and surrounding soft tissue, and refrigerating the specimen wrapped in hydrated tissue paper in a sealed container between dissection and experimental preparation (after Kupczik et al. 2007). All muscular and connective tissue was removed from the mandible, as were the lateral parts of the rhamphotheca (keratinous beak). Part of the rhamphotheca was retained at the anterior tip of the mandible, and this should be borne in mind when interpreting the FE results.

Standard techniques were followed for strain gauge application. The bone surface around the gauge site was abraded with pumice powder and degreased with isopropanol (Vishay Measurements Group, Basingstoke, UK). Four rosette strain gauges (120 ± 0.5 Ω) (1 mm gauge length, 5 mm backing, FRA-1-11-3LT, TML Toyko Sokki Kenkyujo, Japan, obtained from UK distributors Techni Measure, Studley, UK), wired in a three-wire quarter-bridge circuit, were bonded to the mandible with cyanoacrylate glue (Vishay Measurements Group). Gauges were bonded to the lateral surangular (location 1), medial surangular (location 2), dorsal dentary (location 3) and ventral dentary (location 4) (see Fig. 1). All sites were as near flat as possible to avoid gauge distortion and damage.

Fig. 1.

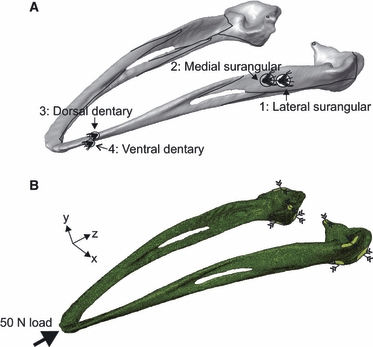
(A) Rendered model of the ostrich mandible (created from jaw 1 computed tomography scans) depicting the location of strain gauges. Black lines indicate sutural junctions. (B) Finite element mesh of jaw 1, illustrating the location and direction of constraints (green surface and converging arrows) and load (thick black arrow).

Mandibles were immobilized at the condyles by a specially designed steel clamp with a flat upper clamp pressed to the dorsal surface of the condyles and a double-convex lower surface in which the ventral, anterior and posterior surfaces of the condyles were snugly wedged (Fig. 2A). The mandible and steel clamp were firmly secured by vice-clamps to the base plate of a hydraulic testing machine (Dartec Ltd, Stourbridge, UK) (Fig. 2B). The gauges were connected to an amplifier (5100B, Vishay Micro-Measurements) with an excitation voltage of 0.5 V. Strain data were recorded in real time on a standard Toshiba laptop and converted to principal strain 1 (ε min) and principal strain 3 (ε max), shear strain and strain orientation using StrainSmart software (Vishay Measurements Group). Each mandible was loaded four times, yet the last trial for mandible 2 recorded seemingly erroneous strain values and one trial for mandible 3 did not achieve the correct loading, thus both of these trials were not included in the analysis further. In total, 10 trials from three specimens were considered. For each mandible, trials were performed in succession to achieve 50 N (6 out of 10 trials) or as close to a 50 N load as possible (2 trials at 52 N; 2 trials at 53 N) (see Table 1 for further details). The average strain per trial was calculated, and trials were subsequently collated to produce an average strain per specimen.

Fig. 2.

Loading apparatus. (A) Close-up of the posterior mandible within the fabricated steel clamp. (B) The mandible and clamp ready for load application by the Dartec hydraulic loading machine.

Table 1.

In-vitro experiment and finite element (FE) model details.

Mandible	Trial	Load achieved in-vitro experiment (N)	No. of elements in corresponding FE model
1	1	53	272 633
1	2	50	272 633
1	3	53	272 633
1	4	52	272 633
2	1	50	321 120
2	2	52	321 120
2	3	50	321 120
2	4	–*	321 120
3	1	–**	293 799
3	2	50	293 799
3	3	50	293 799
3	4	50	293 799

^*Trial did not achieve reliable loading and was not considered further.

^**Error in strain values; trial discarded.

Finite element analysis

The CT data were imported into Simpleware Scanip software v.2.1 (Simpleware Ltd, Exeter, UK). The data were resampled to a voxel size of 1 × 1 × 1 mm and the mandible manually thresholded and masked to separate soft tissue from bone. A floodfill operation was performed to create a solid mandible structure, and the mask data exported to Scanfe v.2.1 (Simpleware Ltd), where a voxel-based FE model was created, and subsequently smoothed, producing a solid mandible mesh of mixed linear tetrahedral and hexahedral elements (Table 1). The mandibular fenestra was included in the FE model (Fig. 1B), but sutures were not included even though they are found in the ostrich mandible. As such, the FE model is a test of how effectively a model without sutural contacts can replicate experimental strain. Models were assigned homogeneous, isotropic material properties (Young's modulus, 13.65 GPa) [as specific data on avian cranial material properties do not exist, an average of all skeletal elements in Table 1 of the paper Cubo & Casinos (2000) was used]. [Poisson's ratio, 0.35 (as an average for bone)]. Based on the results of these FE models, a second set of post-hoc FE models were created with approximately half-magnitude Young's modulus (E = 7 GPa). This value of E created a better fit for the jaw 1 experimental data, and probably accounts in some way for the mixed cancellous-compact composition of the jaw. Some of the lower values for E listed in Cubo & Casinos (2000) encompass this value [i.e. avian femur at 9.69 ± 5.36 GPa (n = 27, 1 SD) and humerus at 10.49 ± 7.79 GPa (n = 29, 1 SD)]. Models were then imported in Abaqus v.6.7 (Simula, Providence, USA), where boundary conditions were applied, analysis executed and postprocessing performed.

The locations at which the clamp contacted the condyles were recorded. At these sites in the FE model, the following constraints were applied directly to appropriate nodes: anterior and posterior surface of the condyle fixed in XZ translation; and dorsal surface fixed in XY translation (Fig. 1B). The area of the beak tip corresponding to the surface loaded by the Dartec was identified in the FE model, and 50 N of load was applied directly to surface nodes (21 nodes for jaw 1, 78 nodes for jaw 2, and 97 nodes for jaw 3). The number of nodes varied, but this represented the relative morphologies of the tip of the jaws. A static linear analysis was then performed.

The location of each gauge on the experimental jaw was measured using digital callipers (Mitutoyo, 10 μm resolution). The exact position of the gauges was subsequently located in the FE model using the distance measurement tool in Abaqus. The nodal strain (ε max and ε min) at all of the surface nodes comprising the 1.5 mm long × 1 mm deep FE ‘gauge site’ was recorded, and an average strain measurement and SD was calculated for each gauge location. The number of nodes selected for each gauge is recorded in Supplementary Table S1. In order to account for error in selecting the gauge site, a wider area of 5 mm diameter around the gauge site was also selected and the average strain and SD was calculated. In general, there are not large differences between average values (Supplementary Table S1). Values from the actual gauge site are recorded in the main text figures. A possible source of error is that this method of estimating average principal strains across the surface of the FE model is different to how principal strains are calculated by the gauges in vitro. The gauges instead measure average strain components in specific directions corresponding to the orientation of the rosette elements. It is possible that these different calculation methods may introduce error when comparing experimental and FE results and this should be borne in mind when comparing results. The difference between experimental and FE-derived strains was determined by calculating the normalized Euclidean distance for ε max and ε min values for each of the models. Lower Euclidean distance measures indicate a better fit of experimental to model data. An absolute value for principal strain orientation was more difficult to achieve in Abaqus. Instead, principal strain vectors were plotted and strain orientations recorded manually.

Results

Experimental loading

All mandibles generated consistent strain readings for successive trials of the same specimen (Table 2). However, strain magnitudes were not consistent between specimens, e.g. strains were much higher in magnitude in jaw 1 than in jaw 2 (Table 2). There was consistency between specimens in the overall strain distribution at gauge sites; strain in the dentary was always greater than in the surangular (Table 2) and gauge location 4, the ventral dentary, always experienced the highest magnitude compressive strain (ε min). The ventral dentary also experienced the largest tensile strains (ε max) in jaws 2 and 3, but the tensile strain was greater in the dorsal dentary in jaw 1. The tensile and compressive strain magnitudes were lowest at either location 1 or 2, the lateral surangular and medial surangular, respectively (Table 2).

Table 2.

Experimental peck strain recording per specimen, per trial, compared with finite element (FE) model result.

	Gauge location
	1	2	3	4	1	2	3	4
Specimen/trial	Lat. surang.	Med. surang.	Dors. dent.	Vent. dent.	Lat. surang.	Med. surang.	Dors. dent.	Vent. dent.
Ostrich jaw 1	ε max	ε max	ε max	ε max	ε min	ε min	ε min	ε min
1	96 ± 2	327 ± 9	1071 ± 9	827 ± 5	−219 ± 5	−175 ± 6	−455 ± 5	−1930 ± 16
2	95 ± 2	305 ± 3	1007 ± 4	783 ± 3	−205 ± 3	−162 ± 3	−425 ± 4	−1819 ± 6
3	104 ± 2	356 ± 6	1092 ± 8	844 ± 6	−230 ± 3	−180 ± 5	−461 ± 4	−1958 ± 15
4	101 ± 2	362 ± 5	1087 ± 7	837 ± 5	−235 ± 3	−182 ± 4	−459 ± 4	−1945 ± 11
Overall mean*	99 ± 9	338 ± 53	1064 ± 79	823 ± 55	−222 ± 26	−175 ± 19	−450 ± 34	−1913 ± 128
FEA mean E = 13.65 GPa	52 ± 26	103 ± 44	612 ± 147	347 ± 37	−33 ± 14	−59 ± 16	−273 ± 48	−765 ± 105
FEA mean E = 7 GPa	102 ± 51	201 ± 85	1193 ± 287	672 ± 69	−65 ± 27	−114 ± 31	−533 ± 94	−1493 ± 204
Ostrich jaw 2	ε max	ε max	ε max	ε max	ε min	ε min	ε min	ε min
1	82 ± 5	130 ± 3	296 ± 4	337 ± 4	−52 ± 3	−264	−159	−818
2	104 ± 10	145 ± 3	309 ± 4	348 ± 8	−53 ± 5	−287	−165	−847
3	104 ± 8	137 ± 3	296 ± 3	332 ± 6	−54 ± 5	−276	−160	−810
Overall mean*	97 ± 25	137 ± 15	300 ± 15	339 ± 16	−53 ± 3	−276 ± 23	−161 ± 6	−825 ± 38
FEA mean E = 13.65 GPa	58 ± 8	31 ± 4	86 ± 52	142 ± 14	−147 ± 18	−76 ± 6	−46 ± 16	−364 ± 40
FEA mean E = 7 GPa	110 ± 16	60 ± 8	162 ± 99	268 ± 26	−278 ± 34	−144 ± 11	−88 ± 29	−690 ± 76
Ostrich jaw 3	ε max	ε max	ε max	ε max	ε min	ε min	ε min	ε min
2	558 ± 15	182 ± 4	482 ± 11	732 ± 5	−231 ± 3	−591 ± 28	−134 ± 5	−1476 ± 44
3	579 ± 10	193 ± 3	499 ± 7	761 ± 5	−241 ± 4	−609 ± 16	−139 ± 3	−1528 ± 22
4	584 ± 10	187 ± 3	507 ± 7	758 ± 4	−245 ± 4	−621 ± 17	−140 ± 3	−1547 ± 26
Overall mean*	574 ± 28	188 ± 11	496 ± 25	751 ± 31	−239 ± 15	−607 ± 29	−137 ± 6	−1517 ± 74
FEA mean E = 13.65 GPa	35 ± 22	116 ± 66	337 ± 55	174 ± 32	−70 ± 64	−58 ± 21	−144 ± 25	−363 ± 98
FEA mean E = 7 GPa	66 ± 42	220 ± 125	638 ± 104	330 ± 61	−133 ± 121	−111 ± 39	−273 ± 47	−687 ± 185

All values in microstrain (με). E, Young's modulus; ε max, maximum principal strain; ε min, minimum principal strain; Lat. surang., lateral surangular; Med. surang., medial surangular; Dors. dent, dorsal dentary; Vent. dent, ventral dentary.

^*Overall mean ± 2 SEM. Trial means and FE analysis (FEA) means ± 2 SD.

The FE strain magnitudes were plotted onto species-specific data for experimental strain (Fig. 3). The grey area indicates the range of experimental strain recorded in all three jaws (± 2 SEM) and the dotted line indicates the grand mean of experimental strain from all three jaws. These data are identical for all graphs in Fig. 3. For the most part, the experimentally derived strain was higher in magnitude than the FE-predicted strain. In all cases, the FE model with a Young's modulus of 7 GPa was a better predictor of experimental strain than the 13.65 GPa models (i.e. Euclidean distance measures were always lower in value for the 7 GPa model, Fig. 3A–C). In jaw 1, the FE-derived strains matched the experimental strains well, and the pattern of peaks and troughs in strain were mirrored (Fig. 3A; ε max peak at gauge 3 dorsal dentary; ε min peak at gauge 4 ventral dentary). In jaw 2, the experimental strain was much lower in value than the average in-vitro strain (Fig. 3B). The FE-derived strain values were lower still, but were still a reasonable fit for the experimental data (Fig. 3B). For jaw 2, there was less variability in strain magnitude between gauge sites, both experimentally and in silico. Despite this, the pattern of high compressive strain at gauge 4, the ventral dentary, was repeated in the jaw 2 FE model (Fig. 3B). Experimental strains were mid-range for jaw 3, and showed variability between gauge location (Fig. 3C). The pattern of experimental strain was different to that observed in jaws 1 and 2. The FE-derived strains matched experimental strain at only half of the gauge sites (ε max locations 2 and 3; ε min locations 1 and 3). The ε min peak at gauge 4 (ventral dentary) was also seen in the FE data, albeit less pronounced than in jaw 1 (compare Fig. 3A and C).

Fig. 3.

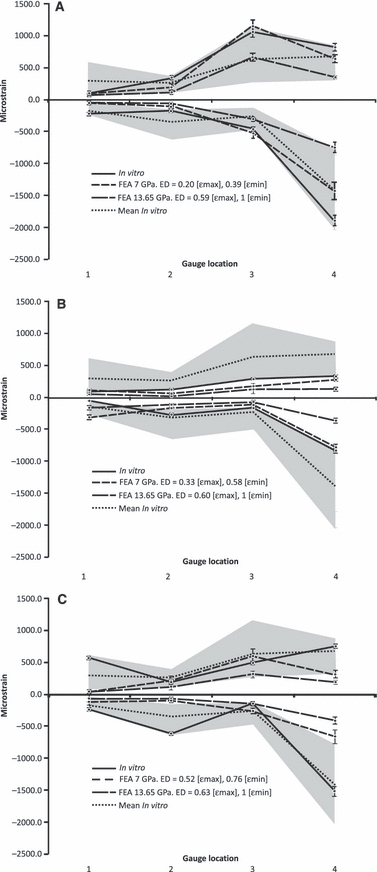
In-vitro compared with finite element (FE) strain data. (A) Jaw 1; (B) jaw 2; (C) jaw 3. The continuity of lines between gauge sites is used to visualize patterns and does not reflect a continuous strain gradient between gauge sites. Grey area is the spread of in-vitro recorded data for all experiments ± 2 SEM for in-vitro data, ± 2 SD for FE data. ED, Euclidean distances; FEA, finite element analysis.

At the dorsal and ventral dentary gauge sites (3 and 4, respectively), similar ratios of ε max : ε min could be seen between experimental and FE results for each specimen (Table 3). As such, tensile strains were always greatest in the dorsal dentary in the experimental jaw and FE, and compressive strains were greatest in the ventral dentary. In the lateral surangular and medial surangular, however, there was less coherence between experimental and FE-derived results. At the lateral surangular, when compression dominated experimentally, tension dominated in the FE model, and vice versa. In the medial surangular, the experimental data and FE results were in agreement in jaws 1 and 2; however, the data for jaw 1 showed that tensile strains dominated, whereas in jaw 2 compressive strains dominated.

Table 3.

Maximum: minimum principal strain ratios for experimental jaws and finite element (FE) models.

	1	2	3	4
Gauge location	Lat. surang.	Med. surang.	Dors. dent.	Vent. dent.
Jaw 1. ε max : ε min experiment	−0.45	−1.93	−2.36	−0.43
Jaw 1. ε max : ε min FEA	−1.56	−1.76	−2.24	−0.45
Jaw 2. ε max : ε min experiment	−1.83	−0.50	−1.87	−0.41
Jaw 2. ε max : ε min FEA	−0.40	−0.41	−1.85	−0.39
Jaw 3. ε max : ε min experiment	−2.40	−0.31	−3.61	−0.49
Jaw 3. ε max : ε min FEA	−0.49	−1.99	−2.34	−0.48

Lat. surang., lateral surangular; Med. surang., medial surangular; Dors. dent, dorsal dentary; Vent. dent, ventral dentary; FEA, FE analysis.

Finite element strain patterns

The Von Mises stress plots of each jaw scaled to the same peak stress (13 MPa) show that jaw 1 experienced a large amount of stress throughout the mandible. Jaw 2 appears relatively unstressed when scaled to a peak of 13 MPa, but high stresses (up to 44 MPa) are present at the constraints (Fig. 4A–C; Table 4). Plots of maximum and minimum principal strains (scaled to 0.001 and −0.001, respectively) show that, for jaws 1 and 3, the dorsal mandible is in tension, whereas the ventral mandible is compressed. Jaw 2 shows a slightly different pattern with large tensile strains at the distal surface of the symphysis, and compressive strain along the medial dentary, just anterior to the mandibular fenestra (Fig. 4D–I). Displacement plots and values (Fig. 4J–O; Table 4) show that jaw 2 does not experience as much displacement as jaws 1 and 3. Overall, jaws 1 and 3 appear to be bending ventrally, whereas, in jaw 2, ventral bending is less pronounced, reflecting the lower strain values recorded here experimentally and in the FE models.

Fig. 4.

Stress, strain and deformation plots for the finite element results. Left column: jaw 1 results; middle column: jaw 2 results; right column: jaw 3 results. (A–C) Von Mises stress, all plots scaled to 13 MPa peak stress. (D–F) Maximum principal strain, all plots scaled to 0.001 peak strain. (G–I) Minimum principal strain, all plots scaled to −0.001 peak strain. (J–L) Displacement, all plots scaled to 1 mm peak displacement. (M–O) Displacement ×10 with original undeformed model plotted in dark blue, all plots scaled to 1 mm peak displacement as before. All plots (A–L) are the deformed contour plots, scaled to a deformation of ×1.

Table 4.

In-vitro peak stress, strain and displacement in each jaw. Values of 13.65 and 7 GPa represent different Young's moduli applied to models.

	Von Mises stress (MPa)	ε max	ε min	Displacement (mm)
Jaw 1: 13.65 GPa	22	0.0016	−0.0017	0.85
Jaw 1: 7 GPa	22	0.0032	−0.0032	1.66
Jaw 2: 13.65 GPa	44	0.0041	−0.0022	0.21
Jaw 2: 7 GPa	44	0.0077	−0.0041	0.39
Jaw 3: 13.65 GPa	13	0.0007	−0.0011	0.65
Jaw 3: 7 GPa	13	0.0013	−0.0019	1.23

ε max, maximum principal strain; ε min, minimum principal strain.

Finite element strain orientation

The observed FE strain orientations matched the in-vitro data very well in the dentary, but did not match well in the postdentary bones. For the in-vitro experimental results, tension was aligned along the long axis of the mandible at the dorsal dentary (Fig. 5A) and mediolaterally in the ventral dentary (Fig. 5B). Lying at 90° to maximum principal strain, the minimum principal strain (compression) was therefore orientated along the long axis of the ventral dentary. The in-vitro data showed little variability in the orientation of these strains. The FE results for the dentary gauges showed the same pattern. In the posterior jaw, experimental strain orientation in jaw 1 was opposite to the pattern in jaws 2 and 3 (Fig. 5C,D). It appears that the posterior region of jaw 1 was bowing inwards (creating tensile strain orientated along the long axis of the mandible on the medial surface). In contrast, the posterior mandible was bowing outwards in jaws 2 and 3, with tension orientated longitudinally on the lateral surface of the mandible. Matching the FE-derived orientations to the experimental data was difficult. In the lateral surangular, orientations matched for jaw 1, but not for jaws 2 and 3 (Fig. 5C). In the medial surangular, none of the experimentally derived orientations matched the FE counterpart data (Fig. 5D), but jaw 1 FE orientation matched jaw 3 experimental data, and jaw 3 FE orientation matched jaw 1 experimental data.

Fig. 5.

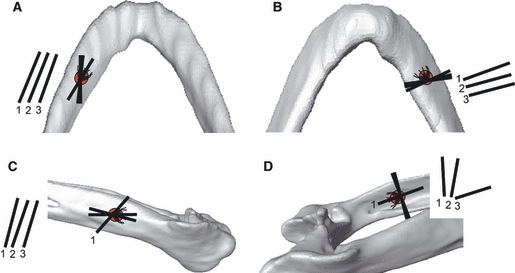
A comparison of maximum principal strain orientation (tension) between experimental and finite element (FE)-derived results. Minimum principal strains (compression) occur orthogonal to the illustrated axes. Axes drawn on the mandible are averaged from experimental trials; axes drawn to the left or right of each figure illustrate the comparable FE model strain orientation. Numbers refer to the relevant jaw experiment or model. Number identifiers are only illustrated for the experimental data when orientations differ markedly. (A) Dorsal dentary; (B) ventral dentary; (C) lateral surangular; (D) medial surangular.

Discussion

Strain data gathered between trials of the same mandible were consistently similar, with low SD per trial, and hence strains were repeatable. There was quite pronounced variability in strain magnitude and polarity between different mandibles. Because this variability was also reproduced in the FE models, it suggested that intraspecific variation was causing such differences. Despite this variability in strain magnitude, consistency between different jaws was observed; the dentary always experienced high magnitude strain, particularly at the ventral dentary, whereas the postdentary bones experienced lower magnitude strain. The jaws were all bending, such that the dorsal surface of the dentary experienced tension, whereas the ventral surface experienced compression. Despite differences in strain magnitude between jaw specimens, strain orientation in the dentary was highly conserved in all three jaws, and reflected the pattern of bending expressed by the gauge recording. The ostrich jaws were obtained from the cohort of farmed ostriches, reared in the same conditions, at the same time. Despite this, jaw 1 was longer than jaws 2 and 3 (166.5, 162.5 and 162.0 mm for jaws 1–3, respectively; see Fig. S2), and this increased length could reflect an increase in deformation. Also, jaw 2 was straighter and broader than jaws 1 and 3 (78.5, 82.0 and 77.0 mm for jaws 1–3, respectively; see Supporting Information) and jaw 2 was more ‘robust’ than the other jaws, having a surface area and volume that were 110 and 124%, respectively, greater than jaw 1. It is possible that the position of the mandibular fenestra, variation in flexibility of the intramandibular suture and differing cross-sectional shape may also influence mechanical behaviour. It seems unlikely that the small portion of the rhamphoteca that was retained at the tip of the jaws affected the results, as the dentary gauges nearest the jaw tips matched the FE data very well. All of these features presumably may have led to jaw 2 being stiffer experimentally and in silico. Different methods of clamping between jaw trials were probably not responsible for the strain differences, as the strain differences between experimental specimens were also reflected in the FE models, which were constrained identically. Clearly the influence of intraspecific morphological variation needs to be addressed in future studies.

The strain patterns and strain orientation data showed that the in-silico FE jaws were also bending and deflecting ventrally under the application of the pseudo-pecking load. Evidence for bending was also provided by the FE stress, strain and deformation plots, patterns that were consistent with this type of deformation. In-vitro strain orientation showed that the posterior jaws were also ‘wishboning’ (sensu Beecher, 1979; Hylander, 1984), with the mandibular rami flexing inwards in jaw 1, and outwards in jaws 2 and 3. The FE models, however, did not distinguish different patterns of wishboning, and FE strain orientations suggested that, in all three jaws, the rami were flexing laterally.

The experimental and FE-derived strain orientations, ratios of ε max : ε min, and (in the case of the 7 GPa model) strain magnitudes matched reasonably well at the dentary gauge sites. This fit of experimental to FE-predicted strain in the dentary was most interesting given the simplicity of the FE models: isotropic and homogeneous properties, and a solid, rather than cancellous, mandible. The FE model predicted strain in the dentary region much more accurately than it predicted strain orientation and ε max : ε min ratios in the postdentary region. At the lateral and medial surangular gauge sites, ε max : ε min ratios and strain orientations were either opposite or did not match. However, strain magnitudes were predicted reasonably well in the postdentary bones. It appeared that the experimental jaws were flexing in a different fashion to the FE jaws (either flexing inwards or outwards), and this could explain the mismatch in ratios and orientation, but the match in strain magnitudes.

Given this explanation, why should the postdentary gauge sites estimate strain less accurately than the dentary gauge sites? Firstly, the postdentary gauge sites were closer to the constraints. Constraints are known to influence the results of FE analyses, quite markedly in some cases (e.g. McHenry et al. 2006), and introduce artificial stiffness or strains to the surrounding region. In this case, the experimental set-up was designed such that the contact surfaces of the clamp holding the condyles could be clearly controlled and observed, and therefore replicated. As such, the FE constraints were modelled as precisely as possible, with only two out of three degrees of freedom invoked at each contact site in order to avoid the effect of over-constraint as much as possible.

Another possibility is that the presence of large, patent sutures at the intramandibular fenestra and in the posterior mandible (Fig. 1A) influenced how strains were transmitted from the dentary to postdentary region. It is possible that in vitro the strains are modulated across the suture but, as the FE model lacks sutures, this modulation cannot be reproduced in the in-silico results. Strains recorded at the two postdentary gauges may be influenced by proximity to sutures. Previous validation studies have shown a surprisingly good match of strains across the crania of macaques, with an exception being the zygomatic arch site (Ross et al. 2005; Strait et al. 2005). Introducing a suture in the zygomatic arch region of a macaque FE model produces strains that are more consistent with in-vitro experimental results (Kupczik et al. 2007), suggesting that strain can be modulated by the presence of a suture. It may be the case that FE models are better able to reproduce experimental strain in primate skulls, which possess a large proportion of interdigitated and partially fused sutures, than in FE models of species with more patent or less complex sutures. The simple morphology of the postdentary sutures in the ostrich are an example of such a suture. In this case, there is a real need to conduct further sensitivity analyses to explore the effect of sutures in experimental and in-silico studies. In Allosaurus and Uromastix, sutures are located in regions of the skull that experience high stress or strain in fused FE models and, when introduced to the model, relieve localized stress or strain hotspots (Rayfield, 2005; Moazen et al. 2009a). It may transpire that there is a need to validate a range of taxa, with varying patterns of suture morphology and suture fusion, in order to fully document the effect of sutures on FE models.

The FE model used here is internally solid, and does not reflect the extremely cancellous nature of many parts of the structure, particularly the postdentary bones approaching and comprising the condyle (personal observation from CT scan data). Introducing a cancellous structure or material properties to the FE model, in some way, may have a marked effect in particular on FE-derived strain patterns in the posterior jaw, and previous studies have found that including subcortical bone properties alongside cortical bone increases the accuracy of FE model predictions (Panagiotopoulou et al. 2010). Following on from this, the elements used here are given the material properties of avian limb bone, as the elastic modulus of avian cranial bone is unknown. Halving the value of E provided by the literature to 7 GPa provides a better fit of FE to the experimental data. The elements used here are isotropic and homogeneous, whereas bone is anisotropic and heterogeneous. Validation studies incorporating experimentally derived material properties recorded a better fit between in-vivo- or in-vitro-derived strain and FE results than homogeneous models (Strait et al. 2005; Kupczik et al. 2007). Although four-noded tetrahedral elements, which are known to be stiffer than 10-noded tetrahedral elements (Dumont et al. 2005), were used here, the good fit between dentary strain values suggests that the choice of lower order elements does not markedly influence the result of this analysis. A sensitivity analysis modifying some or all of the features listed above would permit an exploration into their relevance in influencing FE-derived strain patterns, orientation and magnitudes.

The prospect of this research for palaeontological models is that FEA does seem to replicate overall structural deformation, strain patterns, and strain orientation and, in the absence of flexible sutures, strain magnitude, remarkably well. The simplicity of the FE models used here, with isotropic and homogeneous material properties, offers the possibility that these properties do not have to be estimated with great precision in order to replicate strain patterns, although this requires further study. What may be significant for palaeobiological models is to consider the sutural make-up of the structure, and to represent cancellous bone in some manner, although this remains to be fully determined in future studies.

Concluding remarks

In conclusion, in the dentary of the ostrich, FE-derived strain patterns, orientations and magnitudes from relatively simple models can reproduce experimental strain recorded in vitro surprisingly well. In the postdentary bones, strain magnitudes and patterns are estimated in some instances, but not others, and strain orientations and ε max : ε min ratios are often inaccurate. This leads to the suggestion that sutures or the presence of large volumes of cancellous bone may be modulating the stress, strain and deformation response at the postdentary gauge sites. A more detailed model incorporating and varying cancellous and cortical material properties, sutures and different element types would allow the correlation to be explored further.

Supporting information

Fig. S1. Data from seven trials of experimental pecking study performed on two approximately six month old ostriches.

Fig. S2. (A) Three dissected ostrich jaw specimens used in this analysis. (B) Table documenting measurements of each jaw (surface areas and volumes taken from rendered CT data; linear measurements from (specimens).

Table S1. (A) Nodes selected for gauge sites. (B) Nodes selected for gauge sites and backing. (C) Comparison of number of nodes selected for jaw 1. (D) Comparison of number of nodes selected for jaw 2. (E) Comparison for number of nodes selected for jaw 3.

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer-reviewed and may be re-organized for online delivery, but are not copy-edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.