Biomechanics of the macaque postorbital septum investigated using finite element analysis: implications for anthropoid evolution

Abstract

Finite element analysis was used to assess whether the postorbital septum plays a meaningful biomechanical role as a structural support for the circumorbital region in a species of macaque, an anthropoid primate. A finite element model was constructed of a Macaca fascicularis cranium that was subsequently modified to create a second model in which the septum was removed bilaterally. The models were subjected to forces and constraints simulating a molar bite, and resulting strains and displacements were recorded. Strain magnitudes at selected locations on the models were typically lower or unchanged in the model lacking septae, which would seem to be contrary to expectations. However, more broadly, relative to the model containing septae, the model without septae exhibited a mosaic pattern of strain increases and decreases in the circumorbital region. The model lacking septae also exhibited more asymmetric displacements in the orbital region, although not in precisely the manner predicted by prior experimental studies. Overall, the mechanical impact of the postorbital septum is minimal in macaques. These results, when considered along with those of prior experimental studies, suggest that either the postorbital septum in anthropoids did not evolve for mechanical reasons, or, if it did, it no longer plays such a role in extant taxa.

Anthropoid primates and tarsiers are the only vertebrates to exhibit a postorbital septum (e.g. Ross & Hylander, 1996), a bony plate that separates the orbit from the temporal fossa. Because this trait is unique and because it is so widely recognized as being important in primate systematics, a large number of hypotheses have been proposed purporting to explain its evolution (Cartmill, 1980; Greaves, 1985, 1995; Rosenberger, 1986; Ross, 1995, 1996, 2000; Ross & Hylander, 1996; Heesy et al. 2005). Some of these are mechanical in nature. In particular, it has been suggested that the septum (i) limits the torsion of the face on the braincase caused by asymmetrical bite and joint reaction forces (Greaves, 1985, 1995); (ii) limits the bending of the circumorbital region caused by the posteriorly directed component of the temporalis muscle force (Cartmill, 1980); and/or (iii) limits dorsoventral tension in the postorbital bar caused by the contraction of the masseter muscle (Rosenberger, 1986; Ross & Hylander, 1996). Ross & Hylander (1996) tested these hypotheses using a combination of in vitro and in vivo experimental methods, and found that the skulls of owl monkeys (genus Aotus) did not conform well to the predictions of these simple biomechanical models. However, their in vitro analyses, in which a skull was loaded before and after the postorbital septum was cut, suggested that septum may play at least some role as a structural support and that its presence may have an impact on local strain and deformation patterns. However, unavoidable practical considerations limited their ability to test the functional hypotheses; their in vitro analyses could not account for muscle forces (which figure prominently in two of the hypotheses) and their in vivo studies could not examine the consequences of removing the septum. Here, we use finite element analysis (FEA) to overcome these obstacles by modeling a macaque skull with and without postorbital septae while being exposed to physiologically realistic loads associated with molar bites. In doing so, we test hypotheses suggesting that the postorbital septum has a meaningful impact on feeding biomechanics in extant anthropoid primates.

Hypotheses

Two results emerged from the in vitro experiments of Ross & Hylander (1996) that can be viewed as testable hypotheses:

Hypothesis 1: The presence of a postorbital septum minimizes asymmetrical distortion of the orbits during unilateral loading of the cheek teeth. Asymmetry is caused by the fact that muscle forces are working bilaterally (although with different magnitudes on each side) to pull the cranium inferiorly, but on the working side, this displacement is opposed by a superiorly directed bite force. As a consequence, the working and balancing side postorbital regions deform in different ways. On the balancing side, the inferior displacement caused by the muscles is unimpeded, so the orbit elongates inferiorly. On the working side, the opposing bite and muscle forces minimize vertical displacement, so the orbit also widens laterally. If the septum plays a role in stiffening the circumorbital region structurally, then its removal would have the effect of accentuating the two different working and balancing side deformations. This hypothesis predicts that during molar biting in a skull without septae, there is a greater discrepancy in the vertical displacements of the inferolateral orbital margins on the working and balancing sides than in skulls with septae.

Hypothesis 2: The postorbital septum provides some (albeit minor) structural support to the facial skeleton during molar biting. The removal of the septum would therefore lessen the rigidity of the circumorbital region, and one would expect that deformations due to chewing would increase. This hypothesis predicts that strain magnitudes will be greater in skulls without septae than in those with septae. Ross & Hylander (1996) observed that strains in the dorsal interorbital, dorsal orbital and postorbital regions (running around the orbit from the superior aspect of the center of the supraorbital torus to the postorbital bar just inferior to the orbit's lateral margin) increased by 30–90%.

We tested these hypotheses using FEA, which is an engineering technique used to examine how structures of complex design respond to external loads (Huiskes and Chao, 1983). In FEA, the structure of interest (e.g. a skull) is modeled as a mesh of simple bricks and/or tetrahedra (finite elements) joined at nodes. The elements are then assigned material properties, certain nodes are constrained against motion, forces are applied, and displacements, stresses and strains at each node and within each element are calculated. Recent advances in computer software and imaging technology have made it possible to capture and digitally reconstruct skeletal geometry with great precision, thereby facilitating the generation of detailed finite element models (FEMs) of bony structures (e.g. Richmond et al. 2005; Rayfield, 2007; Panagiotopoulou, 2009). However, the incorporation of realistic muscle forces, bone material properties, modeling constraints, and experimental bone strain data are equally important components of FEA that are necessary to ensure biologically meaningful results (e.g. Richmond et al. 2005; Ross et al. 2005; Strait et al. 2005, 2007, 2008, 2009; Kupczik et al. 2007, 2009).

Our FEA experiments were performed on two models representing a skull of Macaca fascicularis before and after being modified by the bilateral removal of the postorbital septae. In this manner, it was possible to perform a controlled experiment in which strain differences observed between the two models can be explained by the presence or absence of the septum. Macaca fascicularis is a useful subject for this analysis because it has been the subject of numerous in vivo and FEA studies (e.g. Hylander et al. 1991; Hylander & Johnson, 1997; Ross, 2001; Strait et al. 2005, 2007, 2008, 2009; Ross et al. inpress), and thus the bone strain, electromyography, and material properties data needed to construct and validate FE models are readily available. However, the circumorbital morphology of this species does not obviously resemble that of the earliest anthropoids, so our analysis is best interpreted as examining septum mechanics in extant rather than basal anthropoids, and thus only indirectly addresses the issue of why the septum may have evolved.

Materials and methods

Model creation

Serial CT scans were obtained of a subadult male M. fascicularis that had been sacrificed during the course of biomedical research unrelated to the project described here. Those scans were used as the raw material to build an FEM using the software protocol developed by Dumont et al. (2005, 2009). The scans were segmented using medical imaging software (mimics) to produce tesselated (.stl) surfaces of the external and internal surfaces of the skull. Modeling errors in the surface files were removed in surface editing software (geomagic) so as to ensure that the surfaces were ‘watertight’ (i.e. they perfectly enclosed a volume). A mesh of 879 744 tetrahedral elements was then created using finite element analysis software (strand7). A second FEM was then created by modifying the surface file such that the postorbital septum was removed from both sides of skull. A new mesh was then created that contained 875 238 elements. Both models are more densely meshed than our previously validated FE model (Strait et al. 2009). The procedure described above allows for the rapid construction of geometrically precise FEMs.

Material properties

The two FEMs were assigned a single set of isotropic material properties using values of Young's modulus (E = 17.3 Gp) and Poisson's ratio (v = 0.28) derived from average values obtained by Wang & Dechow (2006) and employed in our earlier analyses (Strait et al. 2005). These material properties represent a considerable oversimplification of those present in the primate skull, which are orthotropic and exhibit variation between cranial regions (Wang & Dechow, 2006; Wang et al. 2006). However, it has been shown that although precise assumptions about material properties improve overall model accuracy (Strait et al. 2005), coarse assumptions such as those employed here do not dramatically affect the overall patterning of strains found in FEA. Because the present study entails a simple comparison between FEMs that differ only with respect to the presence or absence of the postorbital septum, the isotropic properties employed here should be sufficient to allow the detection of basic differences in strain patterns. Similarly, as a time-saving step, trabecular bone was not included in the present study and regions of such bone were modeled as empty cavities. Trabecular bone, by volume, is about 30 times less stiff than cortical bone (Ashman et al. 1984), so although trabecular bone in the face certainly plays a role in maintaining the structural integrity of the skull, the vast majority of the load is borne by cortical bone. Thus, in the present study, the omission of trabecular bone should not dramatically impact the results. A sensitivity analysis (see Supporting Information Appendix S1) confirms that the treatment of trabecular bone regions in the cranium as empty cavities has only a small impact on strain results. Likewise, the periodontal ligaments were not modeled because recent sensitivity studies have demonstrated that the ligament does not profoundly affect strains except near the alveolus (Panagiotopoulou et al. 2010; Wood SA, Strait DS, Dumont ER, Ross CF, Grosse IR, in preparation).

Muscle forces

Force vectors corresponding to the right and left anterior temporalis, superficial masseter, deep masseter and medial pterygoid muscles were applied to nodes on the neurocranium, zygomatic arch and lateral pterygoid plate. Vector orientations (Table 1) are equivalent to those used in Strait et al. (2005). Vectors representing the anterior temporalis were applied densely along the temporal lines extending from the superolateral angle of the torus to a point on the line above the articular eminence, and then also diffusely across the wall of the neurocranium above the temporal fossa corresponding to the region defined by muscle scars visible on crania. Vectors representing the superficial and deep masseter were applied to the inferior aspect of the zygomatic arch, with those of the superficial head extending farther anteriorly and being positioned slightly laterally, and those of the deep head extending further posteriorly and being positioned slightly medially. Vectors representing the medial pterygoid arose from the medial aspect of the lateral pterygoid plate. Muscle force magnitudes (Table 1) in M. fascicularis were calculated using a combination of muscle physiologic cross-sectional area and electromyographic data (Antón, 1993; Ross et al. 2005; Strait et al. 2005, 2007, 2008, 2009). These muscle forces reflect the fact that during any given bite, the muscles act slightly out of phase to each other, and thus are never all simultaneously acting at peak levels (Strait et al. 2005, 2007, 2008, 2009). For each muscle, forces were applied as multiple vectors originating from nodes found within the margins of the areas of attachment of the muscle. Note that the forces representing the anterior temporalis had to be modeled slightly differently in the two FEMs because this muscle origin encroaches on the postorbital septum in macaques. In the FEM in which the septum had been removed, the few force vectors that would have originated from the septum were repositioned on the torus and neurocranium.

Table 1.

Muscle force magnitudes and orientation vectors applied to the finite element models.

Muscle	Magnitude (N)	Orientation (x, y, z)*
Working-side
Anterior temporalis	36.6	0.1, −1, −0.1
Superficial masseter	70.6	−0.2, −1, −0.2
Deep masseter	22.6	−0.6, −1, 0
Medial pterygoid	34.8	0.75, −1, 0
Balancing side
Anterior temporalis	15.1	−0.1, −1, −0.1
Superficial masseter	34.7	0.2, −1, −0.2
Deep masseter	8.2	−0.6, −1, 0
Medial pterygoid	6.9	−0.75, −1, 0

^*x, direction is positive to the model's left (working) side; y, direction is positive superiorly; z, direction is positive anteriorly.

Constraints

Constraints were applied to multiple nodes at the right and left articular eminences and the left molars. Muscle forces act to pull the skull models down onto the constrained nodes (fixed points), generating reaction forces representing the joint forces at the temporomandibular joints, and the bite force. The patches of constrained nodes are similar to those employed in, and thus facilitate comparison with our prior analyses (Strait et al. 2005, 2007, 2008, 2009), but arguably may overconstrain the model by, for example, limiting rotation around a mediolateral axis at the temporomandibular joint. However, a sensitivity analysis (see Appendix S1) reveals that the precise manner in which the articular eminences and bite point are constrained does not dramatically impact results (so long, presumably, as all three locations are constrained in at least the vertical direction).

Validation

Before FEA can be used to test hypotheses, it must first be established that the analyses are providing realistic results. This is achieved by comparing strains derived from FEA with those obtained in experimental studies (Fig. 1). An advantage of studying M. fascicularis is that this species has been the subject of numerous in vivo studies examining bone strain during feeding, and these data can be used to validate FEMs of this species (Table 2, Fig. 2). If there is good correspondence between the experimental and FEA strains, then the model is considered to be valid and suitable for use in testing hypotheses.

Fig. 1.

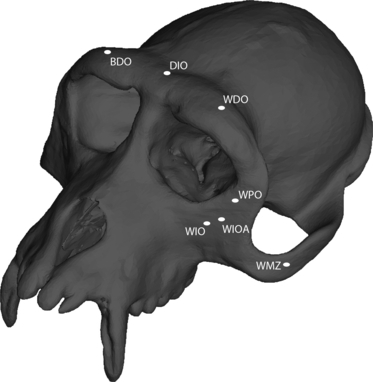
Finite element model of a Macaca fascicularis cranium showing location of some of the regions from which strain (red) and displacement (green) data were collected. BDO, balancing side dorsal orbital region; DIO, dorsal interorbital; WDO, working side dorsal orbital; WPO, working side postorbital bar; WMZ, working side mid-zygomatic arch; WIO, working side infraorbital region; WIOA, working side inferolateral orbital angle. Not shown: balancing side mid-zygomatic arch, balancing side infraorbital, balancing side inferolateral orbital angle.

Table 2.

Validation of FE model.

	FEA strains from model with postorbital septum		Strains recorded from in vivo chewing experiments
Region	Maximum shear strain	Principal strain ratio (Max/Min)	Mean maximum shear strain ± 2 standard deviations	Mean principal strain ratio ± 2 standard deviations*	Experiment	Reference
Dorsal interorbital	72	3.0	169 ± 94	2.1 ± 0.4	5 A (W)	Hylander et al. (1991)
			266 ± 82	2.3 ± 0.2	5 A (B)
			185 ± 78	4.0 ± 0.4	6 (W)
			182 ± 68	4.0 ± 0.6	6 (B)
			139 ± 110	1.8 ± 0.2	2 A (W)
			129 ± 42	1.7 ± 0.2	2 A (B)
			86 ± 38	2.4 ± 0.6	2 B (W)
			117 ± 56	3.1 ± 0.6	5 B (W)
			240 ± 116	2.6 ± 0.4	5 C (W)
			200 ± 84	2.1 ± 1.0	5 C (B)
Working-side dorsal orbital	42	0.4	100 ± 62	0.5 ± 0.2	5 A	Hylander et al. (1991)
			85 ± 44	0.7 ± 0.2	6
Balancing-side dorsal orbital	28	1.0	147 ± 60	1.4 ± 0.2	5 A	Hylander et al. (1991)
			105 ± 29	1.4 ± 0.2	6
Working-side infraorbital	329	1.7	325 ± 174	1.4	2 C	Hylander et al. (1991)
			613 ± 256	1.1	5 C
			180 ± 128	0.1 ± 0.5**	7	Ross et al. (2002)
Balancing-side infraorbital	134	1.4	199 ± 144	2.2	2 C	Hylander et al. (1991)
			295 ± 234	2.4	5 C
			192 ± 160		7	Ross et al. (2002)
Working-side mid-zygomatic	424	1.0	661 ± 414	1.0	2 A	Hylander et al. (1991)
			569 ± 244	0.9	2 B
			250 ± 104	0.7	5 B
			857 ± 360	0.6	2	Hylander & Johnson (1997)
			614 ± 274	0.7	5
			398 ± 204	0.7	7
			391 ± 72	0.7	9
Balancing-side mid-zygomatic	314	0.9	352 ± 238	0.9	2 A	Hylander et al. (1991)
			578 ± 212	0.5	2	Hylander & Johnson (1997)
			440 ± 254	0.6	5
			349 ± 262	0.6	7
			202 ± 168	0.6	9
Working-side postorbital bar	93	1.0	135 ± 113	1.0 ± 0.5	46	Ross CF (unpublished data)
			194 ± 197	47
			142 ± 129	48

^*Standard deviations and, in some cases, means were not reported for all experiments.

^**Data from this experiment were highly skewed, with most chews exhibiting high compression and low tension. However, the highest value observed in this experiment was 1.8.

Fig. 2.

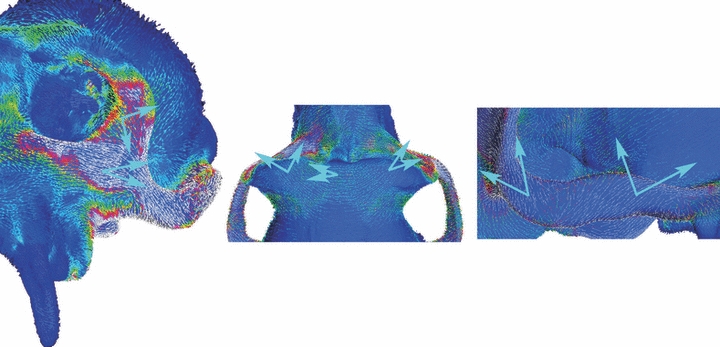
Orientation of maximum principal strain. Vector map indicating orientation of maximum principal strain recorded at each surface element in the FEA of the unmodified macaque cranium. Large blue arrows bracket the angular range of values recorded during in vivo chewing experiments at particular locations on the cranium (Hylander et al. 1991; Hylander & Johnson, 1997; Ross et al. in review). Note the good correspondence between the in vivo and FEA data.

Hypothesis testing

Hypothesis 1 was tested by recording the vertical displacements at nodes on the working and balancing side inferolateral orbital margins of each model. In each model, nodes on each side were selected because they lie at the intersection of a horizontal plane passing through the inferior orbital margin and a vertical plane passing through the lateral orbital margin. Hypothesis 1 predicts that the ratio of the working-to-balancing side vertical displacements will be closer to a value of 1.0 in the model with a postorbital septum, and that displacements will be greatest on the balancing side (where inferior displacements will not be impeded by a bite point).

Hypothesis 2 will be tested by comparing maximum principal, minimum principal, and maximum shear strain from the interorbital, dorsal orbital and postorbital regions in the two FEMs. This hypothesis predicts that strain magnitudes will be higher in the model lacking the septum.

More generally, color maps indicating the distributions of each of these types of strain were examined so as to determine whether there were qualitatively obvious differences in the patterning of strains in the two models.

Results

Validation

Validation of the unmodified macaque model (i.e. with postorbital septae) was good. Shear strain magnitudes (Table 2) at the infraorbital, mid-zygomatic arch and postorbital bar were comfortably within the dispersion observed during in vivo chewing experiments, while magnitudes at the interorbital and dorsal orbital regions were either at or just outside the low end of the in vivo dispersion. Thus, strains along the supraorbital torus are somewhat lower than expected, possibly because the stiffness of cortical bone in the torus is being overestimated in the FEA relative to that observed in life (Wang & Dechow, 2006), or possibly because the specimen used for this model exhibits a robust torus (see below). The orientation of maximum principal strain in the FEM conforms extremely well to the orientations observed in vivo (Fig. 2). These data indicate that the basic nature of the strains is realistic. Moreover, the ratios of maximum to minimum principal strain match the in vivo values at the dorsal interorbital, dorsal orbital, mid-zygomatic and postorbital regions. At two localities (working and balancing side infraorbital), the ratio correctly identifies the ‘mode’ of strain (i.e. primarily tensile), but the values of the ratios in FEA are slightly outside those in the in vivo experiments. On balance, these data indicate that the model is deforming in a broadly realistic fashion, and thus is suitable as the basis for interpretation and experimentation.

Comparing models

Table 3 presents the vertical, horizontal and anteroposterior displacements of nodes found near the inferolateral angles of the working and balancing side orbits. With respect to all directions, working-to-balancing side asymmetry in these displacements was greater in the model lacking postorbital septae. Interestingly, vertical displacements were greater on the working side than on the balancing side in both models. Table 4 presents maximum principal, minimum principal and maximum shear strain magnitudes recorded at the dorsal interorbital and working side dorsal orbital and postorbital regions. At the dorsal interorbital and postorbital regions, strains were nearly identical in the two models. At the working side dorsal orbital region, all types of strain were lower in the model lacking postorbital septae.

Table 3.

Displacement asymmetry of the inferolateral angles of the orbit.^*

Model/side	Vertical displacement	Mediolateral displacement**	Anteroposterior displacement***
With septum
Workingside (mm)	−0.0420	0.0302	−0.0148
Balancingside (mm)	−0.0345	−0.0084	−0.0007
Ratio(working/balancing)	1.25	−3.61	22.91
Without septum
Workingside (mm)	−0.0405	0.0314	−0.0161
Balancingside (mm)	−0.0285	−0.0045	−0.0007
Ratio(working/balancing)	1.45	−6.91	24.60

^*Displacements recorded at the working and balancing side IOA elements labeled in Fig. 1, and described in the text.

^**Positive displacements are towards the left (working) side.

^***Negative displacements are posteriorly directed.

Table 4.

Strains in the supraorbital torus and postorbital bar, in microstrain.

Location*/model	Maximum principal strain	Minimum principal strain	Maximum shear strain
Dorsal interorbital (DIO)
With postorbital septum	54	−18	72
Without postorbitalseptum	54	−17	71
Working side dorsal orbital (WDO)
With postorbital septum	18	−18	36
Without postorbitalseptum	15	−10	25
Working side postorbital (WPO)
With postorbital septum	97	−44	141
Without postorbitalseptum	77	−52	128

^*See Fig. 1 for position of each location.

Figure 3 presents color maps of maximum principal, minimum principal and von Mises strain magnitudes in the two models. The patterns are extremely similar in the two models, although subtle differences are evident. Primarily, the model lacking the postorbital septae exhibits a concentration of elevated minimum principal, von Mises and, to a lesser extent, maximum principal strain on the supraorbital torus near the superolateral angle of the working side orbit that is absent in the model with septae. Strains are also higher in the model without septae near the superomedial angle of the orbit. Close inspection of the working side postorbital bar (lateral to the orbit) and the dorsal orbital region (directly above the orbit just medial to its midline) indicates that strains in these regions are subtly lower in the model lacking septae.

Fig. 3.

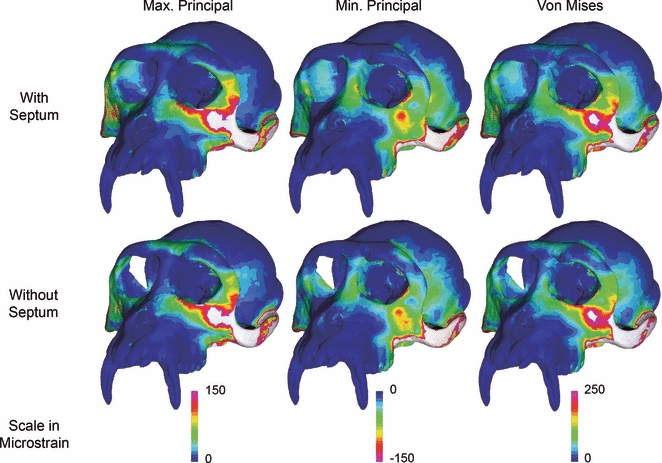
Comparison of strain magnitudes in the finite element models with (top row) and without (bottom row) postorbital septae.

Discussion

The mechanical consequences of variation

The greatest discrepancy between the FEA and in vivo data concerned the strain magnitudes in the dorsal orbital and dorsal interorbital regions; these were lower than expected in the FEA. There are two likely explanations for this. First, bone in the supraorbital torus in macaques is more compliant than bone elsewhere in the cranium (Wang & Dechow, 2006), but such variation in elastic properties is not incorporated into the present analysis. Thus, toral bone in the present study is stiffer than in life, and strains might be correspondingly lower. A second explanation, however, may simply be that the specimen being modeled here has a particularly well developed supraorbital torus and postorbital bar. Figure 4 shows a comparison between the FE model used here and a model used in our prior studies (Strait et al. 2005, 2007, 2008, 2009). It is evident that the model used here has, proportionally, a more pronounced supraorbital torus, a mediolaterally thicker postorbital bar (particularly near the inferolateral margin of the orbits) and a vertically deeper zygomatic arch. Yet, the two models have been subjected to identical muscle forces. Thus, it is reasonable that strains would be lower in the torus in the more robust specimen. Indeed, strains at all of the locations sampled here (Table 2) are universally lower in the current model compared to the older one (Strait et al. 2005: Table 7). These findings illustrate the need for mechanical studies to incorporate information about morphological variation into their analyses. To date, FEA studies have rarely attempted to assess systematically the mechanical consequences of intraspecific cranial shape variation, but clearly this needs to be a priority of the field moving forward.

Fig. 4.

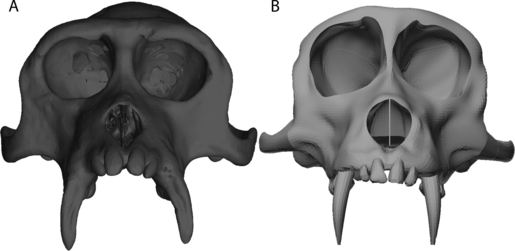
Frontal view of finite element models of Macaca fascicularis. (A) FEM used in the present study. (B) FEM used in Strait et al. (2005). Both FEMs have been scaled to the same maximum bizygomatic breadth.

Hypothesis testing

Results of the FEAs were partially consistent with the predictions of Hypothesis 1 (displacement asymmetry) and Hypothesis 2 (strain magnitude). Vertical and all other displacements near the inferolateral angle of the orbits were more asymmetrical in the model lacking postorbital septae, as predicted by Hypothesis 1. However, it had been expected that vertical displacements would be greater on the balancing side because that side would be ‘unsupported’ by the bite point, resulting in a working-to-balancing side ratio of displacements of < 1.0. In fact, these ratios in both models exceed 1.0. Evidently, the greater working side muscle force compensates for the presence of the bite point to create greater displacement at this location, at least on this side. Thus, although the septum apparently affects working-to-balancing side asymmetry, it does not do so in precisely the manner predicted. Interestingly, the working-to-balancing side asymmetry in our previously constructed M. fascicularis model (Strait et al. 2005) is < 1.0, and thus conforms to predictions, at least in the case in which the postorbital septum is present. Presumably, these differences between the two macaque models (i.e. those from the present and prior studies) are, again, a result of interindividual variation in facial shape. Notably, the macaque used here exhibits a proportionally wider (and shorter) upper face such that the elements from which displacement data were collected are positioned somewhat farther lateral to the bite point. Thus, during the simulated bite, bending of the zygoma in the frontal plane due to the action of the masseter muscle has the effect of accentuating vertical displacements in the circumorbital region of this specimen. This finding highlights the difficulty inherent in interpreting and anticipating deformation patterns in geometrically complex objects (see also Chalk et al. 2010).

Hypothesis 2 predicted that strain magnitudes would be higher at locations on the supraorbital torus and postorbital bar in the model lacking septae, but for the most part this was not observed at the dorsal interorbital and working side dorsal orbital and postorbital regions. Evidently, strains are higher in this model at certain locations, but these locations did not correspond with regions used as gage sites in in vivo experimental studies. There are at least three possible explanations of the discrepancy between the FEA results and the prediction of Hypothesis 2. First, the predictions were derived from the results of in vitro bone strain analyses (Ross & Hylander, 1996) that did not consider the effect of muscle forces acting on the supraorbital torus and zygomatic arch. Rather, in the in vitro analyses, strains in the circumorbital region were generated entirely by the bite force. It is not inconceivable that, in certain regions, the stresses generated by the bite force might be opposed by those associated with the muscle forces, meaning that one could remove the septum without unduly influencing strains. A second explanation could be that the supraorbital torus and postorbital bar in M. fascicularis are shaped differently than those of Aotus trivirgatus, and that whereas the relatively gracile circumorbital structures in owl monkeys experience higher strains when the septae are removed, the more robust structures in macaques do not. Finally, a third explanation might be that the circumorbital regions in both taxa exhibit a mosaic pattern of strain increases and decreases (as is evident in the macaque in Fig. 3), but that due to the shape differences between the species, the strain gage locations on the owl monkey corresponded to areas where strains were elevated, whereas in the macaque those same regions exhibited lower strains.

At present, it is difficult to evaluate these possibilities. However, there is a broader issue about which it seems safe to draw conclusions. Ross & Hylander (1996) suggested that the postorbital septum plays only a minor mechanical role, if any, in supporting the bony orbit, and the results obtained here are consistent with their conclusion. In FEA, removal of the septae resulted in subtle changes in the strains exhibited around the orbits, but given the small magnitude of these changes it would be difficult to conclude that the septae are structurally significant from the standpoint of stress absorption. Thus, our results, in conjunction with those of Ross & Hylander (1996), make it appear unlikely that the postorbital septum plays a mechanically significant role in extant anthropoids. This finding has implications concerning scenarios explaining the evolution of this structure. Namely, it suggests that either the septum did not evolve for mechanical (i.e. stress-absorption) purposes, or that, if it did, it no longer serves that purpose. It might be possible to assess these possibilities using FEA by examining models of tarsiers and basal anthropoids such as Catopithecus.

Perhaps the leading non-mechanical hypothesis purporting to explain the evolution of the anthropoid postorbital septum is one stating that the septum promotes occulomotor stability (e.g. Cartmill, 1980; Ross, 1995, 1996; Heesy et al. 2005) by separating the orbital contents from the anterior temporalis muscle. In vivo experiments (Heesy et al. 2005) in cats and galagos (Felis and Otolemur, respectively) have demonstrated that the contraction of the temporalis can displace the eye and potentially interfere with focus. This problem is hypothesized (Cartmill, 1980; Ross, 1995, 1996) to be accentuated in mammals, such as anthropoids, that exhibit extreme degrees of orbital convergence and frontation (i.e. vertical, forward-facing orbits). Thus, early anthropoids would be under strong selection favoring the evolution of a structure or mechanism to stabilize the eye. The postorbital septum may be such a structure. The present study does not allow an evaluation of the occulomotor stability hypothesis, but it does allow the conclusion that mechanical hypotheses are not obviously more viable.

Conclusion

Biomechanical analyses using FEA (this study) and in vitro and in vivo experimental methods (Ross & Hylander, 1996) agree that the postorbital septum plays a limited role, if any, in providing structural support to the circumorbital region of extant anthropoids. Although these findings do not absolutely preclude the possibility that the septum evolved for mechanical reasons, they do at least suggest that non-mechanical explanations (e.g. Heesy et al. 2005) should be seriously considered.

Supporting information

Appendix S1. A sensitivity analysis was conducted to assess the impact of assumptions regarding trabecular bone and constraints.

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer-reviewed and may be re-organized for online delivery, but are not copy-edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.