Abstract
Reliance on plant exudates is a relatively rare dietary specialization among mammals. One well-studied example of closely related exudate feeders is the New World marmosets and tamarins. Whereas marmosets actively gouge tree bark with their incisors to stimulate the flow of sap, tamarins are opportunistic exudate feeders that do not gouge bark. Several studies of the dentaries and jaw adductors indicate that marmosets exhibit specializations for increased gape at the expense of bite force. Few studies, however, have looked to the cranium of marmosets for evidence of functional specializations. Using 3D finite element models of the marmoset Callithrix jacchus and the tamarin Saguinus fuscicollis, we investigated the performance of the cranium under loading regimes that mimicked unilateral molar biting and bark-gouging. We investigated three measures of performance: the efficiency with which muscle force is transferred to bite force, the extent to which the models are stressed (a predictor of failure), and the work expended by muscles as they deform the skull (total strain energy). We found that during molar biting the two models exhibited similar levels of performance, though the Saguinus model had slightly higher mechanical efficiency, a slightly lower state of stress, and expended more energy on deformation. In contrast, under the bark-gouging load, Callithrix exhibited much higher mechanical efficiency than Saguinas, but did so at the expense of more work and higher levels of von Mises stress. This analysis illustrates that differences in the shapes of the skulls of Callithrix and Saguinus confer differences in performance. Whether these aspects of performance are targets of selection awaits broader comparative analyses.
Keywords: finite element analysis, marmoset, performance, tamarin
Introduction
Primates utilize a broad range of dietary resources. At one end of the spectrum are the largely insect-based diets of small-bodied species such as tarsiers and lorises, and at the other are the plant-based diets of gorillas, langurs and howler monkeys. One of the more rare dietary specializations among primates is a reliance on plant exudates (for reviews see Nash, 1986; Power, 1996). Like any dietary specialization, being an exudate feeder comes with costs and benefits. For example, exudates are rich in carbohydrates and sometimes minerals but contain relatively little protein (Power & Oftedal, 1996; Smith, 2000). All exudate feeders also consume significant quantities of fruit and/or insects (Power, 1996, in press). From a physiological perspective exudates are difficult to digest without fermentation and require long gut transit times. The fact that plant exudates are patchily distributed and can be scarce also has a significant impact on the social organization, range size and foraging patterns of many primate species (Clutton-Brock, 1974; Janson & Goldsmith, 1995). Despite the demands of exudate feeding, it has evolved convergently in four families of primates (Callitrichidae, Cheirogaleidae, Lorisidae and Galagidae) and one family of marsupials (Petaruidae) (Charles-Dominique, 1977; Genin, 2008; Nekaris et al., in press; Smith, in press). The repeated evolution of exudate feeding on several different continents is clear evidence that, despite the costs, it can be a successful dietary strategy.
Many exudate-feeding mammals actively gouge the bark of trees to stimulate the flow of sap (Nash, 1986; Goldingay, 1987; Nekaris et al. in press). During bark-gouging animals open their mouths widely, anchor their upper incisors on the trunk of a tree, and use the lower incisors to scrape upward through the bark. Biologists have long suspected that this unique behavior carries a morphological signature. What that signature is and what it indicates about the underlying mechanics of bark-gouging remain a source of debate.
Several comparative analyses of skeletal morphology have demonstrated that bark-gouging mammals exhibit one or more unique features of the dentary and, to a lesser extent, the skull. The list of features varies among studies but often includes low mandibular condyles, short dentaries, increased corpus and symphysis dimensions, basicranial flexion (klinorhynchy), and a narrowing of the skull at the temporal fossa (Cartmill, 1977; Dumont, 1997; Williams et al. 2002; Vinyard et al. 2003; Viguier, 2004). Unique suites of features in bark-gouging primates have been interpreted in two different ways. Several researchers suggest that some of the unique skeletal features of bark-gougers reflect improved structural strength (i.e. resistance to fracture) in the face of forces imposed by bark-gouging (Szalay & Seligsohn, 1977; Szalay & Delson, 1979; Dumont, 1997; Williams et al. 2002). Others conclude that the most of the unique skeletal features of bark-gougers represent adaptations for the wide gape angles that are required to gouge bark (Williams et al. 2002; Vinyard et al. 2003; Viguier, 2004; Vinyard & Ryan, 2006). These latter interpretations have been reinforced by detailed analyses of muscle architecture in bark-gouging marmosets and non-gouging tamarins (Taylor & Vinyard, 2004; Taylor et al. 2009). Despite similarities between the two species in masticatory muscle mass, the temporalis and masseter muscles of tamarins are capable of producing much more force by virtue of enhanced physiological cross-sectional areas. Based on these data, it appears that marmosets have traded force production for the ability to open the mouth widely.
Most of the skeletal features that are unique to bark-gouging primates are found in the lower jaw. The structure of the skull has received meager attention despite the obvious functional link between skulls and jaws and the likelihood that the skull also plays an important role in feeding. Here we investigate the functional implications of cranial architecture in a bark-gouging primate by comparing two closely related taxa: the common marmoset (Callithrix jacchus) and the saddleback tamarin (Saguinus fuscicollis). The diets of marmosets and tamarins are quite similar and include insects, exudates and fruits (Rylands, 1989). Marmosets use their teeth to gouge through bark and thus stimulate the flow of tree exudate (Coimbra-Filho & Mittermeier, 1977; Rylands, 1989; Garber, 1992). Tamarins, on the other hand, are opportunistic exudate feeders and do not gouge bark themselves. Rather, they rely on exudates that flow from trees whose bark has been breached by insects, abiotic processes or, in some cases, marmosets (Garber, 1992; Passamani & Rylands, 2000). These dietary similarities, behavioral differences and the close relationship between marmosets and tamarins make them excellent choices for a pairwise comparison of skull function.
Here we ask whether bark-gouging is reflected in the structure of the skull in the same way that it is associated with specializations in the morphology of the dentary and masticatory musculature. Specifically, we test the hypothesis that under loading conditions that simulate bark-gouging, the skull of a bark-gouger exhibits one or more elements of enhanced performance relative to that of a non-gouger. We predict that under a bark-gouging load and relative to a non-gouger, the skull of a bark-gouger will (i) be more resistant to structural failure (i.e. exhibit lower stress), (ii) expend less energy on elastic deformation, and (iii) exhibit greater efficiency in its ability to transfer muscle force into bite force. In contrast, we predict that the skull of a non-gouger will perform better under loads that simulate biting with the molar teeth. We test these predictions using finite element models of C. jacchus and S. fuscicollis skulls under loads that simulate both molar biting and bark-gouging. Finite element (FE) modeling and analysis is a technique borrowed from engineering that is increasingly used to evaluate the functional implications of morphological variation among living and extinct organisms (see reviews in Richmond et al. 2005; Rayfield, 2007). Unlike in vivo experimentation, FE modeling provides the opportunity to compare the performance of structures with different shapes, fully controlling for the effects of differences in size (Dumont et al. 2009). This analysis takes full advantage of that capacity.
Materials and methods
Model construction and definition of material properties
Finite element models of the skull were constructed from CT scans of dry skulls (slice thickness = 0.08332 mm) from one adult male saddleback tamarin (S. fuscicollis, AMNH 98286) and one adult male common marmoset (C. jacchus, AMNH 42608) generated by the University of Texas at Austin CT facility. The transformation of CT scans into FE meshes of the skulls involved the use of two different software tools. First, we used mimics® (Materialise NV, Leuven, Belgium) to generate and condition three-dimensional (3D) surface representations of the skulls. These models included both cortical bone and all of the trabecular bone within the lower face, frontal and ear regions; trabecular bone within the occipital region was not modeled (Fig. 1). Secondly, the surface representations were brought into studio geomagic® (Geomagic, Inc., Research Triangle Park, NC, USA) where they were edited to correct small anatomical errors and to make minor geometric adjustments to facilitate the construction of solid finite element meshes. The latter process included rounding of sharp corners, eliminating artifacts caused by the surface extraction process, deleting very small unnamed foramina, and deleting the nasal turbinates (which are thin and complex but unlikely to be load-bearing). We then brought the surface representations back into mimics, where we adjusted the aspect ratios of the triangular surface elements and generated solid finite element models composed of four-noded tetrahedral elements. The completed Callithrix skull model consisted of 1 136 737 elements and the Saguinus skull model of 1 248 605 elements.
Fig. 1.
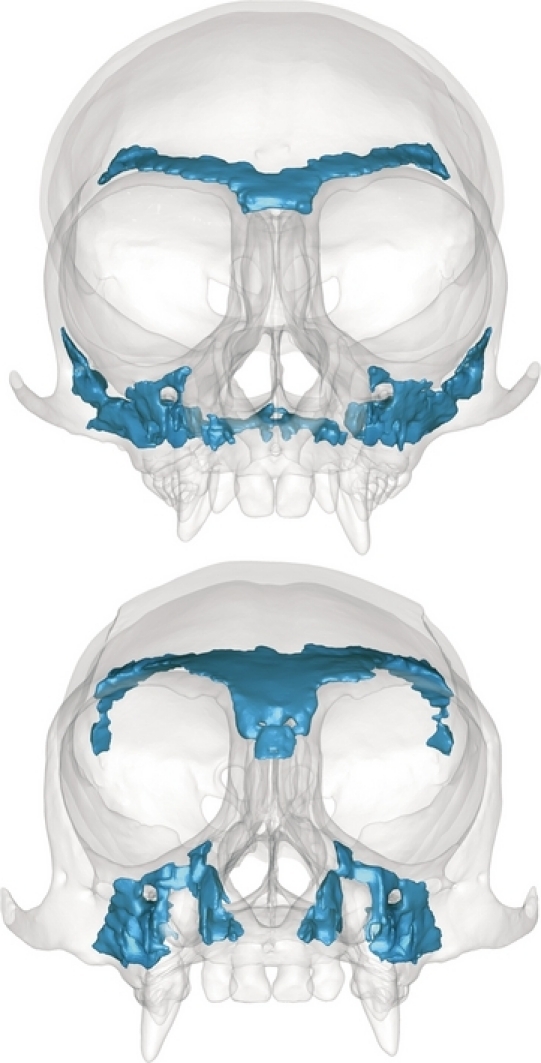
3D surface representations of the Callithrix jacchus (top) and Saguinus fuscicollis (bottom) models. Cortical bone is opaque to illustrate embedded regions of trabecular bone (shown in blue).
To evaluate the relative performance of the skulls of Callithrix and Saguinus during bark-gouging and molar biting, it was critical to account for the position of the dentary under the two different loading conditions. As the jaw is elevated, the locations of the muscle attachments on the jaw and the dentary condyles shift relative to the axis of the temporomandibular joint (TMJ), and these changes may have a significant impact on the moments created by the adductor muscles about the TMJ axis. Taylor & Vinyard (2004) reported an average gape of ∼23 mm in Callithrix during bark-gouging and we achieved this distance in our Callithrix model by depressing the dentary and shifting it anteriorly such that the condyles were in close proximity to the articular eminence (Fig. 2). The 23-mm gape in Callithrix translated into a 50° gape angle as measured in lateral view as the angle from the minimum curvature of the postglenoid process to the upper and lower incisors. We depressed the dentary in our Saguinus model and shifted it anteriorly to achieve the same 50° gape angle. To compare the performance of the skulls of Callithrix and Saguinus during molar biting, we depressed the lower jaws of both models by 15° as measured from the minimum curvature of the postglenoid process to the tips of the M1 protoconid and M1 paracone (Fig. 2). For the 15° gape, the condyles of both species were placed just anterior to the postglenoid process.
Fig. 2.
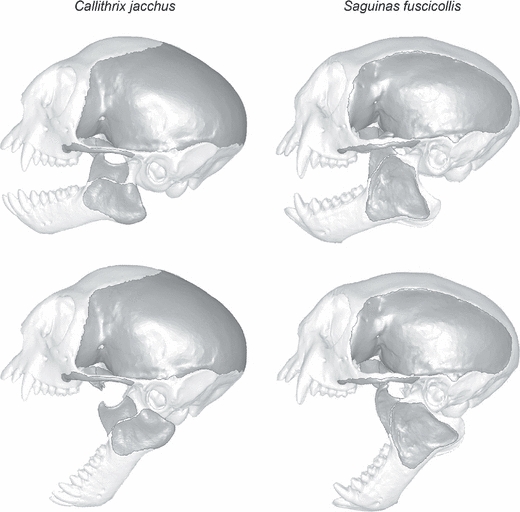
Lateral views of Callithrix jacchus (left) and Saguinus fuscicollis (right) with jaw positions for molar biting (15° gape, top) and bark-gouging (50° gape, bottom) simulations. Muscle attachment areas are darker in color.
No data are available on the material properties of cortical or trabecular bone in marmosets or tamarins. Detailed analyses of macaque craniofacial bone demonstrate that it has different material properties in different orthogonal directions (i.e. it is orthotropic) and that material properties vary from region to region (Dechow & Hylander, 2000; Strait et al. 2005). We do not know whether the same patterns of orthotropy and regional variation apply to marmosets and tamarins. However, we do know that variation in material properties has less of an impact on large-scale patterns of stress and strain than does variation in model shape (Ross et al. 2005; Strait et al. 2005; McHenry et al. 2006; Wroe et al. 2007). For this study the Callithrix and Saguinus models were assigned average isotropic material property values for cortical bone in macaques (Young's modulus = 17.3 GPa, Poisson's ratio = 0.28) and trabecular bone in humans (Young's modulus = 2.23 GPa, Poisson's ratio = 0.28) (Strait et al. 2005; Sebaa et al. 2008).
Constraints against rigid body motion
Each model was constrained from rigid body motion by fixing a series of nodes that represent the contacts between the mandibular condyles and skull, and between either the front teeth and a vertical substrate or the upper right first molar tooth and a food item. Following the methods laid out in previous FE analyses of mammalian masticatory systems (Strait et al. 2002, 2005; Dumont et al. 2005), forces representing the masticatory muscles pull the skull ventrally onto these constraints, generating reaction forces at the TMJ and bite reaction forces at the teeth.
We accounted for the forward translation of the mandibular condyle in the glenoid fossa as the jaw opens by using different pairs of nodes to define the TMJ axis during narrow-gaped molar-biting and wider-gaped bark-gouging positions. For each species, we viewed the glenoid fossa from as planar a perspective as possible and then estimated the locations of the most anterior and posterior contact points along a line drawn between the centers of the postglenoid process and articular eminence (the latter is pronounced in Callithrix and very small in Saguinus). We used the anterior point to represent the TMJ axis during a 50°, bark-gouging gape and the posterior point to represent the center of rotation when the mouth was closed (0° gape). We assumed a linear relationship between gape angle and the point of contact of the condyle and interpolated the location of the contacts at the 15°, molar-biting gape.
For each loading condition (15° and 50°), we used the single node in each glenoid fossa to represent the point of contact of the mandibular condyle and defined a local coordinate system in which the x-axis corresponded to the axis between the two TMJs. To ensure against over-constraining the model, one of the TMJ nodes was fixed in all directions and the other was fixed only in the y and z directions. This allowed the skull to deform laterally (i.e. in a direction of the TMJ axis) when the model was fully constrained against rigid body motion. By themselves, these TMJ constraints were only sufficient to prevent five modes of rigid body motion – translation in all three directions and rotations about the y and z axes. The sixth possible mode of rigid body motion was rotation about the TMJ axis. In the absence of additional nodal constraints, the skull would rotate freely about the TMJ axis when muscle forces were applied. We solved this problem by constraining one or more nodes on the teeth against motion. These constraints allowed the muscle forces we applied to elastically deform the skull and simulated the biomechanics of biting.
To model bite forces during unilateral molar loading, single nodes on the tips of the protocone, paracone and metacone of the right upper first molar were constrained in the direction perpendicular to the occlusal plane of the P3 and M1 paraconids. To model bite reaction forces under the bark-gouging loading condition, we established a coordinate system that defined a plane passing through the long axes of both upper incisors. Three nodes on the occlusal surface of each upper central incisor were fixed against motion in the long axis direction of each plane.
Modeling masticatory muscle forces
During both molar biting and bark-gouging, the primary muscles of mastication (temporalis, masseter, and medial and lateral pterygoid) function in closing the jaw. To model the relative magnitude of these forces we used published values of normalized physiological cross-sectional area (nPCSA) for the temporalis and masseter of C. jacchus and Saguinus oedipus (Taylor et al. 2009), substituting the latter nPCSA values in Saguinus (Table 1). Values of mass for the pterygoid muscles of Callithrix were derived from the dissection of a single adult male and accords reasonably well with the percentages of the pterygoideus internus and pterygoideus externus reported for Callithrix pennicillata (Turnbull, 1970). We assumed the same muscle masses for the pterygoids of Saguinus. nPCSA values for the medial and lateral pterygoid muscles were estimated by multiplying the sum of nPCSA for the temporalis and masseter by the ratio of pterygoid muscle mass to the mass of the temporalis and masseter (A. Taylor and C. Vinyard, personal communication). Independent estimates based solely on the relative contribution of the pterygoids to total muscle mass yielded similar results.
Table 1.
Mass, nPCSA, % nPCSA, and input forces representing the primary jaw adductors in models of Callithrix jacchus and Saguinus fuscicollis at a gape angle representing molar biting (15°). Methods of calculating nPCSA for the pterygoid muscles are described in the text.
| Mass | nPCSA | % nPCSA | Input force (N) | |
|---|---|---|---|---|
| C. jacchus (15°) | ||||
| Temporalis* | 1.53 | 1.6 | 48 | 68.27 |
| Masseter* | 1.1 | 1.31 | 39 | 55.47 |
| Medial pterygoid | 0.3 | – | 10 | 14.22 |
| Lateral pterygoid | 0.2 | – | 3 | 4.27 |
| Sum of input Force | 142.23 | |||
| S. fuscicollis (15°) | ||||
| Temporalis* | 1.79 | 2.72 | 49 | 69.69 |
| Masseter* | 1.29 | 2.19 | 39 | 55.47 |
| Medial pterygoid | 0.3 | – | 9 | 2.80 |
| Lateral pterygoid | 0.1 | – | 3 | 4.27 |
| Sum of input force | 142.23 | |||
To define the vectors of the masticatory muscle forces, we first identified regions of muscle origin on our skull and dentary models based on dissections of Callithrix (ours and A. Taylor, personal communication; Fig. 2). We defined muscle insertion points on the lower jaw as the 3D area centroid of each muscle's area of attachment and used a modified version of the program BoneLoad (Grosse et al. 2007) to apply forces distributed over the muscle origins on the skull and pointing directly to the muscle insertion points. Within each muscle group we accounted for variation in force due to muscle fiber stacking by varying the magnitudes of the force vectors acting on individual elements according to the ratio of the distance from the muscle insertion centroid to the furthest element to the distance from muscle insertion centroid to the element at which the force is applied. We held the relative contribution of each of the primary masticatory muscles to total muscle force constant in our FE analyses at the narrow, 15°, molar-biting gape. This assumed simultaneous, maximum and bilateral activity of the temporalis, masseter, medial and lateral pterygoid muscles at maximum occlusion (De Gueldre & De Vree, 1988; Hylander et al. 2004). However, a preliminary analysis of incisive biting at wide gapes while applying muscle forces in proportion to their relative nPCSA indicated that the temporalis imposed a negative moment about the TMJ axis (i.e. its action was to depress jaw). Because the temporalis was working against the other jaw adductors, it would have been necessary to assume impossibly high muscle forces (357 N, compare to values in Table 1) to achieve the 21 N of bite force known to occur in Callithrix at a wide gape angle (Mork et al. 2005). We resolved this clearly unrealistic situation by applying only those temporalis forces on element faces that imposed a positive moment about the TMJ axis. This eliminated forces applied by the posterior portions of temporalis in both species and resulted in a relative increase in forces applied by masseter and the two pterygoids (Table 2). The marked decrease in the relative contribution of temporalis to total muscle force in Callithrix is a consequence of its lower coronoid process and therefore more inferior location of the temporalis insertion point relative to the TMJ axis.
Table 2.
Percentage of total masticatory nPCSA represented by each muscle, model input forces, resulting applied forces, and % applied forces representing the primary jaw adductors, neck muscles and forces pushing upward through the spine in models of Callithrix jacchus and Saguinus fuscicollis at a gape angle representing bark-gouging (50°). Applied masticatory force is less than input masticatory force because it includes only those portions of temporalis muscles that produce positive moments about the TMJ axis. Note that sums of applied force are identical for each model.
| % Masticatory nPCSA | Input force (N) | Applied force (N) | % Applied force | |
|---|---|---|---|---|
| C. jacchus (50°) | ||||
| Temporalis | 48 | 107.87 | 43.87 | 27 |
| Masseter | 39 | 87.64 | 87.64 | 55 |
| Medial pterygoid | 10 | 22.47 | 22.47 | 14 |
| Lateral pterygoid | 3 | 6.74 | 6.74 | 4 |
| Neck muscle | 69.76 | 69.76 | ||
| Spine | 52.33 | 52.33 | ||
| Sum of applied force | 282.81 | |||
| S. fuscicollis (50°) | ||||
| Temporalis | 49 | 87.46 | 69.70 | 43 |
| Masseter | 39 | 69.61 | 69.61 | 43 |
| Medial pterygoid | 9 | 16.06 | 16.06 | 10 |
| Lateral pterygoid | 3 | 5.35 | 5.35 | 3 |
| Neck muscle | 69.76 | 69.76 | ||
| Spine | 52.33 | 52.33 | ||
| Sum of applied force | 282.81 | |||
Modeling non-masticatory forces associated with bark-gouging
In contrast to molar biting, masticatory muscle forces are only part of the input required for the bark-gouging model. Marmosets also employ their legs to push the head upward through its contact with the spine. Neck muscles are used to assist in prying bark from the tree (Vinyard et al. 2009). We calculated neck and spine forces using a free body diagram (Fig. 3). Measured bite forces were applied at the upper (Fui = 21 N, γ = 67°) and lower incisors (Fli = 28 N, θ = 33°; C. Vinyard, personal communication). We assume the force transmitted to the skull through the spine (Fs) was perpendicular to the plane between the most inferior point of occipital condyle and the occlusal surface of the upper incisor. At the wide gape, this translates to a spine force applied to the skull at an angle (φ) of 34° relative to the x-y plane of the vertical substrate against which the incisors are placed (i.e. xy-plane of the free body diagram). We solved for the magnitude of spine forces and the magnitude and direction of neck forces assuming static equilibrium (Appendix). We also assumed that neck forces acted in the sagittal plane and applied them in the center of the region of attachment of the nuchal musculature. We applied the neck and spine forces derived from these calculations to the finite element model of the Callithrix skull. We then added masticatory muscle forces and scaled their magnitudes to achieve a bite force of 21 N at the upper incisors. For comparison, the same total force was applied to the Saguinus skull.
Fig. 3.

Free body diagram of Callithrix during gouging. Bite forces at the upper incisors (Fui = 21 N, γ = 67°) and lower incisors (Fli = 28 N, θ = 33°) are statically balanced with forces at the neck (Fn y & Fn z) and spine (Fs, φ = 34°).
Comparing model performance
In the context of finite element modeling, performance refers to the mechanical performance of specific structures. These definitions of performance stem from engineering, where structures are evaluated in terms of their strength and/or efficiency. In this study we compared the models of Callithrix and Saguinus on the basis of three mechanically based measures of performance: von Mises stress, strain energy and the efficiency with which muscle force is transferred into bite force.
In practice, the primary challenge in comparing the performance of the Callithrix and Saguinus models is the lack of in vivo data for Saguinus. Bite force data are available for Callithrix, making it possible to estimate total muscle force and predict how those forces deform and are transferred through the skull of a living animal. The lack of similar data for Saguinus makes it impossible to calibrate the model and therefore impossible to generate meaningful estimates of the magnitudes of in vivo stress, strain energy or bite force. Short of collecting in vivo data from Saguinus, the solution to this dilemma is to remove the effects of size and compare the performance of the models solely on the basis of their shapes (Dumont et al. 2009). This approach allows comparisons of models with respect to their structural strength (as evidenced by stress) and efficiency (as evidenced by strain energy and muscle force to bite force ratios) while controlling for the confounding effects of model size. In practice these size-adjusted comparisons can be made by controlling the ratios of force to surface area (for stress) and force squared to volume ratios (for strain energy).
The first performance variable we calculated was von Mises stress, which provides a measure of the ability of structures composed of ductile materials to resist failure by plastic deformation. This ‘failure criterion’ posits that ductile materials will yield and exhibit permanent plastic deformation when the von Mises stress at any given point exceeds the strength of the material. The ratio of the strength of the material to the maximum von Mises stress that occurs in the structure is called the safety factor. When comparing two structures under specified loading conditions, the structure with the higher safety factor (i.e. lower maximum von Mises stress) is less likely to fail and therefore performs better than a structure with a lower safety factor (i.e. higher maximum von Mises stress). However, this deterministic approach does not account for the stochastic nature of material strength. Material strength varies not only across different samples of the same material but also spatially within a given sample of material. This means that the spatial distribution of relatively high stress values is also important. For example, consider two structures of the same material each admitting the same maximum von Mises stress value and therefore having the same deterministic safety factor value. Assume structure A has a relatively higher proportion of its total volume within 90% of the maximum von Mises stress than does structure B. Structure A would have a higher probability of failure simply because there is a greater probability that the stress will exceed the strength at some material point.
To compare stress between the two models without introducing artifacts due to differences in size, it is important to apply the same ratio of muscle force to model surface area (Dumont et al. 2009). We did this by isometrically scaling the Saguinus model to have the same surface area as the Callithrix model and then applying the same total muscle force to each model. For the molar-biting load case both models were loaded with the same ratio of total (masticatory) muscle force to surface area required for the Callithrix model to return a bite reaction force at the upper right molar of 45 N (Mork et al. 2005) perpendicular to the occlusal plane of the P3 and M1 paraconids. Similarly, for the bark-gouging simulation, both models were loaded with the same ratio of total muscle force (neck + spine + masticatory) to surface area required for the Callithrix model to return a total bite reaction force at the upper incisors of 21 N (Mork et al. 2005; C. Vinyard, personal communication) in the opposite direction of Fui (Fig. 3). We compared von Mises stress between the two models by visual inspection of contour plots and by comparing maximum stress values in the most highly stressed region. The latter provided a quantitative estimate of the relative resistance of the two models to failure.
The second performance metric we investigated was strain energy (SE). This metric of energy efficiency quantifies the energy that is expended by external forces to deform a structure and transmit forces through it (Dumont et al. 2009). Models that are stiffer require less energy (i.e., muscle force) to deform them. Assuming that the function of the system under study is to transmit forces rather than to store energy, stiffer models are more efficient compared to models that are more compliant. To remove the effects of size from comparisons of SE in different models, it is important to keep in mind that SE is proportional to force squared and inversely proportional to the cube root of volume. Although our models were scaled to the same surface area and had the same applied force values, the volume of the Saguinus model was higher. Therefore, to compare strain energy performance we simply multiplied the SE obtained from the Saguinus model by (VolumeSaquinas/VolumeCallithrix)1/3 and compared it to the SE value derived from the Callithrix model (Dumont et al. 2009). We calculated strain energy for the two models under the same bark-gouging and molar-biting loading conditions used in our assessment of von Mises stress.
As a third performance variable, we compared the ratio of predicted bite force to applied muscle force resulting from these loading regimes. This measure, the mechanical efficiency of biting, provided a scale-independent estimate of the efficiency with which muscle force is translated into bite force. Note that isometric scaling of a model does not alter its mechanical efficiency. Mechanical efficiency of biting differs from SE in that it speaks to the efficiency of the lever system defined by the TMJ axis, bite points and muscle force vectors, whereas SE provides an estimate of the energy expended on elastic deformation of the skull when it is constrained against rigid body motion and loaded with muscle forces.
Results
Stress contour maps of both models under molar-biting loads exhibited similar patterns in the distribution of von Mises stress (Fig. 4). In both cases, the inferior orbital margin on the working side was stressed, as was the lateral margin of the orbit on the balancing side. Lateral views of the working sides of the skulls revealed elevated stress in the antero-inferior region of the inter-orbital septum and near the junction between the lateral pterygoid plates and maxilla. Ventral views also illustrated stress on the posterior edge of the palate on the working side. The zygomatic arch on the working side was the most highly stressed region in both species, indicating that this was the region with the lowest safety factor and therefore where failure was most likely to occur. Overall, the stress contour maps suggest that Saguinus was less stressed than Callithrix under both loading regimes.
Fig. 4.
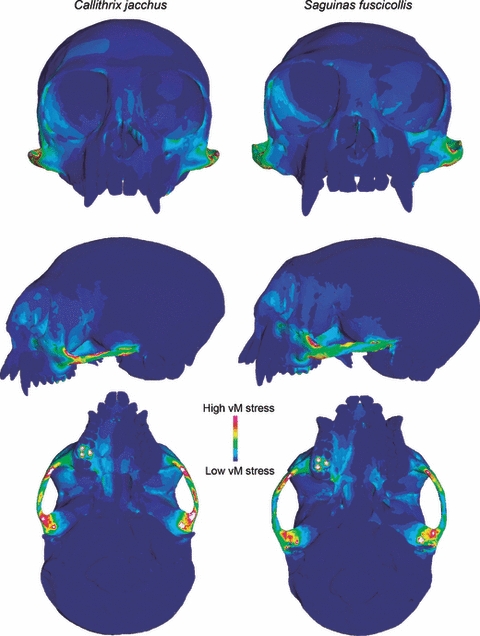
The predicted distribution of von Mises stress in models of Callithrix jacchus (left) and Saguinus fuscicollis (right) during unilateral molar biting (15° gape). Warm colors indicate high von Mises stress and cool colors indicate regions of low stress. White areas indicate stresses that exceed the range specified for the contour plot.
Table 3 presents quantitative performance metrics for molar biting that complement the stress contour plots and illustrate that differences in the performance of the two models were relatively small. As expected, the peak von Mises stress value within the working side zygomatic arch was slightly (10%) lower in Saguinus than in Callithrix. Saguinus also performed 11% better in terms of the efficiency with which muscle force was transferred into bite force. However, in contrast to stress and mechanical efficiency, Saguinus performed 13% more poorly than Callithrix with respect to strain energy. In other words, under simulated molar biting, the Saguinus skull was marginally more resistant to fracture and more mechanically efficient than the Callithrix model, but more energy was spent in deformation. Nevertheless, the magnitudes of these differences were small.
Table 3.
Peak von Mises stress in the working side zygomatic arch, strain energy and mechanical efficiency performance of the Callithrix and Saguinus models under simulated molar-biting (15° gape) and bark-gouging (50° gape) loads. Percent difference is the absolute value of the difference between the two values divided by the value for Callithrix. Higher performance is indicated in bold.
| Loading condition | Peak stress (MPa) | Strain energy (J) | Mechanical efficiency (Fbite/Fmuscle) |
|---|---|---|---|
| Molar biting (15° gape) | |||
| C. jacchus | 52.6 | 1.46 × 10−3 | 0.316 |
| S. fuscicollis | 47.6 | 1.65×10−3 | 0.352 |
| Difference (%) | 10 | 13 | 11 |
| Bark-gouging (50° gape) | |||
| C. jacchus | 168 | 1.01×10−2 | 0.053 |
| S. fuscicollis | 120 | 0.75 × 10−2 | 0.030 |
| Difference (%) | 29 | 26 | 43 |
As in molar biting, stress contour maps for the bark-gouging load revealed similar patterns of stress distribution in the Callithrix and Saguinus models (Fig. 5). In frontal view, both models exhibited elevated stress along the naso-alveolar clivus, the lateral margins of the nasal aperture, the lateral margins of the orbit and post-orbital septum, and near the anterior root of the zygomatic arch. Lateral views further illustrated elevated stress in the sphenoid portion of the infratemporal fossa, and ventral views showed high stress in both the anterior and posterior regions of the palate. Again, the zygomatic arches were the regions of highest stress in both models and Callithrix appeared to be more stressed than Saguinus.
Fig. 5.
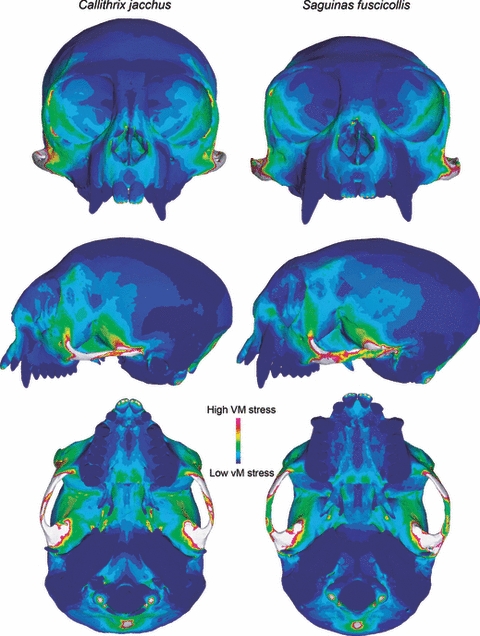
The predicted distribution of von Mises stress in models of Callithrix jacchus (left) and Saguinus fuscicollis (right) during bark-gouging (50° gape). Warm colors indicate high von Mises stress and cool colors indicate regions of low stress. White areas indicate stresses that exceed the range specified for the contour plot.
Not unexpectedly, both models performed more poorly under the bark-gouging load than the molar-biting load (Table 3). However, differences in the performance of the two models were far more dramatic. The peak von Mises stress value was 29% lower in Saguinus relative to Callithrix. Similarly, Saguinus exhibited 26% lower SE values. However, Callithrix performed 43% better with respect to mechanical efficiency under the bark-gouging load. In other words, the Callithrix model had much higher mechanical efficiency than the Saguinus model under the bark-gouging simulation, but it was more stressed and more energy was invested in deformation.
Discussion
This study investigated the impact of skull shape on the performance of models of the skulls of Callithrix (a bark-gouger) and Saguinus (a non-gouger) under both molar-biting and bark-gouging loads. Our hypothesis that under loading conditions that simulate bark-gouging the skull of Callithrix exhibits one or more elements of enhanced performance met with mixed results, as did the prediction that Saguinus would perform better under loads that simulate molar biting. The patterns of variation in performance variables lead to questions about the link between performance variables we described here and selection on organismal form.
Although the distribution of von Mises stress is very similar between the two models, these analyses predict that the skull of Saguinus is more resistant to ductile fracture than Callithrix (i.e. exhibits lower peak von Mises stress) under both molar-biting and bark-gouging loads. In other words, the skull of Saguinus has a higher safety factor and could bear relatively higher loads before it experienced ductile failure. These results are consistent with the idea that marmosets have traded the capacity to generate (and, presumably, bear) high forces at the incisors for the ability to open their mouths widely (e.g. Vinyard et al. 2003; Taylor et al. 2009). One of our predictions was that the energy expended on deformation (i.e. strain energy) would be lowest in Callithrix during bark-gouging and lowest in Saguinus during molar biting. This was not the case. Surprisingly, the Callithrix model expended 26% more energy to deformation than Saguinus during bark-gouging, while the Saguinus model expended 13% more energy to deformation than Callithrix during molar biting. Energy efficiency clearly is not optimized for either bark-gouging in Callithrix or molar biting in Saguinus. This suggests either that energy spent on deformation is so small as to be inconsequential and/or that it is an acceptable cost paid for some other aspect of enhanced performance. For example, within these data we found a consistent, inverse relationship between strain energy and mechanical efficiency.
The performance of the two models with respect to mechanical efficiency during bark-gouging provided clear support for our hypothesis. We found that, during molar biting, the Saguinus and Callithrix models differed in mechanical efficiency by only 11%, but that mechanical efficiency was 43% higher for Callithrix under a bark-gouging load. Mechanical efficiency is based on the configuration of the underlying lever system defined by the TMJ axis, the moments produced by the muscles about the TMJ axis, and the distance from the TMJ axis to the bite point(s). Thus, our results demonstrate that the geometry of the skull in Callithrix is well-suited for the efficient transfer of muscle force to bite force during bark-gouging, whereas differences between the two models during molar biting were only modest.
FEA provides a powerful tool for investigating the mechanical performance of biological structures. One of the next frontiers in comparative FEA studies will be to understand how mechanical performance metrics relate to whole-organism performance and, ultimately, the evolution of organismal form. The concept of whole-organism performance is rooted in the field of ecological morphology, where performance metrics describe an organism's ability to perform an ecologically relevant task that impacts fitness (Arnold, 1983; Lande & Arnold, 1983). In studies of feeding, bite force is often used as a performance variable because it reflects the potential breadth of an animal's diet based on food hardness (Anderson et al. 2008). This very proximate measure of performance speaks to the direct interaction between an organism and its environment, and field studies have demonstrated the rapid evolution of bite force in populations that encounter selection for a more resistant diet (Goheen et al. 2003; Herrel et al. 2008). The question is, how do FEA-based measures of mechanical performance relate to aspects of organismal performance that are seen by natural selection?
This analysis does not predict absolute bite forces for Saguinus. However, it does demonstrate that after controlling for size, the skull of Saguinus would produce relatively higher bite force during molar biting and that of Callithrix would produce relatively higher bite force during bark-gouging. In other words, the geometry of the lever system in Callithrix is most efficient in bark-gouging and that of Saguinus is most efficient in molar biting. This is consistent with what we know of the feeding ecology of these animals. Although it is impossible to identify adaptation in the absence of a more complete phylogenetic sample, these results suggest that the shape of the skull in Callithrix has been optimized for bark-gouging. The implications of our stress and strain energy results for organismal performance are less clear.
To date, there are no data to suggest that the skulls of mammals are stress-limited. With the exception of relatively high frequencies of tooth fracture in some carnivores (Van Valkenberg & Ruff, 1987; Fenton et al. 1998; Van Valkenburgh, 2009), there is no known example of a mammal voluntarily loading its skull to failure during feeding. The von Mises stress values predicted by our FE analyses indicate that the skull of Callithrix is weaker (i.e. less resistant to failure) than that of Saguinus. Studies of muscle structure suggest that Callithrix has traded the capacity to produce high bite forces for the ability to open its mouth widely. From an evolutionary perspective, however, it is not clear whether its elevated stress values reflect selection for decreased structural strength or simply the absence of selection for high structural strength. Although the difference between these alternatives may seem subtle, the answer is fundamental to understanding whether and how stress plays a role in the evolution of skull form.
Dumont et al. (2009) suggested that selection for energy efficiency (i.e. low strain energy) may occur in biomechanical systems that rely on the efficient transfer of forces rather than elastic deformation. If energy efficiency were optimized in Callithrix and Saguinus, we would expect Callithrix to exhibit the lowest strain energy during bark-gouging and Saguinus the lowest strain energy during molar biting. In fact the opposite was true. Moreover, bark-gouging was 26% more costly for Callithrix– the second largest relative difference in any performance variable that we surveyed. This raises the question, how expensive is bark-gouging for Callithrix? One possibility is that the work it expends on deformation is so small as to be biologically meaningless. This analysis predicts that Callithrix expends only 1.01 × 10−2 Joules on deformation each time the skull experiences a bark-gouging load. Depending on the frequency with which Callithrix engages in bark-gouging and the costs/benefits of other components of this foraging strategy (search time, nutritional reward, etc.), it may or may not represent a significant investment of energy.
Conclusions
These analyses highlight two important issues in comparative finite element analyses. First, they illustrate the utility of FEA for making comparisons between animals for which there are limited in vivo data. Even in the absence of absolute values of bite force, stress and strain energy for Saguinus, by controlling for size and loading regime we could compare the relative magnitudes of these quantities as well as mechanical efficiency of biting between Saguinus and Callithrix. Secondly, these analyses demonstrate that the link between measures of mechanical performance and whole-organism performance are not yet well-understood. An important step toward accomplishing that will be to expand comparative FE analyses beyond two-taxon comparisons to include samples of species with known phylogenetic relationships and for which there are in vivo data with which to calibrate (and preferably validate) the results.
Acknowledgments
We are grateful to Sam Cobb for organizing the Craniofacial Biomechanics symposium and to our fellow attendees for many fruitful interactions. We extend special thanks to A. Taylor and C. Vinyard for discussions about nPCSA, muscle attachments and unpublished bite forces. We also thank D. Pulaski for FE model construction, L. Godfrey and L. Curran for access to specimens for dissection, the Mammalogy Department at the American Museum of Natural History for access to specimens for CT-scanning, and S. Santana, T. Eiting and J. Tanner for comments on this manuscript. This work was supported by NSF grant DBI 0743460 to E. R. Dumont and I. R. Grosse and NIH grant RR00168 to the New England Primate Research Center.
Appendix: Determination of neck and spine forces
In this Appendix we present the equations used to determine neck and spine forces during bark gouging. Figure 3 shows the lateral view of the full skull with upper incisor, lower incisor, and neck and spine forces applied. Note that masticating forces are not included as these forces are equal and opposite internal forces for the skull system as defined here. The three unknowns are the y and z components of the neck force and the magnitude of the spine force. Static equilibrium is assumed to exist in the sagittal plane, resulting in the three simultaneous algebraic equations shown below which were then solved for the three unknowns.
References
- Anderson R, McBrayer LD, Herrel A. Bite force in vertebrates: opportunities and caveats for use of a nonpareil whole-animal performance measure. Biol J Linn Soc. 2008;93:709–720. [Google Scholar]
- Arnold SJ. Morphology, performance and fitness. Am Zool. 1983;23:347–361. [Google Scholar]
- Cartmill M. Daubentonia, Dactylopsila, woodpeckers and klinorhynchy. In: Martin RD, Doyle GA, Walker AC, editors. Prosimian Anatomy, Biochemistry and Evolution. London: Duckworth; 1977. pp. 655–670. [Google Scholar]
- Charles-Dominique P. Ecology and Behaviour of Nocturnal Primates. London: Duckworth; 1977. [Google Scholar]
- Clutton-Brock TH. Primate social organization and ecology. Nature. 1974;250:539–542. [Google Scholar]
- Coimbra-Filho AF, Mittermeier RA. Tree-gouging, exudate-eating and the ‘short-tusked’ condition in Callithrix and Cebuella. In: Kleiman DG, editor. The Biology and Conservation of the Callitrichidae. Washington, D.C.: Smithsonian Institute Press; 1977. pp. 105–115. [Google Scholar]
- De Gueldre G, De Vree F. Quanitative electromyography of the masticatory muscles of Pteropus giganteus (Megachiroptera) J Morphol. 1988;196:73–106. doi: 10.1002/jmor.1051960107. [DOI] [PubMed] [Google Scholar]
- Dechow PC, Hylander WL. Elastic properties and masticatory bone stress in the macaque mandible. Am J Phys Anthropol. 2000;112:553–574. doi: 10.1002/1096-8644(200008)112:4<553::AID-AJPA9>3.0.CO;2-R. [DOI] [PubMed] [Google Scholar]
- Dumont ER. Cranial shape in fruit, nectar, and exudate feeders: implications for interpreting the fossil record. Am J Phys Anthropol. 1997;102:187–202. doi: 10.1002/(SICI)1096-8644(199702)102:2<187::AID-AJPA4>3.0.CO;2-W. [DOI] [PubMed] [Google Scholar]
- Dumont ER, Piccirillo J, Grosse IR. Finite-element analysis of biting behavior and bone stress in the facial skeletons of bats. Anat Rec A Discov Mol Cell Evol Biol. 2005;293:319–330. doi: 10.1002/ar.a.20165. [DOI] [PubMed] [Google Scholar]
- Dumont ER, Grosse IR, Slater GS. Requirements for comparing the performance of finite element models of biological structures. J Theor Biol. 2009;256:96–103. doi: 10.1016/j.jtbi.2008.08.017. [DOI] [PubMed] [Google Scholar]
- Fenton MB, Waterman JM, Roth JD, et al. Tooth breakage and diet: a comparison of bats and carnivorans. J Zool. 1998;246:83–88. [Google Scholar]
- Garber PA. Vertical clinging, small body size, and the evolution of feeding adaptations in the callitrichinae. Am J Phys Anthropol. 1992;88:469–482. doi: 10.1002/ajpa.1330880404. [DOI] [PubMed] [Google Scholar]
- Genin F. Life in unpredictable environments: first investigation of the natural history of Microcebus griseorufus. Int J Primatol. 2008;29:303–322. [Google Scholar]
- Goheen JR, Swihart RK, Robins JH. The anatomy of a range expansion: changes in cranial morphology and rates of energy extraction for North American red squirrels from different latitudes. Oikos. 2003;102:33–44. [Google Scholar]
- Goldingay RL. Sap feeding by the marsupial Petaurus australis: an enigmatic behaviour? Oecologia. 1987;73:154–158. doi: 10.1007/BF00376992. [DOI] [PubMed] [Google Scholar]
- Grosse IR, Dumont ER, Coletta C, et al. Techniques for modeling muscle-induced forces in finite element models of skeletal structures. Anat Rec A Discov Mol Cell Evol Biol. 2007;290:1069–1088. doi: 10.1002/ar.20568. [DOI] [PubMed] [Google Scholar]
- Herrel A, Huyghe K, Vanhooydonck B, et al. Rapid large-scale evolutionary divergence in morphology and performance associated with exploitation of a different dietary resource. Proc Natl Acad Sci U S A. 2008;105:4792–4795. doi: 10.1073/pnas.0711998105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hylander WL, Ravosa MJ, Ross C. Jaw muscle recruitment patterns during mastication in anthropoids and prosimians. In: Anapol F, German RZ, Jablonski NG, editors. Shaping Primate Evolution. Cambridge: Cambridge University Press; 2004. pp. 229–257. [Google Scholar]
- Janson CH, Goldsmith ML. Predicting group size in primates: foraging costs and predation risks. Behav Ecol Sociobiol. 1995;6:326–336. [Google Scholar]
- Lande R, Arnold SJ. The measurement of selection on correlated characters. Evolution. 1983;37:1210–1226. doi: 10.1111/j.1558-5646.1983.tb00236.x. [DOI] [PubMed] [Google Scholar]
- McHenry CR, Clausen PD, Daniel WJT, et al. Biomechanics of the rostrum in crocodilians: a comparative analysis using finite-element modeling. Anat Rec A Discov Mol Cell Evol Biol. 2006;288:827–849. doi: 10.1002/ar.a.20360. [DOI] [PubMed] [Google Scholar]
- Mork AL, Wall CE, Williams SH, et al. The biomechanics of tree gouging in common marmosets (Callithrix jacchus) Am J Phys Anthropol. 2005;Suppl 40:153–154. [Google Scholar]
- Nash LT. Dietary, behavioral, and morphological aspects of gummivory in primates. Yearb Phys Anthropol. 1986;29:113–137. [Google Scholar]
- Nekaris KAI, Starr CR, Collins RL, et al. Comparative ecology of exudate feeding by lorises (Nycticebus, Loris) and pottos (Perodicticus, Arctocebus) In: Burrows AM, Nash LT, editors. The Evolution of Exudativory in Primates. in press. [Google Scholar]
- Passamani M, Rylands AB. Feeding behaviour of Geoffroy's marmoset (Callithrix geoffroyi) in an Atlantic forest fragment of south-eastern Brazil. Primates. 2000;41:27–38. doi: 10.1007/BF02557459. [DOI] [PubMed] [Google Scholar]
- Power ML. The other side of callitrichine gumnivory: digestibility and nutritional value. In: Norconk MA, Rosenberger AL, Garber PA, editors. Adaptive Radiations of New World Primates. New York: Plenum Press; 1996. pp. 197–110. [Google Scholar]
- Power ML. Nutritional and digestive challenges to being a gum-feeding primate. In: Burrows AM, Nash LT, editors. The Evolution of Exudativory in Primates. in press. [Google Scholar]
- Power ML, Oftedal OT. Differences among captive callitrichids in the digestive responses to dietary gum. Am J Primatol. 1996;40:131–144. [Google Scholar]
- Rayfield EJ. Finite element analysis and understanding the biomechanics and evolution of living and fossil organisms. Annu Rev Earth Planet Sci. 2007;35:541–576. [Google Scholar]
- Richmond BG, Wright BW, Grosse L, et al. Finite element analysis in functional morphology. Anat Rec A Discov Mol Cell Evol Biol. 2005;283A:259–274. doi: 10.1002/ar.a.20169. [DOI] [PubMed] [Google Scholar]
- Ross CF, Patel BA, Slice DE, et al. Modeling masticatory muscle force in finite element analysis: sensitivity analysis using principal coordinates analysis. Anat Rec A Discov Mol Cell Evol Biol. 2005;283A:288–299. doi: 10.1002/ar.a.20170. [DOI] [PubMed] [Google Scholar]
- Rylands AB. Sympatric Brazilian callitrichids: the black tufted-ear marmoset, Callithrix kuhli, and the golden-headed lion tamarin, Leontopithecus chrysomelas. J Hum Evol. 1989;18:679–695. [Google Scholar]
- Sebaa N, Fellah ZEA, Fellah M, et al. Application of the Biot model to ultrasound in bone: inverse problem. IEEE Trans Ultrason Ferroelectr Freq Control. 2008;55:1516–1523. doi: 10.1109/TUFFC.2008.827. [DOI] [PubMed] [Google Scholar]
- Smith AC. Composition and proposed nutritional importance of exudates eaten by saddleback (Saguinus fuscicollis) and mustached (Saguinus mystax) tamarins. Int J Primatol. 2000;21:69–83. [Google Scholar]
- Smith AC. Exudativory in primates: interspecific patterns. In: Burrows AM, Nash LT, editors. The Evolution of Exudativory in Primates. in press. [Google Scholar]
- Strait DS, Richmond B, Ross CF, et al. Finite-element analysis of a macaque skull: applications for functional morphology. Am J Phys Anthropol. 2002;34:149. [Google Scholar]
- Strait DS, Wang Q, Dechow PC, et al. Modeling elastic properties in finite element analysis: how much precision is needed to produce an accurate model? Anat Rec A Discov Mol Cell Evol Biol. 2005;283A:275–287. doi: 10.1002/ar.a.20172. [DOI] [PubMed] [Google Scholar]
- Szalay FS, Delson E. Evolutionary History of the Primates. New York: Academic Press; 1979. [Google Scholar]
- Szalay FS, Seligsohn D. Why did strepsirhine tooth comb evolve? Folia Primatol. 1977;27:75–82. doi: 10.1159/000155778. [DOI] [PubMed] [Google Scholar]
- Taylor AB, Vinyard CJ. Comparative analysis of masseter fiber architecture in tree-gouging (Callithrix jacchus) and nongouging (Saguinus oedipus) callitrichids. J Morphol. 2004;261:276–285. doi: 10.1002/jmor.10249. [DOI] [PubMed] [Google Scholar]
- Taylor AB, Eng CM, Anapol FC, et al. The functional correlates of jaw-muscle fiber architecture in tree-gouging and nongouging callitrichid monkeys. Am J Phys Anthropol. 2009;139:353–367. doi: 10.1002/ajpa.20991. [DOI] [PubMed] [Google Scholar]
- Turnbull WD. Mammalian masticatory apparatus. Fieldiana Geol. 1970;18:149–356. [Google Scholar]
- Van Valkenberg B, Ruff CB. Canine tooth strength and killing behaviour in large carnivores. J Zool Lond. 1987;212:379–397. [Google Scholar]
- Van Valkenburgh B. Costs of carnivory: tooth fracture in Pleistocene and recent carnivorans. Biol J Linn Soc. 2009;96:68–81. [Google Scholar]
- Viguier B. Functional adaptations in the craniofacial morphology of Malagasy primates: shape variations associated with gumnivory in the family Cheirogaleidae. Ann Anat. 2004;186:495–501. doi: 10.1016/S0940-9602(04)80093-1. [DOI] [PubMed] [Google Scholar]
- Vinyard CJ, Ryan TM. Cross-sectional bone distribution in the mandibles of gouging and non-gouging platyrrhini. Int J Primatol. 2006;27:1461–1490. [Google Scholar]
- Vinyard CJ, Wall CE, Williams SH, et al. Comparative functional analysis of skull morphology of tree-gouging primates. Am J Phys Anthropol. 2003;120:153–170. doi: 10.1002/ajpa.10129. [DOI] [PubMed] [Google Scholar]
- Vinyard CJ, Wall CE, Williams SH, et al. The evolutionary morphology of tree gouging in marmosets. In: Ford SM, Porter LM, Davis LC, editors. The Smallest Anthropoids: The Marmoset/Callimico Radiation. New York: Springer; 2009. pp. 395–410. [Google Scholar]
- Williams SH, Wall CE, Vinyard CJ, et al. A biomechanical analysis of skull form in gum-harvesting galagids. Folia Primatol. 2002;73:197–209. doi: 10.1159/000065429. [DOI] [PubMed] [Google Scholar]
- Wroe S, Moreno K, Clausen P, et al. High-resolution three-dimensional computer simulation of hominid cranial mechanics. Anat Rec A Discov Mol Cell Evol Biol. 2007;290:1248–1255. doi: 10.1002/ar.20594. [DOI] [PubMed] [Google Scholar]


