Abstract
During speech perception, listeners make judgments about the phonological category of sounds by taking advantage of multiple acoustic cues for each phonological contrast. Perceptual experiments have shown that listeners weight these cues differently. How do listeners weight and combine acoustic cues to arrive at an overall estimate of the category for a speech sound? Here, we present several simulations using mixture of Gaussians (MOG) models that learn cue weights and combine cues on the basis of their distributional statistics. We show that a cue-weighting metric in which cues receive weight as a function of their reliability at distinguishing the phonological categories provides a good fit to the perceptual data obtained from human listeners, but only when these weights emerge through the dynamics of learning. These results suggest that cue weights can be readily extracted from the speech signal through unsupervised learning processes.
Keywords: speech perception, speech development, cue weighting, reliability, categorization, statistical learning, unsupervised learning, mixture of Gaussians
1. Introduction
In every domain of perception, multiple sources of information must be combined. A classic example is depth perception, where the distance of an object from an observer is indicated by a number of cues including stereopsis, perspective, binocular disparity, shading, motion, and many others (see Kaufman, 1974, for an extensive list). We use the term cue here to refer to any source of information that allows the perceiver to distinguish between different responses. Each cue provides a continuous estimate of depth, and to get an accurate estimate, observers must combine information across them.
This raises the question of how much weight or importance should be assigned to each cue. An emerging consensus is that cues are weighed as a function of the reliability of the estimates they provide (Jacobs, 1999; Landy & Kojima, 2001; Ernst & Banks, 2002) and that cue reliability can be learned (Atkins et al., 2001). Some depth cues, like stereopsis, provide robust estimates (Johnston, Cumming, & Landy, 1994), whereas other cues, like shading are relatively poor (Bülthoff & Mallot, 1988). Weighting cues based on their reliability (Kalman, 1960; Jacobs, 2002) offers a formal approach for estimating these weights and using them to arrive at a combined estimate. Using this method, the weight of an individual cue at a specific depth is determined by:
| (1) |
where w is the weight of the cue and σ2 is the variance of the estimate provided by that cue at a given depth (i.e. how accurately that cue allows the observer to estimate depth). The overall depth estimate, X, can then be calculated as a linear combination of the weighted cue estimates:
| (2) |
This approach has been shown to be consistent with observers’ performance in a number of tasks (Jacobs, 1999; Battaglia, Jacobs, & Aslin, 2003; Ernst & Banks, 2002).
Weighting-by-reliability works well when cue integration can be described as the linear combination of continuous cues and when their variance is roughly Gaussian. However, for many perceptual problems, the causal factors that give rise to the cues are not themselves continuous. In these cases, the perceptual system faces the joint problem of recovering both a continuous estimate of the perceptual cue and also the underlying categories that shaped it.
Speech perception provides an excellent example of this. In speech, phonological dimensions like voicing (which distinguishes voiced sounds like /b, d, g/ from voiceless sounds like /p, t, k/) are often determined by a large number of continuous acoustic cues. For example, cues to word-initial voicing include voice onset time (VOT; Liberman, Harris, Kinney, & Lane, 1961), vowel length (VL; Summerfield, 1981; Miller & Dexter, 1988), pitch (Haggard, Ambler, & Callow, 1970), and F1 onset frequency (Stevens & Klatt, 1974). Understanding how listeners combine these cues, often described behaviorally using trading relations (a shift in the identification function for one cue with changes in another cue), is central to understanding speech perception (see Repp, 1982, for a review of trading relations in speech).
While these cues are continuous, their statistical distributions are shaped into clusters of cue-values by the phonological categories of the language. The listener’s goal is to determine the underlying phonological category from these cues, not necessarily a continuous estimate (although there is evidence that listeners also estimate continuous values and the likelihood of a category; see McMurray, Tanenhaus & Aslin, 2002; Schouten, Gerrits, & van Hessen, 2003; Massaro & Cohen, 1983). Thus, the goal for speech perception is slightly different than the goal for depth perception. In depth perception, observers must recover the best estimate of the depth (i.e. determine a quantity along a metric dimension), whereas the goal in speech perception is to recover the best estimate of a discrete underlying category.
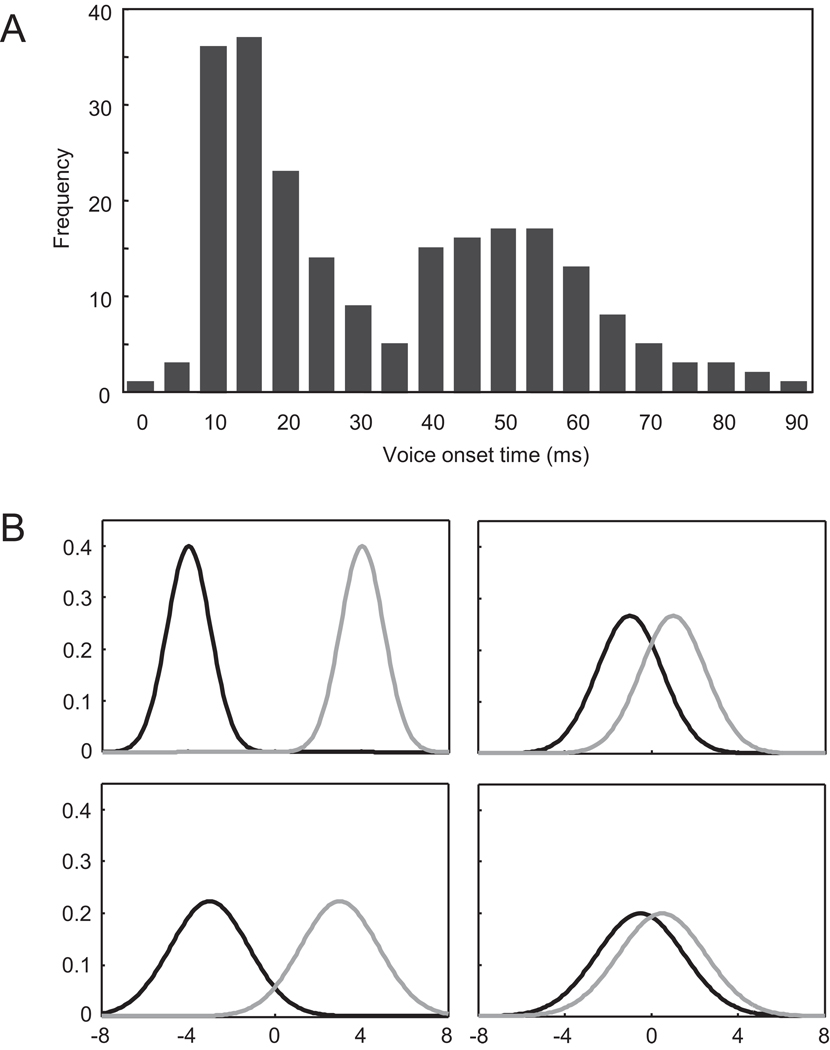
The presence of categories makes it difficult to apply the weighting-by-reliability approach directly, as variance along the cue dimension itself does not map onto how well that cue supports categorization. For example, if we look at the frequency distribution of values for VOT in Fig. 1A, there are clusters of cue-values corresponding to voiced sounds (VOTs near 0 ms) and voiceless sounds (VOTs near 50 ms). This clustering makes a simple computation of reliability from the variance in the estimator of a cue impractical. However, it also enables us to compute a different metric of reliability. That is, the relevant variance for speech perception is the variance in the ability of the cue to support categorization. In a sense, the variance of VOT as an estimator of voicing is a function of both the variability within the categories and the distance between them. Thus, the reliability of a cue or dimension can only be determined with respect to the underlying phonological categories.
Fig. 1.
(A) Distribution of VOT values for voiced and voiceless stops in English (from acoustic measurements in Allen & Miller, 1999). (B) Two-category cues can vary in how reliable they are (and, in turn, how highly they should be weighted) from reliable cues with distinct categories (top left) to unreliable cues with overlapping categories (bottom right). Cues of intermediate reliability (top right and bottom left) require us to take into account both the distance between categories and the variability within them.
Given that the distributional statistics of cues must be learned in order to compute weights based on their reliability, it is fundamental to take into account what is known about development. Thus, whatever solution we adopt to the problem of cue weighting should be based on knowledge and representations that are developmentally plausible. In particular, as we will describe below, the acquisition of speech discrimination abilities may derive from a similar estimation of distributional statistics. The goal of the present work is to adapt the weighting-by-reliability approach in a way that is consistent with the process of speech development.
1.1. Models of cue integration in speech
Formal approaches to cue integration in speech preceded the weighting-by-reliability approach used in depth perception, and thus, do not incorporate an explicit notion of reliability in their solutions to this problem. The Fuzzy Logical Model of Perception (FLMP; Oden & Massaro, 1978; Massaro & Oden, 1980) provides one of the best formal approaches and has successfully modeled a range of cue integration problems. In its mappings between dimensions and categories, it is clear that some notion of weighting emerges. However, it does not completely solve the problem of cue weighting for two reasons. First, it assigns independent weights to different regions of the same dimensions (e.g. VOTs between 0–10 may get substantial weight, but VOTs between 10 and 20 may get less), creating a sparse data problem (i.e. how does a listener deal with a new value along a familiar dimension?). Second, and more importantly, the weights are fit to perceptual data, rather than estimated from the structure of the speech input. Listeners’ responses in speech tasks certainly reflect their own cue weightings, thus, these weighting will be implicitly incorporated into FLMPs integration rules. However, this does not provide an explanation for why listeners would weight one cue over another and does not allow us predict perceptual data from acoustic measurements alone.
Nearey and colleague’s normal a posteriori probability (NAPP) models offer a similar approach to cue integration (Nearey & Hogan, 1986; Nearey & Assmann, 1986; Nearey, 1997). NAPP models use discriminant analysis to assign tokens to categories based on a set of acoustic cues. Like FLMP, these classifications can be probabilistic, allowing the output of the model to be compared to listeners’ identification rates. However, unlike FLMP, NAPP models use measurements from production data along with the intended categories to classify tokens. As in FLMP, the training categories (i.e. the intended production) capture some of the differential variability between dimensions, suggesting that NAPP models may also show implicit weighting effects.
Both NAPP models and FLMP treat cue integration as a category-dependent process. In order for listeners to weight cue dimensions in this way, they would have to know which tokens belong to which category. However, since category membership is not available to listeners’ from the acoustic input, the problem of acquiring categories, as well as learning cue weights, might be better characterized as an unsupervised clustering process (McMurray, Toscano, & Aslin, 2009a; Maye, Werker & Gerken, 2002). Infants tune their phonological discrimination abilities to the native language well before any words are known (e.g. Werker & Tees, 1984; Werker & Curtin, 2005 for a review), and, thus, the development of speech categories must be at least partially category-independent. Given this, it makes sense to seek a category-independent way to describe cue integration and weighting that is sensitive to this unsupervised developmental process.
1.2. Weighting cues in speech
The weighting-by-reliability approach and NAPP models appear to offer some insights for solving the problem of cue weighting, as they allow us to estimate cue weights independently of perception. While, as stated above, the cue-weighting method used in depth perception is not adequate for acoustic cues in speech, it does offer some intuitions about how to proceed. In addition, NAPP models suggest that the distributional statistics of acoustic cues can provide the information needed to weight them. Thus, combining the strengths of these two approaches may yield a more complete model.
Fig. 1B shows several possible categories imposed on a given dimension. The top-left panel shows a dimension that would appear reliable: the categories are far apart and have low variability. Conversely, if categories are close together and have high within-category variability (bottom right panel) this dimension should receive little weight. For more ambiguous cases (top right and bottom left), determining reliability is a function of both the distance between the categories and within-category variability, weighed by their respective variances. In support of this, Clayards, Tanenhaus, Aslin, and Jacobs (2008) demonstrated that artificially manipulating the variance of an acoustic cue changes how listeners weight it perceptually.
These intuitions can be captured formally, by treating each cluster as an independent Gaussian distribution. In this case, we can partial out the overall variance along a dimension into the component due to the difference between category means, and the variance within each category. This leads to a simple way to estimate the reliability of a dimension:
| (3) |
Here, μ1 and μ2 are the means of each category (e.g. /b/ and /p/), and σ1 and σ2 are their standard deviations. This metric would provide listeners with an estimate of cue reliability that is similar to the one provided by the weighting-by-reliability method used in vision. It is similar to standard statistical measures that compare the variance between groups, (μ1 – μ2)2, to the variance within groups, σ1σ2. When both σs are equal, this is a pairwise F-ratio.
This solution requires that listeners are sensitive to the distributional statistics of acoustic cues and that cue weights can be based on and learned from this information. There is growing consensus that listeners are sensitive to these statistics, and, further, that infants use statistical learning mechanisms to acquire speech sound categories. Maye and colleagues, for example, have demonstrated that after a brief exposure to statistically structured input, infants discriminate speech sounds consistent with the number of clusters along dimensions like VOT (Maye, Werker & Gerken, 2002; Maye, Weiss & Aslin, 2008; see also Teinonen, Aslin, Alku, & Csibra, 2008). Thus, at the coarsest level of analysis, listeners are likely to have access to and can learn from the statistics necessary for cue weighting.
However, attempts to implement this approach computationally suggest that statistical category learning is not trivial (e.g. de Boer & Kuhl, 2003; McMurray et al., 2009a). In particular, when the number of categories is not known (since languages can carve up the same dimensions in many ways) and the input is not tagged with the underlying category, there is no analytic solution to the problem of estimating the parameters that describe the means, variances and frequencies of the speech categories. Thus, while at a first approximation, our intuitive modification of the weighting-by-reliability approach seems reasonable, it is significantly underdeveloped from the perspective of learnablity.
The purpose of the present work is to bridge this gap and adapt the weighting-by-reliability approach to the problem of cue integration in speech. Recently McMurray et al. (2009a) presented a mixture of Gaussians (MOG) model that solves many of the problems of unsupervised learning of phonological categories. This model offers a computational-level description (Marr, 1982) of speech sound categorization while also including a mechanistic account of the developmental process. Here, we extend this model to multiple dimensions, and demonstrate how the weighting-by-reliability approach can be implemented in it. In doing so, we reveal some surprising findings about the role of learning processes in statistical cue weighting and the role of context in shifting apparent cue weights.
2. Model architectures
2.1. Mixture of Gaussians models of speech categories
A distribution of acoustic cues can be described as a mixture of probability distributions, in which the likelihood of a given cue value (x) is the product of two factors: (1) the prior probability of each category and (2) the conditional probability of x given each category. This latter probability is usually described as a continuous distribution of cue-values, given the parameters of that category. In typical instantiations, for a particular category, the values of a particular cue cluster around the category mean in a Gaussian distribution (although other distributions are possible).
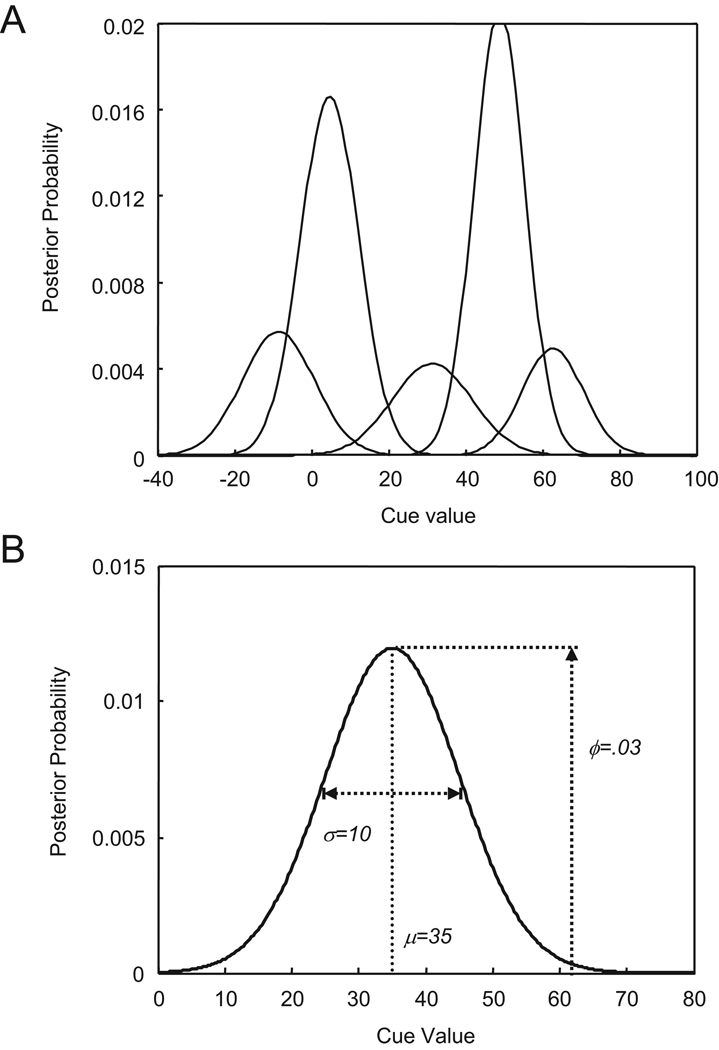
A number of recent studies have modeled the distribution of speech cues using this framework (e.g. McMurray et al., 2009a; de Boer & Kuhl, 2003; Vallabha et al., 2007). Generally, cues in these models are represented by a set of Gaussian distributions (Fig. 2A) each defined by three parameters: frequency of occurrence (ϕ), mean (μ), and standard deviation (σ) (Fig. 2B). Thus, the likelihood of a particular cue-value (x) for each Gaussian is:
| (4) |
and the overall likelihood is the sum of the likelihoods for each Gaussian:
| (5) |
Here, K represents the number of Gaussians in the mixture. For example, the likelihood of a VOT of 30 ms is the sum of the relatively high probability that it arose from a /p/ (μ≈50, σ≈15) and the lower probability it came from a /b/ (μ≈0, σ≈5).
Fig. 2.
(A) A mixture of Gaussians (MOG) with five categories along the dimension. (B) Parameters of a Gaussian distribution used in the mixture model. Each distribution is defined by three parameters – its likelihood (ϕ), its mean (μ), and its standard deviation (σ).
The fact that this model explicitly represents parameters like μ and σ makes it an ideal platform for implementing the variation of the weighting-by-reliability approach described in Equation 3. However, it also raises the critical question of how to determine the mixture’s parameter values. One option would be to simply set the values of K, ϕ, μ, and σ for each category using values extracted from acoustic measurements. However, there is no analytic solution to parameter estimation in a mixture model when the underlying categories for each data point are unknown, and expectation maximization and similar learning algorithms have a difficult time estimating the number of categories in this situation (de Boer & Kuhl, 2003). Simply assigning values on the basis of such measurements, then, assumes that listeners have access to some learning mechanism that is not guaranteed to exist.
McMurray et al. (2009a) demonstrated how gradient descent can be used to model the gradual acquisition of speech categories when learning is unsupervised and the number of categories is not known. Their model uses large values of K (e.g. 20), with the expectation that ϕs will be reduced to near zero for unneeded categories. The idea here is that, over training, K itself doesn’t change, but, because most Gaussians will have very small values for ϕ, the mixture will functionally behave as if K was only 2 (for a two-category dataset). Parameters are updated via maximum likelihood estimation using the derivatives of the probability density function with respect to each parameter. (See Appendix A for these learning rules.) A crucial innovation from this model is the use of a winner-take-all update rule for ϕ such that only one Gaussian updates its ϕ-value on any given trial. This allows the model to suppress unneeded categories and arrive at the correct solution. Without it, the model does not determine the correct number of categories (see McMurray et al., 2009a). This winner-take-all competition is similar to competitive learning approaches used in other unsupervised category learning models like SUSTAIN (Love, Medin, & Gureckis, 2003) as well as various neural network models (McMurray et al., 2009b; Rumelhart & Zipser, 1985). McMurray et al. (2009a) describe how this simple solution allowed 97/100 models in their simulations to arrive at the correct two-category solution for a corpus of VOT measurements, and they demonstrate that the timecourse of learning shows many parallels with infant speech development.
This implementation raises two issues for the cue weighting approach we’ve described. First, since there are more than two categories (even if only two will be used eventually), our weighting metric must be able to handle many categories and factor out unused ones. Second, because this model is based on gradient descent, the learning procedure is not guaranteed to find the globally optimal parameter values based on the distributional statistics of the data (i.e. it may settle in a local minimum). This raises the question of whether the dynamics of learning affect cue weighting. If learning leads to non-optimal representations in the model that reflect human behavior, it would suggest that listeners may be behaving in a way that is not entirely consistent with the statistics of the input. We examine both of these issues in our simulations.
2.2. Cue integration in a mixture of Gaussians
The mixture of Gaussians (MOG) framework allows us to incorporate underlying categories into the reliability estimates described above because it explicitly represents those categories, allowing us to relate the distance between µs to the corresponding σs. The cue weighting strategy we’ve discussed would allow us to combine estimates from different cues into a single overall estimate whose inputs are weighted by the reliability of the individual cues. We also consider, as a comparison, an alternative approach in which multiple cues are represented in a multi-dimensional MOG with individual cues along separate dimensions (e.g. two-dimensional Gaussians for two cues). In this case, weighting emerges implicitly. (This is not necessarily a criticism of the model; indeed, this property is useful since it allows us to model cue integration without having to specify an additional function for determining cue weights.) This multi-dimensional model, which is highly parameterized and can represent distributions completely, serves as a baseline model for comparison with a more constrained cue-weighting model.
2.2.1. Cue-weighting model
In order to compute a cue weight, we must know the variability in the estimate for a given cue-value. Equation 3 describes one way to do this in the specific case of a two-category cue. However, many phonological contrasts contain more than two categories (e.g. voicing in Thai; place of articulation in English). In addition, using the unsupervised learning approach from McMurray et al., (2009a), the model will have many more possible categories than the number of categories in the data. Thus, at some points during learning, it may not be possible to know which Gaussian will become a particular adult category.
Thus, we use a weighting metric that captures a more general case in which the cue dimension may have any number of categories. In our model, the weight of an individual acoustic cue (i) is:
| (6) |
This metric is similar to Equation 3. However, it allows for any number of categories by summing all of the pairwise comparisons between the parameters of the Gaussians in the mixture (i.e. each pair of Gaussians, m and n, from 1 to K) and then halving this sum so that each pair does not contribute twice to the weight.
Two features are worth noting. First, pairs of Gaussians whose means are far apart will increase the weight of the cue, but this is balanced by the within-category variability of those Gaussians. If within-category standard deviations are large, the weight of the cue will be smaller. Thus, as with Equation 3, this metric is similar to measures like d′ or the t statistic, in which both the distance between group means and within-group variances are taken into account.
Second, although K is large, most of the Gaussians are unused after training. This would seem to clutter up the computation with unnecessary comparisons. However, since unused Gaussians will have ϕs near zero, they will not contribute much to the weight. This allows us to compute the weight of a cue regardless of the number of categories and without knowing which specific Gaussians correspond to each category.
After computing the weight for each cue, the weighted estimates are combined to obtain a continuous overall estimate along an underlying phonological dimension. This overall estimate serves as input to an additional MOG that represents the abstract phonological feature distinguished by the cues (e.g. voicing). Thus, the cue-level MOGs are used only to compute weights and inputs to the combined MOG—category judgments are made on the basis of the combined MOG itself. Note that, similar to the cues themselves, this combined MOG is based on a continuous phonological representation. However, it is abstracted away from the input (since it represents a combination of cues). Thus, it is similar to other proposals that phonological representations are continuous (e.g. Frisch, 1996), but it stands in contrast to models that have proposed a more direct mapping between input and phonology, such as exemplar models (Goldinger, 1998; Pierrehumbert, 2001; 2003).
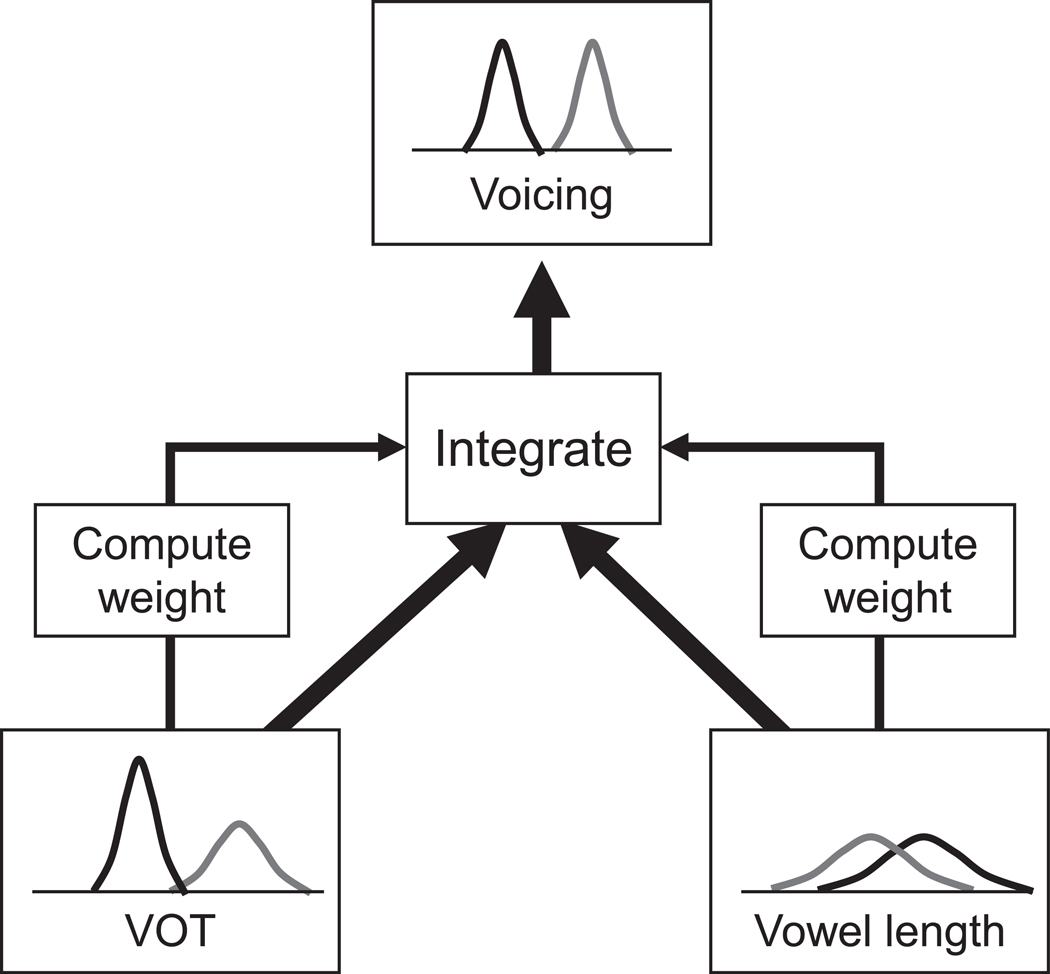
Because different cues give estimates measured on different scales, the combined MOG cannot be based directly on the raw values for each cue. Thus, cue-values are normalized by converting the inputs for individual cues to z-scores using the grand mean and variance of each dimension. Additionally, the particular ordering of categories along each cue dimension may not be the same for all cues. For example, in the specific case of the two acoustic cues studied here (voice onset time [VOT] and vowel length [VL]), voiced sounds are associated with short VOTs but long VLs. Thus, z-scores for VL are multiplied by the sign of the raw correlation between these two cues across all categories (r = −0.196 for VOT/VL data from Allen & Miller, 1999) in order to deal with differences in the relative ordering of categories along each dimension. Finally, the normalized estimates are then weighted (per Equation 6) and summed. Fig. 3 shows a schematic representation of the cue weighting and combination process in the model.
Fig. 3.
Schematic representation of the cue-weighting model. Two MOGs receive input for each cue (VOT and VL). The cue weight for each MOG is computed using Equation 5, and the inputs are converted to z-scores. The inputs are then weighted and summed, providing input to a third MOG that reflects voicing categories based on both cues.
2.2.2. Multi-dimensional model
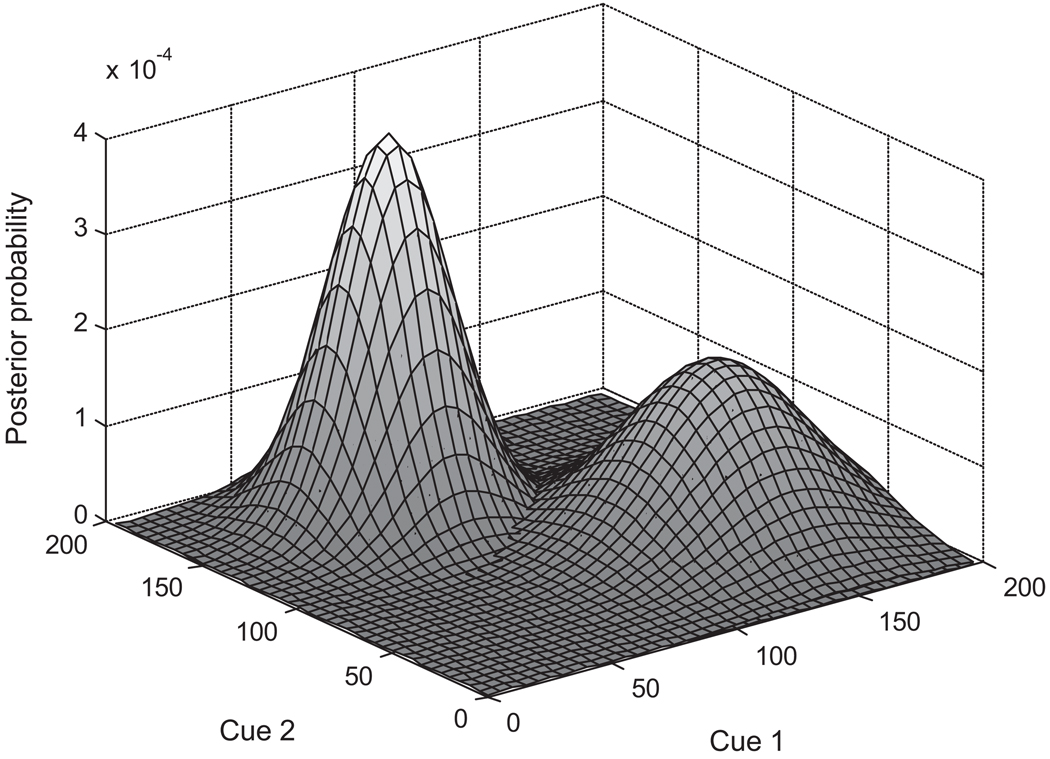
The cue-weighting model can be contrasted with a model that represents categories in a higher-dimensional acoustic space. In this model, categories are multi-dimensional Gaussians, and each cue lies along a separate dimension. Thus, for two cues, categories would be represented by bivariate Gaussian distributions (Fig. 4; Equation 7 in Appendix A). This allows the model to take advantage of the entire acoustic space and does not require it to explicitly weight cues. Cue-weighting can emerge implicitly when the categories along one dimension are wide and overlapping, while the other is narrow.
Fig. 4.
A two-dimensional MOG with two categories. Each Gaussian is determined by cue-values along both dimensions.
This approach raises several problems. First, the number of parameters in the model can be quite large. For a set of categories determined by a large number of cues (which is not uncommon; see Jongman, Wayland, & Wong, 2000; Lisker, 1986), the model would have to estimate a large number of parameters for each category (e.g. for 16 cues [the number reported by Lisker, 1986], the model would have to estimate 168 parameters for each category). In contrast, in the cue-weighting model, only three parameters per category need to be estimated (for each individual dimension), along with an additional set for the combined dimension (e.g. for 16 cues, the model would only need 51 parameters for each category).
Second, since a given input is a point in a high-dimensional space, sampling may be sparse and many regions of acoustic space will never be encountered during training. This makes it difficult to estimate all of the parameters accurately. The cue-weighting model on the other hand considers each dimension independently (not in combination) and may have less trouble with this. Thus, the cue-weighting model may be preferred if it is better able to learn the categories for a larger set of cues.
3. Simulations
3.1. Acoustic and behavioral data
We ran simulations with each of these models using two acoustic cues to word-initial voicing in English: VOT, mentioned above, and vowel length (VL). While VL is a robust cue to word-final voicing in English (Warren & Marslen-Wilson, 1987; Peterson & Lehiste, 1960), the length of the vowel following the consonantal release has long been recognized as a weak cue to word-initial voicing (Summerfield 1981; Miller & Dexter, 1988; Miller & Volaitis, 1989; Allen & Miller, 1999).
Typically, longer vowels are produced for voiced stops and shorter vowels for voiceless stops. For example, Fig. 5A shows a scatter plot of the VOT and VL values from Allen and Miller (1999). Along the VOT dimension, the categories are highly distinct, reflecting the fact that VOT is a strong cue to voicing. Along the VL dimension, the categories are distinguishable, but highly overlapping, suggesting that VL is a weaker cue. Our training data were similar. VOTs were randomly generated from the means reported by Lisker and Abramson (1964) and VLs from the data in Allen and Miller (1999) (see Table 1).
Fig. 5.
(A) Distributions of VOT and VL values for voiced and voiceless stops from the production data in Allen & Miller (1999). The locations of the lines indicate the mean of each category along each dimension, and the lengths of the lines are equal to the standard deviations of each distribution. Voiced and voiceless sounds are primarily distinguished along the VOT dimension, but there is also a small difference along the VL dimension. (B) Identification responses from listeners for sounds varying in both VOT and VL from McMurray et al. (2008). Listeners tend to identify sounds as voiced (/b/) for low VOTs and voiceless (/p/) for long VOTs. The shift in the identification function for the two different VL conditions indicate that they also use VL information when making voicing judgments (i.e. they are more likely to identify sounds as voiced for long VLs and voiceless for short VLs).
Table 1.
Descriptive statistics for the distributions used to generate training data.a
| VOT (ms) | Voiced VL (ms) |
3rd cue | VOT (ms) | Voiceless VL (ms) |
3rd cue | |
|---|---|---|---|---|---|---|
| Mean | 0 | 188 | 260 | 50 | 170 | 300 |
| SD | 5 | 45 | 10 | 10 | 44 | 10 |
VOT and VL cues were used in Simulations 1–4. The “3rd cue” is an additional cue that was used in Simulation 4.
Empirical work has demonstrated trading relations between these cues: the category boundary along a VOT continuum shifts for different VLs (McMurray et al., 2008; Summerfield, 1981; Miller & Volaitis, 1989). Near the boundary, stimuli with long VLs are more often categorized as voiced, and short VLs are more often labeled voiceless (see Fig. 5B for representative results from McMurray et al., 2008). While previous approaches suggested that this trading relation might be an instance of speaking rate compensation (Summerfield, 1981), later work has distinguished it from sentential rate (Wayland, Miller & Volaitis, 1994; see Repp (1982) for a discussion of evidence that VL is distinct from overall speaking rate).
Whatever way we characterize the effect of VL, identification functions like the one in Figure 5B suggest that listeners use both cues, but rely more heavily on VOT, an effect that mirrors the statistical distributions of each cue. Simulations 1 and 2 examined whether the multi-dimensional and cue-weighting models also show a similar trading relation between VOT and VL.
3.2. Simulation 1: VOT and VL in the multi-dimensional model
The first simulation provides a baseline for performance on the VOT/VL task. Fifty repetitions of two-dimensional MOGs were trained using data sampled from the VOT and VL distributions described above. Initial μ-values were randomly chosen from a distribution with a mean of 25 and standard deviation of 75 for the VOT dimension and a mean of 179 and standard deviation of 75 for the VL dimension. Initial σs were set to 3 for the VOT and 10 for the VL dimension. K was set to 20, and initial ϕs were set to 1/K. Learning rates were set to 1 (ημ), 1 (ησ), 0.001 (ηϕ), and 0.001 (ηρ).1 The models were then tested on a range of VOTs (0 to 40 ms in 5 ms steps) and two VLs (125 and 225 ms).2
3.2.1. Procedure
Each model was trained on 200,000 data points. On each trial, a pair of VOT/VL values was selected for input, and the parameters of the Gaussians in the mixture were updated via the gradient descent learning algorithm discussed above. Winner-take-all competition was implemented by selecting the Gaussian with the highest posterior probability for that input and updating only that Gaussian’s ϕ parameter. The ϕs were then normalized so that they summed to 1. Thus, for the winning Gaussian, ϕ increased, and the others decreased slightly. Only Gaussians with a ϕ-value above a threshold of 0.1 were analyzed. Typically, the model arrived at a solution with two above-threshold Gaussians (i.e. the voiced and voiceless categories) with ϕ-values of ≈0.5. Models that over-generalized (i.e. arrived at a one-category solution) or did not have any above-threshold Gaussians at the end of training were excluded from analysis. While this seems like a relatively coarse way to assess model performance, we found that if ϕ falls below a threshold of about 0.1, that Gaussian does not typically recover (other Gaussians ultimately represent the two categories). Moreover, in an analysis of the one-dimensional model, we found that if the model arrived at two categories, μ and σ were almost always accurate.3
After training, the model was tested using a procedure similar to the task used in McMurray et al. (2008). The model was presented with a pair of VOT and VL values, and identification responses were computed from the posterior probability for each category, which were then normalized using the Luce choice rule (Luce, 1959; temperature=1) to obtain the proportion of /p/ responses.
3.2.2. Results and discussion
The model learned this distribution quite well, with every repetition adopting the two-category solution. The parameter estimates were also close to the values in the dataset; the average deviation of μ from the category mean was 1.7 ms for VOT and 5.9 ms for VL (see Table 2).
Table 2.
Mean parameter values at the end of training for Simulations 1, 2 and 4.b
| VOT | Voiced VL |
3rd cue | VOT | Voiceless VL |
3rd cue | ||||
|---|---|---|---|---|---|---|---|---|---|
| Simulation 1 | μ | 1.37 | 188 | - | 51.5 | 178 | - | ||
| σ | 5.58 | 44.8 | - | 10.2 | 44.8 | - | |||
| ϕ | 0.493 | - | 0.491 | - | |||||
| ρ | −0.067 | - | −0.040 | - | |||||
| Simulation 2 | μ | 0.253 | 203 | - | 50.1 | 154 | - | ||
| σ | 5.41 | 38.4 | - | 10.0 | 38.4 | - | |||
| ϕ | 0.499 | 0.502 | - | 0.501 | 0.498 | - | |||
| Simulation 4 | μ | −0.067 | 204 | 260 | 50.0 | 155 | 300 | ||
| σ | 5.35 | 38.7 | 10.1 | 10.1 | 38.3 | 10.2 | |||
| ϕ | 0.501 | 0.498 | 0.502 | 0.499 | 0.502 | 0.498 | |||
Values for the 3rd cue are only applicable to Simulation 4. There is only a single ϕ and ρ for each voicing category in Simulation 1, since there is only a single value for each of these parameters in the two-dimensional Gaussians.
Fig. 6 shows the mean proportion of /p/ responses for the model. A clear effect of VOT is observed, with short VOTs producing more /b/ responses and long VOTs producing more /p/ responses. In contrast, the effect of VL is absent, unlike the effect observed in the empirical data. This was not due to a failure of learning – the model learned the distributions of the two cues and correctly determined the number of categories. In fact, on average the model reported means of 1.63 and 51.3 for VOT, and 188 and 178 for VL, suggesting that it had closely captured the statistics of the input (compare to the means of the training distributions in Table 1). This, however, led to a much weaker trading relation than was observed behaviorally. Since the categories along the VL dimension are highly overlapping, the model relied on VOT instead of VL. Thus, changes along the VOT dimension produced large changes in the model’s identification of voicing category, while changes along the VL dimension did not affect the model’s category judgments. This result does not reflect listeners’ behavior, suggesting that listeners may actually assign more weight to VL than they should based solely on the statistics of the input.
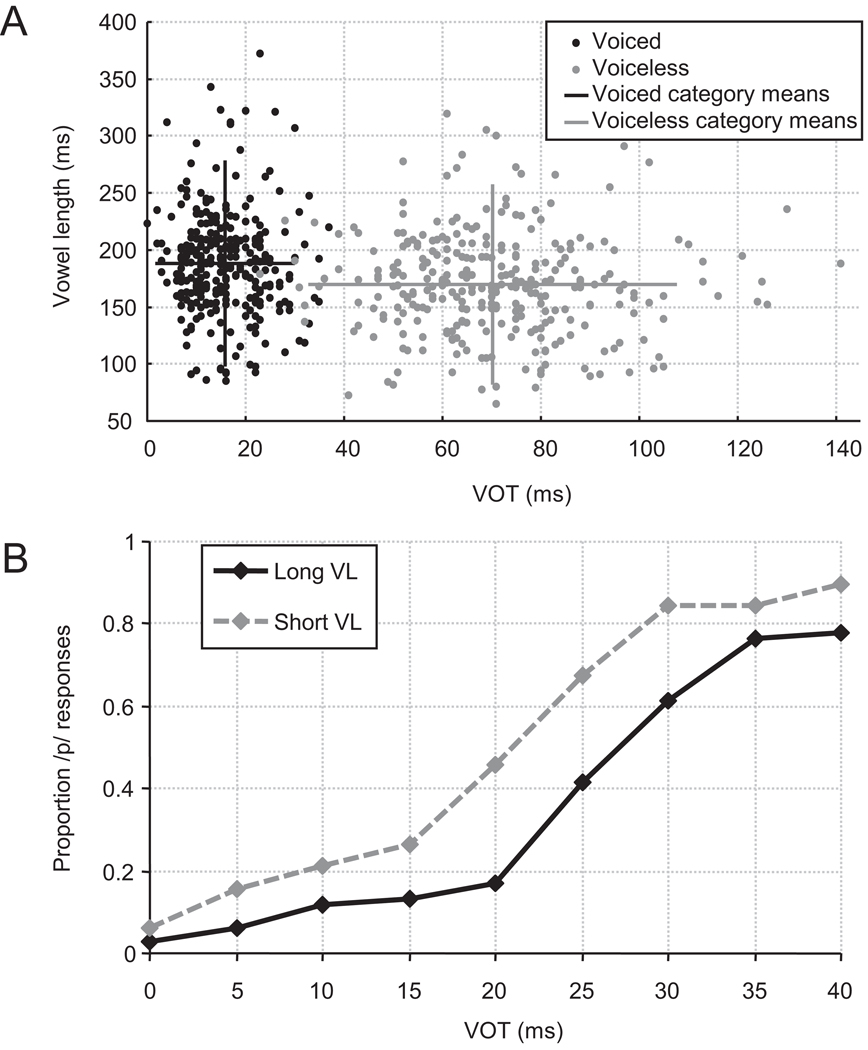
Fig. 6.
Identification results for the multi-dimensional model from Simulation 1. A clear effect of VOT is observed, but the expected trading relation (i.e. the effect of VL) is not.
3.3. Simulation 2: VOT and VL integration in the cue-weighting model
We now consider the cue-weighting model, which consists of three one-dimensional MOGs. The first two represent the VOT and VL dimensions and were used to compute cue weights. The third MOG represents categories based on the combination of the two cues (i.e. a voicing dimension) and is used to compute the actual phonological judgments. Fifty repetitions were trained on data sampled from the same distributions as in Simulation 1. Learning rates, K, and the initial σs and ϕs were the same as in Simulation 1; the initial μ-values were chosen in the same way.
3.3.1. Procedures
As in Simulation 1, parameters were updated using gradient descent learning and winner-take-all competition. Each model was trained on 90,000 data points, and models that over-generalized were excluded from analysis. On each trial during training, the parameters of the Gaussians in the VOT and VL MOGs were updated. Then, weights were computed for each of these cue-level MOGs using Equation 5. Next, the input values for the combined MOG were computed by converting the inputs for the individual cues to z-scores, negating the sign for the VL input (due to the negative correlation between the cues), weighting the inputs, and summing them according to Equation 2. The update procedure is then repeated for the Gaussians in the combined mixture. The testing procedure was the same as the one used for the multi-dimensional model, except that the posteriors for each category were computed from the combined MOG.
3.3.2. Results and discussion
Overall, this model performed similarly to the prior model with 46/50 models showing the correct two-category solution. Of the ones that failed, three overgeneralized (a single category in one of the MOGs) and one did not have any above threshold categories in the combined MOG.
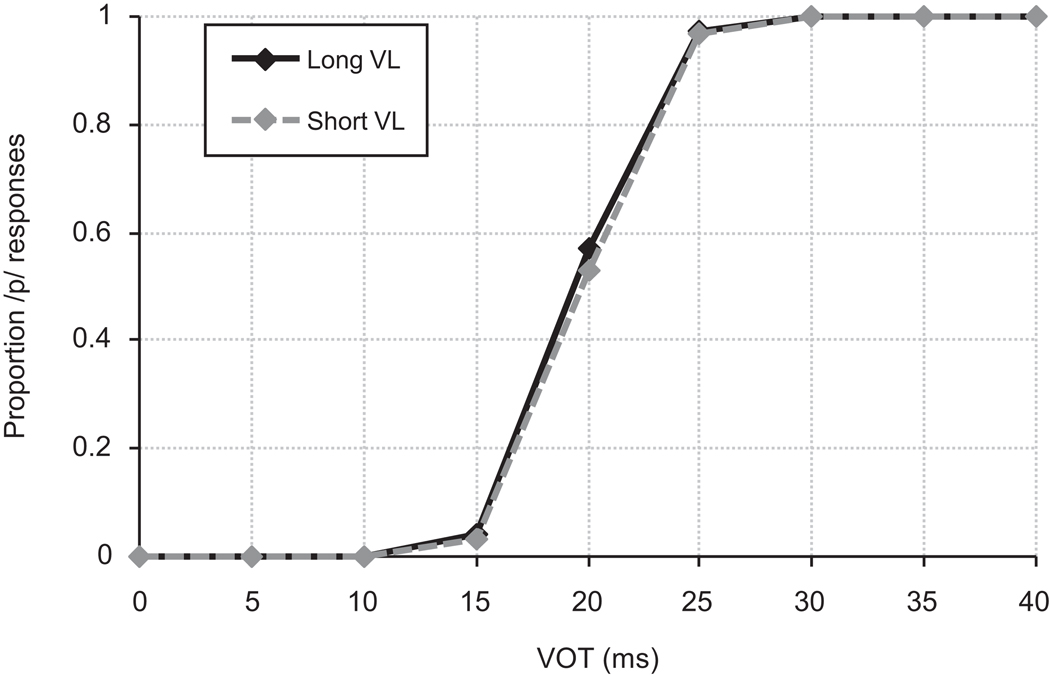
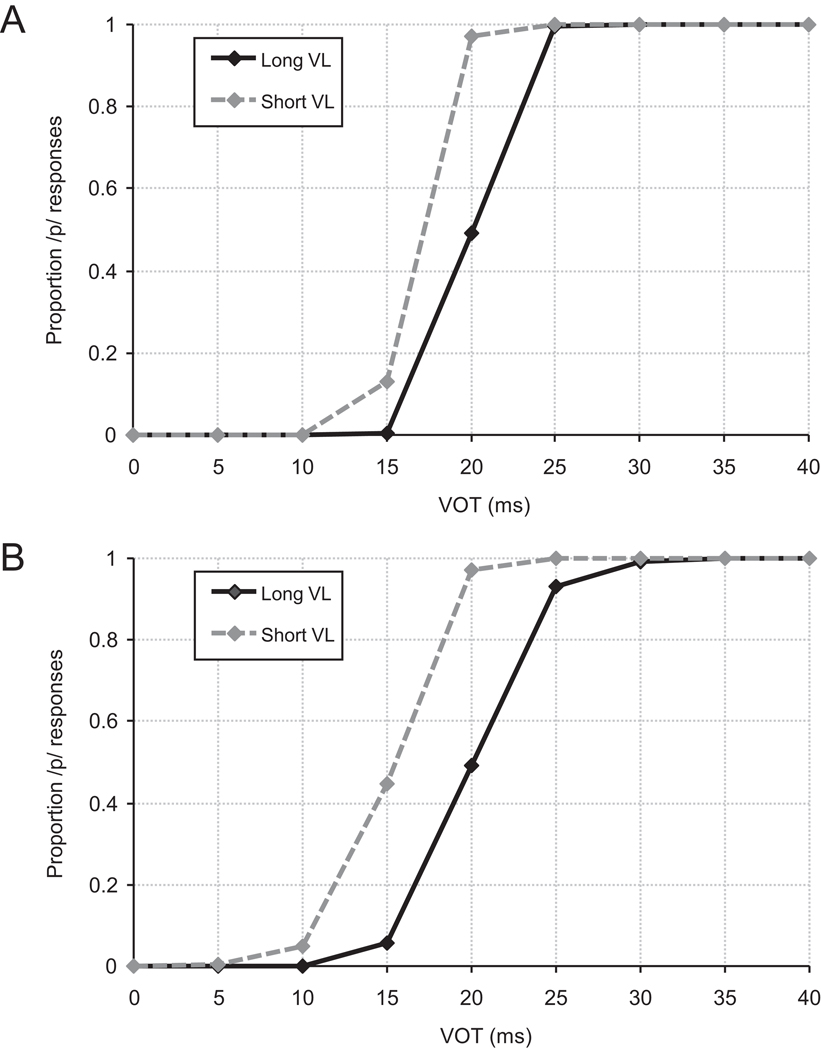
Fig. 7 shows the responses of the model in the categorization task. A moderate trading relation was observed, similar to the behavioral data from McMurray et al. (2008). The average cue weight for the VOT dimension was 0.95, and the average cue weight for VL was 0.05. The results of this simulation suggest that the cue-weighting model shows a good fit to the empirical results, demonstrating that cue-weights can be learned from the distributional statistics of the acoustic cues in the input and that a full multi-dimensional model is not necessary for combining acoustic cues along a single phonological dimension.
Fig. 7.
Identification results for the cue-weighting model from Simulation 2. An effect of both VOT and VL is observed, consistent with responses from listeners.
Why did the cue-weighting model show a trading relation while the multi-dimensional model did not? As mentioned above, the multi-dimensional model correctly fit the statistics of the dataset. In the cue-weighting model, however, the categories for the VL dimension were further apart than the means in the dataset (mean for each category in the model: 203 [/b/] and 154 [/p/] ms; means in the dataset: 188 [/b/] and 170 [/p/] ms). This caused the model to give more weight to VL, resulting in a trading relation.
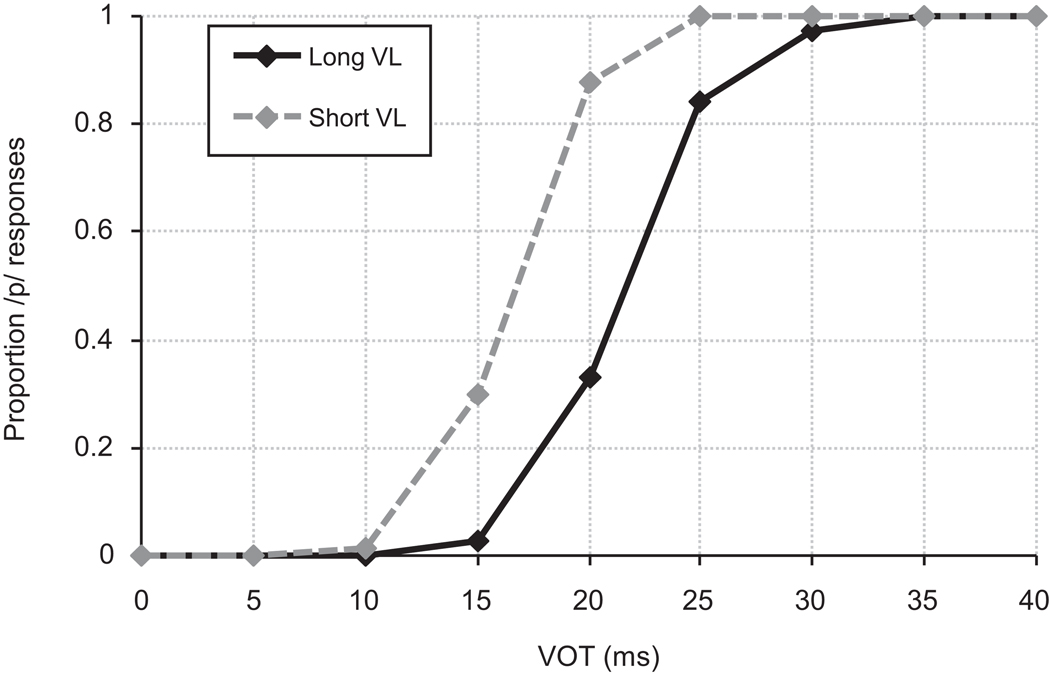
This exaggeration of the VL categories may have been a result of the fact that the categories along the VL dimension are highly overlapping. Since training is unsupervised, this exaggeration cannot be due to a performance benefit for representing categories in this way (though there may be one). Thus, during learning there may have been a local minimum that was more stable than the actual means and variances in the data. Indeed, if we were to compute the cue weights using Equation 6 directly from the acoustic data, we would obtain a relative weight of 0.997 for VOT and 0.003 for VL and, consequently, a significantly reduced trading relation (Fig. 8). This much more closely reflects the behavior of the multi-dimensional model, not the cue-weighting model or listeners. Thus, the cue-weighting model may have produced different results because its parameters and weights were the product of learning, not derived veridically from the input.
Fig. 8.
Predicted results for the cue-weighting model based on the distributional statistics of the two cues. These responses were obtained by setting the parameters of the Gaussians in the input-level MOGs to the means and standard deviations of each cue and training the model (i.e. keeping the parameters at the cue-level MOGs constant while allowing the model to learn the parameters at the combined MOG). The model shows a much smaller trading relation than the one observed in Simulation 2 and in the data from listeners.
3.4. Simulation 3: Effects of learning on VL cue weight
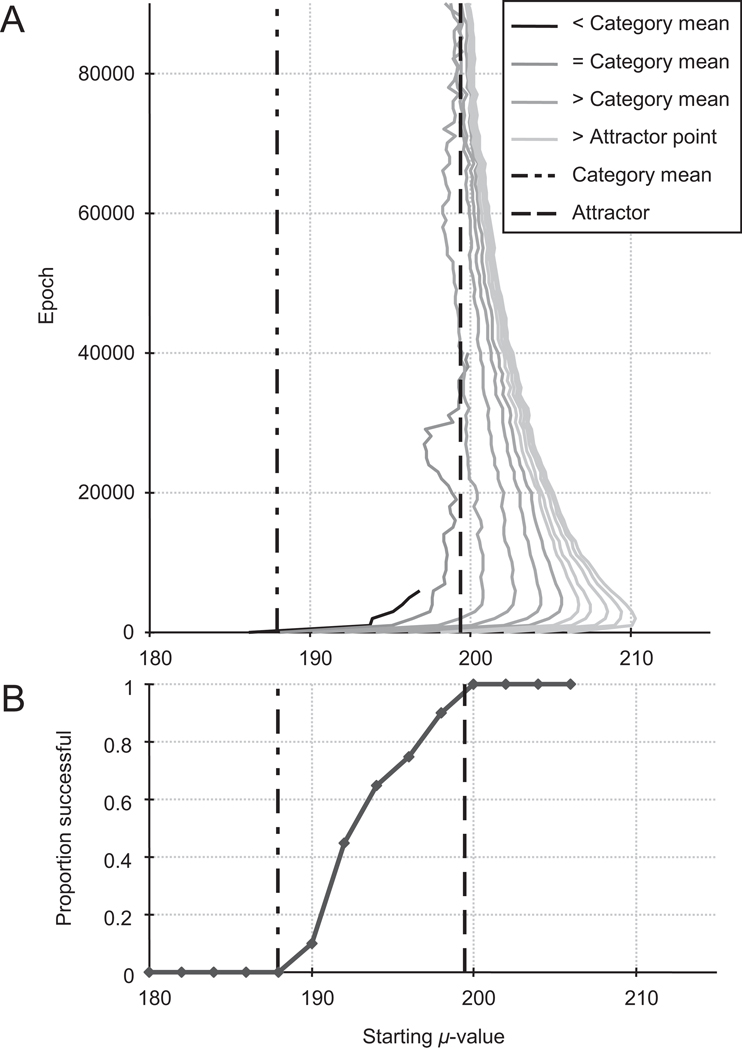
To test the hypothesis that the overweighting of the VL dimension in the cue-weighting model was the product of learning, we ran an additional simulation in which K, the number of Gaussians in the mixture, was set to 2. While this value is quite a bit smaller than the one used in the initial simulations, it allows us to manually set the initial values for μ in order to observe their behavior over the course of learning. Thus, the starting μs were set to different points along the VL dimension (closer together than the category means, exactly equal to them, or further apart) in order to determine what the learning algorithm would do in each case. All other parameters were the same as those used in Simulation 2. This allows us to ask what outcomes the learning rules impose on the models’ representation of VL beyond those determined by the statistics of the input. For example, if the model started with the correct μ-values and the categories were still forced apart, this would suggest that the category means are not a stable point in state space. Fifty repetitions of this simulation were run. Initial σ- and ϕ-values were the same as those in the first two simulations.
3.4.1. Results and discussion
The proportion of successful models, as measured by whether or not the model arrived at a two-category (successful) or one-category (unsuccessful) solution, is shown in Fig. 9B. None of the models with starting μs between the two category means succeeded. Furthermore, every model whose μ-values started outside the observed local minima values was successful. Thus, the model needed to start with μs that were further apart than necessary.4
Fig. 9.
Results of Simulation 3 for the voiced VL category. The bottom panel shows that when the starting μ-values of the Gaussians were initially closer than the means in the data, the model always failed to learn a two-category solution (i.e. it over-generalized the dimension into a single category). As the starting values were moved further apart, the model became more likely to succeed. The top panel shows the μ-values over the course of learning for the different starting values. The point at which each line ends indicates the latest point during training at which one of the models for that starting value still maintained a two-category solution. All of the models that had two categories throughout training settled on μ-values near points further apart than the means in the dataset.
Fig. 9A shows the change in μs over time. For all models, μs were initially pushed apart (even if that pushed them beyond their eventual location), and over time evolved to the values observed in Simulation 2. Thus, the dynamics of learning seem to favor this exaggeration along the VL dimension.
These results suggest that there are attractor points that the model arrives at through learning in which category means are further apart than the means in the data. Thus, learning (instantiated here by our gradient descent update rules) may be critical for determining the weight of individual cues. Indeed, without learning, the cue-weighting model does not reflect the responses from human listeners. With learning, the model only succeeds under conditions in which it learns categories that are more distinct than those in the data. This suggests that human listeners may not behave in a way that optimally reflects the statistics of the input and that this may result from the fact that speech sound categories are acquired in part through an unsupervised process.
3.5. Simulation 4: Co-varying cues in cue-weighting model
So far, we’ve assumed that the magnitude of trading relations directly reflects the relative weight of the cues. However, previous work on cue integration in speech has shown that the presence other cues can influence trading relations. For example, Shinn, Blumstein, and Jongman (1985) examined listeners’ use of VL and formant transition duration (TD) on manner (/b/-/w/) distinctions. In addition to these cues, they simultaneously manipulated additional cues that covaried with TD to produce more natural continua. In this case, the trading relation between TD and VL was reduced. The additional covarying cues may have caused listeners to ignore VL (though see Miller & Wayland, 1993). Utman (1998) found a similar effect, showing that the trading relation between VOT and VL is reduced in natural speech, which contains a large number of voicing cues (see also Lisker, 1975).
Under the assumption that trading relations are determined largely by the relative weight of the available cues, these results imply that listeners perceive synthetic and natural speech differently, re-weighting cues depending on the type of input. However, differences in the observed trading relations may reflect other factors besides the weight of the cues. For example, if changes in a third cue are correlated with changes in one of the other two cues, the relative weight of the correlated cues may appear larger – together they are effectively more reliable.
This is straightforward to test in the cue-weighting model. The model can be tested using different stimuli without changing the weights in order to examine whether additional cues have an effect on trading relations. Thus, we trained the model with a third, artificial cue and tested it under conditions in which, during testing, this cue either covaried with VOT or was held constant at an ambiguous value.
3.5.1. Procedures
While there were no other cues to voicing for which measurements were available, previous research suggested that F1 onset frequency shows a trading relation with VOT similar in size to the one between VOT and VL (e.g. Summerfield & Haggard, 1977). Thus, the distributions used for this third cue were based on a small sample of acoustic measurements of F1 onset frequency for bilabial stops.5 Means and standard deviations for the third cue are given in Table 1.
Training and testing procedures were the same as Simulation 2, except that the model had three cue-level MOGs. Learning rates were the same and initial parameters were determined in the same way as the first two simulations. After training, the models were tested on the VOT/VL pairs used in Simulation 2 under two conditions: (1) the artificial cue was held constant at an ambiguous value of 280 (constant-cue condition) or (2) the artificial cue covaried with VOT in nine steps from 240 to 320 (variable-cue condition).
3.5.2. Results and discussion
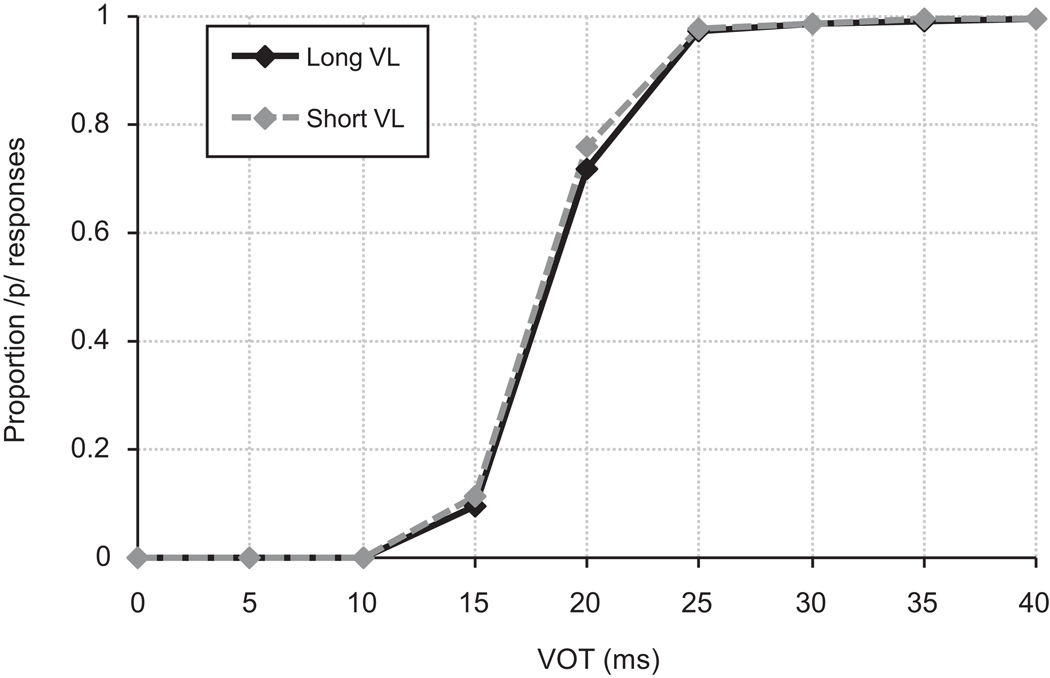
As in the previous simulations, the model performed quite well. Of the fifty models trained, only two were excluded because they overgeneralized. An additional two were excluded because they did not have any above-threshold categories in the combined MOG. Fig. 10 shows performance in the categorization task. In the constant-cue condition (panel A) a moderate VL effect is observed (similar to Simulation 2). In this condition, only VOT and VL are informative, and we see the predicted trading relation between the two cues. In the variable-cue condition (panel B), a decreased trading relation is observed, consistent with results from human listeners (Toscano & McMurray, in preparation). This reflects the fact that the artificial cues are informative about the voicing category, decreasing the apparent effect of VL.
Fig. 10.
Identification responses for Simulation 4. The trading relation is smaller when the third cue covaries with VOT (Panel A) than when it is held constant (Panel B).
These results demonstrate that the size of trading relations can be changed without changes in cue weights. Because additional cues covaried with VOT, variation in responses along the VOT dimension reflected more than the contribution of VOT to the voicing judgment. VL, on the other hand, is uncorrelated with both of the other cues. As a result, the apparent size of the trading relation decreased. Cues are not weighted differently, but, because variation in the primary dimension (VOT) now reflects variation in two cues, the overall contribution of that set of cues to the voicing judgment is greater than the contribution from VL alone. This results in a smaller trading relation between VOT and VL. Thus, both cue weights and the values of the cues used in testing determine the size of a trading relation.
4. General Discussion
These simulations demonstrate that weighting-by-reliability, when adapted to the particular features of acoustic cues in speech, can be used to describe trading relations observed with human listeners. They also suggest that cue weights can be learned using a simple unsupervised competitive learning mechanism and that the learning process itself may play a role in determining how cues are weighted. Further, these models are not speech-specific and could be applied to other categorization tasks as well.
The initial set of simulations revealed that the cue-weighting model provided a better fit to the data from listeners than the multi-dimensional model. The reason for this was counterintuitive: the cue-weighting model over-weighted the less reliable cue, resulting in a trading relation. This was due to the fact that the categories and cue distributions are learned, not estimated directly from the input. Indeed, learning appears to be essential for obtaining the correct cue weights. Thus, the weights that listeners assign to cues may be a function of both the statistics of the input and the history of the learning system. While this result implies that the cue-weighting model represents certain cues sub-optimally, this may generally be the best representation it can achieve given the requirements of learning. There may also be a benefit to this, in that it could allow the system to amplify cues that are generally weak and may be useful in other circumstances (e.g. a noisy environment in which VOT is hard to detect; Miller & Wayland, 1993).
While these results suggest that learning plays a role, we do not argue that any learning process will lead to this outcome. Other types of learning with different dynamics (Rumelhart & Zipser, 1985; Elman, 1993; McMurray et al., 2009b) might lead to different outcomes. Whether it comes from learning, or some other process, however, our simulations suggest that something must exaggerate the difference between overlapping distributions of VL. Statistics alone are not sufficient. Given the success of the MOG framework in accounting for a range of processes in speech development (de Boer & Kuhl, 2003; Vallabha et al, 2007; McMurray et al., 2009a) this approach provides a compelling explanation for listeners’ performance in this task.
The final set of simulations revealed that changes in the trading relation between two cues can be observed without changes in the weights of the individual cues. Trading relations not only reflect cue weights, but also the influence of correlated inputs. Preliminary work with human listeners (Toscano & McMurray, in preparation) confirms the prediction of the cue-weighting model that changes in the VOT/VL trading relation can be observed in a single experiment when additional cues either covary with VOT or are held constant.
In addition to its close correspondence to behavioral data, the cue-weighting model provides a much more compact representation of the input than the multi-dimensional model because it collapses cues into a single dimension. This may offer a better approach for scaling up to a large number of cues. Further, this approach offers a general model of the origin of trading relations in speech, suggesting that they can largely be determined by the statistics of the input and unsupervised learning. This may allow us to explain trading relations between other sets of cues (Repp, 1982) as well as changes in cue weights over development (Nittrouer, 2002; Mayo & Turk, 2004).
The cue-weighting approach may also be informative for describing more general aspects of speech development. For example, during development, listeners face the problem of determining which cues are relevant for different phonological distinctions (Rost & McMurray, 2009). The cue-weighting model would suggest that the irrelevant cues simply receive a weight of zero (i.e. the model learns that they are best described as a single category). Thus, rather than first determining which cues are relevant and then learning the distribution of categories along those dimensions, learning may proceed by first determining the distributional statistics of a set of cues, and then weighting them to determine if they are relevant (or both processes may happen simultaneously). This is a rather counter-intuitive prediction, and it may be informative for understanding how listeners determine which cues to use to distinguish different phonological contrasts. It may also explain why infants at 14 month olds, who’ve tuned their speech categories to their native language, have still not entirely completed this process (Rost & McMurray, 2009; submitted).
4.1. Relationship to other models
The cue-weighting model differs from previous approaches in several important ways. Both FLMP and NAPP models assume that cue integration is a category-dependent process. In contrast, our model suggests that cue weights can be determined independently of the categories along the dimension through an unsupervised learning process that uses the same information for learning the categories themselves. Although this contrasts with previous models, it provides a more realistic characterization of how cue weights are learned. In addition, there is evidence that integration may occur at pre-categorical stages, although it’s not clear if this is due to the fact that cues are estimated and integrated, or whether these cues are only estimated in combination (Delgutte, 1982, Kingston and Diehl, 1994)
Recently, researchers have begun to use Bayesian (i.e. ideal observer) models (Griffiths & Tenenbaum, 2006; Tenenbaum & Griffiths, 2001) to describe various behaviors, including speech perception (Norris & McQueen, 2008; Clayards et al., 2008; Feldman, Griffiths, & Morgan, submitted). These models share a number of properties with ours. They suggest that perceivers are sensitive to the distributional statistics of stimuli and use this information to categorize them. Also, in both approaches, speech categories are described parametrically, allowing us to specify the properties of the model using a simple set of equations (Gaussian distributions in our case).
However, there are many aspects of our models that make them distinctly non-Bayesian. Bayesian models suggest that behavior is based on an optimal encoding of the statistics, whereas our simulations with the cue-weighting model and its close match to the behavioral data suggest that there are limits to how optimally these statistics are estimated. While perception is largely based on the distributional statistics of speech, we highlight a potentially important role for an iterative competitive learning process that leads to non-veridical perception of the input. This learning process eliminates the need to set the number of categories beforehand, using priors on K or pruning techniques. This emphasis on developmental plausibility has a further benefit: McMurray et al. (2009a) show how this iterative learning process can model the developmental timecourse of speech discrimination in infancy.
Other aspects, such as the decision rule, make our models sub-optimal (Nearey & Hogan, 1986), and thus, non-Bayesian. In addition, other features of Bayesian models, such as the size principle (i.e. learners decrease the size of a category with increasing exposure; Tenenbaum, 1999; Tenenbaum & Griffiths, 2001), are not required in our models and they may not obey certain constraints (the size of the category increases over training; see McMurray et al., 2009b). Again, this difference may arise from our commitment to iterative, developmental processes, but the fact that this model can learn quite successfully with rules that seem to violate this principle challenge whether this is necessary.
4.2. Limitations of the model
4.2.1. Perceptual and lexical processes
The MOG approach provides a transparent description of the structure of speech categories and explains how they can be derived from the statistics of the input using an unsupervised learning mechanism and simple form of competition. While this offers a good computational explanation of the system and a model of the learning process, it should not be taken as a model of the perceptual process, which may have additional effects on cue integration. For example, many cues (such as VOT and VL) are temporally asynchronous, and recent eye-tracking data suggests that listeners use cues as they become available during spoken word recognition, rather than waiting until all cues are received (McMurray et al., 2008). This suggests that the order in which cues are heard may have an effect on their functional weighting during perception. Indeed, the simulations presented here demonstrate that the developmental process can provide valuable insights about cue integration; an investigation of perceptual processing may yield further information. Thus, while the MOG provides a mechanistic account of learning, it provides only a descriptive account of listeners’ perceptual processes. More detailed models of online speech processing may be needed to go further (see Toscano & McMurray, 2008; McMurray et al., 2009b).
A second aspect of speech processing that is not considered in these models is the role of feedback and top-down information in learning. The models presented here learn clusters of speech sounds based solely on bottom-up input. Lexical structure may be an important source of information for distinguishing speech sounds. For example, the fact that bear and pear are contrastive words in the lexicon may force the system to make fine-grained phonetic distinctions (Metsala & Walley, 1998; Walley, Metsala, & Garlock, 2003; Charles-Luce & Luce 1990, 1995), and knowing which of the two words is being referred to can provide an error signal for supervised speech category learning (Norris, McQueen & Cutler, 2003; Kraljic & Samuel, 2005). A complete model of speech development should include them. However, feedback is not necessary to account for the effects modeled here. Indeed, if lexical information was used to tag input with the correct category, we might not expect it to exaggerate the differences between the categories along the VL dimension as the cue-weighting model did and as human listeners do. Lexical information would help the model learn the correct distributions, decreasing the relative weight of VL. Thus, if this model included feedback its behavior would be less similar to listeners’ behavior. This is, in effect, the result observed when the parameters of the Gaussians were set to match the distributional statistics of the input (discussed in Simulation 2). However, this does not rule out the utility of feedback. It may be necessary for learning other phonological distinctions, in particular, those for which there are no good individual cues.
4.2.2. Computational limitations
One limitation of the cue-weighing model is its ability to model sets of cues for which the relative order of categories along a dimension is different for each cue. For the case of VOT and VL, this problem can be solved by tracking the sign of the correlation between the two cues. However, for distinctions with more than two categories along each dimension (e.g. place of articulation in English, voicing in Thai), this solution will not necessarily work. For example, both VOT and F2 onset frequency are cues to word-initial place distinctions. However, the relative order of categories along the two dimensions is not the same in the context of the vowels /u/ and /o/ (Kewley-Port, 1982). The cue-weighting model would not be able to collapse these cues into a single dimension (although the weights of each dimension may still be accurate).
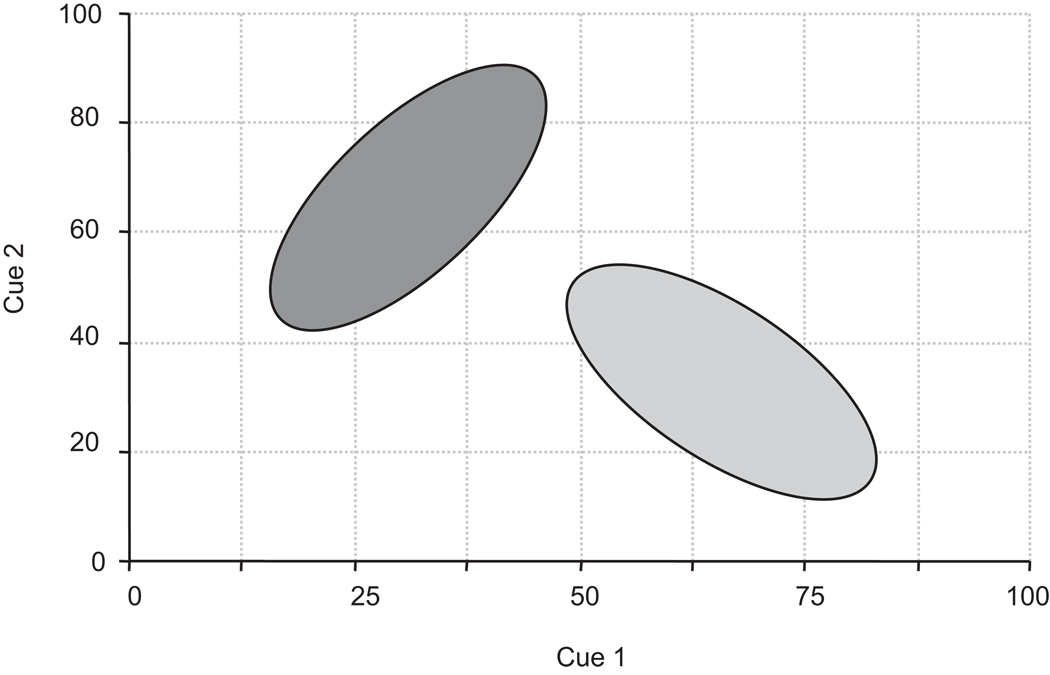
A related limitation is that the model cannot learn sets of cues in which the within-category correlations between cues (i.e. the correlation between tokens within each category) differ for each category. Figure 11 shows a schematic representation of two hypothetical categories with different within-category correlations. Some pairs of cues show these types of relationships in different contexts (e.g. place of articulation: burst center frequency and F2 onset for different vowel contexts; Kiefte & Kluender, 2005; Nearey, 1998).
Fig. 11.
A hypothetical pair of cues for which the within-category correlations for the two categories are different.
Both of these problems are a result of collapsing categories into a single dimension. The multi-dimensional model would not have these problems, since it can represent the entire acoustic space and categories may occur in any relative order along the cue dimensions. Thus, one solution would be to combine aspects of both models, reducing the number of cue dimensions as much as possible using the cue-weighting strategy outlined here and representing cues in a smaller multi-dimensional space. Another possible solution would be to take contextual information into account in determining the values along cue dimensions. That is, inputs to the cue dimensions could be determined by first partialing out context effects (see Cole, Linebaugh, Munson & McMurray, submitted).
4.3. Conclusion
These simulations demonstrate the power of the weighting-by-reliability approach applied to speech. Weights given to acoustic cues can largely be determined from the statistics of the input, and these in turn do a good job predicting behavior. However, by themselves, these statistics are not sufficient to explain all types of cue-weighting—some mechanism by which overlapping categories are enhanced is also needed. We suggest that learning itself, in addition to distributional statistics, may be crucial for determining those weights. While statistical learning approaches to perception have largely focused on statistics, there may also be a unique contribution for learning.
Acknowledgements
Portions of this work were presented at the 30th Meeting of the Cognitive Science Society, July 2008 in Washington, D. C. We are grateful to J. Sean Allen and Joanne Miller for acoustic data used to train the models. We would also like to thank Richard Aslin, Meghan Clayards, and Naomi Feldman for helpful theoretical discussions of the questions addressed in this paper, as well as Lisa Pearl and Terry Nearey for their comments on earlier versions of this manuscript. This research was supported by a University of Iowa Student Government Research Grant to JCT and NIH DC008089 to BM.
Appendix A
Bivariate (two-dimensional) Gaussian distribution for the multi-dimensional model:
| (7) |
This represents a single category in a two-dimensional mixture model, where μxi and μyi are the means along each dimension, σxi and σyi are the standard deviations along each dimension, ρi is the correlation between the two dimensions, and ϕi is the likelihood (frequency) of the category.
Learning rules for cue-weighting model:
| (8) |
| (9) |
| (10) |
These rules update the parameters of the Gaussians in the mixture such that they better approximate the distributions of the data on each training trial. In each equation, η is the learning rate for each parameter. Gi(x) is computed from Equation 4 and M(x) is computed from Equation 5. The update rule for each parameter is determined by taking the derivative of the likelihood function of the mixture distribution (Equation 5) w.r.t. that parameter. Because M(x) is a sum, taking the partial derivative of any single parameter is only a function of the relevant category. This simplifies the learning rules, allowing us to drop all of the terms from the sum except for the one for the relevant category.
Learning rules for multi-dimensional model:
| (11) |
| (12) |
| (13) |
| (14) |
As with the learning rules for the cue-weighting model, η is the learning rate for each parameter, and the update rules are computed by taking the derivative of the likelihood function of the mixture distribution (Equation 7) w.r.t. each parameter.
Footnotes
For the single-cue case, we have explored a range of different starting μ-values and learning rates (Toscano & McMurray, 2005). For initial μ-values, we have not found major differences in the model’s ability to learn or its categorization performance. Learning rates that are ≤1 tend to be the most successful.
We used similar test stimuli to the ones used in McMurray et al. (2008), though they used different VLs for each of their word continua (due to variations in other phonological features of the words). The VL values we chose span a similar range to the ones they used (100 ms in our simulations; 95–100 ms for McMurray et al.) and have similar values.
We chose this loose definition of success because we wanted to include as many repetitions as possible to see how accurately the model reflected listeners’ behavior. At minimum, the model needed to have at least two categories in order to compute identification functions for it. In addition, previous work has demonstrated that for reasonably distinguishable dimensions (e.g. VOT), MOG models show high accuracy in finding the correct parameters. For example, in models learning VOT, the average deviation from the correct VOT was 0.52 ms for μ (see McMurray et al., 2009a). For cases in which the model had more than two above threshold categories at the end of training, the categories with the maximum posterior for the prototypical values of each cue (i.e. the mean value for each category) were used as the voiced and voiceless categories.
Since the model normally starts with a large number of categories whose μ-values are randomly distributed along the cue dimension, it is likely that some of these categories will fall outside this range, allowing the model to successfully learn the number of categories.
While these values were not taken from a complete set of acoustic measurements for a third cue to voicing, we can examine the effects of an additional cue simply by allowing it to covary with VOT.
References
- Allen JS, Miller JL. Effects of syllable-initial voicing and speaking rate on the temporal characteristics of monosyllabic words. Journal of the Acoustical Society of America. 1999;106:2031–2039. doi: 10.1121/1.427949. [DOI] [PubMed] [Google Scholar]
- Atkins JE, Fiser J, Jacobs RA. Experience-dependent visual cue integration based on consistencies between visual and haptic percepts. Vision Research. 2001;41:449–461. doi: 10.1016/s0042-6989(00)00254-6. [DOI] [PubMed] [Google Scholar]
- Battaglia PW, Jacobs RA, Aslin RN. Bayesian integration of visual and auditory signals for spatial localization. Journal of the Optical Society of America. 2003;20:1391–1397. doi: 10.1364/josaa.20.001391. [DOI] [PubMed] [Google Scholar]
- Bülthoff HH, Mallot HA. Integration of depth modules: Stereo and shading. Journal of the Optical Society of America. 1988;5 doi: 10.1364/josaa.5.001749. 174s9-1758. [DOI] [PubMed] [Google Scholar]
- Charles-Luce J, Luce PA. Similarity neighbourhoods of words in young children’s lexicons. Journal of Child Language. 1990;17:205–215. doi: 10.1017/s0305000900013180. [DOI] [PubMed] [Google Scholar]
- Charles-Luce J, Luce PA. An examination of similarity neighbourhoods in young children’s receptive vocabularies. Journal of Child Language. 1995;22:727–735. doi: 10.1017/s0305000900010023. [DOI] [PubMed] [Google Scholar]
- Clayards M, Tanenhaus MK, Aslin RN, Jacobs RA. Perception of speech reflects optimal use of probabilistic speech cues. Cognition. 2008;108:804–809. doi: 10.1016/j.cognition.2008.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole J, Linebaugh G, Munson C, McMurray B. Vowel-to-vowel coarticulation across words in English: Acoustic evidence. (submitted) [Google Scholar]
- de Boer B, Kuhl PK. Investigating the role of infant-directed speech with a computer model. Acoustic Research Letters Online. 2003;4:129–134. [Google Scholar]
- Delgutte B. Some correlates of phonetic distinctions at the level of the auditory nerve. In: Carlson R, Granstöm B, editors. The Representation of Speech in the Peripheral Auditory System. Amsterdam: Elsevier Biomedical Press; 1982. [Google Scholar]
- Elman JL. Learning and development in neural networks: The importance of starting small. Cognition. 1993;48:71–79. doi: 10.1016/0010-0277(93)90058-4. [DOI] [PubMed] [Google Scholar]
- Ernst MO, Banks MS. Humans integrate visual and haptic information in a statistically optimal fashion. Nature. 2002;415:429–433. doi: 10.1038/415429a. [DOI] [PubMed] [Google Scholar]
- Feldman NH, Griffiths TL, Morgan JL. The influence of categories on perception: Explaining the perceptual magnet effect as optimal statistical inference. doi: 10.1037/a0017196. (submitted) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frisch S. Similarity and frequency in phonology. Unpublished doctoral dissertation, Northwestern University; 1996. [Google Scholar]
- Griffiths TL, Tenenbaum JB. Optimal predictions in everyday cognition. Psychological Science. 2006;17:767–773. doi: 10.1111/j.1467-9280.2006.01780.x. [DOI] [PubMed] [Google Scholar]
- Goldinger SD. Echoes of echoes? An episodic theory of lexical access. Psychological Review. 1998;105:251–279. doi: 10.1037/0033-295x.105.2.251. [DOI] [PubMed] [Google Scholar]
- Haggard MP, Ambler S, Callow M. Pitch as a voicing cue. Journal of the Acoustical Society of America. 1970;47:613–617. doi: 10.1121/1.1911936. [DOI] [PubMed] [Google Scholar]
- Jacobs RA. Integration of texture and motion cues to depth. Vision Research. 1999;39:3621–3629. doi: 10.1016/s0042-6989(99)00088-7. [DOI] [PubMed] [Google Scholar]
- Jacobs RA. What determines visual cue reliability? Trends in Cognitive Sciences. 2002;6:345–350. doi: 10.1016/s1364-6613(02)01948-4. [DOI] [PubMed] [Google Scholar]
- Johnson EB, Cummings BG, Landy MS. Integration of stereopsis and motion shape cues. Vision Research. 1994;34:2259–2275. doi: 10.1016/0042-6989(94)90106-6. [DOI] [PubMed] [Google Scholar]
- Jongman A, Wayland R, Wong S. Acoustic characteristics of English Fricatives. Journal of the Acoustical Society of America. 2000;108(3):1252–1263. doi: 10.1121/1.1288413. [DOI] [PubMed] [Google Scholar]
- Kalman RE. A new approach to linear filtering and prediction problems. Transaction of the ASME – Journal of Basic Engineering. 1960;82:35–45. [Google Scholar]
- Kaufman L. Sight and Mind. New York: Oxford University Press; 1974. [Google Scholar]
- Kewley-Port D. Measurement of formant transitions in naturally produced stop consonant-vowel syllables. Journal of the Acoustical Society of America. 1982;72:379–389. doi: 10.1121/1.388081. [DOI] [PubMed] [Google Scholar]
- Kiefte M, Kluender KR. Pattern Playback revisited: Unvoiced stop consonant perception. Journal of the Acoustical Society of America. 2005;118:2599–2606. doi: 10.1121/1.2040047. [DOI] [PubMed] [Google Scholar]
- Kingston J, Diehl R. Phonetic knowledge. Language. 1994;70:419–454. [Google Scholar]
- Kraljic T, Samuel AG. Generalization in perceptual learning for speech. Psychonomic Bulletin & Review. 2006;13:262–268. doi: 10.3758/bf03193841. [DOI] [PubMed] [Google Scholar]
- Landy MS, Kojima H. Ideal cue combination for localizing texture-defined edges. Journal of the Optical Society of America. 2001;43:2307–2320. doi: 10.1364/josaa.18.002307. [DOI] [PubMed] [Google Scholar]
- Lisker L. Is it VOT or a first-formant transition detector? Journal of the Acoustical Society of America. 1975;57:1547–1551. doi: 10.1121/1.380602. [DOI] [PubMed] [Google Scholar]
- Lisker L. “Voicing” in English: A catalogue of acoustic features signaling /b/ versus /p/in trochees. Language and Speech. 1986;29:3–11. doi: 10.1177/002383098602900102. [DOI] [PubMed] [Google Scholar]
- Lisker L, Abramson AS. A cross-linguistic of voicing in initial stops: Acoustical measurements. Word. 1964;20:384–422. [Google Scholar]
- Liberman AM, Harris KS, Kinney JA, Lane H. The discrimination of relative onset-time of the components of certain speech and nonspeech patterns. Journal of Experimental Psychology. 1961;61:379–388. doi: 10.1037/h0049038. [DOI] [PubMed] [Google Scholar]
- Love BC, Medin DL, Gureckis TM. SUSTAIN: A network model of category learning. Psychological Review. 2003;111:309–332. doi: 10.1037/0033-295X.111.2.309. [DOI] [PubMed] [Google Scholar]
- Luce RD. Individual choice behavior: A theoretical analysis. New York: Wiley; 1959. [Google Scholar]
- Marr D. Vision: A Computational Investigation Into the Human Representation and Processing of Visual Information. San Francisco: W. H. Freeman; 1982. [Google Scholar]
- Massaro DW, Cohen MM. Categorical or continuous speech perception: A new test. Speech Communication. 1983;2:15–35. [Google Scholar]
- Massaro DW, Oden GC. Evaluation and integration of acoustic features in speech perception. The Journal of the Acoustical Society of America. 1980;67:996–1013. doi: 10.1121/1.383941. [DOI] [PubMed] [Google Scholar]
- Maye J, Weiss DJ, Aslin RN. Statistical phonetic learning in infants: Facilitation and feature generation. Developmental Science. 2008;11:122–134. doi: 10.1111/j.1467-7687.2007.00653.x. [DOI] [PubMed] [Google Scholar]
- Maye J, Werker JF, Gerken L. Infant sensitivity to distributional information can affect phonetic discrimination. Cognition. 2002;82:B101–B111. doi: 10.1016/s0010-0277(01)00157-3. [DOI] [PubMed] [Google Scholar]
- Mayo C, Turk A. Adult-child differences in acoustic cue weighting are influenced by segmental context: Children are not always perceptually biased toward transitions. Journal of the Acoustical Society of America. 2004;115:3184–3194. doi: 10.1121/1.1738838. [DOI] [PubMed] [Google Scholar]
- McMurray B, Aslin RN, Toscano JC. Statistical learning of phonetic categories: Computational insights and limitations. Developmental Science. 2009a;12:369–378. doi: 10.1111/j.1467-7687.2009.00822.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMurray B, Clayards M, Tanenhaus MK, Aslin RN. Tracking the timecourse of phonetic cue integration during spoken word recognition. Psychonomic Bulletin and Review. 2008;15:1064–1071. doi: 10.3758/PBR.15.6.1064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMurray B, Horst J, Toscano JC, Samuelson LK. Towards an integration of connectionist learning and dynamical systems processing: case studies in speech and lexical development. In: Spencer J, Thomas M, McClelland J, editors. Toward a Unified Theory of Development: Connectionism and Dynamic Systems Theory Re-Considered. London: Oxford University Press; 2009b. pp. 218–249. [Google Scholar]
- McMurray B, Tanenhaus MK, Aslin RN. Gradient effects of within-category phonetic variation on lexical access. Cognition. 2002;86:B33–B42. doi: 10.1016/s0010-0277(02)00157-9. [DOI] [PubMed] [Google Scholar]
- Metsala JL, Walley AC. Spoken vocabulary growth and the segmental restructuring of lexical representations: Precursors to phonemic awareness and early reading ability. In: Metsala JL, Ehri LC, editors. Word Recognition in Beginning Literacy. Mahwah, New Jersey: Erlbaum; 1998. pp. 89–120. [Google Scholar]
- Miller JL, Dexter ER. Effects of speaking rate and lexical status on phonetic perception. Journal of Experimental Psychology: Human Perception & Performance. 1988;14:369–378. doi: 10.1037//0096-1523.14.3.369. [DOI] [PubMed] [Google Scholar]
- Miller JL, Volaitis LE. Effect of speaking rate on the perceptual structure of a phonetic category. Perception & Psychophysics. 1989;46:505–512. doi: 10.3758/bf03208147. [DOI] [PubMed] [Google Scholar]
- Miller JL, Wayland SC. Limits on the limitations of context-conditioned effects in the perception of [b] and [w] Perception & Psychophysics. 1993;54:205–210. doi: 10.3758/bf03211757. [DOI] [PubMed] [Google Scholar]
- Nearey TM. Speech perception as pattern recognition. Journal of the Acoustical Society of America. 1997;101:3241–3256. doi: 10.1121/1.418290. [DOI] [PubMed] [Google Scholar]
- Nearey TM. Locus equations and pattern recognition. Commentary on Sussman, Fruchter, Hilbert, & Sirosh, “Linear correlates in the speech signal: The orderly output constraint”. Behavioral and Brain Sciences. 1998;21:241–259. doi: 10.1017/s0140525x98001174. [DOI] [PubMed] [Google Scholar]
- Nearey TM, Assmann PF. Modeling the role of inherent spectral change in vowel identification. Journal of the Acoustical Society of America. 1986;80:1297–1308. [Google Scholar]
- Nearey TM, Hogan J. Phonological contrast in experimental phonetics: relating distributions of measurements in production data to perceptual categorization curves. In: Ohala J, Jaeger J, editors. Experimental Phonology. New York: Academic Press; 1986. [Google Scholar]
- Nittrouer S. Learning to perceive speech: How fricative perception changes, and how it stays the same. Journal of the Acoustical Society of America. 2002;112:711–719. doi: 10.1121/1.1496082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norris D, McQueen JM. Shortlist B: A Bayesian model of continuous speech recognition. Psychological Review. 2008;115:357–395. doi: 10.1037/0033-295X.115.2.357. [DOI] [PubMed] [Google Scholar]
- Norris D, McQueen JD, Cutler A. Perceptual learning in speech. Cognitive Psychology. 2003;47:204–238. doi: 10.1016/s0010-0285(03)00006-9. [DOI] [PubMed] [Google Scholar]
- Oden GC, Massaro DW. Integration of feature information in speech perception. Psychological Review. 1978;85:172–191. [PubMed] [Google Scholar]
- Peterson GE, Lehiste I. Duration of syllable nuclei in English. Journal of the Acoustical Society of America. 1960;32:693–703. [Google Scholar]
- Pierrehumbert J. Exemplar dynamics: Word frequency, lenition, and contrast. In: Bybee J, Hopper P, editors. Frequency effects and the emergence of lexical structure. Amsterdam: John Benjamins; 2001. pp. 137–157. [Google Scholar]
- Pierrehumbert J. Phonetic diversity, statistical learning, and acquisition of phonology. Language and Speech. 2003;46:115–154. doi: 10.1177/00238309030460020501. [DOI] [PubMed] [Google Scholar]
- Repp BH. Phonetic trading relations and context effects: New experimental evidence for a speech mode of perception. Psychological Bulletin. 1982;82:81–110. [PubMed] [Google Scholar]
- Rost GC, McMurray B. Speaker variability augments phonological processing in early word learning. Developmental Science. 2009;12:339–349. doi: 10.1111/j.1467-7687.2008.00786.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rost GC, McMurray B. Finding the signal by adding noise: The role of non-contrastive phonetic variability in early word learning. doi: 10.1111/j.1532-7078.2010.00033.x. (submitted) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rumelhart DE, Zipser D. Feature discovery by competitive learning. Cognitive Science. 1985;9:75–112. [Google Scholar]
- Schouten B, Gerrits E, van Hessen A. The end of categorical perception as we know it. Speech Communication. 2003;41:71–80. [Google Scholar]
- Shinn PC, Blumstein SE, Jongman A. Limitations of context conditioned effects in the perception of [b] and [w] Perception & Psychophysics. 1985;38:397–407. doi: 10.3758/bf03207170. [DOI] [PubMed] [Google Scholar]
- Stevens KN, Klatt DH. Role of formant transitions in the voiced-voiceless distinction for stops. Journal of the Acoustical Society of America. 1974;55:653–659. doi: 10.1121/1.1914578. [DOI] [PubMed] [Google Scholar]
- Summerfield Q, Haggard M. On the dissociation of spectral and temporal cues to the voicing distinction in initial stop consonants. Journal of the Acoustical Society of America. 1977;62:435–448. doi: 10.1121/1.381544. [DOI] [PubMed] [Google Scholar]
- Summerfield Q. Articulatory rate and perceptual constancy in phonetic perception. Journal of Experimental Psychology: Human Perception and Performance. 1981;7:1074–1095. doi: 10.1037//0096-1523.7.5.1074. [DOI] [PubMed] [Google Scholar]
- Tenenbaum JB. Bayesian modeling of human concept learning. In: Kearns MS, Solla SA, Cohen DA, editors. Advances in Neural Information Processing Systems. Vol. 11. Cambridge: MIT Press; 1999. [Google Scholar]
- Tenenbaum JB, Griffiths TL. Generalization, similarity, and Bayesian inference. Behavioral and Brain Sciences. 2001;24:629–640. doi: 10.1017/s0140525x01000061. [DOI] [PubMed] [Google Scholar]
- Teinonen T, Aslin RN, Alku P, Csibra G. Visual speech contributes to phonetic learning in 6-month-old infants. Cognition. 2008;108:850–855. doi: 10.1016/j.cognition.2008.05.009. [DOI] [PubMed] [Google Scholar]
- Toscano JC, McMurray B. Statistical learning, cross-linguistic constraints, and the acquisition of speech categories: a computational approach. Talk presented at the 11th Midcontinental Workshop on Phonology, University of Michigan; Ann Arbor, MI. 2005. Nov, [Google Scholar]
- Toscano JC, McMurray B. Online processing of acoustic cues in speech perception: Comparing statistical and neural network models. Paper presented at the 156th Meeting of the Acoustical Society of America; Miami, FL. 2008. Nov, [Google Scholar]
- Toscano JC, McMurray B. The time course of cue integration in natural and synthetic speech: Emergent and dynamic effects of multiple perceptual cues. (in preparation) [Google Scholar]
- Utman JA. Effects of local speaking rate context on the perception of voice-onset time in initial stop consonants. Journal of the Acoustical Society of America. 1998;103:1640–1653. doi: 10.1121/1.421297. [DOI] [PubMed] [Google Scholar]
- Vallabha GK, McClelland JL, Pons F, Werker JF, Amano S. Unsupervised learning of vowel categories from infant-directed speech. Proceedings of the National Academy of Sciences. 2007;104:13273–13278. doi: 10.1073/pnas.0705369104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walley AC, Metsala JL, Garlock VM. Spoken vocabulary growth: Its role in the development of phoneme awareness and early reading ability. Reading and Writing. 2003;16:5–20. [Google Scholar]
- Warren P, Marslen-Wilson W. Continuous uptake of acoustic cues in spoken word recognition. Perception & Psychophysics. 1987;41:262–275. doi: 10.3758/bf03208224. [DOI] [PubMed] [Google Scholar]
- Wayland SC, Miller JL, Volaitis LE. The influence of sentential speaking rate on the internal structure of phonetic categories. Journal of the Acoustical Society of America. 1994;95:2694–2701. doi: 10.1121/1.409838. [DOI] [PubMed] [Google Scholar]
- Werker JF, Tees RC. Cross-langauge speech perception: Evidence for perceptual reorganization during the first year of life. Infant Behavior & Development. 1984;7:49–63. [Google Scholar]
- Werker JF, Curtin S. PRIMIR: A developmental framework of infant speech processing. Language Learning & Development. 2005;1:197–234. [Google Scholar]