A joint-modeling approach to assess the impact of biomarker variability on the risk of developing clinical outcome

Abstract

In some clinical trials and epidemiologic studies, investigators are interested in knowing whether the variability of a biomarker is independently predictive of clinical outcomes. This question is often addressed via a naïve approach where a sample-based estimate (e.g., standard deviation) is calculated as a surrogate for the “true” variability and then used in regression models as a covariate assumed to be free of measurement error. However, it is well known that the measurement error in covariates causes underestimation of the true association. The issue of underestimation can be substantial when the precision is low because of limited number of measures per subject. The joint analysis of survival data and longitudinal data enables one to account for the measurement error in longitudinal data and has received substantial attention in recent years. In this paper we propose a joint model to assess the predictive effect of biomarker variability. The joint model consists of two linked sub-models, a linear mixed model with patient-specific variance for longitudinal data and a full parametric Weibull distribution for survival data, and the association between two models is induced by a latent Gaussian process. Parameters in the joint model are estimated under Bayesian framework and implemented using Markov chain Monte Carlo (MCMC) methods with WinBUGS software. The method is illustrated in the Ocular Hypertension Treatment Study to assess whether the variability of intraocular pressure is an independent risk of primary open-angle glaucoma. The performance of the method is also assessed by simulation studies.

1 Introduction

In many clinical trials and epidemiologic studies, information is gathered on both time to event (survival data) and repeated measures of biomarkers (longitudinal data). One primary goal is to see the prognostic effect of a biomarker on survival outcome. This is often modeled in the framework of Cox proportional hazards model where the biomarker is treated as a time-dependent covariate (Cox 1972). In some studies, the variability of a biomarker, in addition to its mean level and/or systematic trend over time, is also predictive of clinical outcomes. In the Honolulu Heart Program, for example, Iribarren et al. (1995) found that the subjects whose weight fluctuated most had a significantly higher risk of death from cardiovascular causes, non-cardiovascular and non-cancerous causes, and death from all causes. Grove et al. (1997) found that the variability of systolic blood pressure is an independent risk factor for the coronary heart disease. In many applications, the effect of biomarker variability is analyzed via a two-step approach where simple descriptive statistics such as standard deviation are first calculated for each individual and then used in regression models as covariates assumed to be free of measurement error. Such a naïve approach possesses some practical advantages. By using the sample-based estimates as time-independent covariates, for instance, one can take advantage of the wealth of theory that have been developed and software that have been written for the conventional Cox model. In addition, the method can produce tangible descriptive statistics that have a natural interpretation for each individual. However, this approach does not use the information in longitudinal data efficiently as it converts the repeated measures into a few summary statistics. More seriously, the method ignores the inherent measurement error in sample-based estimates. It is well known that the error in covariates can bias parameter estimates downward to null values and thus may mislead one into believing that an actually useful biomarker is not related to the outcome (Prentice 1982; Hughes 1993). Given the relatively small number of visits in many longitudinal studies, the influence of measurement error can be substantial, especially in assessing the effect of biomarker variability.

Many methods have been proposed to model longitudinal covariates measured with error and the joint analysis of survival and longitudinal data has received substantial attention in recent years (Hogan and Laird 1997). In general, a joint model consists of two sub-models, a measurement model for longitudinal data and an intensity model describing the time to event, and the two models are linked via shared parameters. There are broadly two classes of joint models, namely selection models and pattern-mixture models, depending on how the joint distribution is factorized (Little 1995). The selection model, though computationally intensive, is more prevalent in practice because of its intuitive construction and easy interpretation. Many of the selection models (Faucett and Thomas 1996; Wulfsohn and Tsiatis 1997; Vonesh et al. 2006) use the conventional linear mixed model (Laird and Ware 1982) to characterize the longitudinal data by a few time-invariant random effects, so that the subject-specific evolution follows a “smooth” trajectory over time. Henderson et al. (2000) extend the above models by introducing a serial correlation into the measurement error and thus allow the trend to vary over time. Guo and Carlin (2004) develop a fully Bayesian version of Henderson et al. (2000). Xu and Zeger (2001) and Lin et al. (2002) propose joint models for survival data and multiple longitudinal data. Tsiatis and Davidian (2004) have provided an excellent overview of recent work on joint analysis. In most models, however, the longitudinal process is linked to the survival process only via random intercept and slope, while assuming all subjects sharing a common variance–covariance structure.

In this paper, we propose a random-effect-dependent selection model to assess the impact of biomarker variability on survival outcome. Our study is motivated by the Ocular Hypertension Treatment Study (OHTS) (Gordon et al. 1999) which is a multicenter randomized trial to evaluate the safety and efficacy of topical ocular hypotensive medication in delaying the onset of primary open-angle glaucoma (POAG). POAG is among the leading causes of blindness in US and worldwide and, as of today, intraocular pressure (IOP) is the only factor that can be modified by current treatment. Although more and more studies including OHTS have confirmed that a decrease in mean IOP level can reduce the risk of developing POAG, the findings from major prospective clinical trials about the impact of IOP fluctuation on POAG remain controversial (Bengtsson et al. 2006; Caprioli and Coleman 2008; Miglior et al. 2007). In this paper, we propose a joint model for this question. Specifically, the time to POAG is described by a full parametric Weibull distribution, the trajectory of IOP is fit using a linear mixed model that incorporates patient-specific variance (Lyles et al. 1999), and the two sub-models are linked via the shared patient-specific random effects. This paper is organized as follows. Section 2 describes model construction and parameter estimation. In Sect. 3, we illustrate the method in the Ocular Hypertension Treatment Study (OHTS). Section 4 assesses the method by a few simulation studies. Finally, Sect. 5 concludes with a discussion.

2 Methods

Suppose there are N subjects. Let T_i = min(D_i, C_i) be the observed survival time for the ith subject, where D_i is the potential failure time and C_i is the potential censoring time independent of D_i. Let Δ_i be the corresponding survival indicator, with Δ_i = 1 if T_i = D_i and Δ_i = 0 otherwise. Let Y_ij denote the longitudinal data for ith individual at time t_ij. In this paper, we assume that all subjects share a common follow-up schedule, with {t_ij} = {t₁, t₂, …, t_J} and t_ij ≤ T_i. Finally, we denote the baseline covariates predictive of longitudinal and survival processes as X_i(t) and Z_i(t) respectively, which may or may not be the same.

2.1 Joint model of longitudinal and survival data

The proposed joint distribution is a random-effect-dependent selection model which consists of two associated sub-models, a measurement model for longitudinal data and an intensity model for survival data. The two sub-models will be conditionally independent given the shared latent random effects and covariates. For the measurement model, the trajectory of longitudinal data is described by a linear mixed model that incorporates patient-specific variance (Lyles et al. 1999),

$$\begin{array}{c}\hfill Y_{\mathit{\text{ij}}}={\beta }_0+{\beta }_1{t}_{\mathit{\text{ij}}}+{\beta }_2{X}_i+\cdots +I_i+S_i{t}_{\mathit{\text{ij}}}+e_{\mathit{\text{ij}}}=\beta \prime X_i(t)+W_{1i},\hfill \\ \hfill \text{with}{I}_i~N(0,{\sigma }_I^2),S_i~N(0,{\sigma }_S^2),\hfill \\ \hfill e_{\mathit{\text{ij}}}~N(0,V_i),\text{ and log}(V_i)~N({\mu }_V,{\sigma }_V^2),\hfill \end{array}$$ (1)

where β is a vector of parameters for fixed effects and X_i(t) is the corresponding covariates. I_i and S_i are the patient-specific random intercept and slope as in the conventional linear mixed model (Laird and Ware 1982). V_i represents the “true” within-subject variability which follows a log-normal distribution with mean μ_V and variance ${\sigma }_V^2$. That is, unlike the conventional linear mixed models, model (1) explicitly allows patient-specific variance. Each of the patient-specific random effects is an independent and identically distributed variable. The term β′X_i(t) reflects the mean response, while W_1i = I_i + S_it_ij + e_ij can be viewed as the “true” individual-level trajectory after adjusting the overall mean response. When the parameter ${\sigma }_V^2$ becomes 0, model (1) reduces to a linear mixed model with a homogenous variance (Lyles et al. 1999).

Turning to the intensity model, the hazard of event at time t is specified as a proportional hazards form,

$$\begin{array}{cc}{\lambda }_i(t)\hfill & ={\lambda }_0(t)\text{exp}({\alpha }_0+{\alpha }_1{Z}_i+\cdots +{\gamma }_1{I}_i+{\gamma }_2{S}_i+{\gamma }_3\text{log}(V_i))\hfill \\ \hfill & ={\lambda }_0(t)\text{exp}(\alpha \prime Z_i(t)+W_{2i}),\hfill \end{array}$$ (2)

where λ₀(t) is the baseline hazard when all the covariates are 0, α′Z_i(t) represents the effects of (possibly time-dependent) explanatory variables, and the term W_2i = γ₁I_i + γ₂S_i + γ₃ log (V_i) induces association between survival and longitudinal processes. Because our previous analysis (unpublished data) with a full parametric Weibull model showed an adequate fit to the OHTS data, we choose λ₀(t) = ρt^(ρ−1), where ρ is the shape parameter of Weibull distribution (with ρ > 1 for a monotone increasing hazard and ρ < 1 for a monotone decreasing hazard).

2.2 Parameter estimation

The unknown parameters in the proposed model are estimated under a Bayesian framework using Markov chain Monte Carlo (MCMC) methods (Gelman et al. 2003). When the conditional distribution of each parameter given others is relatively easy to specify, the MCMC method allows one to work on even very complex models. The full joint distribution is specified in the form of,

$$f(Y,T,\theta )=f(Y|\theta )f(T|Y,\theta )f(\theta ),$$

with $\theta =\{\beta ,\alpha ,\gamma ,{\mu }_V,\rho ,{\sigma }_I^2,{\sigma }_S^2,{\sigma }_V^2\}$, the unknown parameters as given in models (1) and (2). Prior distributions must be specified for all unknown parameters when data are analyzed from a Bayesian perspective. A thorough sensitivity analysis with the OHTS data has been performed in this regard.

Specifically, we use a proper prior for each set of unknown parameters (e.g., a Gaussian distribution for the fixed effects, an Inverse Gamma distribution for the random effects, and a Gamma distribution for the Weibull shape parameter), but try out different levels of variability (with variances of 1,000, 100, 10, and 1 for each distribution). The results indicate that estimates of the fixed effects (β, α, γ, and μ_V) are very robust and hence a rather vague prior is chosen. For the random effects $({\sigma }_I^2,{\sigma }_S^2,\text{and}{\sigma }_V^2)$, especially ${\sigma }_S^2$, a prior of Inverse Gamma (0.001, 0.001) sometime causes numerical difficulties in sampling. The reason may be that ${\sigma }_S^2$ has a relatively small point estimate in the OHTS data $({\sigma }_S^2\approx 0.1)$. We therefore choose a less vague prior for the random effects. Among all the parameters, ρ is very sensitive and has to take a rather informative prior. However, our choice is reassured by the fact that similar results are obtained when an exponential distribution (ρ = 1) is fit instead. In short, following prior distributions are specified and all the parameters are assumed to be mutually independent,

$$\begin{array}{c}\hfill \beta ,\alpha ,\gamma ,{\mu }_v~N(0,1000),\hfill \\ \hfill {\sigma }_I^2,{\sigma }_S^2,{\sigma }_V^2~\text{Inverse Gamma}(0.01,0.01),\hfill \\ \hfill \text{and}\rho ~\text{Gamma}(1,1).\hfill \end{array}$$

2.3 Marginal models

To compare with joint analysis, models (1) and (2) are also fit to longitudinal and survival data separately. The marginal longitudinal model is estimated using the MCMC methods as outlined above. For the marginal survival model, we take a two-step approach and use the variance of residuals from a simple linear regression as a surrogate for the “true” patient-specific variability.

Since the use of two-step approach is so prevalent in medical applications, a simple simulation study is also conducted in Sect. 4 to compare the performance of different estimates for biomarker variability. One of the estimates is the posterior mean of patient-specific variance from model (1). However, this empirical Bayes predictor is known for its unattractive property of over-shrinking the estimates toward population mean. Hence, we also calculate a constrained Bayes estimate that is designed to combat against over-shrinkage and produce estimates whose distribution more closely matches the true underline parameters (Ghosh 1992). Let V̂_EBi denote the empirical estimate of the patient-specific variance for ith individual, and let var(V̂_EBi) be the corresponding variance of V̂_EBi, then the constrained Bayes estimate (V̂_CBi) can be calculated as,

$$\begin{array}{c}\hfill {\widehat{V}}_{{\mathit{\text{CB}}}_i}=w{\widehat{V}}_{{\mathit{\text{EB}}}_i}+(1-w){\overline{\widehat{V}}}_{\mathit{\text{EB}}},\hfill \\ \hfill \text{where}{\overline{\widehat{V}}}_{\mathit{\text{EB}}}=\frac{1}{N}{\displaystyle \sum _{i=1}^N{\widehat{V}}_{{\mathit{\text{EB}}}_i}},w={\left(1+\frac{H_1}{H_2}\right)}^{1/2},\hfill \\ \hfill H_1=\left(1-\frac{1}{N}\right){\displaystyle \sum _{i=1}^N\mathit{\text{var}}({\widehat{V}}_{{\mathit{\text{EB}}}_i})}\text{ and }{H}_2={\displaystyle \sum _{i=1}^N{({\widehat{V}}_{{\mathit{\text{EB}}}_i}-{\overline{\widehat{V}}}_{\mathit{\text{EB}}})}^2}.\hfill \end{array}$$

2.4 Computational implementation

Parameters in the joint model and the marginal longitudinal model are estimated using the Gibbs sampling built into the noncommercial statistical software WinBUGS (http://www.mrc-bsu.cam.ac.uk/bugs/). The estimation procedure is implemented with the R2WinBUGS library in the statistical package R (Sturtz et al. 2005). We use three parallel MCMC sampling chains with difference starting values. The convergence of each chain is monitored by the trace plots and the diagnostic statistics of Gelman et al. (2003). The posterior mean of the parameters are based on 15,000 iterations following a 15,000-iteration of burn-in period. The marginal survival model is fit using the Design library in R (Harrell 2001). Because WinBUGS and R have different parameterizations for Weibull distribution, the estimates from marginal survival models have been re-parameterized to facilitate a fair comparison.

3 Motivating example: ocular hypertension treatment study (OHTS)

3.1 Description of follow-up IOP

In OHTS, 1636 participants who had ocular hypertension were randomized to either an observation group or treatment using commercially available topical ocular hypotensive medication. Follow-up visits were scheduled every 6 months from the date of randomization, and the primary outcome was the time to the development of POAG as evidenced by reproducible visual field abnormality or clinically significant reproducible optic disc deterioration. At the end of study, 104 (12.7%) out of 819 participants in the observation group developed POAG while the incidence rate was 5.4% (44 of 817) among those in the treatment group. Detailed results of OHTS have been described elsewhere (Kass et al. 2002). In this paper, we focus on the relationship between follow-up IOP and time to POAG, especially on the question whether the long-term fluctuation of IOP is predictive of POAG. These 1618 participants who had at least 1 follow-up visit comprise our study cohort. Follow-up IOP (in mmHg) at each visit is the average of two eyes. Only pre-POAG IOP values are included in this study and the follow-up for each patient is ended at the date of POAG onset or last visit, whichever occurs first. The median follow-up time is 6.6 years (with a range of 0.5–8.1 years), the median number of post-randomization IOP measures per subject is 12 (with a range of 1–16), and more than 97% subjects have at least 3 visits (Table 1).

Table 1.

Number of follow-up visits in the OHTS data

Number of follow-up visits	Number of non-POAG (%)	Number of POAG (%)	Total (%)
1	16 (1.1%)	2 (1.4%)	18 (1.1%)
2	17 (1.2%)	9 (6.1%)	26 (1.6%)
3	21 (1.4%)	13 (8.8%)	34 (2.1%)
4	16 (1.1%)	15 (10.1%)	31 (1.9%)
≥5	1,400 (95.2%)	109 (73.6%)	1,509 (93.3%)
Total	1,470 (100%)	148 (100%)	1,618 (100%)

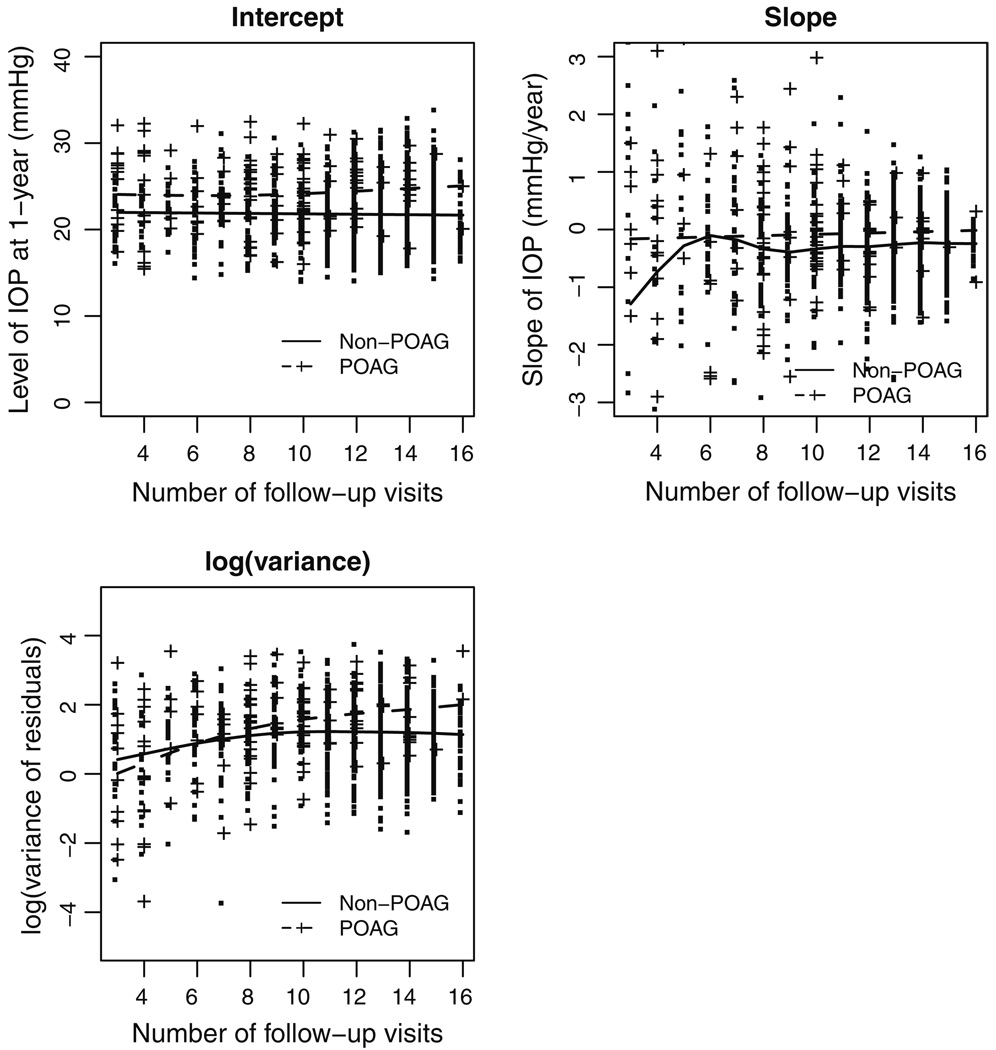
A simple linear regression of IOP against time is fit to each subject who has at least 3 IOP values. Figure 1 presents the estimated intercept, slope, and (logarithm transformed) variance of residuals from these regression models. In each plot, smoothed cubic splines are also imposed for participants with and without POAG respectively. The plots show that, comparing to those who have developed POAG, the POAG-free participants tend to have lower initial IOP levels, smaller slopes, and less variability. Because high IOP is an eligibility criterion in OHTS, the initial values (intercepts) are more likely to suffer from “regression to the mean”. As such, 1-year after randomization is actually used as the time 0 for all the regression models on IOP in this paper.

Fig. 1.

Descriptive statistics for follow-up IOP in the OHTS data, where the intercept, slope, and variance of residuals are estimated from the simple linear regression model fit to each patient. Smoothed cubic-splines are imposed to those who have developed POAG (broken line) and those who are free of POAG (solid line) respectively

3.2 Joint analysis of follow-up IOP and time to POAG

For illustration, treatment group (GRP=0 for observation group and GRP=1 for medication group) and follow-up IOP are included as the only covariates in our analysis. Table 2 shows 7 alternative joint models for the OHTS data and a full description of model selection is given in Sect. 3.4. Based on the fit statistics, Model V and Model VII have similar performance and provide the best fit to OHTS data. The parameter estimates (posterior means) and their 95% posterior intervals from both models are presented in Table 3, where γ₁, γ₂ and γ₃ represent the effects of patient-specific intercept, slope and variance respectively. Because γ₃ (which is absent in Model V) is significantly different from 0 and the two models produce almost identical estimates in all other parameters, Model VII is chosen as the final model,

$${\text{IOP}}_{\mathit{\text{ij}}}={\beta }_0+{\beta }_1{\text{GRP}}_i+{\beta }_2{t}_{\mathit{\text{ij}}}+{\beta }_3{\text{GRP}}_i{t}_{\mathit{\text{ij}}}+I_i+S_i{t}_{\mathit{\text{ij}}}+e_{\mathit{\text{ij}}},$$ (3)

$${\lambda }_i(t)={\rho t}^{(\rho -1)}\text{exp}({\alpha }_0+{\gamma }_1{I}_i^{*}+{\gamma }_2{S}_i^{*}+{\gamma }_3\text{log}(V_i)),$$ (4)

where $I_i^{*}={\beta }_1{\text{GRP}}_i+I_i$ and $S_i^{*}={\beta }_3{\text{GRP}}_i+S_i$ are treatment-modified random intercept and slope respectively.

Table 2.

The expected deviance (D̅), the number of effective parameters (ρD), and the total DIC in the candidate joint models for OHTS data

Models	W1i	W2ia	D̅	ρD	DIC
I	U0i	0	89, 019.8	1,474.6	90,494.4
II	U0i, U1i	0	87,071.9	2,219.2	89,291.1
III	U0i, U1i, Vi	0	82,645.5	3,222.2	85,867.7
IV	U0i, U1i, Vi	${\gamma }_1{I}_i^{*}$	82,599.6	3,211.2	85,810.8
V	U0i, U1i, Vi	${\gamma }_1{I}_i^{*}+{\gamma }_2{S}_i^{*}$	82,578.7	3,213.9	85,792.6
VI	U0i, U1i, Vi	${\gamma }_1{I}_i^{*}+{\gamma }_3\text{log}(V_i)$	82,600.2	3,207.2	85,807.4
VII	U0i, U1i, Vi	${\gamma }_1{I}_i^{*}+{\gamma }_2{S}_i^{*}+{\gamma }_3\text{log}(V_i)$	82,580.3	3,209.4	85,789.7

^a$I_i^{*}={\beta }_1·{\text{GRP}}_i+I_i$, treatment-modified random intercept

^a$S_i^{*}={\beta }_3·{\text{GRP}}_i+S_i$, treatment-modified random slope

Table 3.

Parameter estimates and 95% posterior intervals in the joint models and separate analyses of the OHTS data

Parameters	Model V (with #visit≥1)	Model VII (with #visit≥1)	Model VII (with #visit≥3)	Model VII (with #visit≥5)
Joint models
Longitudinal
Intercept (β0)	24.14(23.96, 24.32)	24.13(23.96, 24.30)	24.11(23.94, 24.29)	24.06(23.89, 24.24)
GRP (β1)	−4.49(−4.74, −4.24)	−4.48(−4.72, −4.23)	−4.51(−4.76, −4.25)	−4.46(−4.71, −4.22)
Time (β2)	−0.20(−0.23, −0.16)	−0.20(−0.24, −0.17)	−0.20(−0.24, −0.17)	−0.20(−0.23, −0.17)
GRP • Time(β3)	−0.05(−0.09, 0.002)	−0.05(−0.09, 0.002)	−0.04(−0.09, 0.006)	−0.05(−0.09, 0.001)
${\sigma }_I^2$	5.32(4.90, 5.77)	5.29(4.87, 5.73)	5.20(4.78, 5.64)	5.07(4.66, 5.52)
${\sigma }_S^2$	0.11(0.10, 0.13)	0.11(0.10, 0.13)	0.11(0.10, 0.13)	0.11(0.10, 0.13)
μV	1.43(1.39, 1.48)	1.44(1.40, 1.48)	1.43(1.39, 1.48)	1.43(1.39, 1.47)
${\sigma }_V^2$	0.53(0.48, 0.59)	0.53(0.48, 0.59)	0.53(0.48, 0.58)	0.53(0.47, 0.58)
Survival
Shape (ρ)	1.76(1.51, 2.02)	1.73(1.40, 2.05)	1.96(1.64, 2.26)	2.82(2.35, 3.22)
α0	−5.47(−5.98, −4.94)	−6.32(−7.25, −5.38)	−6.80(−7.65, −5.88)	−8.83(−9.83, −7.69)
γ1	0.21(0.15, 0.26)	0.18(0.12, 0.23)	0.17(0.11, 0.23)	0.16(0.10, 0.23)
γ2	1.09(0.10, 2.13)	1.05(0.07, 2.07)	1.10(0.21, 2.03)	1.15(0.19, 2.16)
γ3	–	0.54(0.20, 0.87)	0.52(0.23, 0.83)	0.61(0.29, 0.96)
Marginal models
Longitudinal
Intercept (β0)		24.13(23.96, 24.31)	24.11(23.94, 24.28)	24.06(23.88, 24.23)
GRP (β1)		−4.49(−4.73, −4.24)	−4.51(−4.76, −4.26)	−4.46(−4.71, −4.22)
Time (β2)		−0.21(−0.25, −0.17)	−0.21(−0.24, −0.18)	−0.21(−0.24, −0.17)
GRP • Time(β3)		−0.04(−0.09, 0.007)	−0.04(−0.09, 0.009)	−0.04(−0.09, 0.005)
${\sigma }_I^2$		5.27(4.85, 5.72)	5.20(4.78, 5.63)	5.07(4.66, 5.50)
${\sigma }_S^2$		0.11(0.10, 0.13)	0.11(0.10, 0.13)	0.11(0.10, 0.13)
μV		1.44(1.39, 1.48)	1.43(1.39, 1.47)	1.43(1.39, 1.47)
${\sigma }_V^2$		0.53(0.48, 0.59)	0.53(0.48, 0.58)	0.53(0.47, 0.58)
Survival
Shape (ρ)		–	2.05(1.75, 2.39)	3.07(2.58, 3.65)
α0		–	−10.62(−12.13, −9.12)	−12.76(−14.45, 11.07)
γ1		–	0.20(0.15, 0.26)	0.18(0.12, 0.24)
γ2		–	0.50(0.27, 0.73)	0.71(0.43, 1.00)
γ3		–	−0.16(−0.35, 0.02)	0.25(0.01, 0.48)

The estimates of β₀ and β₁ show that the 1-year IOP level in the treatment group (19.7mmHg) is significantly lower than that in the observational group (24.1mmHg). The estimates of β₂ and β₃ reveal that, in average, follow-up IOP decreases over time in both groups but the between-group difference (−0.25mmHg/year in the medication group versus −0.20 mmHg/year in the observation group) is not significant. The estimated ${\sigma }_V^2$ (0.53 with a 95% interval of 0.48–0.59) supports the assumption of heterogeneous variance in follow-up IOP. There is also a strong evidence for the effects of random intercept, slope, and variance on POAG. For every 1-SD (σ_I, σ_S, and σ_V) increase in intercept, slope, and log(variance), for example, there will be 51, 42, and 48% increase in the risk of developing POAG respectively. The WinBUGS model specification of Model VII is given in the Appendix.

3.3 Comparison between joint models and marginal models

To compare with the joint analysis, the follow-up IOP and time to POAG are also analyzed separately using the two sub-models in Model VII. Two sets of marginal models are fit, one for subjects with 3 or more visits and the other for subjects with 5 or more visits. The joint models are also fit in the corresponding subsets of data (Table 3). We see that joint models give consistent estimates across different datasets and the estimates from marginal longitudinal models are almost identical to their counterparts in the joint models. However, the estimates from marginal survival models, especially γ₃, are very sensitive to data selection. In the model including subjects with ≥3 visits, for example, γ₃ shows a trend toward a significant negative effect (γ₃ = −0.16, with 95% interval of −0.35 to 0.02). The other model only excludes less than 5% of subjects from previous data, but γ₃ becomes significantly greater than 0 (γ₃ = 0.25, with 95% interval of 0.01–0.48). Two issues may jointly contribute to such a dramatic change in γ₃. One is the inherent measurement error in the sample-based estimates. Since measurement error in covariates is known to bias estimates toward null values, this may partially explain the underestimation in γ₂. The other problem is the informative dropout. That is, these subjects with the highest risk are more likely to fall out of study earlier and thus are deprived the chance to show fluctuation. This problem will be further explored in the simulation studies.

3.4 Model selection

In the analysis of OHTS data, 7 alternative models are constructed (Table 2),

•	I : W1i = Ii + eij,	W2i = 0, and ${\sigma }_V^2=0$;
•	II : W1i = Ii + Sitij + eij,	W2i = 0, and ${\sigma }_V^2=0$;
•	III : W1i = Ii + Sitij + eij,	W2i = 0;
•	IV : W1i = Ii + Sitij + eij,	W2i = γ1Ii;
•	V : W1i = Ii + Sitij + eij,	W2i = γ1Ii + γ2Si;
•	VI : W1i = Ii + Sitij + eij,	W2i = γ1Ii + γ3 log(Vi);
•	VII : W1i = Ii + Sitij + eij,	W2i = γ1Ii + γ2Si + γ3 log(Vi);

where W_1i and W_2i are the latent Gaussian processes in the longitudinal and survival sub-models respectively, with $I_i~N(0,{\sigma }_I^2),S_i~N(0,{\sigma }_S^2),e_{\mathit{\text{ij}}}~N(0,V_i)\text{and}\text{log}(V_i)~N({\mu }_V,{\sigma }_V^2)$.

Specifically, for the longitudinal sub-model we start with simple models that include only random intercept (Model I) or random intercept and slope (Model II). After adding patient-specific variance (Model III), we observe a dramatic improvement in model fit. As such, patient-specific variance is included in all the subsequent joint models. Regarding the survival sub-model, in the first 3 models we assume that the survival process is associated with longitudinal process only via common baseline covariates (with W_2i = 0), but all 3 models show a very poor fit. Starting from Model IV, we therefore assume that the association is induced by patient-specific random effects as well. To facilitate an easy prediction of future subjects (whose treatment information may be absent), we also assume that treatment itself has no direct effect on time to POAG. Rather, we assume that treatment will modify IOP trajectory which in turn influences the risk of developing POAG. Consequently, treatment-modified intercept and slope are actually used in the survival sub-models.

The best model is selected using Deviance Information Criterion (DIC), a Bayesian generalization of Akaike’s Information Criterion (Spiegelhalter et al. 2002). DIC consists of two components, DIC = D̅ + ρD. D̅ represents the posterior mean of deviance and measures the goodness-of-fit. ρD is the expected effective number of parameters and hence measures model complexity. Since a smaller D̅ indicates a better fit and a smaller ρD indicates a parsimonious model, the model with smallest DIC is preferred. Similar to AIC, however, there are no hard and simple criteria on what would constitute a significant difference in DIC. Following rule of thumb is often used for model selection in practice (Spiegelhalter et al. 2002). A difference larger than 10 is an overwhelming evidence to rule out the model with higher DIC. While a difference between 5 and 10 can be regarded as substantial evidence favoring the model with smaller DIC, a difference less than 5 usually requires judgment calls with other information. Based on DIC alone, therefore, Models V and VII have similar performance and provide the best fit to the OHTS data (Table 2).

4 Simulation studies

Two sets of simulation studies are conducted to assess the performance of the proposed method. The first simulation is designed to compare joint analysis with marginal models. The second simulation compares different estimates of biomarker variability. Each simulation has 100 random samples and each sample includes 300 subjects.

4.1 Simulations comparing joint models and marginal models

For each individual, the survival time T_i and longitudinal data Y_ij are generated from following two models respectively,

$$\begin{array}{c}\hfill {\lambda }_i(t)={\rho t}^{(\rho -1)}\text{exp}({\alpha }_0+{\alpha }_1{X}_i+{\gamma }_1{I}_i+{\gamma }_2{S}_i+{\gamma }_3\text{log}(V_i)),\text{ and}\hfill \\ \hfill Y_{\mathit{\text{ij}}}={\beta }_0+{\beta }_1{t}_{\mathit{\text{ij}}}+{\beta }_2{X}_i+I_i+S_i{t}_{\mathit{\text{ij}}}+e_{\mathit{\text{ij}}},\text{with}{t}_{\mathit{\text{ij}}}\le T_i,\hfill \end{array}$$

where $X_i~N(0,1),I_i~N(0,{\sigma }_I^2),S_i~N(0,{\sigma }_S^2),e_{\mathit{\text{ij}}}~N(0,V_i),\text{and}\text{log}(V_i)~N({\mu }_V,{\sigma }_V^2)$. Most of the parameters are chosen after OHTS data except a few modifications listed below.

• To make simulation feasible, each dataset will only include 300 individuals with a maximum of 7 longitudinal measurements per subject.

• Follow-up visits are scheduled at times t = {0, 0.25, 0.5, 1, 3, 5, 7}, so that roughly 10% subjects are excluded in the marginal survival analysis because of inadequate follow-up visits.

• Censoring is introduced from a uniform distribution U [0, 8] that is independent of survival time.

• The mean slope (β₁) and variance of random slope $({\sigma }_S^2)$ are now β₁ = −0.5 and ${\sigma }_S^2=0.25$ (rather than −0.20 and 0.11 as in OHTS), so that the current sample size could differentiate them from 0.

• The intercept in the survival model (α₀) is chosen to give approximately 50% event rate to ensure similar power for survival analysis as in OHTS.

• We also add a new covariate (X) which has direct effect on both survival time (α₁ = 0.5) and longitudinal data (β₂ = 1.0).

Data are generated under two scenarios: (A) biomarker variability not associated with survival (γ₃ = 0); (B) biomarker variability associated with survival (γ₃ = 0.5). Each dataset is then analyzed using the joint model and two sub-models respectively. The parameter estimates and their 95% posterior intervals are presented in Table 4 and summarized below.

• The joint models perform very well in both scenarios. All the parameters are accurately estimated except that the shape parameter (ρ) is slightly overestimated and γ₂ has a relatively wide 95% posterior interval.

• The marginal longitudinal models produce consistent estimates as their counter-parts in the joint models except that β₁ is significantly underestimated. This finding is consistent with Henderson et al. (2000), who found that informative drop-out can attenuate the observed trend over time. That is, subjects with higher risk are more likely to fall out of study earlier, and the lower risk subjects (who tend to have smaller β₁) will gradually dominate the data as time goes by.

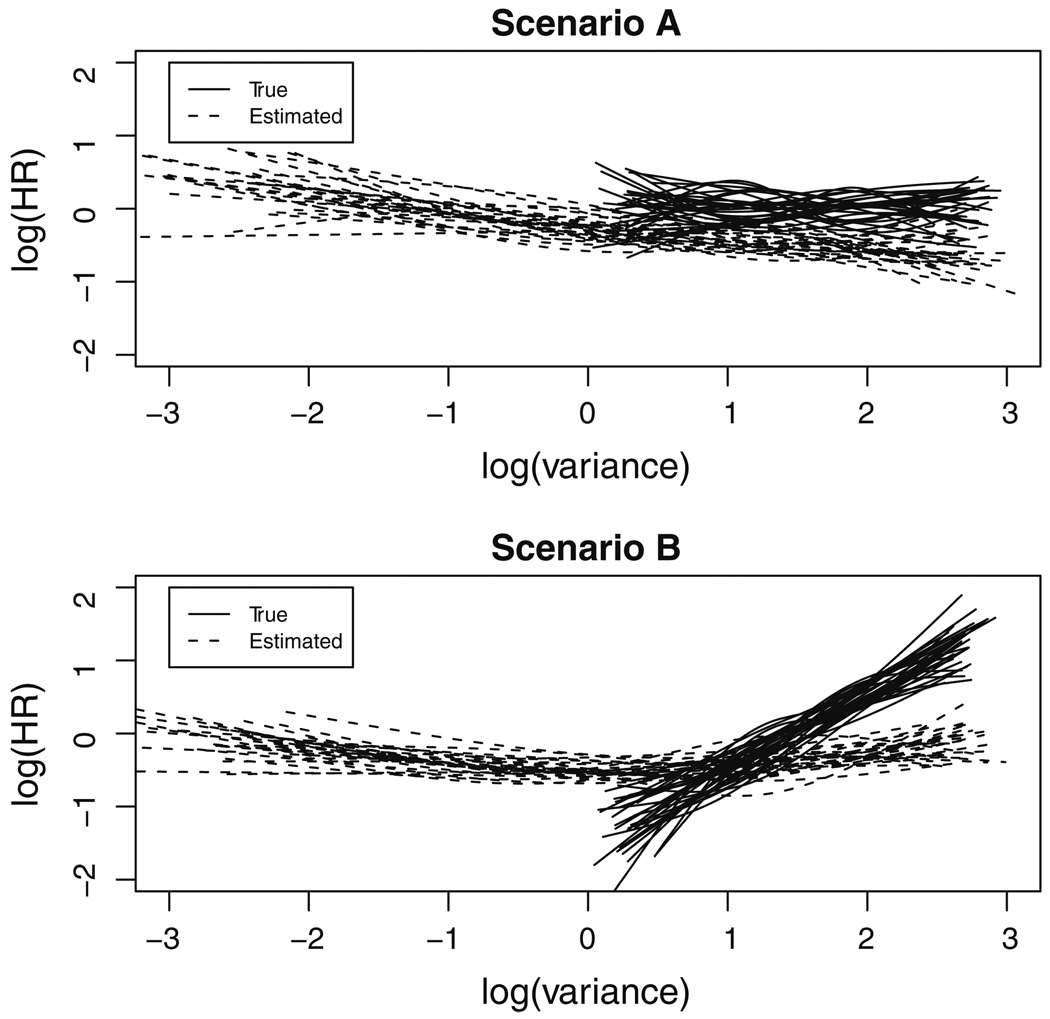
• The marginal survival models have a very poor performance. A totally opposite conclusion is reached for γ₃ and a severe downward bias is observed in the other parameters, especially γ₂. Figure 2 is a graphical presentation of the estimated γ₃ from the first 25 simulated data under scenarios A (γ₃ = 0) and B (γ₃ = 0.5) respectively, with the effects represented as restricted cubic splines (Harrell 2001). The result shows that the estimates using sample-based log(V_i) (dotted lines) are apparently deviated from those based on true log(V_i) (solid lines).

Table 4.

Parameter estimates and 95% posterior intervals for simulation studies comparing joint models and separate analyses

Parameters	True values	Joint model	Marginal modelsa
Scenario A: biomarker variability not associated with survival
Longitudinal
Intercept(β0)	24.0	23.98 (23.68,24.28)	24.02 (23.72, 24.32)
Time(β1)	−0.5	−0.49 (−0.67, −0.30)	−0.72 (−0.87, −0.56)
Covariate X (β2)	1.0	0.97 (0.68, 1.27)	0.93 (0.64, 1.22)
${\sigma }_I^2$	5.0	5.04 (4.03, 6.21)	4.85 (3.87, 5.99)
${\sigma }_S^2$	0.25	0.29 (0.14, 0.51)	0.24 (0.12, 0.42)
μV	1.5	1.51 (1.36, 1.64)	1.51 (1.37, 1.64)
${\sigma }_V^2$	0.5	0.51 (0.33, 0.73)	0.53 (0.34, 0.75)
Survival
Shape (ρ)	2.0	2.43 (1.71, 3.69)	1.84 (1.62, 2.109)
α0	−1.5	−1.49 (−2.36, −0.93)	−4.79 (−5.77, −3.90)
Covariate X (α1)	0.5	0.50 (0.32, 0.79)	0.26 (0.16, 0.37)
γ1	0.2	0.21 (0.13, 0.32)	0.14 (0.10, 0.18)
γ2	1.0	1.14 (0.22, 2.44)	0.09 (0.05, 0.13)
γ3	0	0.01 (−0.33, 0.33)	−0.10(−0.16, −0.03)
Scenario B: biomarker variability associated with survival
Longitudinal
Intercept(β0)	24.0	23.97 (23.67, 24.28)	24.00 (23.70, 24.30)
Time(β1)	−0.5	−0.48 (−0.68, −0.26)	−0.72 (−0.88, −0.56)
Covariate X (β2)	1.0	0.99 (0.70, 1.28)	0.95 (0.66, 1.24)
${\sigma }_I^2$	5.0	4.93 (3.92, 6.11)	4.83 (3.84, 5.97)
${\sigma }_S^2$	0.25	0.29 (0.13, 0.51)	0.23 (0.10, 0.42)
μV	1.5	1.51 (1.37, 1.65)	1.47 (1.33, 1.61)
${\sigma }_V^2$	0.5	0.52 (0.34, 0.74)	0.53 (0.34, 0.76)
Survival
Shape (ρ)	2.0	2.50 (1.72, 3.82)	1.69 (1.49, 1.91)
α0	−1.5	−2.02 (−3.14, −1.29)	−4.66 (−5.68, −3.64)
Covariate X (α1)	0.5	0.51 (0.32, 0.80)	0.26 (0.15, 0.37)
γ1	0.2	0.21 (0.12, 0.33)	0.14 (0.10, 0.18)
γ2	1.0	1.10 (0.20, 2.36)	0.08 (0.04, 0.11)
γ3	0.5	0.53 (0.21, 0.99)	−0.01 (−0.08, 0.07)

^aMarginal survival models only based on subjects with ≥3 longitudinal measurements

Fig. 2.

Estimated effect of biomarker variability on survival (γ₃) in the first 50 simulated data, where the solid lines and dotted lines represent restricted cubic splines of γ₃ using the true log(variance) and sample-based log(variance) respectively. Scenario A γ₃ = 0, Scenario B γ₃ = 0.5

4.2 Simulations comparing different estimates of biomarker variability

In the second simulation, only longitudinal data are generated from a simple model,

$$Y_{\mathit{\text{ij}}}=I_i+S_i{t}_{\mathit{\text{ij}}}+e_{\mathit{\text{ij}}},\text{with}\{t_{\mathit{\text{ij}}}\}=\{0,1,2,\dots ,T_i\},$$

where $I_i~N(2,1),S_i~N(1,1),e_{\mathit{\text{ij}}}~N(0,V_i),\text{and}\text{log}(V_i)~N(1,{\sigma }_V^2)$. Data are generated under three scenarios: (A) homogeneous variance and fixed length of follow-up (${\sigma }_V^2=0$ and T_i = 5); (B) heterogeneous variance and fixed length of follow-up (${\sigma }_V^2=1$ and T_i = 5); (C) heterogeneous variance and varied length of follow-up (${\sigma }_V^2=1$ and varied T_i). Scenario C mimics a study with informative dropout in that these subjects with larger random effects are more likely to have a shorter follow-up. Specifically, T_i follows a binomial distribution with a size of 5 and a success rate of P_i = exp{−0.15 · (I_i + S_i + log(V_i)}(with T_i = 5 if P_i > 1.0), which results in roughly 3% subjects with 1 visit and 10% subjects with 6 visits.

Four estimates of variability are calculated for each individual: the usual sample-based standard deviation (SD_sample), the SD of residuals from simple linear regression fit to each subject (SD_residual), the model-based empirical Bayes estimate (SD_EB), and the constrained Bayes estimate (SD_CB) as described in Sect. 2.3. The performance is summarized as the average bias of the estimated over the true values, with $\text{bias}=\frac{{\text{SD}}_{\mathit{\text{True}}}-{\text{SD}}_{\mathit{\text{Estimated}}}}{{\text{SD}}_{\mathit{\text{True}}}}\times 100.$.

• SD_sample severely overestimates the true variability under all scenarios, with an average bias of −71, −89, and −45% for scenarios A, B, and C respectively. This is as expected because the sample-based SD does not remove the systematic trend over time.

• SD_residual tends to underestimate the true variability (with an average bias of 16, 16, and 28% for scenarios A, B, and C respectively), especially in subjects with less follow-up visits.

• SD_EB (an average bias of <1%, −5%, and −3%) and SD_CB (an average bias of <1%, −5% and −4%) have similar performance under all scenarios. An interesting observation is that, for subjects whose simple estimates cannot be reliably obtained (i.e., with only 1 or 2 visits), the model-based estimates can still provide a reasonable approximation.

5 Discussion

In this paper, we propose a general method for joint analysis of longitudinal data and survival data, specifically focusing on whether the variability of longitudinal data is predictive of survival outcome. Our method has some similarity with the joint modeling approach by Henderson et al. (2000) and Guo and Carlin (2004), who developed a flexible joint model that adds a frailty into survival sub-model to accommodate any effect that cannot be explained by the shared random effects. In contrast, our joint model directly relates the variability of longitudinal data to the survival outcome by incorporating a patient-specific variance. This model possesses some attractive features on modeling biomarker variability. Comparing to the frailty-model framework, the proposed regression approach for variability is relatively straightforward to interpret. When the proportional hazards assumption is holding, for example, the effect of biomarker variability on clinical outcome can be readily quantified as hazard ratio (e.g., HR = exp(γ₃)) which is familiar to clinical investigators. The model also provides the possibility of an individualized prediction by incorporating patient-specific random effects (Lyles et al. 2007).

The method is illustrated with the OHTS data and also evaluated by a few simulation studies. The result shows that the joint model can produce more accurate estimation under various scenarios. In contrast, the widely used two-step approach is very sensitive to the data selection. The discrepancy between joint analysis and naïve approach could be reduced when the analysis is confined to subjects with longer follow-up times. However, this may result in considerable loss of information and even biased estimates. In the OHTS data, for example, the joint model and naïve approach will reach consistent conclusion when the models are fit to subjects with ≥5 visits, but this will exclude nearly 27% of the subjects who have developed POAG. Substantively, our results show that IOP variability is independently predictive of POAG. This finding is consistent with the recent report by Caprioli and Coleman (2008) whose analysis is based on subjects with at least 3-year follow-up. However, the primary purpose of current analysis is for illustration of the method and we include treatment and IOP as the only covariates. A more complete analysis is in progression which will adjust all relevant baseline covariates and also include an independent dataset as an external validation.

Our method is implemented using the Markov chain Monte Carlo (MCMC) methods built in the free-download software WinBUGS. This enables very complex models to be fit rather straightforwardly. The availability of the full posterior estimates for the random effects not only provides a useful tool to gain insight into the model construction, but also permits the possibility of a patient-specific prediction for future cases (Lyles et al. 2007). The Deviance Information Criterion (DIC) facilitates an easy comparison among various complex but realistic models that do not need to be nested. However, all these benefits are not gained for free. One limitation of the proposed method is the intensive computation. In the analysis of OHTS data (N=1,618), each model takes approximately 4 h when using 3 parallel chains with 30,000 iterations each. To make a simulation study feasible, we use a moderate sample size (N=300) and it still takes about 30 min for each replicate. Therefore, each simulation only includes 100 replicates. The other limitation of our method is the potential influence of the prior distributions for unknown parameters. In this study, a sensitivity analysis has been performed to ensure that the data, rather than priors, dominate the posterior estimates.

Appendix

winBUGS specification of the final model to the OHTS data

model {

   for  (i in 1:N)  {
       
        ## For longitudinal sub-model
        ## with 4 fixed effects on Y(t): mu.b0, med, t, med*t
        
        for (j in 1:M) {  
           mu.yy[i,j] <- (beta.y[1] +beta.y[2]*med[i] +b0.i[i]) +
                     (beta.y[3] +beta.y[4]*med[i]+b1.i[i]) *tt[j]
           yy[i,j] ~ dnorm(mu.yy[i,j], tau.vi[i])
        }
        tau.vi[i] <- 1/exp(log.vi[i])

       ## For survival sub-model
       ## 4 effects on S(t): r0, b0i, b1i, log.vi
        
       log(mu.surv[i]) <- r0 + r1 * (beta.y[2]*med[i] + b0.i[i]) +
                               r2 * (beta.y[4]*med[i] + b1.i[i]) +
                               r3 * log.vi[i]
        
       survt[i] ~ dweib(p, mu.surv[i]) I(cent[i],)

         b0.i[i] ~ dnorm(0, tau.b0)
         b1.i[i] ~ dnorm(0, tau.b1)       
       log.vi[i] ~ dnorm(var.alpha, tau.phi)
    }

    ## Use this for Exponential model
    ## p <- 1
    ## Use this for full Weibull model
    p ~ dgamma(1,1)

    var.b0<-1/tau.b0
    var.b1<-1/tau.b1
    var.phi<-/tau.phi

    ## priors
    ## N(0, 1000) for fixed effects
    ## IG(0.01, 0.01) fir random efffects
    beta. y[1:n.para.y] ~ dmnorm ( beta.y.mu[], Sigma.y[,])
          r0 ~ dnorm(0, 0.001)
          r1 ~ dnorm(0, 0.001)
          r2 ~ dnorm(0, 0.001)
          r3 ~ dnorm(0, 0.001)
   var.alpha ~ dnorm(0, 0.001)
      tau.b0 ~ dgamma(0.01, 0.01)
      tau.b1 ~ dgamma(0.01, 0.01)
     tau.phi ~ dgamma(0.01, 0.01)
  }