Feasibility and Sensitivity Study of Helical Tomotherapy for Dose Painting Plans

Abstract

Introduction

Important limitations for dose painting are due to treatment planning and delivery constraints. The purpose of this study was to develop a methodology for creating voxel-based dose painting plans that are deliverable using the clinical TomoTherapy Hi-Art II treatment planning system (TPS).

Materials and Methods

Uptake data from a head and neck patient who underwent a [⁶¹Cu]Cu-ATSM (hypoxia surrogate) PET/CT scan was retrospectively extracted for planning. Non-uniform voxel-based prescriptions were converted to structured-based prescriptions for compatibility with the Hi-Art II TPS. Optimized plans were generated by varying parameters such as dose level, structure importance, prescription point normalization, DVH volume, min/max dose, and dose penalty. Delivery parameters such as pitch, jaw width and modulation factor were also varied. Isodose distributions, quality volume histograms and planning target volume percentage receiving planned dose within 5 percent of the prescription (Q_0.95–1.05) were used to evaluate plan conformity.

Results

In general, the conformity of treatment plans to dose prescriptions was found to be adequate for delivery of dose painting plans. The conformity was better as the dose levels increased from 3 to 9 levels (Q_0.95–1.05: 69% to 93%), jaw decreased in width from 5.0 cm to 1.05 cm (Q_0.95–1.05: 81% to 93%), and modulation factor increased up to 2.0 (Q_0.95–1.05: 36% to 92%). The conformity was invariant to changes in pitch. Plan conformity decreased as the prescription DVH constraint (Q_0.95–1.05: 93% vs. 89%) or the normalization point (Q_0.95–1.05: 93% vs. 90%) deviated from the means.

Conclusion

This investigation demonstrated the ability of the Hi-Art II TPS to create voxel-based dose painting plans. Results indicated that agreement in prescription dose and planned dose distributions for all plans were sensitive to physical delivery parameter changes in jaw width and modulation factors, but insensitive to changes in pitch. Tight constraints on target structures also resulted in decreased plan conformity while under a relaxed set of optimization parameters, plan conformity was increased.

Introduction

Radiation therapy is an integral part of modern cancer treatment with an estimated 60% of all cancer patients receiving some form of radiotherapy as part of their therapeutic regime [1]. Interestingly, most local failures in head and neck and prostate cancers typically occur in regions that received the highest dose [2, 3]. The conventional method to improve failure rates is to uniformly increase the dose to the targeted area. While tumor control probability increases with integral dose, dose escalation is often constrained by a dose-volume trade-off of the normal tissues which tends to limit treatment [4]. Dose painting is an alternate strategy which incorporates functional information into the dose prescription [5]. Selective sub-volume boosting uses this information in defining radioresistant regions within the target while simultaneously integrating a uniform dose boost to these regions [6, 7]. Continuous dose painting, also sometimes referred to as dose painting by numbers, attempts to preserve the integral dose by redistributing the prescription on a smaller spatial scale [8, 9]. This strategy effectively removes dose from the radiosensitive regions of the target in order to increase it to radioresistant parts.

The feasibility of selective sub-volume boosting has been achieved using commercially available software [10]. Continuous dose painting has only been demonstrated in theoretical treatment planning studies using research software capable of prescribing and constraining planned dose on the imaging voxel scale [11, 12]. Most structure-based, commercial treatment planning systems optimize dose on the voxel scale but apply a set of uniform target constraints to each structure [13]. Thus, voxels contained within this structure cannot be constrained independently from their neighbors, which favors dose uniformity. To create a voxel-based non-uniform dose distribution, it is necessary to circumvent the tendency of these TPS to generate uniform dose distributions within the target by allowing for independent fluctuations between target voxels.

The present work investigates the feasibility of continuous dose painting using a commercial treatment planning system. The aim of this study was to develop a methodology for creating voxel-based dose painting plans that are deliverable using the clinical TomoTherapy Hi-Art II (TomoTherapy Inc, Madison, WI) treatment planning system (TPS). Additionally, a sensitivity study was carried out to determine which planning parameters had the greatest impact on plan conformity.

Material and Methods

To overcome limitations of structure-based treatment planning systems, the following workflow was developed from prior theoretical studies and ongoing research [14]. Each step of the process is illustrated within the schematic of figure 1. The procedure was tested on a head and neck squamous cell carcinoma (HNSCC) patient with regional lymph node involvement (T4 N2b M0) who underwent a pre-treatment [⁶¹Cu]Cu-ATSM PET/CT scan three hours post injection over 30 minutes. PET images were reconstructed using ordered subset expectation maximization (OSEM). This patient had heterogeneous tracer uptake within the tumor, which presented a complex and challenging case to dose paint. Imaged PET uptake was segmented to include only values within the clinician-defined, CT-based planning target volume (PTV). Since the spatial resolution of the CT image set was finer than the PET, the CT-defined PTV region containing the PET information had to be downsampled to match the PET image spatial resolution. The PTV delineated PET image was transformed to prescribed radiation dose using a simplistic linear redistribution of boost dose, chosen arbitrarily without biological rationale. This consisted of a base dose of 60 Gy to the target, to which simultaneous integrated dose of 30 Gy was linearly redistributed throughout the PTV based on the PET uptake distribution. The redistribution boost prescription is created as follows:

$$D_i=60\text{ Gy}+30\text{ Gy}·\frac{{\mathit{\text{PET}}}_{\mathrm{i}}}{\langle \mathit{\text{PET}}\rangle }$$ (1)

where D_i is the redistribution dose prescribed to each voxel i inside the PTV, PET_i is the tracer retention in voxel i, and <PET> is the mean tracer retention within the PTV.

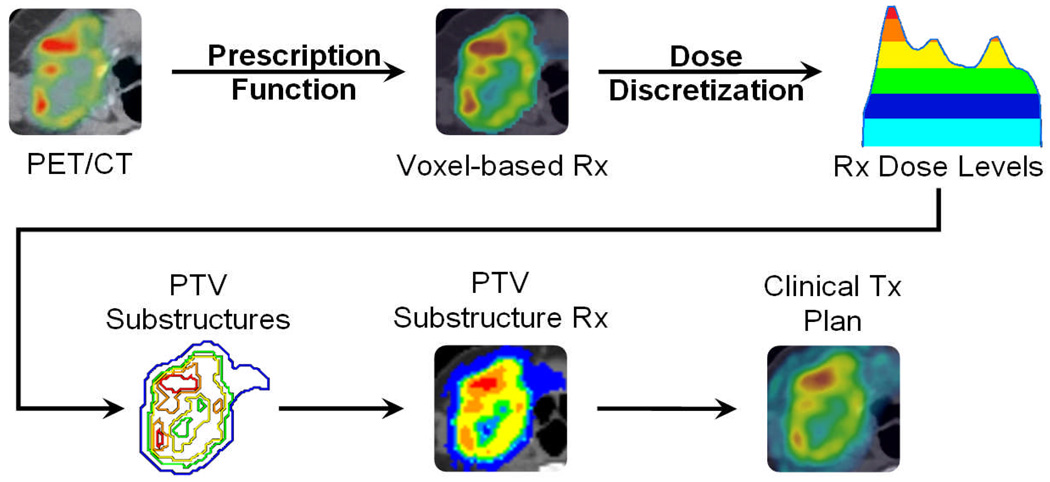
Figure 1. Schematic of workflow for dose painting with clinical treatment planning systems.

From a fused PET/CT image, PET uptake within the target volume is transformed to a voxel-based prescription via a linear redistribution of dose (prescription function). The prescription is discretized into equi-spaced dose levels (e.g. 5 levels), which form the basis for target substructures (dose discretization). Each substructure is prescribed the mean dose representative of the underlying voxel doses, with a DVH objective given by the fractional volume receiving this mean dose or higher. A clinically deliverable treatment plan is generated from IMRT optimization to substructure objectives, yielding a planned dose that can be compared back to the prescribed dose at every voxel.

The non-uniform voxel-based prescription was discretized into a structure-based prescription by binning the dose distribution, whereby each dose bin was equally sized and representative of a distinct target substructure. Integral dose was preserved by prescribing to the mean dose and associated volume of each target substructure based on its underlying voxel dose distribution. Binary masks that made up the target substructures in Cartesian grid space were then converted to contours in polygon mesh space using a MATLAB 7 (The MathWorks, Natick, MA) script. The target contours were exported for use in the TomoTherapy TPS. Note that the procedure up to this point would be similar for any TPS.

The TomoTherapy TPS is guided by several unique, user-defined parameters: primary jaw field width, modulation factor, and pitch, which are described in table 1. Optimized plans were generated by varying each parameter while holding all other parameters constant. All plans were allowed to run for 1000 iterations. Avoidance structures were not considered.

Table 1. Dose conformity for permutations of plan parameters.

Plans were generated from permutations of physical objectives for each prescription sub-volume modifying various plan parameters. Bolded values represent default plan parameters. Pitches equivalent to 0.860 divided by an integer were used in this study to minimize the thread effect [17].

	Parameter	Definition	Value	Q0.95–1.05 (% PTV)
Prescription	Levels	Number of dose levels into which voxel-based prescription was discretized	3	69
			5	87
			7	92
			9	93
			11	93
Physical Delivery	Jaw	Longitudinal slice thickness projected at the machine isocenter	5.00 cm	81
			2.50 cm	87
			1.05 cm	93
	Pitch	Ratio of couch travel distance per rotation to the primary jaw width	0.860	91
			0.430	93
			0.287	93
			0.215	93
			0.172	93
	Modulation Factor	Ratio of the maximum leaf opening time to the average leaf opening time for all non- zero leaves	1	36
			1.5	90
			2	92
			3	93
			6	93
Optimization	DVH Volume Objective	Percentage of target substructure receiving prescribed dose or higher	25 %	91
			75 %	89
			VMean Dose	93
	Normalization Point	Scaling factor to normalize dose to primary target objective	Lowest Level	90
			Mean Dose	93
			Highest Level	92

The quality volume histogram (QVH) was used to compare plan conformity between the original voxel-based dose prescription and the non-uniform dose distribution [11]. QVHs were obtained by calculating the dose deviation normalized to the prescription and then summed for each voxel. Similar to dose volume histogram, the ideal QVH for the PTV would be a step function at 1. To evaluate the overall strength of the plan, Q_0.95–1.05 plots were generated from QVH plots condensed into a single point. The Q_0.95–1.05 values were obtained by summing all the voxels whose planned and prescribed doses were within 5%.

Results

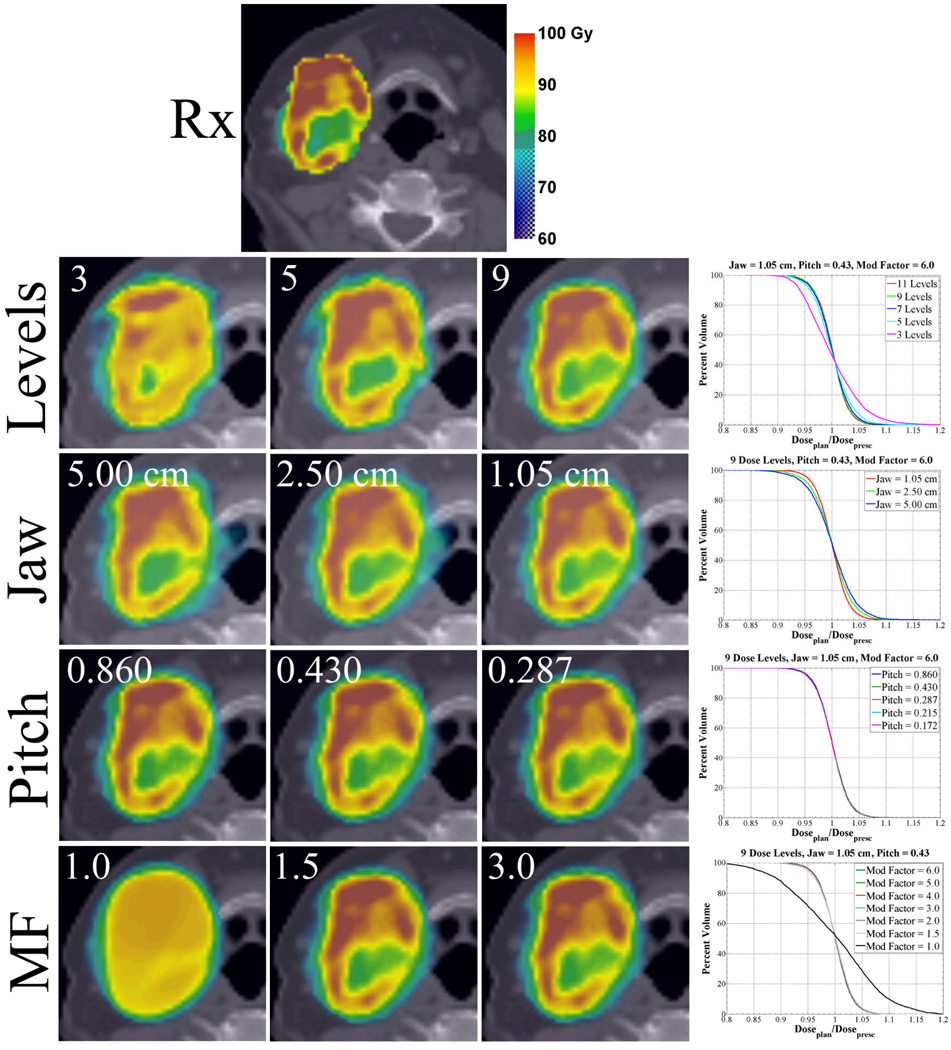
Voxel-based prescriptions created from discretized prescriptions are dependent on the spatial resolution of the delivery system and the expected dose gradient. In figure 2 (Levels), improvements in plan conformity are noticeable as the number of substructures is increased. This trend continues until the delivery spatial resolution and subsequent required dose gradient is exceeded, which for this case is 9 dose levels.

Figure 2. Axial planned dose distributions and QVH plots for varying prescription dose levels and permutations in physical delivery parameters in a head and neck cancer patient.

Variations in plan conformity are quantified by QVH plots. Note that with increasing dose level, increasing modulation factors (MF) up to 2.0, and decreasing jaw width, plan conformity increases. Plan conformity is invariant to changes in pitch.

Optimized isodose distributions, QVH plots, and Q_0.95–1.05 from modifications in physical parameters display variable dose conformity. Figure 2 (Jaw) demonstrates the field width effect for a fixed pitch of 0.430 and modulation factor of 6.0. The planned isodose distributions and QVH plot show increasing conformity with decreasing field width. The most dramatic improvement appears to occur between changes in field widths from 2.50 cm to 1.05 cm, however the Q_0.95–1.05 PTV volume percentage shown in table 1 for each plan shows equal improvement.

Similar to results seen with field width changes, plan conformity improves with increasing modulation factor. Figure 2 (MF) illustrates the effect of modulation factor changes for a fixed pitch of 0.430 and field width of 1.05 cm. The most dramatic improvement occurs between modulation factors of 1.0 and 1.5. Modulation factors greater than 1.5 result only in modest returns with Q_0.95–1.05 PTV volume percentages, quickly converging to 93% after modulation factors greater than 2.0

In contrast to decreases in field width or increases in modulation factor, the dose conformity remains relatively insensitive to changes in pitch. In figure 2 (Pitch), pitches ranging from 0.860 down to 0.172 were coupled to a constant field width of 1.05 cm and modulation factor of 6.0. As pitch is reduced from 0.860 to 0.287, the planned isodose distributions remain indistinguishable and QVH plots for all pitches evaluated generate curves that are superimposed. Comparing the Q_0.95–1.05 PTV volume percentages (table 1), the highest pitch value (0.860) shows a dose conformity drop from 93 to 91% while the remaining pitches (0.430 to 0.172) are isoeffective at 93%.

Due to the large number of optimizations performed it is not possible to illustrate all the resulting dose distributions and QVHs. Instead, Q_0.95–1.05 values for permutations of the optimization parameters are summarized in table 1. In general, the conformity of plans to the non-uniform dose prescription is found to be insensitive to the optimization parameters as long as the prescription DVH volume constraint and the dose normalization point are set to the mean PTV volume and dose. No major changes in plan conformity are noted as dose penalties and structure importance are varied. However, as the prescription DVH volume constraint or the normalization point moves away from the mean volume or dose, plan conformity decreases.

Discussion

This work consists of the creation and implementation of a continuous dose painting methodology utilizing a commercially available, structure-based treatment planning and delivery system. Prior studies have demonstrated the feasibility of multi-level integrated boosts or continuous dose painting but to the author’s knowledge, no continuous dose painting studies have been performed on a commercially available, structured-based treatment planning systems [11, 12, 15]. This study additionally characterizes the sensitivity of the physical delivery and optimization parameters of the clinical treatment planning system on plan conformity.

This study reveals that under the condition of constant integral dose, dose redistribution on a voxel-based level using a structured-based treatment planning system is feasible. Unlike an integrated, uniform boost where the dosimetric margins typically spill over into lower dose regions and result in an overdosing of those target voxels, this methodology takes advantage of those gradients and incorporates them into the targeted region. Specifically, the target prescription in discrete sub-target contours is defined using a simple set of parameters and boundary conditions which characterizes a normal distribution of the underlying voxel doses. The only requirement for each sub-target is the mean dose to the mean volume constraint. This allows the dose to naturally fall or rise to the adjacent dose levels. When the sub-target DVH volume constraint or the normalization point is altered or rigidly constrained, the conformity decreases. This trend is expected since either modification results in a change to the integral dose. Once optimization objectives are met, the only physical limitation is the delivery systems spatial resolution which is dependent on the steepness of the gradient it can create. This is most noticeable in the lowest and highest dose levels where the gradients are quite steep resulting in regions of over- and under-dosing, respectively. In general, this freedom allows a high level of conformity even when presented with a complex spatial distribution as seen in this head and neck case.

Understanding the influence of the individual physical and optimization parameters on the creation of voxel-based dose painting plans is essential to improving the conformity of target coverage. With helical tomotherapy, the dogma has been that smaller field widths, tight pitch values, and high modulation factors (ignoring clinical considerations of time) result in better plans [16]. This may be true when the underlying intention is to treat the entire volume uniformly, but in cases where dose is being redistributed over smaller volumes as in dose painting, this may not be the optimal solution. In general, smaller field widths allow for rapid fall off in the superior-inferior direction which minimizes the smearing of dose between adjacent longitudinal voxels [14]. Logically, continued improvements in dose conformity are expected until the spatial resolution of the delivery system exceeds that of the functional imaging. For simple cases where variation in functional information is small, the smallest field width may not be most desirable or advantageous clinically. Rather, results show that pitches tighter than 0.430 and modulation factors greater than 2.0 may be excessive when the spatial scales of the beamlet, as defined by the field width, is on the order of the underlying functional imaging scale. In essence, the degrees of freedom introduced by tighter pitches or higher modulation factor may be unnecessary in various functional imaging distributions as the optimizer can still find lower beamlet intensities and available projection angle combinations.

Developing this technique as a clinically implementable tool to enhance radiotherapy remains a work in progress and we recognize potential limitations. First, the plans are based on a helical tomotherapy treatment planning and delivery system which is clinically implemented in only a minority of centers worldwide. Despite this, the workflow is robust and allows for generation of similar dose distributions using step-and-shoot or arc-based IMRT delivery. Optimizing plans for the mean dose to the mean volume ratio can be successfully translated between delivery systems (collaborative ongoing research with Korreman et al.). At its basic level, optimization is optimization and any differences are more a product of the physical limitations of each machine to resolve required dose gradients. Second, functional and anatomical images require resampling for fusion onto a common spatial grid. Utilizing upsampled PET or downsampled CT images results in either a degradation of quantitative accuracy in the activity concentration at every PET voxel or a loss of edge detection in target delineation from every CT voxel. However, the degree to which the plans conform to their voxel-based prescriptions is ultimately limited by the spatial resolution attainable by the delivery system. Future investigations to converge PET, CT, and delivery spatial resolutions may potentially address this limitation. Finally, the methodology and workflow is limited to a single clinical case, which may not be completely representative of various clinical presentations. The preliminary trends observed in this study will be expanded on a test population of clinical cases, which will hopefully yield more general conclusions.

This investigation demonstrates that when combined with our robust methodology and workflow, the helical tomotherapy treatment planning system has an adequate delivery spatial resolution to create continuous dose painting plans. Results indicate that agreement in prescription dose and planned dose distributions for all plans are sensitive to physical delivery parameter changes in jaw width and modulation factors, but insensitive to changes in pitch. Conventional planning strategies used on target structures results in a paradoxical decrease in plan conformity while under a relaxed set of optimization parameters, plan conformity increases. In summary this workflow and methodology may have significant value in the clinical implementation of continuous dose painting strategies utilizing dose redistribution with current treatment planning and delivery systems.