Competition of electrostatic and hydrophobic interactions between small hydrophobes and model enclosures

Abstract

The binding affinity between a probe hydrophobic particle and model hydrophobic plates with different charge (or dipole) densities in water was investigated through molecular dynamics simulations free-energy perturbation calculations. We observed a reduced binding affinity when the plates are charged, in agreement with previous findings. With increased charge density, the plates can change from “hydrophobic like” (pulling the particle into the interplate region) to “hydrophilic like” (ejecting the particle out of the interplate region), demonstrating the competition between hydrophobic and electrostatic interactions. The reduction of the binding affinity is quadratically dependent on the magnitude of the charge for symmetric systems, but linear and cubic terms also make a contribution for asymmetric systems. Statistical perturbation theory explains these results and shows when and why implicit solvent models fail.

INTRODUCTION

Hydrophobic interactions give rise to solvent induced attractions between nonpolar particles when solvated in water. They play an important role in protein folding, protein ligand binding, and micelle formation.[1-3] While great efforts have been made by many groups to study the interactions between pure hydrophobic particles or plates, from small to large length scales,[4] relatively less effort has been made to understand the effect of electric charge on the hydrophobic interactions. Yet, most bio-molecular solutes, such as proteins, carry partial charge. It is of interest to further study how the solute-solvent electrostatic interactions affect the binding free energies of nonpolar particles in charged hydrophobic enclosures.

Recent work on the structure and compressibility of water at its interface with single hydrophobic or hydrophilic surfaces[5], connects the hydrophobicity of the surface with the binding affinity of a hard spher probe. Heterogeneous surfaces with mixed hydrophobic and hydrophilic patches were also studied.[6] However, all these studies were concerned with one surface, and the structure and dynamics of water in enclosed systems, where water are surrounded on multiple sides by hydrophobic or hydrophilic moieties, a key motif in many important protein receptors for its molecular recognition, were not studied in those papers. In our present study we investigate, in quantitative detail, the effects of enclosures on a model system containing both hydrophobic and hydrophilic components. Our work on model systems is complementary to our investigation of protein active sites which has already had a significant impact on the drug discovery community.[7]

It is well known that when two sufficiently large hydrophobic plates are closer than a critical distance, the interplate region dewets.[4, 8-10] And in such heterogeneous environments, there is a sensitive coupling of hydrophobicity to the changes in local geometry, dispersion, and electrostatic interactions.[3] Recently, Hansen et al.[11] observed a strong reduction of the critical distance for dewetting between two nanoscale solutes when they were charged, and the effective hydrophobic interactions between the solutes were also reduced. In addition, the reduction of the interactions is sensitive to the charge pattern on the solutes, and there is a significant asymmetry between anionic and cationic solute pairs.[12] The asymmetry between cationic and anionic solvation is a well known fact which has been investigated by many groups.[13-19] Recently, by studying the electric field dependence of the density and polarization density of water between two graphite-like plates,[20] Rasaiah and coworkers found that applying the electric field decreases the density of the water between the plates, contrary to Hansen’s conclusions, and to bulk fluid electrostriction. Rossky et. al. also observed an enhanced hydrophobicity of silica surfaces when the charges on Si and O are inverted compared to that of a fictitious neutral silica surface.[21] Thus, surface polarity is important and sometimes acts in unexpected ways. In addition, Zangi and coworkers [22] have studied the effect of cosolute ions on the potential of mean force (PMF) between two hydrophobic plates, and they found that, for cosolute ions with charge density higher than 0.90, the PMF between the plates will increase; and for cosolute ions with charge density lower than 0.90, the PMF will decrease.

In this paper, we study the binding affinities between a probe hydrophobic particle and model hydrophobic plates through molecular dynamics simulations, and by placing charges or dipoles on the plates, we investigate electrostatically induced interactions between the probe particle and the plate. The plate-water interaction is such that there is no dewetting between the two plates as in the above studies. We find that, for small charges, the binding free energy is negative, indicating the plates remain hydrophobic; however, for large charges, the binding free energy is positive. Thus, as expected, the electrostatic interaction between the charges on the plates and the solvent can drive the plates from being hydrophobic to being hydrophilic.

We also find that the binding affinity of the small particle depends quadratically on the magnitude of the charge (or dipole) on parallel symmetric plates, that is plates with the same sized ions (or dipoles). This is not surprising. The binding affinity between the probe particle and the plates is the difference of electrostatic contribution to the solvation free energy for systems with and without the probe particle. Thus, implicit solvent models such as GB or PB also predict a quadratic dependence on the magnitude of charge.[23-26] However, for plates with different sized ions, the linear and cubic charge (or dipole) dependent terms make small contributions to the solvation free energy, which is contrary to the implicit solvent model predictions.[25] All of the observed effects can be explained by statistical perturbation theory using results from explicit solvent models, but not implicit solvent models.

DETAILS OF SIMULATION

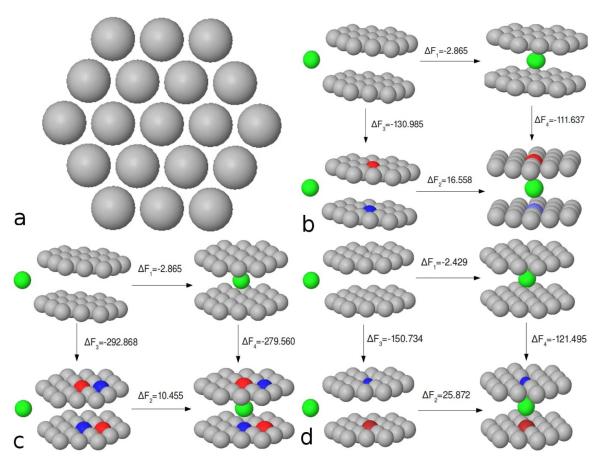
We performed molecular dynamics simulations using the DESMOND program [27] to study the binding affinities between a united-atom methane and two hydrophobic plates. The geometry of the model hydrophobic plate is displayed in figure 1a. It consists of 19 single-layer “atoms” arranged in a triangular lattice with a bond length of 3.2 Å. In two plate systems, the plates are parallel and in-registry with a separation distance of D = 7.46 Å. (which is two times the LJ σ parameter of methane, so the methane can just fit in between the plates.) The plate atoms forming the enclosures all have Lennard Jones parameters σ = 3.73 Å and ε = 0.294 kcal/mol, which are the same as the united-atom methane parameters used in these simulations.[28] The inserted methane particle (displayed in green in figure 1) is placed at the center of the two plates. Then we place opposite charges on the two center atoms of the two plates, or two dipoles pointing in opposite directions, to see how electrostatic perturbation of water affects the binding affinities. The two oppositely charged atoms can be the same size or of different sizes. The plates with the same sized ions (or dipoles) are designated a symmetric system, whereas the plates with different sized ions is designated an asymmetric system.

FIG. 1.

Thermodynamic cycles connecting methane-plates binding affinities and the free energies of charging the plates in water. The gray particles represent the LJ atoms forming the enclosure, the red particles represent negatively charged ions, blue particles represent positively charged ions and green particles represent united-atom methane which will bind to the enclosures. a) the configuration of the plate; b) thermodynamic cycle depicting the effect of charges on the methane-plates binding affinity; c) thermodynamic cycle depicting the effect of dipoles on the methane-plates binding affinity; d)the same process as that in part b, but the center ions were replaced by sodium and chloride ions respectively. The free energy changes for each step of the thermodynamic cycle were given in units of kcal/mol.

The free energy perturbation (FEP) method was used to determine the binding affinities between the inserted methane and the two plates. We used the Maestro System Builder utility [29] to insert each system into a cubic water box with a 10 Å buffer. The water molecules interact through the SPC model.[30] In these simulations, the atoms of the plates were constrained to their initial positions, and only the solvent degrees of freedom were sampled. The united-atom methane was “turned on” inside the two plates over 9 lambda windows with λ=[0, 0.125, 0.25, 0.375, 0.50, 0.625, 0.75, 0.875, 1], where λ is the coupling parameter to turn on/off the LJ interaction between the methane and the rest of the system with initial state and final state correspond to λ = 0 and λ = 1 respectively. The core of the LJ potential for methane is made softer[31] as λ → 0 to avoid singularities and numerical instabilities for FEP simulation. For each of the λ windows, molecular dynamics simulations were performed. The energy of the system was minimized, and then equilibrated to 298 K and 1 atm with Nose-Hoover[32, 33] temperature and Martyna-Tobias-Klein[34] pressure controls over 100 ps of molecular dynamics. A cutoff distance of 9 Å was used to model the Lennard Jones interactions, and the particle-mesh Ewald method[35] was used to model the electrostatic interactions. Following equilibration, a 20 ns production molecular dynamics simulation was performed and configurations of the system were collected every 1.002 ps. The energy difference between neighboring λ windows for each configuration saved was calculated and the Bennett acceptance ratio method[36] was used to calculate the free energy difference between neighboring states. The sum of the free energy differences between neighboring states gives the solvation free energy of methane in the enclosure between the plates. The same procedure was followed to calculate the solvation free energy of methane in bulk water. The difference between the two solvation free energies gives the binding affinity between the methane and the two plates. The error associated with these binding affinities is of order ±0.02 kcal/mol.

As indicated in the thermodynamic cycle in figure 1, the electrostatic contribution to the binding affinity ΔF₂ – ΔF₁, is equal to ΔF₄ – ΔF₃, which is the free energy difference of charging the plates in water with and without the inserted methane. In order to investigate the electrostatic contribution to the binding affinities as a function of charge, we did additional FEP simulations to turn on the electrostatic interaction between the plates and the rest of the system for systems with and without the inserted methane. The FEP protocols were similar to that used for the calculation of the solvation free energy of methane, but here we used 16 lambda windows with λ=[0, 0.02, 0.04, 0.06, 0.08, 0.10, 0.15, 0.20, 0.30, 0.40, 0.50, 0.60, 0.70, 0.80, 0.90, 1.00], and 6ns of data collection for each lambda window, where λ is the coupling parameter to turn on the electrostatic interaction between the charges on the plates and the rest of the system.

RESULTS AND DISCUSSION

Binding affinity results

The free energy results for each process with unit charge on corresponding atoms are depicted on the thermodynamic cycles in figure 1. The free energy changes along different paths of each half cycle only differed by 0.1 kcal/mol, indicating the high accuracy and precision of these free energy results. We see clearly that without charges or dipoles on the hydrophobic plates, there is a strong thermodynamic driving force to pull the methane into the region between the plates (ΔF = −2.865 kcal/mol ); however, if we put charges or dipoles on the plates, the methane is ejected from the enclosed region (ΔF > 10kcal/mol). This agrees with previous findings for the reduction of the hydrophobic interaction between two hydrophobic particles when they are charged.[11, 12] By putting charges or dipoles on the hydrophobic plates, the plates change from “hydrophobic like” (methane absorption) to “hydrophilic like” (methane ejection). It also indicates that even small hydrophilic patches on hydrophobic surface can have a strong effect on the hydrophobicity of the surface, which was observed in previous studies.[6] This behavior is expected: water molecues cannot make hydrogen bonds with uncharged or non-polar plates in which case the water molecules will move away from the interface, and nonpolar methane will preferentially move into the enclosure. However, if there are sufficiently large charges or dipoles on the plates, water molecules will either make hydrogen bonds with the plates, or at least have an attractive polar interaction with the plates, so that they will displace the methan from the enclosure.

The binding affinity difference (ΔF₂ – ΔF₁), as mentioned before, arises from the free energy difference of charging the plates with and without the inserted methane (ΔF₄ – ΔF₃). This is also equal to the difference of the electrostatic contributions to the solvation free energy for the two systems, because the direct electrostatic interactions in solutes for the two systems are the same. It is well known that the more the ions are exposed to water, the more the electrostatic interaction contributes to the solvation free energy.[24] The ions on the plates are more exposed to water without the inserted methane, so ΔF₃ is more negative than ΔF₄, which provides another perspective for understanding the transition from “methane absorption” to “methane ejection” due to putting charges or dipoles on the hydrophobic plates.

Dependence of the binding affinity (Solvation free energy) on the magnitude of charge

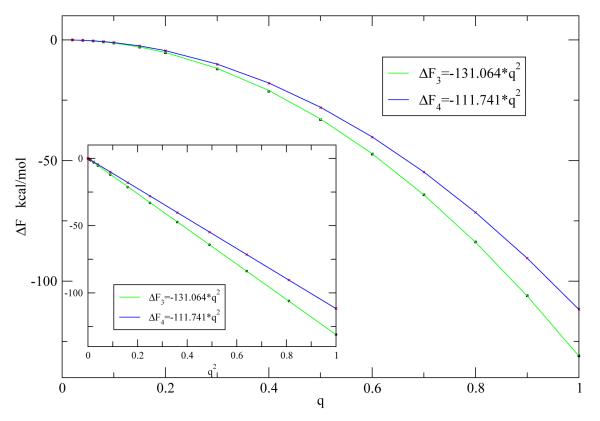
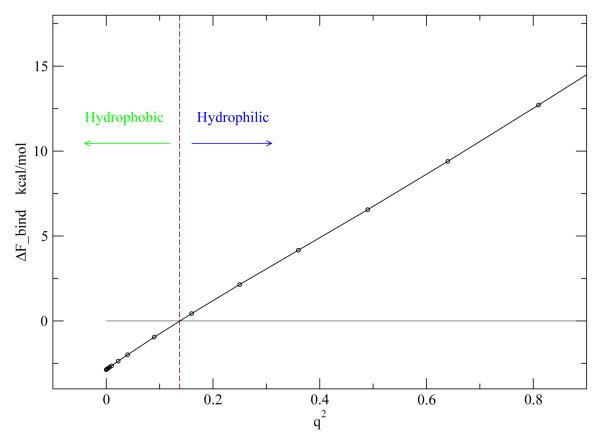
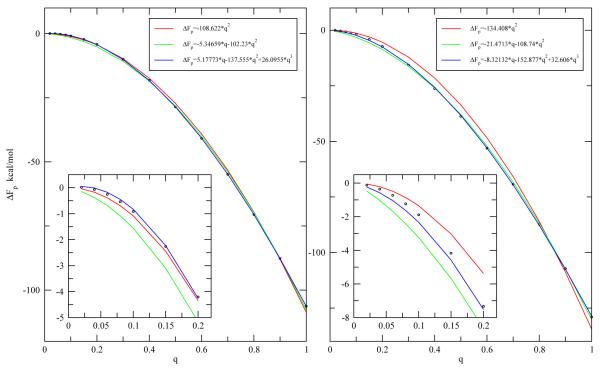
To investigate quantitatively how the magnitude of charges or dipoles affects the hydrophobic or hydrophilic properties of the plates, we calculated the binding affinities of systems with different charge densities on the charged or polar atoms of the plates. (Here the radius of the atoms are fixed and only the magnitudes of the charges are varied.) Figure 2 depicts the relationship between the free energies of charging the plates for the two systems (corresponding to ΔF₃ and ΔF₄ in part b of figure 1) and the magnitude of the charge on the atoms, q, and also q² (Inset of the figure). We see clearly from this figure that the free energy of charging the electrostatic interactions for these two systems are proportional to the square of the magnitude of the charge on the atoms (or the charge density). From these data, we determine the methane-plates binding affinities as a function of the magnitude of the charge. Clearly, the binding affinity should also have a quadratic dependence on the magnitude of the charge. Figure 3 shows the methane-plates binding affinity as a function of q², and can be perfectly fit by a straight line. If we define the plates to be hydrophobic or hydrophilic by the sign of binding affinity, negative binding affinity corresponding to hydrophobic and positive binding affinity corresponding to hydrophilic, then in the low charge region (q < 0.37), the plates are hydrophobic, and in the high charge region (q > 0.37), the plates are hydrophilic. The crossover point occurs at about q ≈ 0.37 (q² ≈ 0.137), where the plates change from being hydrophobic to being hydrophilic. Interestingly, Zangi et.[22] have studied the effect of cosolute ions on the PMF between two hydrophobic plates, and they found that for cosolute with a charge density of 0.90, the PMF was the same as that in pure water, and lower charge density cosolute will decrease the hydrophobic interaction between the plates, and higher charge density cosolute will increase the hydrophobic interaction. However, both the trend and the crossover point charge density observed here is different. This is not surprising: in their studies many ions were dissolved in solvent, while here one ion was placed on one hydrophobic plate and one oppositely charged ion is placed on the other hydrophobic plate. Also the size of the plates and LJ parameters for atoms making up the plates are different, so dewetting occurred in their systems but not here. For hydrophobicity as defined here, the crossover point charge density will depend on the LJ parameters for atoms making up the plates, and the size of the plates, but the trend should be the same. Similar results were observed for systems with dipoles on the two plates,(results not shown) only the slope was different.

FIG. 2.

Free energy of charging the plates in water with and without the inserted methane as a function of the magnitude of charge, q, and the square of the magnitude of charge, q² (inset of the figure). Perfect quadratic dependence of the free energy on the magnitude of charge were displayed by these systems.

FIG. 3.

Methane-plates binding affinity as a function of the square of the magnitude of charge, q². At low charge density, the binding affinity is negative, displaying hydrophobic property of the plates; however, at high charge density, the binding affinity is positive, displaying hydrophilic property of the plates.

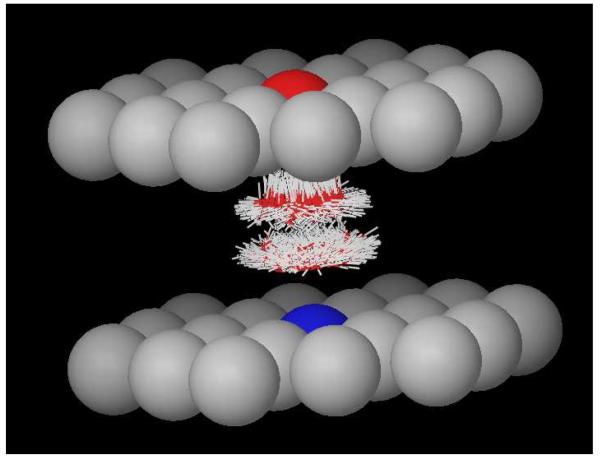
People familiar with implicit solvent models such as PB or GB,[23-26] would not be surprised by the quadratic dependence of the solvation free energy on the magnitude of charge. In these models, the electrostatic potential or the induced surface charge is proportional to the magnitude of the charge on the solute, so the electrostatic contribution to the solvation free energy is proportional the square of the magnitude of the charge.[23-26] The direct electrostatic interactions are trivially proportional to the square of the magnitude of the charge. So the free energy of charging the plates, which is the sum of the two terms, should also have a quadratic dependence on the magnitude of the charge. However, the constant dielectric approximation in such models is clearly not a good approximation for these systems. Figure 4 depicts the projection of the orientation of water molecules in the region between the two plates from 10000 frames with unit charge on the corresponding atoms of plates. Clearly, water molecules are highly structured in this region, and they tend to make hydrogen bonds with the two charged atoms on the plates, so the constant dielectric approximation does not apply here. Although different dielectric constants can be assigned for different regions of the solution when solving the PB equation, it is generally difficult to assign these parameters without prior knowledge of the structure of solvent, and this technique is usually used only for the solute region. In the next section, we will explain this effect by a theory based on explicit solvent models, and the quadratic dependence of the solvation free energy on the magnitude of charge for such systems comes naturally from this theory.

FIG. 4.

Projection of configurations of water between the two plates with two opposite unit charges on the center atoms of the plates from 16000 frames. Water is highly structured in this region, which clearly breaks the constant dielectric assumption of implicit solvent models.

THEORETICAL DERIVATION FOR ELECTROSTATIC CONTRIBUTION TO THE SOLVATION FREE ENERGY

For a solute molecule composed of N_A atoms solvated in N_s solvent molecules, the total interaction energy of the systems is:

$$U({\mathbf{r}}_{\mathbf{A}},{\mathbf{r}}_{\mathbf{s}},∊)=U_A\left({\mathbf{r}}_{\mathbf{A}}\right)+U_s\left({\mathbf{r}}_{\mathbf{s}}\right)+\sum _i^{N_A}\sum _s^{N_s}{u}_{np}({\mathbf{r}}_{\mathbf{i}},{\mathbf{r}}_{\mathbf{s}})+∊\sum _i^{N_A}\sum _s^{N_s}{u}_p({\mathbf{r}}_{\mathbf{i}},{\mathbf{r}}_{\mathbf{s}})$$ (1)

$$=U_A\left({\mathbf{r}}_{\mathbf{A}}\right)+U_s\left({\mathbf{r}}_{\mathbf{s}}\right)+U_{As}^{np}+∊U_{As}^p$$ (2)

where U_A is the intramolecular interactions of the solute and U_s is the intra- and inter- molecular interactions between the N_s solvents molecules, the first summation term on the right hand side is the nonpolar interactions between the solute and the solvent, and the last term on the right hand side is the polar (or electrostatic) interactions between the solute with charge scaled by a scaling parameter ε and the solvent. Through thermodynamic perturbation theory, the electrostatic contribution to the solvation free energy of the solute with charge scaled by ε can be expressed as:

$$\beta \Delta F_p=-\ln {<e^{-\beta ∊U_{As}^p}>}_0$$ (3)

where β⁻¹ = k_BT, k_B is the Boltzmann constant, and < … >₀ means the ensemble average of the mechanical properties over unperturbed state where there is no electrostatic interaction between the solute and the solvent. Here, to make the derivation neater, the solute is kept fixed, and only the solvent degrees of freedom are integrated over. Expanding Eq. 3 in powers of ε we get the electrostatic solvation free energy in powers of the magnitude of charge on the solute,

$$\Delta F_p=∊{<U_{As}^p>}_0-\frac{\beta }{2}{∊}^2{<{(U_{As}^p-{<U_{As}^p>}_0)}^2>}_0+\frac{{\beta }^2}{6}{∊}^3{<{(U_{As}^p-{<U_{As}^p>}_0)}^3>}_0+\cdots$$ (4)

This result is similar to what Hummer et al.[18, 19] get in their studies of ion hydration, except that in their studies the overall charge of the system is not zero, so the finite size effect had to be included explicitly.

Let us now analyze the coefficients of the linear and quadratic terms. The linear term is the average of the electrostatic interaction between the fixed solute and the solvent over the unperturbed configurations of the solvent (ε = 0). For neutral solute molecules, there exists excellent cancellation between interactions from positively charged atoms on solute and interactions from negatively charged atoms on solutes, so the coefficient of the linear term should be small. For symmetric systems like the symmetric parallel plates we studied, this linear term should be exactly zero. For systems with only a single charge, the linear term will be non-negligible and of opposite signs for cations and anions. This explains the asymmetry between cations and anions both for the solvation free energy [13-19] and for the reduction of the PMF.[11, 12] The quadratic term is proportional to the variance of distribution of $U_{As}^p$, which is nonzero, so the coefficient should be a large negative number, which makes sense because the electrostatic solvation free energy is negative for almost all systems studied up till now, and for implicit solvent models such as PB or GB.[23-26] In addition, the coefficient for the second order term is symmetric with respect to charge inversion, which also is consistent with PB or GB predictions. (In other words, if the sign of the charge on the solute was reversed, the coefficient of this term does not change.) The coefficient of the cubic term also depends on the symmetry of the system: for symmetric systems, the distribution of $U_{As}^p$ should also be symmetric, so the cubic term is exactly zero; however, this term is nonzero for asymmetric systems. Again there exists excellent cancellation in the cubic dependence term, so it should also be small.

Furthermore, since $U_{As}^p$, the electrostatic interaction between the solute and the solvent, is long ranged and is the sum of many terms, the distribution function of $U_{As}^p$ is expected to be approximately a Gaussian distribution function according to the central limit theorem. So only the first few lower order terms in Eq.4 make non negligible contributions to the electrostatic solvation free energy. In addition, according to our analysis, the coefficients of the linear and cubic dependence terms are small, so the quadratic dependence term is the dominating contribution.

Comparing the final results of this theory and the implicit solvent models, it is clear that PB or GB models only predict the quadratic dependent term, which is the most important term as predicted from the theory above. This may be the reason why PB or GB models generally give good results for electrostatic solvation free energies, even though the constant dielectric picture is clearly not true for these systems. In the next section, we will present some further evidence that the PB or GB models does not give even qualitatively correct predictions for asymmetric systems.

FURTHER EVIDENCE TO VALIDATE THE THEORY

The four systems studied are all symmetric systems, so the linear and cubic terms should be exactly zero as predicted by theory and indeed FEP gives quadratic dependence of the solvation free energy on the magnitude of charge. In addition, there should also be nonzero linear and cubic terms, if the system is asymmetric, although the magnitude of these terms may be small. For this reason we simulated two plates one with a sodium ion and the other with a chloride ion (parameters for these ions are from ref.[37]) placed on the each center atom on the plates respectively. (Part d of figure 1) Now the solute is asymmetric with respect to the size of the ions because the sodium and chloride ions have different LJ parameters.

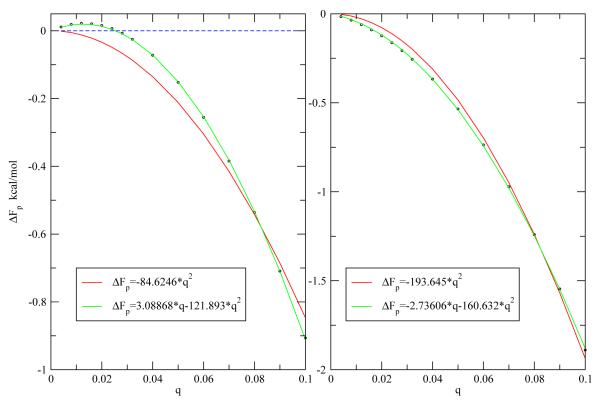
The free energies for each step of the thermodynamic cycle are given in part d of figure 1, and the electrostatic contributions to the solvation free energy in the absence of the inserted methane is given as a function of the magnitude of charge in the left side of figure 5. Overall, the quadratic functional still characterizes the trend, but not as well as those for the equal sized ions in the above four systems, and deviations of the fitted curve from FEP data are observed for medium and large charges. If the linear term is included in the fit, the overall performance of the fitting gets better, but there are still large deviations in the small charge region.(See inset of figure 5) Only if both linear and cubic terms are included does the fit become excellent over the whole charge range. This observation agrees with the theory: both the linear and cubic terms depend on the symmetry of the system, so they both make contributions to the solvation free energy for asymmetric systems. But overall, the quadratic term is still most important, the coefficient of this term being much larger from those of the linear and cubic terms.

FIG. 5.

Electrostatic contributions to the solvation free energies as a function of the magnitude of charge for sodium chloride ions system (left) and the reversed sodium chloride ion systems (right). Insets of the figures depicts the same curves in the small charge region. Deviations from quadratic dependence appear for these systems. Linear and cubic terms also contribute to the electrostatic solvation free energy. The linear term coefficients for these two systems are approximately of the same magnitude but opposite sign.

The theory shows that if the charge on the solute were reversed, the sign of the coefficient for the linear term should also be reversed. So another model system was studied where the charge on the sodium and chloride ions were reversed. (reversed sodium chloride ion system) The electrostatic contribution to the solvation free energy as a function of the magnitude of the charge is shown on the right side of figure 5 for this system. Similar to the sodium chloride ion system, both linear and cubic terms contribute to the solvation free energy. More importantly, the coefficients of both the linear and the quadratic terms were of similar magnitude as the sodium chloride system, but the sign of the linear term was reversed, which agrees well with what the theory predicts. The exact coefficient of the cubic term, should also be of the same magnitude but opposite sign upon charge reversal, just like the linear terms. However, because the cubic term only makes small contributions and we can often ignore the terms of higher order, O(q⁴), in the fitting, but then the coefficients of the cubic terms we obtain from the fitting will have the same sign and will be different in magnitude for charge reversal. This discrepancy points to a deficiency of fitting with polynomials. In addition for asymmetric systems if the fitting is done without the cubic term the observed deviations of the fitted curve from the FEP data in the small charge region is also caused by similar deficiencies of this approach to curve fitting to polynomials in the charge.

Interestingly, implicit solvent models such as PB or GB incorrectly predict identical electrostatic contributions to the solvation free energy for systems with reversed charge distributions, whereas the perturbation theory correctly predicts it. In our situation, the electrostatic contributions to the solvation free energy for the two systems studied with reversed charge distribution were found to be different (−106 kcal/mol vs. −129 kcal/mol for unit charge), which is in agreement with previous findings of the asymmetry between anionic and cationic solutes.[11-19] In addition, the sign of the linear term for these two systems is correctly predicted by the perturbation theory. It is well known that water will break one hydrogen bond at the surface of large hydrophobic plates pointing one of its hydrogen atoms towards the plates.[3, 4] Since the sodium ion is smaller than the chloride ion, hydrogens pointing to the uncharged sodium atom get closer to it than to the uncharged chloride atom in the uncharged state (ε = 0 state). So the interactions between the positive charge on the sodium ion and the unperturbed solvent (ε = 0 state) is larger in magnitude than that for chloride ion, which will result in a overall positive linear term for the sodium chloride ion system and negative linear term for the reversed sodium chloride ion systems. In contrast, the PB or GB models will always predict a negative electrostatic solvation free energy. However, perturbation theory and FEP simulations show that if the coefficient of the linear term is positive, the electrostatic solvation free energy will be positive in the low charge region. To test whether this is true, additional simulations were performed for the two systems with a reversed charge distribution at small charge [0-0.1]. The electrostatic contribution to the solvation free energy as a function of the magnitude of charge is shown in figure 6. From this figure, we can see clearly that the linear term is important for this region, and the electrostatic solvation free energy is positive in the small charge region for the sodium chloride ion system, which further validates the theory presented here.

FIG. 6.

Electrostatic contributions to the solvation free energies as a function of the magnitude of charge for sodium chloride ions systems (left) and the reversed sodium chloride ion systems (right) in the small charge region. It is quite clear that the linear terms are important in this region. The electrostatic solvation free energy is positive at very small charge region for the sodium chloride ion system, which PB or GB models fail to predict. Again, the linear term coefficients are approximately of the same magnitude but opposite sign.

CONCLUSIONS

We have studied the binding affinity between a probe hydrophobic particle and model hydrophobic plates with different charge (or dipole) densities. We found that the binding affinity of the probe particle is strongly decreased by putting charges (or dipoles) on the plates, which agrees with previous observations of the reduction in hydrophobic interaction between two solutes when they were charged.[11] The plates can be either hydrophobic or hydrophilic depending on the charge density of the ions on the plates: in the low charge density regime, the effective free energy of binding of the probe particle in the plate enclosure is negative, and the plates manifest hydrophobic property by pulling the hydrophobic particle into the enclosure; in the high charge density regime, the effective binding free energy is positive, and the plates manifest a hydrophilic property by ejecting the hydrophobic particle out of the enclosure between the plates. The effect of charge on the hydrophobicity of the plates is opposed to the effect of cosolute ions on the PMF between hydrophobic plates studied by Zangi et al,[22] because in the latter case the low charge ions can form a double layer around the plates and act as a surfactant.

Quantitatively, the observed reduction of binding affinity is quadratically dependent on the magnitude of charge (or dipole) on the plates. Although implicit solvent models such as PB or GB can predict the quadratic dependence, the constant dielectric approximation in such implicit solvent models is clearly not valid in the simulated systems. However, from perturbation theory, which does not assume a constant dielectric approximation, the quadratic charge dependence of the solvation free energy for symmetric systems can easily be explained. The quadratic charge dependence of the solvation free energy results from the cancellation of the interactions of the positively and negatively charged atoms on the plates with the solvent molecules. However, for asymmetric plates, the two interactions mentioned above do not cancel exactly, so the theory predicts small linear and cubic terms with charge, which we confirmed by explicit solvent FEP simulations. But implicit solvent models will always predict a quadratic dependence on charge even when the van der Waals radii of the two ions are made different.

In addition, we found that the electrostatic contribution to the solvation free energy is different for asymmetric systems with reversed charge distribution, in agreement with previous observations of the asymmetry between anion and cation pairs,[11-19]. In order to duplicate this behavior it is necessary to make the van der Waals radii of the two ions different in implicit solvent models. This reversed charge effect is easily explained and predicted by perturbation theory. In addition, we observed a small positive value of the electrostatic contribution to the solvation free energy in the low charge density regime for the sodium chloride plates, as predicted by perturbation theory, but not by the implicit solvent models. All of these observations give evidences that perturbation theory provides a guide for understanding the electrostatic contributions to solvation free energy of complicated solutes.

The inability of current implicit solvent models to predict linear and cubic in charge terms in the solvation free energy, the asymmetry between positive and negative ions, and the possible positive electrostatic solvation free energies at low charge, indicates some deficiencies of these models. It has also been shown that the effective solute-solvent interface in these implicit solvent models can vary according to the local electrostatic and dispersion potentials.[38, 39] Recently, there have been some attempts to couple nonpolar and polar solvation free energies into implicit solvent models.[40, 41] The theory and observations in this paper might be helpful for further development of implicit solvent models to incorporate such effects.