Analysis of the stabilities of hexameric amyloid-β (1–42) models using Discrete Molecular Dynamics simulations

Abstract

Amyloid-β (Aβ) oligomers appear to play a pivotal role in Alzheimer’s disease. A 42 residue long alloform, Aβ42, is closely related to etiology of the disease. In vitro results show evidences of hexamers; however structures of these hexamers have not been resolved experimentally. Here, we use Discrete Molecular Dynamics (DMD) to analyze long duration stabilities of Aβ42 hexamer models developed previously in our lab. The hydrophobic core of these models is a six-stranded β-barrel with 3-fold radial symmetry formed by residues 30–40. This core is shielded from water by residues 1–28. The nine models we analyzed differ by the relative positions of the core β-strands, and whether the other segments surrounding the core contain α helices or β-strands. A model of an annular protofibril composed of 36 Aβ peptides was also simulated. Results of these model simulations were compared with results of aggregation simulations that started from six well separated random coils of Aβ42 and with simulations of two known βbarrel structures. These results can be categorized into three groups: stable models with properties similar or superior to those of experimentally-determined β-barrel proteins, aggregation-prone models, and an amorphous aggregate from random coils. Conformations at the end of the simulation for aggregation-prone models have exposed hydrophobic core with dangling β-strands on the surface. Hydrogen bond patterns within the β-barrel were a critical factor for stability of the β-barrel models. Aggregation-prone conformations imply that the association of these hexamers may be possible, which could lead to the formation of larger assemblies.

INTRODUCTION

Oligomers of amyloid-β (Aβ) are thought to be involved closely in etiology of Alzheimer’s disease (AD). Experimental studies revealed various oligomeric assemblies such as low-order oligomers¹, paranuclei², Aβ-derived diffusible ligands (ADDLs)^3;4, globulomers⁵, Aβ*56⁶, β-amyballs⁷, and amylospheroids⁸. Relatively small oligomers of the most toxic alloform, Aβ42, tend to be dimers, tetramers, hexamers, pentamers, and dodecamers, with hexamers and dodecamers being most prevalent⁹. Experimentally derived structural models of oligomeric Aβ are limited due to its aggregation-prone nature. Recently, Shafrir et al. proposed theoretical hexameric Aβ42 models¹⁰, which feature a six-stranded β-barrel core formed by the last third of Aβ42. Here, we report results of DMD simulations to analyze long-term stabilities of nine variants of hexamers with a six-stranded β-barrel core and a 36-mer model of a smooth annular protofibrils. See Methods for details on the nine variants of the β-barrel core model.

DMD has been widely used in protein folding/unfolding, aggregation, and testing stability of protein structures; Kalgin et al. studied folding of SH3 domain structures¹¹; Kesner et al. observed conformational changes on filagin Ig domains¹²; Urbanc et al. showed aggregates of Arctic mutant amyloid-β peptides resembles Aβ42 oligomers more closely than Aβ40 oligomers¹³. Multimodal nature of in vitro oligomer distribution has been reproduced for Aβ42 aggregation^14;15. Recently, effects of DMD on stabilities of both crystal and NMR structures have been analyzed and compared to conventional all atom simulations (NAMD) (See companion manuscript). Two proteins tested for stabilities in the previous study have structural characteristics similar to those of the 252 residue-long Aβ42 hexamer model with a core β-barrel: human serum retinol-binding protein (RBP)¹⁶ has a 174 residue-long antiparallel β-barrel structure, and triosephosphate isomerase (TIM) has a 249 residue-long parallel αβ-barrel structure.

METHODS

DMD and parameters used

DMD is made computationally efficient by utilizing collision-driven molecular dynamics that approximates discretized step potentials (see Zhou and Karplus¹⁷ for detailed description of the DMD algorithm). A simulation step in DMD corresponds to the time between consecutive collisions. A simulation step is roughly estimated by solving kinetic energy for the unit of time, i.e. $E=\frac{1}{2}{mv}^2\to [\mathit{kcal}/\mathit{mol}]=\frac{1}{2}[\mathit{dalton}]{\left[\frac{L}{T}\right]}^2\to [T]=[L]\sqrt{\frac{[\mathit{dalton}]}{2[\mathit{kcal}/\mathit{mol}]}}$ where [T] corresponds to unit of time and [L] is a unit length (1Å). One step roughly corresponds to 0.11 ns, hence 10 million simulation steps correspond to ~1.1 millisecond.

To maximize efficiency of DMD, implicit solvent models and coarse-graining have been implemented. Here we have used an implicit solvent model based on Miyazawa-Jernigan implicit solvent pair potential¹⁸ and four bead peptide model. This implementation has been analyzed on experimentally known structures (See companion manuscript). A DMD temperature of 0.08 was used here because it produced root-mean-squared fluctuations (RMSF) results on known structures similar to those produced by all atom NAMD simulations at 310K. Berendsen thermostat was used. Simulations were performed in constant volume, and the dimension of the system was 200 × 200 × 200 ų. Simulations were performed using the Biowulf parallel computing cluster of the National Institutes of Health (www.biowulf.nih.gov).

Models of hexameric Aβ42

In our nomenclature, the Aβ42 sequence is divided into three segments of equal length, S1, S2, and S3. S1 is composed primarily of hydrophilic residues, most of which are located at odd numbered positions, and is typically disordered in NMR-determined Aβ assemblies. S2 is amphiphilic; hydrophobic residues 17- 21 are flanked by hydrophilic residues. S3 is composed of glycines and hydrophobic residues, and has no polar side chain atoms. S3 is modeled to form the hydrophobic core as a six stranded β-barrel to which each monomer contributes one β-strand. Most residues of S2 and S3 tend to have regular secondary structures which vary between α-helical and β-strand depending upon factors such as the environment, concentration, and time (see Shafrir et al.¹⁰ for more details). We explored antiparallel and parallel orientation for the β-strands of the β-barrel core. All S3 β-barrel models had a shear number of six. For antiparallel β-barrel, three relative positions of ascending or descending S3 were tested (called here 3β-1, 3β-2, and 3β-3; see supplement for relative positions of β-strands). All subunits had identical conformations and interactions in the antiparallel models due to the three-fold symmetry about the axis of the β-barrel and two-fold symmetry from end-to-end. One parallel S3 β-barrel model was developed. All parallel models had two subunit conformations due to lack of end-to-end symmetry. The core β-barrel was shielded from water by S1 and S2 segments. S2 was modeled as either an α-helix (2α) or β-strand (2β). S1 was modeled as a random coil for α-helical S2 or as a β-strand which formed a β-hairpin with S2 for βstranded S2. The S1-S2 hairpins were arranged differently in the 2β3βb-par1 and 2β3βb-par2 models, but the S3 barrels were essentially the same. Details of these models can be found elsewhere¹⁰.

RESULTS AND DISCUSSION

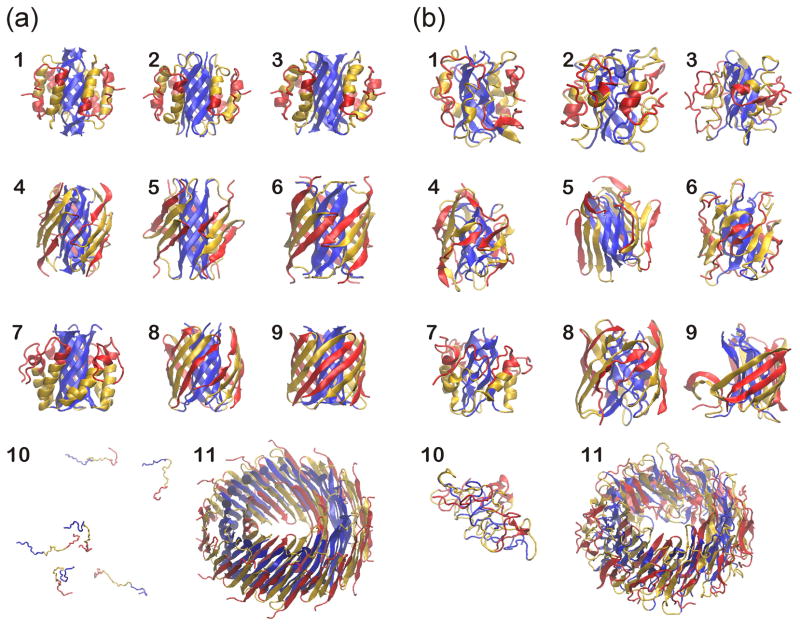
In our original analysis of hexameric Aβ42 models, tentative selections of the 'better' models were based primarily on results of relatively short all-atom molecular dynamics simulations¹⁰. However, long-term stabilities of these models were not analyzed, and thus it was unclear which, if any, of the models should be stable over the long run, and whether the apparent exceptional stability of some of these models was an inherent property of the models or simply a product of the specific method of analysis. DMD simulations were performed to address these issues. DMD simulations use three major approximations to increase computational efficiency: coarse graining in which an amino acid is represented with up to four beads, implicit solvent, and step potentials for interactions among atomic groups. Although these approximations reduce the accuracy of the models, they increase the amount of simulated time by several orders of magnitude. Nine models of Aβ hexamers (Models 1 through 9), six well-separated random coils (Model 10), and an Aβ 36-mer model of an annular protofibril (Model 11) were simulated [Fig. 1]. The nine models share a common characteristic of β-barrel core; however, they differ by whether the barrels are parallel or antiparallel, by the relative positions of the core β-strands, and/or by whether α-helices or β-strands surround the core [Supplementary Fig. 1]. Four trajectories were simulated for each model for 10 million simulation steps each. Starting atom positions and velocities of these four trajectories varied marginally.

Fig. 1.

Snapshots from the simulations of hexameric and 36-meric Aβ42. (a) Starting conformations and (b) typical conformations at 10 millionth step. Models 1 through 9 in (a) are symmetricized β-barrel models at the beginning of the simulations. Model 10 in (a) has six well separated random coils of Aβ42. Model 11 is a 36-mer model of an annular protofibril and consists of three concentric antiparallel β-barrels with a 36-stranded S3 barrel in the middle layer. N-terminal third of Aβ42 (S1) is colored red, the middle third (S2) is gold, and the C-terminal third (S3) is blue. β-strands are shown as arrows and α-helices as ribbons.

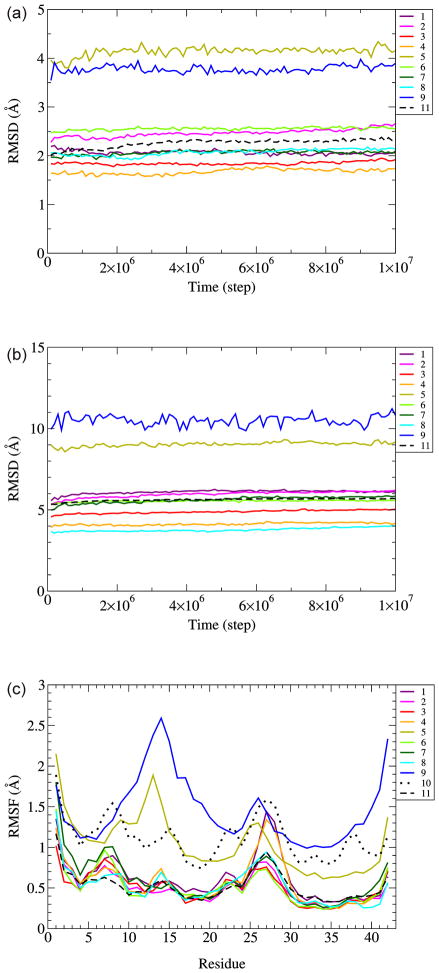
Root mean square deviation (RMSD) vs. time for Cα atoms from corresponding starting conformations for both the S3 core and entire structures showed all the models were equilibrated by having plateaus [Fig. 2(a,b)]. The structures do not change much at the last half of the simulation [Supplementary Fig. 2]. Models 5 and 9 have particularly large RMSDs for both the S3 core and entire structures suggesting large degree of deviation from original structures. Root mean square fluctuations (RMSF) vs. residue that measure standard deviation of α carbons from averaged position between 9 million and 10 million simulation steps were calculated [Fig. 2(c)]. Models 5 and 9 have generally larger RMSF compared to other models and RMSF values of model 10, which began with random coil segments, are about twice as great as those of the other β-barrel models. The similarities of RMSF plots for all the Aβ models are probably due to inherent properties of the residues. Hydrophobic residues have smaller RMSF values because they tend to be more buried in the core where their motions are more restricted, whereas , N-terminal, C-terminal, and hydrophilic residues have larger RMSF values because they tend to be more exposed on the surface where they can have greater mobility.

Fig. 2.

RMSD as a function of time and RMSF for conformations between 9 and 10 millionth step. (a) RMSD for S3, (b) RMSD for whole peptide, (c) RMSF as a function of a residue. Traces are colored differently for each model, as indicated in the figure. Model numbers are the as in Fig. 1. RMSD and RMSF values are for α carbons averaged over four trajectories. RMSD and RMSF for the 36mer (Model 11) are average values for six component hexamers averaged for four trajectories.

Additional analyses were performed by calculating several parameters at the end of the simulation: RMSD and RMSF averaged over S3 or all residues, potential energy by DMD (PE(DMD)), Miyazawa-Jernigan hydropathic energy (MJ energy), number of hydrogen bonds (Hbond #) defined as in DMD¹⁹, or STRIDE in VMD software package²⁰ (geometrical cutoff of either 4.0 Å and 30° or 3.5 Å and 20° between donor and acceptor atoms of hydrogen bonds), and secondary structure persistence (SS) (the percentage of residues at the end of the simulation that retain the secondary structure of the starting model) [Fig. 3].

Fig. 3.

Measured quantities averaged over trajectories used for principal component analysis. The model numbers are the same as in Fig. 1. Best and worst are from the modeling point of view, and coloring roughly follows rainbow color scheme, red for the best, and dark blue and black for the worst. Lowest is the best for RMSD, RMSF, potential energy measured directly by DMD (PE(DMD)), Miyazawa-Jernigan hydropathic energy (MJ energy). Highest is the best for number of hydrogen bonds (Hbond #) based on DMD definition or geometric definitions (cutoffs of either 4.0 Å and 30° or 3.5 Å and 20°), and secondary structure persistence (SS). ‘all’ denotes that the quantity is measured for the whole peptide, and ‘S3’ is for the C-terminal third of the peptide. Quantities are measured at 10 million simulation step for four trajectories, and averaged over the four trajectories. RMSD values for the 36mer (Model 11) are average values for six component hexamers averaged for four trajectories.

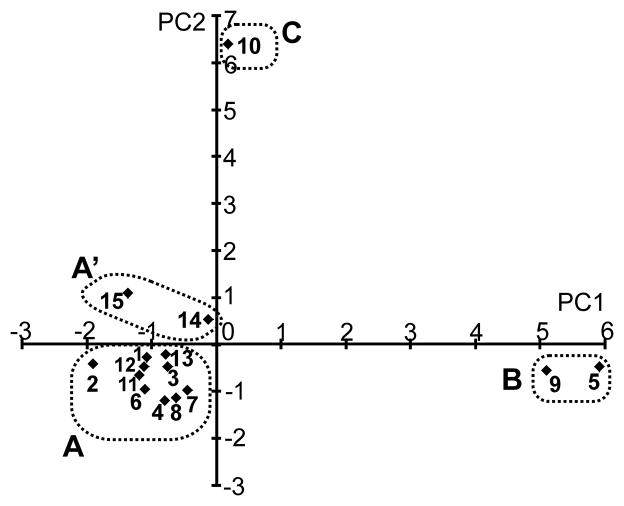
Principal component analysis of results in Fig. 3 showed that models grouped into four categories, A, A’, B, and C [Fig. 4]. Group A and A’ are divided based on negative or positive values for principal component 2 (PC2). Models in Group A (Models 1, 2, 3, 4, 6, 7, 8, 11, 12, and 13) had lower values of RMSD, RMSF, PE, and MJ energy than models in other groups, and include the two experimentally-determined β-barrel protein structures (Models 12 and 13). This indicates that the properties of Group A models of Aβ perform under DMD simulations similarly to those of known β-barrel proteins.

Fig. 4.

Principal component analysis on measured quantities and grouping. The averaged quantities over four trajectories at 10 millionth simulation step in Fig. 2 were subject to principal component analysis. The model numbers are the same as in Fig. 1. PC1 and PC2 are two principal component axes. Results are grouped into A, A’, B, and C as shown by dotted squares.

The Cα RMSDs of Aβ models in Group A were in the range of 4.0 ~ 6.2 Å that is a typical range of Cα RMSD by DMD for two crystal structures with β-barrel cores (RBP RMSD =5.01 Å and TIM RMSD=6.99 Å) [Fig. 3]; for Models 4 and 8 in which residues 2–22 form a β-hairpin, RMSDs were considerably less than for the crystal structures. This stability is remarkable considering that termini tend to be more dynamic than other portions of proteins and the Aβ hexamers have six times as many termini as the crystallized proteins. Models 1, 2, and 7 with helical S2 segments had slightly higher RMSD values that those in which S1-S2 segments form a β-hairpin, consistent with our findings that helical proteins tend to have higher RMSD values than β-barrel proteins and the TIM αβ-barrel structure has a higher RMSD than the antiparallel β-barrel RBP protein (see accompanying manuscript). The core β-barrel regions of Group A models were also exceptionally stable: their average RMSD values were ≤ 2.6 Å (and for Models 3 and 4 were < 2.0 Å) as compared to RMSDs of 3.47 Å and 4.34 Å for the RBP and TIM β-barrels. This exceptional stability is important because six-stranded β-barrels are rare, and thus might be expected to be less stable that the more commonly observed 8-stranded β-barrels of RBP and TIM. The presence of glycine residues at every fourth position is proposed to be essential for the stability of these six-stranded Aβ β-barrels¹⁰. Comparisons of RMSF values of Group A models to those of crystal structures also indicate that these models are relatively static at the ends of the simulations. Averaged RMSF values were < 0.4 Å and 0.6 Å for the core and entire hexamers for all but Model 1, which was 0.64Å. These values are comparable to RMSF values for the crystal structures, which were 0.37Å for the β-barrels and 0.49 Å and 0.60 Å for the entire RBP and TIM structures. Again this is remarkable considering that the most dynamic portions of structures tend to be the termini, and Aβ hexamers have more termini than the crystal structures. The potential energy (PE), which is a sum of hydrogen bonding energy and the MJ contact energies, correlates well with the MJ energies and poorly with the number of H-bonds, indicating that it is dominated in these simulations by the MJ energies. The MJ energies per residue at the end of the simulations are favorable (low) for Group A models, all averages are < −1.2 kcal/mol for all Group A models, as compared to −0.88cal/mol and −1.15 kcal/mol for simulations of RBP and TIM crystal structures. The numbers of hydrogen bonds of Group A models are mostly in the range comparable to those of the crystal structures. H-bond/residue numbers for crystal structures were 0.24 for RBP and 0.52 for TIM with DMD definition, and all the models in Group A were in the range. The secondary structure persistence is variable for Group A models; it ranges from ~ 40% for Model 3 up to ~ 63 % for Model 4. These values are comparable to those obtained from simulations of β-barrel crystal structures: ~38 % for TIM and ~54% for RBP.

Models 1, 4, 7 and 8 in Group A were previously simulated for 20 ns by GROMACS¹⁰. DMD and GROMACS shows consistent Cα RMSD values, but RMSD by GROMACS is always lower than RMSD by DMD by ~1Å [Supplementary Fig. 3 (a)]. This difference is expected since DMD explores much longer time scale than GROMACS, and uses a coarse grained peptide model and simplified potentials. The relative RMSD values of the models to one another is the same for DMD and GRAMACS; i.e., models 8 < 4 < 7 < 1. This suggests that the differences among the RMSD values of the models are due to properties of the models. DMD and GROMACS simulations produce similar RMSF for hydrophilic residues, but RMSF values for hydrophobic residues in S3 are greater with GROMACS than with DMD [Supplementary Fig. 3 (a)]. This effect may be due to negative implicit solvent potentials applied to hydrophobic residues in DMD.

Thus, Group A models appear viable because all parameters appear comparable, or superior, to those obtained from simulations of known crystal structures that have fewer dynamic termini. This is especially true for the antiparallel Model 4 (six parameters of Fig. 3 are superior to those of RBP and the remaining five are comparable; RBP values tend to be better than TIM values). Model 4 is the model that was favored on the basis of much shorter all-atom MD simulations using the program GROMACS¹⁰ and on experimental findings that at least some large Aβ have antiparallel β structures²¹; however, the parallel Model 8 is almost as good with similar values to Model 4 for all but H bonds (Model 8 is better) and secondary structure persistence (it is worse) (see proximity of Models 4 and 8 in Fig. 4).

Models in Group B (Models 5 and 9) produced very different results. The tertiary/quaternary structure of the original models were not well maintained (RMSD values were high), the final structures at the end of the simulations were more dynamic (high RMSF values), and a substantial number of hydrophobic residues became exposed (high MJ energies). Visual inspection confirms that tertiary and quaternary structures were not well maintained for Group B and that hydrophobic portions of the core segments became exposed to water. However, these models also had higher numbers of H-bond and secondary structure persistence, indicating that their secondary structures were maintained even better than in Group A models. We characterize the Group B to be aggregation-prone because exposed hydrophobic residues of such hexamers should self-associate to form larger assemblies. Differences between the two Class B models and their most closely related Class A analogs suggest types of conformational changes that could trigger such transitions. The antiparallel Model 5 differs from Model 4 by the relative positions of ascending and descending S3 strands. The parallel Model 9 differs from Model 8 in the relative positions of the surrounding S1-S2 β strands. Thermodynamic motions might be expected to cause such transitions between these types of model occasionally and when they occur the models may become more prone to aggregation and transitions to larger, more stable assemblies. No models with surrounding α-helices belong to Group B, suggesting the surrounding β-strands might be a necessary condition to be this aggregation-prone group.

In earlier work¹⁰, our group developed models of how six antiparallel hexamer models of Aβ42 could aggregate to form large annular protofibril structures composed of 36 Aβ peptides. In the 'smooth' version of these models the six S3 β-barrels of the hexamers split apart and merge to form a 36-stranded β-barrel. This S3 barrel is shielded from water by β-hairpins formed by S1 and S2 segments; they form a 24-stranded β48-stranded β-barrel inside the S3 barrel and a 48-stranded β-barrel on the outside of the S3 β-barrel [Fig. 1, #11]. We performed DMD simulations on this structure to compare its stability to those of the hexamer models and to known structures. The overall structure remained intact throughout the simulation (total RMSD of 7–8 Å, average RMSD of individual hexamers of 5.7Å; six hexamer per 36mer and four simulations for average of 24 hexamers). This model (Model 11 of the figures) belongs to Group A and in the principal component analysis is nearest the RPB crystal structure. Using the color scheme of Fig. 3, five of the parameters were superior to those of RPM, three were inferior, and three were comparable. This model had the lowest potential energy, PE(DMD) of any model; however none of its other values were superior. Thus in this case, increasing the size of the assembly did not increase the number of H-bonds or preservation of secondary structure substantially relative to other Group A models, but it did not reduce energetically favorable properties either.

Models in Group C (Model 10) were aggregates formed from six well-separated random coils. Simulations of aggregation were performed to use as a reference in comparing the other models. The aggregates do not have regular secondary structural elements such as α helices or β-strands [Fig. 1]. Cα RMSDs for model 10 were extremely high (~ 80 Å) compared to the more highly structured β barrel models (1.7 ~ 11 Å) as expected since the original structure was not designed to be stable [Fig. 3]. The high RMSF values indicate that simulations of random structures were unable to locate structures that are as static as the β-barrel models. PE energies were intermediate between models in Group A and B. The MJ energy was the only 'high ranking' parameter in Fig. 3 for these models, it was comparable to those of Group A models, indicating that the simulations worked well in burying hydrophobic residues. The number of H-bonds was comparable to Group A models but substantially less than Group B models.

Results of simulations of one pre-structured model could also be classified in Group C. This model had a type 2 S3 β-barrel (βb-2), but the structure of the surrounding S1-S2 segments differed from those of Models 3 and 6. This model had the worse features of Groups A and B; i.e., almost all of the parameters would have been colored blue or dark blue in Fig. 3. It was not included in the figure since it was deemed a 'bad' model. However, this result supports the supposition that long simulations with DMD can be useful in classifying some models as unviable.

As a reference, we performed DMD simulations on misfolded models of RBP made by misaligning the sequences by one or two residues toward N-terminus (1up, and 2up) (see companion manuscript). Analyses showed that these (Group A’ models) are close to Group A models, but have opposite sign of principal component 2 values. All of the parameters of Fig. 3 except H-bond # were inferior to those of RPB and except for overall RMSF had 'poor' values; i.e., were colored cyan, blue, or dark blue. Hence DMD could distinguish these structures from the correct structures and from more stable Group A models.

CONCLUSIONS

The major findings of this analysis are that hexameric β-barrel models are exceptionally stable during prolonged DMD simulations (some models were even more stable than β-barrel proteins of known structure), and that specific models (Models 4 and 8) found to be most stable during short all atom simulations with GROMACS¹⁰ were also the most stable with long DMD simulations. The similarities of these results obtained with radically different simulation programs over very different time scales suggest that the stabilities of these models are inherent properties of the models independent of the molecular dynamics program used to analyze the assemblies. Similarities of results for Group A models obtained with parallel and antiparallel β-barrel models, with different antiparallel models, and with α-helical or β-strand S2 segments, suggest that actual assemblies need not be restricted to a single type of model, but could be somewhat polymorphic with each subunit having a different conformation and/or fluctuating among several conformational states. However, the Group B results suggest that some forms of these types of assemblies may undergo large conformational changes that make them more prone to aggregation.