Abstract
New stationary cycles can decrease motion in the frontal and transverse planes with a shank guide. However, there are no studies comparing cycling with and without this guide. The purpose of this study was to compare cycling with and without a shank guide for adolescents with cerebral palsy (CP). Three males and seven females (15.6 ± 1.8 years) with CP, classified as levels III and IV with the Gross Motor Functional Classification System, underwent biomechanical analysis of stationary recumbent cycling with and without a shank guide at 30 and 60 rpm if able. Data collected included three-dimensional lower extremity joint kinematics using motion analysis, surface electromyography of eight lower extremity muscles, cocontraction of six agonist/antagonist pairings, efficiency (power output divided by oxygen consumption), and perceived exertion (OMNI Scale of Perceived Exertion). Non-circular data were analyzed via ANOVAs, and circular data were analyzed using circular t-tests. The shank guide altered joint kinematics in all three planes (p < 0.008), had a minor impact on muscle activity (p < 0.006), and had no impact on cocontraction (p > 0.008), efficiency (p = 0.920), or perceived exertion (p = 0.318). The results suggest that a shank guide during cycling may be beneficial for individuals with CP to decrease the amount of hip and knee frontal and transverse plane motion. Knee movement in these planes has been associated with pain in healthy adults; therefore the guide may help to prevent long-term complications from cycling for adolescents with CP.
Keywords: Cycling, Cerebral palsy, Biomechanics
1. Introduction
Children with cerebral palsy (CP) have decreased muscle strength [1], muscle spasticity [2], decreased joint range of motion [3], altered motor control [2,4], and gait deviations [5,6], and cycling may improve fitness, strength and other impairments while minimizing joint stress [7]. New stationary cycles [8,9] limit lower extremity movement in the frontal and transverse planes through a guide that attaches to the shank. While no studies have reported on their use, this design has implications for children with CP, who show greater frontal and transverse plane motion during gait as compared to typically developing children [5]. Similar deviations have been seen during cycling along with increased cocontraction and decreased efficiency [10]. Limiting these motions at the hip and knee may increase cycling efficiency as forces might be better directed into the pedal. In addition, limiting these motions may reduce stress on joints, as increased knee frontal and transverse plane motion has been associated with pain in healthy adults [7,11].
To limit hip and knee motion with a shank guide, ankle motion in all three planes must be significantly limited, and thus fewer demands may be placed on ankle musculature. This may be undesirable as children with CP are commonly prescribed ankle foot orthoses (AFOs) that constrain the ankle [12] and limit functional use of ankle musculature. Children with spastic diplegia have greater spasticity and less strength in ankle muscles as compared to knee muscles [13]. Therefore, interventions to increase ankle strength are needed and the shank guide may limit this ability. Due to the lack of knowledge about how a shank guide might impact children with CP, a biomechanical analysis is needed to guide decision making for cycling interventions.
The purpose of this study was to compare the three-dimensional (3D) kinematics, electromyographic (EMG) activity, gross mechanical efficiency, and perception of effort of constant load stationary recumbent cycling in adolescents with CP of Gross Motor Function Classification System (GMFCS) Levels III and IV with and without a shank guide.
2. Methods
2.1. Participants
Three males and seven females with spastic CP (15.6 ± 1.8 years) were recruited from an outpatient clinic. Participants 18 years of age and older and a parent of participants less than 18 years old signed an informed consent form approved by the governing Institutional Review Board (IRB). Participants less than 18 years of age signed an IRB approved assent form. Inclusion criteria were ages 13–19 years [10], spastic diplegic or quadriplegic CP, ability to maintain a sitting position, and GMFCS Level III (n = 7) or Level IV (n = 3) [14]. Exclusion criteria were severe spasticity (Modified Ashworth scale ≥4), limited range of motion preventing safe positioning on the cycle, athetoid or ataxic CP, lower extremity surgery or traumatic fracture within past 6 months, joint pain during cycling, spinal fusion to the pelvis, joint instability/dislocation, stress fractures in past year, cardiac disease, uncontrolled seizure disorder, and pulmonary disease or asthma treated with oral steroids.
2.2. Procedures
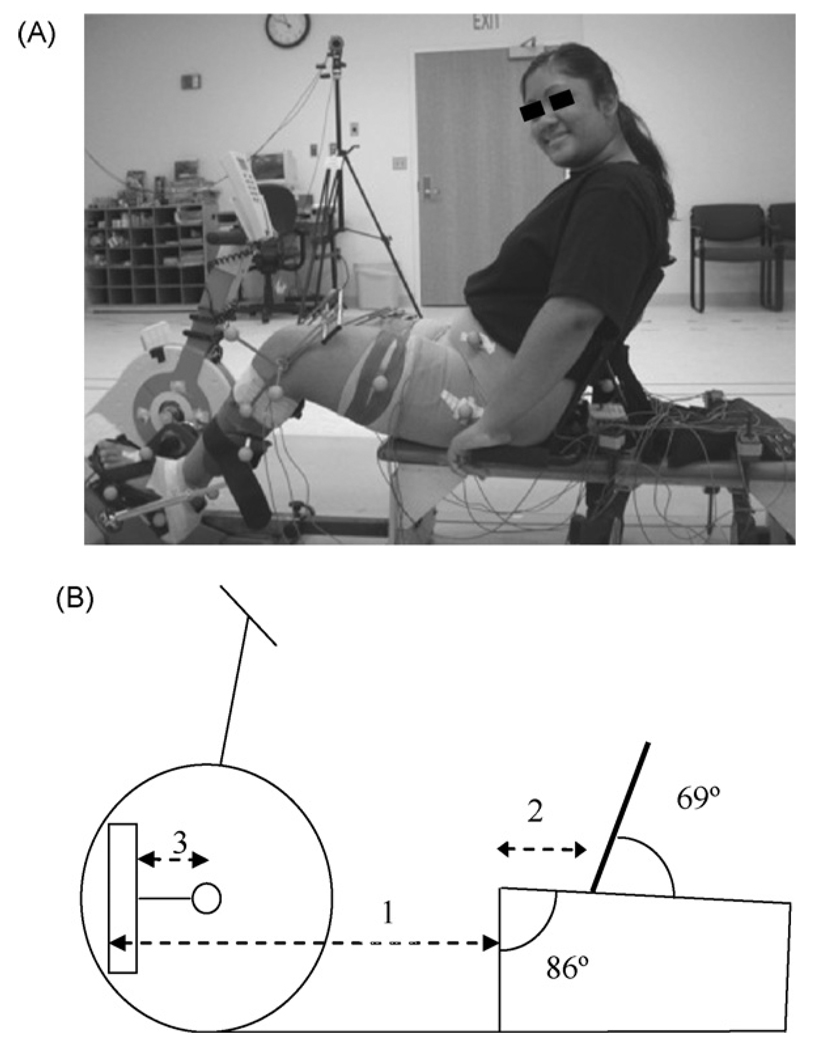
Data collected included left lower extremity kinematics and EMG, energy expenditure, and perceived exertion. The stationary cycle (Restorative-Therapies Inc., Baltimore, MD) had adjustable- length crank arms, adjustable pedals, handlebars, and control pad (Fig. 1A). The pedals had a full footplate, and the pedal spindle was located approximately at the height of the lateral malleolus.
Fig. 1.
Participant using the cycle with the shank guide (A) and bicycle setup (B). All components were adjusted based on anthropometrics: (1) seat to pedal distance = 85% of the distance from the greater trochanter to the base of the calcaneus; (2) seat to greater trochanter distance = 15% of the distance from the greater trochanter to the base of the calcaneus; (3) crank arm length = 30% of tibial length.
Participants sat on a therapy bench (Kaye Products, Hillsborough, NC) attached to the cycle through an adjustable bar (Fig. 1A) and held handgrips attached to the bench. The ranges for adjustability were determined from anthropometric data for typically developing children [15]. The second metatarsal head was aligned with the pedal spindle to maximize ankle power [16], which was set by manipulating the footplate fastened with Velcro to the pedal. Footplate position was also manipulated to accommodate lower extremity deformities.
Each participant was instructed to pedal at a cadence of 30 and 60 revolutions per minute (rpm) using the cycle’s tachometer and received 10–20 min of training. Six of the 10 participants could maintain 60 rpm for the short duration trials (up to 30 s) required for motion analysis. The remaining participants were tested only at 30 rpm. The 60 rpm cadence was selected as developing children without disability cycle most easily at 60–80 rpm, even those with little cycling experience [17]. However it was felt that some participants with CP might not be able to achieve 60 rpm; therefore 30 rpm was also selected. The resistance was set based upon the following formula [18]: load (N m) = 0.49 N/kg × body weight (kg) × crank arm length (m). Using this formula, the resistance used was 3.3 ± 0.9 N m.
Kinematic and EMG data were collected in a motion analysis laboratory. Ten to 15 s trials were conducted once the targeted cadence was reached. For each cadence, three trials were conducted with the shank guide (Fig. 1A) and three without it. The shank guide was placed on the anterior lateral shank and positioned to maintain the ankle in approximately 15° of plantarflexion. This angle was chosen based on an average ankling angle of approximately 15° of plantarflexion reported during upright cycling [19]. Energy expenditure and perceived exertion were measured during 5-min steady-state cycling trials, one with the guide and one without the guide at each cadence.
2.3. Kinematic evaluation
3D kinematics of the hip, knee, and ankle were collected using a seven-camera Vicon 370 motion analysis system (Vicon Motion Systems, Lake Forest, CA) using a standard marker set [21]. A cut-out was made in the seat back to visualize the sacral marker. Hip joint center was calculated as by Davis et al. [20], and hip kinematics were calculated in reference to the pelvis. Data were collected at 60 Hz and digitally filtered (6 Hz low-pass filter). To detect crank arm position, the voltage change of a rotary encoder (US Digital Corporation, Vancouver, WA) on the crank axis was measured in 0.3° increments. Zero degree was defined as the left crank arm being horizontal and farthest from the participant (Fig. 1B). Data were synchronized and processed using customized software using Vicon Plug-in-Gait (Version 1.9, Build 051). Kinematic data were analyzed in 1° increments of the crank position using custom software (MATLAB Version 7.5, The Math Works, Natick, MA). Five cycling revolutions closest to the targeted cadence were analyzed for each cadence for each participant.
2.4. Electromyography
Surface EMG data were collected from eight muscles [16] (gluteus maximus, rectus femoris, vastus lateralis, medial hamstrings, biceps femoris, anterior tibialis, lateral gastrocnemius, and soleus) [21–23]. EMG data were used only to determine timing and cocontraction. EMG placement was confirmed by having the participant contract each muscle against moderate resistance.
EMG data were collected at 1200 Hz using a Motion Lab Systems MA-300 surface EMG recording system (Motion Lab Systems, Baton Rouge, LA) and MA-310 electrodes. EMG data were normalized by establishing a quiet baseline. EMG data were digitally filtered using a band pass filter of 20–350 Hz. To determine activity onset and offset, data were rectified and smoothed using a second-order low-pass Butterworth filter with phase correction and a cut-off frequency of 10 Hz. This smoothed linear envelope was analyzed using 25 ms moving square windows. If the mean voltage within each window was at least three standard deviations (S.D.) above the mean voltage during the quiet baseline, the muscle was identified as being active [24,25]. Crank positions for the onset and offset of muscle activity were determined in 0.3° increments, and activity duration was defined as the difference in degrees between the onset and offset for each muscle for each participant.
Periods of cocontraction around each joint were identified from the percentage of the cycling revolution in which six agonist/antagonist pairings were cocontracting (rectus femoris/biceps femoris, rectus femoris/medial hamstrings, vastus lateralis/biceps femoris, vastus lateralis/medial hamstrings, anterior tibialis/gastrocnemius, and anterior tibialis/soleus).
2.5. Energy expenditure and gross mechanical efficiency
Energy expenditure data were collected via breath-by-breath method (VMax29, SensorMedics Corporation, Yorba Linda, CA). Participants wore a facemask over the mouth and nose that held the flow sensor which measured the volume of oxygen (ml) per kilogram of body weight (VO2/kg). VO2/kg was measured under four consecutive conditions at 30 and 60 rpm if able: (1) sitting quietly for 5 min, (2) cycling for 1 min (warm-up), (3) cycling for 5 min, and (4) sitting quietly for 3 min (recovery). Power output data were downloaded from a computer linked to the cycle’s electronics. Gross mechanical efficiency was calculated by dividing average power output (W) by average metabolic input (VO2/kg) across the 5-min test.
2.6. Perception of effort
Following each test, participants rated their perception of effort using the Children’s OMNI Scale of Perceived Exertion. The version of the scale used in this study shows a child riding a bicycle uphill with “not tired at all” (score of zero) at the bottom of the hill and “very, very tired” (score of 10) at the top of the hill [26].
2.7. Data analysis
Normalized rank transformations were performed secondary to a non-normal distribution [27]. For kinematic data, three-way mixed model ANOVAs with crank position as a random factor were used to determine differences in the joint position based on condition, cadence, and crank position in 1° increments. Bonferroni post hoc analyses were performed for kinematic data not involving crank position. Circular EMG data (muscle activity onset/offset) were analyzed using circular t-tests based on condition and cadence using Oriana 2.0 (Kovach Computing Services, Anglesey, Wales) with a Mardia–Watson–Wheeler test due to a non-normal distribution [28]. A two-way ANOVA was not performed, as a model does not exist for circular data. For the non-circular EMG data (duration of activity), a two-way ANOVA based on condition and cadence was performed. Finally, a two-way ANCOVA based on condition and targeted cadence with actual cadence as a covariate was performed for energy expenditure. There were no differences in achieved cadences between cadences for shorter duration trials for assessing joint kinematics and EMG, so an ANCOVA was not needed for those data. For all analyses, a p-value of less than 0.05 was accepted for significance and adjusted based on the number of variables.
3. Results
3.1. Kinematics
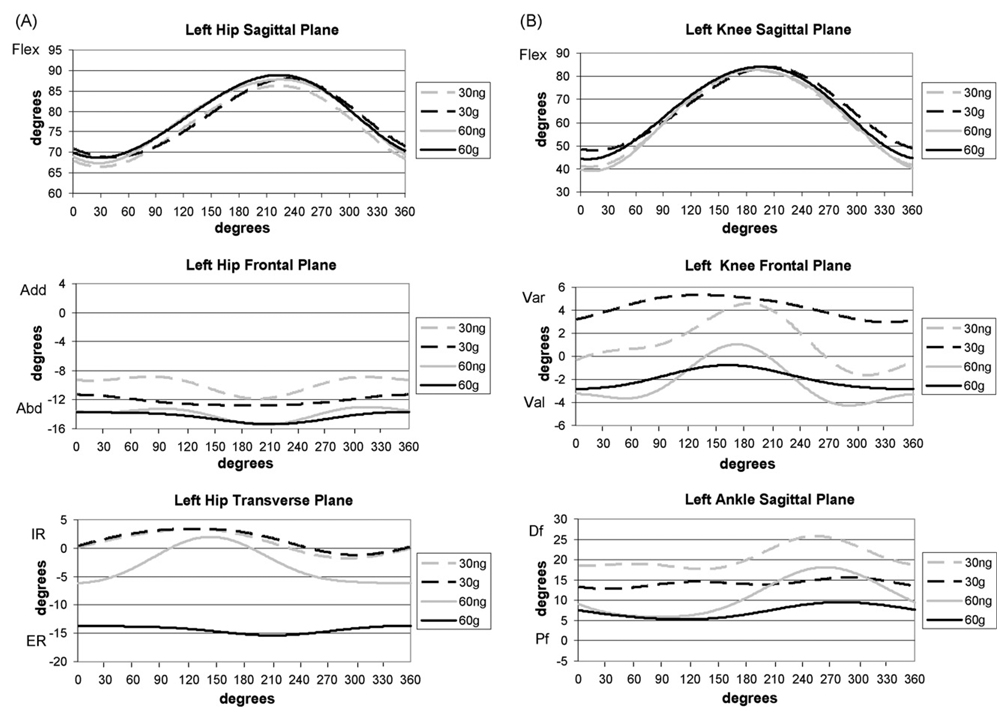
Fig. 2 displays the joint angles. There were no differences in joint kinematics between conditions (guide versus no guide) or cadences when the position of the crank was not included (Table 1). However, differences were seen between conditions when crank position was included, meaning that kinematic curves were compared. This is due to both timing and joint position being taken into account. This interaction effect of condition and crank position was seen for three joint motions with increased hip flexion seen during the flexion phase, decreased knee valgus, and increased plantarflexion seen with the guide. Timing differences were apparent for knee varus/valgus and ankle dorsiflexion/plantarflexion (Fig. 2). There were also interactions of condition, crank position, and cadence for five of the six joint motions (Table 1). These interactions are very complex and are best viewed in Fig. 2.
Fig. 2.
Joint kinematics of the hip (A) and knee and ankle (B). Positive direction indicates flexion, adduction (varus), and internal rotation for sagittal, frontal, and transverse planes, respectively. Flex = flexion, Add = adduction; Abd = abduction; IR = internal rotation; ER = external rotation; Var = varus; Val = valgus; Df = dorsiflexion; Pf = plantarflexion. 30 ng = 30 rpm without guide; 30 g = 30 rpm with guide; 60 ng = 60 rpm without guide; 60 g = 60 rpm with guide.
Table 1.
Statistical results (p values) for the kinematic data
| Condition | Cadence | Crank position |
Condition × cadence | Condition × crank position |
Condition × crank position × cadence |
|
|---|---|---|---|---|---|---|
| Hip flexion and extension | 0.3121 | 0.1855 | <0.0001 | 0.9087 | 0.0023 | <0.0001 |
| Hip adduction and abduction | 0.0386 | 0.3727 | 0.2992 | <0.0001 | 0.7698 | 0.0035 |
| Hip internal and external rotation | 0.8991 | 0.6316 | <0.0001 | <0.0001 | 0.2960 | 0.0024 |
| Knee flexion and extension | 0.1353 | 0.9340 | <0.0001 | 0.0196 | 0.3796 | 0.0050 |
| Knee varus and valgus | 0.0242 | 0.3197 | <0.0001 | 0.0010 | 0.0019 | 0.1174 |
| Ankle dorsiflexion and plantarflexion | 0.0120 | 0.0365 | <0.0001 | <0.0001 | <0.0001 | <0.0001 |
The values in bold type were significant. Interactions involving the crank position indicate that the kinematic curves were compared (*p < 0.008 for significance due to six joint motions being studied). For example, condition × crank position means that the kinematic curves were compared during cycling with and without the guide. In addition, condition by cadence indicates that the mean values were compared between conditions and cadences without taking the crank position, and thus timing differences, into account.
There were differences based on crank position during the cycling revolution, which were expected, and there were interaction effects of combinations of condition, cadence, and crank position for some joint motions. One interaction involved condition and cadence, with differences seen in three joint motions, indicating that there were differences when cycling with and without the guide at different cadences. Bonferroni post hoc testing (p < 0.05) for these interactions showed (Table 1; Fig. 2) increased hip abduction and decreased knee valgus with the guide at 30 rpm, increased plantarflexion with the guide at 60 rpm, and increased plantarflexion when cycling at 60 rpm.
3.2. Electromyography
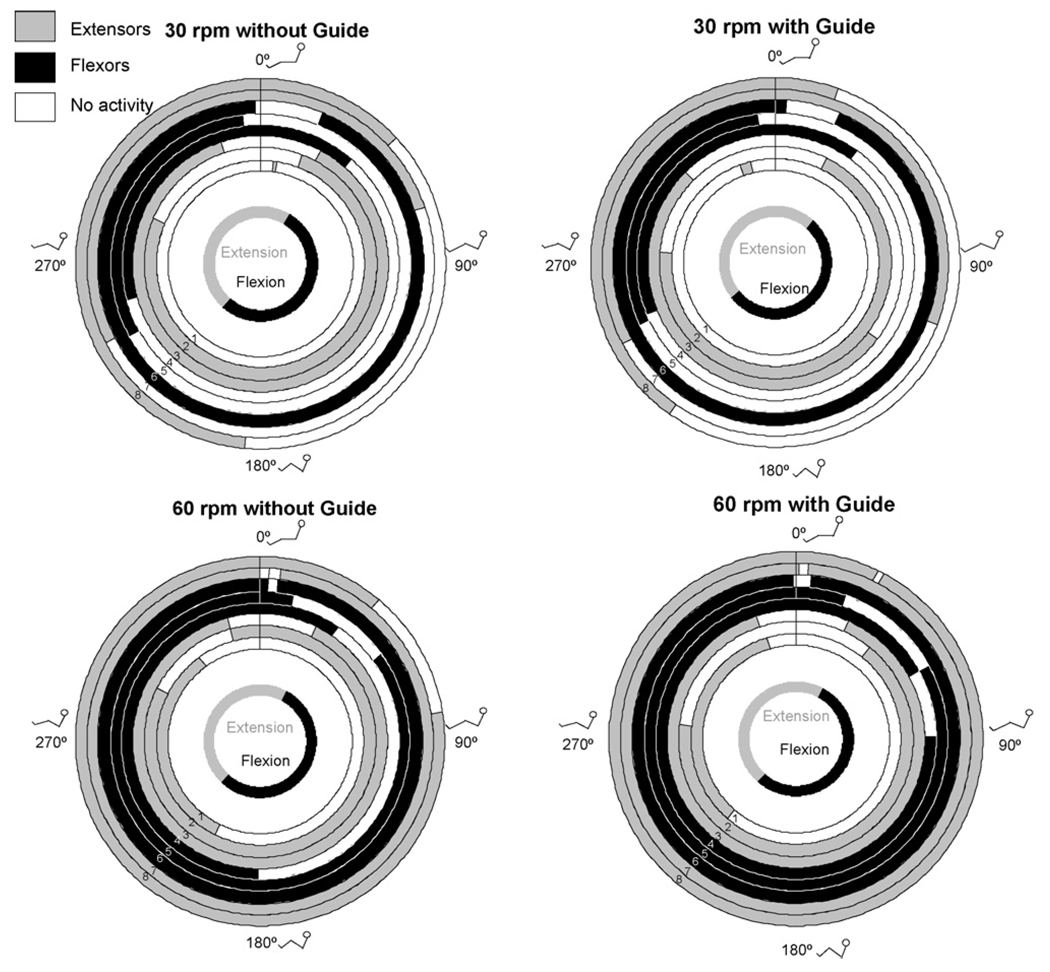
Differences were seen for onset and offset of muscle activity between cadences and between conditions for some muscles (Table 2). Duration of muscle activity differed between cadences for the biceps femoris with increased duration of activity at 30 rpm (Table 2). Fig. 3 displays the activity patterns.
Table 2.
Crank position in degrees for the onset, offset, and duration of muscle activity [mean and (standard deviation)]
| Oneset | Offset | Duration | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Muscle | 30 rpm No guide |
30 rpm Guide |
60 rpm No guide |
60 rpm Guide |
30 rpm No guide |
30 rpm Guide |
60 rpm No guide |
60 rpm Guide |
30 rpm No guide |
30 rpm Guide |
60 rpm No guide |
60 rpm Guide |
| Gluteus maximus | 6.6 (27.2) | 340.3 (33.2) | 206.1 (86.3) | 221.4 (68.8) | 9.4 (33.2) | 346.4 (24.3) | 324.3 (100.1) | 344.2 (57.3) | 210.2 (183.0) | 212.7 (183.4) | 179.9 (131.6 | 146.7 (119.7) |
| Biceps femoris | 240.9 (45.3) | 244.6 (72.4) | 54.4 (67.4) | 61.2 (85.4) | 352.9 (73.6) | 352.6 (84.6) | 12.9 (48.3) | 18.8 (73.5) | 138.8 (82.0) | 102.7 (81.6) | 298.9 (59.2) | 321.5 (42.2) |
| Rectus femoris | 21.0 (40.0) | 25.7 (66.9) | 344.6 (44.8) | 39.0 (71.4) | 292.7 (62.1) | 274.7 (59.2) | 297.2 (63.6) | 277.2 (81.3) | 220.8 (114.9) | 234.8 (99.1) | 270.5 (120.5) | 218.5 (136.3) |
| Vastus lateralis | 27.6 (84.2) | 127.3 (83.1) | 26.4 (115.7) | 23.9 (59.6) | 341.7 (75.1) | 315.0 (79.5) | 345.3 (48.9) | 342.1 (34.3) | 231.0 (122.5) | 186.8 (118.2) | 308.5 (68.3) | 301.4 (85.5) |
| Medial harmstrings | 255.5 (36.2) | 247.8 (68.6) | 180.5 (52.9) | 88.7 (88.7) | 40.8 (50.8) | 35.6 (66.8) | 33.9 (55.8) | 60.5 (67.0) | 148.3 (60.6) | 124.3 (72.2) | 275.5 (103.0) | 302.4 (87.6) |
| Anterior tibialis | 22.1 (87.1) | 22.6 (58.9) | 5.7 (69.8) | 4.6 (44.9) | 357.9 (74.0) | 4.1 (40.2) | 2.5 (52.1) | 358.9 (31.8) | 274.5 (110.2) | 323.4 (52.3) | 342.2 (33.2) | 338.9 (65.9) |
| Lateral gastrocnemius | 242.7 (92.5) | 241.9 (79.0) | 3.4 (75.9) | 1.3 (44.0) | 70.6 (83.7) | 110.6 (73.5) | 6.6 (64.0) | 4.3 (32.7) | 225.5 (106.3) | 236.3 (95.0) | 342.3 (33.4) | 348.5 (32.0) |
| Soleus | 184.7 (30.4) | 214.9 (60.9) | 80.7 (58.9) | 28.3 (86.7) | 46.9 (73.9) | 19.8 (53.5) | 40.3 (42.5) | 26.4 (40.8) | 206.9 (84.3) | 152.1 (85.9) | 319.4 (41.7) | 327.0 (52.5) |
Zero degree is the point at which the left crank arm was horizontal and farthest from the participant (*p-value<0.006 due to eight muscles being studied).As can be seen, onset and offset may show differences while duration does not for most muscles due to different analyses used. Onset and offset data are grouped based on each participant’s actual values, while duration was calculated for each participant and then grouped. Therefore within subject differences are taken into account in the duration values. Light gray = difference between cadences; dark gray = difference between conditions and between cadences. There were no interaction effects.
Fig. 3.
Mean onsets and offsets of muscle activity. Muscles other than the gluteus maximus were labelled as primary extensors and flexors based on actions at the knee and ankle. The duration of activity may differ from those of Table 2 as the durations here represent the difference between mean onset and mean offset. The innermost circle represents when hip flexion and extension occurred. The stick figures show the approximate position of the lower extremities: 1 = gluteus maximus; 2 = rectus femoris; 3 = vastus lateralis; 4 = medial hamstrings; 5 = biceps femoris; 6 = anterior tibialis; 7 = lateral gastrocnemius; 8 = soleus.
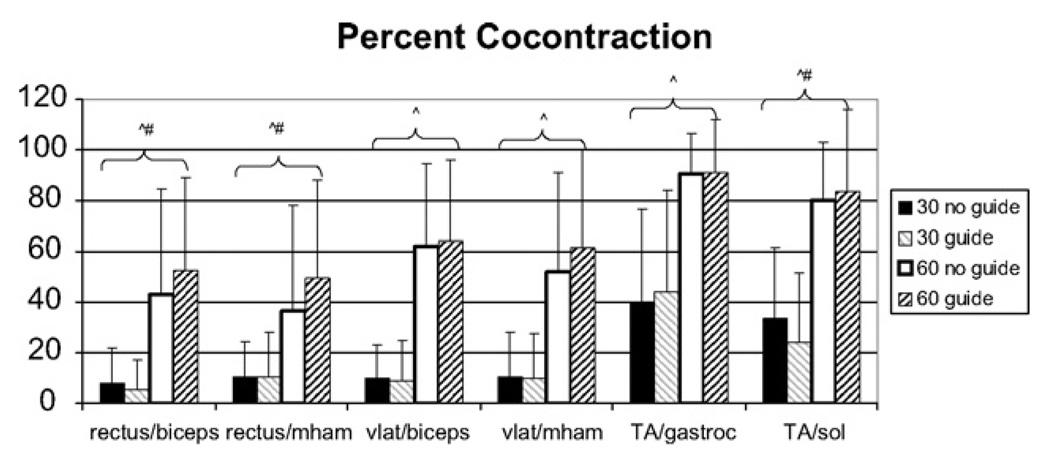
There were differences in percent cocontraction (Fig. 4) between cadences for all agonist/antagonist pairings. There also was an interaction effect of condition and cadence for three pairings (rectus femoris/biceps femoris, rectus femoris/medial hamstrings, and anterior tibialis/soleus); however there were no differences between conditions. Post hoc testing showed that two of these pairings were different with and without the guide at 60 rpm. For the third pairing (anterior tibialis/soleus), there were differences between all combinations except 60 rpm with and without the guide.
Fig. 4.
Percent cocontraction. Percentage (mean and standard deviation) of the cycling revolution in which cocontraction occurred around the knee and ankle. There were no differences between conditions; however there was a difference (p < 0.001) between cadences with greater cocontraction at 60 rpm as compared to 30 rpm. Rectus = rectus femoris; biceps = biceps femoris; vlat = vastus lateralis; mham = medial hamstrings; TA = anterior tibialis; gastroc = gastrocnemius; sol = soleus. ^Difference between cadences, #interaction effect of condition and cadence. Significance was defined as p < 0.008 due to six pairings in the analysis.
3.3. Energy expenditure and gross mechanical efficiency
During the motion laboratory sessions, participants maintained the targeted cadences (29.7 ± 5.7 and 59.9 ± 1.5 rpm without the guide, 31.3 ± 3.7 and 59.8 ± 0.7 rpm with the guide) during the 30 and 60 rpm tests, respectively. However during the 60 rpm energy expenditure test, participants could not maintain the cadence, cycling at of 46.5 ± 5.8 rpm without the guide and 45.6 ± 7.9 rpm with the guide. Participants were successful with the 30 rpm energy expenditure test (29.4 ± 3.0 rpm without the guide, 29.6 ± 6.4 rpm with the guide).
No differences were seen in cycling efficiency between conditions (F = 0.01, p = 0.9196), cadences (F = 0.01, p = 0.9196), or the interaction of the two (F = 0.01, p = 0.9196). Greater perceived exertion was seen at 60 rpm (F = 6.51, p = 0.0216), but there were no differences between conditions (F = 1.08, p = 0.3181) or the interaction of condition and cadence (F = 2.8, p = 0.1199).Without the guide, participants reported median OMNI scores of one (range zero to six) and five (range 2–10) at 30 and 60 rpm, respectively. With the guide, they reported median OMNI scores of two (range zero to eight) and four (range three to eight) at 30 and 60 rpm, respectively.
4. Discussion
The shank guide primarily impacted joint kinematics. The guide decreased hip internal rotation and frontal and transverse plane hip excursions at 60 rpm. In addition, hip extension during the extension phase decreased unexpectedly; however the guide created greater plantarflexion so less hip extension may have been obtained as the leg was effectively longer. At the knee, the guide decreased varus and frontal plane excursion at 30 and 60 rpm, perhaps creating less joint stress.
Overall muscle activity patterns did not differ with versus without the guide. While the differences that were found were statistically significant, they may not be clinically significant as the means differed by only a few degrees. However, cadence did impact muscle activity with muscles turning on sooner and off later when cycling at the higher cadence. This same result was evident in examining the percent cocontraction, with greater cocontraction at the higher cadence. It was anticipated that muscle activity would be altered if the legs were better aligned in the sagittal plane; however, this did not happen. Participants might require more training to optimize muscle patterns and decrease the cocontraction that can accompany a novel task [29]. Participants in this study received 10–20 min of training with the goal of cycling at the two cadences. Thus the effects of additional practice were not evaluated.
Cycling efficiency and perceived exertion were unchanged with the guide. In contrast to the EMG results, there were no differences in cycling efficiency between cadences. However, participants reported higher perceived exertion at 60 rpm than at 30 rpm. While there were no differences with and without the guide, some participants reported greater effort with the guide and others reported less effort.
Overall, the guide was more effective in limiting joint motion in some participants. At times, it was difficult to maintain the shank flush with the guide. The strap was elastic and permitted some motion, but some participants pulled away from the guide more than others. It was also difficult to maintain larger legs in an optimal position; therefore a more proximal guide may be needed [30].
The shank guide was positioned to maintain approximately 15° of plantarflexion [19]. Despite setting this angle statically, this was not the angle seen while cycling and therefore may not have been optimal. Nordeen-Snyder [31] showed that maximum plantarflexion during cycling was approximately 15° with an average of 2–3°. Therefore a smaller angle may have been better. However with children with CP, plantarflexor muscles are shortened, and an angle of 2–3° may be uncomfortable and not optimal for power production. Finally, Nordeen-Snyder [31] showed that ankle plantarflexion increases with increasing seat to pedal distance; therefore increasing this distance might be appropriate if the goal were to obtain greater plantarflexion.
While not examined, the guide might have impacted the direction of forces through the pedals. As participants were better aligned in the sagittal plane, more vertical force may have been directed into the pedal, thus providing greater force in the direction of movement. Future work should examine pedal forces and joint kinetics to understand lower extremity torque and power during cycling.
Clinically, a shank guide during cycling may be beneficial for individuals with CP to decrease the amount of hip and knee frontal and transverse plane motion. As increased knee frontal and transverse plane motion during cycling has been associated with knee pain in healthy adults [7,11], the use of the guide may prevent long-term joint complications; however further study is warranted. As seen in this study, the guide had minimal or no impact on muscle activity and efficiency. Based on the results of this study, it is unknown if the guide would interfere with ankle musculature strengthening following a cycling intervention. Future studies should examine strengthening outcomes and EMG amplitude to address this question. The study results suggest that the guide might be useful for individuals with CP who show increased motion in the frontal and transverse planes during cycling.
5. Conclusions
The use of the shank guide altered the joint kinematics during cycling for these adolescents with CP and had a minor impact on muscle activity. However, the guide did not impact the percentage of agonist/antagonist cocontraction or energy expenditure. Therefore, the guide may be useful for controlling the kinematics of cycling. Future work should examine the impact of extended training, the ankle position, and the kinetics of cycling.
Acknowledgements
Funding provided by Shriners Hospitals for Children, Grant #8530 and a Clinical Research Grant from the Pediatric Section of the American Physical Therapy Association. Dr. Lee is funded by NIH Grant HD043859. The authors thank: Brian Clark, PhD, Drexel University, Philadelphia, PA Temple University, Philadelphia, PA John Gaughan, PhD Kim Nixon-Cave, PT, PhD Shriners Hospitals for Children, Philadelphia, PA Richard Lauer, PhD James McCarthy, MD Patricia Shewokis, PhD (also Drexel University) Emily Slater, MS Brian Smith, MS Carrie Stackhouse, MS
Footnotes
Conflict of interest
None.
References
- 1.Damiano DL, Martellotta TL, Quinlivan JM, Abel MF. Deficits in eccentric versus concentric torque in children with spastic cerebral palsy. Med Sci Sport Exerc. 2001;33:117–122. doi: 10.1097/00005768-200101000-00018. [DOI] [PubMed] [Google Scholar]
- 2.Burtner PA, Qualls C, Woollacott MH. Muscle activation characteristics of stance balance control in children with spastic cerebral palsy. Gait Posture. 1998;8:163–174. doi: 10.1016/s0966-6362(98)00032-0. [DOI] [PubMed] [Google Scholar]
- 3.Bleck EE. Orthopedic management in cerebral palsy. London, UK: MacKeith Press; 1987. [Google Scholar]
- 4.Woollacott MH, Burtner P. Neural and musculoskeletal contributions to the development of stance balance control in typical children and in children with cerebral palsy. Acta Paediatr Suppl. 1996;416:58–62. doi: 10.1111/j.1651-2227.1996.tb14279.x. [DOI] [PubMed] [Google Scholar]
- 5.Sussman MD. Crouched gait consensus. In: Sussman MD, editor. The diplegic child: evaluation and management. Rosemont, IL: American Academy of Orthopaedic Surgeons; 1992. pp. 337–339. [Google Scholar]
- 6.Wren TA, Rethlefsen S, Kay RM. Prevalence of specific gait abnormalities in children with cerebral palsy: influence of cerebral palsy subtype, age, and previous surgery. J Pediatr Orthop. 2005;25:79–83. doi: 10.1097/00004694-200501000-00018. [DOI] [PubMed] [Google Scholar]
- 7.Gregor RJ, Fowler E. Biomechanics of cycling. In: Zachazewski JE, Magee DJ, Quillen WS, editors. Athletic injuries and rehabilitation. Philadelphia, PA: W.B. Saunders Company; 1996. pp. 367–388. [Google Scholar]
- 8.Medica-Medizintechnik,GmbH. [accessed February 8, 2004];2004 http://www.medica-medizin.de/en/produkte/uebersicht/;Available at: http://www.medica-medizin.de/en/produkte/uebersicht.
- 9.Reck, Motomed. [accessed January 8, 2004];2004 http://www.motomed.com;Available at: http://www.motomed.com.
- 10.Johnston TE, Barr AE, Lee SC. Biomechanics of submaximal recumbent cycling in adolescents with and without cerebral palsy. Phys Ther. 2007;78:572–585. doi: 10.2522/ptj.20060261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gregersen CS, Hull ML. Non-driving intersegmental knee moments in cycling computed using a model that includes three-dimensional kinematics of the shank/foot and the effect of simplifying assumptions. J Biomech. 2003;36:803–813. doi: 10.1016/s0021-9290(03)00014-9. [DOI] [PubMed] [Google Scholar]
- 12.Morris C. A review of the efficacy of lower-limb orthoses used for cerebral palsy. Dev Med Child Neurol. 2002;44:205–211. doi: 10.1017/s0012162201001943. [DOI] [PubMed] [Google Scholar]
- 13.Ross SA, Engsberg JR. Relation between spasticity and strength in individuals with spastic diplegic cerebral palsy. Dev Med Child Neurol. 2002;44:148–157. doi: 10.1017/s0012162201001852. [DOI] [PubMed] [Google Scholar]
- 14.Palisano R, Rosenbaum P, Walter S, Russell D, Wood E, Galuppi B, et al. Development and reliability of a system to classify gross motor function in children with cerebral palsy. Dev Med Child Neurol. 1997;39:214–223. doi: 10.1111/j.1469-8749.1997.tb07414.x. [DOI] [PubMed] [Google Scholar]
- 15.Crawford SM. Anthropometry. In: Docherty D, editor. Measurement in pediatric exercise science. Champaign, IL: Human Kinetics; 1996. pp. 17–86. [Google Scholar]
- 16.Ericson MO, Nisell R, Arborelius UP, Ekholm J. Muscular activity during ergometer cycling. Scand J Rehabil Med. 1985;17:53–61. [PubMed] [Google Scholar]
- 17.Jensen JL, Korff T. Adapting to changing task demands: variability in children’s response to manipulations of resistance and cadence during pedaling. Res Q Exerc Sport. 2004;75:361–369. doi: 10.1080/02701367.2004.10609169. [DOI] [PubMed] [Google Scholar]
- 18.Dore E, Bedu M, Franca NM, Diallo O, Duche P, Van Praagh E, et al. Testing peak cycling performance: effects of braking force during growth. Med Sci Sport Exerc. 2000;32:493–498. doi: 10.1097/00005768-200002000-00035. [DOI] [PubMed] [Google Scholar]
- 19.Cavanagh PR, Sanderson DJ. The biomechanics of cycling: studies of the pedaling mechanics of elite pursuit riders. In: Burke ER, editor. Science of cycling. Champaign, IL: Human Kinetics; 1986. pp. 91–122. [Google Scholar]
- 20.Davis RB, Ounpuu S, Tyisurski D, Gage JR. A gait analysis data collection and reduction technique. Human Movement Sci. 1991;20:575–587. [Google Scholar]
- 21.Jorge M, Hull ML. Analysis of EMG measurements during bicycle pedalling. J Biomech. 1986;19:683–694. doi: 10.1016/0021-9290(86)90192-2. [DOI] [PubMed] [Google Scholar]
- 22.Raasch CC, Zajac FE. Locomotor strategy for pedaling: muscle groups and biomechanical functions. J Neurophysiol. 1999;82:515–525. doi: 10.1152/jn.1999.82.2.515. [DOI] [PubMed] [Google Scholar]
- 23.Ericson MO. Muscular function during ergometer cycling. Scand J Rehabil Med. 1988;20:35–41. [PubMed] [Google Scholar]
- 24.Di Fabio RP. Reliability of computerized surface electromyography for determining the onset of muscle activity. Phys Ther. 1987;67:43–48. doi: 10.1093/ptj/67.1.43. [DOI] [PubMed] [Google Scholar]
- 25.Hodges PW, Bui BH. A comparison of computer-based methods for the determination of onset of muscle contraction using electromyography. Electroencephalogr Clin Neurophysiol. 1996;101:511–519. doi: 10.1016/s0013-4694(96)95190-5. [DOI] [PubMed] [Google Scholar]
- 26.Robertson RJ. Perceived exertion for practitioners: rating effort with the OMNI picture system. Champaign, IL: Human Kinetics; 2004. [Google Scholar]
- 27.Conover WJ, Iman RL. Rank transformations as a bridge between parametric and nonparametric statistics. Am Stat. 1981;35:124–129. [Google Scholar]
- 28.Sparto PJ, Schor RH. Directional statistics. In: Stergiou N, editor. Innovative analysis of human movement: analytical tools for human movement research. Champaign, IL: Human Kinetics; 2004. pp. 121–161. [Google Scholar]
- 29.Gribble PL, Mullin LI, Cothros N, Mattat A. Role of cocontraction in arm movement accuracy. J Neurophysiol. 2003;89:2396–2405. doi: 10.1152/jn.01020.2002. [DOI] [PubMed] [Google Scholar]
- 30.Trumbower RD, Faghri PD. Kinematic analyses of semireclined leg cycling in able-bodied and spinal cord injured individuals. Spinal Cord. 2005;43:543–549. doi: 10.1038/sj.sc.3101756. [DOI] [PubMed] [Google Scholar]
- 31.Nordeen-Snyder KS. The effect of bicycle seat height variation upon oxygen consumption and lower limb kinematics. Med Sci Sport. 1977;9:113–117. [PubMed] [Google Scholar]